

Калькулятор процентов онлайн.
Найти число, зная чему равен указанный процент от него.
Этот калькулятор онлайн решает задачу на нахождение числа, зная его процент.
Онлайн калькулятор для нахождения числа по его процентам не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Понятие о проценте
Проценты – одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно
прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%,
промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка
и т.д. Ясно, что понимание такой информации необходимо в современном обществе.
Одним процентом от любой величины – денежной суммы, числа учащихся школы и т.д. – называется одна сотая ее часть. Обозначается
процент знаком %, Таким образом,
1% – это 0,01, или ( frac{1}{100} ) часть величины
Приведем примеры:
– 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) – это 2300/100 = 23 рубля;
– 1% от населения России, равного примерно 145 млн. человек (2007 г.), – это 1,45 млн. человек;
– 3%-я концентрация раствора соли – это 3 г соли в 100 г раствора (напомним, что концентрация раствора – это часть, которую
составляет масса растворенного вещества от массы всего раствора).
Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке
“хлопок 100%” означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих
учеников.
Слово “процент” происходит от латинского pro centum, означающего “от сотни” или “на 100”. Это словосочетание можно встретить и в
современной речи. Например, говорят: “Из каждых 100 участников лотереи 7 участников получили призы”. Если понимать это выражение
буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших
призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое
понимание соответствует происхождению слова “процент”: 7% – это 7 из 100, 7 человек из 100 человек.
Знак “%” получил распространение в конце XVII века. В 1685 году в Париже была издана книга “Руководство по коммерческой
арифметике” Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали “cto” (сокращенно от cento). Однако
наборщик принял это “с/о” за дробь и напечатал “%”. Так из-за опечатки этот знак вошел в обиход.
Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.
Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:
( 58% = frac{58}{100} = 0,58; ;;; 4,5% = frac{4,5}{100} = 0,045; ;;; 200% = frac{200}{100} = 2 )
Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить
на 100:
( 0,58 = (0,58 cdot 100)% = 58% )
( 0,045 = (0,045 cdot 100)% = 4,5% )
В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина – 50%,
четверть – 25%, три четверти – 75%, пятая часть – 20%, три пятых – 60% и т.д.
Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью
процентов. Например, в сообщениях “Минимальная заработная плата повышена с февраля на 50%” и “Минимальная заработная плата повышена
с февраля в 1,5 раз” говорится об одном и том же.
Точно так же увеличить в 2 раза – это значит увеличить на 100%, увеличить в 3 раза – это значит увеличить на 200%, уменьшить
в 2 раза – это значит уменьшить на 50%.
Аналогично
– увеличить на 300% – это значит увеличить в 4 раза,
– уменьшить на 80% – это значит уменьшить в 5 раз.
Задачи на проценты
Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби.
В простейших задачах на проценты некоторая величина а принимается за 100% (“целое”), а ее часть b выражается числом p%.
В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и
соответствующие задачи на дроби, но перед их решением число р% выражается дробью.
1. Нахождение процента от числа.
Чтобы найти ( frac{p}{100} ) от a, надо a умножить на ( frac{p}{100} ):
( b = a cdot frac{p}{100} )
Итак, чтобы найти р% от числа, надо это число умножить на дробь ( frac{p}{100} ). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг,
а 118% от х равны 1,18x
2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью ( frac{p}{100} , ; (p neq 0) ), надо b разделить на ( frac{p}{100} ):
( a = b : frac{p}{100} )
Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на ( frac{p}{100} ).
Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.
3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а ( (a neq 0) ), надо сначала узнать, какую часть b составляет от а, а
затем эту часть выразить в процентах:
( p = frac{b}{a} cdot 100% )
Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат
умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют ( frac{9 cdot 100}{180} = 5% ) раствора.
Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило
называют правилом нахождения процентного отношения двух чисел.
Нетрудно заметить, что формулы
( b = a cdot frac{p}{100}, ;; a = b : frac{p}{100}, ;; p = frac{b}{a} cdot 100% ;; (a,b,p neq 0 ) )
взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу
считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании,
можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.
Составные задачи на проценты решаются аналогично задачам на дроби.
Простой процентный рост
Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется “пеня” (от латинского роеnа
– наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма
составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р.,
а всего 1019 р.
Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую
формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.
Пусть S – ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n – число просроченных дней. Сумму,
которую должен заплатить человек после n дней просрочки, обозначим Sn.
Тогда за n дней просрочки пеня составит рn% от S, или ( frac{pn}{100}S ), а всего придется заплатить
( S + frac{pn}{100}S = left( 1+ frac{pn}{100} right) S )
Таким образом:
( S_n = left( 1+ frac{pn}{100} right) S )
Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.
Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов.
Как и выше, нетрудно убедиться, что в этом случае
( S_n = left( 1- frac{pn}{100} right) S )
Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает.
Рост в этом случае “отрицательный”.
Сложный процентный рост
В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный
договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете
доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход –
“проценты”, как его обычно называют.
Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего
года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются “проценты на проценты”,
или, как их обычно называют, сложные проценты.
Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех
лет не будет брать деньги со счета.
10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)
10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)
10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)
Нетрудно представить себе, сколько при таком непосредственном, “лобовом” подсчете понадобилось бы времени для нахождения суммы
вклада через 20 лет. Между тем подсчет можно вести значительно проще.
А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1
раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма
увеличится в 1,1 • 1,1 = 1,12 раз.
Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,12 = 1,13
раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое:
1,13 • 1000 = 1,331 • 1000 – 1331 (р.)
Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма,
которая будет на счете через n лет, равна Sn р.
Величина p% от S составляет ( frac{p}{100}S ) р., и через год на счете окажется сумма
( S_1 = S+ frac{p}{100}S = left( 1+ frac{p}{100} right)S )
то есть начальная сумма увеличится в ( 1+ frac{p}{100} ) раз.
За следующий год сумма S1 увеличится во столько же раз, и поэтому через два года на счете будет сумма
( S_2 = left( 1+ frac{p}{100} right)S_1 = left( 1+ frac{p}{100} right) left( 1+ frac{p}{100} right)S = left( 1+ frac{p}{100} right)^2 S )
Аналогично ( S_3 = left( 1+ frac{p}{100} right)^3 S ) и т.д. Другими словами, справедливо равенство
( S_n = left( 1+ frac{p}{100} right)^n S )
Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.
Как найти число по его проценту?
Апр 10, 2021 | 4 класс |

Как найти число, если известен его процент?
Давайте разбираться.
Задание 1.
Надо найти число, если известно, что 23% — это 138.
Решение:
1). Сначала найдем чему равен 1%.
Нам известно, что 23% это 138, значит, чтобы найти 1%, надо — 138 : 23 = 6.
Т.е. 1% — это 6.
2). Теперь надо найти целое число.
Мы знаем, что в целом – 100%.
А, чтобы найти целое, надо 1% умножить на 100.
Т.е. 6 х 100 = 600.
Значит, 100% — это 600 и это – целое число.
Ответ: 600.
Задание 2.
Найти число, если 12% — это 48.
Решение:
1). Превратим 12 % в десятичную дробь.
Если 1% = 1/100, то 12% =12/100
2). 12/100 – это 48,
Найдем 1/100, для этого 48 разделим на 12 и умножим на 100, 48 : 12 х 100.
Заменим знак «:» дробной чертой, будет 48/12 х 100, или по правилу работы с дробями – 48 х 100/12.
Получается — 48 : 12 х 100 = 48/12 х 100 = 48х100/12 = 48 х 100/12.
Таким образом, видно, что часть мы умножаем на обратную дробь или делим на дробь.
Т.е. 48 х 100/12 = 4800/12 = 400
Ответ: 400.
При решении примеров надо выбирать удобный для вас вариант.

Похожие статьи
Задача. За контрольную по математике в пятом классе отметку «(5)» получили четверо учеников,
что составляет
16%
от всех учеников класса. Сколько учеников в классе?
I способ.
Найдём, какая часть всех учащихся класса приходится на
1%
:
Все ученики класса составляют целое:
100%
.
Умножим найденное число на (100):
Ответ: в классе (25) учеников.
Решение задачи можно записать по-другому.
В задаче надо найти такое число,
16%
которого равны (4).
Обозначим неизвестное число за (x), тогда получим равенство:
16%отxравно4;0,16отxравно4;0,16⋅x=4;x=4:0,16;x=400:16;x=25.
Ответ: в классе (25) учеников.
III способ.
Выразим проценты обыкновенной или десятичной дробью и
количество учеников, которые получили отметку «(5)», разделим на эту дробь:
,
или
Ответ: в классе (25) учеников.
Чтобы найти число по его проценту, надо:
1) выразить проценты обыкновенной или десятичной дробью;
2) разделить данное число на полученную дробь.
Рассмотрим три основных типа задач на проценты.
Нахождение процента от числа
Запомните!
![]()
Чтобы найти процент от числа, нужно число умножить на процент.
Разбор примера
Предприятие изготовило за квартал 500 насосов, из которых
60% имели высшую категорию качества. Сколько насосов высшей категории качества
изготовило предприятие?
Решение:
Найдем 60% от 500 (общее количество насосов).
60 % = 0,6
500 · 0,6 = 300 насосов высшей категории качества.
Ответ: 300 насосов высшей категории качества.
Нахождение числа по его проценту
Запомните!
![]()
Чтобы найти число по его проценту, нужно его известную часть разделить на то,
сколько процентов она составляет от числа.
Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто
не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать
текст. Если вам встречаются слова «который», «что составляет» и «который составляет»,
скорее всего перед вами задача «число по его проценту».
Разбор примера
Ученик прочитал 138 страниц, что составляет 23%
числа всех страниц в книге. Сколько страниц в книге?
Решение:
Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую
прочитал ученик (138 страниц) составляет 23% от общего количества
страниц в книге.
Так как 138 стр. — это всего лишь часть, само количество
страниц, естественно, будет больше 138. Это поможет нам при проверке.
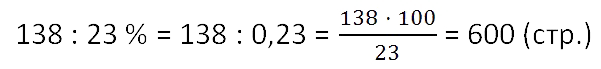
Проверка: 600 > 138 (это означает, что 138 является частью 600).
Ответ: 600 (стр.) — общее количество страниц в книге.
Сколько процентов одно число составляет от другого
Запомните!
![]()
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается,
разделить на общее количество и умножить на 100%.
Разбор примера
Из 200 арбузов 16 оказались незрелыми.
Сколько процентов всех арбузов составили незрелый арбузы?
Решение:
О чем спрашивают? О незрелых арбузах. Значит, 16
делим на общее количество арбузов и умножаем на 100%.
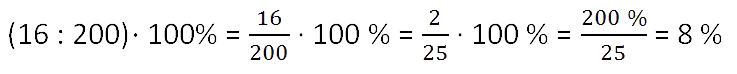
Ответ: 8% — составляют незрелые арбузы от всех арбузов.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
8 апреля 2023 в 0:03
Надежда Горскова

Профиль
Благодарили: 0
Сообщений: 1

Надежда Горскова
Профиль
Благодарили: 0
Сообщений: 1
Благодарю.
0
Спасибо
Ответить
9 января 2020 в 14:39
Владислав Кругомов

Профиль
Благодарили: 0
Сообщений: 1

Владислав Кругомов
Профиль
Благодарили: 0
Сообщений: 1
Масса сплава меди и серебра равна 7,2 кг.Масса серебра состовляет 80% массы меди. Сколько килограммов меди в сплаве?
Можно пожалуйста решения не уравнением!
0
Спасибо
Ответить
11 января 2020 в 18:02
Ответ для Владислав Кругомов
Иван Войт

Профиль
Благодарили: 0
Сообщений: 2

Иван Войт
Профиль
Благодарили: 0
Сообщений: 2
Т.к. серебро — 0.8 (80%) от меди, а медь — 1 (100%), то их сумма =1,8. Т.к. 1.8 (180%) это 7.2 кг, то (7.2/1.8)= 4 (кг) — это медь, а серебро = 3,2 (7,2-4 или 4*0.8 (80%))
Ответ: серебро — 3,2 кг, медь -4 кг
0
Спасибо
Ответить
11 января 2020 в 18:02
Ответ для Владислав Кругомов
Иван Войт

Профиль
Благодарили: 0
Сообщений: 2

Иван Войт
Профиль
Благодарили: 0
Сообщений: 2
Т.к. серебро — 0.8 (80%) от меди, а медь — 1 (100%), то их сумма =1,8. Т.к. 1.8 (180%) это 7.2 кг, то (7.2/1.8)= 4 (кг) — это медь, а серебро = 3,2 (7,2-4 или 4*0.8 (80%))
Ответ: серебро — 3,2 кг, медь -4 кг
0
Спасибо
Ответить
4 сентября 2016 в 9:48
София Ниязова

Профиль
Благодарили: 0
Сообщений: 1

София Ниязова
Профиль
Благодарили: 0
Сообщений: 1
40% числа 15 и 9,5% числа 280… Если знаете как решать это напишите прошу вас!
0
Спасибо
Ответить
4 сентября 2016 в 16:15
Ответ для София Ниязова
Юлия Анарметова

Профиль
Благодарили: 0
Сообщений: 11

Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
1. (40 · 15): 100=6
2.(9.5 · 280) :100=26.6
0
Спасибо
Ответить
10 мая 2016 в 23:58
Илья Московец

Профиль
Благодарили: 0
Сообщений: 1

Илья Московец
Профиль
Благодарили: 0
Сообщений: 1
У Первого человека было 50 рублей, у второго тоже 50 рублей вместе у них 100 рублей. это 100%. Первый человек добавил 25 рублей всего стало 125 рублей. Вопрос: в процентах как это поменялось? и как вы считаете?
0
Спасибо
Ответить
11 мая 2016 в 19:13
Ответ для Илья Московец
Дмитрий Захаров

Профиль
Благодарили: 0
Сообщений: 3

Дмитрий Захаров
Профиль
Благодарили: 0
Сообщений: 3
либо 1% стал меньше, либо стало 125 %
0
Спасибо
Ответить
22 сентября 2016 в 11:42
Ответ для Илья Московец
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Чтобы расчитать изменение в процентах, нужно понять относительно чего изменения? Если относительно первоначальной суммы, то увеличилось на 25%. Если относительно количества денег у каждого из людей, то у первого увеличилось на 50% от вервоначальной суммы.
1
Спасибо
Ответить
12 апреля 2016 в 15:41
Денис Захарченко

Профиль
Благодарили: 0
Сообщений: 1

Денис Захарченко
Профиль
Благодарили: 0
Сообщений: 1
Ёмкость с водой на 1000л имеет 3 одинаковых трубы снизу, ведущие в 3 бочки, на каждой трубе кран, 1-й открыт на 100%, второй и третий на 30%, на сколько литров наполниться каждая из бочек?
0
Спасибо
Ответить
13 апреля 2016 в 7:51
Ответ для Денис Захарченко
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Спасибо за интересную задачу. Тянет на олимпиадную, на правильность не претендую, но логика вроде верная.
Т.к. трубы в равных условиях, то вытекает вода из них одно и тоже время. Обозначим это время за Х. Скорость, с которой вытекает из первый трубы, возьмём условно за 1. А из двух оставшихся за 0,3. Тогда количество воды вытекающей из первой трубы будет равно 1 · Х, а из двух оставшихся 0,3 · Х. Т.к. известно, что всего в ёмкости 1000 литров, составим уравнение и решим:
1 · x+0,3 · x+0,3 · x=1000
1,6 · x=1000
x=625
Проверка:
625+0,3 · 625+0,3 · 625=625+187,5+187,5=1000
1000=1000
Вытекло в 1ую бочку: х =625
Вытекло во 2ую бочку: 0,3 · х=187,5
Вытекло в 3ю бочку: 0,3 · х=187,5
Ответ: 625л;187,5л; 187,5л.
Если будет возможность, прошу предоставить правильный ответ.
Заранее благодарен!
0
Спасибо
Ответить
1 октября 2015 в 17:39
Дима Дима

Профиль
Благодарили: 0
Сообщений: 1

Дима Дима
Профиль
Благодарили: 0
Сообщений: 1
масса сушёных груш состовляет 20% массы свежих.Сколько кг сушёных груш получится из 100кг;350кг;25кг свежих? Сколько процентов массы свежих груш теряется при сушке?
0
Спасибо
Ответить
1 июля 2016 в 17:06
Ответ для Дима Дима
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для вычисления процента от числа необходимо умножить на количество процентов и разделить на 100. Следовательно 20: 100 = .
100 · =100: 5 = 20 (кг).
Аналогично с остальными примерами:
350 : 5 = 70 (кг)
25: 5 = 5 (кг)
Масса свежей груши 100%. масса сушеной груши 20%. Значит груша теряет 100%-20%=80% своей массы при высыхании.
Ответ: 20 кг, 70 кг, 5 кг, 80%.
0
Спасибо
Ответить
11 мая 2015 в 23:20
Эдуард Селивоненко

Профиль
Благодарили: 0
Сообщений: 1

Эдуард Селивоненко
Профиль
Благодарили: 0
Сообщений: 1
в цветочном магазине 35%гвоздик -крассные, и их 105 штук ,25%-белых, а остольные розавые. вапрос сколько белых и сколько розавых?
0
Спасибо
Ответить
17 апреля 2016 в 16:18
Ответ для Эдуард Селивоненко
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В этом разделе подробно описан вопрос про проценты: http://math-prosto.ru/index.php?page=pages/percent/percent1.php
Решение:
35% это 0,35
Обозначим общее количество гвоздик за Х, тогда
0,35 · x=105
x=300 — всего в магазине 300 гвоздик.
Найдём количество белых:
300 · 0,25 = 75 — белых гвоздик в магазине.
Найдём количество розовых:
Для этого из общего количества гвозик отнимаем количество красных и белых:
300 — 75 — 105 = 120 — розовых гвоздик.
Ответ: 75 белых и 120 розовых гвоздик было в магазине.
0
Спасибо
Ответить
19 апреля 2015 в 14:16
Маша Галлямова

Профиль
Благодарили: 0
Сообщений: 2

Маша Галлямова
Профиль
Благодарили: 0
Сообщений: 2
Цену на товар сначала снизили на 20%, а затем увеличили на 20%. Больше или меньше станет цена на товар относительно его первоначальной стоимости и на сколько процентов?
0
Спасибо
Ответить
20 апреля 2015 в 21:49
Ответ для Маша Галлямова
Константин Лебедев

Профиль
Благодарили: 0
Сообщений: 1

Константин Лебедев
Профиль
Благодарили: 0
Сообщений: 1
Пусть х цена товара. Снижение на 20% равносилно умножению цены на 0.8=1-20/100, следовательно цена стала равна х*0.8. Затем увеличили на 20% это означает, что новую цену умножили 1.2. В итоге получили окончательно новую цену х*0.8*1.2 =х*0.96. Таким образом первоначальная цена стала меньше т.к. умножилась на величину меньшую единицы. Так же видно, что цена уменьшилась на 4%. Видно и то, что от порядка выполнения операций снижения, а потом увеличения цены на одно и тоже число процентов, или наоборот повышения а потом снижения, окончательная цена будет меньше первоночальной и приводит к снижению цены. В общем виде обозначим число процентов pb пусть а=р/100, тогда новая цена будет равна х*(1-а)(1+а)=x*(1-а^2). Мы доказали что цена уменьшается на а^2*100%.
0
Спасибо
Ответить
16 апреля 2015 в 15:17
Лёня Стародубцев

Профиль
Благодарили: 0
Сообщений: 1

Лёня Стародубцев
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
14 апреля 2016 в 11:32
Ответ для Лёня Стародубцев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В статье подробно описано, как это делается: http://math-prosto.ru/index.php?page=pages/percent/percent1.php
А именно: “Чтобы перевести проценты в дробь, нужно убрать знак % и разделить число на 100.”
33
%= %
Переведём проценты в дробь:
: 100=
60 · =20
Ответ: 20
0
Спасибо
Ответить
Принцип нахождения числа по данным его процентам такой же, как и обычное нахождение числа по его дроби. То есть это задача на нахождение числа по дроби. А как решать подобные задания мы уже знаем.
Принцип нахождения числа по данным его процентам такой же, как и обычное нахождение числа по его дроби. То есть это задача на нахождение числа по дроби. А как решать подобные задания мы уже знаем.
Но так как проценты можно представить и в виде обыкновенной, и виде десятичной дроби, то найти число по его процентам можно разными способами, и по-разному записать решение.
Но так как проценты можно представить и в виде обыкновенной, и виде десятичной дроби, то найти число по его процентам можно разными способами, и по-разному записать решение.
Чтобы найти число по его проценту, надо его известную часть разделить на то, сколько процентов она составляет от числа. Не забудьте, проценты перевести или в десятичную дробь, или в обыкновенную!
Чтобы найти число по его проценту, надо его известную часть разделить на то, сколько процентов она составляет от числа. Не забудьте, проценты перевести или в десятичную дробь, или в обыкновенную!
Давайте решим задачу.
Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?
Решение:
Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик (138 страниц) составляет 23% от общего количества страниц в книге.
Так как 138 стр. — это всего лишь часть, само количество страниц, естественно, будет больше 138. Это поможет нам при проверке.
1) переведём проценты в десятичную дробь – 23% = 23 : 100 = 0,23
2) 138 : 0,23 = 600 (стр)
Проверка: 600 > 138 (это означает, что 138 является частью 600).
Ответ: 600 стр. — общее количество страниц в книге.
Можно, по-другому:
1) переведём проценты в обыкновенную дробь – 23% = 23/100
2) 138 : 23 = 6 (стр) – это 1%
3) 6 * 100 = 600(стр)
Проверка: 600 > 138 (это означает, что 138 является частью 600).
Ответ: 600 стр. — общее количество страниц в книге.
Чтобы найти число по данным его процентам, надо:
Чтобы найти число по данным его процентам, надо:
1) выразить проценты обыкновенной дробью;
2) разделить данную часть числа на числитель полученной обыкновенной дроби (тем самым, найдя 1% от искомого числа);
2) умножить полученный результат на знаменатель обыкновенной дроби. Это и будет ответ.
1) перевести проценты в десятичную дробь, разделив количество процентов на 100;
2) разделить данную часть числа на полученную десятичную дробь.
Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать текст. Если вам встречаются слова «который», «что составляет», «который составляет» и «это», скорее всего перед вами задача «число по его проценту».
Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать текст. Если вам встречаются слова «который», «что составляет», «который составляет» и «это», скорее всего перед вами задача «число по его проценту».
Если, всё равно, сложно понять сразу, то попробуйте перефразировать задачу, заменив слова «который», «что составляет», «который составляет», местоимением “это”. Если у вас получилась замена, то перед вами задача «число по его проценту».
Если, всё равно, сложно понять сразу, то попробуйте перефразировать задачу, заменив слова «который», «что составляет», «который составляет», местоимением “это”. Если у вас получилась замена, то перед вами задача «число по его проценту».
Решим ещё задачи:
- Сливочное мороженое содержит 14% сахара. Сколько килограммов мороженого изготовлено, если было использовано 49 кг сахара?
Решение:
Перефразируем задачу: сколько килограммов мороженого изготовлено, если было использовано 49 кг сахара, и это составляет 14% мороженного?
Мы знаем, что 49 кг сахара – это 14% мороженного
1) 14% = 14/100
1) 49 : 14 = 3,5 (кг) составляет 1% мороженого;
2) 3,5 · 100 = 350 (кг) изготовлено мороженого.
(Или можно записать, по-другому: 14% = 0,14 ; 49 : 0,14 = 350 (кг))
Ответ. 350 кг.
- Масса сушёной малины составляет 15% массы свежей. Сколько взяли свежей малины, если получили 3 кг сухой?
Решение:
Перефразируем: 3 кг сухой малины – это 15% свежей. Сколько взяли свежей малины?
1) 15% = 0,15
2) 3 : 0,15 = 20(кг) – свежей малины
Ответ: взяли 20 кг свежей малины.
- Мясо при варке теряет 30% веса. Сколько надо взять сырого мяса, чтобы получилось 560 г варёного?
Решение:
Если мясо при варке теряет 30% веса, то варёное мясо – это 70% от свежего, т.к. 100% – 30% = 70%
Мы знаем, что получилось 560 г варёного мяса. И это 70% свежего.
1) 100% – 30% = 70% – варёное мясо
2) 70% = 0,7
3) 560 : 0,7 = 800 (г) – сырого мяса
Ответ: необходимо взять 800 г сырого мяса.
При решении задач на проценты находите сначала 1%, а затем смотрите по смыслу.
При решении задач на проценты находите сначала 1%, а затем смотрите по смыслу.
