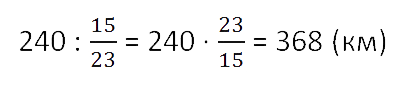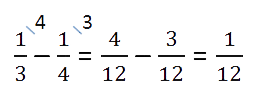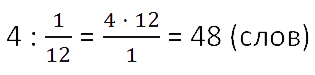Если известно сколько составляет часть от целого, то по известной части можно “восстановить”
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Эта информация доступна зарегистрированным пользователям
В этом уроке мы научимся, зная дробь от числа, находить все число.
Также мы узнаем, как делать аналогичные действия для процентов, то есть по данному количеству процентов находить все число.
Потом применим полученные навыки для решения задач.
Сформулируем, в чем состоит задача нахождения числа по его дроби.
Имеется дробь; она говорит о том, какая часть от числа нам дана.
Имеется число, равное данной дробной части от искомого числа.
Мы уже умеем находить дробь от числа. Вспомним как это делать.
Эта информация доступна зарегистрированным пользователям
Чтобы найти дробь от числа нам нужно исходное число умножить на эту дробь, тогда получится какое-то значение, обозначающее дробь от числа.
В этой задаче было известно все число и то, какую дробную часть от него необходимо получить. Дробь от числа оставалась неизвестной.
В задаче этого урока дробь от числа нам уже известна, а все число, напротив, только предстоит найти.
Для его нахождения можно составить уравнение, аналогичное тому, которое было на картинке выше. Отличие будет только в том, какие переменные нам известны.
Решая это уравнение, вы переносите известный нам множитель, то есть дробь, в правую часть.
Как делить на дробь мы изучили в прошлом уроке. Напомним, что для этого надо домножить на взаимно обратное число к этой дроби.
Итак, вы получили выражение для неизвестного числа.
Сформулируем правило: чтобы найти дробь от числа необходимо разделить известную часть числа на дробь.
Эта информация доступна зарегистрированным пользователям
Пример 1
(mathbf{frac{3}{4}}) от числа равны 21-му, найдите исходное число.
Для решения необходимо разделить известную часть на дробь, то есть 21 разделить на (mathbf{frac{3}{4}})
(mathbf{21divfrac{3}{4}=21cdotfrac{4}{3}=frac{21cdot4}{3}=frac{7cdot4}{1}=28})
Пример 2
(mathbf{frac{2}{7}}) от числа равны 12, найдите исходное число.
Для решения надо разделить данную часть числа на данную дробь, то есть 12 разделить на (mathbf{frac{2}{7}})
(mathbf{12divfrac{2}{7}=12cdotfrac{7}{2}=frac{12cdot7}{2}=frac{6cdot7}{1}=42})
Пример 3
Далеко не всегда часть числа делится на числитель данной дроби; в таких случаях мы будем получать в ответе не целые числа, а дроби или смешанные числа.
(mathbf{frac{2}{3}}) от числа равны 11, найдите исходное число.
Во всем остальном решение ничем не будет отличаться- также разделим дробь от числа, равную (mathbf{frac{2}{3}}), на величину дроби, равную 11 и получим результат.
(mathbf{11divfrac{2}{3}=11cdotfrac{3}{2}=frac{11cdot3}{2}=frac{33}{2}=16frac{1}{2}})
Для получения ответа нам понадобилось выделить целую часть.
Важен еще один случай.
Никто не гарантирует, что данная нам часть числа сама по себе не будет являться дробью.
Такого случая не стоит пугаться, а стоит придерживаться алгоритма, а именно делить часть числа на то, какой дробью она является.
Пример 4
(mathbf{frac{5}{6}}) от числа равны (mathbf{frac{2}{3}}), найдите все число.
Для решения этого примера разделим (mathbf{frac{2}{3}})- часть числа, на (mathbf{frac{5}{6}})- дробь.
(mathbf{frac{2}{3}divfrac{5}{6}=frac{2}{3}cdotfrac{6}{5}=frac{2cdot6}{3cdot5}=frac{2cdot2}{5}=frac{4}{5}})
Все исходное число равняется (mathbf{frac{4}{5}})
Эта информация доступна зарегистрированным пользователям
Теперь представим, что дан какой-то определенный процент от числа и необходимо найти, от какого числа брали процент.
Вспомним, что процент- это способ записи десятичной дроби.
То есть, чтобы из процента получить десятичную дробь, которую он обозначает, надо величину процента разделить на 100.
Поэтому для решения такого рода задач надо преобразовать процент в десятичную дробь, а дальше сделать все то же самое: разделить число на эту дробь.
Пример 1
Известно, что зарплата работника увеличилась на 2 000 рублей или на 25 процентов. Какая зарплата у работника была изначально?
Решение:
Переведем проценты в дроби: (mathbf{25%=25div100=0.25})
Разделим число на дробь: (mathbf{2000div0.25=8000})
Ответ: изначально зарплата работника была 8000 рублей.
Сформулируем правило.
Чтобы найти число по проценту от него, надо перевести процент в десятичную дробь, а после разделить данную часть числа на полученную дробь.
Пример 2
Сказано, что 9% от числа равны 81. Необходимо найти все число.
Решение:
Первым действием переводим проценты в десятичную дробь.
(mathbf{9%=9div100=0.09})
Вторым действием делим данное число на эту дробь.
(mathbf{81div0.09=900})
Ответ: искомое число 900
Эта информация доступна зарегистрированным пользователям
Задачи, в которых фигурируют дроби от числа часто встречаются не только в школьных учебниках и задачниках, но и в реальной жизни, поэтому стоит уделить им особое внимание.
Сначала разберем некоторые из таких задач вместе, а дальше вы попробуете свои силы в самостоятельном решении задач.
Часть задач тривиальна, иными словами, их решение очевидно, достаточно лишь увидеть в них формулу, подставить в нее данные значения и получить результат.
Пример:
Айсберг возвышается над водой на (mathbf{frac{1}{11}}) своей высоты.
Капитан корабля заметил, что от воды до макушки айсберга по вертикали 16 метров.
Какова общая высота айсберга?
Решение:
В данном случае мы сразу можем сказать, что все число- это общая высота айсберга, дробь от числа- 16 (метров), а величина дроби- (mathbf{frac{1}{11}}).
Соответственно, по правилу, для получения ответа мы делим 16 на (mathbf{frac{1}{11}}) и получаем результат.
(mathbf{16divfrac{1}{11}=16cdot11=176}) (метр)- общая высота айсберга
Ответ: 176 (метров).
Некоторые задачи для своего решения требуют более глубокого анализа.
Пример:
Магазин продал (mathbf{frac{2}{3}}) пар новых кроссовок специальной партии, после чего на складе осталось 56 пар.
Какого размера была специальная партия?
Решение:
В данной задаче, если не вчитываться в условие, интуитивно хочется просто поделить 56 на (mathbf{frac{2}{3}}) и получить ответ, но ответ не будет правильным.
Если посмотреть внимательно, то 56 пар соответствуют оставшейся части партии, в то время как дробь (mathbf{frac{2}{3}}) описывает проданную часть.
Но мы пока не знаем общего количества пар и не можем сказать, какому числу соответствует (mathbf{frac{2}{3}})
Зато мы можем вычислить размер оставшейся части.
Если вся партия – это 1, и продано (mathbf{frac{2}{3}}), значит осталась (mathbf{frac{1}{3}}) товара.
Эта дробь соответствует 56 оставшимся парам.
Дальнейшие действия аналогичны рассмотренным в предыдущей задаче.
Теперь оформим решение:
1) (mathbf{1-frac{2}{3}=frac{1}{3}}) составляет оставшаяся часть от всего размера партии
2) (mathbf{56divfrac{1}{3}=56cdot3=168}) (пар) кроссовок всего было в партии
Ответ: 168 (пар).
Вам могут встретиться задачи и с более сложными условиями, все их разобрать невозможно, но главное:
- не давать себя запутать
- расписать, какой части какая дробь и какое число соответствует
- понять, где данных достаточно, чтобы узнать что- то новое
- и так постепенно продвигаться к ответу
Эта информация доступна зарегистрированным пользователям
Задачи математики часто диктуются другими науками, в том числе экономикой.
Существуют поднауки других наук, связанные с математикой. Примерами таких могут служить математическая физика, изучающая, как следует из названия, физические модели, а также математическая экономика, о которой мы вам сейчас расскажем.
Предметом изучения этой теории является математическое описание экономических объектов, явлений и процессов.
В самом деле, интересно применить мощнейший математический аппарат к таким насущным вопросам, как изменение цен и доходов, изменение предпочтений покупателей и пр.
Истоки математической экономики идут с XVII века. Тогда преподаватели германских университетов начали использовать новый стиль преподавания, который включал в себя статистику. Там, где появляется статистика, то есть множество чисел, появляется и математика, которая выявляет какие-то закономерности.
К примеру, расчет среднего дохода крестьян не является сложной задачей и сводится к вычислению среднего арифметического, но тоже является задачей математики.
В это же время группа английских ученых создала метод «численной аргументации государственной политики», который затрагивал темы налогов, сборов, таможенных пошлин, и прочие экономические процессы, в которых участвует государство.
К XIX веку появляется и развивается классическая школа политической экономики, чьим лицом принято считать Адама Смита.
Эта информация доступна зарегистрированным пользователям
Именно в этот период математика начала активно применяться в экономике.
В дальнейшем все большее количество математических инструментов переходило в экономику, а в наши дни на нее трудятся еще и информационные технологии.
Так что в наши дни великим экономистом может быть не тот, кто изначально учился на экономиста, а успешный математик или программист.
Как число находить по известной его части и значению этой части. Алгоритм.
В начале параграфа нас учат, как находить число по его дроби:
“Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь”
Здесь мы разбирали, как число делить на дробь, а значит, найти число по дроби – дело техники. Ниже смотрите примеры.
№ 686
Условие звучит так:
“Из бочки вылили 7/12 находившегося там керосина. Сколько литров керосина было в бочке, если из неё вылили 84 л?”
Видим, что у нас имеется дробь – 7/12 и её значение – 84 л. Нужно найти целое.
Решение простое:
№ 687
Условие звучит так:
“Володя прочитал 234 страницы, что составляет 36% всей книги. Сколько страниц в этой книге?”
Может быть, кого – то испугает 36% я часть.
Но 1% – это ведь 1/100 часть чего – либо. Значит 36% – 36/100.
Дальше действуем по алгоритму нахождения числа по его дроби.
Вот решение с ответом:
№ 688
Ещё раз вспомним, что, чтобы найти число по известной его части, нужно значение этой части разделить на эту часть.
Итак, записываем условие – и вперёд!
“Использование нового трактора для вспашки поля дало экономию времени в 70% и заняло 42 ч. Сколько времен потребовалось бы для выполнения этой работы на старом тракторе?”
Записываем условие в виде краткой записи:
И снова, как и в прошлой задаче, мы переводим проценты в дробь. Далее по алгоритму нахождения числа по дроби.
Важно!
ЭКОНОМИЯ времени в 70% – значит, что времени на новом тракторе стало на 70% МЕНЬШЕ, чем было на старом.
Решение:
№ 689
Условие таково:
“Столб, врытый в землю на 2/13 своей длины, возвышается над землёй на (5 + 1/2)м. Найдите всю длину столба.”
Тут мы разбирали, как найти число по известным части и значению этой части.
Если в условие невнимательно вчитаться, то можно подумать, что (5 + 1/2) м нужно разделить на 2/13 м.
Но!
2/13 – это ведь часть столба ПОД землёй, а (5 + 1/2) м – часть столба НАД землёй. То есть, прошлый путь решения неверный.
На самом деле, нам нужно узнать часть столба, которая находится над землёй, и уже с ней и её значением выполнять действия.
Вот решение:
№ 690
Условие:
“Токарь, выточив на станке 145 деталей, перевыполнил план на 16%. Сколько деталей надо было выточить по плану?”
Может возникнуть резонный вопрос – “Почему план обозначен как 100%, а не (100 – 16)%?”
Это произошло, потому что, если посмотреть вперёд в решение, то можно понять, что при делении числа на 86/100, получится число БОЛЬШЕЕ делимого. А токарь план не недовыполнил, сделав 145 деталей, хоть по плану должно было быть БОЛЬШЕ, а перевыполнил, при этом в плане заведомо МЕНЬШЕ, чем 145 деталей.
То есть, нужно 145 делением сделать “МЕНЬШЕ”, что как раз получится. Значит, план действительно должен быть обозначен, как 100%.
Здесь мы разбирали, как решать подобные задачи.
Решение с ответом:
№ 691
Условие звучит так:
“Точка C делит отрезок АВ на два отрезка АС и СВ. Длина отрезка АС составляет 0,65 длины отрезка СВ. Найдите длины отрезков СВ и АВ, если АС = 3,9 см.”
С первого взгляда не очень понятно, не так ли? Давайте лучше для понимания начертим чертёж:
Стало понятнее? Надеюсь, что да. Теперь мы можем легко увидеть, что на что надо делить для узнавания целого по нашему алгоритму.
Главное – не запутаться, что с чем складывать.
Решение ниже:
№ 692
Условие:
“Лыжная дистанция разбита на три участка. Длина первого – 0,48 длины всей дистанции, длина второго составляет 5/12 длины первого участка. Какова длина всей дистанции, если длина второго участка 5 км? Какова длина третьего участка?”
Ух… Довольно сложное условие. Но давайте разбираться. Давайте сначала начертим схему.
Во – первых, нам нужно найти длину первого участка – мы знаем сколько составляет определённая часть от неё (второй участок), а значит, можем вычислить её саму.
Затем, зная, какую часть от всей дистанции она составляет, а также ё длину, мы можем вычислить длину всей дистанции.
И потом вычисляем длину третьего участка.
Вот решение:
№ 693
Условие такое:
“Из полной бочки взяли 14,4 кг квашеной капусты и затем ещё 5/12 этого количества. После этого в бочке осталось 5/8 находившейся там ранее квашеной капусты. Сколько килограммов квашеной капусты было в полной бочке?”
Тут нам понадобятся знания по двум темам – по параграфу 14 и по этой теме, чтобы найти дробь по числу, а потом число по дроби. Но сначала давайте начертим схему, чтобы разобраться в условии.
Теперь решение – дело техники. Главное – не сделать дробное число в числителе. Сначала ищем дробь по числу, а затем число по дроби.
Решение:
№ 694
Условие:
“Когда Костя прошёл 0,3 всего пути от дома до школы, ему ещё осталось пройти до середины пути 150 м. Какой длины путь от дома Кости до школы?”
Чертим схему, чтобы всё понять:
Нужно лишь помнить, что десятичные дроби легко переводятся в обыкновенные, а значит 0,3 можно превратить в 3/10. Потом по плану нахождения числа по дроби находим весь путь.
Вот решение:
№ 695
Условие:
“Три группы школьников посадили деревья вдоль дороги. Первая группа посадила 35% всех имеющихся деревьев, вторая – 60% оставшихся деревьев, а третья группа – остальные 104 дерева. Сколько всего деревьев посадили?”
Давайте начертим схему:
Эту задачу нужно решать с конца – со 104 деревьев, высаженных 3й группой. Снова вспоминаем, что процент – 1/100, затем ищем число по дроби.
Потом повторяем то же самое, только уже находя общее количество деревьев.
Решение:
№ 696
Условие такое:
“В цехе имелись токарные, фрезерные и шлифовальные станки. Токарные станки составляли 5/11 всех этих станков. Число шлифовальных станков составляло 2/5 числа токарных станков. Сколько всего станков этих видов было в цехе, если фрезерных станков было на 8 меньше, чем токарных?”
Давайте начертим схему. Она, кстати, довольно простая:
Далее давайте решать. Сначала, пользуясь параграфом 14, мы находим, чему равно количество шлифовальных станков.
Затем, вычитая из единицы 5/11 и часть “для” шлифовальных станков, получаем, что фрезерных станков – 4/11 от всего.
Далее – дело техники.
Решение ниже:
Спасибо за просмотр! Подписывайтесь, ставьте лайк и рассказывайте друзьям о канале!
Представим
себе такую историю…
–
Саша, чем ты занимаешься? – спросил у друга Паша.
–
Да я вчера с родителями ездил на дачу, – начал Саша. – Папа сказал, что за
поездку наш автомобиль израсходовал бака
бензина, что составляет 36 литров. Вот мне и стало интересно, какой же тогда
объём всего бака в литрах нашей машины.
–
В 5-м классе мы решали похожие задачи, – вспомнил Паша. – Чтобы ответить на
твой вопрос, сначала нужно вычислить, сколько литров составляет часть
объёма бака машины. Получим литров.
А затем уже посчитать объём всего бака. Получим литров.
–
То есть объём бака нашей машины всего лишь 60 литров? – удивился Саша. – Паша,
ты уверен, что всё правильно посчитал?
–
Вроде бы, да… – задумался Паша. – Но давай лучше уточним у Мудряша.
–
Ребята, прежде чем я расскажу вам о нахождении числа по заданному значению дроби,
давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
–
Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было
получиться!
–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Зная, что 36 литров
составляют объёма
всего бака машины, вы нашли весь объём бака в литрах Сашиной машины. Подобные
задачи называют задачами на нахождение числа по заданному значению его
дроби. Нахождение числа по заданному значению его дроби выполняется
тогда, когда известно, сколько составляет часть от целого, и нужно
«восстановить» само целое.
–
Вы правильно вычислили объём в литрах бака машины, – продолжил Мудряш, – однако
найденный ответ — 60 литров — можно было получить и другим способом. Сейчас мы
с вами вместе его выведем. Итак, давайте объём всего бака машины, то есть
целое, обозначим за х. Мы знаем, что всего
бака, то есть часть от целого, равны 36 литрам.
–
Мне кажется я догадываюсь, – сказал Паша. – Нам поможет нахождение дроби от
числа. Чтобы найти дробь от числа, можно число умножить на эту дробь. Так
как х литров – это целое, а –
это часть от целого, то можем х умножить на и
получим 36.
–
Правильно! – сказал Мудряш.
–
Чтобы найти неизвестный множитель, – продолжил Саша, – нужно произведение
разделить на известный множитель. Применим правило деления дробей. Тогда х
= 60 литров.
–
Молодцы! – похвалил ребят Мудряш. – А теперь давайте подумаем, что же мы
сделали для того, чтобы узнать, чему равно наше целое?
–
Мы известную нам часть разделили на долю, которую она составляла, – ответили
мальчишки.
–
Правильно! – согласился Мудряш. – То есть для того, чтобы выяснить, какой объём
всего бака машины, достаточно число 36 разделить на дробь .
Рассмотренный пример иллюстрирует следующее правило.
Запомните! –
сказал Мудряш. – Чтобы найти число по заданному значению его дроби, можно данное
значение разделить на эту дробь.
–
Продолжу автомобильную тему, – улыбнулся Мудряш. – Давайте решим такую задачу: машина
проехала 72 километра, что составило 30 % всего пути. Какой путь должна
проехать машина?
–
Запишем 30 % в виде десятичной дроби, – начал Паша. – Нам известно, что 72 километра
– это 30 % всего пути. Значит, чтобы найти весь путь, который должна проехать
машина, нужно 72 разделить на 0,3. Получим, что машина должна проехать 240
километров.
–
Молодец! – похвалил Пашу Мудряш. – Рассмотренный пример иллюстрирует следующее
правило. Запомните! Чтобы найти число по его процентам, можно
представить проценты в виде дроби и разделить значение процентов на эту дробь.
–
А теперь давайте потренируемся и найдём следующие числа по известным их частям,
– предложил Мудряш.
–
Нам нужно найти число, если известно, что от
него равны 3,6, – начал Паша. – Чтобы найти число по заданному значению его
дроби, можно данное значение разделить на эту дробь. Десятичную дробь 3,6
представим в виде смешанного числа .
Можем сократить числитель и знаменатель дробной части на 2. Затем смешанное
число представим в виде неправильной дроби .
Применим правило деления дробей. Сократим числитель и знаменатель на 2. Получим
дробь .
Это неправильная дробь, так как числитель больше знаменателя. Выделим целую
часть. Получим .
–
Перейдём к следующему пункту, – продолжил Саша. – Нам нужно найти число, если от
него равно 0,7. Разделим 0,7 на дробь .
Десятичную дробь 0,7 представим в виде обыкновенной дроби. Применим правило
деления дробей. Сократим на 7. Получим дробь .
–
В следующем пункте нам нужно найти число, если 25 % от него равно ,
– сказал Саша. – 25 % представим в виде обыкновенной дроби. Это будет .
А теперь разделим
на .
Воспользуемся правилом деления дробей. Сократим на 4. И получим 1.
–
В последнем пункте нужно найти число, если %
от него равно 5, – сказал Паша. – %
представим в виде обыкновенной дроби. Мы знаем, что для того, чтобы проценты
перевести в число, нужно убрать знак процента и разделить число на 100. Тогда
получим дробь .
А теперь 5 разделим на .
Воспользуемся правилом деления дробей. Получим 1250.
–
А теперь, ребята, давайте посмотрим, как вы всё поняли, и решим несколько
задач.
Задача
первая: спортсмен пробежал 300 метров, что составило всей
дистанции. Какова длина дистанции?
Решение:
нам известно, что спортсмен пробежал 300 метров и это составляет всей
дистанции. Чтобы найти число по заданному значению его дроби, можно данное
значение разделить на эту дробь. Следовательно, 300 разделим на .
Применим правило деления дробей. Сократим на 3. Получим, что вся дистанция
равна 800 метрам. Не забудем записать ответ.
Задача
вторая: в киоске в первый день продали 40 % всех пакетов, во
второй день 53 % всех пакетов, а в третий день – остальные 847 пакетов. Сколько
пакетов продал киоск за три дня?
Решение: так
как в первый день продали 40 % всех пакетов, а во второй день 53 % всех
пакетов, то за два дня продали всех
пакетов. Следовательно, в третий день продали всех
пакетов. Мы знаем, что эти 7 % пакетов, проданных в третий день, равны 847.
Чтобы найти число по его процентам, можно представить проценты в виде дроби и
разделить значение процентов на эту дробь. 7 % представим в виде обыкновенной
дроби. Затем 847 разделим на .
Применим правило деления дробей. Сократим дробь на 7. Получим, что за три дня в
киоске продали 12 100 пакетов. Запишем ответ.
И
последняя задача: на школьной выставке 220 рисунков
выполнены красками, а остальные – карандашами. Сколько всего рисунков на
выставке, если карандашами выполнено всех
рисунков?
Решение: обозначим
за х количество всех рисунков на выставке. Тогда –
это количество рисунков, нарисованных карандашами. Нам известно, что карандашами
нарисовано всех
рисунков. Чтобы найти число по заданному значению его дроби, можно данное
значение разделить на эту дробь. Следовательно, можем составить уравнение: .
Решим это уравнение. Умножим левую и правую часть нашего равенства на .
Получим уравнение .
Перенесём все числа с переменной в левую часть равенства, а без переменной в
правую. Упростим уравнение. Получим .
Чтобы найти неизвестный множитель, нужно произведение разделить на известный
множитель. Применим правило деления дробей. Сократим на 4. Отсюда .
Получим, что всего 385 рисунков на выставке. Не забудем записать ответ.