Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция – arcsin(y)=x
sin(arcsin(y))=y
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Рассчитать арксинус
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

sin(α) = BC/AB
sin(-α) = -sin(α)
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
sin(α ± 2π) = sin(α)
Пример sin(5π) = sin(4π + π) = sin(π)
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451
Таблица Брадиса синусы
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Похожие калькуляторы
Знаки тригонометрических функций
5 ноября 2011
- Знаки триг. функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
Синус угла α — это ордината (координата
y
) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Косинус угла α — это абсцисса (координата
x
) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Тангенс угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты
y
к координате
x
.
Обозначение: sin α =
y
; cos α =
x
; tg α =
y
:
x
.
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
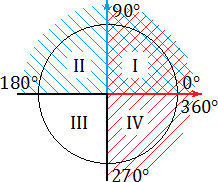
Синим цветом обозначено положительное направление оси
OY
(ось ординат), красным — положительное направление оси
OX
(ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
- sin α > 0, если угол α лежит в
I
или
II
координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата
y
). А координата
y
будет положительной именно в
I
и
II
координатных четвертях;
- cos α > 0, если угол α лежит в
I
или
IV
координатной четверти. Потому что только там координата
x
(она же — абсцисса) будет больше нуля;
- tg α > 0, если угол α лежит в
I
или
III
координатной четверти. Это следует из определения: ведь tg α =
y
:
x
, поэтому он положителен лишь там, где знаки
x
и
y
совпадают. Это происходит в
I
координатной четверти (здесь
x
> 0,
y
> 0) и
III
координатной четверти (
x
< 0,
y
< 0).
Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:
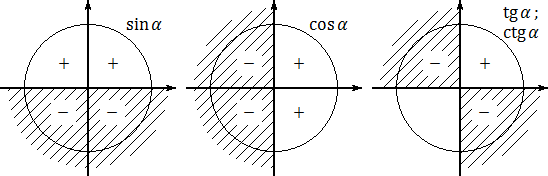
Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.
Теперь предлагаю рассмотреть примеры, похожие на задачи B11 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.
Задача. Определите знаки тригонометрических функций и выражений (значения самих функций считать не надо):
- sin (3π/4);
- cos (7π/6);
- tg (5π/3);
- sin (3π/4) · cos (5π/6);
- cos (2π/3) · tg (π/4);
- sin (5π/6) · cos (7π/4);
- tg (3π/4) · cos (5π/3);
- ctg (4π/3) · tg (π/6).
План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:
- sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из
II
координатной четверти. Но синус во
II
четверти положителен, поэтому sin (3π/4) > 0;
- cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из
III
координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;
- tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в
IV
четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;
- sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это
II
четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова
II
четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;
- cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это
II
координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это
I
четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;
- sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о
II
координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это
IV
координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
- tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это
II
четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это
IV
четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;
- ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это
III
координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это
I
координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это
II
координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о
III
координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это
IV
координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это
I
координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
Смотрите также:
- Радианная мера угла

- Тест к уроку «Знаки тригонометрических функций» (1 вариант)

- Тест к параграфу «Что такое логарифм» (легкий)

- Сводный тест по задачам B12 (1 вариант)

- Изюм и виноград (смеси и сплавы)

- Задача B4: транзит нефти

Примеры:
(sin{30^°}=)(frac{1}{2})
(sin)(frac{π}{3})(=)(frac{sqrt{3}}{2})
(sin2=0,909…)
Содержание:
- Аргумент и значение
Синус острого угла
Синус числа
Синус любого угла
Связь с другими функциями
Функция
Аргумент и значение

Синус острого угла
Синус острого угла можно определить с помощью прямоугольного треугольника – он равен отношению противолежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить синус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить (sinA).

Синус числа

Числовая окружность позволяет определить синус любого числа, но обычно находят синус чисел как-то связанных с Пи: (frac{π}{2}), (frac{3π}{4}), (-2π).
Например, для числа (frac{π}{6}) – синус будет равен (0,5). А для числа (-)(frac{3π}{4}) он будет равен (-)(frac{sqrt{2}}{2}) (приблизительно (-0,71)).

Подробнее как вычисляется синус разных чисел можно прочитать в этой статье.
Значение синуса всегда лежит в пределах от (-1) до (1). При этом вычислен он может быть для абсолютно любого угла и числа.
Синус любого угла
Благодаря единичному кругу можно определять тригонометрические функции не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать – проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить (sin∠КОА) с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам (sin∠KOA).
Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) – всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) – целых семь.
Как вы могли заменить, и синус числа, и синус произвольного угла определяется практически одинаково. Изменяются только способ нахождения точки на окружности.
Связь с другими тригонометрическими функциями:
– косинусом того же угла (или числа): основным тригонометрическим тождеством (sin^2x+cos^2x=1)
– тангенсом и косинусом того же угла (или числа): формулой (tgx=)(frac{sinx}{cosx})
– котангенсом того же угла (или числа): формулой (1+сtg^2x=)(frac{1}{sin^2x})
Другие наиболее часто применяемые формулы смотри здесь.
Функция (y=sinx)
Если отложить по оси (x) углы в радианах, а по оси (y) – соответствующие этим углам значения синуса, мы получим следующий график:

График данной функции называется синусоида и обладает следующими свойствами:
– область определения – любое значение икса: (D(sinx )=R)
– область значений – от (-1) до (1) включительно: (E(sinx )=[-1;1])
– нечетная: (sin(-x)=-sinx)
– периодическая с периодом (2π): (sin(x+2π)=sinx)
– точки пересечения с осями координат:
ось абсцисс: ((πn;0)), где (n ϵ Z)
ось ординат: ((0;0))
– промежутки знакопостоянства:
функция положительна на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
– промежутки возрастания и убывания:
функция возрастает на интервалах: ((-)(frac{π}{2})(+2πn;) (frac{π}{2})(+2πn)), где (n ϵ Z)
функция убывает на интервалах: (()(frac{π}{2})(+2πn;)(frac{3π}{2})(+2πn)), где (n ϵ Z)
– максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=)(frac{π}{2})(+2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=-)(frac{π}{2})(+2πn), где (n ϵ Z).
Смотрите также:
Косинус
Тангенс
Котангенс
Решение уравнения (sinx=a)
$$ctg(pi-alpha)=-ctg(alpha);$$
Давайте вместо угла (alpha) возьмем какой-нибудь реальный угол. Суть от этого не изменится. Чтобы усложнить задачу, я не буду рисовать рисунок. Нарисуйте окружность сами и по пунктам сделайте пример.
Пример 7
$$cos(3pi+frac{pi}{6})=?;$$
- Угол ((3pi+frac{pi}{6})) лежит в третьей четверти. Действительно, (3pi=2pi+pi) можно представить как полный круг плюс еще половина;
- В третьей четверти косинус отрицательный. Знак минус;
- (3pi) лежит на горизонтальной оси в точке (C). Значит косинус не меняется на синус;
$$cos(3pi+frac{pi}{6})=-cos(frac{pi}{6})=-frac{sqrt{3}}{2};$$
До этого мы рассматривали примеры, когда угол (alpha) был острым. А что, если он больше (90^o)?
В этом случае нам придется сделать из него острый угол. Рассмотрим пример:
Пример 8
$$tg(frac{pi}{2}-frac{5pi}{6})=?;$$
Угол (frac{5pi}{6}) – тупой угол. Для того, чтобы воспользоваться формулой приведения, можно представить:
$$frac{5pi}{6}=pi-frac{pi}{6};$$
Подставим в исходный пример
$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{2}-pi+frac{pi}{6})=tg(frac{pi}{6}-frac{pi}{2});$$
Угол (frac{pi}{6}) острый и теперь можно воспользоваться правилом лошади.
- ((frac{pi}{6}-frac{pi}{2})) лежит в четвертой четверти. Отмечаем (frac{pi}{6}) и по часовой стрелке вычитаем из него (frac{pi}{2});
- В четвертой четверти тангенс отрицательный;
- (frac{pi}{2}) лежит на вертикальной оси, тангенс меняется на котангенс;
$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{6}-frac{pi}{2})=-ctg(frac{pi}{6})=-sqrt{3};$$
У любопытного читателя может возникнуть вопрос: а почему данный алгоритм называется правилом лошади? При чем тут, казалось бы, лошадь?
Лошадь, действительно, не при чем. Но дело в том, что когда вы определяете в третьем пункте, меняется ли наша тригонометрическая функция на противоположную или нет, то в случае, если дополнительный угол к (alpha) лежит на вертикальной оси, мы как бы смотрим вверх-вниз, киваем головой, как лошадь, говоря себе: «Да, меняем». Или если угол лежит на горизонтальной оси, то мы киваем влево вправо вдоль горизонтальной оси, как бы говоря: «Нет, не меняем». Такое вот странное название у правила.
Методы решения тригонометрических уравнений
Составной частью ЕГЭ являются тригонометрические уравнения.
К сожалению, не существует общего единого метода, следуя которому можно было бы решить любое уравнение, в котором участвуют тригонометрические функции. Успех здесь могут обеспечить лишь хорошие знания формул и умение видеть те или иные полезные комбинации, что вырабатывается лишь практикой.
Общая цель обычно состоит в преобразовании входящего в уравнение тригонометрического выражения к такому виду, чтобы корни находились из так называемых простейших уравнений:
| сos px = a; | sin gx = b; | tg kx = c; | ctg tx = d. |
Для этого необходимо уметь применять тригонометрические формулы. Полезно знать и называть их “именами”:
1. Формулы двойного аргумента, тройного аргумента:
сos 2x = cos 2 x – sin 2 x = 1 – 2 sin 2 x = 2 cos 2 x – 1;
sin 2x = 2 sin x cos x;
tg 2x = 2 tg x/1 – tg x;
ctg 2x = (ctg 2 x – 1)/2 ctg x;
sin 3x = 3 sin x – 4 sin 3 x;
cos 3x = 4 cos 3 x – 3 cos x;
tg 3x = (2 tg x – tg 3 x)/(1 – 3 tg 2 x);
ctg 3x = (ctg 3 x – 3ctg x)/(3ctg 2 x – 1);
2. Формулы половинного аргумента или понижения степени:
sin 2 x/2 = (1 – cos x)/2; сos 2 x/2 = (1 + cos x)/2;
tg 2 x = (1 – cos x)/(1 + cos x);
ctg 2 x = (1 + cos x)/(1 – cos x);
3. Введение вспомогательного аргумента:
рассмотрим на примере уравнения a sin x + b cos x = c а именно, определяя угол х из условий sin y = b/v(a 2 + b 2 ), cos y = a/v(a 2 + b 2 ), мы можем привести рассматриваемое уравнение к простейшему sin (x + y) = c/v(a 2 + b 2 ) решения которого выписываются без труда; тем самым определяются и решения исходного уравнения.
4. Формулы сложения и вычитания:
sin (a + b) = sin a cos b + cos a sin b;
sin (a – b) = sin a cos b – cos a sin b;
cos (a + b) = cos a cos b – sin a sin b;
cos (a – b) = cos a cos b + sin a sin b;
tg (a + b) = ( tg a + tg b)/(1 – tg a tg b);
tg (a – b) = ( tg a – tg b)/(1 + tg a tg b);
5. Универсальная тригонометрическая подстановка:
sin a = 2 tg (a/2)/(1 + (tg 2 (a/2));
cos a = (1 – tg 2 (a/2))/(1 + (tg 2 (a/2));
tg a = 2 tg a/2/(1 – tg 2 (a/2));
6. Некоторые важные соотношения:
sin x + sin 2x + sin 3x +…+ sin mx = (cos (x/2) -cos (2m + 1)x)/(2 sin (x/2));
cos x + cos 2x + cos 3x +…+ cos mx = (sin (2m+ 1)x/2 – sin (x/2))/(2 sin (x/2));
7. Формулы преобразования суммы тригонометрических функций в произведение:
sin a + sin b = 2 sin(a + b)/2 cos (a – b)/2;
sin a – sin b = 2 cos (a + b)/2 sin (a – b)/2;
cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2;
cos a – cos b = -2 sin(a + b)/2 sin (b – a)/2;
tg a + tg b = sin (a + b)/(cos a cos b);
tg a – tg b = sin (a – b)/(cos a cos b).
А также формулы приведения.
В процессе решения надо особенно внимательно следить за эквивалентностью уравнений, чтобы не допустить потери корней (например, при сокращении левой и правой частей уравнения на общий множитель), или приобретения лишних корней (например, при возведении обеих частей уравнения в квадрат). Кроме того, необходимо контролировать принадлежат ли получающие корни к ОДЗ рассматриваемого уравнения.
Во всех необходимых случаях (т.е. когда допускались неэквивалентные преобразования), нужно обязательно делать проверку. При решении уравнении необходимо научить учащихся сводить их к определенным видам, обычно начиная с легких уравнении.
Ознакомимся с методами решения уравнений:
1. Сведение к виду аx 2 + bx + c = 0
2. Однородность уравнений.
3. Разложение на множители.
4. Сведение к виду a 2 + b 2 + c 2 = 0
5. Замена переменных.
6. Сведение уравнения к уравнению с одной переменной.
7. Оценка левой и правой части.
8. Метод пристального взгляда.
9. Введение вспомогательного угла.
10. Метод “ Разделяй и властвуй ”.
1. Решить уравнение: sin x + cos 2 х = 1/4.
Решение: Решим методом сведения к квадратному уравнению. Выразим cos 2 х через sin 2 x
sin x + 1 – sin 2 x = 1/4
4 sin 2 x – 4 sin x – 3 = 0
sin x = -1/2, sin x = 3/2(не удовлетворяет условию х€[-1;1]),
т.е. х = (-1) к+1 arcsin 1/2 + k, k€z,
2. Решить уравнение: 2 tg x cos x +1 = 2 cos x + tg x,
решим способом разложения на множители
2 tg x cos x – 2 cos x + 1 – tg x = 0,где х /2 + k, k€z,
2 cos x (tg x – 1) – (tg x – 1) = 0
(2 cos x – 1) (tg x – 1) = 0
2 cos x – 1 = 0 или tg x – 1 = 0
cos x = 1/2, tgx = 1,
т.е х = ± /3 + 2k, k€z, х = /4 + m, m€z.
Ответ: ± /3 + 2k, k€z, /4 + m, m€z.
3. Решить уравнение: sin 2 x – 3 sin х cos x + 2 cos 2 х = 0.
Решение: sin 2 x – 3 sin х cos x + 2 cos 2 х = 0 однородное уравнение 2 степени. Поскольку cos x = 0 не является корнем данного уравнения, разделим левую и правую часть на cos 2 х. В результате приходим к квадратному уравнению относительно tg x
tg 2 x – 3 tg x + 2 = 0,
tg x = 1 и tg x = 2,
откуда х = /4 + m, m€z,
х = arctg 2 + k, k€z.
Ответ: /4 + m, m€z, arctg 2 + k, k€z.
4. Решить уравнение: cos (10x + 12) + 42 sin (5x + 6) = 4.
Решение: Метод введения новой переменной
Пусть 5х + 6 = у, тогда cos 2у + 4 2 sin у = 4
1 – 2 sin 2 у + 4 2 sin у – 4 = 0
sin у = t, где t€[-1;1]
2t 2 – 4 2t + 3 = 0
t = 2/2 и t = 3 2/2 (не удовлетворяет условию t€[-1;1])
sin (5x + 6) = 2/2,
5x + 6 = (-1) к /4 + k, k€z,
х = (-1) к /20 – 6/5 + k/5, k€z.
Ответ: (-1) к ?/20 – 6/5 + ?k/5, k€z.
5. Решить уравнение: (sin х – cos у) 2 + 40х 2 = 0
Решение: Используем а 2 +в 2 +с 2 = 0, верно, если а = 0, в = 0, с = 0. Равенство возможно, если sin х – cos у = 0, и 40х = 0 отсюда:
х = 0, и sin 0 – cos у = 0, следовательно, х = 0, и cos у = 0, отсюда: х = 0, и у = /2 + k, k€z, также возможна запись (0; /2 + k) k€z.
6. Решить уравнение: sin 2 х + cos 4 х – 2 sin х + 1 = 0
Решение: Преобразуем уравнение и применим метод “разделяй и властвуй”
(sin 2 х – 2 sin х +1) + cos 4 х = 0;
(sin х – 1) 2 + cos 4 х = 0; это возможно если
(sin х – 1) 2 = 0, и cos 4 х = 0, отсюда:
sin х – 1 = 0, и cos х = 0,
sin х = 1, и cos х = 0, следовательно
х = /2 + k, k€z
7. Решить уравнение: sin 5х + sin х = 2 + cos 2 х.
Решение: применим метод оценки левой и правой части и ограниченность функций cos и sin.
– 1 sin 5х 1, и -1 sin х 1
0 cos 2 х 1
0 + 2 2 + cos 2 х 1 + 2
2 2 + cos 2 х 3
sin 5х + sin х 2, и 2 + cos 2 х 2
-2 sin 5х + sin х 2, т.е.
sin 5х + sin х 2,
имеем левая часть 2, а правая часть 2,
равенство возможно если, они оба равны 2.
cos 2 х = 0, и sin 5х + sin х = 2, следовательно
х = /2 + k, k€z (обязательно проверить).
8. Решить уравнение: cos х + cos 2х + cos 3х+ cos 4х = 0.
Решение: Решим методом разложения на множители. Группируем слагаемые, расположенные в левой части, в пары.
(В данном случае любой способ группировки приводит к цели.) Используем формулу cos a+cos b=2 cos (a + b)/2 cos (a – b)/2.
2 cos 3/2х cos х/2 + 2 cos 7/2х cos х/2 = 0,
cos х/2 (cos 3/2х + cos 7/2х) = 0,
2 cos 5/2х cos х/2 cos х = 0,
- cos х/2 = 0, х/2 = /2 + k, k€z, х = + 2k, k€z;
- cos 5/2х = 0, 5/2х = /2 + k, k€z, х = /5 + 2/5k, k€z;
- cos х = 0, х = /2 + k, k€z.
Ответ: + 2k, /5 + 2/5k, /2 + k, k€z.
Обратим внимание на то, что второй случай включает в себя первый. (Если во втором случае взять к = 4 + 5, то получим + 2n). Поэтому нельзя сказать, что правильнее, но во всяком случае “культурнее и красивее” будет выглядеть ответ: х1 = /5 + 2/5k, х2 = /2 + k, k€z. (Вновь типичная ситуация, приводящая к различным формам записи ответа). Первый ответ также верен.
Рассмотренное уравнение иллюстрирует весьма типичную схему решения – разложение уравнения на множители за счёт попарной группировки и использования формул:
sin a + sin b = 2 sin (a + b)/2 cos (a – b)/2;
sin a – sin b = 2 cos (a + b)/2 sin (a – b)/2;
cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2;
cos a – cos b = -2 sin (a + b)/2 sin (b – a)/2.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений весьма специфична и обычно оказывается более сложной, чем это имело место для уравнений алгебраических. Приведём решения уравнений, иллюстрирующие типичные случаи появления лишних (посторонних) корней и методы “борьбы” с ними.
Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнений. Приведём примеры.
9. Решить уравнение: (sin 4х – sin 2х – cos 3х + 2sin х -1)/(2sin 2х – 3) = 0.
Решение: Приравняем нулю числитель (при этом происходит расширение области определения уравнения – добавляются значения х, обращающие в нуль знаменатель) и постараемся разложить его на множители. Имеем:
2 cos 3х sin х – cos 3х + 2sin х – 1 = 0,
(cos 3х + 1) (2 sin х – 1) = 0.
Получаем два уравнения:
Посмотрим, какие k нам подходят. Прежде всего, заметим, что левая часть нашего уравнения представляет собой периодическую функцию с периодом 2. Следовательно, достаточно найти решение уравнения, удовлетворяющее условию 0 х < 2 (один раз “обойти” круг), затем к найденным значениям прибавить 2k.
Неравенству 0 х < 2 удовлетворяют три числа: /3, , 5/3.
Первое не подходит, поскольку sin 2/3 = 3/2, знаменатель обращается в нуль.
Ответ для первого случая: х1 = + 2k, х2 = 5/3 + 2k (можно х2 = – /3 + 2k), k€z.
Найдём решение этого уравнения, удовлетворяющие условию 0 х < 2. Их два: /6, 5/6. Подходит второе значение.
Ответ: + 2k, 5/3 + 2k, 5/6 + 2k, k€z.
10. Найти корни уравнений: v(cos 2х + sin 3х) = v2 cos х.
Решение этого уравнения распадается на два этапа:
1) решение уравнения, получающегося из данного возведением в квадрат обеих его частей;
2) отбор тех корней, которые удовлетворяют условию cos х 0. При этом (как и в случае алгебраических уравнений) заботиться об условии cos 2х + sin 3х 0 нет необходимости. Все значения k, удовлетворяющие возведённому в квадрат уравнению, этому условию удовлетворяют.
Первый шаг приводит нас к уравнению sin 3х = 1, откуда х1 = /6 + 2/3k.
Теперь надо определить, при каких k будет иметь место cos (/6 + 2/3k) 0. Для этого достаточно для k рассмотреть значения 0, 1, 2, т.е. как обычно “обойти один раз круг”, поскольку дальше значения косинуса будут отличаться от уже рассмотренных на величину, кратную 2.
Ответ: /6 + 2k, 3/2/3 + 2k, 5/6 + 2k, k€z.
11. Решить уравнение: sin 8 х – cos 5 х = 1.
Решение этого уравнения основывается на следующем простом соображении: если 0 < a < 1 то a t убывает с ростом t.
Значит, sin 8 х sin 2 х, – cos 5 х cos 2 х;
Сложив почленно эти неравенства, будем иметь:
sin 8 х – cos 5 х sin 2 х + cos 2 х = 1.
Следовательно, левая часть данного уравнения равна единице тогда и только тогда, когда выполняются два равенства:
sin 8 х = sin 2 х, cos 5 х = cos 2 х,
т.е. sin х может принимать значения -1, 0
Для полноты картины рассмотрим ещё пример.
12. Решить уравнение: 4 cos 2 х – 4 cos 2 3х cos х + cos 2 3х = 0.
Решение: Будем рассматривать левую часть данного уравнения как квадратный трёхчлен относительно cos х.
Пусть D – дискриминант этого трёхчлена:
1/4 D = 4 (cos 4 3х – cos 2 3х).
Из неравенства D 0 следует cos 2 3х 0 или cos 2 3х 1.
Значит, возникают две возможности: cos 3х = 0 и cos 3х = ± 1.
Если cos 3х = 0, то из уравнения следует, что и cos х = 0, откуда х = /2 + k.
Эти значения х удовлетворяют уравнению.
Если cos 3х = 1, то из уравнения cos х = 1/2 находим х = ± /3 + 2k. Эти значения также удовлетворяют уравнению.
Ответ: /2 + k, /3 + 2k, k€z.
13. Решить уравнение: sin 4 x + cos 4 x = 7/2 sin x cos x.
Решение: Преобразуем выражение sin 4 x + cos 4 x,выделив полный квадрат: sin 4 x + cos 4 x = sin 4 x + 2 sin 2 х cos 2 х + cos 4 x – 2 sin 2 х cos 2 х = (sin 2 х + cos 2 х) 2 – 2 sin 2 х cos 2 х, откуда sin 4 x + cos 4 x = 1 – 1/2 sin 2 2х. Пользуясь полученной формулой, запишем уравнение в виде
1-1/2 sin 2 2х = 7/4 sin 2х.
обозначив sin 2х = t, -1 t 1,
получим квадратное уравнение 2t 2 + 7t – 4 = 0,
решая которое, находим t1 = 1/2, t2 = – 4
уравнение sin 2х = 1/2
2х = (- 1) к /6 + k, k€z, х = (- 1) к //12 + k /2, k€z .
уравнение sin 2х = – 4 решений не имеет.
Ответ: (- 1) к //12 + k /2, k€z .
14. Решить уравнение: sin 9х + sin х = 2.
Решение: Решим уравнение методом оценки. Поскольку при всех значениях а выполнено неравенство sin а1,то исходное уравнение равносильно sin х = 1 и sin 9х =1,откуда получаем х = /2 + 2k, k€z и х = /18 + 2n, n€z.
Решением будут те значения х, при которых выполнено и первое, и второе уравнение. Поэтому из полученных ответов следует отобрать только х = /2 + 2k, k€z.
15. Решить уравнение: 2 cos x = 1 – 2 cos 2 x – v3 sin 2х.
Решение: воспользуемся формулой:
сos 2x = cos 2 x – sin 2 x = 1 – 2 sin 2 x = 2 cos 2 x – 1;
и перепишем уравнение в виде
2 cos x = – cos 2х – 3 sin 2х.
Применим к правой части процедуру введения дополнительного аргумента. Получим уравнение:
2 cos x = – 2 (1/2 cos 2х + 3/2 sin 2х),
которое можно записать в виде
2 cos x = – 2 (cos а cos 2х + sin а sin 2х),
где очевидно, а = /3. Преобразуя правую часть полученного уравнения с помощью формулы:
cos (a – b) = cos a cos b + sin a sin b;
приходим к уравнению
2 cos x = – 2 cos (2х – /3),
cos x + cos (2х – /3) = 0.
Последнее уравнение легко решить, преобразовав сумму косинусов в произведение по формуле:
cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2,
cos x + cos (2х – /3) = 2 cos (3х/2 – /6) cos (/6 – х/2) = 0
Это уравнение расщепляется на два уравнения
решение которых уже не представляет сколь нибудь значительных трудностей.
Ответ: 2/9(2 + 3n), 2/3(2 + 3 k), n, k€z.
16. При каких значениях параметра а, уравнение а sin x – 4 cos x = 5, имеет решения?
Решение: преобразуем левую часть уравнения, используя формулу введения дополнительного аргумента:
а sin x – 4 cos x = (а 2 + 16) sin (x – y), где y определяется из условий sin y = – 4/(а 2 + 16), и cos y = а /(а 2 + 16).
Но значение y нас не интересует. Поэтому данное уравнение перепишем в виде
(а 2 + 16) sin (x – y) = 5,
sin (x – y) = 5/(а 2 + 16), это уравнение имеет решение при условии 5/(а 2 + 16) 1.
Решим это неравенство:
5/(а 2 + 16) 1, обе части умножим на (а 2 + 16):
5 (а 2 + 16),
(а 2 + 16) 5,
а 2 + 16 25,
а 2 9, или
а 3, следовательно
а € (-;-3] U [3; ).
17. При каких значениях параметра а, уравнение 2 sin 2 x + 3 cos (x +2 а) = 5, имеет решения?
Решение: поскольку 0 sin 2 x 1, и -1 cos (x +2а) 1 левая часть уравнения может равняться 5 тогда и только тогда, когда одновременно выполняются равенства sin 2 x = 1, и cos (x +2 а) = 1.
Это означает, что исходное уравнение равносильно системе уравнений sin 2 x = 1, и cos (x +2 а) = 1.
sin x = – 1, sin x = 1, cos (x +2 а) = 1;
х = /2 + n, n€z, и x +2 а = 2 к, к€z;
х = /2 + n, и x = – 2 а + 2 к;
/2 + n = – 2 а + 2 к;
2 а = 2 к – /2 – n;
а = к – /4 – n/2;
а = – /4 + /2 (2к – n);
а = – /4 + m/2, m€z.
Ответ: – /4 + m/2, где m€z.
Рассмотренные выше примеры лишь иллюстрируют несколько общих рекомендаций, которые полезно учитывать при решении тригонометрических уравнений. Из приведённых примеров видно, что дать общий рецепт в каждом конкретном случае невозможно.
Ежегодно варианты экзаменационных материалов ЕГЭ содержат от 4-х до 6-ти различных задач по тригонометрии. Поэтому параллельно с повторением теоретического материала значительное время должно быть отведено решению конкретных задач, в том числе и тригонометрических уравнений. А умение можно выработать, только получив практические навыки в решении достаточного числа тригонометрических уравнений.
Тригонометрические уравнения — формулы, решения, примеры
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`

2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| leq 1` имеет бесконечное множество решений.
Формула корней: `x=pm arccos a + 2pi n, n in Z`


Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + pi n, n in Z`

4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + pi n, n in Z`

Формулы корней тригонометрических уравнений в таблице
Для синуса: Для косинуса:
Для косинуса: Для тангенса и котангенса:
Для тангенса и котангенса: Формулы решения уравнений, содержащих обратные тригонометрические функции:
Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+frac pi 6)-3sin(frac pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+frac pi 6)-3cos(x+frac pi 6)+1=0`,
делаем замену: `cos(x+frac pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+frac pi 6)=1`, `x+frac pi 6=2pi n`, `x_1=-frac pi 6+2pi n`.
2. `cos(x+frac pi 6)=1/2`, `x+frac pi 6=pm arccos 1/2+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Ответ: `x_1=-frac pi 6+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =pi n`, `x_1=2pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ pi n`, `x/2=pi/4+ pi n`, `x_2=pi/2+ 2pi n`.
Ответ: `x_1=2pi n`, `x_2=pi/2+ 2pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x ne 0` — для первого случая, и на `cos^2 x ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x ne 0`, получим:
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+pi n`, `n in Z`
- `tg x=1`, `x=arctg 1+pi n`, `x_2=pi/4+pi n`, ` n in Z`.
Ответ. `x_1=arctg (-2)+pi n`, `n in Z`, `x_2=pi/4+pi n`, `n in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2pi n`, `n in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Ответ. `x_1=2 arctg 2+2pi n, n in Z`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt `:
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `frac a>=cos varphi`, ` frac b> =sin varphi`, `frac c>=C`, тогда:
`cos varphi sin x + sin varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt `, получим:
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos varphi` , `4/5=sin varphi`. Так как `sin varphi>0`, `cos varphi>0`, то в качестве вспомогательного угла возьмем `varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos varphi sin x+sin varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`x+varphi=(-1)^n arcsin 2/5+ pi n`, `n in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `frac =1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x ne 0`, `cos x ne -1`, ` x ne pi+2pi n, n in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=pi n`, `n in Z`
- `1-sin x=0`, `sin x=-1`, `x=pi /2+2pi n, n in Z`.
Учитывая, что ` x ne pi+2pi n, n in Z`, решениями будут `x=2pi n, n in Z` и `x=pi /2+2pi n`, `n in Z`.
Ответ. `x=2pi n`, `n in Z`, `x=pi /2+2pi n`, `n in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Решение уравнения sinx=a
учебно-методический материал
Решение уравнений sin  =a. Арксинус.
=a. Арксинус.
Синусом угла  называется ордината (то есть координата по оси ОУ ) точки на единичной окружности, соответствующей повороту на данный угол
называется ордината (то есть координата по оси ОУ ) точки на единичной окружности, соответствующей повороту на данный угол  .
.
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение 
Этому уравнению удовлетворяют все такие значения угла поворота  , которые соответствуют точкам окружности, ордината которых равна
, которые соответствуют точкам окружности, ордината которых равна 
Отметим на оси ординат точку с ординатой 

Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату  .Эти точки соответствуют углам поворота на
.Эти точки соответствуют углам поворота на  и
и  радиан:
радиан:

Если мы, выйдя из точки, соответствующей углу поворота на  радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на
радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на  радиан и имеющую ту же ординату. То есть это угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно “холостых” оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число “холостых” оборотов обозначим буквой k (или n). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, k (или n ) могут принимать любые целые значения, записывается это так k
радиан и имеющую ту же ординату. То есть это угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно “холостых” оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число “холостых” оборотов обозначим буквой k (или n). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, k (или n ) могут принимать любые целые значения, записывается это так k  — множество целых чисел.
— множество целых чисел.
То есть первая серия решений исходного уравнения имеет вид:
 + 2
+ 2  — множество целых чисел (1)
— множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:

 + 2
+ 2  — множество целых чисел (2)
— множество целых чисел (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на  .
.
Эти две серии решений можно объединить в одну запись:
х =( 
 +
+  /
/
Если мы в этой записи возьмем k = 2n ( то есть четное k), то мы получим первую серию решений.
Если мы в этой записи возьмем k = 2n + 1 ( то есть нечетное k ), то мы получим вторую серию решений.
Отметим на окружности точки, ордината которых равна 0:

х = 
2. 
Отметим на окружности единственную точку, ордината которой равна 1:

х =  + 2
+ 2 
3. 
Отметим на окружности единственную точку, ордината которой равна -1:

Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
х = —  +2
+2  , где n
, где n 
Уравнение sinx = a
Если | a |>1 , то уравнение sinx = a не имеет корней.
Например, уравнение sinx =2 не имеет корней.
Если | a |≤1 , то корни уравнения выражаются формулой,
x =  arcsina + πk , k ∈ Z
arcsina + πk , k ∈ Z
Что же такое arcsina ?
Арксинус в переводе с латинского означает «дуга и синус». Это обратная функция.
Если | a |≤1 , то arcsina (арксинус a ) — это такое число из отрезка [  ] , синус которого равен a .
] , синус которого равен a .
аrcsina = x ⇒ sinx = a , где | a |≤1, x ∈ [ −  ] .
] .
Найти arcsiт 
Выражение arcsiт 
показывает, что синус угла x равен />, т. е. sinx = />.
Далее просто находим точку этого синуса на числовой окружности, что и является ответом:

Точка  , находящаяся на оси y , соответствует точке
, находящаяся на оси y , соответствует точке  на числовой окружности.
на числовой окружности.
Значит, arcsin  =
= 
Если sin  =
=  , то arcsin
, то arcsin  =
= 
В первом случае по точке на числовой окружности находим значение синуса, а во втором — наоборот, по значению синуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арксинус.
Для любого a ∈ [ − 1;1] справедлива формула arcsin (− a )=− arcsina .
Например: arcsin (-  ) = — arcsin
) = — arcsin  = —
= — 
Если | a |>1 , то уравнение sinx = a не имеет корней.
Если | a |≤1 , то корни уравнения выражаются формулой,
x =  arcsina + πk , k ∈ Z
arcsina + πk , k ∈ Z
х = 
х =  + 2
+ 2 
х = —  +2
+2  , где n
, где n 
Формулы: arcsin(sin 
Например: arcsin(sin />) = />
sin(arcsin />) = />
Это частный случай. Если синус равен 1, то угол равен  + 2
+ 2 
2х =  + 2
+ 2 
х =  +
+ 
Ответ: х =  +
+ 
2. 2sin  —
—  = 0
= 0
2 sin  =
= 
sin 
 =
=  arcsin
arcsin  + πk , k ∈ Z
+ πk , k ∈ Z
 =
=  + πk , k ∈ Z,
+ πk , k ∈ Z,
х =  πk , k ∈ Z,
πk , k ∈ Z,
Ответ: х =  πk , k ∈ Z,
πk , k ∈ Z,
3. sin(x-  ) = 0.
) = 0.
Это частный случай. Синус равен нулю, если угол равен 
В нашем случае угол равен x-  x-
x-  =
= 
х =  +
+  . Ответ: х =
. Ответ: х =  +
+  .
.
2х =  + πk , k ∈ Z,
+ πk , k ∈ Z,
2х =  0,3 + πk , k ∈ Z
0,3 + πk , k ∈ Z
х=  , k ∈ Z
, k ∈ Z
Ответ:  , k ∈ Z
, k ∈ Z
5. sin4xcos2x = cos4xsin2x
sin4xcos2x – cos4xsin2x = 0,
2x = 
х =  ,
, 
Ответ: х =  ,
, 
