Привет! Продолжаем разбирать ОГЭ по информатике 2023. Сегодня посмотрим 3 задание.
Третье задание из ОГЭ по информатике проверяет умение работать с логическим выражением.
В логическом выражении могут использоваться союз И и союз ИЛИ.
Пусть 0 – это ложь, 1 – Истина. Тогда напишем таблицу истинности для союза И и для союза ИЛИ.
Таблица истинности для союза И
| Выражение | Результат |
| 0 И 0 | 0 |
| 0 И 1 | 0 |
| 1 И 0 | 0 |
| 1 И 1 | 1 |
Союз И похож на умножение в математике. Если в логическом выражении присутствует 0 (ложь), то в итоге тоже получается 0 (ложь). Лишь две единицы дают тоже единицу.
Таблица истинности для союза ИЛИ
| Выражение | Результат |
| 0 ИЛИ 0 | 0 |
| 0 ИЛИ 1 | 1 |
| 1 ИЛИ 0 | 1 |
| 1 ИЛИ 1 | 1 |
Эта операция похоже на суммирование в математике. Лишь 1 или 1 даёт не 2, как в математике, а 1.
Перейдём к решению примерных задач из ОГЭ по информатике 2023.
Задача (Классическая)
Напишите наименьшее число X, для которого истинно высказывание:
(X > 16) И НЕ (X нечётное)
Решение:
Нужно, чтобы высказывание было истинным. Посмотрим, когда единица (истина) получается для союза И. Такое происходит только когда слева и справа стоят 1 (единицы).
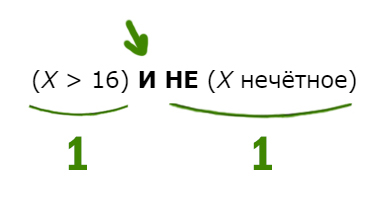
Получается наш X должен быть больше 16, и число должно быть не нечётное, т.е. чётное! Наименьшее чётное число большее 16 будет 18.
Ответ: 18
Задача (Закрепление)
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 6) И НЕ (X >= 11)
Решение:
Опять высказывание должно быть истинным.
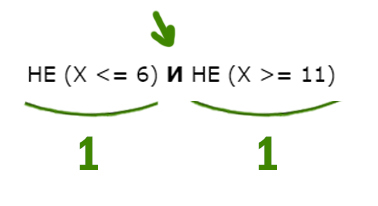
С одной стороны X должен быть НЕ меньше или равно 6, т.е значит, X нужно взять больше 6 (X > 6). Причём само число 6 не входит в этот диапазон.
С другой стороны X НЕ больше или равно 11, т.е. X должен быть меньше 11 (X < 11).
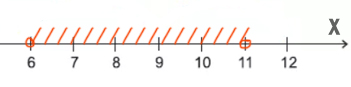
Наибольшее целое число будет 10.
Ответ: 10
Задача (Союз И)
Напишите наименьшее натуральное двузначное число, для которого истинно высказывание:
НЕ (первая цифра нечётная) И (число делится на 3)
Решение:
Высказывание должно быть истинным.
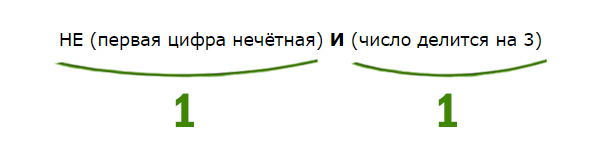
Первая цифра должна быть НЕ нечётная. Значит, она должна быть чётная. Число должно делится на 3. Найдём наименьшее двухзначное число, у которого первая цифра чётная, и оно делится на 3. Это будет 21.
Ответ: 21
Задача (Союз ИЛИ)
Для какого целого числа X ЛОЖНО высказывание:
(X > 3) ИЛИ НЕ (X > 2)
Решение:
В этой задаче используется союз ИЛИ. Нужно, чтобы высказывание было ложным. Ложь при союзе ИЛИ получается только в одном случае, когда слева и справа стоят нули.
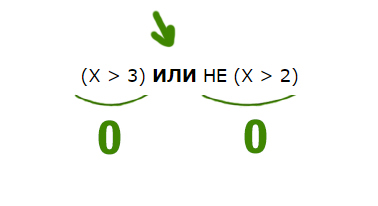
Утверждение, что X > 3 должно быть ложно, значит, если его перевернуть, получится X <= 3. Второе утверждение НЕ (X > 2) тоже должно быть ложно. Значит, если перевернём это утверждение, частицу НЕ нужно убрать. Получается просто X > 2.
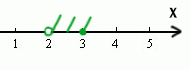
Получается, что только одно целое число входит в допустимый диапазон. Это тройка.
Ответ: 3
Задача (Частица НЕ над всем выражением)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((x<=200) ИЛИ (x<=100))
Решение:
Нам нужно сделать выражение истинным. Но всё выражение находится под влиянием частицы НЕ. Можно эту частицу полностью убрать, но воспринимать, как будто нужно сделать выражение ложным. А дальше всё как обычно.
Ложь у союза ИЛИ получается в одном случае.
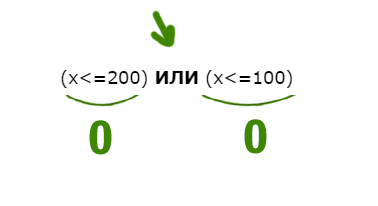
Первое выражение выдаёт ноль, когда x>200 (равно 200 не входит). Второе выражение выдаёт ноль, когда x>100. Объединив эти два условия получаем:
x > 200
Наименьшее число получается 201.
Ответ: 201
Задача (Крепкий орешек)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((x <= 100) ИЛИ (x>=200)) И (x чётное)
Решение:
В этой примерной задаче из ОГЭ по информатике применим все приёмы, которые мы разбирали до этого.
Когда союз И выдаёт единицу ?
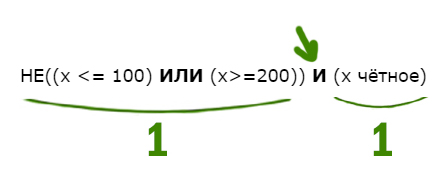
Посмотрим, когда левое выражение выдаёт 1. Уберём частицу НЕ, но тогда будем смотреть, когда левое выражение выдаёт 0.
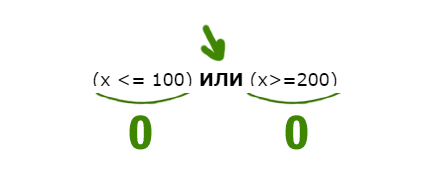
Перевернём оба выражения, которые находятся по обе стороны от союза ИЛИ. С одной стороны X>100, с другой X<200.
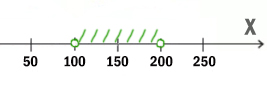
Учтём правое от союза И выражение. Наименьшее чётное число получается 102.
Ответ: 102
Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.

Алгебра высказываний
Под высказыванием понимаем всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является оно истинным или ложным. Например, «5-3 = 2» или «В неделе семь дней» — истинные высказывания, а «5 > 8» или «В русском языке 35 букв» — ложные высказывания. Синонимами слова «высказывания» можно считать: логическое высказывание, булевское выражение, суждение, утверждение и т.п. Фразы: «Ура!», «Который час?» — не являются высказываниями.
Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА» , «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «О», «НЕТ», «Л», «-«, «false»). Совокупность возможных значений высказывания образует множество истинности {0,1} и {И,Л}.
Есть два вида высказываний: простые и составные (сложные). Под простым будем понимать высказывание, которое не может быть разбито на более простые высказывания. Про него всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи логических операций можно строить сложные высказывания, которые всегда только истинны или только ложные. Высказывания обозначаются заглавными латинскими буквами: 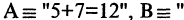 сегодня вторник
сегодня вторник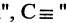 если студент успешно сдал сессионные экзамены, то переводится на следующий курс и будет получать стипендию».
если студент успешно сдал сессионные экзамены, то переводится на следующий курс и будет получать стипендию».
Логические операции
Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.
Отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 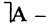 отрицание высказывания А, которое истинно, когда А ложно, и ложно, когда А истинно. Символ
отрицание высказывания А, которое истинно, когда А ложно, и ложно, когда А истинно. Символ 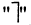 соответствует логическому союзу «не».
соответствует логическому союзу «не». 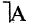 читается «не А» или «не верно, что А». Отрицание — одноместная (или унарная) операция. Последующие операции — двухместные (или бинарные). Например, если
читается «не А» или «не верно, что А». Отрицание — одноместная (или унарная) операция. Последующие операции — двухместные (или бинарные). Например, если 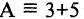
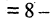 истинное высказывание, то
истинное высказывание, то 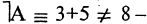 ложное высказывание (отрицание А), или если
ложное высказывание (отрицание А), или если 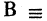 в комнате холодно»,
в комнате холодно», 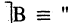 в комнате не холодно». Отметим, что высказывание «в комнате жарко» не является отрицанием В.
в комнате не холодно». Отметим, что высказывание «в комнате жарко» не является отрицанием В.
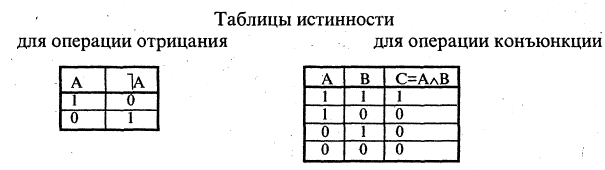
Конъюнкция высказываний
Конъюнкцией высказываний А и В называется высказывание 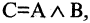 которое истинно только в том случае, когда и А, и В одновременно истинны. Выражение
которое истинно только в том случае, когда и А, и В одновременно истинны. Выражение  читается «А и В». Пример: пусть
читается «А и В». Пример: пусть 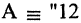 делится на
делится на 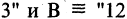 делится на 4″. Тогда формула
делится на 4″. Тогда формула  имеет смысл: «12 делится на 3 и на 4».
имеет смысл: «12 делится на 3 и на 4».
Операцию конъюнкции можно определить и для нескольких высказываний как связку высказываний, объединенных союзом «и». Конъюнкция из п высказываний — новое высказывание, причем высказывание
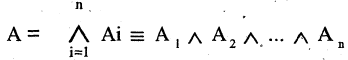
имеет значение «истина», если 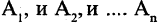 истинны. Во всех других случаях эта конъюнкция имеет значение «ложь». Пусть, например,
истинны. Во всех других случаях эта конъюнкция имеет значение «ложь». Пусть, например, 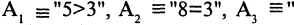 отец старше сына
отец старше сына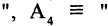 Мурманск севернее Смоленска». Тогда высказывание
Мурманск севернее Смоленска». Тогда высказывание 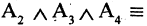 («8=3 и отец старше сына, и
(«8=3 и отец старше сына, и
Мурманск севернее Смоленска») — ложное высказывание. В то время как 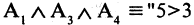 и отец старше сына, и Мурманск севернее Смоленска» — истинное высказывание.
и отец старше сына, и Мурманск севернее Смоленска» — истинное высказывание.
Дизъюнкция высказываний
Дизъюнкцией высказываний А и В называется высказывание 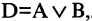 которое ложно только тогда, когда и А, и В ложны одновременно. Дизъюнкция имеет значение «истина», если хотя бы одно из высказываний, входящее в дизъюнкцию, является истинным. Выражение
которое ложно только тогда, когда и А, и В ложны одновременно. Дизъюнкция имеет значение «истина», если хотя бы одно из высказываний, входящее в дизъюнкцию, является истинным. Выражение  читается «А или В». Пусть
читается «А или В». Пусть 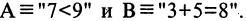 Тогда
Тогда 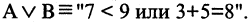
Операцию дизъюнкции можно определить для нескольких высказываний как связку высказываний, объединенных союзом «или»,
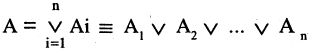
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Импликация высказываний
Импликацией высказываний А и В называется высказывание 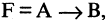 которое ложно только в том случае, когда А — истинно, а В — ложно. Во всех других случаях импликация
которое ложно только в том случае, когда А — истинно, а В — ложно. Во всех других случаях импликация 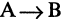 имеет значение «истина». Символ
имеет значение «истина». Символ 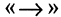 соответствует логическому союзу: «если А, то В». Например, А — «целое число делится на 4, то оно делится на 2». Для иллюстрации содержательного смысла импликации рассмотрим следующий пример: А
соответствует логическому союзу: «если А, то В». Например, А — «целое число делится на 4, то оно делится на 2». Для иллюстрации содержательного смысла импликации рассмотрим следующий пример: А  «папа завтра получит премию», В
«папа завтра получит премию», В  «папа завтра купит сыну велосипед». Тогда импликация
«папа завтра купит сыну велосипед». Тогда импликация 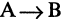 может быть сформулирована так: «если папа завтра получит премию, то купит сыну велосипед».
может быть сформулирована так: «если папа завтра получит премию, то купит сыну велосипед».

Пусть А и В истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Когда же папа не купит сыну велосипед (В — ложно), получив премию (А — истинно), то это, мягко говоря, не логичный поступок, а импликация имеет значение «ложь». Если же папа не получит премию (А — ложно), но купит велосипед (В -истинно), то результат положителен. В том случае, если, не получив премии (А ложно), папа не купит велосипед (В — ложно) -обещание не нарушено, результат можно считать истинным.
Эквивалентность высказываний
Эквивалентностью высказываний А и В называется высказывание 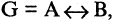 которое истинно, когда высказывания и А, и В оба истинны или оба. ложны. Символ логической эквивалентности
которое истинно, когда высказывания и А, и В оба истинны или оба. ложны. Символ логической эквивалентности 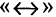 соответствует связке «тогда и только тогда». Пример. Пусть А
соответствует связке «тогда и только тогда». Пример. Пусть А  «число З
«число З является четным», В
является четным», В  «число
«число  является четным». Высказывание «число З
является четным». Высказывание «число З является четным тогда и только тогда, когда
является четным тогда и только тогда, когда  -четное число» есть эквивалентность высказываний А и В. Эквивалентность высказываний может быть задана следующей таблицей истинности:
-четное число» есть эквивалентность высказываний А и В. Эквивалентность высказываний может быть задана следующей таблицей истинности:
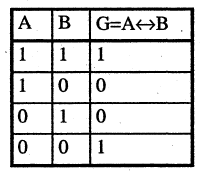
Замечание. Характерной особенностью операций над высказываниями является введение логических союзов с точно определенным смыслом, не допускающим никакой двусмысленности в толковании этих символов. Таким образом, математическая логика применима не для любых высказываний, а только для таких, которые допуск кают четкую оценку в двоичной системе «истина — ложь». Для преодоления такого рода ограничений в рамках нечеткой математики разрабатывается нечеткая логика.
Если в выражении встречаются различные логические операции, то в качестве естественного порядка (выполняемого поочередно слева направо) используется следующая последовательность: 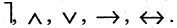 Это означает, что сначала выполняются операции отрицания, затем конъюнкции и т. д. Для нарушения порядка служат скобки. Рассмотрим пример. Пусть высказывания А и В имеют значения «истина», а высказывания С и Б — «ложь». Тогда формула
Это означает, что сначала выполняются операции отрицания, затем конъюнкции и т. д. Для нарушения порядка служат скобки. Рассмотрим пример. Пусть высказывания А и В имеют значения «истина», а высказывания С и Б — «ложь». Тогда формула 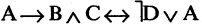 имеет значение «ложь», т.к.:
имеет значение «ложь», т.к.:
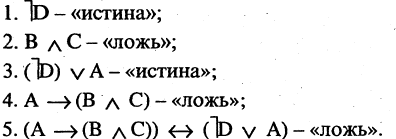
Введя скобки, получим формулу 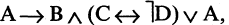 которая уже имеет другое значение — «истина». Действительно:
которая уже имеет другое значение — «истина». Действительно:
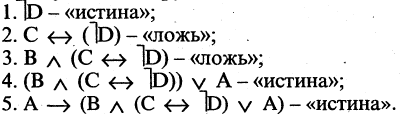
Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:
Использование различных операций позволяет в удобной аналитической форме задавать различные множества.
Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:
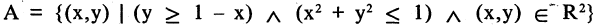
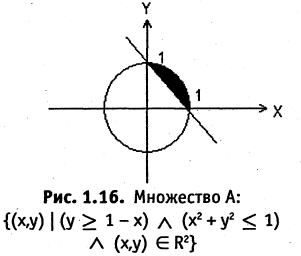
Система операций 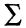 называется полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы
называется полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы 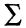 . Система введенных пяти операций (отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности) полная, хотя вообще говоря, избыточна, так как одни логические операции могут быть выражены через другие. Например, импликация и эквивалентность можно выразить через отрицание, конъюнкцию и дизъюнкцию следующим образом:
. Система введенных пяти операций (отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности) полная, хотя вообще говоря, избыточна, так как одни логические операции могут быть выражены через другие. Например, импликация и эквивалентность можно выразить через отрицание, конъюнкцию и дизъюнкцию следующим образом:
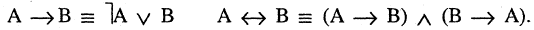
Булевы функции
Всякую формулу логики высказываний можно рассматривать как некоторую функцию: каждая буква (высказывание) может принимать одно из двух значений — «истина» или «ложь», при этом сложное высказывание, заданное этой формулой, также может быть истинным или ложным. Так формула
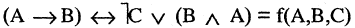
выражает функцию от переменных А, В и С.
Такого рода функции называются булевыми, а их аргументы — булевыми переменными. Аргументы булевых функций могут представлять собой, сокращенные обозначения некоторых конкретных высказываний. Тогда функция обозначает сокращенную запись некоторого сложного высказывания. Например, 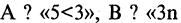 делится на 3», С ? «Мурманск севернее Смоленска». В этом случае
делится на 3», С ? «Мурманск севернее Смоленска». В этом случае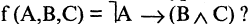 «если
«если 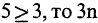 делится на 3 и Мурманск севернее Смоленска». Сравните с известной формулой физики
делится на 3 и Мурманск севернее Смоленска». Сравните с известной формулой физики 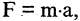 где m — масса тела, а — его ускорение, а F — сила, вызвавшая это ускорение. Буквы в булевых функциях могут выступать в качестве переменных. Подставляя вместо них любые высказывания, можно по формуле вычислить соответствующее значение функции. Действительно, если в формуле
где m — масса тела, а — его ускорение, а F — сила, вызвавшая это ускорение. Буквы в булевых функциях могут выступать в качестве переменных. Подставляя вместо них любые высказывания, можно по формуле вычислить соответствующее значение функции. Действительно, если в формуле 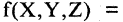
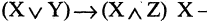 «истина», Y — «ложь», Z — «истина», то
«истина», Y — «ложь», Z — «истина», то 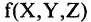 — «истина». Если же Z будет иметь ложное значение, то
— «истина». Если же Z будет иметь ложное значение, то 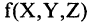 поменяет значение на противоположное и будет «ложью».
поменяет значение на противоположное и будет «ложью».
Целый ряд булевых функций обладает тем свойством, что они принимают одни и те же значения при любых значениях истинности аргументов. Такие формулы называются тождественно истинными. Например, при любых X и Y истинны формулы 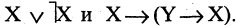 Тождественно ложные функции при любых значениях аргументов имеют значение «ложь». Так формулы
Тождественно ложные функции при любых значениях аргументов имеют значение «ложь». Так формулы 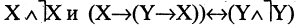 всегда имеют значение «ложь».
всегда имеют значение «ложь».
Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.
Основные законы математической логики
1.Коммутативность
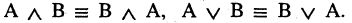
2.Ассоциативность
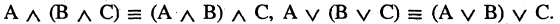
3.Дистрибутивность
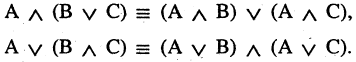
4.Законы де Моргана
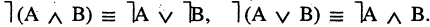
5.Закон поглощения
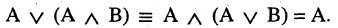
6.Закон идемпотентности
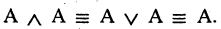
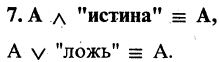
8.Закон противоречия
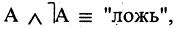
9.Закон исключения третьего
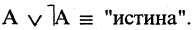
10.Закон двойного отрицания
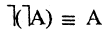
Пример:
Упростить выражение, используя тождественны преобразования
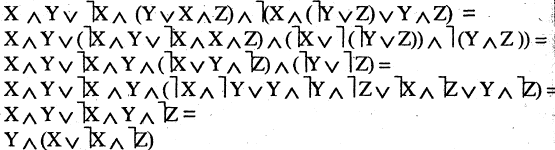
Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.
Основные методы доказательств
При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.
Формально каждая теорема может быть выражена в форме импликации 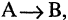 где посылка А называется условием теоремы, а следствие В — заключением. Теорема верна, если выражающая ее импликация тождественно истинна, т. е. является тавтологией. Тавтологии рассматривают как некоторые логически истинные схемы рассуждений. В этой связи тавтологии играют роль законов, определяющих построение правильных умозаключений. Существует бесконечное множество тавтологий. Некоторые из них легли в основу методов доказательства. Основные методы доказательств.
где посылка А называется условием теоремы, а следствие В — заключением. Теорема верна, если выражающая ее импликация тождественно истинна, т. е. является тавтологией. Тавтологии рассматривают как некоторые логически истинные схемы рассуждений. В этой связи тавтологии играют роль законов, определяющих построение правильных умозаключений. Существует бесконечное множество тавтологий. Некоторые из них легли в основу методов доказательства. Основные методы доказательств.
Метод цепочек импликаций
Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из  -импликаций, последним высказыванием в которой является заключение теоремы В, т. е.
-импликаций, последним высказыванием в которой является заключение теоремы В, т. е.
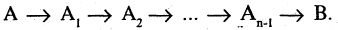
В основе этого метода лежит закон цепного высказывания или закон силлогизма 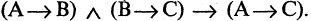
Метод от противного
Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:
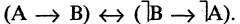
Метод необходимого и достаточного
Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:
а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);
б) если имеет место В, то имеет место и А (В достаточно для А).
Доказательство таким методом базируется на законе тавтологии:
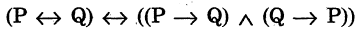
Алгебра предикатов
Предикатом 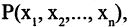 заданным на множествах
заданным на множествах 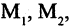
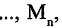
называется функция Р, отображающая их прямое произведение на двоичное множество, т. е. 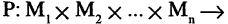
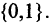 Множество М называется предметной областью предиката,
Множество М называется предметной областью предиката, 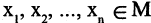 называются предметными переменными или термами. Предикат представляет собой логическую функцию, принимающую, как и булевская функция, значение «истина» или «ложь», когда ее предметные переменные принимают определенные значения.
называются предметными переменными или термами. Предикат представляет собой логическую функцию, принимающую, как и булевская функция, значение «истина» или «ложь», когда ее предметные переменные принимают определенные значения.
Рассмотрим примеры, 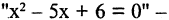 одноместный предикат на множестве комплексных чисел, при этом, например, если
одноместный предикат на множестве комплексных чисел, при этом, например, если 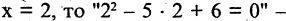 истинное высказывание, а
истинное высказывание, а
положив 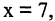 получим
получим 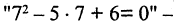 «ложь». Выражение «X — брат Y» — двухместный предикат, заданный на множестве людей. Здесь термы X и Y указывают места, на которые нужна поставить имена двух людей, чтобы получить правильно построенное высказывание. Очевидно, что X — лицо мужского пола, а Y может выбираться из всего множества людей.
«ложь». Выражение «X — брат Y» — двухместный предикат, заданный на множестве людей. Здесь термы X и Y указывают места, на которые нужна поставить имена двух людей, чтобы получить правильно построенное высказывание. Очевидно, что X — лицо мужского пола, а Y может выбираться из всего множества людей.
Всякий предикат  определяет отношение R, такое, что
определяет отношение R, такое, что 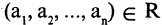 тогда и только тогда, когда
тогда и только тогда, когда 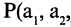
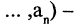 «истина». В этом случае говорят, что отношение R задается областью истинности предиката
«истина». В этом случае говорят, что отношение R задается областью истинности предиката  . Например, отношение
. Например, отношение 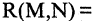 «расстояние на плоскости между точками
«расстояние на плоскости между точками 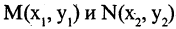 больше величины 1″ можно задать предикатом
больше величины 1″ можно задать предикатом 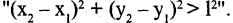
Если в  -местный предикат на место одного из термов подставить определенный элемент из соответствующего множества, то предикат станет
-местный предикат на место одного из термов подставить определенный элемент из соответствующего множества, то предикат станет 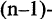 местным. Заменив все термы на конкретные значения из предметной области предиката, получим 0 — местный предикат, т. е. высказывание. Например, «Х- брат Y» — двухместный предикат, «X — брат Маши» — одноместный предикат, «Саша — брат Маши» — высказывание.
местным. Заменив все термы на конкретные значения из предметной области предиката, получим 0 — местный предикат, т. е. высказывание. Например, «Х- брат Y» — двухместный предикат, «X — брат Маши» — одноместный предикат, «Саша — брат Маши» — высказывание.
Логические операции над предикатами
Отрицание предиката
Пусть предикат  задан на множествах
задан на множествах 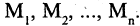 Предикат
Предикат  называется отрицанием предиката
называется отрицанием предиката  тогда и только тогда, если при одних и тех же кортежах
тогда и только тогда, если при одних и тех же кортежах 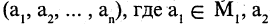
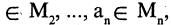 высказывание
высказывание 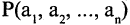 истинно, когда
истинно, когда 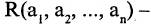 ложно и наоборот. Обозначение
ложно и наоборот. Обозначение
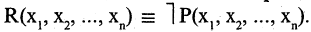
Например, предикат « — четное число» есть отрицание предиката «
— четное число» есть отрицание предиката « — нечетное число» на множестве целых чисел.
— нечетное число» на множестве целых чисел.
Конъюнкция предикатов
Пусть на множествах 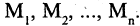 заданы два
заданы два  — местных предиката
— местных предиката 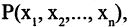 и
и  . Конъюнкцией этих предикатов называется предикат
. Конъюнкцией этих предикатов называется предикат
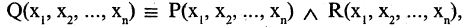
который истинен для одних и тех же кортежей только тогда, когда оба предиката — и  и
и 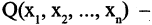 истинны.
истинны.
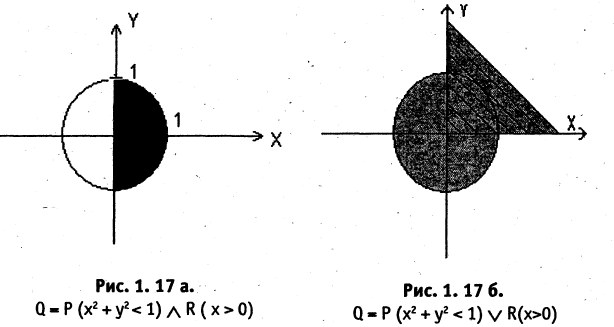
Например, конъюнкция предикатов 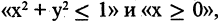 где
где 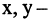 вещественные числа, определяет предикат «точки правой половины единичного круга» (см. рис. 1.17а).
вещественные числа, определяет предикат «точки правой половины единичного круга» (см. рис. 1.17а).
Дизъюнкция предикатов
Дизъюнкция предикатов  и
и  есть новый предикат
есть новый предикат  который имеет значение «ложь» для тех и только тех кортежей из
который имеет значение «ложь» для тех и только тех кортежей из 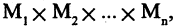 для которых оба предиката — и
для которых оба предиката — и  и
и  — имеют значение «ложь». На рис. 1.17 6 иллюстрируется дизъюнкция предиката
— имеют значение «ложь». На рис. 1.17 6 иллюстрируется дизъюнкция предиката 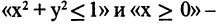 (заштрихованная область).
(заштрихованная область).
Импликация предикатов
Импликация предикатов  и
и  есть новый предикат
есть новый предикат 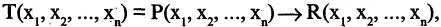 который имеет значение «ложь» для тех и только тех кортежей из
который имеет значение «ложь» для тех и только тех кортежей из 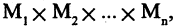 для которых предикат
для которых предикат  имеет значение «истина», а предикат
имеет значение «истина», а предикат  имеет значение «ложь».
имеет значение «ложь».
Например, импликация « делится на 4″ —» »
делится на 4″ —» »  делится на 2″ есть предикат: «если
делится на 2″ есть предикат: «если  делится на 4, то
делится на 4, то  делится на 2″.
делится на 2″.
Эквивалентность предикатов
Эквивалентность предикатов  и
и  есть новый предикат
есть новый предикат 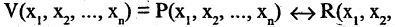
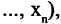 который имеет значение «истина» для тех и только тех кортежей из
который имеет значение «истина» для тех и только тех кортежей из  для которых предикат
для которых предикат  и предикат
и предикат  имеют одинаковые значение или оба «истина» или оба «ложь». Два предиката, заданные на одних и тех же множествах, называются равносильными, если при всех наборах входящих в них предметных переменных эти предикаты принимают одинаковые значения. Равносильность называют также логической эквивалентностью. Например, эквивалентность предикатов
имеют одинаковые значение или оба «истина» или оба «ложь». Два предиката, заданные на одних и тех же множествах, называются равносильными, если при всех наборах входящих в них предметных переменных эти предикаты принимают одинаковые значения. Равносильность называют также логической эквивалентностью. Например, эквивалентность предикатов 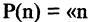 делится на 6» и
делится на 6» и 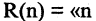 делится на 2 и
делится на 2 и  делится на 3» есть предикат
делится на 3» есть предикат 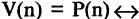
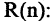 «если
«если  делится на 6, то
делится на 6, то  делится на 2 и на 3». Предикаты
делится на 2 и на 3». Предикаты 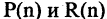 логически эквивалентны.
логически эквивалентны.
Наряду с логическими операциями важную роль играют операции, называемые кванторами. Квантор всеобщности есть операция, которая предикат  превращает в высказывание: «все
превращает в высказывание: «все  обладают свойством
обладают свойством  ». Знак квантора всеобщности
». Знак квантора всеобщности 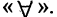 Он заменяет фразы: «для всех», «каждый», «любой» и т.п. Обозначение
Он заменяет фразы: «для всех», «каждый», «любой» и т.п. Обозначение  читается так: «для всех
читается так: «для всех  таких, что Р от
таких, что Р от  ». Например,
». Например, 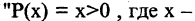 вещественное число», есть предикат «
вещественное число», есть предикат « — положительное число». Тогда
— положительное число». Тогда  есть высказывание «каждое число — положительно». Это ложное высказывание. Если же
есть высказывание «каждое число — положительно». Это ложное высказывание. Если же  — любое натуральное число
— любое натуральное число 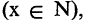 то
то  есть выражение: «каждое натуральное число — положительно» — истинное высказывание. Квантор всеобщности есть обобщение серии конъюнкций единичных высказываний. Пусть М — множество очков, которое может выпасть при бросании игральной кости, т. е.
есть выражение: «каждое натуральное число — положительно» — истинное высказывание. Квантор всеобщности есть обобщение серии конъюнкций единичных высказываний. Пусть М — множество очков, которое может выпасть при бросании игральной кости, т. е. 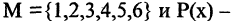 предикат: «при бросании игральной кости один раз выпадает
предикат: «при бросании игральной кости один раз выпадает  очков», где
очков», где 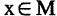 . Применение квантора всеобщности позволяет вместо сложного высказывания
. Применение квантора всеобщности позволяет вместо сложного высказывания 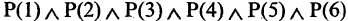 записать равносильное ему компактное высказывание
записать равносильное ему компактное высказывание 
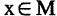 : «при бросании игральной кости один раз может выпасть любое из шести первых натуральных чисел».
: «при бросании игральной кости один раз может выпасть любое из шести первых натуральных чисел».
Квантор существования
Квантор существования есть операция, которая предикат  превращает в высказывание: «существует хотя бы один
превращает в высказывание: «существует хотя бы один 
из М, обладающий свойством  ». Знак квантора существования
». Знак квантора существования 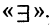 Он заменяет фразы: «существует хотя бы один», «найдется», «некоторый» и т.п. Обозначение
Он заменяет фразы: «существует хотя бы один», «найдется», «некоторый» и т.п. Обозначение  читается так: «существует хотя бы один
читается так: «существует хотя бы один  такой, что Р от
такой, что Р от  ». Например,
». Например,  — предикат: «
— предикат: « — студент», где
— студент», где  — элемент множества жителей Москвы. Тогда выражение
— элемент множества жителей Москвы. Тогда выражение  есть высказывание «хотя бы один житель Москвы является студентом». Квантор существования есть обобщение серии дизъюнкций единичных высказываний. Если задано множество
есть высказывание «хотя бы один житель Москвы является студентом». Квантор существования есть обобщение серии дизъюнкций единичных высказываний. Если задано множество 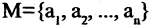 и на нем определен предикат
и на нем определен предикат 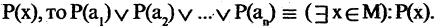
Кванторы обладают свойствами, являющимися аналогами законов де Моргана:
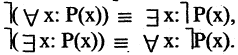
С помощью кванторов можно выражать ряд часто используемых на практике отношений между множествами. Например, высказывание «все объекты  из данного множества, обладающие свойством
из данного множества, обладающие свойством  , обладают также и свойством
, обладают также и свойством 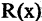 » формально можно записать —
» формально можно записать — 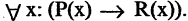
Переход от 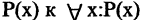 или
или  называется квантификацией или связыванием переменной
называется квантификацией или связыванием переменной  . Связанная переменная фактически не является переменной, т. е. переход от
. Связанная переменная фактически не является переменной, т. е. переход от 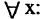
 или от
или от 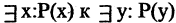 не меняет истинности выражений. Навешивание переменной на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных
не меняет истинности выражений. Навешивание переменной на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных
Рассмотрим пример. На множестве чисел задан двухместный предикат 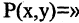 число
число  делится на число
делится на число  ». Связывая одну переменную, можно получить следующие одноместные предикаты:
». Связывая одну переменную, можно получить следующие одноместные предикаты:
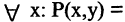 «каждое число делится на
«каждое число делится на  » — ложь;
» — ложь;
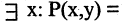 «существует число, которое делится на
«существует число, которое делится на  » — истина;
» — истина;
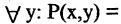 «число
«число  делится на любое число» — ложь;
делится на любое число» — ложь;
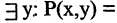 «существует число, на которое делится
«существует число, на которое делится  » — истина.
» — истина.
Связывая обе переменные данного предиката, получим высказывания:
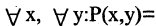 «каждое число делится на любое число» -ложное высказывание,
«каждое число делится на любое число» -ложное высказывание,
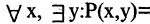 «существует число, на которое делится любое число» — истина, т.к. такое число есть 1,
«существует число, на которое делится любое число» — истина, т.к. такое число есть 1,
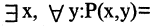 «существует число, которое делится на любое число» — ложное высказывание,
«существует число, которое делится на любое число» — ложное высказывание,
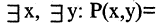 «существует число, которое делится на какое-нибудь число» — истинное высказывание.
«существует число, которое делится на какое-нибудь число» — истинное высказывание.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Каталог заданий.
Задания 3. Значение логического выражения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 3 № 10632 

i
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 2) И (X < 5).
Решение
·
Помощь
2
Тип 3 № 10633 

i
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 2) И (X чётное).
Решение
·
Помощь
3
Тип 3 № 10634 

i
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 7) И (X чётное).
Решение
·
Помощь
4
Тип 3 № 10635 

i
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 6) И (X нечётное).
Решение
·
Помощь
5
Тип 3 № 10636 

i
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 9) И НЕ (X нечётное).
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Скачать материал

Скачать материал




- Сейчас обучается 87 человек из 36 регионов


- Сейчас обучается 89 человек из 28 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Подготовка к ЕГЭ
Основы Логики -

2 слайд
Типы задач
Определить истинность высказывания
Определить равносильны ли выражения
Решить уравнение
Найти значение переменнойРешить задачу
Установить соответствие выражения таблице истинности -

3 слайд
Определить истинность высказывания
(№92 – №95)Для какого числа Х истинно высказывание:
№92
¬((Х>3)(X>4))?
1) 1
2) 2
3) 3
4) 4№94
((Х>3) V (X<3))(X<1)?
1) 1
2) 2
3) 3
4) 4
№93
((Х>2) V (X<2))(X>4)?
1) 1
2) 2
3) 3
4) 4№95
(Х>4) V ((X>1)(X>4))?
1) 1
2) 2
3) 3
4) 4 -

4 слайд
Решение: №92 – №95
№92 Способ 1
Поочередно подставляем значения X в высказывание:
1) ¬((1>3) (1>4)) = ¬(ложь ложь) = ¬(истина) = ложь;
2) ¬((2>3) (2>4)) = ¬(ложь ложь) = ¬(истина) = ложь;
3) ¬((3>3) (3>4)) = ¬(ложь ложь) = ¬(истина) = ложь;
4) ¬((4>3) (4>4)) = ¬(истина ложь) = ¬(ложь) = истина. Ответ: 4.
Способ 2
По условию ¬ ((Х>3) (Х>4)) = истина, поэтому ((Х>3) (Х>4)) = ложь.
Из определения импликации следует, что высказывание (Х>3) истинно, а (Х>4) — ложно. Этим условиям из целых чисел удовлетворяет только 4. Ответ: 4.
№93 Удобен способ 1
Поочередно подставляем значения X в высказывание:
1) ((1>2) V (1<2))(1>4) =(ложь V истина) ложь = истина ложь = ложь;
2) ((2>2) V (2<2))(2>4) =(ложь V ложь) ложь = ложь ложь = истина;
3) ((3>2) V (3<2))(3>4) =(истина V ложь) ложь = истина ложь = ложь;
4) ((4>2) V (4<2))(4>4) =(истина V ложь) ложь = истина ложь = ложь; Ответ: 2.
№94 Удобен способ 1
Поочередно подставляем значения X в высказывание:
1) ((1>3) V (1<3))(1<1)=(ложь V истина) ложь = истина ложь = ложь;
2) ((2>3) V (2<3))(2<1)=(ложь V истина) ложь = истина ложь = ложь;
3) ((3>3) V (3<3))(3<1)=(ложь V ложь) ложь = ложь ложь = истина;
4) ((4>3) V (4<3))(4<1)=(истина V ложь) ложь = истина ложь = ложь; Ответ: 3.
№95 Удобен способ 1
Поочередно подставляем значения X в высказывание:
1) (1>4) V ((1>1)(1>4)) = ложь V (ложь ложь) = ложь V истина = истина;
2) (2>4) V ((2>1)(2>4)) = ложь V (истина ложь) = ложь V ложь = ложь;
3) (3>4) V ((3>1)(3>4)) = ложь V (истина ложь) = ложь V ложь = ложь;
4) (4>4) V ((4>1)(4>4)) = ложь V (истина ложь) = ложь V ложь = ложь; Ответ: 1.
№92
¬((Х>3)(X>4))?
1) 1
2) 2
3) 3
4) 4№93
((Х>2) V (X<2))(X>4)?
1) 1
2) 2
3) 3
4) 4№94
((Х>3) V (X<3))(X<1)?
1) 1
2) 2
3) 3
4) 4
№95
(Х>4) V ((X>1)(X>4))?
1) 1
2) 2
3) 3
4) 4 -

5 слайд
(№96 – №97)Для какого слова истинно высказывание:
№96
¬(Первая буква слова согласная (Вторая буква слова гласная V Последняя буква слова гласная))?1) ГОРЕ
2) ПРИВЕТ
3) КРЕСЛО
4) ЗАКОН№97
(Первая буква слова гласная V Пятая буква слова согласная) Вторая буква слова гласная?1) АРБУЗ
2) ОТВЕТ
3) КРЕСЛО
4) ПРИВАЛ -

6 слайд
Решение: №96, 97
№96
¬(Первая буква слова согласная(Вторая буква слова гласная V Последняя буква слова гласная))?1) ГОРЕ ; 2) ПРИВЕТ; 3) КРЕСЛО; 4) ЗАКОН
1) ГОРЕ: ¬(истина (истина V истина)) = ¬(истина истина) = ¬(истина)= ложь;
2) ПРИВЕТ: ¬(истина (ложь V ложь)) = ¬ (истина ложь) = ¬ (ложь)= истина;
3) КРЕСЛО: ¬ (истина (ложь V истина)) = ¬(истина истина) = ¬(истина)= ложь;
4) ЗАКОН: ¬(истина (истина V ложь)) = ¬(истина истина) = ¬(истина)= ложь;
Ответ: 2.
№97
(Первая буква слова гласная V Пятая буква слова согласная) Вторая буква слова гласная?1) АРБУЗ; 2) ОТВЕТ; 3) КРЕСЛО; 4) ПРИВАЛ
1) АРБУЗ: (истина V истина) ложь = истина ложь = ложь;
2) ОТВЕТ: (истина V истина) ложь = истина ложь = ложь;
3) КРЕСЛО: (ложь V истина) ложь = истина ложь = ложь;
4) ПРИВАЛ: (ложь V ложь) ложь = ложь ложь = истина;
Ответ: 4. -

7 слайд
Найти значение переменной
№ 103
Каково наибольшее целое число Х, при котором истинно высказывание: (90< Х *Х) (Х < (Х-1)) ?№ 104
А, В, С – целые числа, для которых истинно высказывание:¬(А=В)&(( А>В) (В >С)) &((В >А) (С >В))
Чему равно В, если А=45, С=43?№ 105
А, В, С – целые числа, для которых истинно высказывание:¬(А=В)&((В<А) (2С >А))&((А < В) (А > 2С))
Чему равно А, если С=8,В=18?№ 106
Каково наибольшее целое число Х, при котором истинно высказывание: (50< Х *Х) (50>(Х+1)*(Х+1)) ?№ 107
Укажите значения логических переменных K,L,M,N, при которых логическое выражение:
(K V M)(M V ¬L V N) ложно.
Ответ запишите в виде строки из четырех символов: значений переменных K,L,M,N (в указанном порядке). Так, например, строка 0101 соответствует тому, что K=0,L=1,M=0,N=1.№ 109
Дано логическое выражение: (M V ¬L V ¬ N) (K V ¬L V ¬ N ).
Укажите значения логических переменных K,L,M,N, при которых логическое выражение ложно.
Ответ запишите в виде строки из четырех символов: значений переменных K,L,M,N (в указанном порядке). Так, например, строка 0101 соответствует тому, что K=0,L=1,M=0,N=1. -

8 слайд
№ 103
Каково наибольшее целое число Х, при котором истинно высказывание:
(90< Х *Х) (Х < (Х-1)) ?Решение: № 103 – 109
(90< Х *Х) (Х < (Х-1)) = истина
(90< Х *Х) (Х < Х-1) = истина
(90< Х *Х) (0 < -1) = истина
Так как (0 < -1)= ложь, то (90< Х *Х) = ложь, значит (90>= Х *Х), тогда Х=1,2,3,4,5,6,7,8,9. По условию Х – наибольшее целое, значит Х=9.
Ответ: 9.
№ 106
Каково наибольшее целое число Х, при котором истинно высказывание:
(50< Х *Х) (50>(Х+1)*(Х+1)) ?Найдем значения Х, при которых высказывание ложно:
(50< Х *Х) (50>(Х+1)*(Х+1)) = ложь (только в одном случае)
(50< Х *Х) = истина, а (50>(Х+1)*(Х+1)) = ложь
(50< Х *Х) = истина и (50 < = (Х+1)*(Х+1)) = истина
Эти два неравенства выполняются одновременно при Х >= 8.
Итак, (50< Х *Х) (50>(Х+1)*(Х+1)) = ложь при Х >= 8, значит
(50< Х *Х) (50>(Х+1)*(Х+1)) = истина при Х=1,2,3,4,5,6,7.
По условию Х – наибольшее целое, значит Х=7.
Ответ: 7. -

9 слайд
Решение: № 103 – 109
№ 104А, В, С – целые числа, для которых истинно высказывание: ¬(А=В)&(( А>В) (В >С)) &((В >А) (С >В))
Чему равно В, если А=45, С=43?А < > В = истина
(( А>В) (В >С)) = истина
((В >А) (С >В)) = истина учтем, что А В = ¬А V ВА < > В = истина
( А <= В) V (В >С) = истина
(В <= А) V (С >В) = истинаВ < > 45 = истина
(45 < В) V (В > 43) = истина
(В < 45) V (43 > В) = истинаВведем обозначения:
В < > 45 =М, (45 < В) = Т, (В > 43) = Н
М = истина
Т V Н = истина
¬ Т V ¬ Н = истина
Составим таблицу истинности
Из таблицы видно, что возможны 2 случая:
В < > 45 = истина, (45 < В) = ложь, (В > 43) = истина
В < > 45 = истина, (В < 45) = истина, (В > 43) = истина, тогда В= 442) В < > 45 = истина, (45 < В) = истина, (В > 43) = ложь
В < > 45 = истина, (45 < В) = истина, (43 > В) = истина, а это невозможно.
Ответ: 44. -

10 слайд
№ 105
А, В, С – целые числа, для которых истинно высказывание:
¬(А=В)&((В<А) (2С >А))&((А < В) (А > 2С))
Чему равно А, если С=8,В=18?
Решение: № 103 – 109
А < > В = истина
((В < А ) (2С > А )) = истина
((А < В ) (А > 2С )) = истина учтем, что А В = ¬А V ВА < > В = истина
(А <= В ) V (2С > А ) = истина
(А >= В) V А > 2С ) = истинаА < > 18 = истина
(18 > А ) V (16 > А) = истина
(18 < А ) V (16 < А) = истинаВведем обозначения:
А < > 18 =М, (18 > А ) = Т, (16 > А)= Н
М = истина
Т V Н = истина
¬ Т V ¬ Н = истина
Составим таблицу истинности
Из таблицы видно, что возможны 2 случая:
А < > 18 = истина, (18 > А) = ложь, (16 > А) = истина
А < > 18 = истина, (18 < А) = истина, (16 > А) = истина, а это невозможно.
2) А < > 18 = истина, (18 > А) = истина,(16 > А) = ложь
А < > 18 = истина, (18 > А) = истина, (16 < А) = истина, тогда А =17. Ответ: 17. -

11 слайд
Решение: № 103 – 109
№ 107
Укажите значения логических переменных K,L,M,N, при которых логическое выражение:
(K V M)(M V ¬L V N) ложно.
Ответ запишите в виде строки из четырех символов: значений переменных K,L,M,N (в указанном порядке). Так, например, строка 0101 соответствует тому, что K=0,L=1,M=0,N=1.
Ответ: 1100. -

12 слайд
Решение: № 103 – 109
№ 109
Дано логическое выражение: (M V ¬L V ¬ N) (K V ¬L V ¬ N ).
Укажите значения логических переменных K,L,M,N, при которых логическое выражение ложно.
Ответ запишите в виде строки из четырех символов: значений переменных K,L,M,N (в указанном порядке). Так, например, строка 0101 соответствует тому, что K=0,L=1,M=0,N=1.
Ответ: 0111. -

13 слайд
Решить уравнение
№ 108
Сколько различных решений имеет уравнение: ((K V L) & (M V N)) = 1,
где K,L,M,N – логические переменные?В ответе не нужно перечислять все различные наборы значений K,L,M,N, при которых выполнено данное равенство. В качестве ответа вам нужно указать количество таких наборов.
№ 110
Сколько различных решений имеет уравнение: ((K V L) (L & M & N)) = 0,
где K,L,M,N – логические переменные?В ответе не нужно перечислять все различные наборы значений K,L,M,N, при которых выполнено данное равенство. В качестве ответа вам нужно указать количество таких наборов.
-

14 слайд
Решение: № 108
№ 108
Сколько различных решений имеет уравнение: ((K V L) & (M V N)) = 1,
где K,L,M,N – логические переменные?В ответе не нужно перечислять все различные наборы значений K,L,M,N, при которых выполнено данное равенство. В качестве ответа вам нужно указать количество таких наборов.
Ответ: 9. -

15 слайд
Решение: № 110
№ 110
Сколько различных решений имеет уравнение: ((K V L) (L & M & N)) = 0,
где K,L,M,N – логические переменные?В ответе не нужно перечислять все различные наборы значений K,L,M,N, при которых выполнено данное равенство. В качестве ответа вам нужно указать количество таких наборов.
Ответ: 10. -

16 слайд
Определить равносильны ли выражения
(№98 – №102)Какое логическое выражение равносильно выражению…№98
¬(А&В) & ¬ С?1) ¬А V В V ¬С
2) (¬А V ¬ В) & ¬С
3) (¬А V ¬ В) & С
4) ¬А & ¬ В & ¬С№99
¬(¬А&В) V ¬ С?1) ¬А V В V ¬С
2) ¬А V ¬ В V ¬С
3) А V ¬ В V ¬С
4) А V В V ¬С№100
¬А V ¬ (В V С)?1) ¬А V ¬ В V ¬С
2) А V (В & С)
3) А V В V С
4) ¬ А V (¬В & ¬С )№101
¬(¬ А V В) V ¬ С?1) (А & ¬В) V ¬С
2) А V ¬ В V ¬С
3) ¬А V В V ¬С
4) (¬А & В) V ¬С№102
¬( А V ¬ В V С)?1) ¬А V В V ¬С
2) А & ¬ В & С
3) ¬А V ¬ В V ¬С
4) ¬А & В & ¬С -

17 слайд
Решение: №98 – 97
№98
¬(А&В) & ¬ С?1) ¬А V В V ¬С
2) (¬А V ¬ В) & ¬С
3) (¬А V ¬ В) & С
4) ¬А & ¬ В & ¬С
Ответ: 2.
Способ 1: Составить таблицу истинности
Способ 2: Преобразовать с помощью законов логики¬(А&В) & ¬ С = (¬А V¬ В) & ¬ С .
Ответ: 2.
-

18 слайд
№99
¬(¬А&В) V ¬ С?1) ¬А V В V ¬С
2) ¬А V ¬ В V ¬С
3) А V ¬ В V ¬С
4) А V В V ¬СРешение: №99 – 102
¬(¬А&В) V ¬ С = (¬ (¬ А ) V ¬ В) V ¬ С= А V ¬ В V ¬ СОтвет: 3.
№100
¬А V ¬ (В V С)?1) ¬А V ¬ В V ¬С
2) А V (В & С)
3) А V В V С
4) ¬ А V (¬В & ¬С )¬А V ¬(В V С)= ¬ А V (¬ В &¬ С)
Ответ: 4.
№101
¬(¬ А V В) V ¬ С?1) (А & ¬В) V ¬С
2) А V ¬ В V ¬С
3) ¬А V В V ¬С
4) (¬А & В) V ¬С¬(¬А V В) V ¬ С = (¬ (¬ А ) & ¬ В) V ¬ С= (А & ¬ В) V ¬ С
Ответ: 1.
№102
¬( А V ¬ В V С)?1) ¬А V В V ¬С
2) А & ¬ В & С
3) ¬А V ¬ В V ¬С
4) ¬А & В & ¬С¬(А V ¬ В V С) = (¬ А ) & ¬ (¬ В) & ¬ С= ¬ А & В & ¬ С
Ответ: 4.
-

19 слайд
Решить задачу
№ 111В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.
Один считает, что первой будет Наташа, а Маша будет второй. Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место. Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на чемпионате заняли Наташа, Маша, Люда и Рита?
Н – 1, М – 2
Л – 2, Р – 4
Р – 3, Н – 2
Только одна часть каждого высказывания истинна
Пусть
Н – 1= ложь, то М – 2= истина, тогда
Л – 2= ложь, а Р – 4= истина, значит
Р – 3= ложь, а Н – 2= истина
Получаем противоречие
Пусть
Н – 1= истина, то М – 2 = ложь, тогда
Л – 2= истина, а Р – 4=ложь, значит
Р – 3=истина, а Н – 2= ложь
Противоречия не получаем
Ответ: 1,4,2,3. -

20 слайд
№ 112
Восемь школьников, остававшихся в классе на перемене, были вызваны к директору. Один из них разбил окно в кабинете. На вопрос директора, кто это сделал, были получены следующие ответы:
Егор: «Разбил Андрей!». Света: «Вика разбила».
Оля: «Разбила Света». Миша: «Это кто-то с улицы!»
Надя: «Да, Оля права…» Коля: «Это либо Вика, либо Света!»
Андрей: «Ни Вика, ни Света этого не делали». Вика: «Андрей не бил!»
Кто разбил окно, если известно, что из этих восьми высказываний истинно ровно три?
Ответ запишите в виде первой буквы имени.Имеем высказывания:
А
В
С
Кто – то с улицы
С
В V С
¬ В & ¬ С = ¬(В V С)
¬ А
Истинно ровно три
Пусть
А= истина, то
В= ложь
С= ложь
Кто – то с улицы = ложь
С= ложь
В V С= ложь
¬ В & ¬ С = ¬(В V С)= истина
¬ А= ложь
Получили, что истинно только 2 высказывания, что противоречит условиюПусть
А = ложь, а
В= истина, то
С = ложь,
Кто – то с улицы = ложь
С = ложь
В V С = истина
¬ В & ¬ С = ¬(В V С)= ложь
¬ А= истина
Получили, что истинно 3 высказывания, значит, окно разбила Вика.Ответ: В.
Пусть
А = ложь,
В= ложь, а
С= истина,
Кто – то с улицы = ложь
С = истина,
В V С = истина
¬ В & ¬ С = ¬(В V С)= ложь
¬ А= истина
Получили, что истинно 4 высказывания, что противоречит условию. -

21 слайд
№ 113
Восемь школьников, остававшихся в классе на перемене, были вызваны к директору. Один из них разбил окно в кабинете. На вопрос директора, кто это сделал, были получены следующие ответы:
Соня:«Это сделал Володя».
Миша:«Это ложь!»
Володя:«Я разбил!»
Аня:«Это я разбила!»
Оля:«Аня не разбивала!»
Рома:«Разбила либо Соня, либо Оля…»
Коля:«Девочки этого не делали».
Толя:«Коля разбил!»
Кто разбил окно, если известно, что из этих восьми высказываний истинно только два?
Ответ запишите в виде первой буквы имени.Имеем высказывания:
В
¬ В
В
А
¬ А
С V О
¬ А & ¬ С & ¬ О
К
Истинно ровно два
Пусть
В = истина
¬ В = ложь
В = истина
А = ложь
¬ А = истина
С V О = ложь
¬ А & ¬ С & ¬ О = истина
К = ложь
Противоречие с условием, что истинно ровно два.
Пусть
В = ложь
¬ В = истина
А = истина
¬ А = ложь
С V О = ложь
¬ А & ¬ С & ¬ О = К V В = ложь
К = ложь
Противоречие с условием не получили, значит наше предположение верно.Пусть
В = ложь
¬ В = истина
А = ложь
¬ А = истина
С V О = ложь
¬ А & ¬ С & ¬ О = К V В = истина
К = истина
Противоречие с условием, что истинно ровно два.
Пусть
В = ложь
¬ В = истина
А = ложь
¬ А = истина
С V О= истина
¬ А & ¬ С & ¬ О = К V В = ложь
К = ложь
Противоречие с условием, что истинно ровно два.
Ответ: А. -

22 слайд
№ 114
Три школьника, Миша (М), Коля (К) и Сергей (С), остававшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:
Миша: «Я не бил окно, и Коля тоже…»
Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!»
Сергей: «Я не делал этого, стекло разбил Миша».
Стало известно, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил. Зная это директор смог докопаться до истины.
Кто разбил стекло в классе? В ответе запишите только первую букву имени.
Имеем высказывания:
¬ М , ¬ К
¬ М, С
¬ С , М
Один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил.
Пусть
¬ М = истина , ¬ К= истина, тогда
¬ М = истина, С = ложь
¬ С = истина , М = ложьПротиворечие с условием, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил.
Пусть
¬ М = истина, ¬ К= истина, тогда
¬ М = истина, С = истина,
¬ С = ложь, М = ложьПротиворечие с условием, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил.
Ответ: М.
Пусть
¬ М = ложь, ¬ К= истина, тогда
¬ М = ложь, С = ложь
¬ С = истина , М = истинаПротиворечие с условием, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил, не получаем, значит окно разбил Миша.
-

23 слайд
Установить соответствие выражения таблице истинности
(№115 – №118)Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?
№1151)¬X V Y V ¬ Z
2) X & ¬ Y & ¬ Z
3) ¬X & Y & Z
4) X V ¬ Y V Z
№1161)¬X V Y V ¬ Z
2) X & ¬ Y & ¬ Z
3) ¬X & Y & Z
4) X V ¬ Y V Z
№1171)¬X V Y V ¬ Z
2) X & Y & ¬ Z
3) ¬X & ¬ Y & Z
4) X V ¬ Y V Z
№1181)¬X V ¬ Y V ¬ Z
2) X & ¬ Y & ¬ Z
3) X & Y & Z
4) X V Y V Z -

24 слайд
Решение (№115 – №118)
№1151)¬X V Y V ¬ Z
2) X & ¬ Y & ¬ Z
3) ¬X & Y & Z
4) X V ¬ Y V Z
Ответ: 3.
№1161)¬X V Y V ¬ Z
2) X & ¬ Y & ¬ Z
3) ¬X & Y & Z
4) X V ¬ Y V Z
Ответ: 4. -

25 слайд
Решение (№115 – №118)
№117
1)¬X V Y V ¬ Z
2) X & Y & ¬ Z
3) ¬X & ¬ Y & Z
4) X V ¬ Y V Z
Ответ: 2.
№118
1)¬X V ¬ Y V ¬ Z
2) X & ¬ Y & ¬ Z
3) X & Y & Z
4) X V Y V Z
Ответ: 4.
Краткое описание документа:
Разбор задач по ЕГЭ. Из раздела алгебры логики..
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 255 934 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 18.01.2015
- 4488
- 35
- 18.01.2015
- 646
- 0
- 18.01.2015
- 2130
- 1
- 18.01.2015
- 1906
- 16
- 18.01.2015
- 1122
- 20
- 18.01.2015
- 1456
- 0
- 18.01.2015
- 535
- 0
Задание №3. Определение истинности составного высказывания.
Уровень сложности: базовый; макс. балл за задание: 1; примерное время выполнения: 3 минуты.
Знать: логические значения, операции, выражения.
Уметь: определять истинность составного высказывания.
Пример задания.
Напишите наименьшее число x, для которого истинно высказывание:
(x > 16) И НЕ (x нечётное).
Разбор задания.
Мы имеем составное высказывания из двух простых связанных между собой конъюнкцией (операцией логического умножения). Конъюнкция истинна только в одном случае, когда оба простых высказывания истинны. Следовательно требуемое число должно быть больше 16 и не нечётное (т.е. чётное). Наименьшее такое число – 18.
Ответ: 18.
Пример задания.
Напишите наибольшее число x, для которого ложно высказывание:
НЕ ((x < 54) И (x простое число)) ИЛИ НЕ (x <= 16)
Разбор задания.
Это задание гораздо сложнее предыдущего. Для решения таких логических примеров не мешало бы знать законы алгебры логики для того, чтобы можно было упростить выражение.
Сначала “избавимся” от отрицания:
(x >= 54) ИЛИ (x не простое число) ИЛИ (x > 16)
В данном примере трудно сообразить, для какого наибольшего числа x это высказывание будет ложно. Но можно ко всему выражению применить “отрицание” и найти для какого наибольшего числа x это высказывание будет истинным!
(x < 54) И (x простое число) И (x <= 16)
Глядя на это выражение можно понять, что наибольшее простое число х , которое меньше 54, меньше либо равно 16 – это число 13, что и будет ответом к нашему заданию.
Ответ: 13.
Проводя анализ результатов пробного ОГЭ по информатике в нашем районе и увидев процент решаемости заданий на логику (задание №3), я пришел к такому выводу, что просто необходимо разобрать побольше типичных задач. Предлагаю Вам решить некоторые такие задания.
Задание №1. Напишите наибольшее число x, для которого ложно высказывание:
(x > 72) ИЛИ НЕ (x чётное).
Задание №2. Напишите наибольшее число x, для которого ложно высказывание:
НЕ (x ≤ 26) ИЛИ (x нечётное).
Задание №3. Напишите наименьшее число x, для которого истинно высказывание:
НЕ (x ≤ 25) И (x кратное 5) И (x ≠ 30).
Задание №4. Напишите наибольшее число x, для которого ложно высказывание:
(x ≥ 90) ИЛИ НЕ (x кратное 3) ИЛИ (x ≠ 87).
Задание №5. Напишите наибольшее число x, для которого истинно высказывание:
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) И НЕ (x > 25).
Задание №6. Напишите наименьшее число x, для которого ложно высказывание:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) ИЛИ НЕ (x > 125).
Задание №7. Напишите наибольшее число x, для которого ложно высказывание:
НЕ ((x < 54) И (x простое число)) ИЛИ НЕ (x ≤ 16).
Дальше разберём каждое задание по отдельности, и вы сможете сравнить свои ответы с правильными.
Задание №1. Напишите наибольшее число x, для которого ложно высказывание:
(x > 72) ИЛИ НЕ (x чётное).
Разбор задания №1. Для успешного решения заданий такого типа необходимо знать, что такое конъюнкция, дизъюнкция, отрицание и законы Де Моргана. Также, необходимо для конъюнкции и дизъюнкции уметь строить таблицы истинности.
Итак, перед нами сложное высказывание, состоящее из двух простых:
(x > 72) ИЛИ НЕ (x чётное).
Для удобства я выделил высказывания разным цветом. Необходимо помнить, что связками между простыми высказываниями будут конъюнкция (логическое И), дизъюнкция (логическое ИЛИ), а также и другие логические операции, но их изучают в старших классах и в заданиях ОГЭ они не встречаются.
Когда же это сложное высказывание будет ложным? А ложным оно будет тогда и только тогда, когда оба простых высказывания будут ложными. Следовательно (x > 72) должно давать ложь и НЕ (x чётное) тоже должно давать ложь.
Теперь всё делаем по порядку.
- Все числа x, которые меньше или равны 72, нам подойдут. Из условия знаем, что число должно быть наибольшим. Следовательно, возьмём число 72. Проверяем условие 72 > 72 – нет, это ложь.
- Разберём второе высказывание НЕ (x чётное). Сначала «избавимся» от отрицания. НЕ (x чётное) – это тоже самое, что (x нечётное). При проверке первого высказывания мы выяснили, что число не может быть больше 72. Подставим его во вторую часть высказывания. (72 нечётное) – нет, это ложь, следовательно, нам вполне подходит.
Ответ: 72.
Задание №2. Напишите наибольшее число x, для которого ложно высказывание:
НЕ (x ≤ 26) ИЛИ (x нечётное).
Разбор задания №2. По аналогии с первым заданием выполняем и это. Мы имеем сложное высказывание. Связаны высказывания между собой дизъюнкцией, а дизъюнкция ложна тогда и только тогда, когда ложны все её составляющие!
- Разберём первую часть – НЕ (x ≤ 26). По законам Де Моргана «избавляемся» от отрицания. НЕ (x ≤ 26) = (x > 26). Чтобы эта часть высказывания была ложной нам подойдут все числа, которые меньше, чем 26 и само число 26, т.к. (26 > 26) – это ложь.
- По условию нам нужно наибольшее число x. Подставим во вторую часть высказывания (x нечётное) число 26. (26 нечётное) – нет, это ложь. Нам подходит, следовательно, оно и будет ответом.
Ответ: 26.
Это были задачи попроще. Теперь разберём немного потруднее.
Задание №3. Напишите наименьшее число x, для которого истинно высказывание:
НЕ (x ≤ 25) И (x кратное 5) И (x ≠ 30).
Разбор задания №3. Мы имеем сложное высказывание, но только оно состоит из трёх простых высказываний, связанных между собой конъюнкцией (логической операцией И). Конъюнкция истинна тогда и только тогда, когда все части составного высказывания будут истинны!
- Рассмотрим первую часть НЕ (x ≤ 25). По закону Де Моргана «избавимся» от отрицания. НЕ (x ≤ 25) = (x > 25). Нам подойдёт любое число больше, чем 25, т.е. от 26 до бесконечности. Из условия мы знаем, что нам нужно наименьшее из таких чисел – это 26.
- Рассмотрим вторую часть составного высказывания – (x кратное 5). Число 26 нам не подходит, т.к. оно не кратно пяти. Все числа кратные пяти заканчиваются на пять или на ноль. Нам бы подошло число 30. Оно больше, чем 25 и оно кратно 5.
- Рассмотрим третью часть составного высказывания, она то и даст верный ответ на нашу задачу. Число x не должно равняться 30, следовательно, наш x – это число больше 25, кратное 5, но не равняется 30. Такое ближайшее число – это 35. Оно полностью подходит всем условиям и является ответом к нашему заданию.
Ответ: 35.
Задание №4. Напишите наибольшее число x, для которого ложно высказывание:
(x ≥ 90) ИЛИ НЕ (x кратное 3) ИЛИ (x ≠ 87).
Разбор задания №4. Как и в предыдущем задании, мы имеем сложное, которое состоит из трёх простых, высказывание, только все они связаны дизъюнкцией (логической операцией ИЛИ). А ложно составное высказывание будет ложно только в том случае, когда будут ложны все его части!
- Рассмотрим первую часть (x ≥ 90). Она будет ложной в том случае, когда x будет строго меньше 90, т.е. от 89 до минус бесконечность. Так как от нас требуется найти наибольшее из этих чисел, то пока остановимся на числе 89.
- Далее рассмотрим второе высказывание НЕ (x кратное 3). Если «избавится» от отрицания, то мы имеем выражение (x не кратно 3). Это высказывание будет ложным в тех случаях, когда число на три делится! Ближайшее наибольшее число из диапазона от минус бесконечность до 89 будет число 87. Остановимся пока на нём и перейдем к третьему высказыванию.
- Из высказывания (x ≠ 87) становится ясным, что число 87 нам вполне подходит, т.к. выражение (87 ≠ 87) ложно.
Ответ: 87.
Задание №5. Напишите наибольшее число x, для которого истинно высказывание:
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) И НЕ (x > 25).
Разбор задания №5. Обратите внимание, что всё наше сложное высказывание включает в себя одно сложное высказывание (выделено красными скобками) НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) и одно простое высказывание НЕ (x > 25), это всё связано конъюнкцией (логической операцией И). Всё выражение будет истинным только в том случае, когда обе его части будут истинны!
- В данном примере сразу применим закон Де Моргана. Когда мы отрицаем всё то, что заключено в скобках, то все знаки внутри скобок «переворачиваем».
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) = ((x < 23) И (x нечётное))
Следовательно, наше число x должно быть меньше, чем 23 и нечётное. Подойдёт число 21. Проверим его в следующей части выражения.
- Имеем высказывание НЕ (x > 25). «Избавимся» от отрицания и подставим в него для проверки число 21. Проверяем: (21 ≤ 25) – это истина.
Ответ: 21.
Задание №6. Напишите наименьшее число x, для которого ложно высказывание:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) ИЛИ НЕ (x > 125).
Разбор задания №6. По структуре задание напоминает предыдущее. Оно также включает в себя одно сложное высказывание (выделено красными скобками) НЕ ((x ≥ 100) И НЕ (x кратно 4)) и одно простое высказывание НЕ (x > 125), это всё связано дизъюнкцией (логической операцией ИЛИ). И это всё должно быть ложно.
- «Избавляемся» от отрицания – все знаки внутри скобок «переворачиваем»:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) = ((x < 100) ИЛИ (x кратно 4))
Мы имеем вот такое выражение ((x < 100) ИЛИ (x кратно 4)), осталось понять, когда же оно ложно. А ложно оно будет тогда и только тогда, когда ложны его обе части, т.е. x – это число от 100 до плюс бесконечности и оно не должно делиться нацело на 4. Такое наименьшее число – 101.
- Подставим для проверки это число во вторую часть выражения. НЕ (101 > 125). К сожалению, это выражение истинно, а из условия мы знаем, что всё выражение должно быть ложно. Значит, число x должно быть строго больше 125 и не должно делится на 4. Такое минимальное число – 126.
Ответ: 126.
