Что такое возрастание функции
В начале прочитаем определение возрастания функции.
Запомните!
Функция « y(x) » называется возрастающей на некотором промежутке, если
для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких, что « x2 > x1 »
выполняется неравенство
« y( x2 ) > y( x1 )».
Определение сложно понять без наглядного примера.
Поэтому сразу перейдём к разбору задачи на возрастание функции.
По-другому можно сказать, что, если каждому бóльшему значению « x »
соответствует бóльшее значение « y », значит,
функция « y(x) » возрастает.
|
x2 > x1 |
Обязательное условие возрастания функции |
Давайте разберем определение возрастания функции на конкретном примере.
Разбор примера
Возрастающей или убывающей является функция « y = 9x − 4 » ?
Для начала определим
область определения функции
« y = 9x − 4 ».
y = 9x − 4
D(y): x ∈ R ,
то есть « x » —
любое действительное число.
Построим график функции
« y = 9x − 4 ».
Так как функция
« y = 9x − 4 »
линейная, ее график — прямая.
Используем правила построения графика линейной функции. Нам достаточно найти две точки, чтобы построить ее график.
Область определения функции
« y = 9x − 4 » — все действительные числа,
поэтому можно подставить любое число вместо « x » и вычислить « y » по
формуле функции
« y = 9x − 4 ». Например, возьмем
« x = 0 ».
x = 0
y(x) = 9x − 4
y(0) = 9 · 0 − 4 = −4
Для второй точки возьмем « x = 1 ».
x = 1
y(x) = 9x − 4
y(1) = 9 · 1 − 4 = 5
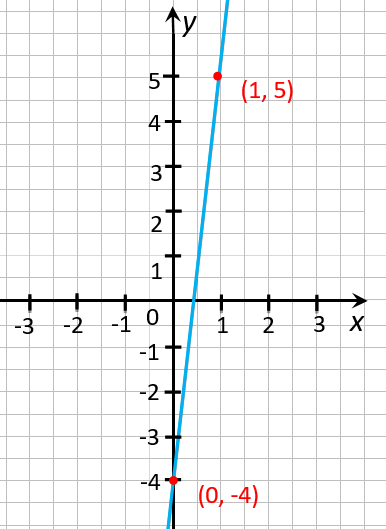
Отметим две полученные
точки «(0; −4)» и «(1; 5)» на
координатной плоскости
и проведем через них прямую.
Докажем, что функция
« y = 9x − 4 » возрастает на всей своей области определения двумя способами: по ее графику и
аналитически
(по ее формуле).
Как определить по графику, что функция возрастает
По определению возрастания функции мы знаем, что
если « x » увеличивается,
то « y » тоже должен увеличиваться.
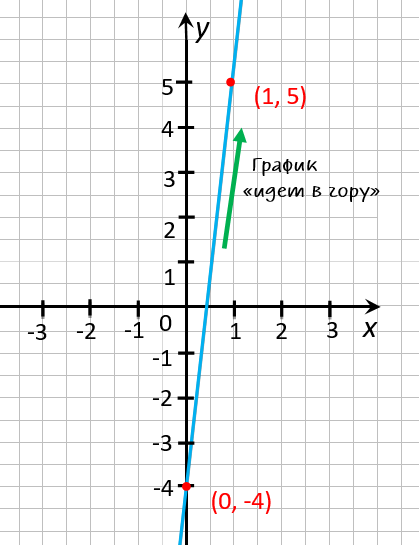
На рисунке ниже видно, что график функции « y = 9x − 4 »
«идет в гору». Другими словами, при увеличении « x »
↑ растет
значение « y » ↑.
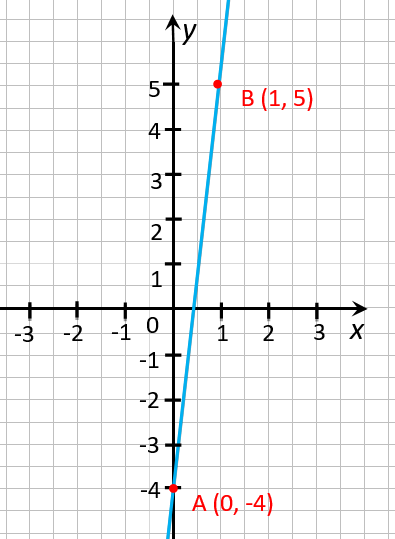
В этом можно убедиться, если взять две любые точки на графике. Например, точки, по
которым мы построили график функции. Назовем эти точки:
« (·)A » и « (·)B ».
У первой точки « (·)A »
координаты:
x1 = 0 ; y1 = − 4
У второй точки « (·)B » координаты:
x2 = 1 ; y2 = 5
На примере точек « (·)A » и « (·)B » видно, что
при увеличении
« x ↑ ( x2 > x1 )»
растет
« y ↑ ( y2 > y1 ) ».
Поэтому график зрительно «идет в гору».
Как по формуле доказать, что функция возрастает
Вернёмся к нашей функции
« y = 9x − 4 ».
По графику мы поняли, что
функция « y = 9x − 4 » возрастает,
так как ее график «идет в гору».
Но как доказать по формуле, что функция
возрастает на всей своей области определения?
Запомните!
Функция возрастает на всей области определения, когда при
« x2 > x1 »
выполняется условие
« y( x2 ) > y( x1 ) ».
Формулировка выше не самая простая для понимания. Давайте разберем ее на практике.
По определению возрастания функции нам нужно доказать, что при
« x2 > x1 » увеличивается значение функции
« y( x2 ) > y( x1 ) ».
Но как нам найти значения функции
« y( x1 )» и
«y( x2 ) »?
Для нахождения « y( x1 )» и
«y( x2 ) »
достаточно подставить « x1 » и
« x2 » в исходную формулу « y = 9x − 4 ».
y( x1 ) = 9x1 − 4
y( x2 ) = 9x2 − 4
Теперь запишем обязательное условие возрастания функции.
|
x2 > x1 |
Обязательное условие возрастания функции |
Подставим в неравенство
« y( x2 ) >
y( x1 ) » полученные формулы
« y( x1 ) = 9x1 − 4» и
« y( x2 ) = 9x2 − 4 » .
y( x2 ) > y( x1 )
9x2 − 4 > 9x1 − 4
Упростим полученное
неравенство.
9x2 − 9x1 > − 4 + 4
9x2 − 9x1 > 0
Вынесем общий множитель
в левой части неравенства.
9(x2 − x1) > 0
Разделим левую и правую часть на «9».
При делении нуля на любое число получается ноль.
x2 − x1 > 0
x2 > x1
Мы доказали, что выполняется исходное условие возрастания функции «x2 > x1».
Отсюда следует, что функция
« y = 9x − 4 » возрастает на всей области определения.
В завершении вместо ответа следует написать фразу:
«Что и требовалось доказать».
Посмотрим другой пример, где требуется доказать, что функция возрастает.
Разбор примера
Доказать, что функция возрастает на всей области определения: y = 13x − 1
По аналогии с предыдущим примером составим неравенства, которые доказывают, что функция возрастает.
|
x2 > x1 |
Обязательное условие возрастания функции |
Вместо « y( x1 )» и
«y( x2 ) » запишем
формулу функции « y = 13x − 1 » и упростим полученное неравенство.
y( x2 ) > y( x1 )
13x2 − 1 > 13x1 − 1
13x2 − 13x1 > 1 − 1
13(x2 − x1) > 0 |: 13
>
x2 − x1 > 0
x2 > x1
Что и требовалось доказать.
Что такое убывание функции
Запомните!
Функция « y(x) » называется убывающей на некотором промежутке, если для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких,
что « x2 > x1 »
выполняется неравенство « y( x2 ) < y( x1 )».
|
x2 > x1 |
Обязательное условие убывания функции |
Как по графику понять, что функция убывает
Разбор примера
Доказать, что функция убывает на всей области определения: y = 1 − 3x
По определению убывания функции мы знаем, что,
если « x »
↑ растет, то
« y » ↓ должен уменьшаться.
Построим график функции
« y = 1 − 3x ». Ее график — прямая, поэтому нам будет достаточно двух точек.
Область определения функции
« y = 1 − 3x » — все действительные числа,
поэтому можно поставить любое число вместо « x » и вычислить « у » по
формуле функции
« y = 1 − 3x ». Например, возьмем
« x = 0 »
и « x = 1 ».
x = 0
y(x) = 1 − 3x
y(0) = 1 − 3 · 0 = 1
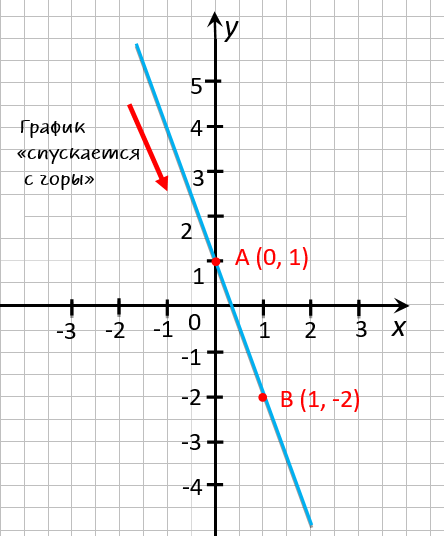
(·) А (0; 1)
x = 1
y(1) = 1 − 3x
y(1) = 1 − 3 · 1 = 1 − 3 = −2
(·) B (1; −2)
Построим график функции
« y = 1 − 3x » по полученным точкам
« (·)A » и « (·)B ».
На графике функции видно, что зрительно график «спускается с горы», то есть функция убывает. Другими словами, при увеличении
« x »
↑ уменьшается
значение
« y » ↓.
Как по формуле доказать, что функция убывает
Вернёмся к нашей функции
« y = 1 − 3x ».
По ее графику мы поняли, что функция убывает, так как график «спускается с горы». Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?
Запомните!
Чтобы доказать, что функция убывает требуется доказать, что при любых
« x2 > x1 » выполняется
« y( x2 ) < y( x1 ) ».
Давайте разберем на примере функции
« y = 1 − 3x ». Докажем, что она убывает
на всей своей области определения.
|
x2 > x1 |
Обязательное условие убывания функции |
Подставим « y( x1 )» и
«y( x2 ) » в
формулу функции « y = 1 − 3x » и упростим полученное неравенство.
y( x2 ) < y( x1 )
1 − 3x2 < 1 − 3x1
3x1 − 3x2 < 1 − 1
3(x1 − x2) < 0 | :3
<
x1 − x2 < 0
−x2 < −x1
Умножим на « −1 » левую и правую часть неравенства. При
умножении неравенства на отрицательное число знак неравенства поменяется на
противоположный.
−x2 < −x1 | · (−1)
x2 > x1
Что и требовалось доказать.
Как по графику функции определить
возрастание и убывание
Потренируемся только по графику функции определять промежутки возрастания и убывания функции.
Разбор примера
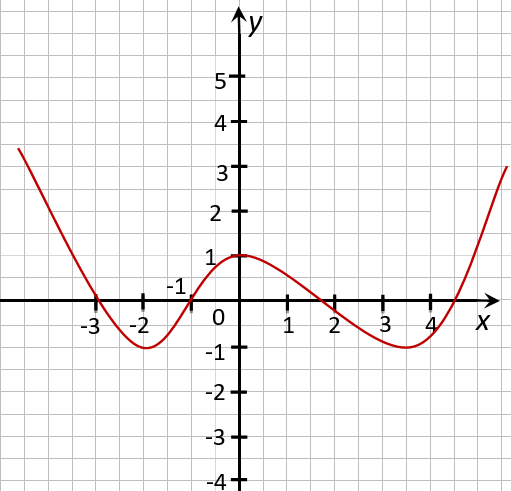
На рисунке ниже изображён график функции, определенной на множестве действительных чисел.
Используя график, найдите промежутки возрастания и промежутки убывания функции.
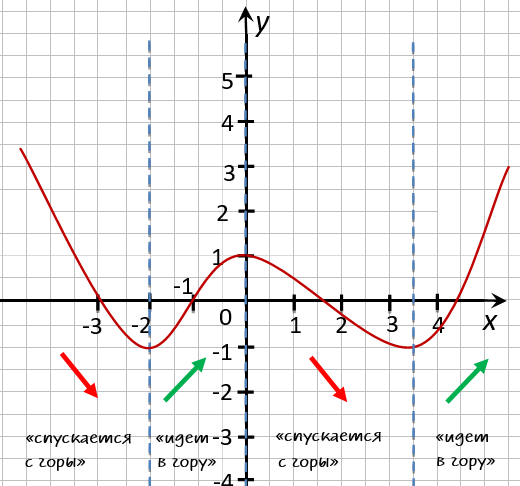
Отметим с помощью штриховых линий промежутки, где график функции убывает
(«спускается с горы») и где он возрастает («идет в гору»).
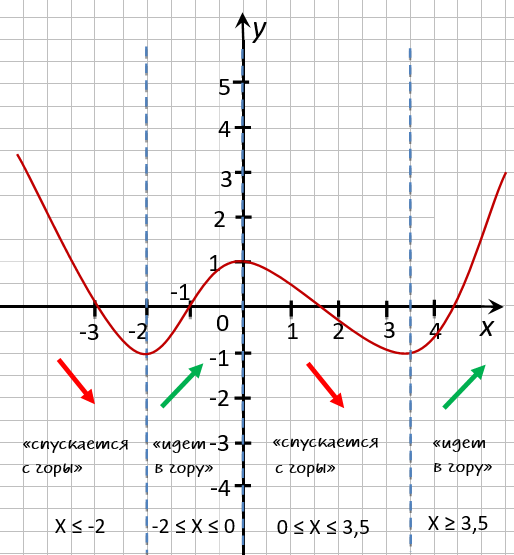
Запишем через знаки неравенств,
какие значения принимает « x » на полученных промежутках.
Обратите внимание, что во всех случаях при указании промежутков, мы указываем, что их
концы входят в промежуток, то есть используем знаки нестрогого неравенства.
Остаётся записать полученные промежутки возрастания и убывания функции в ответ.
Ответ:
- функция убывает при
x ≤ −2; 0 ≤ x ≤ 3,5 - функция возрастает при
−2 ≤ x ≤ 0 ; x ≥ 3,5
Более грамотно будет записать ответ с помощью специальных
математических символов.
Ответ:
- функция убывает на промежутках
x ∈ (−∞ ; −2] ∪ [0; 3,5] - функция возрастает на промежутках x ∈ [−2 ; 0] ∪ [3,5 ; +∞]
При каких значениях
« m »
функция является убывающей или возрастающей
Ещё один тип заданий, в которых требуется определить,
при каких
« m » ( « а, b » или других буквах) функция убывает или возрастает.
Разбор примера
При каких значениях « m » функция
« y = mx − m − 3 + 2x » является убывающей?
Обратимся снова к определению убывания функции. Вспомним, как записать условия убывания функции с точки зрения формул.
|
x2 > x1 |
Обязательное условие убывания функции |
Запишем эти условия, используя формулу функции « y = mx − m − 3 + 2x », заданную в
задаче. Вместо
« x »
подставим « x1 » и « x2 ».
y( x2 ) < y( x1 )
mx2 − m − 3 + 2x2 < mx1 − m − 3 + 2x1
Упростим полученное неравенство. Перенесем из правой части все члены неравенства в левую часть с противоположными знаками.
mx2 − m − 3 + 2x2 − mx1
+ m
+ 3
− 2x1
< 0
Упростим полученное выражение. Некоторые члены неравенства взаимоуничтожатся.
mx2 − mx1
− m + m − 3 + 3 + 2x2 − 2x1
< 0
mx2 − mx1 + 2x2 − 2x1
< 0
Вынесем общие множители за скобки.
m( x2 − x1) + 2(x2 − x1)
< 0
Теперь
вынесем общий множитель
« ( x2 − x1 ) ».
( x2 − x1) (m + 2)
< 0
Вспомним обязательное условие убывания функции.
|
x2 > x1 |
Обязательное условие убывания функции |
Преобразуем исходное условие убывания функции « x2 > x1 ».
Перенесем все в левую часть.
x2 > x1
x2 − x1 > 0
По условию убывания функции
« x2 − x1 > 0 »,
значит, чтобы
произведение
«( x2 − x1) (m + 2)
» было меньше нуля, требуется, чтобы множитель «(m + 2)» был меньше нуля. Так как по
правилу знаков:
плюс на минус даёт минус.
| + | · | − | < 0 |
| (x2 − x1) | · | (m + 2) | < 0 |
Решим полученное неравенство.
m + 2 < 0
m < −2
Ответ: при «m < −2» функция
« y = mx − m − 3 + 2x »
является убывающей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | – | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f”(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x – 3.
Решение: Находим производную: f′(x) = 2x – 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
Алгебра и начала математического анализа, 11 класс
Урок №15. Возрастание и убывание функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение промежутков монотонности функции,
2) Определение алгоритма нахождения промежутков возрастания и убывания функции,
3) Решение задачи на нахождения промежутков возрастания и убывания функции
Глоссарий по теме
Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)
- Найти D(f)
- Найти f‘(x).
- Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) <f(x2)
2. Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) >f(x2)
Теоремы
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежутки монотонности функции
у = -3х3 + 4х2 + х – 10.
Решение
1.Найдем область определения функции.
D(y) =
2.Найдем производную функции.
y’ = (x – 1)(-9x – 1)
3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).
Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так как на интервале 
Так как на интервале 
Так как на интервале 
Так как в точках 
Следовательно, функция возрастает на 


Ответ: Функция возрастает на
Функция убывает на 

№2. Определите промежутки монотонности функции
у = х5–5х4 +5х3 – 4.
Решение:
y‘ =
- Функция возрастает на
; функция убывает на
.
Ответ: Функция возрастает на 
функция убывает на 
Как найти промежутки возрастания и убывания функции
Определение промежутков возрастания и убывания функции – это один из основных аспектов исследования поведения функции наряду с нахождением точек экстремумов, в которых происходит перелом от убывания к возрастанию и наоборот.

Инструкция
Функция y = F(x) является возрастающей на определенном интервале, если для любых точек x1 F(x2), где x1 всегда > x2 для любых точек на интервале.
Существуют достаточные признаки возрастания и убывания функции, которые вытекают из результата вычисления производной. Если производная функции положительна для любой точки интервала, то функция возрастает, если отрицательна – убывает.
Чтобы найти промежутки возрастания и убывания функции, нужно найти область ее определения, вычислить производную, решить неравенства вида F’(x) > 0 и F’(x)
Рассмотрим пример.
Найти промежутки возрастания и убывания функции для y = (3·x² + 2·x – 4)/x².
Решение.
1. Найдем область определения функции. Очевидно, что выражение, стоящее в знаменателе, должно всегда быть отличным от нуля. Поэтому точка 0 исключается из области определения: функция определена при x ∈ (-∞; 0)∪(0; +∞).
2. Вычислим производную функции:
y’(x) = ((3·x² + 2·x – 4)’ ·x² – (3·x² + 2·x – 4) · (x²)’)/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x – 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^4 = (8·x – 2·x²)/x^4 = 2· (4 – x)/x³.
3. Решим неравенства y’ > 0 и y’ 0;
(4 – x)/x³
4. Левая часть неравенства имеет один действительный корень х = 4 и обращается в бесконечность при x = 0. Поэтому значение x = 4 включается и в промежуток возрастания функции, и в промежуток убывания, а точка 0 не включается никуда.
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
Рассмотрим пример.
Найти промежутки возрастания и убывания функции для y = (3·x² + 2·x – 4)/x².
Решение.
1. Найдем область определения функции. Очевидно, что выражение, стоящее в знаменателе, должно всегда быть отличным от нуля. Поэтому точка 0 исключается из области определения: функция определена при x ∈ (-∞; 0)∪(0; +∞).
2. Вычислим производную функции:
y’(x) = ((3·x² + 2·x – 4)’ ·x² – (3·x² + 2·x – 4) · (x²)’)/x^4 = ((6·x + 2) ·x² – (3·x² + 2·x – 4) ·2·x)/x^4 = (6·x³ + 2·x² – 6·x³ – 4·x² + 8·x)/x^4 = (8·x – 2·x²)/x^4 = 2· (4 – x)/x³.
3. Решим неравенства y’ > 0 и y’ 0;
(4 – x)/x³
4. Левая часть неравенства имеет один действительный корень х = 4 и обращается в бесконечность при x = 0. Поэтому значение x = 4 включается и в промежуток возрастания функции, и в промежуток убывания, а точка 0 не включается никуда.
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
4. Левая часть неравенства имеет один действительный корень х = 4 и обращается в бесконечность при x = 0. Поэтому значение x = 4 включается и в промежуток возрастания функции, и в промежуток убывания, а точка 0 не включается никуда.
Итак, искомая функция возрастает на промежутке x ∈ (-∞; 0) ∪ [2; +∞) и убывает при x (0; 2].
Источники:
- как найти на функции промежутки убывания
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Определение
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!
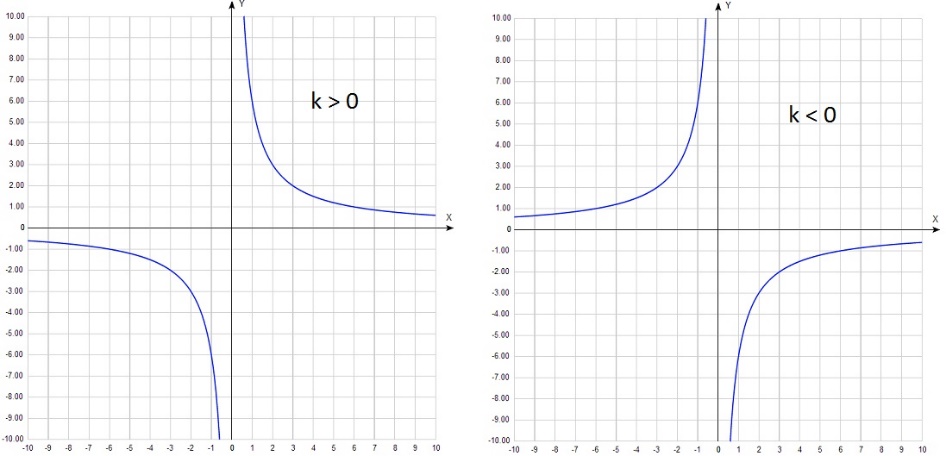
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом:
По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?
- Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
- Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.
Рассмотрим примеры нахождения нулей функции.
Пример №1. Найти нули функции (если они существуют):
а) у= –11х +22
б) у= (х + 76)(х – 95)
в) у= – 46/х
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Получим х=2.
Таким образом, мы нашли нуль функции: х=2
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.
в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Определение
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.
На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.
Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Определение
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Даниил Романович | Просмотров: 16.1k








 ; функция убывает на
; функция убывает на  .
.