Сергей Андреевич Дремук
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Количество путей в графе — это общее число маршрутов, которые приводят из одной вершины графа к другой его вершине.
Введение
Определение 2
Под путём в графе понимают последовательный набор его вершин, в котором все вершины соединяются со следующей за ней вершиной посредством ребра.
Если G является неориентированным графом, то путём в графе G будет такой конечный или бесконечный набор последовательных рёбер и вершин S = (…, a0, E0, a1, E1, …, En-1, an), для которого пара соседних рёбер Ei и Ei-1 обладают общей вершиной ai. То есть справедливы следующие выражения E0 = (a0, a1), E1 = (a1, a2), …, En = (an, an+1)
Следует заметить, что возможна неоднократная встреча с одним и тем же ребром при прохождении путевого маршрута. В случае, когда нет рёбер, которые предшествуют E0, то a0 считается исходной вершиной S. А когда не существует рёбер, которые идут за E(n-1), то an считается последней вершиной S. Все вершины, которые принадлежат паре соседних рёбер, считаются внутренними.
Следует заметить, что поскольку возможно повторение рёбер и вершин при прохождении путевого маршрута, то внутренняя вершина может быть, как начальной, так и конечной вершиной.
При совпадении начальной и конечной вершин, путь считается циклическим. В случае, когда каждое ребро графа при обходе путевого маршрута, попадается всего один раз (повтор вершин допускается), такой путь считается цепью, а циклический путь считается циклом.
Путь, при котором нет рёбер графа, соединяющих две вершины пути, носит название индуцированного пути. Пара путей считается независимой в смысле вершин, когда у них нет одинаковых внутренних вершин. И по аналогии пара путей считается независимой в плане рёбер, когда у них нет общих внутренних рёбер.
«Количество путей в графе» 👇
Количество путей в графе
В случае, когда в город S возможно доехать лишь из городов X, Y, и Z, то количество разнообразных путевых маршрутов из города А в город S равняется суммарному количеству разных путей движения из А в Х, из А в Y и из А в Z, что можно выразить следующей формулой:
$N_S = N_X + N_Y + N_Z$
Обозначим как NM количество путевых маршрутов из вершины А в некую вершину М. Количество путей будет конечным, если в графе отсутствуют замкнутые пути, то есть циклы. Рассмотрим конкретный пример. Имеется структурная схема дорог, которые соединяют города А, Б, В, Г, Д, Е, Ж, И, К, Л. Передвижение по всем дорогам возможно только в одну сторону, в которую указывает стрелка. Необходимо определить количество возможных путей из города А в город Л.
Рисунок 1. Путевые маршруты. Автор24 — интернет-биржа студенческих работ
Обозначим как $N_X$ число разных маршрутов из города А в город Х. Считаем, что город А является исходным пунктом путевого маршрута, и, следовательно, NA = 1. А для произвольно выбранного города Х число путей $N_X$ возможно определить по формуле:
$N_X = N_Y + … + N_Z$.
Здесь суммарный путь принят по всем вершинам, имеющим прямую связь с вершиной Х, то есть, к примеру:
$N_Л = N_Д + N_И + N_Ж + N_К$
Сформируем таблицу, где каждому городу сопоставлено общее число прямых маршрутов в этот город. Вычислим общее число путей из начальной точки маршрута, города А.
В пункты Б и В ведут единственные дороги из А. В пункт В можно попасть из пунктов А, Б, и Г, т.е. $N_В = N_А + N_Б + N_Г = 3$.
Рисунок 2. Таблица. Автор24 — интернет-биржа студенческих работ
В пункт Е можно попасть только из Г, количество путей равно количеству путей в пункт Г. В пункт Ж ведут прямые пути из пунктов Е и В, т.е. $N_Ж = N_В + N_Е = 4$. В пункт Д ведут прямые пути из пунктов Б и В, т.е. $N_Д = N_В + N_Б = 4$.
Рисунок 3. Таблица. Автор24 — интернет-биржа студенческих работ
В пункт И можно попасть только из Д, количество путей равно количеству путей в пункт Д = 4. В пункт К ведет путь только из пункта Е, т.е. $N_К = N_Е = 1$. В пункт Л ведут прямые пути из пунктов Д, И, Ж и К, т.е. $N_Л = N_Д + N_И + N_Ж + N_К = 13$.
Рисунок 4. Таблица. Автор24 — интернет-биржа студенческих работ
Итоговый результат тринадцать путей.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
| Задача: |
| Задан ациклический граф и две вершины и . Необходимо посчитать количество путей из вершины в вершину по рёбрам графа . |
Содержание
- 1 Решение задачи
- 1.1 Перебор всех возможных путей
- 1.2 Метод динамического программирования
- 1.3 Псевдокод
- 2 Пример работы
- 3 См. также
- 4 Источники информации
Решение задачи
Перебор всех возможных путей
Небольшая модификация алгоритма обхода в глубину. Запустим обход в глубину от вершины . При каждом посещении вершины проверим, не является ли она искомой вершиной . Если это так, то ответ увеличивается на единицу и обход прекращается. В противном случае производится запуск обхода в глубину для всех вершин, в которые есть ребро из , причем он производится независимо от того, были эти вершины посещены ранее, или нет.
Функция принимает граф в виде списка смежности, начальную вершину и конечную вершину .
countPaths(g, v, t)
if v == t
return 1
else
s = 0
for to in g[v]
s += countPaths(g, to, t)
return s
Время работы данного алгоритма в худшем случае , где — число путей в графе из в . Например, на следующем графе данный алгоритм будет иметь время работы . Если же использовать метод динамического программирования, речь о котором пойдет ниже, то асимптотику можно улучшить до .
![Пример графа, на котором алгоритм имеет время работы [math]O(2^{n/2})[/math]](https://neerc.ifmo.ru/wiki/images/thumb/0/00/Dp-countpaths-example.png/600px-Dp-countpaths-example.png)
Метод динамического программирования
Пусть — число путей от вершины до вершины .
Тогда зависит только от вершин, ребра из которых входят в . Тогда таких , что есть ребро из в . Мы свели нашу задачу к меньшим подзадачам, причем мы также знаем, что . Это позволяет решить задачу методом динамического программирования.
Псевдокод
Пусть — стартовая вершина, а — конечная, для нее и посчитаем ответ. Будем поддерживать массив , где — число путей из вершины до вершины и массив , где , если ответ для вершины уже посчитан, и в противном случае. Изначально для всех вершин , кроме , а . Функция будет возвращать ответ для вершины . Удобнее всего это реализовать в виде рекурсивной функции с запоминанием. В этом случае значения массива будут вычисляться по мере необходимости и не будут считаться лишний раз:
count(g, v)
if w[v]
return d[v]
else
sum = 0
w[v] = true
for c in g[v]
sum += count(g, c)
d[v] = sum
return sum
countPaths(g, s, t)
d[s] = 1
w[s] = true
answer = count(t)
return answer
Значение функции считается для каждой вершины один раз, а внутри нее рассматриваются все такие ребра . Всего таких ребер для всех вершин в графе , следовательно, время работы алгоритма в худшем случае оценивается как , где — число вершин графа, — число ребер.
Пример работы
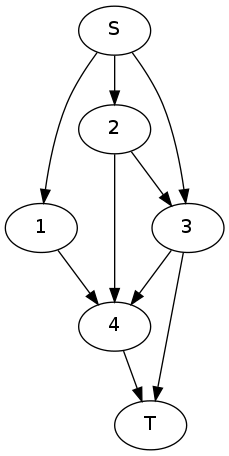
Рассмотрим пример работы алгоритма на следующем графе:
Изначально массивы и инициализированы следующим образом:
| вершина | S | 1 | 2 | 3 | 4 | T |
| w | true | false | false | false | false | false |
| d | 1 | 0 | 0 | 0 | 0 | 0 |
Сначала функция будет вызвана от вершины . Ответ для нее еще не посчитан (), следовательно будет вызвана от вершин и . Для вершины ответ также не посчитан (), следовательно будет вызвана уже для вершин и . А вот для них ответ мы уже можем узнать: для он равен , так как это — единственная вершина, ребро из которой входит в нее. Непосредственно для ответ нам также известен. На текущий момент таблица будет выглядеть следующим образом:
| вершина | S | 1 | 2 | 3 | 4 | T |
| w | true | false | true | false | false | false |
| d | 1 | 0 | 1 | 0 | 0 | 0 |
Теперь мы знаем значения для вершин и , что позволяет вычислить . Также обновим значения в массиве : .
| вершина | S | 1 | 2 | 3 | 4 | T |
| w | true | false | true | true | false | false |
| d | 1 | 0 | 1 | 2 | 0 | 0 |
В самом начале для вычисления нам требовались значения и . Теперь нам известно значение , поэтому проследим за тем, как будет вычисляться . , но , следовательно значения и мы уже знаем, и нам необходимо вызвать . Ответ для этой вершины равен , так как это единственная вершина, ребро из которой входит в . Обновим соответствующие значения массивов и :
| вершина | S | 1 | 2 | 3 | 4 | T |
| w | true | true | true | true | false | false |
| d | 1 | 1 | 1 | 2 | 0 | 0 |
Теперь нам известны все три значения, требующиеся для вычисления ответа для вершины . :
| вершина | S | 1 | 2 | 3 | 4 | T |
| w | true | true | true | true | true | false |
| d | 1 | 1 | 1 | 2 | 4 | 0 |
Наконец, вычислим и обновим таблицы и :
| вершина | S | 1 | 2 | 3 | 4 | T |
| w | true | true | true | true | true | true |
| d | 1 | 1 | 1 | 2 | 4 | 6 |
Этот алгоритм позволяет вычислить количество путей от какой-либо вершины не только до , но и для любой вершины, лежащей на любом из путей от до . Для этого достаточно взять значение в соответствующей ячейке .
См. также
- Динамическое программирование
- Кратчайший путь в ациклическом графе
- Задача о расстановке знаков в выражении
- Задача о порядке перемножения матриц
Источники информации
- Акулич И.Л. Глава 4. Задачи динамического программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9..
На уроке рассмотрен материал для подготовки к ОГЭ по информатике, рассмотрены примеры того, как решать 9 задание. Дан теоретический материал по теме «Анализирование информации, представленной в виде схем и поиск количества путей».
Содержание:
- ОГЭ по информатике 9 задания объяснение
- Поиск количества путей
- 9 задание как решать
- Актуальное
- Тренировочные
9-е задание: «Анализирование информации, представленной в виде схем».
Уровень сложности — повышенный,
Максимальный балл — 1,
Примерное время выполнения — 4 минуты.
* до 2020 г — это было задание № 11 ОГЭ
Поиск количества путей
- Если в город R из города A можно добраться только из городов X, Y и Z, то количество различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть:
- где NR — это количество путей из вершины A в вершину R
- Число путей не бесконечно, исключением является только схема, в которой есть циклы – замкнутые пути.
- Часто подобные задания целесообразней решать с конца (рассмотрим пример ниже).
NR = NX + NY + NZ
9 задание как решать
-
Подробный видеоразбор по ОГЭ 9 задания:
- Рассмотрено 3 задачи. Перемотайте видеоурок на решение нужной задачи.
Актуальное
Решение задания 9.3. Демонстрационный вариант огэ по информатике 2022 г.:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, проходящих через город В?
✍ Решение:
-
✎ 1 способ (дерево):
- Поскольку нас интересуют пути, проходящие через город В, то вычеркнет те дороги, которые минуют город В:
- Как видим, таких дорог получилось две — Б->Д и А->Г. Учтем это при дальнейших расчетах.
- Решим задание с конца. Т.е. так как траектория поиска путей — от А до K, то мы будем рассматривать сначала город K.
- В город K можно попасть из трех городов — Д, E и Ж; запишем это так:
K = Д + Е + Ж
Д = В (Б -> Д не учитываем) Е = Д + В Ж = В + Г
К = Д + Е + Ж Д = В Е = Д + В Ж = В + Г ----- Б = А = 1 A = 1 В = Б + А Д = B Ж = B + Г Г = В (А - Г не учитываем) Теперь возвращаемся, подставляя найденные значения: ↑ В = Б + А = 2 Г = В = 2 Д = В = 2 Ж = B + Г = 2 + 2 = 4 Е = Д + В = 2 + 2 = 4
К = Д + Е + Ж = 2 + 4 + 4 = 10
✎ 2 способ (дерево):
К Д - Е - К -------------- Е - К Д - К Б - В - Е - К Ж - К Г - Ж - К А ---------------- Д - К Е - К В - Е - К Ж - К Г - Ж - К ---------------- Г - Ж - К
К Д - Е - К -------------- Е - К Д - К Б - В - Е - К Ж - К Г - Ж - К А ---------------- Д - К Е - К В - Е - К Ж - К Г - Ж - К ---------------- Г - Ж - К
Ответ: 10
Решение задания 9.4:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, проходящих через город Ж?
✍ Решение:
-
✎ 1 способ (с конца):
- Поскольку нас интересуют пути, проходящие через город Ж, то вычеркнем те дороги, которые минуют город Ж:
- Решим задание с конца. Т.е. так как траектория поиска путей — от А до K, то мы будем рассматривать сначала город K.
- В город K можно попасть из трех городов — И, E и Ж; запишем это так:
K = И + Ж
И = Ж Ж = Д + В + Е
К = И + Ж И = Ж Ж = Д + В + Е ----- Д = Б + В Е = В + Г В = Б + А + Г А = 1 Г = А = 1 Б = А = 1 Теперь возвращаемся, подставляя найденные значения: ↑ В = Б + А + Г = 1 + 1 + 1 = 3 Д = Б + В = 1 + 3 = 4 Е = В + Г = 3 + 1 = 4 Ж = Д + В + Е = 4 + 3 + 4 = 11 И = Ж = 11 К = И + Ж = 22
Ответ: 22
Тренировочные
Решение задания 9.1:
На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город H?
Типовые задания для тренировки
✍ Решение:
- Решим задание с конца. Т.е. так как траектория поиска путей от А до Н, то мы будем рассматривать сначала город Н.
- В город Н можно попасть из трех городов — C, D и G; запишем это так:
H = C + D + G
C = D + A D = A + E G = D + E + F
Далее, рассмотрим каждый город, дойдя до первого — города А. Для него существует только одни путь. Также, для городов, выходящих только из города А, тоже существует только 1 путь. Таким образом имеем:
H = C + D + G C = D + A D = A + E G = D + E + F ----- D = Е + A A = 1 E = A + B F = B B = 1 Теперь возвращаемся, подставляя найденные значения: ↑ F = B = 1 E = A + B = 1 + 1 = 2 D = Е + A = 2 + 1 = 3 G = D + E + F = 3 + 2 + 1 = 6 D = A + E = 1 + 2 = 3 C = D + A = 3 + 1 = 4 H = C + D + G = 4 + 3 + 6 = 13
Ответ: 13
Решение задания 9.2:
На карту нанесены 4 города (A, B, C и D).
Известно, что:
между городами A и C — три дороги,
между городами C и B — две дороги,
между городами A и B — две дороги,
между городами C и D — две дороги,
между городами B и D — четыре дороги.
По каждой из этих дорог можно ехать в обе стороны.
Сколькими различными способами можно проехать из A в D, посещая каждый город не более одного раза?
Типовые задания для тренировки
✍ Решение:
- Построим все возможные ветви для движения из города A. Будем выполнять произведение количества дорог для каждой ветви, так как движение возможно в обе стороны:
A * B * C * D = 2 * 2 * 2 = 8 (A и B - две дороги, C и B - две дороги, C и D - две дороги) A * B * D = 2 * 4 = 8 (A и B - две дороги, B и D - четыре дороги) A * C * D = 3 * 2 = 6 (A и C - три дороги, C и D - две дороги) A * C * B * D = 3 * 2 * 4 = 24 (A и C - три дороги, C и B - две дороги, B и D - четыре дороги)
8 + 8 + 6 + 24 = 46
Ответ: 46

Наши выездные компьютерные курсы предоставляют услуги индивидуального и корпоративного обучения с выездом на дом или на предприятие.
- Подробности
- Опубликовано: 13 Май 2013
-
Просмотров: 4449
Подробнее…

Широкий выбор компьютерных курсов
- Подробности
- Опубликовано: 05 Март 2013
-
Просмотров: 2922
Подробнее…

Кто Ваши преподаватели?
Кадровая политика наших курсов строится таким образом, что работать у нас могут только преподаватели соответствующие следующим критериям: наличие стажа педагогической деятельности и соответствующий склад характера, отличное знание профильных компьютерных программ и практический опыт работы с ними, пунктуальность и коммуникабельность.
- Подробности
- Опубликовано: 05 Март 2013
-
Просмотров: 3130
Подробнее…