Как найти число распадов ядер

ΔN=N(t)-N(t+Δt)=N(t)(1-e^–λΔt)

Если
интервал времени распада Δt
очень мал по
сравнению с периодом полураспада T,
то число ядер, распавшихся за время Δt,
можно найти по приближенной формуле:

ΔN=λN(t)Δt

Период
полураспада T–
это промежуток времени, за который число
нераспавшихся ядер уменьшается в два
раза (см. рис. 1.1).

За
время 2T
число ядер
снижается в 4 раза и т.д. Связь между
периодом полураспада и постоянной
распада

Число ядер, содержащихся в массе m радиоактивного вещества:

где
μ
– молярная масса вещества; N_A–
число Авогадро (N_A=6,02·10²³
моль^-1).

Активность
радиоактивного препарата – это число
ядер, распавшихся в единицу времени:

или

,

где
a₀₌λN₀–
активность в начальный момент времени.

Единица
активности в СИ – беккерель (Бк): 1 Бк –
активность изотопа, при которой за 1 с
происходит один акт распада.

Внесистемная
единица – кюри (Ku)
: 1 Ku=3,7·10¹⁰
Бк.

Удельной
активностью называется число распадов
в 1 с на единицу массы распадающегося
вещества.

1.8 Правила смещения при радиоактивном распаде

В
процессах радиоактивного распада имеют
место так называемые правила смещения,
позволяющие определить массовое число
и заряд ядра нового элемента, возникающего
в результате α-
и β-
превращений:

при
α – распаде

при

–
распаде

при
γ- излучении
значения A
и Z
у ядра не изменяются.

Если
дочернее ядро Y
также оказывается
радиоактивным, то возникает цепочка
радиоактивных превращений. Из правил
смещения видно, что массовое число при
α –
распаде уменьшается на 4, а при β
–распаде не
меняется. Следовательно, для всех ядер
одного и того же радиоактивного семейства
остаток от деления массового числа на
4 одинаков, т.е. существует четыре
различных семейства, для каждого из
которых массовые числа определяются
значениями

A
= 4n,
4n+1,
4n+2,
4n+3,

где
n
– целое
положительное число.

Семейства
начинаются на наиболее долгоживущем (
с наибольшим периодом полураспада )
«родоначальнике» семейства: тории ,
уране и актинии

и
заканчиваются после цепочки α-
и β-
превращений на устойчивых изотопах
свинца:

Семейство
4n+1
нептуния
состоит из цепочки искусственно-радиоактивных
ядер и заканчивается висмутом.

1.9 Ядерные реакции

Ядерные
реакции – это превращения атомных ядер,
вызванные взаимодействиями их друг с
другом или с элементарными частицами.

Как
правило, в ядерных реакциях участвуют
два ядра и две частицы. Развернутый вид
ядерной реакции выглядит, к примеру,
следующим образом:

При
ядерных реакциях выполняются законы
сохранения массового и зарядового числа

A₁+A₂=A₃+A₄
и
Z₁+Z₂=Z₃+Z₄,

где
индексы 1 и 2 относятся к исходным
реагентам, а 3 и 4 – к продуктам реакции.
В законе сохранения зарядового числа
учитывается знак заряда реагента
(алгебраическая сумма). Кроме того,
выполняются закон сохранения импульса
и релятивистской полной энергии.

Широко
распространен сокращенный способ записи
ядерных реакций согласно следующему
правилу: вначале записывается
бомбардируемое ядро (ядро- мишень), затем
в скобках указывается на первом месте
налетающая частица (частица-снаряд), а
за ней – все частицы, вылетевшие в
результате реакции; после скобок
обозначается окончательно получившееся
ядро (ядро-продукт). Сокращенная запись
реакции представима в виде:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Появление «ручных» сцинтилляционных счетчиков и, главным образом, счётчиков Гейгера–Мюллера, которые помогли автоматизировать подсчёты частиц (см. § 15-е), привело физиков к важному выводу. Любой радиоактивный изотоп характеризуется самопроизвольным ослабеванием радиоактивности, выражающимся в уменьшении количества распадающихся ядер в единицу времени.

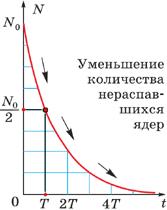
Построение графиков активности различных радиоактивных изотопов приводило учёных к одной и той же зависимости, выражающейся показательной функцией (см. график). По горизонтальной оси отложено время наблюдения, а по вертикальной – количество нераспавшихся ядер. Кривизна линий могла быть различной, однако сама функция, которой выражались описываемые графиками зависимости, оставалась одной и той же:

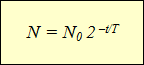N – количество нераспавшихся ядер N0 – начальное количество ядер t – время наблюдения, с T – период полураспада, с

Эта формула выражает закон радиоактивного распада: количество нераспавшихся с течением времени ядер определяется как произведение начального количества ядер на 2 в степени, равной отношению времени наблюдения к периоду полураспада, взятой с отрицательным знаком.

Как выяснилось в ходе опытов, различные радиоактивные вещества можно охарактеризовать различным периодом полураспада – временем, за которое количество ещё нераспавшихся ядер уменьшается вдвое (см. таблицу).

Йод-129	15 млн лет		Углерод-14	5,7 тыс лет
Йод-131	8 дней		Уран-235	0,7 млрд лет
Йод-135	7 часов		Уран-238	4,5 млрд лет

Период полураспада – общепринятая физическая величина, характеризующая скорость радиоактивного распада. Многочисленные опыты показывают, что даже при очень длительном наблюдении за радиоактивным веществом его период полураспада постоянен, то есть не зависит от числа уже распавшихся атомов. Поэтому закон радиоактивного распада нашёл применение в методе определения возраста археологических и геологических находок.

Метод радиоуглеродного анализа. Углерод – очень распространённый на Земле химический элемент, в состав которого входят стабильные изотопы углерод-12, углерод-13 и радиоактивный изотоп углерод-14, период полураспада которого составляет 5,7 тысяч лет (см. таблицу). Живые организмы, потребляя пищу, накапливают в своих тканях все три изотопа. После прекращения жизни организма поступление углерода прекращается, и с течением времени его содержание убывает естественным путём, за счёт радиоактивного распада. Поскольку распадается только углерод-14, с течением веков и тысячелетий изменяется соотношение изотопов углерода в ископаемых останках живых организмов. Измерив эту «углеродную пропорцию», можно судить о возрасте археологической находки.

Метод радиоуглеродного анализа применим и для геологических пород, а также для ископаемых предметов быта человека, но при условии, что соотношение изотопов в образце не было нарушено за время его существования, например, пожаром или действием сильного источника радиации. Неучёт подобных причин сразу после открытия этого метода приводил к ошибкам на несколько веков и тысячелетий. Сегодня применяются «вековые калибровочные шкалы» для изотопа углерода-14, исходя из его распределения в долгоживущих деревьях (например, в американской тысячелетней секвойе). Их возраст можно подсчитать весьма точно – по годовым кольцам древесины.

Предел применения метода радиоуглеродного анализа в начале XXI века составлял 60 000 лет. Для измерения возраста более древних образцов, например горных пород или метеоритов, используют аналогичный метод, но вместо углерода наблюдают за изотопами урана или других элементов в зависимости от происхождения исследуемого образца.

Недавно проводил очередные занятия по физике со своими учениками и заметил некоторые трудности в решении задач на радиоактивный распад. По моим наблюдениям в школе и в интернете разбираются самые тривиальные задачи на распад. Задачи из ЕГЭ бывают немного сложнее. Но для интереса я добавил в статью разборы еще 6 задач, которые смело можно назвать задачами «со звёздочкой*», то есть повышенной сложности. На написание теории и подробные решения было потрачено много времени, поэтому, если Вам понравится статья, поддержите своей активностью.

💡 Крупные статьи я выкладываю в pdf в своём канале в telegram Репетитор IT mentor. Подписывайтесь, там публикуется контент, которого на Дзен не будет.

Прежде всего хотелось бы сделать замечание. Для успешного решения задач по физике (в целом, любых задач) Вам понадобятся:
◼ 1. Уверенные знания в математике на уровне физ-мат лицея (это минимум)
◼ 2. Базовые знания по дифференциальному и интегральному исчислению, а также умение применять начальные условия (НУ) и граничные условия (ГУ).
◼ 3. Понимание ограничений и сути процесса ( у вас не должны получаться отрицательная масса или отрицательное время, дробное количество, околосветовые скорости макроскопических объектов )
◼ 4. Хорошее воображение, 3D-видение эксперимента у себя в голове, а также возможность представить как выглядит график функции, описываемой в определенном законе (например: закон радиоактивного распада).
◼ 5. Умение разбивать большую задачу на малые подзадачи (например: определить амплитуду колебаний изображения математического маятника — у вас две задачи: механическая и оптическая — решайте их отдельно, потом сшивайте).
◼ 6. Чувствуйте абстракции. Вы никогда не решите задачу, если попытаетесь учесть всё. Пример: определите траекторию полёта камня, брошенного под углом к горизонту с учётом… эффекта Магнуса, динамического сопротивления ветра, фазы Луны, функции плотности воздуха, динамики вихрей потоков воздуха, распада вещества, из которого состоит камень, термодинамического расширения камня. Сложно? Вот поэтому чувствуйте абстракции.
◼ 7. Программирование. Да… внезапно. Для физики полезно знать какой-нибудь язык программирования. Попробуйте решенную задачу замоделировать и закодить в виде графической анимации. Так ваши решения станут куда более интересными и наглядными. А меняя входные параметры, вы станете лучше понимать поведение физических систем.

Основные определения

Радиоактивность – свойство некоторых нуклидов подвергаться радиоактивному распаду.

Радиоактивность – превращение одних атомных ядер в другие ядра, сопровождающееся испусканием различных частиц и электромагнитного излучения. На латыни radio – излучаю, activus – действенный.

Радиоактивность – самопроизвольное превращение неустойчивых изотопов одного химического элемента в изотоп другого элемента, сопровождающееся испусканием элементарных частиц, ядер и жесткого электромагнитного излучения.

Нуклид – разновидность атома, характеризуемая числом протонов и нейтронов, а в некоторых случаях энергетическим состоянием ядра.

Радионуклид – нуклид, испускающий ионизирующее излучение.

Радиация или ионизирующее излучение – это частицы или гамма-кванты, энергия которых достаточна велика, чтобы при воздействии на вещество создавать ионы и катионы (т.е. ионизировать молекулы на своём пути).

Ионизирующее излучение – поток заряженных или нейтральных частиц и квантов электромагнитного излучения, прохождение которых через вещество приводит к ионизации и возбуждению атомов или молекул среды. По своей природе делится на фотонное (гамма-излучение, тормозное излучение, рентгеновское излучение) и корпускулярное (альфа-излучение, электронное, протонное, нейтронное, мезонное).

Теория для решения задач

Закон радиоактивного распада – закон, который описывается зависимость интенсивности радиоактивного распада от времени и от количества радиоактивных атомов в образце. Закон был открыт Фредериком Содди и Эрнестом Резерфордом. Оба получили Нобелевскую премию. Они обнаружили закон экспериментальным путем. Ещё в далеком 1903 году в работах «Сравнительное изучение радиоактивности радия и тория» этот закон формулировался:

Во всех случаях, когда отделяли один из радиоактивных продуктов и исследовали его активность независимо от радиоактивности вещества, из которого он образовался, было обнаружено, что активность при всех исследованиях уменьшается со временем по закону геометрической прогрессии.

То есть скорость превращения всё время пропорционально количеству элементов, ещё не подвергнувшихся превращению.

Данную формулировку можно записать в виде дифференциального уравнения: dN/dt = – λ·N, где dN – изменение количества ядер за время dt.

Это изменение отрицательно, потому что при распаде уменьшается количество оставшихся элементов. Опытным путем было установлено, что эта скорость распада dN/dt пропорционально количеству оставшихся ядер N и некоторой постоянной λ, которая называется постоянной распада и характеризует вероятность радиоактивного распада за единицу времени (имеет размерность 1/c). Данное уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными. Решение подобных уравнений можно найти в любом учебнике по высшей математике.

В итоге решение будет иметь вид N = N₀ · exp(- λ·t) :

Отсюда видно, что число радиоактивных атомов какого-либо вещества уменьшается со временем по экспоненциальному (показательному) закону. Помимо постоянной распада λ используются другие характеристики.

Среднее время жизни

Зная закон распада, можно посчитать среднее время жизни радиоактивного атома. Вспоминаем, что dN обозначает количество атомов, которое распадется за время от t до t + dt. Тогда среднее время можно будет найти подобно тому, как мы ищем среднее или математическое ожидание случайной непрерывной величины:

В вычислениях была использована формула для интегрирования по частям. Теория интегрирования также описана в любой книге с конспектами по высшей математике (или математическому анализу, или интегральному исчислению).

Подставим результат для тау (время жизни τ) в экспоненциальную зависимость в формуле распада:

Отсюда видно, что за среднее время жизни τ число радиоактивных атомов образца ( а также его активность – количество распадов в секунду) уменьшается в e ≈ 2.718 раз.

Период полураспада

И всё же большей популярностью пользуется другая характеристика для радиоактивных элементов. Называется она периодом полураспада T. Если немного подумать, то из названия понятно, что это время, в течение которого количество радиоактивных атомов исходного элемента уменьшается в 2 раза. Выведем связь этой величины с постоянной распада:

A – массовое число (число нуклонов в составе ядра атома)
Z – атомный номер в таблице Менделеева (число протонов в ядре)
Для нейтрального атома:

Законы сохранения в распадах

При радиоактивном распаде сохраняются следующие параметры:

1. Заряд. Электрический заряд не может создаваться или исчезать. Общий заряд до и после реакции должен сохраняться, хотя может по-разному распределяться среди различных ядер и частиц. Единичный положительный и отрицательный заряды нейтрализуют друг друга. Аналогично, возможно для нейтральной частицы (типа нейтрона) произвести один заряд каждого знака.
2. Массовое число или число нуклонов. Число нуклонов после реакции должно быть равно числу нуклонов до реакции.
3. Общая энергия. Кулоновская энергия и энергия эквивалентных масс должна сохраняться во всех реакциях и распадах.
4. Импульс и угловой момент. Сохранение линейного импульса ответственно за распределение кулоновской энергии среди ядер, частиц и/или электромагнитного излучения. Угловой момент относится к спину частиц.

Потенциальная энергия взаимодействия α-частицы и остаточного ядра с зарядом Z·e

Вид волновой функции можно получить из решения уравнения Шредингера для взаимодействия ядра атома и α-частицы. Способы решения можно почитать в книгах по физике вузовского уровня или в книгах по ММФ (методы математической физики). В целом, для понимания вам будет полезна теория решения дифференциальных уравнений из конспектов лекций по высшей математике или конкретно по теме – дифференциальное и интегральное исчисление.

По причинам исторического характера ядро He называют альфа-частицей. Установлено, что многие тяжелые ядра с зарядовым числом Z > 82 (Z = 82 имеет свинец) испытывают радиоактивный распад с испусканием альфа-частицы. В альфа-частице удельная энергия связи больше, чем в тяжелых ядрах, поэтому альфа-распад возможен энергетически. К примеру, образце урана U-238 испускает альфа-частицы с периодом полураспада 4.5 млрд. лет. Самопроизвольно происходит реакция:

Спустя 4.5 млрд. лет половина ядер урана U-238 распадается. Разность масс U-238 и продуктов распада равна энергии 4.2 МэВ. Рисунок выше позволяет получить представление о том, почему происходит альфа-распад. Ea – кинетическая энергия вылетающей альфа-частицы. Первоначально альфа-частицы находится в области I и может быть описана стоячей волной с амплитудой Ψвнутр (волновая функция в данной области пространства). Однако, возможно проникновение сквозь барьер, потому что в области вдали от ядра имеется небольшой «хвост» волновой функции Ψвнеш. Вероятность вылета альфа-частицы в момент её соударения с барьером можно оценить выражением: |Ψвнеш|²/|Ψвнутр|².

Число таких столкновений в 1 секунду приблизительно v/2R, где v – скорость альфа-частицы в области I. Таким образом, вероятность испускания альфа-частицы в единицу времени можно записать так:

В образце, содержащем n ядер, число распадов в секунду (скорость уменьшения n) равна

Отсюда с помощью интегрирования и подстановки начальных условий можно снова получить закон радиоактивного распада:

Можно получить ещё одну формулу для оценки периода полураспада:

Формула иллюстрирует применение квантовой механики для объяснения радиоактивности. Квантовая механика дает исчерпывающее объяснение альфа-распада и других радиоактивных превращений. Природа вероятности интересна тем, что если в силу редкой случайности текущее ядро уцелело на протяжении большого числа периодов полураспада, то эта предыстория абсолютно не влияет на вероятность распада в будущем. Этот же эффект имеет место при бросании монеты. Если у вас пять раз выпал орёл, вероятность шестой раз выпасть орлу остаётся по-прежнему равной 0.5.

Вероятность распада ядер одного вещества всегда одна и та же, независимо от их возраста. Допустим, половина ядер какого-либо изотопа распадается за один год. Какое-то ядро, избежавшее распада в первый год, по-прежнему будет иметь вероятность ½ распасться на протяжении второго года. Если сохранится на протяжении двух лет, то вероятность распада на третий год снова будет ½.

💡 Теперь перейдем к практике и поучимся решать основные задачи. Здесь имеются две задачи из ЕГЭ по физике, но также я добавил более сложные задачи, которые не встречались мне в ЕГЭ, однако встречались в вузовской программе для физиков.

Практика решения задач

Задача 1. Какая доля радиоактивных ядер распадается через интервал времени, равный половине периода полураспада? Ответ приведите в процентах и округлите до целых.

Решение:

Задача 2. После крупной радиационной аварии, произошедшей в 1986 году на Чернобыльской атомной электростанции, некоторые участки местности оказались сильно загрязнены радиоактивным изотопом цезия-137 с периодом полураспада 30 лет. На некоторых участках норма максимально допустимого содержания цезия-137 была превышена в 1000 раз. Через сколько периодов полураспада после загрязнения такие участки местности вновь можно считать удовлетворяющими норме? Ответ округлите до целого числа.

Решение:

Задача 3. Период полураспада элемента 1 в три раза больше периода полураспада элемента 2. За некоторое время число атомов элемента 1 уменьшилось в 8 раз. Во сколько раз за это же время уменьшилось число атомов элемента 2?

Решение:

Задача 4*. Вычислить постоянную распада λ для изотопов радия:
а) ²¹⁹Ra; б) ²²⁶Ra; в) ²³⁰Ra. Чему равна вероятность распада изотопов радия за время t = 1 час ?

Решение:

Задача 5*. При определении периода полураспада короткоживущего радиоактивного изотопа использовался счётчик импульсов. За минуту в начале наблюдения было насчитано Δn₀ = 250 импульсов, а через время τ = 1 час было зарегистрировано Δn = 92 импульса. Чему равен период полураспада данного изотопа?

Решение:

Задача 6*. Известно, что из радиоактивного полония ²¹⁰Po массой m = 2.5 грамм за время t = 32 дня в результате его распада образуется гелий объемом V = 40 см³ при нормальных условиях: p₀ = 10⁵ Па и τ₀ = 273 К. Определить по этим данным период полураспада данного изотопа полония.

Решение:

Задача 7*.Оценить количество тепла, которое выделяет полоний ²¹⁰Po массой m = 1 мг за время, равное периоду полураспада этих ядер, если испускаемые α-частицы имеют кинетическую энергию Wα = 5.3 МэВ.

Решение:

Задача 8*. Пусть в ядре урана ²³⁸U альфа-частица сталкивается с потенциальным барьером 5·10²⁰ раз в секунду и Ψвнеш/Ψвнутр = 10⁻¹⁹.
а) Какова вероятность распада этого ядра в 1 сек ?
б) Каково среднее время жизни этого ядра?

Решение:

Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram

При всем разнообразии реакций самопроизвольного (спонтанного) распада ядер в этом процессе наблюдается общая закономерность, которую можно описать математически. Интересно, что зависимость количества распавшихся ядер от времени задается одной и той же функцией для различных ядер, участвующих в распаде. Перейдем к количественному описанию процессов радиоактивного распада.

Большинство изотопов любого химического элемента превращается в более устойчивые изотопы путем радиоактивного распада. Каждый радиоактивный элемент распадается со своей, присущей только ему «скоростью». При этом для каждого радиоактивного ядра существует характерное время, называемое периодом полураспада , спустя которое в исходном состоянии остается половина имевшихся ядер. Таким образом, периодом полураспада  называется промежуток времени, за который распадается половина начального количества  радиоактивных ядер. Другая половина ядер превращается в более устойчивые изотопы посредством распада.
Отметим, что период полураспада не зависит от того, в каком состоянии находится вещество: твердом, жидком или газообразном. Кроме того, период полураспада радиоактивного вещества не зависит от его количества, от времени, места и условий, в которых оно находится. Поэтому количество радиоактивных ядер «тогда»  и «сейчас»  непосредственно определяет промежуток времени ,  прошедший с момента уменьшения числа ядер от  до .
Невозможно точно предсказать, когда произойдет распад данного ядра. Однако можно оценить среднее число ядер, которые распадутся за данный промежуток времени. Таким образом, закон радиоактивного распада является статистическим и он справедлив только при достаточно большом количестве радиоактивных ядер.

Для записи закона радиоактивного распада будем считать, что в начальный момент времени () число радиоактивных ядер . Через промежуток времени, равный периоду полураспада, это число будет , еще через такой же промежуток времени —  (рис. 218). Спустя промежуток времени, равный n периодам полураспада , радиоактивных ядер останется:

(1)

Это соотношение выражает закон радиоактивного распада, который можно сформулировать следующим образом:

число нераспавшихся радиоактивных ядер убывает с течением времени по закону, представленному соотношением (1).

Закон радиоактивного распада позволяет найти число нераспавшихся ядер в любой момент времени. Полученное выражение хорошо описывает распад радиоактивных ядер, если их количество достаточно велико.
Приведем экспериментальные результаты, которые показывают, что при малом количестве радиоактивных ядер это выражение неприменимо. На рисунке 219 изображен график распада 47 ядер изотопа фермия , период полураспада которого .  Из рисунка 219 видно, что пока ядер было достаточно много — от 47 до 12, то показательная функция хорошо описывала закон распада. Однако при меньшем числе ядер истинная зависимость существенно отличается от показательной функции.
Периоды полураспада некоторых радиоактивных изотопов веществ приведены в таблице 11.

Таблица 11. Периоды полураспада радиоактивных изотопов веществ
Вещество	Период полураспада
	30,17 лет
	5,3 года
	8,04 суток
	24 390 лет
	1600 лет
	3,8 суток
	700 млн лет
	4,5 млрд лет

Впервые процесс радиоактивного распада для измерения промежутков времени был использован в 1904 г. Резерфордом. По отношению концентрации урана и его дочернего продукта распада (гелия) он определил возраст урановой породы. Эта работа положила начало ядерной геохронологии — определению возраста различных минералов Земли по радиоактивным долгоживущим веществам. В дальнейшем исследование процессов ядерного синтеза позволило перейти к ядерной космохронологии, т.е. к определению продолжительных промежутков времени, прошедших с момента образования элементов в масштабах Галактики и Вселенной. В основу ядерной космохронологии положена неизменность «скорости» радиоактивного распада. В 1927 г. американский ученый Г. Блюмгарт, используя изотоп  , впервые определил скорость кровотока у людей. В 1934 г. венгерский ученый Дьердь фон Хевеши, используя дейтерий, впервые установил, что в организме человека вода полностью обновляется в течение 14 суток.  В 1943 г. Дьердь фон Хевеши была присуждена Нобелевская премия по химии «за работу по использованию изотопов в качестве меченых атомов при изучении химических процессов».