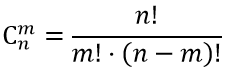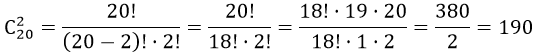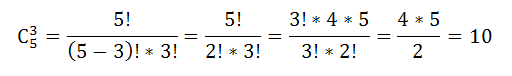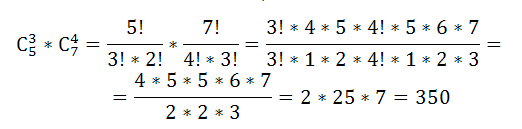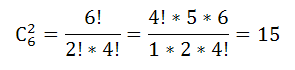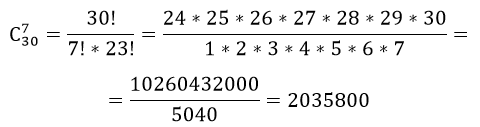Сочетания
- Сочетания без повторений
- Сочетания с повторениями
- Биномиальные коэффициенты и их свойства
- Примеры
п.1. Сочетания без повторений
Сочетаниe без повторений – это неупорядоченная ⟨n,k⟩-выборка без повторений, k ≤ n. Общее количество сочетаний без повторений: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$
Внимание! Главным отличием сочетаний от размещений является неупорядоченность выборок. Если для размещения выборки (a,b)≠(b,a) не равны, то для сочетания (a,b)=(b,a) – одна и та же выборка.
Сочетания используются тогда, когда порядок выборки не важен.
Например:
Из 10 программистов нужно отобрать 4 для участия в проекте. Сколькими способами это можно сделать?
$$mathrm{ n = 10, k=4 }$$ В данном случае, порядок отбора не важен (выборка неупорядоченная); каждый кандидат может войти только один раз в выборку (выборка без повторений). Поэтому рассматриваем неупорядоченные ⟨10,4⟩ –выборки без повторений. Количество способов отбора равно: $$mathrm{ C_{10}^4=frac{10!}{6! 4!}=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 }$$ Ответ: 210.
п.2. Сочетания с повторениями
Сочетаниe с повторениями – это неупорядоченная ⟨n,k⟩-выборка с повторениями. Общее количество сочетаний с повторениями: $$ mathrm{ overline{C}_n^k=frac{(n+k-1)!}{(n-1)k!} } $$
$$ mathrm{ overline{C}_n^k=C_{n+k-1}{k} } $$
Например:
Нужно отобрать 4 программистов для участия в проекте. Многочисленных претендентов можно разделить на две категории: желающих работать удаленно и предпочитающих работу в офисе. Сколько всего комбинаций из любителей офиса и удалёнки может оказаться в выбранной четвёрке? $$mathrm{ n = 2, k=4 }$$ Порядок отбора не важен; кандидатов из каждой категории может быть несколько или ни одного. Поэтому рассматриваем неупорядоченные ⟨2,4⟩ –выборки с повторениями: $$ mathrm{ overline{C}_2^4=frac{(2+4-1)!}{(2-1)4!}=frac{5!}{4!}=5 } $$ Всего – 5 комбинаций: OOOO,OOOD,OODD,ODDD,DDDD
где O – любитель офиса; D – любитель удалёнки. Напоминаем, что порядок не важен – важен только состав группы.
Ответ: 5.
п.3. Биномиальные коэффициенты и их свойства
Подробно о биноме – см. §28 справочника для 7 класса.
Для n-й степени бинома справедливо выражение: $$ mathrm{ (apm b)^n=a^n+C_n^1a^{n-1}bpm C_n^2a^{n-2}b^2+…+C_n^{n-1}b^n } $$ где (mathrm{C_n^k}) – биномиальные коэффициенты, к оторые одновременно являются количествами сочетаний без повторений из n по k: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$ Таким образом, биномиальные коэффициенты можно определять как с помощью треугольника Паскаля, так и с помощью данной формулы.
Заметим, что в литературе также часто встречается обозначение (mathrm{left(_k^nright)}) для биномиальных коэффициентов (mathrm{left(C_n^kright)}).
Свойства биномиальных коэффициентов
Свойство симметрии
$$mathrm{ C_n^k=C_n^{n-k} }$$
Свойство Паскаля
$$mathrm{ C_n^k=C_{n-1}^{k-1}+C_{n-1}^k }$$
Замена индексов
$$mathrm{ C_n^mC_m^{n-k}=C_{n}^{k}C_{k}^{n-m} }$$
Вынесение за скобки
$$mathrm{ C_n^k=frac{n}{k}C_{n-1}^{k-1} }$$
Рекуррентные формулы
begin{gather*}mathrm{ C_n^k=frac{n-k+1}{k}C_{n}^{k-1} }\ mathrm{ C_n^k=frac{n}{n-k}C_{n-1}^k } end{gather*}
Свойство суммы
$$mathrm{ C_n^0+C_n^1+C_n^2+…+ C_n^n=sum_{k=0}^nC_n^k=2^n }$$
Свойство разности
$$mathrm{ C_n^0-C_n^1+C_n^2-…+(-1)^nC_n^n=sum_{k=0}^n(-1)^kC_n^k=0 }$$
Свойства максимума
Если n – четное, то максимальное значение (mathrm{C_n^k}) имеет при (mathrm{k=frac{n}{2}}).
Если n – нечетное, то максимальное значение имеют два коэффициента (mathrm{C_n^k}), при (mathrm{k=frac{n-1}{2}}) и (mathrm{k=frac{n+1}{2}})
Свёртка Вандермонда
$$mathrm{ sum_{r=0}^kC_n^rC_m^{k-r}=C_{n+m}^k }$$
Сумма квадратов
$$mathrm{ sum_{k=0}^n(C_n^k)^2=C_{2n}^n }$$
Взвешенное суммирование
begin{gather*} mathrm{ sum_{k=0}^nnC_n^k=n2^{n-1} }\ mathrm{ sum_{k=0}^nn^2C_n^k=n(n+1)2^{n-2} } end{gather*}
Связь с числами Фибоначчи
$$mathrm{ C_n^0+C_{n-1}^1+…+C_{n-k}^{k}+…+C_{0}^{n}=F_{n+1} }$$
п.4. Примеры
Пример 1. На столе лежит 10 яблок и 5 груш.
1) Сколькими способами можно выбрать 7 фруктов?
2) Сколькими способами можно выбрать 7 фруктов, чтобы среди них было 3 груши?
1) Всего у нас n = 10 + 5 = 15 фруктов. Нужно выбрать k = 7 фруктов.
Порядок выбора не важен, т.е. выборка неупорядоченная. Находим: $$ mathrm{ C_n^k=C_{15}^7=frac{15cdot 14cdot 13cdot 12cdot 11cdot 10cdot 9}{1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7}=6435 } $$ Существует 6435 способов выбрать 7 фруктов из 15.
2) Выбираем 4 яблока из 10 и 3 груши из 5.
Для яблок: $$ mathrm{ C_{10}^4=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 } $$ Для груш: $$ mathrm{ C_3^5=C_{5}^2=frac{5cdot 4}{1cdot 2}=10 } $$ По правилу произведения, общее количество способов выбрать 4 яблока и 3 груши: $$ mathrm{ C_{10}^3cdot C_{5}^3=210cdot 10=2100 } $$ Ответ: 1) 6435; 2) 2100.
Пример 2. В кондитерском магазине продаётся 4 вида пирожных. Сколькими способами можно купить 7 пирожных? $$ mathrm{ n=4, k=7 } $$ Порядок выбора пирожных неважен – выборка неупорядоченная; пирожные одного вида могут повторяться. Значит, находим количество сочетаний с повторениями: $$ mathrm{ overline{C}_4^7=C_{7+4-1}^7=C_{10}^7=C_{10}^3=frac{10cdot 9cdot 8}{1cdot 2cdot 3}=120 } $$ Ответ: 120
Пример 3. Рота состоит из 3 офицеров, 6 сержантов и 15 рядовых. Сколькими способами можно выбрать из них отряд, состоящий из 1 офицера, 2 сержантов и 5 рядовых?
По всем трём множествам делаем неупорядоченную выборку (т.е., сочетания) без повторений.
Выбираем офицеров: (mathrm{C_3^1=frac31=3})
Выбираем сержантов: (mathrm{C_6^2=frac{6cdot 5}{1cdot 2}=15})
Выбираем рядовых: (mathrm{C_{15}^6=frac{15cdot 14cdot 13cdot 12cdot 11}{1cdot 2cdot 3cdot 4cdot 5}=3003})
По правилу произведения, отряд можно выбрать:
(mathrm{3cdot 15cdot 3003=135135}) способами.
Ответ: 135135.
Пример 4. Найдите сумму
a) (mathrm{C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6})
По свойству суммы (mathrm{sum_{k=0}^6C_6^k=2^6}). Получаем: $$ mathrm{ C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6=sum_{k=0}^6C_6^k-C_6^0=2^6-1=64-1=63 } $$
б) (mathrm{C_n^1+6C_n^2+6C_n^3}) $$ mathrm{ C_n^1=n, C_n^2=frac{n(n-1)}{2}, C_n^3=frac{n(n-1)(n-2)}{6} } $$ Получаем begin{gather*} mathrm{ C_n^1+6C_n^2+6C_n^3=n+6cdot frac{n(n-1)}{2}+6cdot frac{n(n-1)(n-2)}{6}=}\ mathrm{ =n(1+3(n-1)+(n-1)(n-2))=n(3n-2+n^2-3n+2)=n^3 } end{gather*} Ответ: а) 63; б) n3.
Пример 5. Рассчитайте все (mathrm{C_{10}^k}) по рекуррентной формуле (mathrm{C_{n}^k=frac{n-k+1}{k}C_n^{k-1}}).
Постройте график (mathrm{C_{10}^k(k)}). Сделайте выводы.
Начальное значение (mathrm{C_{10}^0=1}).
|
0 $$mathrm{ C_{10}^0=1 }$$ 1 $$mathrm{ C_{10}^1=frac{10-1+1}{1}C_{10}^0=10 }$$ 2 $$mathrm{ C_{10}^2=frac{10-2+1}{2}C_{10}^1=45 }$$ 3 $$mathrm{ C_{10}^3=frac{10-3+1}{3}C_{10}^2=120 }$$ 4 $$mathrm{ C_{10}^4=frac{10-4+1}{4}C_{10}^3=210 }$$ 5 $$mathrm{ C_{10}^4=frac{10-5+1}{5}C_{10}^4=252 }$$ 6 $$mathrm{ C_{10}^6=frac{10-6+1}{6}C_{10}^5=210 }$$ 7 $$mathrm{ C_{10}^7=frac{10-7+1}{7}C_{10}^6=120 }$$ 8 $$mathrm{ C_{10}^6=frac{10-8+1}{8}C_{10}^7=45 }$$ 9 $$mathrm{ C_{10}^9=frac{10-9+1}{9}C_{10}^8=10 }$$ 10 $$mathrm{ C_{10}^{10}=frac{10-10+1}{10}C_{10}^9=1 }$$ |
 |
На графике видно симметрию коэффициентов: (mathrm{C_{10}^k=C_{10}^{10-k}}).
Т.к. n = 10 – чётное, максимальный коэффициент при (mathrm{k=frac{n}{2}=5, C_{10}^5=252}).
Можем также проверить свойство суммы: (mathrm{sum_{k=0}^{10}C_{10}^k=1024=2^{10}}).
Рейтинг пользователей
Число сочетаний
- Главная
- /
- Математика
- /
- Комбинаторика
- /
- Число сочетаний
Для того чтобы найти число сочетаний из n по k без повторений воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Сколько сочетаний будет из
n=
объектов по
k=
?
Ответ:
0
Просто введите общее число объектов (n) и длину одного сочетания (k).
Число сочетаний формула
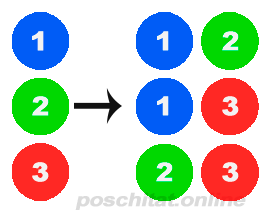
По данной формуле можно найти только сочетания с неповторяющимися объектами и без учета позиции элемента. То есть у нас есть три объекта: 1 2 3. И нам надо определить все варианты по 2 элемента. Тогда мы получим только три варианта: 1 и 2, 1 и 3, 2 и 3. Варианты 2 и 1, 3 и 1, 3 и 2 считаются идентичными предыдущим. А варианты с повторяющимися объектами (1 и 1, 2 и 2, 3 и 3) не рассматриваются вообще.
Пример
Определим какое количество неповторимых паролей можно создать из 26 букв латинского алфавита, если длина пароля будет 5 символов.
С526 = 26! / (26-5)! ⋅ 5! = 26! / 21! ⋅ 5! = 22⋅23⋅24⋅25⋅26/1⋅2⋅3⋅4⋅5 = 7893600 / 120 = 65780
Итого мы получили 65780 вариантов паролей
См. также
Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.
Обозначение: $С_n^m$
Допустим, имеется три буквы А, В и С.
Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС.
При подсчете числа сочетаний элементов — порядок не важен.
Запишем формулу сочетания
Пример 1
В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем
Пример 2
Пусть имеется множество, содержащие 4 буквы: {А,В,С,D}.
Записать все возможные сочетания из указанных букв по три.
Решение
По формуле сочетания имеем,
$C_4^3 =frac{{4!}}{{left( {4 — 3} right)!cdot3!}} = frac{{4!}}{{3!}} = frac{{1cdot2cdot3cdot4}}{{1cdot2cdot3}} = 4$
Пример 3
В ящике 15 деталей, среди которых 6 бракованных. Наугад выбирается комплект из 5 деталей. Сколькими способами можно составить такой комплект, в котором 2 детали бракованные?
Решение
$C_{6}^2$ — количество способов выбора двух бракованных деталей из шести
$C_{9}^3$ — количество способов выбора трех исправных деталей из девяти
Тогда количество комбинаций по правилу умножения будет
$C_{6}^2·C_{9}^3=frac{{6!}}{{(6-2)!2!}}·frac{{9!}}{{(9-3)!3!}}=15·84=1260$
Пример 4
Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?
Решение
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно
Пример 5
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?
Решение
Из пяти женщин необходимо выбрать по три. Следователь, число таких способов отбора равно $С_5^3$
Число способов отбора мужчин, четырех из семи равно $С_7^4$
По формуле комбинаторики – сочетания, группу можно сформировать способами:
Пример 6
Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?
Решение
Число способов выбора офицера: $С_3^1$
сержантов $С_6^2$
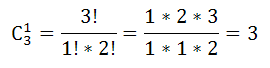
по аналогии, число комбинаций выбора курсантов, получаем $С_30^7$
Итак, получаем число способов составления суточного наряда
$$C_3^1cdot{C_6^2}cdot{C_{30}^7}=3cdot15cdot2035800=91611000$$
Формулы комбинаторики
Рассмотрим задачу
подсчета числа выборок из данного
множества в общем виде. Пусть имеется
некоторое множество N,
состоящее из n
элементов. Любое подмножество, состоящее
из m
элементов можно рассматривать без учета
их порядка, так и с его учетом, т.е. при
изменении порядка переходим к другой
m
– выборке.
Сформулируем
следующие определения:
Размещения без повторения
Размещением без
повторения из n
элементов по m
называется всякое упорядоченное
подмножество множества N,
содержащее m
различных элементов.
Из определения
следует, что два размещения отличаются
друг от друга, как элементами, так и их
порядком, даже если элементы одинаковы.
Теорема 3.
Число размещений без повторения равно
произведению m
сомножителей, наибольшим из которых
является число n.
Записывают:
Перестановки без повторений
Перестановками
из n
элементов называются различные
упорядочения множества N.
Из этого определения
следует, что две перестановки отличаются
только порядком элементов и их можно
рассматривать как частный случай
размещений.
Теорема 4.
Число различных перестановок без
повторений вычисляется по формуле
Сочетания без повторений
Сочетанием без
повторения из n
элементов по m
называется любое неупорядоченное
подмножество множества N,
содержащее m
различных элементов.
Из определения
следует, что два сочетания различаются
только элементами, порядок не важен.
Теорема 5.
Число сочетаний без повторений вычисляют
по одной из следующих формул:
Пример 1.
В комнате 5 стульев. Сколькими способами
можно разместить на них
а) 7 человек; б) 5
человек; в) 3 человека?
Решение:
а) Прежде всего надо выбрать 5 человек
из 7 для посадки на стулья. Это можно
сделать
способом. С каждым выбором конкретной
пятерки можно произвестиперестановок местами. Согласно теореме
умножения искомое число способов посадки
равно.
Замечание:
Задачу можно решать, используя только
теорему произведения, рассуждая следующим
образом: для посадки на 1-й стул имеется
7 вариантов, на 2-й стул-6 вариантов, на
3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов
посадки 7 человек на 5 стульев равно
.
Решения обоими способами согласуются,
так как
б) Решение очевидно
–
в)
– число выборов занимаемых стульев.
– число размещений
трех человек на трех выбранных стульях.
Общее число выборов
равно
.
Не трудно проверить
формулы
;
;
–
число всех подмножеств множества,
состоящего из n
элементов.
Размещения с повторением
Размещением с
повторением из n
элементов по m
называется всякое упорядоченное
подмножество множества N,
состоящее из m
элементов так, что любой элемент ожжет
входить в это подмножество от 1 до m
раз, либо вообще в нем отсутствовать.
Число
размещений с повторением обозначают
и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
Пример 2.
Пусть дано множество из трех букв N
= {a,
b,
c}.
Назовем словом любой набор из букв,
входящих в это множество. Найдем
количество слов длиной 2, которые можно
составить из этих букв:
.
Замечание:
Очевидно, размещения с повторением
можно рассматривать и при
.
Пример 3.
Требуется из букв {a,
b},
составить всевозможные слова длиной
3. Сколькими способами это можно сделать?
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Перестановки, размещения и сочетания. Формулы.
Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:
- Введение. Множества и выборки.
- Размещения без повторений из $n$ элементов по $k$.
- Размещения с повторениями из $n$ элементов по $k$.
- Перестановки без повторений из $n$ элементов
- Перестановки с повторениями.
- Сочетания без повторений из $n$ элементов по $k$.
- Сочетания с повторениями из $n$ элементов по $k$.
Введение. Множества и выборки.
В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.
Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме “Понятие множества. Способы задания множеств”.
Очень краткий рассказ про множества: показатьскрыть
Рассмотрим некое непустое конечное множество $U$, мощность которого равна $n$, $|U|=n$ (т.е. в множестве $U$ имеется $n$ элементов). Введём такое понятие, как выборка (некоторые авторы именуют её кортежем). Под выборкой объема $k$ из $n$ элементов (сокращённо $(n,k)$-выборкой) будем понимать набор элементов $(a_1, a_2,ldots, a_k)$, где $a_iin U$. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Две упорядоченные выборки, различающиеся лишь порядком элементов, являются различными. Если порядок следования элементов выборки не является существенным, то выборку именуют неупорядоченной.
Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.
Для примера рассмотрим множество $U={a,b,c,d,e}$. Множество $U$ содержит 5 элементов, т.е. $|U|=5$. Выборка без повторений может быть такой: $(a,b,c)$. Данная выборка содержит 3 элемента, т.е. объём этой выборки равен 3. Иными словами, это $(5,3)$-выборка.
Выборка с повторениями может быть такой: $(a,a,a,a,a,c,c,d)$. Она содержит 8 элементов, т.е. объём её равен 8. Иными словами, это $(5,8)$-выборка.
Рассмотрим ещё две $(5,3)$-выборки: $(a,b,b)$ и $(b,a,b)$. Если мы полагаем наши выборки неупорядоченными, то выборка $(a,b,b)$ равна выборке $(b,a,b)$, т.е. $(a,b,b)=(b,a,b)$. Если мы полагаем наши выборки упорядоченными, то $(a,b,b)neq(b,a,b)$.
Рассмотрим ещё один пример, немного менее абстрактный 🙂 Предположим, в корзине лежат шесть конфет, причём все они различны. Если первой конфете поставить в соответствие цифру 1, второй конфете – цифру 2 и так далее, то с конфетами в корзине можно сопоставить такое множество: $U={1,2,3,4,5,6}$. Представьте, что мы наугад запускаем руку в корзинку с целью вытащить три конфеты. Вытащенные конфеты – это и есть выборка. Так как мы вытаскиваем 3 конфеты из 6, то получаем (6,3)-выборку. Порядок расположения конфет в ладони совершенно несущественен, поэтому эта выборка является неупорядоченной. Ну, и так как все конфеты различны, то выборка без повторений. Итак, в данной ситуации говорим о неупорядоченной (6,3)-выборке без повторений.
Теперь подойдём с иной стороны. Представим себе, что мы находимся на фабрике по производству конфет, и на этой фабрике производятся конфеты четырёх сортов. Множество $U$ в этой ситуации таково: $U={1,2,3,4 }$ (каждая цифра отвечает за свой сорт конфет). Теперь вообразим, что все конфеты ссыпаются в единый жёлоб, около которого мы и стоим. И, подставив ладони, из этого потока отбираем 20 конфет. Конфеты в горсти – это и есть выборка. Играет ли роль порядок расположения конфет в горсти? Естественно, нет, поэтому выборка неупорядоченная. Всего 4 сорта конфет, а мы отбираем двадцать штук из общего потока – повторения сортов неизбежны. При этом выборки могут быть самыми различными: у нас даже могут оказаться все конфеты одного сорта. Следовательно, в этой ситуации мы имеем дело с неупорядоченной (4,20)-выборкой с повторениями.
Рассмотрим ещё пару примеров. Пусть на кубиках написаны различные 7 букв: к, о, н, ф, е, т, а. Эти буквы образуют множество $U={к,о,н,ф,е,т,а}$. Допустим, из данных кубиков мы хотим составить “слова” из 5 букв. Буквы этих слов (к примеру, «конфе», «тенко» и так далее) образуют (7,5)-выборки: $(к,о,н,ф,е)$, $(т,е,н,к,о)$ и т.д. Очевидно, что порядок следования букв в такой выборке важен. Например, слова «нокфт» и «кфтон» различны (хотя состоят из одних и тех же букв), ибо в них не совпадает порядок букв. Повторений букв в таких «словах» нет, ибо в наличии только семь кубиков. Итак, набор букв каждого слова представляет собой упорядоченную (7,5)-выборку без повторений.
Еще один пример: мы составляем всевозможные восьмизначные числа из четырёх цифр 1, 5, 7, 8. Например, 11111111, 15518877, 88881111 и так далее. Множество $U$ таково: $U={1,5,7,8}$. Цифры каждого составленного числа образуют (4,8)-выборку. Порядок следования цифр в числе важен, т.е. выборка упорядоченная. Повторения допускаются, поэтому здесь мы имеем дело с упорядоченной (4,8)-выборкой с повторениями.
Размещения без повторений из $n$ элементов по $k$
Размещение без повторений из $n$ элементов по $k$ – упорядоченная $(n,k)$-выборка без повторений.
Так как элементы в рассматриваемой выборке повторяться не могут, то мы не можем отобрать в выборку больше элементов, чем есть в исходном множестве. Следовательно, для таких выборок верно неравенство: $n≥ k$. Количество размещений без повторений из $n$ элементов по $k$ определяется следующей формулой:
$$
begin{equation}
A_{n}^{k}=frac{n!}{(n-k)!}
end{equation}
$$
Что обозначает знак “!”? : показатьскрыть
Пример №1
Алфавит состоит из множества символов $E={+,*,0,1,f}$. Определим количество таких трёхсимвольных слов в этом алфавите, которые не содержат повторяющихся букв.
Решение
Под трёхсимвольными словами будем понимать выражения вида “+*0” или “0f1”. В множестве $E$ пять элементов, поэтому буквы трехсимвольных слов образуют (5,3)-выборки. Первый вопрос: эти выборки упорядочены или нет? Слова, которые отличаются лишь порядком букв, полагаются различными, поэтому порядок элементов в выборке важен. Значит, выборка является упорядоченной. Второй вопрос: допускаются повторения или нет? Ответ на этот вопрос даёт условие: слова не должны содержать повторяющихся букв. Подводим итоги: буквы каждого слова, удовлетворяющего условию задачи, образуют упорядоченную (5,3)-выборку без повторений. Иными словами, буквы каждого слова образуют размещение без повторений из 5 элементов по 3. Вот примеры таких размещений:
$$
(+,*,f), ; (*,+,f), ; (1,+,0)
$$
Нас же интересует общее количество этих размещений. Согласно формуле (1) количество размещений без повторений из 5 элементов по 3 будет таким:
$$
A_{5}^{3}=frac{5!}{(5-3)!}=frac{5!}{2!}=60.
$$
Т.е. можно составить 60 трёхсимвольных слов, буквы которых не будут повторяться.
Ответ: 60.
Размещения с повторениями из $n$ элементов по $k$
Размещение с повторениями из $n$ элементов по $k$ – упорядоченная $(n,k)$-выборка с повторениями.
Количество размещений с повторениями из $n$ элементов по $k$ определяется следующей формулой:
$$
begin{equation}
bar{A}_{n}^{k}=n^k
end{equation}
$$
Пример №2
Сколько пятизначных чисел можно составить из множества цифр ${5,7,2}$?
Решение
Из данного набора цифр можно составить пятизначные числа 55555, 75222 и так далее. Цифры каждого такого числа образуют (3,5)-выборку: $(5,5,5,5,5)$, $(7,5,2,2,2)$. Зададимся вопросом: что это за выборки? Во-первых, цифры в числах могут повторяться, поэтому мы имеем дело с выборками с повторениями. Во-вторых, порядок расположения цифр в числе важен. Например, 27755 и 77255 – разные числа. Следовательно, мы имеем дело с упорядоченными (3,5)-выборками с повторениями. Общее количество таких выборок (т.е. общее количество искомых пятизначных чисел) найдём с помощью формулы (2):
$$
bar{A}_{3}^{5}=3^5=243.
$$
Следовательно, из заданных цифр можно составить 243 пятизначных числа.
Ответ: 243.
Перестановки без повторений из $n$ элементов
Перестановка без повторений из $n$ элементов – упорядоченная $(n,n)$-выборка без повторений.
По сути, перестановка без повторений есть частный случай размещения без повторений, когда объём выборки равен мощности исходного множества. Количество перестановок без повторений из $n$ элементов определяется следующей формулой:
$$
begin{equation}
P_{n}=n!
end{equation}
$$
Эту формулу, кстати, легко получить, если учесть, что $P_n=A_{n}^{n}$. Тогда получим:
$$
P_n=A_{n}^{n}=frac{n!}{(n-n)!}=frac{n!}{0!}=frac{n!}{1}=n!
$$
Пример №3
В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?
Решение
Пусть первому мороженому соответствует цифра 1, второму – цифра 2 и так далее. Мы получим множество $U={1,2,3,4,5}$, которое будет представлять содержимое морозилки. Порядок съедения может быть таким: $(2,1,3,5,4)$ или таким: $(5,4,3,1,2)$. Каждый подобный набор есть (5,5)-выборка. Она будет упорядоченной и без повторений. Иными словами, каждая такая выборка есть перестановка из 5 элементов исходного множества. Согласно формуле (3) общее количество этих перестановок таково:
$$
P_5=5!=120.
$$
Следовательно, существует 120 порядков выбора очередности съедения.
Ответ: 120.
Перестановки с повторениями
Перестановка с повторениями – упорядоченная $(n,k)$-выборка с повторениями, в которой элемент $a_1$ повторяется $k_1$ раз, $a_2$ повторяется $k_2$ раза так далее, до последнего элемента $a_r$, который повторяется $k_r$ раз. При этом $k_1+k_2+ldots+k_r=k$.
Общее количество перестановок с повторениями определяется формулой:
$$
begin{equation}
P_{k}(k_1,k_2,ldots,k_r)=frac{k!}{k_1!cdot k_2!cdot ldots cdot k_r!}
end{equation}
$$
Пример №4
Слова составляются на основе алфавита $U={a,b,d}$. Сколько различных слов из семи символов может быть составлено, если в этих словах буква “a” должна повторяться 2 раза; буква “b” – 1 раз, а буква “d” – 4 раза?
Решение
Вот примеры искомых слов: “aabdddd”, “daddabd” и так далее. Буквы каждого слова образуют (3,7)-выборку с повторениями: $(a,a,b,d,d,d,d)$, $(d,a,d,d,a,b,d)$ и т.д. Каждая такая выборка состоит из двух элементов “a”, одного элемента “b” и четырёх элементов “d”. Иными словами, $k_1=2$, $k_2=1$, $k_3=4$. Общее количество повторений всех символов, естественно, равно объёму выборки, т.е. $k=k_1+k_2+k_3=7$. Подставляя эти данные в формулу (4), будем иметь:
$$
P_7(2,1,4)=frac{7!}{2!cdot 1!cdot 4!}=105.
$$
Следовательно, общее количество искомых слов равно 105.
Ответ: 105.
Сочетания без повторений из $n$ элементов по $k$
Сочетание без повторений из $n$ элементов по $k$ – неупорядоченная $(n,k)$-выборка без повторений.
Общее количество сочетаний без повторений из $n$ элементов по $k$ определяется формулой:
$$
begin{equation}
C_{n}^{k}=frac{n!}{(n-k)!cdot k!}
end{equation}
$$
Пример №5
В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?
Решение
Итак, в данной задаче исходное множество таково: $U={1,2,3,4,5,6,7,8,9,10}$. Из этого множества мы выбираем четыре элемента (т.е., четыре карточки из корзины). Номера вытащенных элементов образуют (10,4)-выборку. Повторения в этой выборке не допускаются, так как номера всех карточек различны. Вопрос вот в чём: порядок выбора карточек играет роль или нет? Т.е., к примеру, равны ли выборки $(1,2,7,10)$ и $(10,2,1,7)$ или не равны? Тут нужно обратиться к условию задачи. Карточки вынимаются для того, чтобы потом найти сумму элементов. А это значит, что порядок карточек не важен, так как от перемены мест слагаемых сумма не изменится. Например, выборке $(1,2,7,10)$ и выборке $(10,2,1,7)$ будет соответствовать одно и то же число $1+2+7+10=10+2+1+7=20$. Вывод: из условия задачи следует, что мы имеем дело с неупорядоченными выборками. Т.е. нам нужно найти общее количество неупорядоченных (10,4)-выборок без повторений. Иными словами, нам нужно найти количество сочетаний из 10 элементов по 4. Используем для этого формулу (5):
$$
C_{10}^{4}=frac{10!}{(10-4)!cdot 4!}=frac{10!}{6!cdot 4!}=210.
$$
Следовательно, общее количество искомых наборов равно 210.
Ответ: 210.
Сочетания с повторениями из $n$ элементов по $k$
Сочетание с повторениями из $n$ элементов по $k$ – неупорядоченная $(n,k)$-выборка с повторениями.
Общее количество сочетаний с повторениями из $n$ элементов по $k$ определяется формулой:
$$
begin{equation}
bar{C}_{n}^{k}=frac{(n+k-1)!}{(n-1)!cdot k!}
end{equation}
$$
Пример №6
Представьте себе, что мы находимся на конфетном заводе, – прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных “конфетных комбинаций” может оказаться в горсти?
Решение
Если принять, что первому сорту соответствует число 1, второму сорту – число 2 и так далее, то исходное множество в нашей задаче таково: $U={1,2,3,4}$. Из этого множества мы выбираем 20 элементов (т.е., те самые 20 конфет с конвейера). Пригоршня конфет образует (4,20)-выборку. Естественно, повторения сортов будут. Вопрос в том, играет роль порядок расположения элементов в выборке или нет? Из условия задачи следует, что порядок расположения элементов роли не играет. Нам нет разницы, будут ли в горсти располагаться сначала 15 леденцов, а потом 4 шоколадных конфеты, или сначала 4 шоколадных конфеты, а уж потом 15 леденцов. Итак, мы имеем дело с неупорядоченной (4,20) выборкой с повторениями. Чтобы найти общее количество этих выборок используем формулу (6):
$$
bar{C}_{4}^{20}=frac{(4+20-1)!}{(4-1)!cdot 20!}=frac{23!}{3!cdot 20!}=1771.
$$
Следовательно, общее количество искомых комбинаций равно 1771.
Ответ: 1771.