Формула числа сочетаний
Спасибо за ваши закладки и рекомендации
Определение числа сочетаний
Пусть имеется $n$ различных объектов и требуется найти число сочетаний из $n$ объектов по $k$. Будем выбирать комбинации из $k$ объектов всеми возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен, в отличие от размещений).
Например, есть три ($n=3$) объекта {1,2,3}, составляем сочетания по $k=2$ объекта в каждом. Тогда выборки {1,2} и {2,1} – это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: {1,2}, {1,3}, {2,3}.
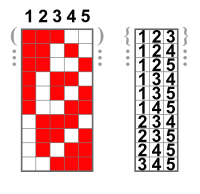
На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6, см. калькулятор сочетаний ниже, который даст формулу расчета).
Общая формула, которая позволяет найти число сочетаний из $n$ объектов по $k$ имеет вид:
$$C_n^k=frac{n!}{(n-k)!cdot k!}.$$
Чаще всего сочетания используются в комбинаторных задачах и задачах на расчет вероятности по формуле классической вероятности (см. теорию и примеры).
Смотрите также другие онлайн-калькуляторы
Чтобы вычислить число сочетаний $C_n^k$ онлайн, используйте калькулятор ниже.
Видеоролик о сочетаниях
Не все понятно? Посмотрите наш видеообзор для формулы сочетаний: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи и использовать онлайн-калькулятор.
Расчетный файл из видео можно бесплатно скачать
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
- Онлайн учебник по теории вероятностей
- Основные формулы комбинаторики
- Примеры решений задач по теории вероятностей
- Заказать свои задачи на вероятность
Решебник по ТВ
Решебник с задачами по комбинаторике и теории вероятностей:
Число сочетаний из n по k элементов очень важное понятие в комбинаторике. Оно показывает сколько существует вариантов выбора k элементов из множества n элементов. При нахождении числа сочетаний используют формулу:
Формула числа сочетаний
{C_n^k = frac {n!}{k! cdot (n-k)!}}
Читается обозначение следующим образом – “C из n по k“.
В сочетаниях не имеет значение порядок, в котором расставлены элементы множества k. Для быстрого нахождения сочетаний в режиме онлайн используйте наш калькулятор.
Рассмотрим понятие сочетаний на примере.
Пример нахождения числа сочетаний
Задача 1
Вспомним известную лотерею “5 из 36” и ответим на вопрос, сколько возможных комбинаций в ней существует.
Решение
Итак, из множества в 36 элементов мы выбираем множества элементов по 5. Подставив значения в формулу получим результат:
C_{36}^5 = dfrac {36!}{5! cdot (36-5)!} = dfrac {36!}{5! cdot 31!}
Далее, вспомним, что такое факториал и упростим выражение. Так как 36! = 1 * 2 * 3 * … * 36, а 31! = 1 * 2 * 3 * … * 31, то числитель и знаменатель можно упростить.
C_{36}^5 = dfrac {36!}{5! cdot 31!} = dfrac {32 cdot 33 cdot 34 cdot 35 cdot 36}{1 cdot 2 cdot 3 cdot 4 cdot 5} = dfrac{45 239 040}{120} = 376 992
Это и будет искомый ответ.
Ответ: 376 992
Полученный ответ очень легко проверить с помощью калькулятора .
1. Даны (3) элемента 
.
a) Сколькими способами можно выбрать (2) из них, если порядок неважен?
Это можно сделать (3) способами — 
; 
; 
— по формуле:
C32=3!2!⋅3−2!=3⋅2!2!⋅1!=3
.
b) Сколькими способами можно выбрать (1) элемент, если порядок неважен?
Это тоже можно сделать (3) способами — 
; 
; 
— по формуле:
C31=3!1!⋅3−1!=3⋅2!1!⋅2!=3
.
2. У Светланы есть (12) платьев. Сколькими способами из них можно выбрать (3) платья для поездки на курорт?
Решение:
так как порядок выбора платьев неважен, нужно вычислить сочетания по (3) элемента из (12) элементов, т. е. (n = 12) и (m = 3).
.
Ответ: три платья из (12) можно выбрать (220) различными способами.
3. Из (6) человек ((2) женщин и (4) мужчин) нужно выбрать (1) женщину и (2) мужчин. Сколькими способами это можно сделать?
Решение:
так как порядок выбора неважен (в конце концов команда будет той же), нужно вычислить, сколькими способами из (2) женщин можно выбрать (1), а из (4) мужчин — двоих.
Количество сочетаний женщин ((n = 2) и (m = 1)):
.
Количество сочетаний мужчин ((n = 4) и (m = 2)):
.
Чтобы получить ответ, используем закон умножения:
Ответ: из данных людей (1) женщину и (2) мужчин можно выбрать (12) различными способами.
4. Четырём игрокам домино раздаётся (28) костей поровну. Сколькими различными способами можно разделить кости домино?
Решение:
первому игроку дать кости можно
C287
способами.
Второму игроку дать кости можно
C217
способами.
Третьему игроку дать кости можно
C147
способами.
Четвёртому игроку дать кости можно
C77=1
способом.
Всего кости можно раздать
C287⋅C217⋅C147⋅C77
способами.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 декабря 2021 года; проверки требуют 4 правки.
В комбинаторике сочетанием из 
по 
называется набор из элементов, выбранных из -элементного множества, в котором не учитывается порядок элементов.
Соответственно, сочетания, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми — этим сочетания отличаются от размещений. Так, например, 3-элементные сочетания 2 и 3 ((нестрогие) подмножества, для которых 
) из 6-элементного множества 1 (
) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов 1.
В общем случае число всех возможных -элементных подмножеств -элементного множества стоит на пересечении -й диагонали и -й строки треугольника Паскаля.[1]
3х элементные подмножества 5 элементного множества
Число сочетаний[править | править код]
Число сочетаний из по равно биномиальному коэффициенту
При фиксированном производящей функцией последовательности чисел сочетаний 
, 
, 
, … является
Двумерной производящей функцией чисел сочетаний является
Сочетания с повторениями[править | править код]
Сочетанием с повторениями из по называется такой -элементный набор из -элементного множества, в котором каждый элемент может участвовать несколько раз, но в котором порядок не учитывается (мультимножество). В частности, число монотонных неубывающих функций из множества 
в множество 
равно числу сочетаний с повторениями из по .
Число сочетаний с повторениями из по равно:
При фиксированном производящая функция чисел сочетаний с повторениями из по равна
![{displaystyle sum _{k=0}^{infty }left[(-1)^{k}{-n choose k}right]x^{k}=(1-x)^{-n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bd6c56f3688025f4714e0d033caee38511f649d)
Двумерной производящей функцией чисел сочетаний с повторениями является
См. также[править | править код]
- Комбинаторика
- Многочлен
- Мультиномиальный коэффициент
- Перестановка
- Размещение
Примечания[править | править код]
- ↑ Удивительный треугольник великого француза. Дата обращения: 20 апреля 2010. Архивировано 21 апреля 2010 года.
Ссылки[править | править код]
- Стенли Р.ruen. Перечислительная комбинаторика. — М.: Мир, 1990.
Число сочетаний
Пусть имеется n различных объектов. Будем выбирать из них k объектов всевозможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок
(он тут не важен, в отличие от размещений).
Например, есть три объекта {1,2,3}, составляем сочетания по 2 объекта в каждом. Тогда выборки {1,2} и {2,1} – это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: {1,2}, {1,3}, {2,3}.
Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид:
Ckn = n!k! ⋅ (n – k)!
Данный онлайн калькулятор позволяет найти число сочетаний из n элементов по k.
Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний – нет), причем именно в k! раз, то есть верна формула связи:
Akn = Ckn ⋅ Pk
Поделиться страницей в социальных сетях:
