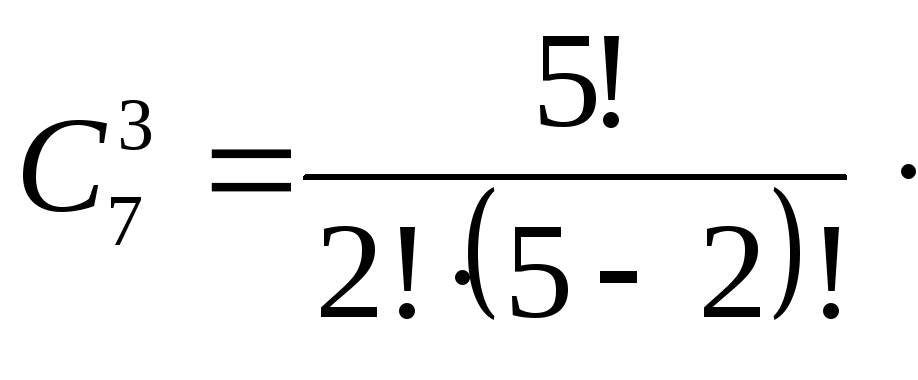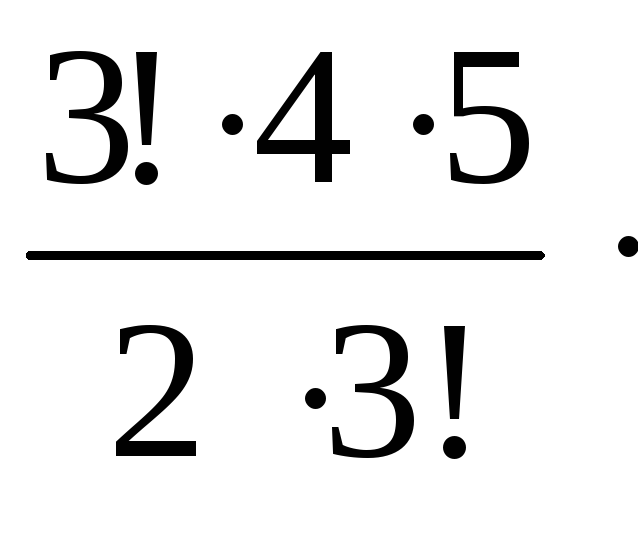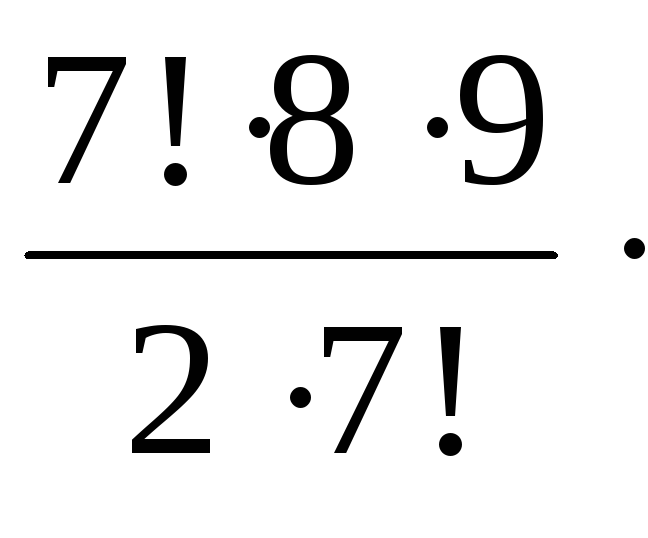Как найти число сочетаний с повторениями

Формула числа сочетаний с повторениями

Раньше мы выяснили, что число способов разложить $k$ различных шаров по $n$ ящикам есть число размещений с повторениями $overline{A}_n^k=n^k.$

А сколько получится способов, если шары одинаковые (в ящике может быть любое число шаров)?

Поступим следующим образом. Обозначим шары нулями, их будет $k$, а также введем $n-1$ единиц, которые будут обозначать “перегородки”. Тогда любая последовательность из $k$ нулей и $n-1$ единиц однозначно зафиксирует способ разложения шаров: число нулей до первой единицы – это число шаров в первом ящике, число нулей между первой и второй единицей – это число шаров во втором ящике и так далее. А расставить $k$ единиц в последовательности из $k+n-1$ объектов можно (мы уже знаем – это число сочетаний)

$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$

способами.

Эта формула носит название числа сочетаний с повторениями из $n$ объектов по $k$. Она описывает, сколькими способами можно составить комбинацию по $k$ элементов из элементов $n$ типов (элементы в комбинации могут повторяться, но порядок их не важен).

Примеры решений

Рассмотрим решение типовых задач.

Пример 1. В магазине продаются булочки трех видов: с маком, изюмом и повидлом. Мама послала Колю купить 6 булочек. Сколько возможных вариантов выбора у него есть?

Решение. По условию задачи требуется составить комбинацию из $k=6$ элементов, которые выбираются (возможны повторения) из объектов $n=3$ типов (с маком, изюмом, или повидлом). Всего возможных наборов булочек будет (по формуле сочетаний с повторенями):

$$overline{C}_3^6=C_{3+6-1}^6=C_{8}^6=frac{8!}{2!cdot 6!}=28.$$

Пример 2. Сколько решений в неотрицательных числах имеет уравнение $x+y+z+q=8?$

Решение. Переформулируем задачу в терминах шаров и ящиков (см. выше вывод формулы). Пусть у нас есть $k=8$ шаров/единичек, их нужно разместить в $n=4$ ящиках (каждый ящик – это слагаемое в выражении слева, вместе как раз шаров во всех ящиках будет 8, то есть равенство выполнится). Так как решение требуется в неотрицательных числах, то ящик в том числе может быть пустым (дополнительных ограничений нет). Применяем формулу числа сочетаний с повторениями:

$$overline{C}_4^8=C_{4+8-1}^8=C_{11}^8=frac{11!}{3!cdot 8!}=165.$$

Найти сочетания с повторениями из n по k

Чтобы вычислить число сочетаний с повторениями $overline{C}_n^k$ онлайн, используйте калькулятор ниже.

Видеоролик о сочетаниях с повторениями

Не все понятно? Посмотрите наш видеообзор для формулы сочетаний с повторениями: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи.

Расчетный файл из видео можно бесплатно скачать

Полезные ссылки

• Онлайн учебник по теории вероятностей
• Основные формулы комбинаторики
• Примеры решений задач по теории вероятностей
• Заказать свои задачи на вероятность

Решебник с задачами по комбинаторике и теории вероятностей:

Сочетания

1. Сочетания без повторений
2. Сочетания с повторениями
3. Биномиальные коэффициенты и их свойства
4. Примеры

п.1. Сочетания без повторений

Сочетаниe без повторений – это неупорядоченная ⟨n,k⟩-выборка без повторений,     k ≤ n. Общее количество сочетаний без повторений: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$

Внимание! Главным отличием сочетаний от размещений является неупорядоченность выборок. Если для размещения выборки (a,b)≠(b,a) не равны, то для сочетания (a,b)=(b,a) – одна и та же выборка.
Сочетания используются тогда, когда порядок выборки не важен.

Например:
Из 10 программистов нужно отобрать 4 для участия в проекте. Сколькими способами это можно сделать?
$$mathrm{ n = 10, k=4 }$$ В данном случае, порядок отбора не важен (выборка неупорядоченная); каждый кандидат может войти только один раз в выборку (выборка без повторений). Поэтому рассматриваем неупорядоченные ⟨10,4⟩ –выборки без повторений. Количество способов отбора равно: $$mathrm{ C_{10}^4=frac{10!}{6! 4!}=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 }$$ Ответ: 210.

п.2. Сочетания с повторениями

Сочетаниe с повторениями – это неупорядоченная ⟨n,k⟩-выборка с повторениями. Общее количество сочетаний с повторениями: $$ mathrm{ overline{C}_n^k=frac{(n+k-1)!}{(n-1)k!} } $$

$$ mathrm{ overline{C}_n^k=C_{n+k-1}{k} } $$

Например:
Нужно отобрать 4 программистов для участия в проекте. Многочисленных претендентов можно разделить на две категории: желающих работать удаленно и предпочитающих работу в офисе. Сколько всего комбинаций из любителей офиса и удалёнки может оказаться в выбранной четвёрке? $$mathrm{ n = 2, k=4 }$$ Порядок отбора не важен; кандидатов из каждой категории может быть несколько или ни одного. Поэтому рассматриваем неупорядоченные ⟨2,4⟩ –выборки с повторениями: $$ mathrm{ overline{C}_2^4=frac{(2+4-1)!}{(2-1)4!}=frac{5!}{4!}=5 } $$ Всего – 5 комбинаций: OOOO,OOOD,OODD,ODDD,DDDD
где O – любитель офиса; D – любитель удалёнки. Напоминаем, что порядок не важен – важен только состав группы.
Ответ: 5.

п.3. Биномиальные коэффициенты и их свойства

Подробно о биноме – см. §28 справочника для 7 класса.
Для n-й степени бинома справедливо выражение: $$ mathrm{ (apm b)^n=a^n+C_n^1a^{n-1}bpm C_n^2a^{n-2}b^2+…+C_n^{n-1}b^n } $$ где (mathrm{C_n^k}) – биномиальные коэффициенты, к оторые одновременно являются количествами сочетаний без повторений из n по k: $$ mathrm{ C_n^k=frac{n!}{(n-k)!k!} } $$ Таким образом, биномиальные коэффициенты можно определять как с помощью треугольника Паскаля, так и с помощью данной формулы.
Заметим, что в литературе также часто встречается обозначение (mathrm{left(_k^nright)}) для биномиальных коэффициентов (mathrm{left(C_n^kright)}).

Свойства биномиальных коэффициентов

Свойство симметрии

$$mathrm{ C_n^k=C_n^{n-k} }$$

Свойство Паскаля

$$mathrm{ C_n^k=C_{n-1}^{k-1}+C_{n-1}^k }$$

Замена индексов

$$mathrm{ C_n^mC_m^{n-k}=C_{n}^{k}C_{k}^{n-m} }$$

Вынесение за скобки

$$mathrm{ C_n^k=frac{n}{k}C_{n-1}^{k-1} }$$

Рекуррентные формулы

begin{gather*}mathrm{ C_n^k=frac{n-k+1}{k}C_{n}^{k-1} }\ mathrm{ C_n^k=frac{n}{n-k}C_{n-1}^k } end{gather*}

Свойство суммы

$$mathrm{ C_n^0+C_n^1+C_n^2+…+ C_n^n=sum_{k=0}^nC_n^k=2^n }$$

Свойство разности

$$mathrm{ C_n^0-C_n^1+C_n^2-…+(-1)^nC_n^n=sum_{k=0}^n(-1)^kC_n^k=0 }$$

Свойства максимума

Если n – четное, то максимальное значение (mathrm{C_n^k}) имеет при (mathrm{k=frac{n}{2}}).
Если n – нечетное, то максимальное значение имеют два коэффициента (mathrm{C_n^k}), при (mathrm{k=frac{n-1}{2}}) и (mathrm{k=frac{n+1}{2}})

Свёртка Вандермонда

$$mathrm{ sum_{r=0}^kC_n^rC_m^{k-r}=C_{n+m}^k }$$

Сумма квадратов

$$mathrm{ sum_{k=0}^n(C_n^k)^2=C_{2n}^n }$$

Взвешенное суммирование

begin{gather*} mathrm{ sum_{k=0}^nnC_n^k=n2^{n-1} }\ mathrm{ sum_{k=0}^nn^2C_n^k=n(n+1)2^{n-2} } end{gather*}

Связь с числами Фибоначчи

$$mathrm{ C_n^0+C_{n-1}^1+…+C_{n-k}^{k}+…+C_{0}^{n}=F_{n+1} }$$

п.4. Примеры

Пример 1. На столе лежит 10 яблок и 5 груш.
1) Сколькими способами можно выбрать 7 фруктов?
2) Сколькими способами можно выбрать 7 фруктов, чтобы среди них было 3 груши?

1) Всего у нас n = 10 + 5 = 15 фруктов. Нужно выбрать k = 7 фруктов.
Порядок выбора не важен, т.е. выборка неупорядоченная. Находим: $$ mathrm{ C_n^k=C_{15}^7=frac{15cdot 14cdot 13cdot 12cdot 11cdot 10cdot 9}{1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7}=6435 } $$ Существует 6435 способов выбрать 7 фруктов из 15.

2) Выбираем 4 яблока из 10 и 3 груши из 5.
Для яблок: $$ mathrm{ C_{10}^4=frac{10cdot 9cdot 8cdot 7}{1cdot 2cdot 3cdot 4}=210 } $$ Для груш: $$ mathrm{ C_3^5=C_{5}^2=frac{5cdot 4}{1cdot 2}=10 } $$ По правилу произведения, общее количество способов выбрать 4 яблока и 3 груши: $$ mathrm{ C_{10}^3cdot C_{5}^3=210cdot 10=2100 } $$ Ответ: 1) 6435; 2) 2100.

Пример 2. В кондитерском магазине продаётся 4 вида пирожных. Сколькими способами можно купить 7 пирожных? $$ mathrm{ n=4, k=7 } $$ Порядок выбора пирожных неважен – выборка неупорядоченная; пирожные одного вида могут повторяться. Значит, находим количество сочетаний с повторениями: $$ mathrm{ overline{C}_4^7=C_{7+4-1}^7=C_{10}^7=C_{10}^3=frac{10cdot 9cdot 8}{1cdot 2cdot 3}=120 } $$ Ответ: 120

Пример 3. Рота состоит из 3 офицеров, 6 сержантов и 15 рядовых. Сколькими способами можно выбрать из них отряд, состоящий из 1 офицера, 2 сержантов и 5 рядовых?

По всем трём множествам делаем неупорядоченную выборку (т.е., сочетания) без повторений.
Выбираем офицеров: (mathrm{C_3^1=frac31=3})
Выбираем сержантов: (mathrm{C_6^2=frac{6cdot 5}{1cdot 2}=15})
Выбираем рядовых: (mathrm{C_{15}^6=frac{15cdot 14cdot 13cdot 12cdot 11}{1cdot 2cdot 3cdot 4cdot 5}=3003})
По правилу произведения, отряд можно выбрать:
(mathrm{3cdot 15cdot 3003=135135}) способами.
Ответ: 135135.

Пример 4. Найдите сумму
a) (mathrm{C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6})
По свойству суммы (mathrm{sum_{k=0}^6C_6^k=2^6}). Получаем: $$ mathrm{ C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6=sum_{k=0}^6C_6^k-C_6^0=2^6-1=64-1=63 } $$
б) (mathrm{C_n^1+6C_n^2+6C_n^3}) $$ mathrm{ C_n^1=n, C_n^2=frac{n(n-1)}{2}, C_n^3=frac{n(n-1)(n-2)}{6} } $$ Получаем begin{gather*} mathrm{ C_n^1+6C_n^2+6C_n^3=n+6cdot frac{n(n-1)}{2}+6cdot frac{n(n-1)(n-2)}{6}=}\ mathrm{ =n(1+3(n-1)+(n-1)(n-2))=n(3n-2+n^2-3n+2)=n^3 } end{gather*} Ответ: а) 63; б) n³.

Пример 5. Рассчитайте все (mathrm{C_{10}^k}) по рекуррентной формуле (mathrm{C_{n}^k=frac{n-k+1}{k}C_n^{k-1}}).
Постройте график (mathrm{C_{10}^k(k)}). Сделайте выводы.

Начальное значение (mathrm{C_{10}^0=1}).

0 $$mathrm{ C_{10}^0=1 }$$ 1 $$mathrm{ C_{10}^1=frac{10-1+1}{1}C_{10}^0=10 }$$ 2 $$mathrm{ C_{10}^2=frac{10-2+1}{2}C_{10}^1=45 }$$ 3 $$mathrm{ C_{10}^3=frac{10-3+1}{3}C_{10}^2=120 }$$ 4 $$mathrm{ C_{10}^4=frac{10-4+1}{4}C_{10}^3=210 }$$ 5 $$mathrm{ C_{10}^4=frac{10-5+1}{5}C_{10}^4=252 }$$ 6 $$mathrm{ C_{10}^6=frac{10-6+1}{6}C_{10}^5=210 }$$ 7 $$mathrm{ C_{10}^7=frac{10-7+1}{7}C_{10}^6=120 }$$ 8 $$mathrm{ C_{10}^6=frac{10-8+1}{8}C_{10}^7=45 }$$ 9 $$mathrm{ C_{10}^9=frac{10-9+1}{9}C_{10}^8=10 }$$ 10 $$mathrm{ C_{10}^{10}=frac{10-10+1}{10}C_{10}^9=1 }$$

На графике видно симметрию коэффициентов: (mathrm{C_{10}^k=C_{10}^{10-k}}).
Т.к. n = 10 – чётное, максимальный коэффициент при (mathrm{k=frac{n}{2}=5, C_{10}^5=252}).
Можем также проверить свойство суммы: (mathrm{sum_{k=0}^{10}C_{10}^k=1024=2^{10}}).

Рейтинг пользователей

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 декабря 2021 года; проверки требуют 4 правки.

В комбинаторике сочетанием из по называется набор из элементов, выбранных из -элементного множества, в котором не учитывается порядок элементов.

Соответственно, сочетания, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми — этим сочетания отличаются от размещений. Так, например, 3-элементные сочетания 2 и 3 ((нестрогие) подмножества, для которых ) из 6-элементного множества 1 () являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов 1.

В общем случае число всех возможных -элементных подмножеств -элементного множества стоит на пересечении -й диагонали и -й строки треугольника Паскаля.^[1]

Число сочетаний[править | править код]

Число сочетаний из по равно биномиальному коэффициенту

При фиксированном производящей функцией последовательности чисел сочетаний , , , … является

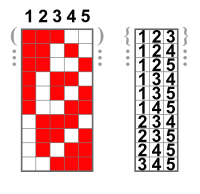
Двумерной производящей функцией чисел сочетаний является

Сочетания с повторениями[править | править код]

Сочетанием с повторениями из по называется такой -элементный набор из -элементного множества, в котором каждый элемент может участвовать несколько раз, но в котором порядок не учитывается (мультимножество). В частности, число монотонных неубывающих функций из множества в множество равно числу сочетаний с повторениями из по .

Число сочетаний с повторениями из по равно:

При фиксированном производящая функция чисел сочетаний с повторениями из по равна

Двумерной производящей функцией чисел сочетаний с повторениями является

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

• Стенли Р.^ru_en. Перечислительная комбинаторика. — М.: Мир, 1990.

Пусть
задано 5 различных элементов a,
b,
c,
d,
e
(в достаточном количестве
комплектов) и пусть требуется составить
из этих пяти элементов по 3 элемента
сочетания с повторениями.

Это значит, что
каждое соединение должно содержать три
элемента и одно от другого должно
отличаться, по крайней мере, одним
элементом.

Если бы сочетания
составлялись без повторений, то они
должны были быть различными:

abc
abd abe acd ace ade bcd bce bde
cde.

Сочетания же с
повторениями по три элемента из заданных
пяти элементов будут иметь вид:

aaa aab aac aad aae abb abc abd abe acb acd ace add ade aee

bbb bbc bbd bbe bce bcd bce bdd bde bee

ccc ccd cce cdd cde cee ddd dde dee eee

Таким образом,
сочетания же с повторениями из n
элементов по m
элементов (при 0≤ m
≤ n)
может содержать любой элемент сколько
угодно раз от

до m
включительно, или не содержать его
совсем, т. е. каждое сочетание из n
элементов по m
элементов может состоять не только из
m
различных элементов, но и из m
каких угодно и как угодно повторяющихся
элементов.

Следует отметить,
что если два соединения по m
элементов отличаются друг от друга
только порядком расположения элементов,
то они не считаются различными сочетаниями.

Число сочетаний
с повторениями из n
элементов по m
будем обозначать символом
.

Существует формула
для вычисления числа сочетаний с
повторениями:

.
(1.8.1)

Здесь m
может быть и больше n.

Пример 1.8.1.
В магазине
продается

видов тортов. Очередной покупатель
выбил чек на три торта. Считая, что любой
набор товаров равно-возможен, определить
число возможных заказов.

Решение.
Число равновозможных заказов по формуле
(1.8.1) равно

Ответ:
220.

2. Решение задач

2.1. Разные задачи

Лучший способ
освоения комбинаторики – решение задач.
Начинать естественно, надо с
простейших. Именно о простых, типовых
(и в тоже время важнейших) задачах и
пойдет речь.

Пример 2.1.1.
В студенческой
группе

человек. Необходимо выбрать старосту,
его заместителя и профорга. Сколько
существует способов это сделать?

Решение.
Старостой может быть выбран любой из
20 человек, его заместителем – любой из
оставшихся 19, а профоргом – любой из 18
студентов, т. е. n₁
= 20, n₂
= 19, n₃
= 18. По правилу произведения общее число
способов выбора старосты, его заместителя
и профорга равно

n₁
·
n₂
· n₃
= 20 · 19 · 18 =
6
840 способов.

Ответ:
6 840.

Пример
2.1.2.
Четыре
юноши и четыре девушки садятся на 8
расположенных подряд стульев, причем
юноши садятся на места с четными номерами,
а девушки – на места с нечетными номерами.
Сколькими способами это можно сделать?

Решение.
Первый
юноша может сесть на любое из четырех
четных мест, второй
– на любое из оставшихся трех мест,
третий – на любое из оставшихся двух
мест. Последнему юноше предоставляется
всего одна возможность. Согласно правилу
произведения, юноши могут занять четыре
места 4 · 3 · 2 · 1 = 24 способами.
Столько же возможностей имеют и девушки.

Таким
образом, согласно правилу произведения,
юноши и девушки могут занять все стулья
24 · 24 = 576 способами.

Ответ:
576.

Пример 2.1.3.
В
ящике
250
изделий.
Известно, что
100
из них – первого,
120 –
второго,
а остальные – третьего сорта. Сколько
способов выбора извлечения из ящика
одной детали первого или третьего
сорта?

Решение.
Деталь первого сорта может быть извлечена
n₁
= 100 способами, третьего сорта – n₂
= 30.

По правилу суммы
существует n₁
+ n₂
= 100 + 30 + 130
способов извлечения одной детали первого
или третьего сорта.

Ответ:
130.

Пример 2.1.4. В
высшей лиге чемпионата страны по футболу
16 команд. Борьба идет за золотые,
серебряные и бронзовые медали. Сколькими
способами медали могут быть распределены
между командами?

Решение.
Число разных способов распределения
медалей равно

.

Ответ:
3 360.

Примечание.
Необходимо
различать сочетания и размещения.
Например, в группе – 25 студентов,

из них вышли из аудитории на перерыв.
Студенты стоят вместе и беседуют. Тогда
порядок,
в котором
они стоят, – не существенен.
Число всех возможных групп из 25 человек
по

в этом случае – сочетания.
Если же студенты отправились на перерыве
в буфет или в кассу за стипендией, то
тогда существенно,
в каком порядке они стоят,
т. е. кто из них первый, второй и т.д.
В этой ситуации при подсчете возможных
групп из 25 человек по

необходимо составлять размещения.

Пример 2.1.5.
У туриста
есть семь консервных банок с ухой. В
походе он будет находиться девять
дней; из них какие-то семь дней будет
есть уху, а три дня будет питаться
всухомятку. Сколько у туриста есть
способов выбрать дни с горячим питанием?

Решение.
Число способов равно
.
Используя
формулу (1.5.1), находим:

Ответ:
36.

Пример 2.1.6. В
спортивной секции занимается

баскетболистов. Сколько может быть
организовано тренером разных спортивных
пятерок?

Решение.
Число разных спортивных пятерок равно

.
Используя формулу (1.5.1), находим:

.

Ответ:
792.

Пример 2.1.7. Из
группы, состоящей из

человек, выбирают троих для поездки на
соревнование. Сколькими способами это
может быть сделано?

Решение.
Число способов равно
.
Используя формулу (1.5.1), находим:

.

Ответ:
2 300.

Пример 2.1.8.
Для подарков
ко дню 8 Марта молодой человек должен
приобрести две броши и три браслета. В
магазине ему предложили на выбор пять
брошей и семь браслетов. Сколькими
способами человек может сделать выбор?

Решение.
Две броши из пяти можно выбрать числом
способов, равным
,
а три браслета из семи – числом способов

.
Каждый из способов выбора броши нужно
скомбинировать с каждым из способов
выбора браслета. Следовательно, полное
число способов, какими человек может
выбрать две броши и три браслета,
есть

.

Ответ:
350.

Пример 2.1.9.
Восемь человек
должны расположиться в двух комнатах,
причем так, чтобы в каждой было не менее
трех человек. Сколькими способами это
можно сделать?

Решение.
Есть два варианта. Первый вариант: в
одной комнате три человека, а в другой
пять. Второй: в каждой комнате по четыре
человека.

В первом варианте
количество способов расположения восьми
человек в двух комнатах равно числу
сочетаний трех из восьми

(или пяти из восьми, что
одно и то же), во втором варианте – числу
сочетаний четырех из восьми
.

Полное число
способов расположения восьми человек
в двух комнатах должно учитывать как
первый, так и второй варианты:

.

Ответ:
126.

Пример 2.1.10.
Группу
из девяти человек надо разбить на три
подгруппы:
в одной два человека, в другой три, в
третьей четыре. Сколькими способами
можно выполнить такое разбиение?

Решение.
Сначала выясняем, сколькими способами
можно выбрать двух человек из девяти.
Это число способов равно
.
После того, как этот выбор состоялся,
осталось семь человек. Из них надо
организовать подгруппы из трех и четырех
человек. Это можно сделать числом
способов, равным

(или
,
что одно и то же). Итак, девять человек
можно разбить на два, три и четыре
следующим числом способов:

.

Примечание.
Можно было бы сначала выяснить, сколькими
способами можно выбрать трех человек
из девяти. Тогда ответ на вопрос задачи
дало бы произведение
.
А можно было бы сначала выяснить, сколько
есть выборок четырех человек из девяти.
Тогда ответ дало бы произведение
.
Докажите самостоятельно, что
.

Ответ:
1260.

Пример 2.1.11.
Сколькими
способами можно из 40 человек, поступающих
в вуз, создать 4 группы разных специальностей
по 10 человек в каждой?

Решение.
Первую группу можно создать

способами. Вторую группу можно создать
из оставшихся 30 человек

способами.
Третью
группу можно создать из оставшихся 20
человек

способами.
Оставшиеся
10 человек составят четвертую группу.
Итак, число всех различных способов
составляет четырех групп из 40 человек
равно

Ответ:

.

Пример 2.1.12.
Сколькими
способами можно группу из 12 человек
разбить на две подгруппы, в одной из
которых должно быть не более пяти,
а во второй – не более девяти человек?

Решение.
Первая
подгруппа может состоять либо из трех,
либо из четырех, либо из пяти человек.
Подгруппу из трех человек можно выбрать

способами. Подгруппу из четырех человек
можно выбрать

способами, а подгруппу из пяти
человек –

способами. Учитывая, что выбор первой
подгруппы первой подгруппы однозначно
определяет вторую, найдем по правилу
суммы искомое число способов:
.

Ответ:
1 507.

Пример 2.1.13.
Сколькими
способами можно рассадить за столом
пять гостей, если стол накрыт на семь
персон?

Решение.
Пять гостей из семи можно выбрать

способами.
Но это не ответ на поставленный в
задаче вопрос, поскольку при рассаживании
гостей за столом необходимо принимать
во внимание также число перестановок
пяти гостей (оно равно P₅).
Ведь занявших те или иные пять стульев
можно поменять местами. Таким образом,
пять гостей можно рассадить за столом,
накрытым на семь персон, числом способов,
равным

.

Ответ:
2
520.

Пример 2.1.14.
Десять
команд участвуют в розыгрыше первенства
по футболу, лучшие из которых занимают
1-е, 2-е и 3-е места. Две команды, занявшие
последние места, не будут участвовать
в следующем первенстве.

Сколько
различных вариантов результата первенства
может быть, если учитывать только
положение первых трех и последних двух
команд?

Решение.
Задачу
решим тремя способами.

Способ
1. Первые
три места могут быть распределены

способов. В результате останется семь
команд, две из которых выбывают из
следующего первенства.

Так
как в этом случае порядок выбывших
команд не важен, то это может произойти

способами. Согласно правилу умножения
получаем, что число различных результатов
первенства равно
.

Способ
2. Выберем
без учета порядка пять команд из общего
числа команд. В эту группу входят
три команды, занявшие призовые места,
и две выбывшие команды. Такую операцию
можно выполнить

способами. Из этих пяти команд без
учета порядка выделим две команды,
которые выбывают, что можно сделать

способами. Для оставшихся трех команд
распределение призовых мест возможно
P₃
способами. По правилу умножения все три
операции можно выполнить
P₃
= 15 120.

Способ
3. Распределение
всех 10 мест в первенстве возможно
P₁₀
=
10! способами.

Однако
перестановки команд, занявших места с
4-го по 8-е, и перестановки команд, занявших
9-е и 10-е места, на результаты первенства
не оказывают влияния. Число таких
перестановок равно 5! · 2!, а число различных
результатов первенства равно
.

Ответ:
15 120.

Пример 2.1.15. Для
освещения аудитории может быть включена
каждая из имеющихся

ламп.
Сколько
существует различных способов
освещения аудитории?

Решение.
Очевидно, что

и число
способов равно 2¹⁰
= 1 204. При этом учитывается и тот способ
«освещения», при котором ни одна лампочка
не горит.

Ответ:
1
024.

Пример 2.1.16. В
кондитерском магазине
продавались
пирожные четырех видов: корзиночки,
наполеоны, песочные и эклеры. Сколькими
способами можно выбрать 7
пирожных?

Решение. В
данной задаче
подразумевается,
что количество пирожных каждого сорта
не ограничено. Для ответа на поставленный
вопрос воспользуемся формулой сочетаний
с повторениями (1.8.1):

.

Ответ:

.

Пример 2.1.17.
На конкурс
представлено 10 студенческих работ.
Денежные премии будут присуждаться
по следующим номинациям: оригинальная
научная идея; использование современного
экономико-математи-ческого аппарата;
применение компьютерного обеспечения;
презентация результатов на научной
конференции.

Сколько существует
вариантов распределения премий, если
по каждой комбинации установлены:

а) различные
денежные премии;

б) одинаковые
премии.

Решение

А. Каждый из
вариантов распределения премий
представляет собой комбинацию 4 работ
из 10, отличающуюся от других комбинаций
как самими работами, так и их порядком
расположения по номинациям; причем одни
и те же работы могут повторяться несколько
раз, так как любая научная работа может
получить премии как по одной, так и по
нескольким (даже всем четырем)
номинациям.

Число возможных
вариантов распределения денежных премий
представляет собой число размещений с
повторениями из 10
элементов по 4 и определяется по формуле
(1.8.1):

Б.
Если по каждой номинации установлены
одинаковые премии, то порядок следования
работ в комбинации четырех премиальных
работ значения не имеет. И тогда
число вариантов распределения премий
представляет собой число сочетаний с
повторениями из 10 элементов по 4,
определяемое по формуле (1.8.1):

Ответ:
а)
;
б)
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

Число сочетаний с повторениями

Пусть имеются предметы n различных типов. Сколькими способами можно составить из них комбинацию из k элементов, если не принимать во внимание порядок элементов в комбинации, но при этом предметы одного и того же типа могут повторяться? Иными словами, различные комбинации должны отличаться количеством предметов хотя бы одного типа. Такие комбинации называются сочетаниями с повторениями.

Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить шесть сочетаний с повторениями по два элемента: ab, ac, bc, aa, bb, cc.

Таким образом, сочетание с повторениями из n элементов по k элементов (при этом допускается, что k>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т.е. каждое сочетание с повторениями из n элементов по k элементов может состоять не только из k различных элементов, но и k каких угодно и как угодно повторяющихся элементов.

Следует отметить, что если, например, две комбинации по k элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.

Формула для вычисления числа сочетаний с повторениями:

C^~_kⁿ
= (k + n – 1)! (n – 1)! ⋅ k!
= C_k ^k+n-1

Данный онлайн калькулятор позволяет найти число сочетаний с повторениями из n элементов по k.

Поделиться страницей в социальных сетях: