Как найти число спектров

Самым простым из всех атомов является атом водорода, и он выступил в свое время в качестве своеобразного тест-объекта для теории Бора. К моменту появления теории атом водорода был тщательно исследован в ходе экспериментов: имелось знание о том, что он содержит единственный электрон. Ядром атома является протон.

Протон – это частица с положительным зарядом, модуль которого равен модулю заряда электрона, а масса больше массы электрона в 1836 раз.

Серия Бальмера и формула Ридберга

Начало XIX века ознаменовалось открытием линейчатого спектра.

Линейчатый спектр – это дискретные спектральные линии в видимой области излучения атома водорода.

В последующем закономерности, в соответствии с которыми ведут себя длины волн (или частоты) линейчатого спектра, подробно в количественном отношении исследовал И. Бальмер (в 1885 г.)

Серия Бальмера – совокупность спектральных линий атома водорода в видимой части спектра.

Позднее подобные серии спектральных линий обнаружились в ультрафиолетовой и инфракрасной частях спектра. В 1890 г. И. Ридберг составил запись эмпирической формулы для частот спектральных линий (формула Ридберга): 

νnm=R1m2-1n2.

Для серии Бальмера m = 2, n = 3, 4, 5, …. Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, … .

Неизменяемая R в формуле для частот спектральных линий носит название постоянной Ридберга и равна: R=3,29·1015 Гц.

До того, как Бор сформулировал постулаты, вопросы, каким же образом возникают линейчатые спектры и каков смысл целых чисел, входящих в формулы спектральных линий водорода (и некоторых других атомов), оставались без ответа.

Правило квантования

Постулаты Бора задали направление для развития новой науки – квантовой физики атома. Однако в них не было «рецепта», как определить параметры стационарных состояний (орбит) и соответствующих им значений энергии En.

Бором было сформулировано правило квантования, которое приводило к соотносимым с опытом значениям энергий стационарных состояний атома водорода. Ученый выдвинул гипотезу, что момент импульса электрона, совершающего вращение вокруг ядра, может принимать лишь дискретные значения, кратные постоянной Планка.

Правило квантования Бора дает возможность путем вычисления определить радиусы стационарных орбит электрона в атоме водорода и отыскать значения энергий. Скорость электрона, который совершает вращение по круговой орбите некоторого радиуса r в кулоновском поле ядра, записывается в виде соотношения (в соответствии с 2 законом Ньютона):

ν2=e24πε0mer.

Самой близкой к ядру орбите соответствует значение n=1.

Радиусы последующих орбит получают возрастание пропорционально n2.

Полная механическая энергия E системы из атомного ядра и электрона, вращающегося по стационарной круговой орбите радиусом rn, имеет запись:

En=Ek+Ep=meν22-e24πε0rn.

Заметим, что Ep<0, поскольку имеет место действие сил притяжения между электроном и ядром. Подставим в это выражение записи для υ2 и rn и получаем:

En=-mee48e02h2·1n2.

В квантовой физике атома целое число n=1, 2, 3, … носит название главного квантового числа.

В соответствии со вторым постулатом Бора: когда электрон переходит с одной стационарной орбиты с энергией En на другую стационарную орбиту с энергией Em<En, атом испускает квант света с частотой νnm, равной ΔEnmh:

νnm=∆Enmh=mee48ε02h31m2-1n2.

Это выражение полностью идентично с эмпирической формулой Ридберга для спектральных серий атома водорода, если за постоянную R взять:

R=mee48ε02h3.

Подставим в это выражение числовые значения всех переменных, получим

R=3,29·1015 Гц.

Полученное значение отлично коррелируется с эмпирическим значением R.

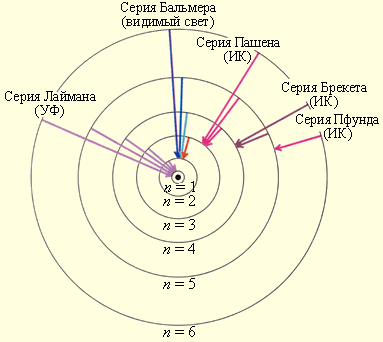
На рисунке 6.3.1 проиллюстрировано образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.

Рисунок 6.3.1. Стационарные орбиты атома водорода и образование спектральных серий.

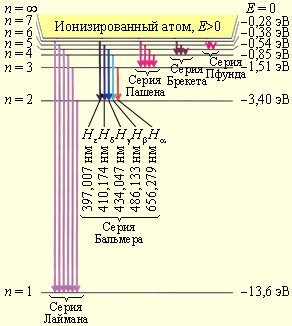
Рисунок 6.3.2 демонстрирует диаграмму энергетических уровней атома водорода с указанием переходов для различных спектральных серий.

Рисунок 6.3.2. Диаграмма энергетических уровней атома водорода с указанием переходов для различных спектральных серий. Также имеется указание длин волн для первых пяти линий серии Бальмера.

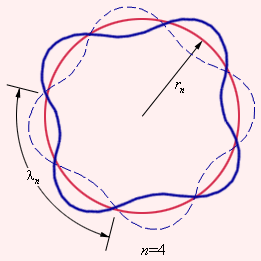
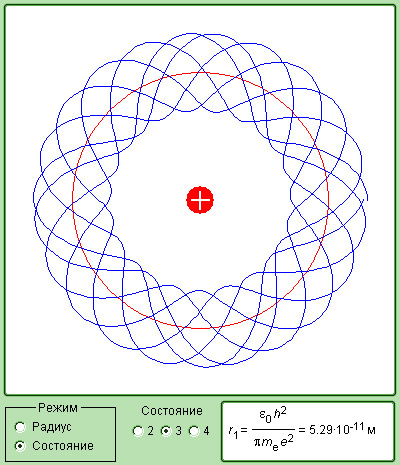
Тот факт, что теория Бора для атома водорода и результаты эксперимента оказались так отлично согласованы между собой, стал весомым аргументом в пользу верности этой теории. Но при этом попытка использовать теорию применительно к более сложным атомам закончилась провалом. Бору не удалось дать физическую интерпретацию правилу квантования – это позже, спустя десятилетие, сделал де Бройль, опираясь на представления о волновых свойствах частиц. Его предположение заключалось в том, что каждая орбита в атоме водорода соответствует волне, получающей распространение по окружности около ядра атома. Стационарная орбита имеет место тогда, когда волна постоянно повторяет себя после каждого оборота вокруг ядра. Иначе говоря, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. 6.3.3). Такое явление подобно стационарной картине стоячих волн в струне с закрепленными концами.

Рисунок 6.3.3. Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая n=4.

Согласно дебройлевским идеям, в стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться целое число длин волн λ:

nλn=2πrn

Если подставить сюда формулу длины волны де Бройля λ=hp, где p=meυ – импульс электрона, то:

nhneν=2πrn или meνrn=nh2π.

Итак, правило квантования Бора находится во взаимосвязи с волновыми свойствами электронов.

Вообще можно сказать, что Бор достиг поразительных успехов в попытках объяснить спектральные закономерности. Появилось утверждение, что атомы являются квантовыми системами, а энергетические уровни стационарных состояний атомов дискретны. Практически одномоментно с возникновением боровской теории экспериментально было доказано, что существуют стационарные состояния атома и квантование энергии. Дискретность энергетических состояний атома опытным путем продемонстрировали в 1913 г. Д. Франк и Г. Герц, исследуя столкновение электронов с атомами ртути. Выяснилось, что при энергии электронов менее 4,9 эВ их столкновение с атомами ртути протекает согласно закону абсолютно упругого удара. А, когда энергия электронов равна 4,9 эВ, столкновение с атомами ртути будет иметь черты неупругого удара. Таким образом, выходит, что, столкнувшись с неподвижными атомами ртути, электроны лишаются всей своей кинетической энергии, что, в свою очередь, означает факт поглощения атомами ртути энергии электрона и перевода электронов из основного состояния в первое возбужденное состояние:

E2-E1=4,9 эВ.

В соответствии с концепцией Бора, когда будет происходить обратный самопроизвольный переход атома, ртуть будет испускать кванты с частотой

ν=E2-E1h=1,2·1015 Гц.

Линия спектра с подобной частотой в самом деле нашлась в ультрафиолетовой части спектра излучения атомов ртути.

Утверждения о дискретных состояниях находились в противоречии с классической физикой, в связи с чем также возник закономерный вопрос: не опровергает ли квантовая теория законы классической физической теории.

Квантовая физика отнюдь не стремилась отменить фундаментальные основы, такие как законы сохранения энергии, импульса, электрического разряда и подобное. По сформулированному Бором принципу соответствия квантовая физика вмещает в себя классические представления, и при некоторых условиях можно заметить планомерный переход от квантовых представлений к классическим. Энергетический спектр атома водорода как раз дает нам такой пример (рис. 6.3.2): при больших квантовых числах n≫1 дискретные уровни постепенно становятся ближе, что задает плавный переход в область непрерывного спектра, вытекающего из классической физики.

Постулаты Бора со своей «половинчатостью», «полуклассикой» стали важной ступенью развития квантовых основ, введение которых в физику потребовало серьезной перестройки механики и электродинамики, произошедшей в 20-е – 30-е годы XX века.

Квантовые числа

Видение Бора о том, что существуют определенные орбиты для движения электронов в атоме, оказалось очень условным. В действительности, траектория движения электрона в атоме почти не имеет общего с движением планет или спутников. Физический смысл есть лишь в возможности обнаружить электрон в том или ином месте, и эта вероятность описывается квадратом модуля волновой функции |Ψ|2. Волновая функция Ψ служит решением базового уравнения квантовой механики – уравнения Шредингера. Выяснилось, что состояние электрона в атоме описывается целым набором квантовых чисел.

Квантовое число m введено в связи с тем, что проекция момента импульса на любое выделенное в пространстве направление (к примеру, направление вектора B→ магнитного поля) также принимает дискретный ряд значений.

Все виды квантовых чисел (n, l, m) находятся во взаимосвязи с правилами квантования. К примеру, орбитальное квантовое число l может принимать значения целого числа от 0 до (n – 1). Магнитное квантовое число m может принимать любые значения целого числа в интервале ±l. Тогда каждому значению главного квантового числа n, описывающему состояние энергии атома, соответствует целый ряд комбинаций квантовых чисел l и m. Одновременно с этим, с каждой такой комбинацией соотносится определенное распределение вероятности |Ψ|2 обнаружения электрона в разных точках пространства («электронное облако»).

Когда l>0 сферическая симметрия электронного облака нарушается.

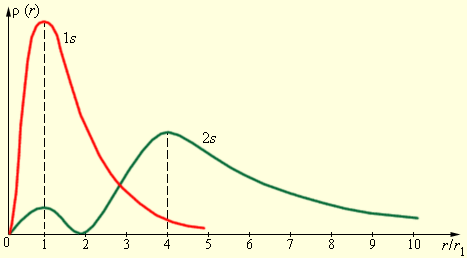
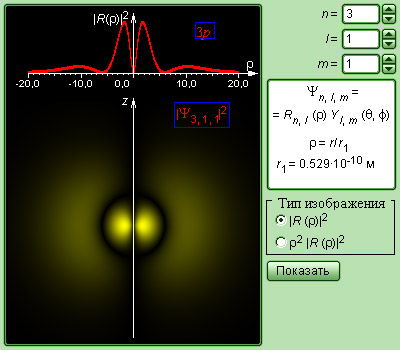
Рис. 6.3.4 иллюстрирует кривые распределения вероятности ρ (r)=4πr2|Ψ|2 обнаружения электрона в атоме водорода на разных расстояниях от ядра в состояниях 1s и 2s.

Рисунок 6.3.4. Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1s и 2s. r1=5,29·10–11 м – радиус первой орбиты Бора.

На рисунке 6.3.4 наглядно продемонстрировано, что электрон в состоянии 1s (основное состояние атома водорода) имеет возможность быть обнаруженным на различных расстояниях от ядра. С самой высокой вероятностью электрон обнаружится на расстоянии, равном радиусу r1 первой боровской орбиты. Вероятность нахождения электрона в состоянии 2s достигает максимума на расстоянии r=4r1 от ядра. И в том, и в том случае атом водорода возможно представить, как сферически симметричное электронное облако, в центре которого расположено ядро.

Рисунок 6.3.5. Модель квантования электронных орбит.

Рисунок 6.3.6. Модель атома водорода.

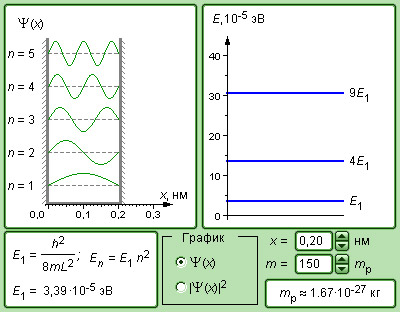
Рисунок 6.3.7. Модель частицы в потенциальной яме.

Как определить наибольший порядок спектра дифракционной решетки

Проходя через дифракционную решетку луч света отклоняется от своего направления под несколькими разными углами. В результате по другую сторону решетки получается картина распределения яркости, в которой яркие участки чередуются с темными. Вся эта картина называется дифракционным спектром, а число ярких участков в ней определяет порядок спектра.

Инструкция

В расчетах исходите из формулы, которая связывает между собой угол падения света (α) на дифракционную решетку, длину его волны (λ), период решетки (d), угол дифракции (φ) и порядок спектра (k). В этой формуле произведение периода решетки на разницу между синусами углов дифракции и падения приравнивается к произведению порядка спектра на длину волны монохроматического света: d*(sin(φ)-sin(α)) = k*λ.

Выразите из приведенной в первом шаге формулы порядок спектра. В результате у вас должно получиться равенство, в левой части которого останется искомая величина, а в правой будет отношение произведения периода решетки на разность синусов двух известных углов к длине волны света: k = d*(sin(φ)-sin(α))/λ.

Так как период решетки, длина волны и угол падения в полученной формуле являются величинами постоянными, порядок спектра зависит только от угла дифракции. В формуле он выражен через синус и стоит в числителе формулы. Из этого вытекает, что чем больше синус этого угла, тем выше порядок спектра. Максимальное значение, которое может принимать синус, равно единице, поэтому просто замените в формуле sin(φ) на единичку: k = d*(1-sin(α))/λ. Это и есть окончательная формула вычисления максимального значения порядка дифракционного спектра.

Подставьте численные величины из условий задачи и рассчитайте конкретное значение искомой характеристики дифракционного спектра. В исходных условиях может быть сказано, что падающий на дифракционную решетку свет составлен из нескольких оттенков с разными длинами волн. В этом случае используйте в расчетах ту из них, которая имеет меньшее значение. Эта величина стоит в числителе формулы, поэтому наибольшее значение периода спектра будет получено при наименьшем значении длины волны.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Спектр матрицы и собственные векторы матрицы

Собственные числа и собственные векторы матрицы.

Из курса линейной алгебры известно, что если А х = l х , то вектор х называется собственным вектором матрицы А , а число l – собственным числом, соответствующим данному собственному вектору. Совокупность всех собственных чисел матрицы называется спектром матрицы. Если в спектре матрицы одно и тоже собственное число встречается k раз, то говорят, что кратность этого собственного числа равна k .

Для нахождения собственных чисел матрицы А используется команда eigenvalues(A). Для нахождения собственных векторов матрицы А используется команда eigenvectors(A). В результате выполнения этой команды будут получены собственные числа, их кратность и соответствующие собственные векторы.

Чтобы понять, в каком виде получаются результаты выполнения команды eigenvectors, внимательно разберитесь со следующим примером: матрица имеет 3 собственных вектора: , отвечающий собственному числу кратности 1, , отвечающий собственному числу кратности 1, , отвечающий собственному числу кратности 1. Найдем их в Maple :

В строке вывода перечислены в квадратных скобках собственное число, его кратность и соответствующий собственный вектор в фигурных скобках , затем следующие наборы таких же данных.

Характеристический и минимальный многочлены матрицы.

Для вычисления характеристического многочлена матрицы A используется команда charpoly(A,lambda).

Минимальный многочлен (делитель) матрицы А можно найти с помощью команды minpoly(A,lambda).

Канонические и специальные виды матрицы.

Привести матрицу А к нормальной форме Жордана можно командой jordan(A).

К треугольному виду матрицу А можно привести тремя способами:

команда gausselim(A) приводит матрицу А к треугольному виду методом Гаусса;

команда ffgausselim(A) приводит матрицу А к треугольному виду методом Гаусса без деления. Эта команда предпочтительней для работы с символьными матрицами, так как не производит нормировку элементов и исключает возможные ошибки, связанные с делением на нуль;

команда gaussjord(A) приводит матрицу А к треугольному виду методом Гаусса-Жордана.

Характеристическую матрицу можно вычислить командой charmat(A,lambda).

Задание 3.

1. Дана матрица . Найти ее собственные векторы и собственные числа.

,

Дана матрица . Найти собственные векторы, собственные числа, характеристический многочлен и минимальный многочлен, Жорданову форму.

Дана матрица .

Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.

Самостоятельно проверьте, чем будет отличаться результат выполнения команды ffgausselim(A) от gausselim(A) на этом примере.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Характеристический полином, собственные числа, собственные векторы матрицы

В настоящем разделе $ n_<> $ означает порядок квадратной матрицы $ A_<> $.

Характеристический полином

определяется для произвольной квадратной матрицы $ A_<> $ как 1) $ det (A_<>-lambda E) $, где $ E_<> $ – единичная матрица одинакового с $ A_<> $ порядка.

Пример. Для $ n=2_<> $:

Теорема 1.

Пример. Характеристический полином матрицы Фробениуса

$$ mathfrak F= left( begin 0 & 1 & 0 & 0 & dots & 0 & 0 \ 0 & 0 & 1 & 0 & dots & 0 & 0 \ 0 & 0 & 0 & 1 & dots & 0 & 0 \ vdots& &&&ddots & & vdots \ 0 & 0 & 0 & 0 & dots & 0 & 1 \ a_n & a_ & a_ & & dots & a_2 & a_1 end right)_ $$ равен $ (-1)^n(lambda^n-a_1lambda^-dots-a_) $.

Характеристический полином линейного оператора

определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее ☞ ЗДЕСЬ.

Характеристический полином линейного однородного разностного уравнения

$ n_<> $-го порядка $$ x_=a_1 x_+ dots+ a_n x_K, quad a_n ne 0, $$ определяется как $$ lambda^n – a_1 lambda^ – dots – a_n . $$ Подробнее ☞ ЗДЕСЬ.

Свойства

Теорема 2. Характеристический полином матрицы не меняется

1. при ее транспонировании: $$ det (A-lambda E) = det (A^<top>-lambda E_<>) , ;$$ 2. при переходе к подобной матрице: если $ B=C^<-1>AC^<> $ при произвольной неособенной матрице $ C_<> $, то $$ det (A-lambda E) equiv det (B-lambda E_<>) , . $$

Теорема 3. Пусть матрица $ A_<> $ имеет порядок $ mtimes n_<> $, а $ B_<> $ — порядок $ ntimes m_<> $. Тогда эти матрицы допускают умножение в любом порядке, т.е. определены $ AB_<> $ и $ BA_<> $ и оба произведения будут квадратными матрицами — порядков $ m_<> $ и $ n_<> $ соответственно. Тогда характеристические полиномы этих произведений различаются лишь на степень $ lambda_<> $:

$$ lambda^n det (AB – lambda E_)equiv lambda^m det (BA – lambda E_) . $$

Если матрицы $ A_<> $ и $ B_<> $ — квадратные одинакового порядка, то характеристические полиномы матриц $ AB_<> $ и $ BA_<> $ тождественны.

Теорема 4. Если характеристический полином матрицы $ A_<> $ равен

$$ f(lambda)=(-1)^n lambda^n+a_1lambda^+dots+a_lambda+a_n $$ и $ a_ ne 0 $, то характеристический полином матрицы $ A^<-1>_<> $ равен $$ f^<ast>(lambda)=frac<(-lambda)^n> f(1/lambda) = frac<(-1)^n> left[ (-1)^n+a_1 lambda + dots+ a_lambda^+a_nlambda^ right] . $$

Теорема Гамильтона-Кэли

Теорема 5. Результатом подстановки в характеристический полином $ det (A_<>-lambda E) $ самой матрицы $ A_<> $ будет нулевая матрица:

$$ det (A-lambda E)= (-1)^n lambda^n +a_1 lambda^+dots+a_lambda+ a_n Rightarrow $$ $$ Rightarrow (-1)^n A^n +a_1 A^+dots+a_A+ a_n E = <mathbb O>_ . $$

матрица является корнем своего характеристического полинома.

Доказательство ☞ ЗДЕСЬ.

Пример. Для $ n_<>=2 $:

$$ left(begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right)^2 – (a_<11>+a_<22>)left(begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right) + (a_<11>a_<22>-a_<12>a_<21>) left(begin 1 & 0 \ 0 & 1 end right) = left(begin 0 & 0 \ 0 & 0 end right) . $$

Собственное число

определяется для квадратной матрицы $ A_<> $ как произвольный корень ее характеристического полинома $ det (A_<>-lambda E) $. Набор всех собственных чисел матрицы $ A_<> $ (с учетом их кратностей) называется спектром матрицы (таким образом спектр матрицы $ A_<> $ порядка $ n_<> $ всегда состоит из $ n_<> $ чисел, часть из которых могут быть одинаковыми). Максимальный из модулей собственных чисел матрицы $ A_<> $ называется ее спектральным радиусом, он иногда обозначается $ rho(A) $.

Пример. Найти спектр матрицы

$$ A= left(begin 0&1&2&3\ -1&0&4&7\ -2&-4&0&2\ -3&-7&-2&0 endright). $$ Решение. Характеристический полином $$ det (A-lambda E)=left|begin -lambda&1&2&3\ -1&-lambda&4&7\ -2&-4&-lambda&2\ -3&-7&-2&-lambda endright|=lambda^4+ 83lambda^2 $$ имеет корни $ lambda_1=0, lambda_2 = <mathbf i>sqrt<83>, lambda_3 = – <mathbf i>sqrt <83>$, причем $ lambda_ <1>$ — второй кратности.

Ответ. Спектр матрицы $ A_<> $: $ <0,0, <mathbf i>sqrt<83>,- <mathbf i>sqrt <83>> $. Спектральный радиус матрицы $ A_<> $: $ rho(A)= sqrt <83>$.

Теорема 6. Если $ <lambda_<1>,lambda_<2>,dots,lambda_ > $ — спектр матрицы $ A_<> $, то

$$ lambda_1+lambda_<2>+dots+lambda_n = operatorname(A)=a_<11>+a_<22>+dots+a_, $$ $$ lambda_1cdotlambda_<2>times dots times lambda_n = (-1)^ndet (A) . $$

Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета. ♦

Для того, чтобы матрица $ A_<> $ была неособенной необходимо и достаточно, чтобы среди ее собственных чисел не было нулевого.

Теорема 7. Пусть $ g(x)=b_<0>x^m+dots+b_m in <mathbb C>[x] $ — произвольный полином. Вычислим полином от матрицы $ A_<> $: $ g(A)=b_<0>A^m+dots+b_m E $. Тогда если $ <lambda_<1>,dots,lambda_ > $ — спектр матрицы $ A_<> $, то $ ),dots,g(lambda_n) > $ — спектр матрицы $ g(A_<>) $.

Результат теоремы обобщается и на более широкий класс функций $ g_<>(x) $ — фактически на любую функцию, которая может быть определена на спектре матрицы $ A_<> $. В частности, если $ det A_<> ne 0 $, то спектр матрицы $ A^<-1>_<> $ совпадает с $ <1/lambda_j>_^n $.

Имеет место следующее равенство, связывающее степени матрицы $ A_<> $ с суммами Ньютона ее характеристического полинома:

$$ operatorname(A^k)=lambda_1^k+dots+lambda_n^k . $$ Здесь $ operatorname_<> $ обозначает след матрицы (т.е. сумму ее диагональных элементов). Утверждение остается справедливым и для отрицательных показателей $ k_<> $ при условии, что $ det A_<> ne 0 $.

Имеет место следующее равенство:

$$ det g(A) = (-1)^ <mathcal R>(f,g_<>) , $$ где $ <mathcal R>(f,g_<>) $ означает результант полиномов $ f(x) =det (A-x_<> E) $ и $ g_<>(x) $.

Теорема 8. Собственные числа вещественной симметричной матрицы $ A_<> $ все вещественны.

Доказательство ☞ ЗДЕСЬ.

Теорема 9. Собственные числа вещественной кососимметричной матрицы $ A_<> $ все мнимы, за исключением, возможно, $ lambda_<> = 0 $.

Доказательство ☞ ЗДЕСЬ.

Теорема 10. Собственные числа вещественной ортогональной матрицы все равны $ 1_<> $ по абсолютной величине (модулю). Характеристический полином ортогональной матрицы является возвратным если $ +1 $ не является его корнем или является корнем четной кратности. Хотя бы одно собственное число ортогональной матрицы нечетного порядка равно $ +1 $ или $ (-1) $.

Доказательство ☞ ЗДЕСЬ.

Теорема 11. Спектр циклической матрицы

$$ left(begin a_1 & a_2 & a_3 & dots & a_n \ a_n & a_1 & a_2 & dots & a_ \ a_ & a_n & a_1 & dots & a_ \ vdots & & & & vdots \ a_2 & a_3 & a_4 & dots & a_1 end right) . $$ совпадает с набором чисел $$ ) > ,$$ при $$ f(x)=a_<1>+a_2x+a_3x^2+dots+a_nx^ $$ и $$ varepsilon_k=cos frac<2,pi k> + <mathbf i>sin frac<2,pi k> $$ — корне n-й степени из единицы.

Доказательство ☞ ЗДЕСЬ.

Локализация собственных чисел

Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть

$$A=left[a_ right]_^n quad , quad B=left[b_ right]_^n . $$ Обозначим $$M= max_> left <|a_|, |b_ | right> quad , quad delta = frac<1>sum_^n |a_ – b_ | . $$ Тогда любому собственному числу $ lambda_<ast>^<> $ матрицы $ A_<> $ можно поставить в соответствие такое собственное число $ mu_<ast>^<> $ матрицы $ B_<> $, что $$ |lambda_<ast>-mu_ <ast>| le (n+2) M sqrt[n] <delta> . $$

Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы ☞ ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы. Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.

Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.

Пример [Уилкинсон] [2]. Найти собственные числа матрицы

$$ A= left( begin 20 & 20 & & & & \ & 19 & 20 & & & \ & & 18 & 20 & & \ & & & ddots & ddots & \ & & & & 2 & 20 \ <colorvarepsilon > & & & & & 1 \ end right)_ <20times 20>$$ при $ <colorvarepsilon >=10^ <-10>$ (все неуказанные элементы матрицы считаются равными нулю).

Решение. Характеристический полином $$ det(A-lambda E) = prod_^ <20>(j-lambda) – 20^ <19> <colorvarepsilon > = $$ $$ =lambda^<20>-<scriptstyle 210>,lambda^<19>+<scriptstyle 20615>,lambda^<18>-<scriptstyle 1256850>, lambda^ <17>+<scriptstyle 53327946>, lambda^<16>-<scriptstyle 1672280820>, lambda^<15>+ <scriptstyle 40171771630>, lambda^<14>-<scriptstyle 756111184500>, lambda^<13>+ $$ $$ +<scriptstyle 11310276995381>, lambda^ <12>- <scriptstyle 135585182899530>, lambda^ <11>+<scriptstyle 1307535010540395>, lambda^<10>-<scriptstyle 10142299865511450>, lambda^9 + $$ $$ +<scriptstyle 63030812099294896>, lambda^8 – <scriptstyle 311333643161390640>, lambda^7+<scriptstyle 1206647803780373360>, lambda^6 -<scriptstyle 3599979517947607200>, lambda^5 +<scriptstyle 8037811822645051776>, lambda^4- $$ $$ -<scriptstyle 12870931245150988800>, lambda^3 +<scriptstyle 13803759753640704000>, lambda^2 -<scriptstyle 8752948036761600000>,lambda + <scriptstyle 2432377720176640000>$$ очень похож на полином из другого ☞ ПРИМЕРА Уилкинсона. Он имеет корни $$ lambda_1=0.995754, lambda_2=2.109241, lambda_3=2.574881, $$ $$ lambda_<4,5>=3.965331pm 1.087735, mathbf i, lambda_<6,7>=5.893977pm 1.948530 , mathbf i, $$ $$ lambda_<8,9>=8.118073 pm 2.529182 , mathbf i, lambda_<10,11>=10.5pm 2.733397 , mathbf i, $$ $$ lambda_<12,13>=12.881926pm 2.529182 , mathbf i, lambda_<14,15>=15.106022 pm 1.948530 , mathbf i, $$ $$ lambda_<16,17>=17.034669pm 1.087735 , mathbf i, $$ $$ lambda_<18>=18.425118, lambda_<19>=18.890758, lambda_<20>=20.004245 . $$ Итак, нановозмущение 2) в одном-единственном элементе матрицы приводит к существенному изменению спектра: из $ 20 $ вещественных собственных чисел «остаются в живых» только $ 6_<> $; кроме того, у образовавшихся мнимых корней оказываются достаточно большими мнимые части. В данном примере допустимые возмущения для $ <colorvarepsilon > $, т.е. такие, при которых сохранится свойство вещественности всех корней характеристического полинома, находятся в пределах 3) $$ -8.636174times 10^<-14> ♦

Теорема 13 [Гершгорин]. 4) Обозначим $ mathbb D_ $ круг на комплексной плоскости $ mathbb C_<> $ с центром в точке $ a_^<> $ и радиуса

$$ r_j=sum_<ell=1 atop ellne j>^n left|a_right| .$$ Тогда спектр матрицы $ A_<> $ лежит внутри объединения этих кругов: $$ <lambda_1,dots, lambda_n >subset bigcup_^n mathbb D_j . $$ Иными словами: любое собственное число матрицы должно удовлетворять хотя бы одному из неравенств $$ |z- a_ |

Если все главные миноры $ A_1,A_2,dots,A_ $ симметричной матрицы $ A_<> $ отличны от нуля, то число положительных собственных чисел матрицы $ A_<> $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:

$$ operatorname < det (A-lambda E) =0 | lambda>0 > = <mathcal P>(1,A_1,dots,A_n), $$ $$ operatorname < det (A-lambda E) =0 | lambda ненулевойстолбец $$ X_<ast>= left( begin x_<1>^ <ast>\ vdots \ x_^ <ast>end right) in mathbb^n $$ такой, что $$ AX_<ast>=lambda_ <ast>X_ <ast>quad iff quad (A -lambda_<ast>E) X_ <ast>= mathbb O_ . $$ По определению собственного числа, $ det (A^<> -lambda_<ast>E) = 0 $ и, следовательно, система однородных уравнений $ (A -lambda_<ast>E) X^<> = mathbb O $ всегда имеет нетривиальное решение; более того, этих решений бесконечно много. Таким образом, одному и тому же собственному числу матрицы принадлежит бесконечное множество собственных векторов. Эту бесконечность можно описать с помощью фундаментальной системы решений (ФСР).

Пример. Найти собственные векторы матрицы

Решение. Спектр матрицы найден выше. $$(A-0 cdot E)X=mathbb O quad Longrightarrow mbox< ФСР>= left< <mathfrak X>_1=left(begin 4 \ -2 \ 1 \ 0 endright), <mathfrak X>_2=left(begin 7 \ -3 \ 0 \ 1 end right) right>.$$ Любой вектор вида $ alpha_ <1><mathfrak X>_1 + alpha_2 <mathfrak X>_2 $ будет собственным, принадлежащим $ lambda_<>=0 $. $$ begin (A- mathbf i, sqrt <83>E)X=mathbb O \ \ Downarrow \ \ <mathfrak X>_3= left(begin 1- mathbf i , sqrt <83>\ 8-2, mathbf i , sqrt <83>\ 12 \ 17+mathbf i , sqrt <83>endright) end qquad begin (A+mathbf i sqrt <83>E)X=mathbb O \ \ Downarrow \ \ <mathfrak X>_4= left(begin 1+mathbf i , sqrt <83>\ 8+2mathbf i , sqrt <83>\ 12 \ 17- mathbf i ,sqrt <83>endright) end . $$ ♦

Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.

Теорема 15. Пусть $ lambda_<ast>^<> $ — собственное число матрицы $ A_<> $. Обозначим частное от деления характеристического полинома на линейный множитель $ lambda_<> – lambda_ <ast>$ через $ f_<ast>(lambda)^<> $:

$$ f_<ast>(lambda) equiv f(lambda) / (lambda-lambda_<ast>) . $$ Тогда любой ненулевой столбец матрицы $ f_<ast>(A)^<> $ является собственным вектором, принадлежащим $ lambda_<ast>^<> $.

Доказательство следует из равенства $$(A-lambda_ <ast>E)f_<ast>(A)=mathbb O_ . $$ На основании определения любой ненулевой столбец $ f_<ast>(A)^<> $ должен быть собственным вектором матрицы $ A_<> $. ♦

Пример. Найти собственные векторы матрицы

$$ A=left( begin 9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5 end right) . $$

Решение. $$ det (A-lambda E)=-lambda^3+ 7, lambda + 6 equiv -(lambda_<>-3) (lambda+2)(lambda+1) , .$$ Пренебрегая знаком – , имеем: $$ begin f_1(lambda)=lambda^2+3lambda+2 & u & f_1(A)= left( begin 40 & 80 & -20 \ 0 &0 & 0 \ 40 & 80 & -20 end right) , \ f_2(lambda)=lambda^2-2lambda-3 & u & f_2(A)= left( begin -10 & -30 & 10 \ 5 &15 & -5 \ 0 & 0 & 0 end right) , \ f_3(lambda)=lambda^2-lambda-6 & u & f_3(A)= left( begin -4 & -8 & 4 \ 4 & 8 & -4 \ 8 & 16 & -8 end right) . end $$

Если $ lambda_<ast>^<> $ является простым корнем характеристического полинома 5) , то ненулевые столбцы $ f_<ast>(A)^<> $ будут пропорциональными. Или, что то же, $ operatorname f_<ast>(A)^<> = 1 $.

Тогда очевидно, что и строки матрицы $ f_<ast>(A)^<> $ тоже должны быть пропорциональны!

Доказать, что любая ненулевая строка матрицы $ f_<ast>(A)^<> $ является собственным вектором матрицы $ A^<^<top>>_<> $, принадлежащим $ lambda_<ast>^<> $. Доказать, что собственный вектор матрицы $ A_<> $ ортогонален собственному вектору матрицы $ A^<top>_<> $, если эти векторы принадлежат различным собственным числам 6) .

На практике вычисление полинома $ f_<ast>(lambda)^<> $ может быть осуществлено с помощью схемы Хорнера.

Пример. Вычислить собственный вектор матрицы

$$ A=left( begin 23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87 end right) , $$ принадлежащий ее вещественному собственному числу.

Решение. Характеристический полином $$ f(lambda)= -lambda^3+184,lambda^2-14751,lambda+611404 $$ имеет единственное вещественное собственное число $ lambda_ <ast>approx 96.8817 $. Составляем схему Хорнера $$ begin & -1 & 184 & -14751 & 611404 \ hline 96.8817 & -1 & 87.1183 & -6310.8310 & -0.0352 end $$ За счет ошибок округления мы получили ненулевое значение для $ f(lambda_<ast>) $. В качестве частного от деления $ f(lambda) $ на $ lambda-lambda_ <ast>$ берем $$ f_<ast>(lambda)= -lambda^2 + 87.1183, lambda – 6310.8310 . $$ Подставляем в него матрицу $ A_<> $ и вычисляем первый столбец матрицы $$ -A^2+87.1183,A -6310, E = left( begin -1882.1101 & * & * \ -2723.2902 & * & * \ -708.6229 & * & * end right) .$$ Проверяем: $$ left( begin 23 & 75 & -92 \ 6 & 74 & 72 \ 37 & -23 & 87 end right) left( begin -1882.1101 \ -2723.2902 \ -708.6229 end right) – 96.8817 left( begin -1882.1101 \ -2723.2902 \ -708.6229 end right)= left( begin 0.0356 \ 0 \ -0.0002 end right) . $$ ♦

Можно развить последний метод далее: найти универсальную формулу для собственного вектора как функции ее собственного числа. Действительно, найдем частное от деления характеристического полинома $$ f(lambda) =a_0lambda^n+a_0lambda^+dots+ a_n, quad a_0=(-1)^n $$ на линейный полином $ lambda- lambda_ <ast>$, где $ lambda_ <ast>$ — произвольное число из $ mathbb C $. С помощью той же схемы Хорнера, получаем $$ q(lambda)=a_0lambda^+(a_0lambda_<ast>+a_1)lambda^+(a_0lambda_<ast>^2+a_1lambda_<ast>+a_2)lambda^+dots+ (a_0lambda_<ast>^+a_1lambda_<ast>^+dots+a_) , . $$ Если $ lambda_ <ast>$ является собственным числом матрицы $ A_<> $, то любой ненулевой столбец матрицы $$ q(A)= a_0A^+(a_0lambda_<ast>+a_1)A^+(a_0lambda_<ast>^2+a_1lambda_<ast>+a_2)A^+dots+ (a_0lambda_<ast>^+a_1lambda_<ast>^+dots+a_)E $$ будет собственным вектором, принадлежащим $ lambda_ <ast>$.

Пример. Найти представление всех собственных векторов матрицы

$$ A=left( begin 9 & 22 & -6 \ -1 &-4 & 1 \ 8 & 16 & -5 end right) $$ в виде функции ее собственных чисел.

Решение. Характеристический полином матрицы был вычислен выше: $ f(lambda)=-lambda^3+ 7, lambda + 6 $. Имеем, $$ q(lambda)=-lambda^2-lambda_<ast>lambda+(7-lambda_<ast>^2) $$ и $$ q(A)=-A^2-lambda_<ast>A+(7-lambda_<ast>^2)E= left(begin -lambda_<ast>^2-9lambda_<ast>-4 & -22lambda_<ast>-14 & 6lambda_<ast>+2 \ lambda_<ast>-3 & -lambda_<ast>^2+4lambda_<ast>-3 & -lambda_<ast>+3 \ -8lambda_<ast>-16 & -16lambda_<ast>-32 & -lambda_<ast>^2+5lambda_<ast>+14 end right) , . $$ Берем произвольный столбец этой матрицы, например, первый: $$ X_<ast>(lambda_<ast>)= left(begin -lambda_<ast>^2-9lambda_<ast>-4 \ lambda_<ast>-3 \ -8lambda_<ast>-16 end right) , . $$ Утверждается, что $ X_ <ast>(lambda_<ast>) $ — универсальное представление всех собственных векторов матрицы. Действительно, $$ X_<ast>(-1) = left(begin 4 \ -4 \ -8 end right), X_<ast>(-2) = left(begin 10 \ -5 \ 0 end right), X_<ast>(3) = left(begin -40 \ 0 \ -40 end right) , . $$ ♦

Теорема 16. Пусть $ g(x)=b_0x^m+dots+b_ in <mathbb C>[x] $ – произвольный полином. Если $ X_<ast>in mathbb C^ $ — собственный вектор матрицы $ A_<> $, соответствующий собственному числу $ lambda_<ast>^<> $, то он же будет собственным и для матрицы $ g(A)^<> $, принадлежащим собственному числу $ g(lambda_<ast>)^<> $.

Доказательство. Домножим равенство $ A<mathfrak X>_<ast>=lambda_<ast>^<><mathfrak X>_ <ast>$ слева на матрицу $ A_<> $: $$ A^2<mathfrak X>_<ast>=lambda_<ast>A<mathfrak X>_<ast>=lambda_<ast>^2<mathfrak X>_ <ast>.$$ По индукции доказывается и общее равенство: $$ A^k<mathfrak X>_<ast>=lambda_<ast>^k<mathfrak X>_ <ast>.$$ Домножим его на $ b_^<> $ и просуммируем по $ k_<> $ от $ 0_<> $ до $ m_<> $: $$ g(A)<mathfrak X>_<ast>=g(lambda_<ast>)<mathfrak X>_ <ast>,$$ что и доказывает утверждение теоремы. ♦

Если матрица $ A $ невырождена, то теорема остается справедливой и для произвольного полинома от $ A^ <-1>$. В частности, собственные векторы $ A^ <-1>$ совпадают с собственными векторами матрицы $ A $.

Теорема 17. Собственные векторы, принадлежащие различным собственным числам матрицы $ A_<> $, линейно независимы.

Теорема 18. Собственные векторы, принадлежащие различным собственным числам вещественной симметричной матрицы $ A_<> $, ортогональны, т.е. если $ mathfrak X_1 $ принадлежит собственному числу $ lambda_ <1>$, а $ mathfrak X_2 $ принадлежит собственному числу $ lambda_ <2>$ и $ lambda_1 ne lambda_2 $, то

$$ langle mathfrak X_1, mathfrak X_2 rangle =0 , $$ где $ langle , rangle $ означает скалярное произведение, определяемое стандартным образом: $ langle X,Y rangle =x_1y_1+dots+x_ny_n $.

Доказательство ☞ ЗДЕСЬ.

Теорема Перрона-Фробениуса

Теорема 19 [Перрон, Фробениус]. Для положительной матрицы $ A_<> $ существует положительное собственное число $ lambda_ <+>$ такое, что все остальные собственные числа этой матрицы меньше $ lambda_ <+>$ по абсолютной величине (модулю). Соответствующий этому собственному числу собственный вектор может быть выбран положительным:

$$ exists mathfrak X_ <+>> mathbb O: quad A mathfrak X_ <+>= lambda_ <+>mathfrak X_ <+> . $$

Число $ lambda_ <+>$ из теоремы называется собственным числом Перрона или собственным числом Перрона-Фробениуса матрицы $ A_<> $, а соответствующий ему произвольный положительный собственный вектор — собственным вектором Перрона-Фробениуса матрицы $ A_<> $.

Спектральный радиус положительной матрицы $ A_<> $ совпадает с ее собственным числом Перрона-Фробениуса:

Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы

$$ A= left(begin 2 & 7 & 18 & 28 \ 1 & 8 & 2 & 8 \ 3 & 1 & 4 & 1 \ 5 & 9 & 26 & 5 end right) , . $$

Решение. Характеристический полином матрицы $ A_<> $ $$ det(A-lambda E)=lambda^4-19, lambda^3-175, lambda^2-285, lambda+10390 $$ имеет корнями $$ lambda_ <1,2>approx -6.260463 pm 5.452465 mathbf i, lambda_3 approx 5.878976, lambda_4 approx 25.641950 . $$ Числом Перрона-Фробениуса является $ lambda_4 $, а соответствующий ему собственный вектор Перрона-Фробениуса можно взять равным $$ left( begin 1 \ 0.365240 \ 0.184802 \ 0.634244 end right) quad mbox < или >quad left( begin 2.737922 \ 1 \ 0.505974 \ 1.736510 end right) quad mbox < или >left( begin 5.411185 \ 1.976383 \ 1 \ 3.432010 end right) quad mbox < или >quad left( begin 1.576681 \ 0.575868 \ 0.291374 \ 1 end right) quad mbox < или >quad left( begin 0.798133 \ 0.291510 \ 0.147496\ 0.506210 end right) quad mbox < или >dots $$ (напоминаю: собственный вектор определяется с точностью до ненулевого сомножителя!). Последний вектор имеет длину равную $ 1_<> $. ♦

1. Собственное число Перрона-Фробениуса всегда простое для характеристического полинома матрицы $ A_<> $. Отсюда следует, что собственный вектор Перрона-Фробениуса определяется единственным образом — с точностью до домножения на положительный скаляр.

2. Любой собственный вектор положительной матрицы $ A_<> $, не соответствующий собственному числу Перрона-Фробениуса, не может состоять исключительно только из положительных элементов. Иными словами, хотя бы одна компонента такого вектора должна быть либо отрицательной либо мнимой.

3. Для собственного числа Перрона-Фробениуса справедливо неравенство $$ min_> sum_^n a_ le lambda_ <+>le max_> sum_^n a_ . $$

4. Собственное число Перрона-Фробениуса матрицы $ A_<> $ совпадает с собственным числом Перрона-Фробениуса матрицы $ A^ <top>$.

Какие из перечисленных свойств можно распространить на случай неотрицательных матриц ? Каждую такую матрицу можно рассматривать как предел последовательности (строго) положительных матриц. Воспользовавшись теоремой о непрерывной зависимости собственных чисел матрицы от ее элементов, можем сделать вывод, о том, что для неотрицательной матрицы $ A_<> $ всегда найдется вещественное неотрицательное собственное число, которое будет являться максимальным по модулю среди всех собственных чисел матрицы. Другое дело, что в данном случае — в отличие от случая положительных матриц — такое мажорирующее собственное число может оказаться не единственным.

Пример. Спектр неотрицательной матрицы

$$ A=left( begin 0 & 1 \ 1 & 0 end right) $$ состоит из чисел $ lambda_1=+1 $ и $ lambda_1=-1 $ одинакового модуля. ♦

Однако, по-прежнему, хотя бы одно неотрицательное вещественное число $ lambda_ <+>$ со свойством $ rho(A) = lambda_ <+>$ существовать будет; более того, ему будет соответствовать неотрицательный собственный вектор $ mathfrak X ge mathbb O $. Это число (вектор) по-прежнему называются числом (вектором) Перрона-Фробениуса 7) матрицы $ A_<> $.

Частным случаем неотрицательных матриц являются стохастические матрицы, т.е. неотрицательные матрицы, в которых сумма элементов каждой строки равна $ 1_<> $: $$ P=left[p_right]_^n, \ge 0 >_^n, sum_^n p_ = 1 npu quad j in <1,2,dots,n> . $$

Теорема 20. Собственное число Перрона-Фробениуса стохастической матрицы равно $ 1_<> $. Этому собственному числу соответствует собственный вектор $ X=[1,1,dots,1]^ <top>$.

Доказательство существования собственного числа равного $ 1_<> $ и соответствующего ему собственного вектора $ X=[1,1,dots,1]^ <top>$ следует из равенства $$ P left( begin 1 \ 1 \ vdots \ 1 end right) = left( begin 1 \ 1 \ vdots \ 1 endright) . $$ Далее, из теоремы Гершгорина следует, что любое собственное число $ lambda_<>in mathbb C $ стохастической матрицы должно удовлетворять неравенству $$|lambda – p_|le sum_ |p_|=1-p_ $$ хотя бы при одном $ j_<> $. Воспользовавшись следствием к неравенству треугольника получаем: $$|lambda| – |p_|le |lambda – p_| le 1-p_ Rightarrow |lambda| le 1 . $$ ♦

Методы вычисления характеристического полинома

Вычисление коэффициентов характеристического полинома матрицы $ A_<> $ непосредственным разложением определителя $ det (A-lambda_<> E) $ на $ n!_<> $ слагаемых — крайне неэффективно. Элементами этого разложения являются выражения, полиномиально зависящие от параметра $ lambda_<> $. На каждом этапе вычислений мы получаем проблему символьных вычислений: хранения таких полиномов и действий над ними.

Основной метод вычисления числовых определителей — метод Гаусса — также неэффективен в приложении к вычислению определителя, элементы которого зависят от параметра. Источником вычислительных проблем является неудобное расположение переменной $ lambda_<> $ — на главной диагонали матрицы. Первый же шаг метода Гаусса приводит к делению на элемент $ a_ <11>- lambda $, и, в дальнейшем, элементы преобразованной матрицы будут уже не полиномами, а рациональными функциями относительно $ lambda_<> $. Следующие шаги метода приводят к возрастанию степеней знаменателей. Необходимость в организации хранения рациональных функций и программировании действий с ними кажется тем более неоправданной, если вспомнить, что окончательный ответ — выражение для $ det (A-lambda_<> E) $ — должно быть полиномом по $ lambda_<> $; т.е. знаменатели дробей в конечном ответе сократятся.

А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.

Какой выход предлагается? — Предварительно преобразовать определитель $ det (A-lambda_<> E) $ к виду, когда переменная $ lambda_<> $ оказывается «выметенной» с диагонали на крайний ряд (в столбец или в строку). При этом допускается увеличение размеров (порядка) определителя. Такое представление дает возможность разложения определителя по этому исключительному ряду, и, тем самым, позволяет свести задачу к вычислению числовых определителей — а уж для этой задачи применение метода Гаусса вполне эффективно.

Метод Леверье

Метод основан на формуле (см. следствие к теореме $ 7 $ ☞ ЗДЕСЬ ): $$ operatorname (A^k)=lambda_1^k+dots+lambda_n^k=s_k , $$ т.е. след $ k_<> $-й степени матрицы $ A_<> $ равен $ k_<> $-й сумме Ньютона ее характеристического полинома $ f(lambda)=det (A-lambda E ) $. Вычисляем последовательные степени матрицы $ A_<> $: $$s_1=operatorname (A), s_2=operatorname (A^2), dots, s_n=operatorname (A^n) .$$ Неизвестные коэффициенты $ f(lambda)=(-1)^n(lambda^n+a_1lambda^+ dots+a_n) $ находим по рекурсивным формулам Ньютона: $$ a_1=-s_1, a_2=-(s_2+a_1s_1)/2, $$ $$ a_k=-(s_+a_1s_+a_2s_+dots+a_s_1)/k npu k le n. $$ Очевидно, что не имеет смысла вычислять все элементы матрицы $ A^ $ — достаточно обойтись лишь элементами ее главной диагонали.

Пример [Леверье]. Найти характеристический полином матрицы

$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$

Решение. $$ A^2=left(begin 30.91795128&-30.56848188&2.878480155&0.0031325713\ -4.705449283&164.6764010&-141.3504639&-0.4143169528\ 0.3341843103&-106.6094396&193.1869924& -6.756396001\ 0.0022236138&-1.904168948&-41.16923134& 309.9628536 end right), $$ $$ A^3=left(begin -179.0125092&431.2849919&-198.8601505& -0.9173897610\ 66.38829278&-2562.954533& 2771.458834& -15.49709921\ -23.08728044&2090.291485&-3124.010318& 156.9329019\ -0.649145142&-71.21907809&956.2502143& -5463.723497 end right), $$ $$ A^4=left(begin 1100.720103& ast& ast& ast \ ast& 42332.23816& ast& ast \ ast& ast& 52669.62534& ast \ ast& ast& ast& 96355.91518 end right) . $$ Вычисляем следы матриц: $$s_1=-47.888430, s_2=698.7441983, s_3=-11329.70086, s_4= 192458.4988 ,$$ и по формулам Ньютона получаем: $$a_1= 47.888430, a_2 = 797.278764_ <displaystyle 8>, a_3 = 5349.45551_<displaystyle 3>, a_4 = 12296.550_ <displaystyle 68> . $$ ♦

После нахождения коэффициентов характеристического полинома можно найти его корни каким-либо 8) методом. Если $ lambda_<ast>^<> $ — одно из собственных чисел, то для нахождения соответствующего собственного вектора воспользуемся алгоритмом из ☞ ПУНКТА. Предположив дополнительно, что это собственное число простое 9) , обозначим $$ f_<ast>(lambda)= f(lambda)/(lambda-lambda_<ast>)=(-1)^n(lambda^ +p_1lambda^+dots+p_lambda+p_) $$ т.е. частное от деления $ f(lambda_<>) $ на $ lambda-lambda_ <ast>$. Тогда любой ненулевой столбец матрицы $ f_<ast>(A)^<> $ будет собственным вектором, принадлежащим $ lambda_<ast>^<> $. Как правило, собственным вектором можно взять комбинацию

Степени матрицы $ A_<> $ уже нами посчитаны при вычислении коэффициентов характеристического полинома.

Пример. Для приведенного выше примера находим собственные числа:

$$ lambda_1=-17.86326, lambda_2=-17.15242, lambda_3=-7.57404, lambda_4= -5.29869 . $$ Коэффициенты $ f_1(lambda) $ можно определить по схеме Хорнера: $$ begin &1 & 47.888430 & 797.2787648 & 5349.455513 & 12296.55068 \ hline -17.86326 & 1 & underbrace<30.025170>_>& underbrace<260.9313465>_> &underbrace<688.371028>_>& approx 0 \ end $$ Собственным вектором, принадлежащим $ lambda_ <1>$, будет $$left[ -0.0256_<displaystyle 67>, 0.21938_<displaystyle 0>, -0.24187_<displaystyle 1>, 1.044526 right]^<^<top>> .$$ ♦

Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:

$$ f(lambda)=frac<1>left| begin s_1 &1 & & & &\ s_2&s_1& 2 & &mathbb O & \ s_3&s_2&s_1&3& & \ vdots& & & ddots &ddots & \ s_n&s_& s_ & dots &s_1&n \ lambda^n&lambda^&lambda^& dots &lambda&1 end right|_ <(n+1)times (n+1)> . $$

Биографические заметки о Леверье ☞ ЗДЕСЬ.

Метод Крылова

Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_<1>^<[0]>,dots,y_^ <[0]>right]^<^<top>> in mathbb C^n $. Cоставим итерационную векторную последовательность $$ Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_=Acdot Y_ . $$

Теорема 22. Определитель

$$ det left[begin Y_0&Y_<1>&dots&Y_&Y_\ 1& lambda&dots&lambda^&lambda^n end right]_ <(n+1)times (n+1)>$$ совпадает — с точностью до постоянного множителя — с характеристическим полиномом матрицы $ A_<> $. Здесь $ |_<> $ означает конкатенацию.

Доказательство. Легко видеть, что $$ Y_K=A^KY_0 quad npu quad K in <1,dots,n> . $$ Если $$ f(lambda)=det(A-lambda E) =(-1)^n lambda^n+a_1 lambda^+a_2 lambda^+dots+a_n , $$ то по теореме Гамильтона-Кэли: $$ (-1)^n A^n+a_1A^+dots+a_nE=mathbb O_ . $$ Это равенство останется справедливым и после умножения его на произвольный вектор, в том числе на $ Y_ <0>$: $$ (-1)^n A^ncdot Y_0+a_1A^ cdot Y_0 +dots+a_ncdot Y_0=mathbb O_ iff $$ $$ iff quad (-1)^n Y_n+a_1Y_ +dots+a_nY_0=mathbb O . $$ Последнее равенство представляет линейную систему относительно неизвестных коэффициентов характеристического полинома. Можно решать ее по формулам Крамера, но мы пойдем другим путем. Дополним эту систему тождеством $ f(lambda)=(-1)^n lambda^n+a_1 lambda^+a_2 lambda^+dots+a_n $. Рассмотрим получившуюся систему как линейную однородную относительно столбца $ left[ a_n,a_,dots,a_1,1right]^ <top>$. Поскольку эта система имеет нетривиальное решение, то ее определитель должен равняться нулю: $$ 0=det left[begin Y_0&Y_<1>&dots&Y_&(-1)^nY_\ 1& lambda&dots&lambda^&(-1)^nlambda^n-f(lambda) end right]= $$ (представляем последний столбец в виде суммы двух столбцов и используем свойство 5 определителя) $$ =det left[begin Y_0&Y_<1>&dots&Y_&(-1)^nY_\ 1& lambda&dots&lambda^&(-1)^nlambda^n end right]-f(lambda) det left[begin Y_0&Y_<1>&dots&Y_ end right] . $$ Таким образом, $$ f(lambda)=(-1)^n frac<det left[begin Y_0&Y_<1>&dots&Y_&Y_\ 1& lambda&dots&lambda^&lambda^n end right]><det left[begin Y_0&Y_<1>&dots&Y_ end right]> , $$ если только знаменатель в этой дроби не обратится в нуль. ♦

Пример. Найти характеристический полином матрицы примера Леверье

$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$

Решение. Возьмем $ Y_0=left[ 1,0,0,0 right]^ <top>$. Имеем $$ begin Y_1=A Y_0= & Y_2=AY_1= & Y_3=AY_2= & Y_4=AY_3= \ left(begin -5.509882\ 0.287865 \ 0.049099 \ 0.006235 end right), & left(begin 30.917951\ -4.705449 \ 0.334184 \ 0.002223 end right), & left(begin -179.012509\ 66.388293 \ -23.087280\ -0.649145 end right), & left(begin 1100.720101\ -967.597333\ 576.522644\ -4.040153 end right) . end $$ $$ det left[begin Y_0&Y_<1>&Y_2& Y_<3>& Y_<4>\ 1& lambda&lambda^2 &lambda^<3>&lambda^4 end right]= left| begin 1 & -5.509882 & 30.917951 & -179.012509 & 1100.720101 \ 0 & 0.287865 & -4.705449 & 66.388293 & -967.597333\ 0 & 0.049099 & 0.334184 & -23.087280 & 576.522644\ 0 & 0.006235 & 0.002223 & -0.649145 & -4.040153 \ 1 & lambda & lambda^2 & lambda^3 & lambda^4 end right|= $$ $$ =0.348621 lambda^4+16.694915lambda^3+277.948166lambda^2+1864.932835lambda+4286.836454 = $$ $$ =0.348621 left(lambda^4+47.888430lambda^3+797.27876_<displaystyle 3>lambda^2+5349.4555_<displaystyle 0>lambda+12296.550_ <displaystyle 5>right) . $$ ♦

После нахождения характеристического полинома можно найти его корни каким-либо 10) методом. Пусть $ lambda_<ast>^<> $ — одно из собственных чисел, и оно — простое; тогда для нахождения соответствующего собственного вектора можно воспользоваться тем же приемом, что был задействован в предыдущем ПУНКТЕ. Вычислим 11) частное от деления $ f(lambda_<>) $ на $ lambda-lambda_ <ast>$ $$ f_<ast>(lambda)= f(lambda)/(lambda-lambda_<ast>)=(-1)^n(lambda^ +p_1lambda^+dots+p_lambda+p_) . $$ Тогда любой ненулевой столбец матрицы $ f_<ast>(A)^<> $ будет собственным вектором, принадлежащим $ lambda_<ast>^<> $. Но тогда и произвольная комбинация столбцов этой матрицы тоже будет собственным вектором (если только не обратится в нулевой вектор). В частности, это относится и к комбинации, записываемой в матричном виде $$ (-1)^n f_<ast>(A) Y_0 = A^Y_0 +p_1A^Y_0+dots+p_Y_0=Y_+p_1Y_+dots+p_Y_0 . $$ А комбинируемые векторы уже посчитаны.

Теперь обсудим исключительные случаи. При неудачном выборе $ Y_ <0>$ определитель $$ det left[begin Y_0&Y_<1>&dots&Y_ end right] $$ может обратиться в нуль. Эта неприятность обязательно произойдет если, например, наш выбор пал на вектор $ Y_0 $, совпадающий с собственным вектором матрицы $ A_<> $. Вероятность такого события — нулевая. В общем же случае, трудно ожидать, чтобы $ n_<> $ почти произвольных столбцов $ Y_0,Y_<1>,dots,Y_ $ оказались линейно зависимыми — если только сама матрица $ A_<> $ не обладает «скрытым дефектом» — типа рассмотренного в следующем примере.

Пример. Найти характеристический полином матрицы

Решение. При любом выборе $ Y_0 $ векторы $ $ оказываются линейно зависимыми: $$ Y_0= left(begin 1\ 0\ 0 end right), Y_1= left(begin 2\ 1\ 1 end right), Y_2= left(begin 6\ 5\ 5 end right),dots ; Y_0= left(begin 1\ 1\ 1 end right), Y_1= left(begin 4\ 4\ 4 end right),dots $$ Объяснение этого феномена состоит в том, что для матрицы $ A_<> $ ее аннулирующий полином имеет степень меньшую ее порядка: $$ A^2-5 A+4 E = mathbb O . $$ Домножение этого равенства на произвольный столбец $ Y_0 $ и доказывает линейную зависимость системы $ $. ♦

Такая ситуация возможна только в случае, когда характеристический полином матрицы $ A_<> $ имеет кратные корни (в рассмотренном выше примере $ lambda_<>=1 $ являлся двойным корнем $ det (A-lambda_<> E) $); она исключительно редко встречается на практике.

Поиск всех собственных чисел

Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.

QR-алгоритм

Этот алгоритм основан на QR-разложении матрицы $ A $.

Теорема 23. Спектр матрицы $ A $ совпадает со спектром матрицы $ P^ <top>A P $ при произвольной ортогональной матрице $ P $.

Доказательство. $$ det (P^ <top>A P-lambda E)=det (P^ <top>A P- lambda P^ <top>E P)=det P^ <top>(A -lambda E ) P = det (A -lambda E ) P P^ <top>= det (A -lambda E ) , . $$ ♦

Пусть QR-разложение матрицы $ A $ имеет вид $$ A=Q_1R_1 , , $$ где $ Q_1 $ — ортогональная, а $ R_1 $ — верхнетреугольная матрицы. Тогда матрица $$ A_2=R_1Q_1 $$ имеет тот же спектр, что и матрица $ A $. Действительно, поскольку $$ A_2=Q_1^ <top>A Q_1 , $$ то сработает предыдущая теорема. Вычислим QR-разложение матрицы $ A_2 $ $$ A_2=Q_2R_2 $$ и переставим местами матрицы этого произведения: $$ A_3=R_2Q_2 , . $$ Матрица $$ A_3= Q_2^ <top>A_2 Q_2=Q_2^ <top>Q_1^ <top>A Q_1 Q_2 $$ продолжаем иметь те же собственные числа, что и матрица $ A $. Утверждается, что бесконечная последовательность матриц $$ Q_>_^ <infty>$$ как правило, сходится к матрице $ A_ <infty>$, которая будет верхнетреугольной.

Теорема 24 [4]. Если все собственные числа матрицы $ A $ различны по модулю, то матрица $ A_ <infty>$ является верхнетреугольной и на ее главной диагонали стоят собственные числа матрицы $ A $.

Пример. Найти все собственные числа матрицы $$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & 4 end right) , . $$

Решение. $$ A_1=Aapprox underbrace<left(begin 0.272165 & 0.759752 & 0.590511 \ 0.952579 & -0.299517 & -0.053683 \ -0.136083& -0.577119 & 0.805242 end right)>_ underbrace<left(begin 7.348469 & 3.946400 & 2.041241\ 0 & 2.534941 & -3.966781 \ 0 & 0 & 2.469409 end right)>_ $$ Теперь переставляем матрицы произведения местами и строим QR-разложение получившейся матрицы: $$ quad Rightarrow quad A_2 = R_1Q_1approx left(begin 5.481481 & 3.222957 & 5.771191 \ 2.954542 & 1.530046 & -3.3303021 \ -0.336044 & -1.425143 & 1.988472 end right)approx $$ $$ approxunderbrace<left(begin -0.878992 & 0.022595 & 0.476300\ 0.473781 & -0.154267 & -0.867026 \ 0.053886 & -0.987771 & 0.146304 end right)>_ underbrace<left(begin -6.236096& -3.634658 & -3.387848\ 0 & 1.244502 & -1.319999\ 0 & 0 & 5.927198 end right)>_ $$ Продолжим процесс: $$ quad Rightarrow quad A_3 = R_2Q_2approx left(begin 7.020952& 3.766220 & -0.314568\ -0.660752 & 1.111870 & -1.272137\ 0.319398 & -5.854713 & 0.867177 end right) approx $$ $$ approx underbrace<left(begin -0.994581 & -0.065879 & 0.080426 \ 0.093601 & -0.230749 & 0.968501 \ -0.045246 & 0.970780 & 0.235665 end right)>_ underbrace<left(begin -7.059205 & -3.376839 & 0.154554 \ 0 & -6.188319 & 1.156106 \ 0 & 0 & -1.053002 end right)>_ $$ Замечаем тенденцию убывания элементов матриц $ $, стоящих под главной диагональю. $$ Rightarrow dots Rightarrow A_ <10>approx left(begin mathbf<6.>_ <246022>& 2.758769 & -2.160057\ -0.0467437 & mathbf<4.4>_ <09292>& -5.341014\ 0.000018 &-0.005924 & mathbf<-1.6>_ <55314>end right) approx $$ $$ underbrace<left(begin -0.999972 & -0.007483 & 0.000007 \ 0.007483 & -0.999971 & 0.001339 \ -0.000003 & 0.001339 & 0.999999 end right)>_> underbrace<left(begin -6.246197 & -2.725694 & 2.120031\ 0 & -4.429817 & 5.354807 \ 0 & 0 & -1.662479 end right)>_> , . $$ Матрица $ Q_j $ уже близка к диагональной (с элементами $ pm 1 $), верхнетреугольность матрицы $ A_j $ также заметна, но точность приближения еще не достаточна. $$ Rightarrow dots Rightarrow A_ <20>approx left(begin mathbf<6.17>_ <5608>& 2.805821 & -2.020513 \ -0.001776 & mathbf<4.48>_ <4917>& -5.388407\ 0 & 0 & -mathbf <1.660525>end right) approx $$ Точность приближения минимильного собственного числа существенно выше точностей приближения остальных чисел. $$ Rightarrow dots Rightarrow A_ <30>approx left(begin mathbf<6.172>_ <778>& 2.807524 & -2.015076\ -0.000073 & mathbf<4.487>_ <747>& -5.390442\ 0 & 0 & -mathbf <1.660525>end right) , . $$ ♦

К сожалению условие теоремы достаточно ограничительно: собственные числа вещественной матрицы $ A $ могут оказаться и мнимыми, но тогда они одинаковы по модулю.

Как это обстоятельство сказывается на структуре матрицы $ A_ <infty>$ и дальнейшее развитие метода ☞ ЗДЕСЬ

Частичная проблема собственных чисел

Задача. Найти максимальное по модулю собственное число матрицы $ A_<> $.

Предположение . Будем считать сначала, что максимальное по модулю собственное число матрицы единственно.

Излагаемый ниже метод поиска этого собственного числа называется методом степенны́х итераций 12) .

Рассмотрим произвольный ненулевой столбец $ Y_0=left[ y_<1>^<[0]>,dots,y_^ <[0]>right]^<^<top>> in mathbb C^n $. Cоставим такую же итерационную векторную последовательность, как и в методе Крылова $$ Y_1=Acdot Y_0, Y_2=Acdot Y_1, dots, Y_=Acdot Y_,dots , $$ (только теперь, в отличие от метода Крылова, считаем ее неограниченно продолжающейся) и выделим последовательность первых элементов этих векторов: $$y_<1>^<[1]>,y_<1>^<[2]>,dots,y_<1>^<[K]>,dots $$

Теорема 25. Как правило, предел

$$ lim_frac^<[K+1]>>^<[K]>> $$ существует и он равен максимальному по модулю собственному числу матрицы $ A_<> $.

Доказательство. Перенумеруем собственные числа $ lambda_<1>,dots,lambda_n $ матрицы $ A_<> $ так, чтобы $ lambda_ <1>$ обозначило максимальное по модулю: $$|lambda_1|= max_> |lambda_j| , quad |lambda_1|>|lambda_j| quad npu quad jin <2,dots,n> . $$ Очевидно, $$ Y_=A^Kcdot Y_0 ; $$ отсюда следует, что любой элемент столбца $ Y_ $ может быть линейно выражен через $ lambda_<1>^K,dots,lambda_n^K $. В частности, это справедливо и для первого элемента: $$ y_<1>^<[K]>=C_1lambda_1^K+C_2lambda_2^K+dots+C_nlambda_n^K . $$ В этом представлении $ _^n $ — будут константами из $ mathbb C_<> $ в случае если все собственные числа являются простыми, и полиномами из $ mathbb C[K] $ в случае, если имеются кратные собственные числа. Действительно, в первом случае существует базис пространства $ mathbb C^n $, состоящий из собственных векторов матрицы $ A_<> $: $$ A<mathfrak X>_j=lambda_j<mathfrak X>_j quad npu quad jin <1,dots,n>. $$ Вектор $ Y_0 $ можно разложить по этому базису: $$Y_0=alpha_1<mathfrak X>_1+dots+alpha_n<mathfrak X>_n .$$ Тогда последовательным домножением на матрицу $ A_<> $ получаем : $$begin Y_1=AY_0&=& alpha_1 lambda_1<mathfrak X>_1+dots+alpha_nlambda_n<mathfrak X>_n, \ dots & & dots \ Y_K=A^KY_0&=& alpha_1 lambda_1^K<mathfrak X>_1+dots+alpha_nlambda_n^K<mathfrak X>_n end $$ откуда и следует доказываемое равенство.

Во втором случае — когда имеются кратные собственные числа матрицы $ A_<> $ — придется применять «тяжелую артиллерию» в виде жордановой нормальной формы; см. теорему $ 5 $ ☞ ЗДЕСЬ. Для простоты рассуждений, будем в оставшейся части доказательства считать все собственные числа матрицы различными. Имеем тогда $$ lim_ frac^<[K+1]>>^<[K]>>= lim_ frac <lambda_1^left[C_1+ C_2(lambda_2/lambda_1)^+dots+ C_n(lambda_n/lambda_1)^ right]> <lambda_1^left[C_1+C_2(lambda_2/lambda_1)^+dots+ C_n(lambda_n/lambda_1)^ right]> =lambda_1 $$ поскольку $$ lim_ left| frac<lambda_j> <lambda_1>right|^K = 0 quad npu quad jin <2,dots,n> . $$ Исключительным случаем является ситуация $ C_1=0 $, в этом случае утверждение теоремы может оказаться несправедливым 13) . ♦

Как правило, вектор

$$ left[1, lim_frac^<[K]>>^<[K]>>,dots, lim_frac^<[K]>>^<[K]>>right]^<^<top>> $$ будет собственным, принадлежащим максимальному по модулю собственному числу матрицы $ A_<> $.

Пример. Для матрицы

$$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & -4 end right) $$ найти максимальное по модулю собственное число и принадлежащий ему собственный вектор.

Решение. Возьмем в качестве стартового столбца $ Y_0=[1,0,0]^<^<top>> $. Имеем: $$ Y_1=AY_0=left( begin 2 \ 7 \ -1 end right), Y_2=AY_1=left( begin 26 \ 32 \ -12 end right), Y_3=AY_2=left( begin 160 \ 242 \ -42 end right),dots, $$ $$ Y_<19>=left( begin <scriptstyle 4259667747238636>\ <scriptstyle 6435097324667832>\ <scriptstyle -1571397155909260>end right), Y_<20>=AY_<19>=left( begin <scriptstyle 29396024624390028>\ <scriptstyle 44408774736946168>\ <scriptstyle -10844273772937260>end right) $$ Смотрим на отношения первых элементов векторов: $$ begin K & 1 & 2 & 3 & 4 & 5 & dots & 15 & dots & 19 \ hline y_<1>^<[K+1]>/y_<1>^ <[K]>& 2 & 13 & 6.153846 & 6.8 & 7.180147 & dots & 6.900726 & dots & mathbf<6.90101>_ <displaystyle 3>end $$ Далее, в соответствии со следствием, собственный вектор, принадлежащий найденному числу $$ approx left[1, frac^<[20]>>^<[20]>>,frac^<[20]>>^<[20]>>right]^<^<top>> approx left[1, 1.51070_<displaystyle 6>, -0.368902 right]^<^<top>> $$ ♦

Теперь обсудим исключительные случаи алгоритма.

1. Нарушение сходимости итерационного процесса за счет неудачного выбора стартового вектора. Если в качестве $ Y_ <0>$ оказался случайно взят собственный вектор $ mathfrak X_ <ast>$ матрицы $ A_<> $, принадлежащий произвольному ее собственному числу $ lambda_ <*>$, то предел последовательности из теоремы будет равен именно этому числу; если при этом $ |lambda_ <*>| ne max_ <1le j le n>| lambda_j | $, то мы выйдем за пределы смысла выражения «как правило». Понятно, что вероятность настолько плохого выбора нулевая, но и выбор $ Y_0 $ вблизи $ mathfrak X_ <ast>$ также может существенно замедлить скорость сходимости. Поэтому если возникает ситуация медленной «стабилизации» значащих цифр в десятичном приближении собственного числа, попробуйте сменить начальный вектор.

2. Нарушение условия предположения , выдвинутого в начале пункта: максимальное по модулю собственное число неединственно.

Пример. Найти максимальное по модулю собственное число матрицы примера Леверье

$$ A=left(begin -5.509882&1.870086&0.422908&0.008814 \ 0.287865&-11.811654&5.711900&0.058717 \ 0.049099&4.308033&-12.970687&0.229326 \ 0.006235&0.269851&1.397369&-17.596207 end right) . $$

Решение. Для столбца $ Y_0=[1,0,0,0]^<^<top>> $ имеем $$y_<1>^<[100]>/y_<1>^<[99]>=-17.8_ <displaystyle 3113> ,$$ т.е. на $ 100 $-й итерации получаем лишь $ 3_<> $ истинные десятичные цифры в представлении собственного числа. При этом компонентами векторов $ Y_ $ являются числа порядка $ 10^ <123>$. Если мы посмотрим на ответ примера Леверье, то увидим, что имеются два собственных числа матрицы, близких по модулю. ♦

К сожалению, вероятность того факта, что у случайно выбранной матрицы два ее собственных числа будут иметь одинаковый модуль становится ненулевой если эта матрица выбирается из множества вещественных матриц. Дело в том, что в этом случае ее характеристический полином будет иметь вещественные коэффициенты, а мнимые корни такого полинома всегда пáрные — для любого невещественного корня $ lambda_<ast>^<> $ полинома, комплексно сопряженное к нему число $ overline<lambda_<ast>> $ также будет корнем. При этом $ |lambda_<ast>|= |overline<lambda_<ast>> | $.

Пример. Для матрицы

Предположение 2 . Пусть два максимальных по модулю собственных числа матрицы разнесены по величине, например $$ |lambda_1| > | lambda_2 | > | lambda_ j | quad npu j in <2,dots, n >. $$

Обобщение степенного метода основывается на использовании последовательностей из каких-то двух компонент векторов $ Y_=AY_K $, например, наряду с уже использованной выше последовательностью первых компонент $$y_<1>^<[1]>,y_<1>^<[2]>,dots,y_<1>^<[K]>,dots $$ возьмем еще и аналогичную для вторых: $$y_<2>^<[1]>,y_<2>^<[2]>,dots,y_<2>^<[K]>,dots $$

Теорема 26 [Эйткен]. При практически любом выборе стартового вектора $ Y_0 ne mathbb O $ для последовательности

Доказательство. Построим квадратное уравнение $$ p_0x^2+p_1x+p_2 = 0 $$ имеющее корнями $ lambda_1 $ и $ lambda_2 $. Если существует базис рпостранства $ mathbb C^n $ $$Y_0=alpha_1<mathfrak X>_1+alpha_2<mathfrak X>_2+dots+alpha_n<mathfrak X>_n .$$ Тогда последовательным домножением на матрицу $ A_<> $ получаем : $$begin Y_K=& alpha_1 lambda_1^K<mathfrak X>_1 &+alpha_2 lambda_2^K<mathfrak X>_2+dots &+alpha_nlambda_n^K<mathfrak X>_n, \ Y_=& alpha_1 lambda_1^<mathfrak X>_1 &+alpha_2 lambda_2^<mathfrak X>_2+dots &+alpha_nlambda_n^<mathfrak X>_n,\ Y_=& alpha_1 lambda_1^<mathfrak X>_1 & +alpha_2 lambda_2^<mathfrak X>_2+dots &+alpha_nlambda_n^<mathfrak X>_n. end $$ Отбрасываем из правых частей равенств слагаемые порядков возрастания ниже, чем $ lambda_2^K, lambda_2^, lambda_2^ $ соответственно, домножаем получившиеся приближенные равенства $$begin Y_K & approx alpha_1 lambda_1^K<mathfrak X>_1 &+alpha_2 lambda_2^K<mathfrak X>_2, & color times p_2 \ Y_& approx alpha_1 lambda_1^<mathfrak X>_1 &+alpha_2 lambda_2^<mathfrak X>_2, & color times p_1\ Y_ & approx alpha_1 lambda_1^<mathfrak X>_1 & +alpha_2 lambda_2^<mathfrak X>_2, & color times p_0 end $$ и складываем: $$ p_2 Y_K + p_1Y_ + p_0 Y_ approx mathbb O , . $$ В получившемся векторном равенстве выбираем первые две компоненты: $$ left< begin p_2 y_1^ <[K]>+ p_1 y_1^ <[K+1]>+ p_0 y_1^ <[K+2]>approx 0 , , \ p_2 y_2^ <[K]>+ p_1 y_2^ <[K+1]>+ p_0 y_2^ <[K+2]>approx 0 , , end right. $$ которые и позволят определить приближенное значение набора $ p_0,p_1,p_2 $. С точностью до числового сомножителя, искомый полином можно представить в виде определителя $$ p_0x^2+p_1x+p_2 approx left|begin y_1^ <[K]>& y_1^ <[K+1]>& y_1^ <[K+2]>\ y_2^ <[K]>& y_2^ <[K+1]>& y_2^ <[K+2]>\ 1 & x & x^2 end right| , . $$ Формулы Виета завершат доказательство. ♦

При выполнении условия предположения 2 имеет место равенство

Пример. Для матрицы

$$ A=left(begin 2 & 3 &-1\ 7 & 3 & 3 \ -1 & -2 & 4 end right) $$ найти первые два по порядку убывания модулей собственных числа.

Задачи

Источники

[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94

[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960

[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989

Спектральная кластеризация

Дата публикации Feb 21, 2019

Введение

В этом посте мы рассмотрим тонкости спектральной кластеризации для графиков и других данных. Кластеризация является одной из главных задач в машинном обучении без учителя. Цель состоит в том, чтобы назначить немаркированные данные группам, где, возможно, аналогичные точки данных будут назначены в одну группу.

Спектральная кластеризация – это метод с корнями в теории графов, где этот подход используется для идентификации сообществ узлов в графе на основе соединяющих их ребер. Этот метод является гибким и позволяет кластеризовать не графовые данные.

Спектральная кластеризация использует информацию из собственных значений (спектра) специальных матриц, построенных из графика или набора данных. Мы узнаем, как построить эти матрицы, интерпретировать их спектр и использовать собственные векторы для назначения наших данных кластерам.

Собственные векторы и собственные значения

Критическим для этой дискуссии является концепция собственных значений и собственные векторы. Для матрицы A, если существует вектор x, который не является всеми 0 и скалярным λ, таким, что Ax = λx, то x называется собственным вектором A с соответствующим собственным значением λ.

Мы можем думать о матрице A как о функции, которая отображает векторы на новые векторы. Большинство векторов окажутся где-то совершенно разными, когда к ним будет применен A, но собственные векторы меняются только по величине. Если вы проведете линию через начало координат и собственный вектор, то после отображения собственный вектор все равно попадет на линию. Величина, по которой вектор масштабируется вдоль линии, зависит от λ.

Мы можем легко найти собственные значения и собственные векторы матрицы, используя numpy в Python:

Собственные векторы являются важной частью линейной алгебры, потому что они помогают описать динамику систем, представленных матрицами. Существует множество приложений, в которых используются собственные векторы, и мы будем использовать их непосредственно здесь для выполнения спектральной кластеризации.

диаграммы

Графики являются естественным способом представления многих типов данных. Граф – это набор узлов с соответствующим набором ребер, которые соединяют узлы. Края могут быть направленными или ненаправленными и даже иметь веса, связанные с ними.

Сеть роутеров в интернете легко представить в виде графика. Маршрутизаторы – это узлы, а ребра – это соединения между парами маршрутизаторов. Некоторые маршрутизаторы могут разрешать трафик только в одном направлении, поэтому границы могут быть направлены в направлении направления трафика. Веса на краях могут представлять полосу пропускания, доступную вдоль этого края. При такой настройке мы могли бы затем запросить график, чтобы найти эффективные пути для передачи данных от одного маршрутизатора к другому по сети.

Давайте использовать следующий неориентированный граф в качестве рабочего примера:

Этот граф имеет 10 узлов и 12 ребер. Он также имеет два соединенных компонента <0,1,2,8,9>и <3,4,5,6,7>. Связанный компонент – это максимальный подграф узлов, у всех из которых есть пути к остальным узлам подграфа.

Связанные компоненты кажутся важными, если наша задача – назначить эти узлы сообществам или кластерам. Простая идея – сделать каждый связанный компонент отдельным кластером. Это кажется разумным для нашего примера графа, но возможно, что весь граф может быть связан, или что связанные компоненты очень велики. Могут также быть меньшие структуры в связанном компоненте, которые являются хорошими кандидатами для сообществ. Вскоре мы увидим важность идеи связанного компонента для спектральной кластеризации.

Матрица смежности

Мы можем представить наш примерный граф в виде матрицы смежности, где индексы строк и столбцов представляют узлы, а записи представляют отсутствие или наличие ребра между узлами. Матрица смежности для нашего примера графа выглядит следующим образом:

В матрице мы видим, что строка 0, столбец 1 имеет значение 1. Это означает, что существует ребро, соединяющее узел 0 с узлом 1. Если ребра были взвешены, веса ребер были бы в этой матрице вместо только 1 и 0. Так как наш график не направлен, записи для строки i, col j будут равны записи в строке j, col i. Последнее, что следует отметить, это то, что диагональ этой матрицы равна 0, поскольку ни один из наших узлов не имеет ребер.

Степень Матрица

Степень узла – это количество ребер, соединенных с ним. В ориентированном графе мы могли бы говорить о степени и степени, но в этом примере у нас просто есть степень, так как ребра идут в обе стороны. Глядя на наш график, мы видим, что узел 0 имеет степень 4, поскольку он имеет 4 ребра. Мы также можем получить степень, взяв сумму строки узла в матрице смежности.

Матрица степеней – это диагональная матрица, где значение на входе (i, i) является степенью узла i Давайте найдем матрицу степеней для нашего примера:

Сначала мы взяли сумму по оси 1 (строки) нашей матрицы смежности, а затем поместили эти значения в диагональную матрицу. Из матрицы степеней мы легко видим, что узлы 0 и 5 имеют 4 ребра, в то время как остальные узлы имеют только 2.

График лапласианский

Теперь мы собираемся вычислить граф Лапласа. Лапласиан – это просто еще одно матричное представление графа. У него есть несколько прекрасных свойств, которыми мы воспользуемся для спектральной кластеризации. Чтобы вычислить нормальный лапласиан (есть несколько вариантов), мы просто вычитаем матрицу смежности из нашей матрицы степеней:

Диагональ лапласиана – это степень наших узлов, а вне диагонали – вес отрицательного края. Это представление, которое мы ищем для выполнения спектральной кластеризации.

Собственные значения графа лапласиана

Как уже упоминалось, лапласиан обладает некоторыми прекрасными свойствами. Чтобы понять это, давайте рассмотрим собственные значения, связанные с лапласианом, когда я добавлю ребра в наш граф:

Мы видим, что когда граф полностью отключен, все десять наших собственных значений равны 0. Когда мы добавляем ребра, некоторые из наших собственных значений увеличиваются. Фактически, число собственных значений 0 соответствует числу связанных компонент в нашем графе!

Посмотрите внимательно, как добавлен этот последний край, соединяя два компонента в один. Когда это происходит, все собственные значения, кроме одного, были отменены:

Первое собственное значение равно 0, потому что у нас есть только один связный компонент (весь граф связен). Соответствующий собственный вектор всегда будет иметь постоянные значения (в этом примере все значения близки к 0,32).

Первое ненулевое собственное значение называется спектральной щелью. Спектральная щель дает нам некоторое представление о плотности графика. Если бы этот граф был плотно связан (все пары из 10 узлов имели ребро), то спектральный разрыв был бы 10.

Второе собственное значение называется значением Фидлера, а соответствующий вектор является вектором Фидлера. Значение Фидлера приблизительно соответствует минимальному срезу графа, необходимому для разделения графа на два связанных компонента. Напомним, что если бы в нашем графе уже было два связанных компонента, то значение Фидлера было бы равно 0. Каждое значение в векторе Фидлера дает нам информацию о том, какой стороне разреза принадлежит этот узел. Давайте раскрасим узлы в зависимости от того, положительна ли их запись в векторе Филдера:

Этот простой трюк разделил наш график на две группы! Почему это работает? Помните, что нулевые собственные значения представляют связанные компоненты. Собственные значения около нуля говорят нам, что существует почти разделение двух компонентов. Здесь у нас есть одно преимущество: если бы его не было, у нас было бы два отдельных компонента. Таким образом, второе собственное значение мало.

Подводя итог, что мы знаем до сих пор: первое собственное значение 0, потому что у нас есть один связанный компонент. Второе собственное значение около 0, потому что мы на расстоянии одного края от двух соединенных компонентов. Мы также видели, что вектор, связанный с этим значением, говорит нам, как разделить узлы на эти приблизительно связанные компоненты.

Возможно, вы заметили, что следующие два собственных значения также довольно малы. Это говорит нам о том, что мы «близки» к четырем отдельным подключенным компонентам. В общем, мы часто ищем первый большой разрыв между собственными значениями, чтобы найти число кластеров, выраженных в наших данных. Видите разрыв между собственными значениями четыре и пять?

Наличие четырех собственных значений перед разрывом указывает на то, что, вероятно, существует четыре кластера. Векторы, связанные с первыми тремя положительными собственными значениями, должны дать нам информацию о том, какие три разреза необходимо сделать на графике, чтобы назначить каждый узел одному из четырех приближенных компонентов. Давайте построим матрицу из этих трех векторов и выполним кластеризацию K-средних для определения назначений:

График был сегментирован на четыре квадранта, причем узлы 0 и 5 произвольно назначены одному из их связанных квадрантов. Это действительно круто, и это спектральная кластеризация!

Подводя итог, мы сначала взяли наш граф и построили матрицу смежности. Затем мы создали лапласиан графа, вычтя матрицу смежности из матрицы степеней. Собственные значения лапласиана указывали на наличие четырех кластеров. Векторы, связанные с этими собственными значениями, содержат информацию о том, как сегментировать узлы. Наконец, мы выполнили K-средства для этих векторов, чтобы получить метки для узлов. Далее мы увидим, как это сделать для произвольных данных.

Спектральная кластеризация произвольных данных

Посмотрите на данные ниже. Точки нарисованы из двух концентрических кругов с добавлением шума Нам бы хотелось, чтобы алгоритм позволял группировать эти точки в два круга, которые их генерировали.

Эти данные не в форме графика. Итак, во-первых, давайте просто попробуем алгоритм обрезки печенья, такой как K-Means. K-Means найдет два центроида и пометит точки, в зависимости от того, к какому центроиду они ближе всего. Вот результаты:

Очевидно, K-Means не собирался работать. Он действует на евклидовом расстоянии и предполагает, что скопления примерно сферические. Эти данные (и часто данные реального мира) нарушают эти предположения. Давайте попробуем решить эту проблему с помощью спектральной кластеризации.

График ближайших соседей

Есть несколько способов обработать наши данные как график. Самый простой способ – построить граф k-ближайших соседей. Граф k-ближайших соседей обрабатывает каждую точку данных как узел в графе. Затем ребро рисуется от каждого узла до его k ближайших соседей в исходном пространстве. Как правило, алгоритм не слишком чувствителен к выбору k. Меньшие числа, такие как 5 или 10, обычно работают довольно хорошо.

Посмотрите на изображение данных еще раз и представьте, что каждая точка связана со своими 5 ближайшими соседями. Любая точка во внешнем кольце должна быть в состоянии следовать по пути вдоль кольца, но во внутреннем круге не будет никаких путей. Довольно легко увидеть, что этот график будет иметь два связанных компонента: внешнее кольцо и внутренний круг.

Поскольку мы разделяем эти данные только на два компонента, мы должны использовать наш векторный метод Фидлера ранее. Вот код, который я использовал для спектральной кластеризации этих данных:

И вот результаты:

Другие подходы

Граф ближайших соседей – хороший подход, но он основан на том факте, что «близкие» точки должны принадлежать одному кластеру. В зависимости от ваших данных, это может быть не так. Более общий подход заключается в построении аффинной матрицы. Матрица сходства похожа на матрицу смежности, за исключением того, что значение для пары точек показывает, насколько эти точки похожи друг на друга. Если пары точек сильно различаются, то сродство должно быть 0. Если точки идентичны, то сродство может быть 1. Таким образом, сродство действует как вес для ребер нашего графа.

Как решить, что означает совпадение двух точек данных, является одним из наиболее важных вопросов в машинном обучении. Часто знание предметной области – лучший способ построить меру подобия. Если у вас есть доступ к экспертам по доменам, задайте им этот вопрос.

Есть также целые поля, посвященные изучению того, как строить метрики подобия непосредственно из данных. Например, если у вас есть некоторые помеченные данные, вы можете обучить классификатор, чтобы предсказать, похожи ли два входа или нет, основываясь на том, имеют ли они одинаковую метку. Затем этот классификатор можно использовать для присвоения сходства парам немаркированных точек.

Вывод

Мы рассмотрели теорию и применение спектральной кластеризации для графов и произвольных данных. Спектральная кластеризация – это гибкий подход для поиска кластеров, когда ваши данные не соответствуют требованиям других распространенных алгоритмов.

Сначала мы сформировали график между нашими точками данных. Края графика отражают сходство точек. Собственные значения графа лапласиана могут затем использоваться для поиска наилучшего числа кластеров, а собственные векторы могут использоваться для поиска фактических меток кластеров.

Я надеюсь, что вам понравился этот пост, и вы нашли спектральную кластеризацию полезной в вашей работе или исследовании.

[spoiler title=”источники:”]

http://vmath.ru/vf5/algebra2/charpoly

http://www.machinelearningmastery.ru/spectral-clustering-aba2640c0d5b/

[/spoiler]