Как найти число степеней свободы формула - Сайт, где вы сможете решить свои вопросы

Степени свободы (D_f, C) – это количество параметров (точек контроля) Модели (Model). Они указывают количество независимых значений, которые могут изменяться в ходе анализа без нарушения каких-либо ограничений.

Пример.

Рассмотрим Выборку (Sample) данных, состоящую для простоты из пяти положительных целых чисел. Значения могут быть любыми числами без известной связи между ними. Эта выборка данных теоретически должна иметь пять степеней свободы.
Четыре числа в выборке – это {3, 8, 5 и 4}, а среднее значение всей выборки данных равно 6.
Это должно означать, что пятое число равно 10. Иначе быть не может. У пятого значения нет свободы варьироваться.
Таким образом, степень свободы для этой выборки данных равна 4.

Формула степени свободы выглядит следующим образом:

$$D_f = N – 1$$

где

D_f – степень свободы

N – количество значений

Математически степени свободы часто представляют, используя греческую букву “ню”, которая выглядит так: ν. Вы наверняка встретите и такие сокращения: ‘d.o.f.’, ‘dof’, ‘d.f.’ или просто ‘df’.

Степени свободы в статистике

Степени свободы в статистике – это количество значений, используемых при вычислении переменной.

Степени свободы = Количество независимых значений – Количество статистик

Пример. У нас есть 50 независимых значений, и мы хотим вычислить одну-единственную статистику “среднее”. Согласно формуле, степеней свободы будет 50 – 1 = 49.

Степени свободы в Машинном обучении

В прогностическом моделировании, степени свободы часто относятся к количеству параметров, включая данные, используемые при вычислении ошибки модели. Наилучший способ понять это – рассмотреть модель линейной регрессии.

Рассмотрим модель линейной регрессии для Датасета (Dataset) с двумя входными переменными. Нам потребуется один коэффициент в модели для каждой входной переменной, то есть модель будет иметь еще и два параметра.

$$hat{y} = x_1 * β_1 + x_2 * β_2$$

где

y – целевая переменная
x_1, x_2 – входные переменные
β_1, β_2 – параметры модели

Эта модель линейной регрессии имеет две степени свободы, потому что есть два параметра модели, которые должны быть оценены на основе обучающего датасета. Добавление еще одного столбца к данным (еще одной входной переменной) добавит модели еще одну степень свободы. Сложность обучения модели линейной регрессии описывается степенью свободы, например, “модель четвертой степени сложности” означает наличие четырех входных переменных, а также степень свободы, равную четырем.

Степени свободы для ошибки линейной регрессии

Количество обучающих примеров имеет значение и влияет на количество степеней свободы регрессионной модели. Представьте, что мы создаем модель линейной регрессии на базе датасета, состоящего из ста строк.

Сравнивая предсказания модели с реальными выходными значениями, мы минимизируем ошибку. Итоговая ошибка модели имеет одну степень свободы для каждого ряда за вычетом количества параметров. В нашем случае ошибка модели 98 степеней свободы (100 рядов – 2 параметра).

Итоговые степени свободы для линейной регрессии

Конечные степени свободы для модели линейной регрессии рассчитываются как сумма степеней свободы модели плюс степени свободы ошибки модели. В нашем примере это 100 (2 степени свободы модели + 98 степеней свободы ошибки). Как вы уже заметили, степеней свободы столько, сколько рядов в датасете.

Теперь рассмотрим набор данных из 100 строк, но теперь у нас есть 70 входных переменных. Это означает, что модель имеет еще и 70 коэффициентов, что дает нам d.o.f. ошибки, равной 30 (100 строк – 70 коэффициентов). d.o.f. самой модели по-прежнему равен ста.

Отрицательные степени свободы

Что происходит, когда у нас больше столбцов, чем строк данных? Отрицательные значения вполне допустимы здесь. Например, у нас может быть 100 строк данных и 10 000 переменных, к примеру, маркеры генов для 100 пациентов. Следовательно, модель линейной регрессии будет иметь 10 000 параметров, то есть модель будет иметь 10 000 степеней свободы.

Тогда степени свободы рассчитываются следующим образом:

Степень свободы модели = Количество независимых значение – Количество параметров = 100 – 10 000 = -9 900

В свою очередь, степени свободы модели линейной регрессии будут следующими:

Степени свободы модели линейной регрессии = Степени свободы модели – Степени свободы ошибки модели = 10 000 – 9 900 = 100

Фото: @mickeyoneil

Источник

What Are Degrees of Freedom?

Degrees of freedom are the maximum number of logically independent values, which may vary in a data sample. Degrees of freedom are calculated by subtracting one from the number of items within the data sample.

Key Takeaways

Degrees of freedom refer to the maximum number of logically independent values, which may vary in a data sample.
Degrees of freedom are calculated by subtracting one from the number of items within the data sample.
The earliest concept of degrees of freedom was noted in the early 1800s with the works of mathematician and astronomer Carl Friedrich Gauss.
Degrees of freedom are commonly discussed in various forms of hypothesis testing in statistics, such as a chi-square.
Degrees of freedom can describe business situations where management must make a decision that dictates the outcome of another variable.

Understanding Degrees of Freedom

Degrees of freedom are the number of independent variables that can be estimated in a statistical analysis and tell you how many items can be randomly selected before constraints must be put in place.

Within a data set, some initial numbers can be chosen at random. However, if the data set must add up to a specific sum or mean, for example, the number in the data set is constrained to evaluate the values of all other values in a data set, then meet the set requirement.

Examples of Degrees of Freedom

Example 1: Consider a data sample consisting of five positive integers. The values of the five integers must have an average of six. If four items within the data set are {3, 8, 5, and 4}, the fifth number must be 10. Because the first four numbers can be chosen at random, the degree of freedom is four.

Example 2: Consider a data sample consisting of five positive integers. The values could be any number with no known relationship between them. Because all five can be chosen at random with no limitations, the degree of freedom is four.

Example 3: Consider a data sample consisting of one integer. That integer must be odd. Because there are constraints on the single item within the data set, the degree of freedom is zero.

Degrees of Freedom Formula

The formula to determine degrees of freedom is:

−

where:

degrees of freedom

sample size

begin{aligned} &text{D}_text{f} = N – 1 \ &textbf{where:} \ &text{D}_text{f} = text{degrees of freedom} \ &N = text{sample size} \ end{aligned}

Df=N−1where:Df=degrees of freedomN=sample size

For example, imagine a task of selecting ten baseball players whose batting average must average to .250. The total number of players that will make up our data set is the sample size, so N = 10. In this example, 9 (10 – 1) baseball players can be randomly picked, with the 10th baseball player having a specific batting average to adhere to the .250 batting average constraint.

Some calculations of degrees of freedom with multiple parameters or relationships use the formula Df = N – P, where P is the number of different parameters or relationships. For example, in a 2-sample t-test, N – 2 is used because there are two parameters to estimate.

Applying Degrees of Freedom

In statistics, degrees of freedom define the shape of the t-distribution used in t-tests when calculating the p-value. Depending on the sample size, different degrees of freedom will display different t-distributions. Calculating degrees of freedom is critical when understanding the importance of a chi-square statistic and the validity of the null hypothesis.

Degrees of freedom also have conceptual applications outside of statistics. Consider a company deciding the purchase of raw materials for its manufacturing process. The company has two items within this data set: the amount of raw materials to acquire and the total cost of the raw materials.

The company freely decides one of the two items, but their choice will dictate the outcome of the other. Because it can only freely choose one of the two, it has one degree of freedom in this situation. If the company decides the amount of raw materials, it cannot decide the total amount spent. By setting the total amount to spend, the company may be limited in the amount of raw materials it can acquire.

Chi-Square Tests

There are two different kinds of chi-square tests: the test of independence, which asks a question of relationship, such as, “Is there a relationship between gender and SAT scores?”; and the goodness-of-fit test, which asks something like “If a coin is tossed 100 times, will it come up heads 50 times and tails 50 times?”

For these tests, degrees of freedom are utilized to determine if a null hypothesis can be rejected based on the total number of variables and samples within the experiment. For example, when considering students and course choice, a sample size of 30 or 40 students is likely not large enough to generate significant data. Getting the same or similar results from a study using a sample size of 400 or 500 students is more valid.

T-Test

To perform a t-test, you must calculate the value of t for the sample and compare it to a critical value. The critical value will vary, and you can determine the correct critical value by using a data set’s t distribution with the degrees of freedom.

Sets with lower degrees of freedom have a higher probability of extreme values, and higher degrees of freedom, such as a sample size of at least 30, will be much closer to a normal distribution curve. Smaller sample sizes will correspond with smaller degrees of freedom and result in fatter t-distribution tails.

In the examples above, many of the situations may be used as a 1-sample t-test. For instance, ‘Example 1,’ where five values are selected but must add up to a specific average, can be defined as a 1-sample t-test. This is because there is only one constraint being placed on the variable.

History of Degrees of Freedom

The earliest and most basic concept of degrees of freedom was noted in the early 1800s, intertwined in the works of mathematician and astronomer Carl Friedrich Gauss. The modern usage and understanding of the term were expounded upon first by William Sealy Gosset, an English statistician, in his article “The Probable Error of a Mean,” published in Biometrika in 1908 under a pen name to preserve his anonymity.

In his writings, Gosset did not specifically use the term “degrees of freedom.” He did explain the concept throughout developing what would eventually be known as “Student’s T-distribution.” The term was not popular until 1922. English biologist and statistician Ronald Fisher began using the term “degrees of freedom” when he published reports and data on his work developing chi-squares.

How Do You Determine Degrees of Freedom?

When determining the mean of a set of data, degrees of freedom are calculated as the number of items within a set minus one. This is because all items within that set can be randomly selected until one remains; that one item must conform to a given average.

What Does Degrees of Freedom Tell You?

Degrees of freedom tell you how many units within a set can be selected without constraints to still abide by a given rule overseeing the set. For example, consider a set of five items that add to an average value of 20. Degrees of freedom tell you how many of the items (4) can be randomly selected before constraints must be put in place. In this example, once the first four items are picked, you no longer have the liberty to randomly select a data point because you must “force balance” to the given average.

Is the Degree of Freedom Always 1?

Degrees of freedom are always the number of units within a given set minus 1. It is always minus one because, if parameters are placed on the data set, the last data item must be specific so all other points conform to that outcome.

The Bottom Line

Some statistical analysis processes may call for an indication of the number of independent values that can vary within an analysis to meet constraint requirements. This indication is the degrees of freedom, the number of units in a sample size that can be chosen randomly before a specific value must be picked.

Источник

Степени свободы в статистике

Уровень сложности
Простой

Время на прочтение
6 мин

Количество просмотров 1.1K

Автор статьи: Артем Михайлов

Статистический анализ играет важную роль в научных исследованиях, коммерческих деятельностях и в других областях. Однако, его результаты могут быть неточными, если не учитывать имеющиеся степени свободы. Степени свободы – это концепция, которая широко используется в статистике, и она позволяет более точно определить, насколько можно доверять полученным результатам.

В данной статье мы рассмотрим понятие степеней свободы, их роль в статистических расчетах, а также примеры их использования. Мы узнаем, как степени свободы помогают улучшить точность статистических выводов и в каких случаях их использование особенно важно.

Что такое степень свободы?

Степень свободы (Degree of Freedom, df) в статистике – это количество значений или наблюдений в выборке, которые могут быть изменены независимо друг от друга без изменения ее структуры. Можно сказать, что это количество переменных, которые оставляются свободными для варьирования после того, как структура выборки была определена.

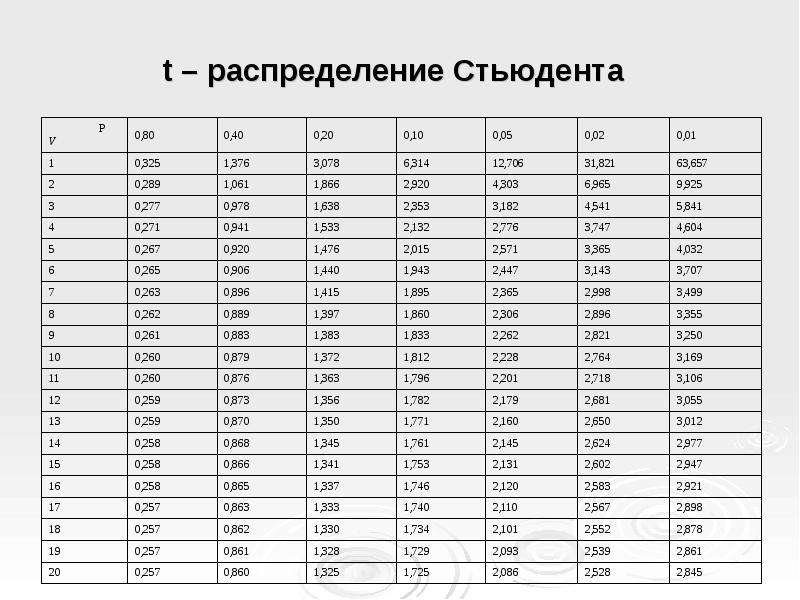
Например, рассмотрим тест Стьюдента (t-Test), который используется для проверки гипотезы о равенстве средних значений двух выборок. В этом тесте степень свободы определяется как сумма степеней свободы двух выборок минус два (df = n1 + n2 – 2), где n1 и n2 – размеры выборок.

Чем больше степень свободы, тем меньше вероятность ложных выводов и тем более точными будут результаты теста. В случае же, если степень свободы будет низкой, то мы можем получить ложные результаты, так как мы не имеем достаточно информации для адекватной оценки статистических характеристик выборки.

Одним из важных факторов, влияющих на степень свободы, является размер выборки. Чем больше выборка, тем больше степень свободы, значит, чем больше выборка, тем менее вероятно получение ошибочных результатов в статистических тестах.

Также степень свободы важна при выборе статистической модели. К примеру, при построении линейной регрессии, степень свободы может использоваться для определения того, сколько переменных необходимо использовать в модели. Выбор модели слишком сложной или, наоборот, слишком простой (т.е. с недостаточной степенью свободы) может привести к неправильным выводам.

Таблица степеней свободы

Таблица степеней свободы – это таблица, которая заполняется в соответствии с типом и количеством переменных, которые используются в анализе статистических данных. Она используется для определения правильной формулы для расчета критических значений при проведении статистических тестов, таких как t-критерий, F-критерий и хи-квадрат тест.

В таблице степеней свободы могут быть два типа переменных: независимые (IV) и зависимые (DV). Количество степеней свободы для каждой переменной определяется путем вычитания единицы от общего количества наблюдений.

Для каждого теста, количество степеней свободы может быть разным в зависимости от характеристик выборки и типа теста. Например:

В t-критерии Стьюдента, количество степеней свободы зависит от размера выборки и количества групп, участвующих в сравнении. Если у нас есть две группы, количество степеней свободы будет равно n1+n2-2 (где n1 и n2 – это размер первой и второй групп соответственно).
В анализе дисперсии (ANOVA), количество степеней свободы будет зависеть от количества групп и количества элементов в каждой группе. Если есть количество групп (k) и общее количество элементов (N), то количество степеней свободы для межгрупповой дисперсии будет равно k-1, а для остаточной дисперсии будет равно N-k.
В хи-квадрат тесте, количество степеней свободы зависит от размера матрицы сопряженности. Если у нас есть матрица 2×2, то количество степеней свободы будет равно 1.

Таблица степеней свободы помогает убедиться, что мы используем правильные статистические формулы для расчетов, что позволяет получать более точные и надежные результаты при анализе статистических данных.

Примеры использования степеней свободы

Рассмотрим несколько практических примеров использования степеней свободы в статистике:

t-критерий Стьюдента. Это статистический тест, который используется для проверки значимости различия между средними двух независимых выборок. Для расчета t-критерия Стьюдента используется формула, которая включает в себя показатели меры центральной тенденции (среднее значение) и меры разброса (стандартное отклонение) для каждой выборки, а также степени свободы. В частности, степени свободы в расчете t-критерия Стьюдента определяются как сумма степеней свободы выборок, возведенная в степень двух, деленная на сумму квадратов степеней свободы выборок. Этот тест дает возможность оценить значимость различий между двумя выборками и узнать, велика ли вероятность случайного различия.

Предположим, что вы хотите определить, отличаются ли средние зарплаты мужчин и женщин в вашей компании. Вы можете использовать t-критерий для проверки этой гипотезы. Для этого вам нужно знать выборочные средние и стандартные отклонения для мужчин и женщин, а также общее число человек в каждой группе. После этого можно использовать формулу для расчета t-критерия, учитывая количество степеней свободы (количество людей в каждой группе минус 1).
Анализ дисперсии (ANOVA). Это статистический тест, который используется для сравнения средних значений нескольких групп. ANOVA расчитывается разнесением общего отклонения между группами на внутреннюю дисперсию (внутригрупповое отклонение) и межгрупповую дисперсию. Степени свободы в расчете ANOVA определяются как разность между общим числом наблюдений и числом использованных для расчета средних значений степеней свободы (то есть на 1 меньше числа групп). Внутригрупповые и межгрупповые степени свободы могут быть вычислены отдельно.

Предположим, что у вас есть несколько групп людей, проходящих тренировку для улучшения своего здоровья. Вы хотите определить, есть ли значимые различия в потере веса между этими группами. Для решения этого вопроса можно использовать ANOVA, для этого вам нужно знать выборочные средние и стандартные отклонения для каждой группы, а также общее количество участников в каждой группе. Затем используйте формулу для расчета F-критерия, учитывая количество степеней свободы, которое будет различаться в зависимости от количества групп и количества участников в каждой группе.
Хи-квадрат тест. Это статистический тест, в котором измеряется отклонение между фактическим и ожидаемым количеством наблюдений в наборе данных. Хи-квадрат тест может использоваться для проверки независимости двух переменных в категориальных данных, таких как таблицы сопряженности. Степени свободы в расчете Хи-квадрат теста определяются как разность между общим количеством наблюдений в таблице и количеством ограничений (то есть размерность таблицы минус 1, по каждому измерению). Если степени свободы достаточно высоки, то можно считать, что тест говорит о статистически значимых различиях между переменными.

Предположим, что у вас есть две переменных – пол (мужчина или женщина) и предпочитаемый вид спорта (баскетбол, футбол, хоккей и т.д.), и вы хотите проверить, есть ли статистически значимая связь между этими переменными. Для этого вы можете использовать хи-квадрат тест, для которого нужно разбить каждую категориальную переменную на несколько групп, затем измерить общее количество наблюдений в каждой ячейке таблицы. После того как вы подсчитаете значения статистики хи-квадрат, вы можете использовать таблицу степеней свободы, чтобы определить, является ли полученный результат значимым для определенного уровня доверия.
В корреляционном анализе, степени свободы используются для вычисления коэффициента корреляции между двумя переменными и определения статистической значимости этой связи. Обычно, чем больше степеней свободы, тем точнее оценки корреляции. Количество степеней свободы определяется как общее число наблюдений минус число неизвестных параметров.

Например, если мы исследуем связь между уровнем образования и доходом, то количество степеней свободы будет равно количеству наблюдений минус два, так как два параметра (уровень образования и доход) неизвестны.

Преимущества и недостатки

Преимущества использования степеней свободы в статистике включают следующее:

Корректность статистических тестов: использование степеней свободы позволяет правильно оценивать дисперсию и скорректировать стандартные ошибки. Это обеспечивает более точные тесты на статистическую значимость.
Увеличение мощности тестов: использование правильных степеней свободы может увеличить мощность статистических тестов. Это позволяет увидеть статистически значимые различия там, где их может не быть при использовании неправильных степеней свободы.
Более надежные выводы: правильное использование степеней свободы позволяет избежать ошибок первого и второго рода. Это позволяет давать более точные и надежные научные выводы.

Однако, использование степеней свободы также имеет некоторые ограничения:

Количество данных: необходимо иметь достаточно большое количество данных, чтобы определить степени свободы. В противном случае могут возникнуть ошибки в статистических тестах.
Некоторые статистические тесты зависят от предположений: некоторые статистические тесты, такие как t-тесты, предполагают нормальность распределения данных. Если данные не соответствуют этим предположениям, использование степеней свободы может привести к ошибкам.
Ошибки вязкости: иногда степени свободы могут быть неверными из-за ошибок в вычислениях. Это может привести к неправильным выводам из статистических тестов.

Заключение

Таким образом, степени свободы являются одним из ключевых параметров в статистических расчетах и оказывают большое влияние на результаты анализа данных. При этом, важно понимать, что оптимальное количество степеней свободы зависит от многих факторов, включая размер выборки и число независимых переменных. Поэтому, для правильного выбора количества степеней свободы, необходим обширный опыт в анализе данных и статистике.

Также следует отметить, что степени свободы являются только одним из аспектов статистического анализа, и их применение требует определенных знаний в области статистики.

Полезные рекомендации

Напоследок хочу порекомендовать несколько полезных бесплатных вебинаров от OTUS. Регистрация доступна по ссылкам ниже:

Построение архитектуры с иcпользованием облачных сервисов AWS
Профессия Системный Аналитик. Путь с нуля до Middle
Бережливое управление требованиями

Источник

Число степеней
свободы это число свободно варьирующих
единиц в составе выборки. Так, если вся
выборка состоит из п
элементов
и характеризуется средней X,
то любой элемент этой совокупности
может быть получен как разность между
величиной n
• X
и суммой
всех остальных элементов, кроме самого
этого элемента.

Пример. Рассмотрим
ряд 4.5: 2468 10. Мы помним, что средняя
этого ряда равна 6.
В этом ряду
5 чисел, следовательно N
= 5. Предположим,
что мы хотим получить последний элемент
ряда

– 10, зная все
предыдущие элементы и среднее этого
ряда. Тогда:

5-6-2-4-6-8= 10

Предположим, что
мы хотим получить первый элемент ряда

– 2, зная все
последующие элементы и среднее этого
ряда. Тогда:

5-6-4-6-8-10 = 2и т.д.

Следовательно,
один элемент выборки не имеет свободы
вариации и всегда может быть выражен
через другие элементы и среднее. Это
означает, что число степеней свободы у
выборочного ряда обозначаемое в
таких случаях символом k
будет
определяться как k
= п -1, где п
— общее
число элементов ряда (выборки).

При наличии не
одного, а нескольких ограничений свободы
вариации, число степеней свободы,
обозначаемое как v
(гречес-и.ш буква ню) будет равно v
= п – k,
где k
соответствует
числу ограничений свободы вариации.

В общем случае для
таблицы экспериментальных данных число
степеней свободы будет определяться
по следующей формуле:

v
= (с – 1)•(n–
1)
(4.8)

где с
— число
столбцов, а п
— число
строк (число испытуемых).

Следует подчеркнуть,
однако, что для ряда статистических
методов расчет числа степеней свободы
имеет свою специфику.

4.7. Понятие нормального распределения

Нормальное
распределение играет большую роль в
математической статистике, поскольку
многие статистические методы предполагают,
что, анализируемые с их помощью
экспериментальные данные распределены
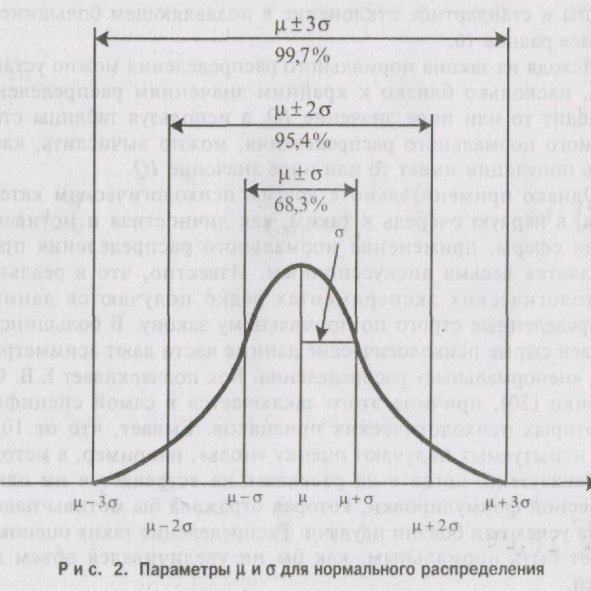
нормально. График нормального распределения
имеет вил колоколообразной кривой (см.
рис. 2).

Его важной
особенностью является то, что форма и
положение графика нормального
распределения определяется только
двумя параметрами: средней µ(мю) и
стандартным отклонением о (сигма).
Если стандартное отклонение σ постоянно,
а величина средней µ меняется, то
собственно форма нормальной кривой
остается неизменной, а лишь ее график
смещается вправо (при увеличении µ)
или влево (при уменьшении µ) по оси
абсцисс –ОХ.
При условии
постоянства средней ц изменение сигмы
влечет за собой изменение только ширины
кривой: при уменьшении сигмы кривая
делается более узкой, и поднимается при
этом вверх, а при увеличении сигмы кривая
расширяется, но опускается вниз.
Однако во всех случаях нормальная кривая
оказывается строго симметричной
относительно средней, сохраняя правильную
колоколообразную форму.

Для нормального
распределения характерно также
совпадение величин средней
арифметической, моды и медианы. Равенство
этих показателей указывает на нормальность
данного распределения. Это распределение
обладает еще одной важной особенностью:
чем больше величина признака отклоняется
от среднего значения, тем меньше
будет частота встречаемости (вероятность)
этого признака в распределении.
«Нормальным» такое распределение было
названо потому, что оно наиболее часто
встречалось в естественно-научных
исследованиях и казалось «нормой»
распределения случайных величин.

В психологических
исследованиях нормальное распределение
используется в первую очередь при
разработке и применении тестов
интеллекта и способностей. Так, отклонения
показателей интеллекта IQ
следуют
закону нормального распределения, имея
среднее значение равное 100 для любой
конкретной возрастной группы и стандартное
отклонение в подавляющем большинстве
случаев равное 16.

Исходя из закона
нормального распределения можно
установить, насколько близко к крайним
значениям распределения подходит то
или иное значение IQ,
а используя
таблицы стандартного нормального
распределения, можно вычислить, какая
часть популяции имеет то или иное
значение IQ.

Однако применительно
к другим психологическим категориям,
в первую очередь к таким, как личностная
и мотиваци-онная сферы, применение
нормального распределения представляется
весьма дискуссионным. Известно, что в
реальных психологических экспериментах
редко получаются данные, распределенные
строго по нормальному закону. В большинстве
случаев сырые психологические данные
часто дают асимметричные, «ненормальные»
распределения. Как подчеркивает Е.В.
Сидоренко (30), причина этого заключается
в самой специфике некоторых психологических
признаков. Бывает, что от 10 до 20% испытуемых
получают оценку «ноль», например, в
методике Хекхаузена, когда в их
рассказах не встречается ни одной
словесной формулировки, которая отражала
бы мотивы надежды на успех или боязни
неудачи. Распределение таких оценок не
может быть нормальным, как бы ни
увеличивался объем выборки.

Несмотря на это,
при обработке экспериментальных данных
всегда целесообразно проводить оценку
характера распределения (см. главу 8,
раздел 8.2). Эта оценка важна, потому что
в зависимости от характера распределения
решается вопрос о возможности
применения того или иного статистического
метода. Как будет понятно из дальнейшего
изложения, при нормальном распределении
экспериментальных данных применяются
особые методы статистической обработки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 октября 2019 года; проверки требует 1 правка.

Количество степеней свободы — это количество значений в итоговом вычислении статистики, способных варьироваться. Иными словами, количество степеней свободы показывает размерность вектора из случайных величин, количество «свободных» величин, необходимых для того, чтобы полностью определить вектор.

Количество степеней свободы может быть не только натуральным, но и любым действительным числом, хотя стандартные таблицы рассчитывают p-value наиболее распространённых распределений только для натурального числа степеней свободы.

Степени свободы распределений[править | править код]

Хи-квадрат[править | править код]

Если случайные величины $Z_{1};ldots ;Z_{n}$ независимы и все имеют стандартное нормальное распределение (), то тогда говорят, что случайная величина , являющаяся суммой квадратов стандартных нормальных величин в количестве штук, имеет распределение хи-квадрат с степенями свободы ( $chi _{n}^{2}$ ):

$X=sum limits _{{i=1}}^{n}Z_{i}^{2}sim chi _{n}^{2}$

t-распределение Стьюдента[править | править код]

Если случайная величина имеет стандартное нормальное распределение (), случайная величина имеет распределение хи-квадрат с степенями свободы ( $chi _{n}^{2}$ ) и и независимы (их корреляция равна нулю), то случайная величина $T={frac {Z}{{sqrt {{frac {X}{n}}}}}}$ имеет распределение Стьюдента с степенями свободы ( $t_{n}$ ):

$T={frac {{mathcal {N}}(0;1)}{{sqrt {{frac {chi _{n}^{2}}{n}}}}}}sim t_{n}$

Распределение Фишера—Снедекора[править | править код]

Если случайная величина $X_{1}$ имеет распределение хи-квадрат с степенями свободы, а случайная величина $X_{2}$ имеет распределение хи-квадрат с степенями свободы, то случайная величина $F={frac {X_{1}/n}{X_{2}/m}}$ имеет распределение Фишера—Снедекора с и степенями свободы ( $t_{n}$ ):

$F={frac {chi _{n}^{2}/n}{chi _{m}^{2}/m}}sim {mathrm {F}}_{{n;m}}$

$(t_{m})^{2}=left({frac {{mathcal {N}}(0;1)}{{sqrt {{frac {chi _{m}^{2}}{m}}}}}}right)^{2}={frac {{bigl (}{mathcal {N}}(0;1){bigr )}^{2}}{left({sqrt {{frac {chi _{m}^{2}}{m}}}}right)^{2}}}={frac {chi _{1}^{2}}{chi _{m}^{2}/m}}={frac {chi _{1}^{2}/1}{chi _{m}^{2}/m}}sim {mathrm {F}}_{{1;m}}$

Теория вероятностей[править | править код]

Пусть $X_{i}$ — одномерная случайная величина. Тогда будут верны следующие утверждения о количестве степеней свободы:

Замена случайной величины ${bar X}(X_{1};ldots ;X_{n})$ на её истинное математическое ожидание даёт прибавку в одну степень свободы по следующей причине. Рассмотрим случайную величину $xi _{k}=X_{k}-{bar X}$ . Далее, $sum limits _{{i=1}}^{n}xi _{i}=sum limits _{{i=1}}^{n}(X_{i}-{bar X})=sum limits _{{i=1}}^{n}X_{i}-sum limits _{{i=1}}^{n}{bar X}=n{bar X}-n{bar X}=0$ . Следовательно, имеется штук зависимых случайных величин. Поэтому n-1 штук величин независимы, поэтому в формуле с bar X в числителе на одну степень свободы меньше, чем в формуле с истинным матожиданием.

Регрессионный анализ[править | править код]

В регрессионном анализе при использовании метода наименьших квадратов сопоставляются наблюдения $Y_{i}$ с расчётными значениями ${hat Y}_{i}$ (полученными из уравнения регрессии). Если {bar Y} — это арифметическое среднее всех наблюдений, то в соответствии с многомерной теоремой Пифагора имеет место равенство:

$underbrace {sum limits _{i}(Y_{i}-{bar Y})^{2}}_{{TSS}}=underbrace {sum limits _{i}({hat Y}_{i}-{bar Y})^{2}}_{{ESS}}+underbrace {sum limits _{i}(Y_{i}-{hat Y})^{2}}_{{RSS}}$

При этом TSS (Total Sum of Squares) распределён как $chi ^{2}$ с (n-1) степенями свободы, ESS (Estimated Sum of Squares; не путать с Error!) распределён как $chi ^{2}$ с одной степенью свободы, RSS (Residual Sum of Squares; не путать с Regression!) распределён как $chi ^{2}$ с (n-2) степенями свободы.

См. также[править | править код]

Распределение вероятностей
Теория вероятностей

Источник

Степени свободы в статистике

Степени свободы в Машинном обучении

Степени свободы для ошибки линейной регрессии

Итоговые степени свободы для линейной регрессии

Отрицательные степени свободы

What Are Degrees of Freedom?

Key Takeaways

Understanding Degrees of Freedom

Examples of Degrees of Freedom

Degrees of Freedom Formula

Applying Degrees of Freedom

Chi-Square Tests

T-Test

History of Degrees of Freedom

How Do You Determine Degrees of Freedom?

What Does Degrees of Freedom Tell You?

Is the Degree of Freedom Always 1?

The Bottom Line

Степени свободы в статистике

Автор статьи: Артем Михайлов

Что такое степень свободы?

Таблица степеней свободы

Примеры использования степеней свободы

Преимущества и недостатки

Заключение

Полезные рекомендации

4.7. Понятие нормального распределения

Степени свободы распределений[править | править код]

Хи-квадрат[править | править код]

t-распределение Стьюдента[править | править код]

Распределение Фишера—Снедекора[править | править код]

Теория вероятностей[править | править код]

Регрессионный анализ[править | править код]

См. также[править | править код]

Вам также может понравиться

Как найти файлы драйвера на компьютере

Как нашли произведения гомера

Как найти электронную оболочку элемента

Добавить комментарий Отменить ответ