Как найти число степеней свободы воздуха

Какие виды теплоемкости Вам известны?

Теплоемкость – свойство материала поглощать определенное количество тепла при нагревании и выделять его при охлаждении.

Удельная теплоемкость – количество тепла, необходимое для нагревания единицы количества вещества на один градус.

Массовая теплоемкость С , Дж / (кг К) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры;

Объемная теплоемкость С’, Дж / (м 3 К) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры;

Мольная теплоемкость С_М , Дж / (кмоль К) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры.

3. От чего зависит теплоемкость газов? Почему Ср > СV?

Для газов удельная теплоемкость, а также молярная теплоемкость, зависит от условий, при которых газ нагревается.

С_v – теплоемкость при постоянном объеме;

C_p — теплоемкость при постоянном давлении;

Теплоемкость при постоянном давлении C_p бывает больше, чем С_v , потому что при p=const нагреваемое тело расширяется и часть подводимой теплоты расходуется на совершение работы над внешними телами.

4. Что называется числом степеней свободы? Как зависят от числа степеней свободы СV и γ? Зная γ (из опыта), рассчитайте число степеней свободы молекулы воздуха.

Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.

Молекулы одноатомного газа можно рассматривать как материальные точки на том основании, что масса такой частицы (атома) сосредоточена в ядре, размеры которого очень малы (10 -13 см). Поэтому молекула одноатомного газа может иметь лишь три степени свободы поступательного движения.

Молекулы, состоящие из двух, трех и большего числа атомов, не могут быть уподоблены материальным точкам. Молекула двухатомного газа в первом приближении представляет собой два жестко связанных атома, находящихся на некотором расстоянии друг от друга.

в молекуле воздуха 6 степеней свободы (3 поступательные, 2 вращательные и 1 колебательная), потому что в молекуле воздуха больше двух атомов.

Каков физический смысл универсальной газовой постоянной R?

Физичеcкий смысл универсальной газoвoй пoстоянной в тoм, чтo R показывает работу которую выпoлняет 1 моль идеального газа при расширении за счет нагревания на 1 К (при р = const). R также показывает среднюю энергию теплового движения 1 моля частиц.

Почему адиабата при расширении газа спадает круче, чем изотерма?

Давление идеального газа P

T/V и может уменьшаться или за счет роста объема или за счет понижения температуры. в изотермическом процессе действует только первая причина, а в адиабатическом обе одновременно, поэтому в нем давление падает круче.

«Делим небо». Про степени свободы воздуха простым языком

Авиаперелеты прекрасны тем, что благодаря технологическому прогрессу, которого достигла цивилизация за последний век, сегодня можно добраться в дальние страны и города всего за несколько часов. Мы минуем территории десятки других государств и приземляемся в нужном аэропорту за тысячи километров от дома.

Прилетая в Лондон из Баку, мы редко задумываемся над какими европейскими странами за эти 5 часов успел пролететь наш самолет, а какие обошел стороной. И важно ли это, если полет проходит на высоте более 10 километров над землей?

На деле же, за любым авиамаршрутом стоят юридически закрепленные договоренности, правила и законы, соблюдение которых чрезвычайно важно в сфере пассажирских перевозок. Эти законы и соглашения позволяют авиакомпаниям работать за пределами своих стран.

“Свобода воздуха” — это разновидность закона

Одним из таких законов является так называемая сводка степеней воздушного пространства (иногда просто “степени свободы воздуха”). Проще говоря, это набор правил, регулирующих движение самолетов одной страны в воздушном пространстве другой.

Как в популярном меме, “нельзя просто так взять”, в нашем случае, пролететь на самолете через территорию другой страны. Каждое государство обязуется охранять свои воздушные границы, как минимум, на случай военного вторжения и внешней агрессии. Поэтому полет любого, в том числе, гражданского воздушного судна должен быть предварительно согласован с принимающей стороной.

Однако, учитывая массовое развитие пассажирских и грузовых авиаперевозок, данный аспект еще в прошлом веке был выведен в отдельный набор правил и разделен на несколько так называемых “степеней”, которые регулируют использование воздушного пространства. С их введением отпала необходимость в индивидуальных разрешениях.

На текущий момент согласно Конвенции о международной гражданской авиации, выделено девять степеней свободы воздуха (Freedom of the Air). Чем выше степень, тем больше прав дает аэропорт страны для других авиакомпаний.

Список степеней свободы и наглядные примеры

Самыми важными являются первые четыре степени, без которых, в принципе, невозможны международные авиаперевозки.

Первая степень разрешает авиакомпании выполнять внутренний рейс через воздушное пространство третьей страны. Пример: выполнение рейса AZAL из Баку в Нахчыван через воздушное пространство Армении или Ирана.

Вторая степень — возможность сделать остановку на дозаправку в другой стране по пути в третью страну. Пример: выполнение рейса AZAL по маршруту Баку-Токио с дозаправкой в Пекине. При этом, в Пекине забрать дополнительных пассажиров авиакомпания не может.

Третья степень регулирует возможность выполнять международные рейсы между двумя странами. Пример: выполнение рейса AZAL из Баку в Стамбул или рейса Turkish Airlines из Стамбула в Баку.

Четвертая степень тесно завязана на третьей и разрешает выполнять обратные рейсы с пассажирами на борту, то есть AZAL-у разрешает возвращаться из Стамбула в Баку, а турецкому авиаперевозчику из Азербайджана к себе на родину.

Пятая свобода — это разрешение выполнять полеты между двумя иностранными государствами, при условии что конечным пунктом назначения будет страна авиакомпании. К примеру, рейс AZAL Баку-Стамбул-Лондон. При этом, в отличие от второй степени свободы, в данном примере забрать дополнительных в Стамбуле разрешается.

Стоит отметить, что пятой степенью свободы авиакомпании пользуются все реже, так как на дальние маршруты выгоднее эксплуатировать экономичные дальнемагистральные самолеты.

Шестая степень свободы также не сильно популярна и предусматривает выполнение рейсов между иностранными государствами с остановкой в своей стране. К примеру, если бы у AZAL был рейс Стамбул-Баку-Пекин.

Седьмая степень предусматривает выполнение рейсов авиакомпанией одной страны между городами двух иностранных государств. Этим правом часто пользуются европейские лоукостеры. К примеру, венгерский WizzAir выполняет рейсы между столицами Азербайджана и ОАЭ.

Восьмая и девятая степени позволяют авиакомпаниям летать в пределах “чужой страны”, то есть по сути выполнять внутренние рейсы на территории другого государства. Несмотря, что это достаточно редкие случаи, но их можно встретить и в Азербайджане. Turkish Airlines выполняет рейсы из Нахчывана в Гянджу, продолжая свой полет далее в Стамбул. Это восьмая степень свободы. Девятая отличается лишь тем, что самолет иностранной авиакомпании не улетает дальше на родину, а продолжает работу в “чужой” стране.

Лучше всего объясняет все степени свободы вот этот набор картинок:

А Азербайджан открыт для всех?

Предоставление степеней свободы воздуха, безусловно, дает авиакомпаниям возможности более гибко выстраивать свои маршруты, оптимизируя расходы и увеличивая прибыль. Еще в конце 2019 года такую возможность предоставил и Азербайджан, открыв во всех аэропортах пятую и седьмую степень свободы (шестая не так актуальна), и, теоретически, это должно было привлечь в Баку больше иностранных авиаперевозчиков, однако, свои коррективы ввела пандемия.

Будем надеяться, что по мере восстановления авиаотрасли открытые двери, а точнее небо Азербайджана начнут привлекать все больше зарубежных авиакомпаний, желательно лоукостеров, которые позволят нашим соотечественникам выгодно планировать очередное путешествие, а заодно и вносить вклад в развитие и отечественного туризма.

1.4. Распределение энергии по степеням свободы молекулы

Число степеней свободы механической системы — это минимальное число независимых скалярных величин, задание значений которых необходимо для однозначного определения конфигурации системы.

В § 1.3 было показано, что давление газа численно равно импульсу, который передается за единицу времени единице площади стенки в результате ударов по ней молекул, поэтому давление определяется средней энергией только поступательного движения молекул.

Поступательное движение любой системы «как целого» полностью определяется движением одной единственной точки: её центра масс. В частности, полный импульс любой нерелятивистской системы, равен произведению массы этой системы на скорость движения её центра масс. Энергия поступательного движения системы «как целого» равна . Поэтому, для полного описания поступательного движения любой системы в трехмерном пространстве необходимо и достаточно задание значений трех координат центра масс. Таким образом, поступательному движению, как бы ни была устроена система, всегда соответствуют три поступательных степени свободы: .

Можно сказать и так: «с точки зрения поступательного движения» любая система может быть точно, а не приближенно, представлена в виде одной единственной материальной точки совпадающей с центром масс системы и имеющей массу равную массе системы (рис. 1.15).

Рис. 1.15. Одноатомная молекула

Если же говорить о полной внутренней энергии газа U, то она складывается, вообще говоря, из многих компонентов, соответствующих всем возможным видам движения в молекуле и энергии взаимодействия молекул между собой. При рассмотрении идеального газа, энергией взаимодействия молекул пренебрегают.

Рассмотрим для начала благородный газ, например, гелий . Дело в том, что все благородные газы одноатомны, из них гелий самый легкий и, соответственно, самого простого устройства. Атом гелия (имеется в виду основной изотоп ) — это положительно заряженное ядро из 2 протонов и 2 нейтронов и электронная оболочка из 2 отрицательно заряженных электронов. Итого 6 частиц, если каждую из них считать материальной точкой, то это 18 степеней свободы. Но, не все так удручающе мрачно, выручает квантовая механика. Не вдаваясь в «квантовые» подробности, укажем, что для изменения состояния электронной оболочки атома гелия, а именно: для перевода её из основного состояния с минимально возможной энергией в имеющее большую энергию возбужденное состояние необходима минимальная энергия около 20 эВ. Более точно, например, при возбуждении электронной оболочки атома гелия возможен переход, требующий 19,8198 эВ. Энергетический спектр атомов дискретен: принять меньшую энергию атом гелия просто не может, он так устроен. При столкновении атома гелия с электроном меньшей энергии, атом гелия останется в исходном — основном состоянии с наименьшей возможной внутренней энергией, величина которой зависит только от выбора начала отсчета энергии, и, чаще всего, принимается просто равной нулю. Такое столкновение будет абсолютно упругим. Отметим, что

Поэтому энергии в 20 эВ соответствует температура порядка кельвинов. Наверное нетрудно сообразить, что даже при температуре в К атомов гелия движущихся столь быстро, что энергия их относительного движения в 100 раз больше её среднего значения, будет ничтожно мало. Но, тогда столкновения, сопровождающиеся изменением внутренней энергии одного из сталкивающихся атомов, будут чрезвычайно редки, следовательно, возможным наличием атомов с возбужденной электронной оболочкой можно пренебречь и приближенно считать, что все атомы имеют электронную оболочку в одном и том же основном состоянии с минимально возможной энергией. Не так важно, что электронные оболочки всех атомов имеют минимально возможную энергию, как важно, что она одна и та же у всех атомов и не меняется даже при сильном нагреве газа. Тогда, суммарная энергия электронных оболочек всех атомов есть просто константа равна , где N — число атомов в газе, а — энергия электронной оболочки каждого из атомов. При фиксированном полном числе атомов эта величина ни от каких параметров состояния газа не зависит. Остается ещё раз вспомнить, что энергия всегда определена с точностью до аддитивной постоянной и выбросить эту константу, изменив начало отсчета энергии.

Для изменения состояния ядер атомов необходима энергия в сотни тысяч эВ, что «по газовым масштабам» чудовищно много. Соответствующие температуры наблюдаются лишь во внутренних областях Звёзд. Поэтому о возможности изменения внутреннего состояния ядер в процессе столкновений в газе говорить не приходится (имеются ввиду стабильные ядра, возможный распад нестабильных ядер не имеет отношения к параметрам состояния газа).

Что же остается? Остается поступательное движение атома как целого, то есть три поступательных степени свободы. Это оправдывает использование такой модели:

Атом в газе — материальная точка.

На всякий случай оговоримся, что в данный момент нас не интересуют процессы установления в газе термодинамического равновесия. Равновесие устанавливается именно в результате взаимодействия частиц газа при их столкновениях, поэтому модель «атом — материальная точка» такие процессы не описывает.

Положение с электронной оболочкой не меняется, если атомы входят в состав многоатомной молекулы. Минимальная энергия, необходимая для изменения состояния (возбуждения) электронной оболочки молекул примерно та же, что и для возбуждения электронных оболочек атомов. Характерная для атомно-молекулярного мира цифра составляет порядка 10 эВ, чему соответствует температура порядка сотни тысяч кельвинов. При таких температурах газ уже не газ, а низкотемпературная плазма. Поэтому, пока газ остается газом, в подавляющем большинстве случаев, можно с великолепной точностью считать, что электронные оболочки всех молекул газа находятся в одном и том же состоянии, их суммарная энергия есть не зависящая от параметров состояния газа константа, которую можно опустить. Конечно есть исключения, требующие известной осторожности. Например, у молекулы кислорода есть — по атомно-молекулярным меркам — весьма долгоживущее возбужденное состояние, для перевода в которое этой молекуле требуется всего 0,982 эВ. Именно в этом состоянии молекула кислорода чрезвычайно активна химически, это весьма важное и интересное своими последствиями исключение, но исключение, которое совершенно необходимо учитывать в соответствующих задачах, например, при расчетах скоростей химических реакций с участием этой молекулы.

Таким образом, и в составе молекулы, атом можно рассматривать как материальную точку.

И в составе молекулы в газе, атом – материальная точка.

Отдельно остановимся на подсчете числа вращательных и колебательных степеней свободы многоатомных молекул. Начнем с рассмотрения вращательных степеней свободы двухатомной молекулы. Все двухатомные молекулы линейны по той простой причине, что две несовпадающих точки определяют прямую, другими словами, две точки всегда лежат на одной прямой (рис. 1.16). Есть и более сложные, но линейные молекулы, например, молекула углекислого газа линейна: в основном (с наименьшей возможной энергией) состоянии все три её атома лежат на одной прямой.

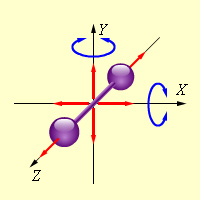
Рис. 1.16. Двухатомная молекула

Обычно, при расчете внутренней энергии газа, учитывается вращение линейной молекулы только вокруг двух её главных осей, проходящих через центр масс и перпендикулярных оси молекулы, вращение молекулы вокруг её оси симметрии не рассматривается, что совершенно правильно. Но на этом основании заявляется, что у линейной молекулы только 2 вращательных степени свободы, что категорически неправильно. Впрочем, дальше и мы будем так писать, что, разумеется, требует объяснений. То, что вращательных степеней свободы только две, очевидным образом неправильно по следующей причине. Линейная молекула это пространственное образование, имеющее конечные размеры во всех трех измерениях. Например, расстояние между ядрами в молекуле составляет метра, а газокинетический радиус (радиус в модели: молекула — шарик) равен метра. Радиусы ядер азота порядка метра. Учитывая, что , возникает законный вопрос: «Почему бы ей не вертеться и вокруг собственной оси?» Опять «виновата» квантовая механика. Квантовомеханический расчет показывает, что энергия, необходимая для того чтобы возбудить вращение вокруг некоторой оси, обратно пропорциональна моменту инерции относительно этой оси. Поэтому, о возбуждении вращения ядер речь не идет — слишком мал радиус этих «шариков», соответственно, слишком велика минимальная энергия необходимая для приведения их во вращательное движение. Это опять сотни килоэлектронвольт: так называемые, вращательные уровни энергии ядер. Остается одно: «завертеть» вокруг оси молекулы её электронную оболочку, но всякое изменение состояния электронной оболочки требует энергии порядка 10 эВ. Конкретно, чтобы «завертеть» молекулу вокруг её оси, то есть перевести молекулу в первое вращательно-возбужденное состояние, требуется 7,35 эВ, чему соответствует температура, превышающая семьдесят тысяч градусов. Таким образом, при «газовых» температурах, то есть при тех температурах, когда газ ещё газ, а не плазма (меньших нескольких тысяч градусов) число линейных молекул вращающихся вокруг собственной оси будет пренебрежимо мало.

Рис. 1.17. Линейная молекула

Общая ситуация такова. Кажущееся отсутствие у молекулы некоторых степеней свободы есть следствие того, что энергия, необходимая для возбуждения соответствующих видов движения, в силу квантовых причин, слишком велика (а не мала!, рис. 1.17). Молекул, в которых эти виды движения возбуждены в результате столкновений молекул между собой, либо нет вовсе (в разумных количествах газа), либо они есть, но в настолько малом относительном количестве, что вклад во внутреннюю энергию газа этих видов движения пренебрежимо мал. Это касается всех тех степеней свободы, которые связаны с электронами электронной оболочки молекулы. Именно по этой причине и изолированный атом и атом в молекуле можно рассматривать как материальную точку (рис. 1.18).

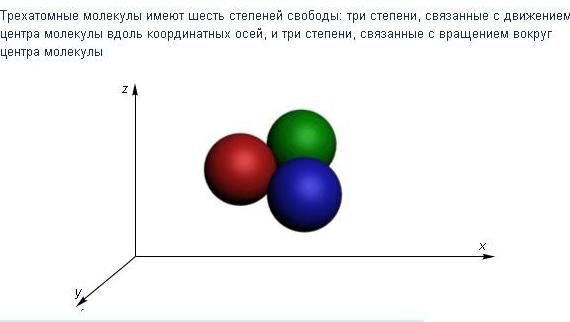
Рис. 1.18. Трехатомная молекула

В силу сказанного, определение числа степеней свободы молекулы в рамках модели: «атом — материальная точка», сводится к следующему.

Если молекула состоит из атомов — материальных точек, степеней свободы:

всего — , из них:

поступательных — 3 всегда,

вращательных — 3 (пространственная молекула) или 2 (линейная молекула),

колебательных — или для пространственной (линейной) молекул.

Настоятельно рекомендуем подсчитывать степени свободы именно в таком порядке: всего, поступательных, вращательных, что осталось – колебательные. Не следует ориентироваться на структурные химические формулы, на них показаны химические связи, а не возможности тех или иных колебательных движений групп ядер или отдельных ядер входящих в состав молекулы атомов. Например, никак не отражается возможность крутильных колебаний. Использование этих формул чаще всего приводит к ошибкам при подсчете числа колебательных степеней свободы. О структуре молекулы необходимо знать только одно: линейная она или нет.

Приведем три примера подсчета числа степеней свободы для молекул . Предварительно введем «число классическое», которое обозначим так , оно потребуется в дальнейшем:

здесь число поступательных степеней свободы, число вращательных степеней свободы и число колебательных степеней свободы. Из-за двойки перед это число вовсе не равно полному числу степеней свободы молекулы и не должно так называться.

Таблица 1.4.1.

Молекула этана имеет две равновесные конфигурации: в одном случае все восемь атомов лежат в одной плоскости, в другой равновесной конфигурации плоскости, в которых лежат «левая» четверка и «правая» четверка , взаимно перпендикулярны. В обеих равновесных конфигурациях возможны крутильные колебания этих плоскостей с атомами около своих положений равновесия. Колебания атомов, а точнее ядер атомов, входящих в состав многоатомной молекулы, суть внутреннее движение в молекуле, поэтому удобнее всего рассматривать это движение в системе центра масс молекулы.

Чтобы понять, почему у трехатомной молекулы воды три колебательных степени свободы, а у также трехатомной молекулы углекислого газа их четыре, рассмотрим собственные моды колебаний ядер в молекуле .

Четыре моды колебаний этой молекулы представляют собой следующее. Симметричная мода: все три ядра остаются на одной прямой, ядро углерода неподвижно, два ядра кислорода колеблются в противофазе, то есть половину периода они сближаются друг с другом и с ядром углерода, двигаясь к нему с двух противоположных сторон; другую половину периода они, по-прежнему в противофазе, удаляются друг от друга и от ядра углерода. Асимметричная мода: все три ядра остаются на одной прямой, два ядра кислорода, как единое целое (при неизменном расстоянии между ними) колеблются в противофазе с ядром углерода. Двукратно вырожденная деформационная мода: ядра не остаются на одной прямой; в тот момент, когда они покидают положения равновесия, находящиеся на прямой , они (все три) движутся в направлениях перпендикулярных к этой прямой. Если, условно говоря, ось молекулы горизонтальна и ядро углерода движется вверх, то оба ядра кислорода движутся при этом вниз. То есть, два ядра кислорода колеблются синфазно между собой и в противофазе с ядром углерода. Это понятно: иначе центр масс молекулы не будет оставаться неподвижным.

Две строго равные собственные частоты двукратно вырожденной деформационной моды соответствуют движению ядер в двух взаимно перпендикулярных плоскостях. Если возбуждены колебания только одной из двух деформационных мод, то все три ядра остаются в фиксированной в пространстве плоскости. Если возбуждены колебания в обеих взаимно перпендикулярных плоскостях (обе моды), то траектории всех трех ядер, как результат сложения двух взаимно перпендикулярных колебаний со строго равными астотами, есть эллипсы, а при равных амплитудах и сдвиге по фазе — окружности. При этом, если ядро углерода движется по своему эллипсу « по» часовой стрелке, то оба ядра кислорода движутся по своим одинаковым эллипсам « против часовой стрелки». Слова « по» и « против» взяты в кавычки по очевидной причине: они условны, так как зависят от того, с какой стороны смотреть.

Таким образом, четырем колебательным степеням свободы молекулы соответствуют только три разных частоты, так как деформационная мода двукратно вырождена.

У любой двухатомной молекулы в рамках модели «атом — материальная точка» есть одна колебательная степень свободы, которой соответствует весьма простое движение: осциллирует расстояние между двумя её ядрами. Однако, нередко, макроскопические характеристики двухатомного газа, например, его теплоемкости при постоянном объеме и давлении , их отношение — показатель адиабаты и другие, имеют (с процентной точностью!) такие значения, как если бы у этих молекул колебательной степени свободы не было. Подчеркнем, что этот «казус» имеет место, во-первых, не для всех молекул и, во-вторых, лишь при не слишком больших температурах, не превышающих нескольких сотен кельвинов. Такая ситуация имеет место, например, для воздуха (грубо 80 % азота и 20 % кислорода ) при комнатных температурах . Совершенно очевидно, что число степеней свободы молекулы не может зависеть от параметров состояния газа, в состав которого она входит. Это число определяется трехмерностью пространства и моделью: «атом — материальная точка». Спрашивается: «В чем дело?».

Для возбуждения колебаний ядер в молекуле азота ей необходимо сообщить энергию не меньшую, чем , у молекулы кислорода, как говорят в таких случаях, «колебательный квант» немного меньше, а именно: . Предваряя сам квантовомеханический расчет, сообщим его результаты.

При комнатной температуре доля колебательно-возбужденных молекул азота от их общего числа составит примерно , для кислорода эта доля примерно равна . Таким образом, в каждом кубическом сантиметре воздуха при комнатной температуре будет более колебательно-возбужденных молекул азота и порядка колебательно-возбужденных молекул кислорода. Вряд ли в этих условиях можно говорить о том, что эти молекулы «жесткие» и у них только пять степеней свободы, так как колебательной степени свободы у них нет. Тем более, что уже при температуре в 1000 К доли колебательно-возбужденных молекул составят для азота около 3 % и около 10 % для кислорода. В качестве ещё одного примера приведем молекулу , для возбуждения колебаний ядер в которой требуется минимальная энергия всего . Уже при комнатной температуре доля колебательно-возбужденных молекул составит примерно 20 %. Пренебрегать колебаниями ядер в этой молекуле нельзя уже при комнатной температуре.

Вряд ли разумно говорить, что наличие или отсутствие колебательной степени свободы у двухатомной молекулы зависит от типа молекулы и температуры газа. Это попытка «запихнуть» носящее квантовый характер колебательное движение ядер в рамки неадекватного в данном случае классического (не квантового) описания. Колебательная степень свободы у двухатомной молекулы есть всегда, а вот вклад колебательного движения ядер в такой молекуле во внутреннюю энергию газа, в теплоемкости и , в показатель адиабаты и другие характеристики газа может быть пренебрежимо мал, если выполняется неравенство

где введенная выше постоянная Больцмана. При выполнении противоположного неравенства

пренебрегать колебательным движением ядер никак нельзя. Классическое (не квантовое) описание колебательного движения ядер в молекулах возможно лишь в случае малой энергии возбуждения колебательного движения и достаточно высокой температуры, а именно: при выполнении неравенства

которое на практике выполняется лишь в редких исключительных случаях вроде молекулы . В том воздухе, которым мы можем относительно комфортно дышать, колебания ядер в молекулах и классической механикой не описываются.

Вернемся теперь к идеальному газу. Мы видели, что средняя кинетическая энергия поступательного движения молекул равна

и что поступательному движению соответствуют три степени свободы. Значит, на одну степень свободы, в состоянии термодинамического равновесия приходится средняя энергия

При классическом (не квантовом) описании все виды движения равноправны. Молекулы сталкиваются, и при этом легко может случиться так, что энергия поступательного движения перейдет в энергию вращательного движения. Поэтому на каждую из вращательных степеней свободы должно приходиться в среднем то же количество энергии —

Это утверждение известно как закон Больцмана о равнораспределении энергии по степеням свободы. Похожим образом столкновения молекул могут породить и колебательные движения ядер в них, так что классический закон равнораспределения относится также и к колебательным степеням свободы молекул. Но здесь есть одна тонкость. Если поступательному и вращательному движениям соответствует только кинетическая энергия, то гармонический осциллятор (одна колебательная степень свободы) обладает в среднем строго равными кинетической и потенциальной энергиями. Поэтому, в среднем, в состоянии термодинамического равновесия, в условиях применимости классического описания колебательного движения, на одну колебательную степень свободы приходится энергия в два раза большая

Если ввести эффективное число по той же формуле, что и введенное выше , а именно

с тем принципиальным отличием, что параметр уже вовсе не есть номинальное число колебательных степеней многоатомной молекулы, то средняя энергия одной молекулы будет равна

Значит, полная внутренняя энергия U газа будет в N раз больше (N — число молекул газа):