Как найти число точек разрыва функции

Нахождение точек разрыва функции является одним из обязательных моментов исследования на непрерывность. Для кого-то это может прозвучать непонятно, а для остальных будет слишком банально.

Но и тем, и другим не стоит делать поспешные выводы: материал этой темы действительно предельно прост, но вместе с тем для успешного решения практических задач потребуется осмыслить и запомнить несколько технических приемов и нюансов.

Как минимум необходимо понимать, что за «зверь» кроется под понятием предела функции. И конечно же, нужно уметь их решать. Не менее полезным станет понимание геометрического смысла, дополненное графиком — большинство задач подобного характера требуют построения чертежа после решения.

Определение точки разрыва

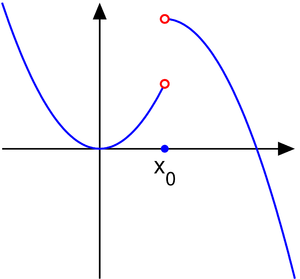
Как уже упоминалось, их поиск напрямую связан с темой непрерывности. Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:

Он более чем очевидно иллюстрирует определение понятия. Если функция прерывается в X0, то непрерывность в этом месте нарушена одним из двух возможных способов:

• первый род;
• второй род.

Задачи похожего типа, где необходимо находить точки разрыва, могут выступать не только, как один из этапов полного исследования на непрерывность, но и в качестве самостоятельных заданий. Чтобы определить их вид, потребуется отыскать предел для найденных значений. Поэтому, если вы еще не умеете их решать, самое время ненадолго отвлечься, чтобы изучить базовые основы.

К счастью, на практике это не так сложно — самый трудный этап заключается в приведении примера к одному из табличных. Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.

Классификация точек разрыва.

Точки разрыва первого и второго рода

Если функция не определена, но односторонние пределы имеют конечное значение, то ее относят к случаю первого рода. Который, в свою очередь, может иметь характеристику устранимого или конечного:

• Точки устранимого разрыва функции. Значения вычислений обоих пределов для них равны. Но также имеется возможность «исправить ситуацию»: нахождения между двумя координатами такой, левый и правый пределы которой будут одинаковы, а сама она — соединит «порванный» участок, сделав график непрерывным.

• Точки конечного разрыва первого рода — скачок функции. Пределы могут быть вычислены, но в то же время не равны друг другу, и поэтому доопределение уравнения невозможно. Разница первого и второго называется скачком.
• Точки разрыва второго рода отличаются тем, что вычисляемые пределы не просто различны по значению, но результат хотя бы одного из них обязательно должен быть равен бесконечности или несуществующему числу.

Как найти точки разрыва функции

Если в условиях задачи не были даны координаты проверяемого отрезка, то процесс решения делится на несколько этапов. Для начала нужно найти область определенных значений, с которой в дальнейшем пойдет работа. После это вычисляются односторонние пределы функции. Полученные результаты необходимо будет сравнить, чтобы однозначно определить род и характеристику разрыва.

Рассмотрим более подробно каждый из этих моментов на примере нахождения нужных нам точек у конкретного примера f (y)=(y² – 25)/(y – 5):

1. Областью определения называют множество значений, в котором существует функция. Здесь не нужны никакие сложные вычисления, достаточно взять лишь знаменатель. Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
2. Вычисление односторонних пределов. Это самая сложная для учеников часть, т. к. пределы не всегда бывают удобными для вычисления, да не все на них «собаку съели». Но в этом случае функцию можно значительно упростить еще до начала вычисления: f (y) = (y ²-25)/(y — 5) = ((y-5)(y+5)) /(y — 5) = y+5. Никогда не пренебрегайте такой возможностью, если она есть. Заметим, что новая функция непрерывна при любом численном значении, т. ч. по всем математическим правилам пределы будут равны: lim (y + 5) = 5 + 5 = 10.
3. Проверяя совпадение результатов, мы выяснили, что левый и правый предел функции в точке y=5 одинаковые. Но вместе с тем функция f(y) не может быть определена в этой координате, иначе ее знаменатель обращается в ноль, что невозможно по условиям. Следовательно, она действительно является разрывом, а именно: устранимым и первого рода.

Видео

Из этого видео вы узнаете, как исследовать непрерывность функции.

Функция

является непрерывной в некоторой точке
,
если выполняются следующие условия:

Т.е.
предел функции

при стремлении

(слева), равен пределу функции при стремлении

(справа) и равен значению функции в точке
.

Если хотя бы одно из условий нарушается, тогда говорят, что функция

имеет разрыв в точке
.

Все
точки разрыва функции
делят на точки разрыва первого рода и точки разрыва второго рода.

Eсли существуют конечные односторонние пределы

и
, тогда точка

называется точкой разрыва
первого рода.

Точки разрыва первого рода в свою очередь подразделяются на точки устранимого разрыва и скачки.

Если

– является точкой разрыва первого рода и при этом
, точка

называется точкой
устранимого разрыва.

График соответствующей функции приведён на рисунке ниже:

Eсли же
, тогда в точке
.
происходит скачок функции

Величина скачка определяется по формуле
. Соответствующий график приведён на рисунке:

Если хотя бы один из пределов

или

равен
, точка

называется точкой разрыва
второго рода. Пример соответствующего графика функции представлен на рисунке ниже:

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha вычисляет точки разрыва заданной функции с описанием подробного хода решения.

Содержание:

Точки разрыва и их классификация

Непрерывность или разрыв функции может зависеть от конкретных условий, в которых рассматривается задача. Рассмотрим, например, численность населения земного шара как функцию времени. Она увеличивается на 1 в момент рождения каждого человека и уменьшается на 1 в момент смерти. Но рождения и смерти следуют друг за другом через бесконечно малые интервалы времени и изменение численности населения планеты на 1 настолько мало его меняет, что практически функцию можно рассматривать непрерывной. По стоит перейти от численности населения земного шара к численности населения одной квартиры, как рождение или смерть отдельного ее жителя будут так заметно менять ее численность, что функцию нельзя будет рассматривать как непрерывную.

Если хотя бы одно из условий определения непрерывности функции в точке (см. п. 3.1) не выполнено, то в данной точке функция терпит разрыв. Различают три вида точек разрыва непрерывной функции.

1. Точка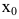

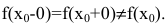
Чтобы устранить разрыв в точке 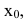достаточно положить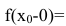 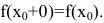В этом случае говорят, что функция доопределена до непрерывной в точке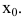

2. Точка 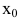называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные пределы слева 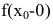и справа 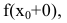не равные друг другу:

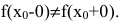
При этом величина 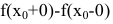называется скачком функции f(x) в точке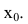

3. Если хотя бы один из односторонних пределов 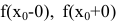равен бесконечности или не существует, то 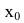называется точкой разрыва второго рода функции f(x).

Пример №32

Исследовать функции на непрерывность. В случае устранимого разрыва доопределить функцию до непрерывной.

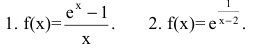
Решение:

1. Данная функция элементарная, т.к. получена с помощью конечного числа арифметических действий над основными элементарными функциями: экспоненциальной, постоянной и степенной. Следовательно, она непрерывна в области определения 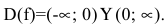При х=0 функция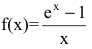

не определена и поэтому разрывна. Исследуем характер точки разрыва. Так как 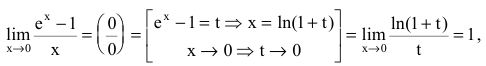то х=0 – точка устранимого разрыва.

Если положить f(0)=0, то функция 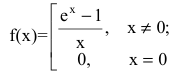будет непрерывной для всех х.

2. Функция 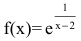является элементарной как композиция основных элементарных функций. Следовательно, она непрерывна в области определения 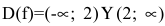и х=2 – точка разрыва. Для исследования характера точки разрыва найдем односторонние пределы:

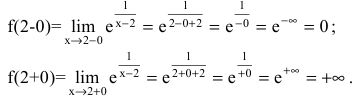Так как один из односторонних пределов равен бесконечности, то х=2 -точка разрыва второго рода.

Пример №33

Исследовать функцию на непрерывность. Построить схематично график функции.

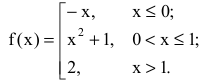
Решение:

Область определения этой функции – вся числовая прямая: 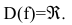Однако функция является составной. Составляющие ее функции непрерывны на множестве действительных чисел как элементарные. Поскольку функция задана различными аналитическими выражениями, то проверить на непрерывность нужно точки «стыка» 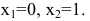Исследуем точку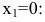

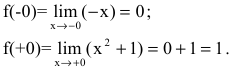Так как 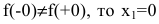– точка разрыва первого рода. Скачок функции в данной точке равен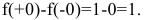

Исследуем точку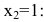

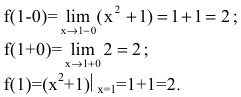
Поскольку 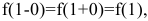то в точке 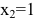функция непрерывна. Следовательно, искомая функция непрерывна для всех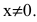

Построим график функции.

——

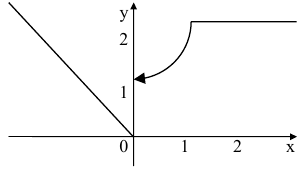
Точки разрыва и их классификация

Точка, в которой функция не является непрерывной, называется точкой разрыва функции, а сама функция называется разрывной в этой точке.

Точка 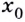 будет точкой разрыва функции  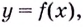если выполняется одно из условий:

1. функция в точке 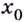 не определена;
2. не существует предела функции в точке 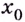 или он равен бесконечности;
3. предел функции в точке 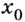 не совпадает со значением функции в этой точке.

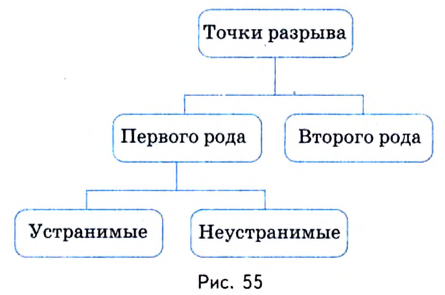
Различают два вида точек разрыва — первого рода и второго рода (рис.55).

Исследуя точки разрыва, используют односторонние пределы. Это означает, что рассматривают поведение функции для значений 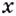 только справа или слева от точки  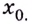Таким образом получают соответственно правосторонний или левосторонний пределы.

Обозначают:

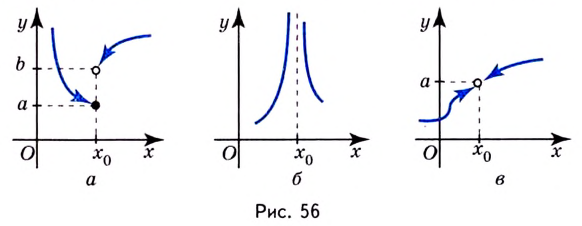
Точку 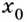 называют точкой разрыва первого рода, если в ней существуют конечные односторонние пределы (рис. 56, а).

Точку 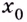 называют точкой разрыва второго рода, если хоть один из односторонних пределов является бесконечным, либо вообще не существует (рис. 56, б).

Если левосторонний и правосторонний пределы в точке 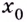 — конечные и равные между собой, но не равны значению функции в этой точке, то точку  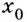называют устранимой точкой разрыва (рис. 56, в).

Пример №522

Найдите точки разрыва функции 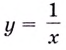 и выясните их характер.

Решение:

Поскольку на ноль делить нельзя, то точкой разрыва данной функции является 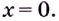 Для выяснения её характера вычислим односторонние границы данной функции в этой точке.

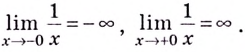 Итак, односторонние пределы равны бесконечности, поэтому  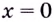— точка разрыва второго рода.

Пример №523

Исследуйте функцию 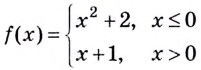 на непрерывность и постройте её график.

Решение:

На каждом из интервалов 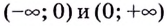 функция непрерывна как многочлен. Поскольку вся область определения функции разделена на два промежутка точкой  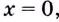то в этой точке функция может иметь разрыв. Выясним, существует ли предел функции в этой точке.

Если 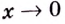 слева, то функция имеет вид

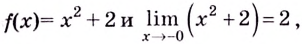  а при 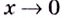 справа  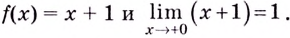Следовательно,  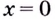— точка разрыва первого рода, неустранимый разрыв. График этой функции изображён на рисунке 57.

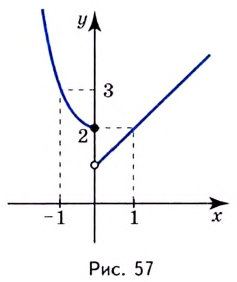
Односторонние пределы используют для нахождения вертикальных асимптот кривых.

Прямая  называется вертикальной асимптотой кривой, если при 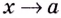 (справа или слева) значение функции стремится к бесконечности, т.е. выполняется одно из условий:

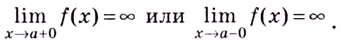
Например, ось 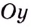 является вертикальной асимптотой для графиков функций  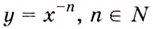(см. рис. 17, б) и  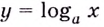(см. рис. 33).

• Заказать решение задач по высшей математике

Пример №524

Найдите вертикальные асимптоты кривой

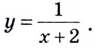
Решение:

Поскольку функция не определена в точке 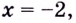 то в этой точке кривая может иметь вертикальную асимптоту. Вычислим пределы:

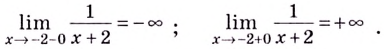
Следовательно, 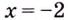 вертикальная асимптота данной кривой.

Замечание: Если 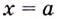 — вертикальная асимптота функции  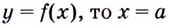— точка разрыва второго рода.

Пример №525

Исследуйте заданные функции на непрерывность и выясните характер их точек разрыва:

Решение:

Заданные в условии функции элементарные, а потому непрерывные в каждой точке области определения, а именно на множестве 

а) Функция 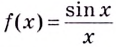 не определена в точке  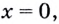следовательно, эта точка является точкой разрыва. Поскольку  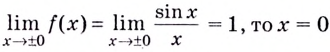является точкой разрыва первого рода, устранимый разрыв.

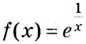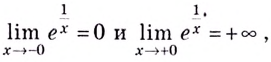б) Функция  не определена в точке  эта точка является точкой разрыва. Поскольку  то 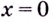 является точкой разрыва второго рода.

Пример №526

Заданные функции до определить в точке 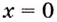 так, чтобы они стали непрерывными в этой точке:

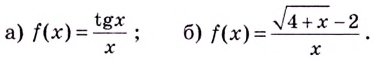
Решение:

а) Имеем 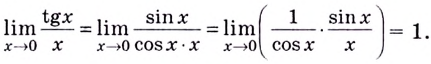 Положив  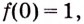получим, что  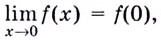т.е. функция непрерывна в точке  Итак,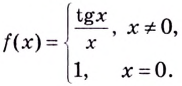 

б) Вычислим предел заданной функции в точке 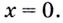 Имеем:

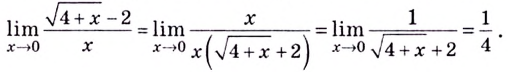
Если теперь за значение функции в точке 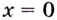 взять число  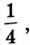, то функция станет непрерывной в этой точке.

Итак,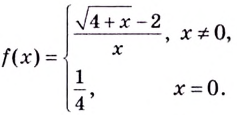 

Пример №527

Имеет ли уравнение 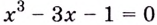 хотя бы один действительный корень на отрезке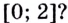 

Рассмотрим функцию 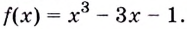 Эта функция непрерывна на отрезке  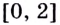и на его концах приобретает различные по знаку значения:  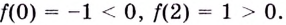Итак, согласно теореме Больцано—Коши существует по крайней мере одна точка  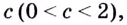в которой значение функции равно нулю. Число-с и является корнем заданного уравнения.

Пример №528

Имеет ли горизонтальные и вертикальные асимптоты кривая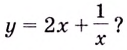 

Решение:

1) Найдём вертикальные асимптоты. Заданная функция не определена в точке 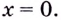 Поскольку  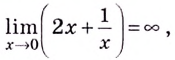то прямая  — вертикальная асимптота. 2) Найдём горизонтальные асимптоты.

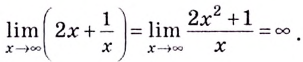
Горизонтальных асимптот нет.

Данный калькулятор предназначен для нахождения точек разрыва функции онлайн.
Точки разрыва функции – это точки, в которых функция имеет разрыв, при этом функция в этих точках не является непрерывной.
Существует определенная классификация точек разрыва функции. Точки разрыва функции (нули знаменателя) делятся на точки разрыва первого рода и точки разрыва второго рода.

Точки разрыва первого рода при x=a имеют место быть, если существуют левосторонний и правосторонний пределы: lim(x→a-0)⁡f(x) и lim(x→a+0)⁡f(x). Эти пределы должны быть конечны. Если хотя бы один из односторонних пределов равен нулю или бесконечности, то в таком случае функция имеет точки разрыва второго рода.
Для того чтобы найти точки разрыва функции онлайн, необходимо указать функцию и значение аргумента.

Для получения полного хода решения нажимаем в ответе Step-by-step.

Точки разрыва функции

Назначение

Сервис предназначен для определения типа точек разрыва функции.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Решение сохраняется в формате MS Word

Классификация точек разрыва

Для точек разрыва принята следующая классификация.

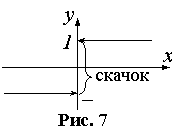1. Если в точке имеются конечные пределы, но они не равны f(x0+0)≠f(x0-0), то x₀ называется точкой разрыва первого рода, при этом разрыв называют скачком функции.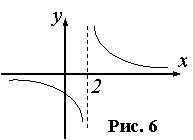
2. Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.
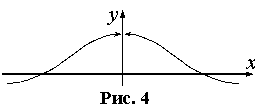3. Точка x=x₀ называется точкой устранимого разрыва, если f(x0+0)=f(x0-0)≠f(x0). Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) функцию и функция станет непрерывной в точке x₀.

см. также Непрерывность функции: основные понятия и свойства (разрывы функции и их классификации с подробными примерами).

Пример №1. Установить непрерывность или определить характер точек разрыва. Нарисовать график функции f(x) в окрестностях этих точек:


Решение. Найдем точки разрыва функции внутри указанной области.

Находим переделы в точке x=1.





В этой точке функция терпит разрыв. Предел равен ∞, поэтому это точка разрыва II-го рода.

Находим переделы в точке x=0





В этой точке функция терпит разрыв. Пределы существуют, но не равны, поэтому это точка разрыва I-го рода.



Ответ: точка x₁=1 является точкой разрыва II-го рода, точка x₂=0 является точкой разрыва I-го рода.

Пример №2. Найти точки разрыва функции, если они существуют. Сделать чертеж.



Решение. Исследуем точку стыка промежутков x=π/2





В этой точке пределы существуют и они равны, поэтому функция в этой точке непрерывна.

Исследуем поведение функции на отрезке (π/2;π).





Пределы существуют, на указанном промежутке функция непрерывна.

Исследуем точку стыка промежутков x=π





В этой точке пределы существуют, но они разные, поэтому это точка разрыва I-го рода.

Исследуем поведение функции на отрезке (pi;∞).





Пределы существуют, на указанном промежутке функция непрерывна.



Ответ: Точка x=π является точкой разрыва I-го рода.

Пример №3. Найти точки разрыва функции и определить их тип.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).