Мы уже знакомы с действиями сложения и вычитания матриц. Прежде чем начать изучение умножения матрицы на число, вам следует повторить тему «Что такое матрица». Особое внимание необходимо уделить размеру матрицы. Приступим к рассмотрению темы.
Онлайн-калькулятор
Умножение матрицы на число
Произведением матрицы AA и числа kk называется новая матрица BB, полученная из исходной путем умножения соответствующих элементов матрицы AA на число kk.
Элемент b11=k⋅a11b_{11}=kcdot a_{11}, b12=k⋅a12,…b_{12}=kcdot a_{12}, …
Так можно получить все элементы матрицы BB.
В общем виде умножение матрицы на число выглядит следующим образом. Даны некоторое число kk и матрица
A=(a11a12…a1na21a22…a2n…………am1am2…amn)A=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix}.
Найдем произведения k⋅Akcdot A и A⋅kAcdot k:
B=k⋅A=A⋅k=(k⋅a11k⋅a12…k⋅a1nk⋅a21k⋅a22…k⋅a2n…………k⋅am1k⋅am2…k⋅amn)B=kcdot A=Acdot k=begin{pmatrix}kcdot a_{11}&kcdot a_{12}&…&kcdot a_{1n}\kcdot a_{21}&kcdot a_{22}&…&kcdot a_{2n}\…&…&…&…\kcdot a_{m1}&kcdot a_{m2}&…&kcdot a_{mn}end{pmatrix}.
Свойства умножения матрицы на число
Пусть kk и nn — числа, AA и BB — матрицы.
- При умножении произвольной матрицы на единицу получаем исходную матрицу:
1⋅A=A1cdot A=A.
- При умножении произвольной матрицы на нуль получаем нулевую матрицу, размер которой равен размеру исходной матрицы:
0⋅A=O0cdot A=O, где OO — нулевая матрица.
- При умножении числа на матрицу, которая также умножается на число можно найти произведение этих чисел, а затем умножить на матрицу
k⋅(n⋅A)=(k⋅n)⋅Akcdot (ncdot A)=(kcdot n)cdot A.
- При умножении суммы чисел на матрицу можно каждое из этих чисел умножить на матрицу, а полученные результаты сложить
(k+n)⋅A=k⋅A+n⋅A(k+n)cdot A=kcdot A+ncdot A.
- При умножении числа на сумму матриц можно это число умножить на каждую из матриц, а полученные результаты сложить
k⋅(A+B)=k⋅A+k⋅Bkcdot (A+B)=kcdot A+kcdot B.
Умножить матрицу H=(13261481925172320)H=begin{pmatrix}13&26&14\8&19&25\17&23&20end{pmatrix} на число 22.
Умножим каждый элемент матрицы HH на 22:
2⋅H=(2⋅132⋅262⋅142⋅82⋅192⋅252⋅172⋅232⋅20)=(265228163850344640)2cdot H=begin{pmatrix}2cdot13&2cdot26&2cdot14\2cdot8&2cdot19&2cdot25\2cdot17&2cdot23&2cdot20end{pmatrix}=begin{pmatrix}26&52&28\16&38&50\34&46&40end{pmatrix}
Умножить матрицу T=(1014915251347381510)T=begin{pmatrix}10&14&9&15\25&13&4&7\3&8&15&10end{pmatrix} на число 1515.
Умножим каждый элемент матрицы TT на 1515:
15⋅T=15⋅(1014915251347381510)=(15⋅1015⋅1415⋅915⋅1515⋅2515⋅1315⋅415⋅715⋅315⋅815⋅1515⋅10)=15cdot T=15cdotbegin{pmatrix}10&14&9&15\25&13&4&7\3&8&15&10end{pmatrix}=
begin{pmatrix}15cdot10&15cdot14&15cdot9&15cdot15\15cdot25&15cdot13&15cdot4&15cdot7\15cdot3&15cdot8&15cdot15&15cdot10end{pmatrix}=
=(1502101352253751956010545120225150)=begin{pmatrix}150&210&135&225\375&195&60&105\45&120&225&150end{pmatrix}
Не знаете, где заказать решение задач по математике? Наши специалисты быстро помогут вам с заданиями!
Тест по теме «Умножение матрицы на число»
Содержание:
- Определение
- Свойства умножения матрицы на число
Определение
Произведением матрицы $A$ на ненулевое
число $ lambda $ называется матрица $ B=lambda A $ того же порядка, полученная из исходной умножением на заданное
число всех ее элементов:
$$ B=lambda A Longrightarrow b_{i j}=lambda a_{i j} $$
Итак, в результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент
которой является результатом произведения соответствующего элемента исходной матрицы на заданное число.
Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число, то есть $ lambda A = A lambda $.
Из определения следует, что общий множитель всех
элементов матрицы можно выносить за знак матрицы.
Данная операция, вместе с операцией
сложения матриц, относится к
линейным операциям над матрицами.
Пример
Задание. Чему равна матрица $-3A$, если матрица $ A=left( begin{array}{rr}{-1} & {3} \ {0} & {2}end{array}right) $ ?
Решение. $ -3 A=3 cdot left( begin{array}{rr}{-1} & {3} \ {0} & {2}end{array}right)=left( begin{array}{rr}{-3 cdot(-1)} & {-3 cdot 3} \ {-3 cdot 0} & {-3 cdot 2}end{array}right)=left( begin{array}{cc}{3} & {-9} \ {0} & {-6}end{array}right) $
Ответ. $ -3 A=left( begin{array}{ll}{3} & {-9} \ {0} & {-6}end{array}right) $
Свойства умножения матрицы на число:
- $ 1 cdot A=A $
- $ 0 cdot A=Theta $
- $ lambda(A+B)=lambda A+lambda B $
- $ (lambda+mu) A=lambda A+mu A $
- $ (lambda mu) A=lambda(mu A) $
Читать дальше: сложение и вычитание матриц.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
В данной публикации мы рассмотрим, каким образом матрицу можно умножить на определенное число. Также мы приведем практические примеры и перечислим основные свойства рассматриваемого произведения.
- Правило умножения матрицы на число
- Свойства произведения матрицы и числа
- Примеры задач
Правило умножения матрицы на число
Результатом умножения матрицы (A) на любое число (m), не равное нулю, является матрица того же порядка (размера), элементы которой равны произведению соответствующих элементов исходной матрицы на данное число.
B = m ⋅ A
В общем виде это выглядит примерно так:

Согласно законам умножениям, порядок сомножителей неважен, т.е.:
m ⋅ A = A ⋅ m = B
Следствие: если у всех элементов матрицы есть общий множитель, его можно вынести за пределы матрицы.
Свойства произведения матрицы и числа
1. Если матрицу умножить на единицу (или наоборот), в результате получится та же самая матрица.
1 ⋅ A = A ⋅ 1 = A
2. Результатом произведения матрицы на ноль является Θ, где Θ – нулевая матрица (все ее элементы равны нулю).
0 ⋅ A = A ⋅ 0 = Θ
3. Умножение числа на сумму матриц – это то же самое, что и сумма произведений данного числа с каждой матрицей по отдельности.
m ⋅ (A + B) = mA + mB
4. Произведение суммы чисел и матрицы – это то же самое, что и сумма произведений каждого числа и матрицы.
(m + n ) ⋅ A = mA + nA
5. Сочетательный закон при умножении применим и к матрицам:
(m ⋅ n ) ⋅ A = m ⋅ (n ⋅ A)
Примеры задач
Пример 1
Определите, чему равняется 4A, если исходная матрица A выглядит так:

Решение:

Пример 2
Выясните, есть ли у матрицы ниже общий множитель, и, если да, вынесите его за ее пределы.

Решение:
Наименьшим общим делителем всех элементом заданной матрицы является число 2, следовательно, его можно вынести за скобки.

На чтение 7 мин. Просмотров 11.4k.
Как умножить матрицу на матрицу и как умножить матрицу на число — обсуждаем на примерах с решением и объяснением. Произведение матрицы на число и произведение матрицы на матрицу просто и на примерах.
Умножение матрицы на число
Произведением матрицы ![]() на число
на число ![]() называется такая матрица
называется такая матрица ![]() , каждый элемент которой равен
, каждый элемент которой равен ![]() , то есть, если
, то есть, если
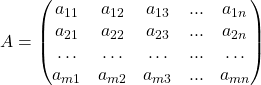 ,
,
то
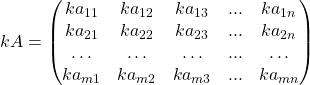 .
.
Правило умножения матрицы на число
Умножение матрицы на число — есть умножение на это число всех элементов матрицы.
Рассмотрим умножение матрицы на число на примере:
Пример 1
Умножьте матрицу ![]() на число
на число ![]() .
.
Решение: Чтобы умножить матрицу ![]() на число 2, нужно умножить на это число каждый элемент матрицы. Итак, получим:
на число 2, нужно умножить на это число каждый элемент матрицы. Итак, получим:
![]() .
.
Пример 2
Найдите матрицу, противоположную матрицу 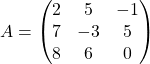 .
.
Решение: Чтобы найти противоположную матрицу надо умножить исходную матрицу на ![]() .
.
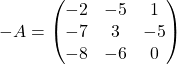 .
.
Пример 3
Даны матрицы 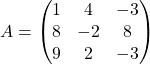 и
и 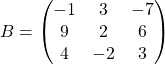 . Вычислите
. Вычислите ![]() .
.
Решение:
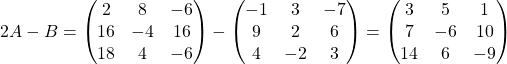 .
.
Умножение матрицы на матрицу
Чтобы умножить матрицу на матрицу необходимо умножать последовательно каждый элемент каждой строки первой матрицы на каждый элемент каждого столбца второй матрицы и сумму этих произведений записать в соответствующем элементе матрицы-произведения.
Давайте рассмотрим умножение матрицы на матрицу на примере. Пусть нам нужно умножить две квадратные матрицы ![]() и
и ![]() .
.
 ,
, 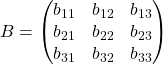
Умножением матрицы на матрицу называется матрица:
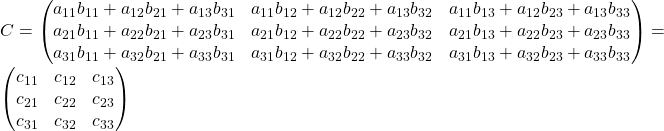 .
.
Таким образом, получаем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Правило умножения матрицы на матрицу
Чтобы получить элемент ![]() надо все элементы
надо все элементы ![]() -й строки матрицы A умножить на соответствующие элементы
-й строки матрицы A умножить на соответствующие элементы ![]() -го столбца матрицы B и полученные произведения сложить.
-го столбца матрицы B и полученные произведения сложить.
Рассмотрим умножение матрицы на матрицу на примерах.
Пример 1
Найдите произведение матриц:
![]() и
и ![]() .
.
Решение:
Находим произведение матриц ![]() .
.
Таким образом, для прямоугольных матриц правило умножения матрицы на матрицу такое же, как и для квадратных матриц.
Пример 2
Найдите произведение AB, если
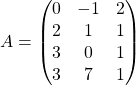 ,
, 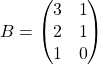 .
.
Решение:
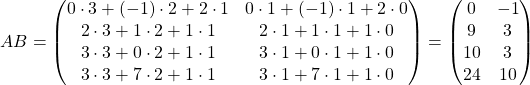 .
.
Мы смогли найти произведение AB, однако, мы не сможем найти произведение BA.
Правила умножения матриц
Не все матрицы можно перемножать, для того, чтобы произведение матриц было возможным, необходимо соблюдение следующих правил:
Умножение матрицы A на матрицу B имеет смысл только в том случае, когда число столбцов матрицы A равно числу строк матрицы B.
В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.
Свойства умножения матриц
Рассмотрим умножение двух матриц ![]() и
и ![]() . Найдем произведение
. Найдем произведение ![]() и произведение
и произведение ![]() , а затем сравним эти произведения.
, а затем сравним эти произведения.
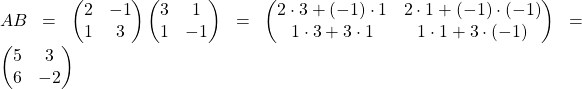 ;
;
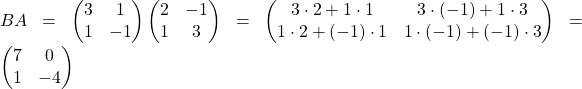 .
.
Очевидно, что ![]() . Таким образом, для произведения матриц переместительный закон не выполняется. Однако, два других закона умножения, сочетательный закон и распределительный закон выполняются:
. Таким образом, для произведения матриц переместительный закон не выполняется. Однако, два других закона умножения, сочетательный закон и распределительный закон выполняются:
![]() — сочетательный закон умножения,
— сочетательный закон умножения,
![]() — распределительный закон.
— распределительный закон.
Из школьного курса математики известно, что произведение двух отличных от нуля чисел равно отличному от нуля числу. Однако при умножении двух ненулевых матриц можно получить нулевую матрицу, смотрите:
Возьмем две матрицы ![]() и
и ![]() . Найдем произведение этих матриц:
. Найдем произведение этих матриц:
![]()
Вот такими удивительными свойствами обладает умножение матриц.
Читайте еще статьи про матрицы:
Умножение матрицы на число
Произведением матрицы А на число k
называется матрица В= kA, элементы
которой bij = kaij
для i = 1, 2, …, m; j = 1,2,…, n
Рис.9
Иначе говоря, при умножении матрицы
на постоянную каждый элемент этой
матрицы умножается на эту постоянную
k*Aij = (k*aij
).
Например, для матриц A и B из
предыдущего примера (1) и (2)

В частности, произведений матрицы А
на Число «0» есть нулевая матрица,
то есть А х 0 = 0.
В MS Excel для выполнения операции умножения
матри цы на число могут быть использованы
формулы, вводи мые в соответствующие
ячейки.
Выаолнить Задание 5. Умножить
матрицу на число
Пусть, как и в предыдущем примере (1)
матрица A введена в диапазон А1:
С2. Необходимо получить матрицу С =
3 х A.
Порядок выполнения.
1. Табличный курсор поставьте в левый
верхний угол результирующей матрицы,
напри мер в El.
2. Введите формулу =3*А1 для вычисления
первого элемента результирующей
матрицы (предварительно установив
английскую раскладку клавиатуры).
3. Скопируйте введенную формулу в
остальные ячейки результирующей
матрицы: поставьте табличный курсор в
ячейку Е1; наведите указатель мыши на
точку в правом нижнем углу ячейки,
так чтобы указатель мыши принял вид
тонкого крестика;
при нажатой левой кнопке мыши протяните
указатель до ячейки G1; таким же образом
протяните указатель мыши до ячейки G2.
В результате в ячейках E1:G2 появится
матрица, равная исходной матрице,
умноженной на постоянную —3.
![]()
Умножение матриц
Произведение матриц определено, если
число столбцов первой матрицы равно
числу строк второй.
Пусть A = (aij) m
х
n , B = (bij) n х
p, тогда размерность произведения
А х В равна m х
p .
При этом матрица С (размера m х
p) называется произведением матриц
A и В, если каждый ее элемент
сij, равен сумме произведений
элементов i-й строки матрицы А
на соответствующие элементы j-гo
столбца матрицы В:
![]()
Таким образом, перемножение матриц
осуществляется по следующему правилу:

Пусть например

Рис.10
Многие свойства, присущие операциям
над числами, справедливы и для операций
умножения матриц (что следует из
определений этих операций).
Для матриц верны общие свойства операции умножения.
1. А(ВС) = (АВ)С — ассоциативность.
2. А(В + С) = АВ + АС — дистрибутивность.
3. (А + В)С= АВ + ВС.
4. (αА)В = А(αВ) = α(АВ), α ─ константа.
Однако имеются и специфические свойства
операций умножения матриц.
5. Умножение матриц некоммутативно —
АВ ≠ ВА.
В частном случае коммутативным законом
обладает произведение любой квадратной
матрицы А i-го порядка на единичную
матрицу Е того же порядка, причем это
произведение равно А.
6. Если Е — единичная матрица, то ЕА =
А; ВЕ = В.
Таким образом, единичная матрица
играет при умножении ту же роль, что и
число 1 при умножении чисел.
7. Из того, что А х В = 0, не следует,
что А = 0 или В = 0.
В алгебре матриц нет действия деления.
Выражение А/В не имеет смысла.
Его заменяют два различных выражения
В-1 х
А и А х
В-1 , если существует
В-1
Для квадратных матриц возможна
операция возведения в степень. По
определению полагают, что А0
= Е и А1 = А. Целой
положительной степенью Аm
(m > 1) квадратной матрицы А
называется произведение m матриц,
равных А, то есть:

Для нахождения произведения двух
матриц в Excel используется функция
МУМНОЖ, которая вычисляет
произведение матриц (матрицы хранятся
в массивах).
Функция имеет вид МУМНОЖ (массив1,
массив 2). Здесь массив1 и массив2 —
это перемножаемые массивы. При этом
количество столбцов аргумента массив
1 должно быть таким же, как количество
строк аргумента массив2, и оба массива
должны содержать только числа. Результатом
является массив с таким же числом строк,
как массив1 и с таким же числом
столбцов, как массив2.
![]() Массив
Массив
С, который является произведением
двух массивов А и В, определяется
следующим образом:
где i — номер строки, a j — номер
столбца.
Рассмотрим примеры умножения матриц.
Выполнить Задание 6. Найти
произведение матриц А и В из
выше приведенного примера Рис.10.
Пусть матрица А из рассмотренного
примера введена в диапазон A1:D3, а
матрица В в диапазон А4 : В7.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
