Логарифмы степени числа — свойства с примерами, как решать задачи
Содержание:
- Что такое логарифм степени числа и как его посчитать
- Основные свойства логарифмов
- Примеры логарифмов с решением, пояснения
- Задачи для самостоятельной работы
Что такое логарифм степени числа и как его посчитать
Логарифм по основанию а от b представляет собой число t, демонстрирующее степень, в которую требуется возвести а для получения в результате b:
(Large{{log_a{b}=tquadLeftrightarrowquad a^t=b }})
Здесь a>0, b отлично от нуля и является положительным.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По той причине, что степень может иметь любое значение без какого-либо предела, имеем:
(tin mathbb{R})
В результате получается вывести главное логарифмическое тождество.
Основное логарифмическое тождество является соотношением, записанным в виде:
(Large{a^{log_ab}=b})
Исходя из рассмотренных закономерностей, справедливы следующие соотношения:
({large{begin{array}{|ll|l|} hline qquad qquad qquad qquad {small{text{Формулы}}} && qquad qquad{small{text{Ограничения}}}\ &&\ hline textbf{(1)} log_a1=0&&a>0, ane 1\ &&\ textbf{(2)} log_aa=1 &&a>0, ane 1\ &&\ textbf{(3)} log_{a}{b^m}=mlog_a|b|&(m – {small{text{четн.}}})&a>0, ane 1, bne 0\ &&\ textbf{(4)}log_{a}{b^m}=mlog_ab& (m – {small{text{нечетн.}}})&a>0, ane 1, b>0\ &&\ textbf{(5)} log_{a^n}{b}=frac 1nlog_{|a|}b&(n – {small{text{четн.}}})&ane 0, ane 1, b>0\ &&\ textbf{(6)}log_{a^n}b=frac1nlog_ab&(n – {small{text{нечетн.}}})&a>0, ane 1, b>0\ &&\ textbf{(7)} log_a{bc}=log_a|b|+log_a|c|&&a>0, ane 1, bcne 0\ &&\ textbf{(8)} log_a{dfrac bc}=log_a|b|-log_a|c|&&a>0, ane 1,bcne 0 \ &&\ textbf{(9)} a^{log_ab}=b &&a>0, ane 1, b>0\ &&\ textbf{(10)}c^{log_ab}=b^{log_ac}&&a>0, ane 1, b>0, c>0\ &&\ textbf{(11)} log_abcdot log_bc=log_ac && a>0, ane 1,b>0, bne 1, c>0\ &&\ textbf{(11′}) log_bc=dfrac{log_ac}{log_ab}&&a>0, ane 1,b>0, bne 1, c>0\ &&\ &&\ {small{text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \ textbf{(12)} log_abcdot log_ba=1 && a>0, ane 1, b>0, bne 1\ &&\ textbf{(12′}) log_ab=dfrac1{log_ba}&&a>0, ane 1, b>0, bne 1\ &&\ hline end{array}}})
Если все условия, связанные с ограничениями, выполняются, то эти формулы справедливы в прямом и обратном направлениях.
Логарифм степени какого-либо числа представляет собой результат умножения логарифма модуля основания данной степени и показателя этой степени:
(log_{a}x^r=r cdot log_{a}|x|)
В данном случае (x^r,a > 0), (a ne 1).
Разберем наглядный пример такой взаимосвязи. Предположим, что имеется некое выражение, значение которого требуется определить:
(log_{5}frac{1}{125}+log_{11}121)
Рассмотрим выражение, записанное под знаком логарифма, и решим, что с ним делать. Заметим, что его можно переписать как основание логарифма в степени. Воспользуемся свойством логарифма степени, изученным ранее, и выполним преобразования:
(log_{5}frac{1}{125}+log_{11}121=log_{5}5^{-3}+log_{11}11^2=-3log_{5}5+2log_{11}11)
Известно, что:
(log_{a}a=1)
Доведем вычисления до конца:
(log_{5}frac{1}{125}+log_{11}121=log_{5}5^{-3}+log_{11}11^2=-3log_{5}5+2log_{11}11=-3+2=-1)
Ответ: (log_{5} frac{1}{125}+log_{11}121=-1.)
В процессе решения задач в разных главах разделов тригонометрии может потребоваться обратный перевод определения логарифма степени числа. Заметим, что оно также является справедливым.
Коэффициент, записанный перед знаком логарифма, допустимо заносить в степень выражения, находящегося под знаком логарифма:
(s log_{a}x=log_{a}x^s)
Здесь a и b > 0, a≠1.
Рассмотрим наглядный пример. Пусть дано выражение, которое требуется упростить:
(6 log_{13}x^2-log_{13}x^7)
Воспользуемся логарифмическим свойством, чтобы записать степень за знаком логарифма:
(6 log_{13}x^2-log_{13}x^7=6 cdot 2 log_{13}x-7 log_{13}x=12 log_{13}x-7 log_{13}x=5 log_{13}x)
Если под логарифмический знак записать коэффициент в виде числа 5, то получим:
(6 log_{13}x^2-log_{13}x^7=6 cdot 2 log_{13}x-7 log_{13}x=12 log_{13}x-7 log_{13}x=5 log_{13}x=log_{13}x^5.)
Основные свойства логарифмов
При решении задач на логарифмы, в том числе, для вычисления логарифма степени числа и поиск натуральных корней, полезно знать несколько свойств. Благодаря несложным закономерностям, можно сделать проще даже самое сложное выражение.
1. Рассмотрим свойство степени аргумента, записанное в виде уравнения:
({{log }_{a}}{{a}^{x}}=x)
Докажем, что записанное соотношение справедливо. Предположим, что:
({{log }_{a}}b=x)
В таком случае:
({{a}^{x}}=b)
В результате получим:
(frac{{{log }_{c}}b}{{{log }_{c}}a}=frac{{{log }_{c}}{{a}^{x}}}{{{log }_{c}}a}=frac{x{{log }_{c}}a}{{{log }_{c}}a}=x={{log }_{a}}b)
Данное свойство доказано.
2. Следующее свойство суммы логарифмов состоит в том, что при сложении логарифмов, имеющих одинаковые основания, получается в результате логарифм произведения:
({{log }_{a}}b+{{log }_{a}}c={{log }_{a}}left( bcdot c right))
Начнем доказательство со следующего предположения:
({{log }_{a}}b=x)
В таком случае:
({{a}^{x}}=b)
Представим, что:
({{log }_{a}}c=y)
В таком случае:
({{a}^{y}}=c)
В результате получим, что:
({{log }_{a}}left( bcdot c right)={{log }_{a}}left( {{a}^{x}}cdot {{a}^{y}} right)={{log }_{a}}{{a}^{x+y}}underset{text{по правилу 1}}{mathop{=}},x+y={{log }_{a}}b+lo{{g}_{a}}c)
Свойство суммы логарифмов доказано.
3. Свойство разности логарифмов звучит так: разность двух логарифмов, имеющих идентичные основания, равна логарифму частного. Это утверждение можно выразить формулой:
(lo{{g}_{a}}b-{{log }_{a}}c={{log }_{a}}frac{b}{c})
Доказательство данного свойства аналогично сумме логарифмов. Предположим, что:
({{log }_{a}}b=x)
В таком случае:
({{a}^{x}}=b)
Представим, что:
({{log }_{a}}c=y)
В таком случае:
({{a}^{y}}=c)
В результате получим, что:
({{log }_{a}}left( frac{b}{c} right)={{log }_{a}}left( frac{{{a}^{x}}}{{{a}^{y}}} right)={{log }_{a}}{{a}^{x-y}}=x-y={{log }_{a}}b-{{log }_{a}}c)
({{log }_{a}}b-{{log }_{a}}c={{log }_{a}}left( frac{b}{c}cdot c right)-{{log }_{a}}c={{log }_{a}}frac{b}{c}+{{log }_{a}}c-{{log }_{a}}c={{log }_{a}}frac{b}{c}.)
4. Следующее свойство призвано упростить вынесение показателя степени из аргумента логарифма. Оно состоит в следующем: при наличии в аргументе логарифма степени ее показатель допустимо выносить за знак логарифма. Справедливым является следующее соотношение:
({{log }_{a}}{{b}^{n}}=ncdot {{log }_{a}}b)
Доказать данное утверждение можно с помощью определения логарифма. Представим, что:
({{log }_{a}}b=x)
В таком случае:
({{a}^{x}}=b)
Получим, что:
({{log }_{a}}{{b}^{n}}={{log }_{a}}{{left( {{a}^{x}} right)}^{n}}={{log }_{a}}{{a}^{nx}}=nx=ncdot {{log }_{a}}b)
Утверждение доказано. Также существует другой вариант записи свойства:
({{log }_{a}}{{b}^{n}}={{log }_{a}}left( underbrace{bcdot bcdot …cdot b}_{ntext{ раз}} right)text{ }underset{text{правило} text{2}}{mathop{=}},text{ }underbrace{{{log }_{a}}b+lo{{g}_{a}}b+…+{{log }_{a}}b}_{ntext{ раз}}=ncdot {{log }_{a}}b.)
Таким образом, степень аргумента допустимо записывать перед логарифмом в виде коэффициента.
5. Следующее свойство позволит выносить показатель степени из основания логарифма. Такое действие реализуемо, так как при наличии в основании логарифма степени ее показатель допустимо выносить за знак логарифма:
({{log }_{{{a}^{n}}}}b=frac{1}{n}cdot {{log }_{a}}b)
Докажем записанное соотношение, предположив, что:
({{log }_{a}}b=x), тогда (displaystyle {{a}^{x}}=b)
В таком случае:
({{log }_{{{a}^{n}}}}b={{log }_{{{a}^{n}}}}{{a}^{x}}={{log }_{{{a}^{n}}}}{{a}^{frac{xcdot n}{n}}}={{log }_{{{a}^{n}}}}{{left( {{a}^{n}} right)}^{frac{x}{n}}}=frac{x}{n}=frac{1}{n}cdot {{log }_{a}}b.)
Свойство доказано. Здесь следует отметить, что степень можно вынести из основания в виде обратного числа.
6. Существует свойство, позволяющее выносить показатель степени из основания и аргумента логарифма. Свойство заключается в следующем: при наличии степеней в основании и аргументе логарифма их показатели допустимо выносить за знак логарифма, то есть:
({{log }_{{{a}^{n}}}}{{b}^{m}}=frac{m}{n}cdot {{log }_{a}}b)
В том случае, когда степени не отличаются друг от друга, применимо следующее правило:
({{log }_{{{a}^{n}}}}{{b}^{n}}={{log }_{a}}b.)
7. Другое свойство логарифма оговаривает процесс перехода к новому основанию. В том случае, когда логарифмы обладают разными основаниями, целесообразно при решении задачи перейти к логарифмам, имеющим одинаковое основание:
({{log }_{a}}b=frac{{{log }_{c}}b}{{{log }_{c}}a}text{ }left( c>0;text{ }ne text{1} right))
Здесь доказательство свойства построено на следующем предположении:
({{log }_{a}}b=x,) тогда (displaystyle {{a}^{x}}=b)
В таком случае:
(frac{{{log }_{c}}b}{{{log }_{c}}a}=frac{{{log }_{c}}{{a}^{x}}}{{{log }_{c}}a}=frac{x{{log }_{c}}a}{{{log }_{c}}a}=x={{log }_{a}}b.)
8. В большинстве случаев при решении заданий на логарифмы используют свойство смены мест основания и аргумента логарифма. Допустимо переставлять основание и аргумент логарифма. При этом следует «перевернуть» все выражение, то есть записать логарифм в знаменатель:
({{log }_{a}}b=frac{1}{{{log }_{b}}a},text{ }left( bne 1 right))
Данное свойство является частным случаем записанного ранее правила. При подстановке c=b получается, что:
({{log }_{a}}b=frac{{{log }_{b}}b}{{{log }_{b}}a}=frac{1}{{{log }_{b}}a}.)
Примеры логарифмов с решением, пояснения
Задача 1
Дано выражение, значение которого требуется определить:
(log _{2} frac{1}{8}+log _{5} 25)
Решение
Данное выражение можно преобразовать. Для этого следует вспомнить свойство логарифма степени. С его помощью нужно вынести имеющиеся степени за знак логарифма. Далее пригодится следующее соотношение:
(log _{a} a=1.)
Выполним вычисления:
(log _{2} frac{1}{8}+log _{5} 25=log _{2} 2^{-3}+log _{5} 5^{2}=-3 cdot log _{2} 2+2 cdot log _{5} 5=-3+2=-1)
Ответ: ( log _{2} frac{1}{8}+log _{5} 25=-1)
Требуется упростить следующее выражение:
(2 log _{7} 4-log _{7} 8)
Решение
Данное выражение можно упростить. Перепишем его с помощью свойства логарифма степени. В процессе следует записать число 2 под знак логарифма. Затем удобно применить свойство разности логарифмов. Выполним вычисления:
(2 log _{7} 4-log _{7} 8=log _{7} 4^{2}-log _{7} 8=log _{7} 16-log _{7} 8=log _{7} frac{16}{8}=log _{7} 2)
Ответ: (2 log _{7} 4-log _{7} 8=log _{7} 2)Задача 2
Задача 3
Дано выражение, значение которого необходимо вычислить:
(lo{{g}_{5}}250-{{log }_{5}}2)
Решение
Воспользуемся свойствами логарифма и выполним вычисления:
({{log }_{5}}250={{log }_{5}}left( 125cdot 2 right)={{log }_{5}}left( {{5}^{3}}cdot 2 right)={{log }_{5}}{{5}^{3}}+{{log }_{5}}2=3+{{log }_{5}}2)
Заметим, что:
({{log }_{5}}250-{{log }_{5}}2=3+{{log }_{5}}2-{{log }_{5}}2=3)
Ответ: 3.
Задача 4
Нужно упростить следующее выражение:
(log _{2}^{2}2sqrt{3}-log _{2}^{2}sqrt{3}-{{log }_{2}}3)
Решение
Воспользуемся формулами сокращенного умножения, а именно — разностью квадратов:
(log _{2}^{2}2sqrt{3}-log _{2}^{2}sqrt{3}=left( {{log }_{2}}2sqrt{3}-{{log }_{2}}sqrt{3} right)left( {{log }_{2}}2sqrt{3}+{{log }_{2}}sqrt{3} right).)
Тогда, согласно свойствам логарифма:
(log _{2}^{2}2sqrt{3}-log _{2}^{2}sqrt{3}-{{log }_{2}}3= left( {{log }_{2}}2sqrt{3}-{{log }_{2}}sqrt{3} right)left( {{log }_{2}}2sqrt{3}+{{log }_{2}}sqrt{3} right)-{{log }_{2}}3={{log }_{2}}frac{2sqrt{3}}{sqrt{3}}cdot {{log }_{2}}left( 2sqrt{3}cdot sqrt{3} right)-{{log }_{2}}3={{log }_{2}}2cdot {{log }_{2}}left( 2cdot 3 right)-{{log }_{2}}3=1cdot left( 1+{{log }_{2}}3 right)-{{log }_{2}}3=1)
Ответ: 1.
Задача 5
Необходимо определить значение следующего выражения:
(frac{{{log }_{2}}25}{{{log }_{2}}5})
Решение
Воспользуемся свойствами логарифма и запишем вычисления:
(frac{{{log }_{2}}25}{{{log }_{2}}5}=frac{{{log }_{2}}{{5}^{2}}}{{{log }_{2}}5}=frac{2{{log }_{2}}5}{{{log }_{2}}5}=2)
Ответ: 2.
Задачи для самостоятельной работы
Задача 6
Даны выражения, которые нужно упростить, используя свойства логарифма:
({{log }_{3}}4-{{log }_{3}}12)
({{log }_{0,3}}3-{{log }_{0,3}}10)
({{log }_{1,75}}28+{{log }_{1,75}}2-{{log }_{1,75}}32)
(lg sqrt{0,05}-lg sqrt{5})
({{lg }^{2}}2sqrt{5}-{{lg }^{2}}5sqrt{2}-frac{3}{2}lg sqrt{frac{2}{5}})
Задача 7
Требуется найти значения для следующих выражений:
(displaystyle frac{{{log }_{2}}81}{{{log }_{2}}3})
(displaystyle frac{{{log }_{3}}125}{{{log }_{3}}625})
(displaystyle frac{log _{5}^{2}25sqrt{10}-log _{5}^{2}sqrt{10}}{{{log }_{5}}250})
Задача 8
Нужно определить значения записанных ниже выражений:
({{log }_{5}}75+{{log }_{5}}frac{1}{3})
({{log }_{3}}36-2{{log }_{3}}2)
({{log }_{8sqrt[5]{4}}}left( 32sqrt[5]{2} right))
(frac{log _{5}^{2}25sqrt{10}-log _{5}^{2}sqrt{10}}{{{log }_{5}}250})
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Логарифм степени основания
Определение 1
Значением логарифма степени числа, которое равно основанию логарифма, является показатель этой степени:
$log_{a}a^s=s$
при $a > 0$, $a ne 1$,
$s$ – любом числе.
Данное свойство вытекает из определения логарифма. С его помощью можно сразу найти значение логарифма при условии, что число, которое стоит под знаком логарифма, можно записать в виде степени числа, являющегося основанием данного логарифма.
Пример 1
$log_{11}{11^8}=8$;
$lg10^{-17}=-17$;
$log_{sqrt{8,7}}(sqrt{8,7})^{7,23}=7,23$.
Логарифм степени числа
Определение 2
Логарифм степени любого числа равен произведению логарифма модуля основания этой степени на показатель степени:
$log_{a}x^r=r cdot log_{a}|x|$
при $x^r,a > 0$, $a ne 1$.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 2
Найти значение выражения $log_{5}frac{1}{125}+log_{11}121$.
Решение.
Представим подлогарифмические выражения в виде основания логарифма в степени и используем свойство логарифма степени:
$log_{5}frac{1}{125}+log_{11}121=log_{5}5^{-3}+log_{11}11^2=-3log_{5}5+2log_{11}11=$
воспользуемся равенством $log_{a}a=1$:
$=-3+2=-1$.
Ответ: $log_{5} frac{1}{125}+log_{11}121=-1$.
При вычислении логарифмов справедливым является и обратное определение:
Определение 3
Коэффициент, который стоит перед логарифмом можно внести в степень подлогарифмического выражения:
$s log_{a}x=log_{a}x^s$
при $a,b > 0$, $a ne 1$.
Пример 3
Упростить $6 log_{13}x^2-log_{13}x^7$.
Решение.
Используем свойство логарифма степени и вынесем степень за знак логарифма:
$6 log_{13}x^2-log_{13}x^7=6 cdot 2 log_{13}x-7 log_{13}x=12 log_{13}x-7 log_{13}x=5 log_{13}x=$
внесем коэффициент $5$ под знак логарифма:
$=log_{13}x^5$.
Ответ: $6 log_{13}x^2-log_{13}x^7=log_{13}x^5$.
«Логарифм степени» 👇
Логарифм корня
Определение 4
Следствием из свойства логарифма степени числа является свойство логарифма степени в виде дроби:
$log_{a}sqrt[r]{x}=frac{1}{r} cdot log_{a}x$
при $a,x > 0$, $a ne 1$, $r$ – натуральное число, $r > 1$.
Пример 4
$log_{7,8}sqrt[6]{2}=log_{7,8}2^{frac{1}{6}}=frac{1}{6}log_{7,8}2$.
Пример 5
Найти значение выражения $lgsqrt[3]{10x}$, если $lgx=frac{5}{7}$.
Решение.
Используем свойство логарифма корня:
$lgsqrt[3]{10x}=frac{1}{3}lg10x=$
воспользуемся свойством логарифма произведения:
$frac{1}{3} (lg10+lgx )=frac{1}{3} (1+frac{5}{7})=frac{1}{3} cdot frac{12}{7}=frac{12}{21}$.
Ответ: $lgsqrt[3]{10x}=frac{12}{21}$.
Также можно применять и обратное свойство:
Определение 5
Если перед логарифмом стоит дробь, то ее можно внести в степень подлогарифмического выражения:
$frac{1}{r} cdot log_{a}x=log_{a}sqrt[r]{x}$
при $a,x > 0$, $a ne 1$, $r$ – натуральное число, $r > 1$.
Пример 6
Вычислить $frac{1}{4}log_{12}16+log_{12}6$.
Решение.
Применим свойство логарифма корня:
$frac{1}{4}log_{12}16+log_{12}6=log_{12}sqrt[4]{16}+log_{12}6=log_{12}2+log_{12}6=$
используем свойство суммы логарифмов:
$=log_{12}2 cdot 6=log_{12}12=1$.
Ответ: $frac{1}{4}log_{12}16+log_{12}6=1$.
При вычислении логарифмов зачастую встречаются случаи, когда основание логарифма и число, для которого вычисляется логарифм, можно записать в виде степени одного и того же числа. Тогда для упрощения вычислений пользуются формулой:
$log_{a^x}a^y=frac{y}{x}$.
Данная формула дает возможность практически моментально получить значение рассматриваемого логарифма при его кажущейся сложности записи.
Рассмотрим пример, который покажет удобство использования данной формулы.
Пример 7
Вычислить $log_{27}9sqrt[7]{81}$.
Решение.
Запишем основание логарифма $27$ и подлогарифмическое выражение $9sqrt[7]{81}$ в виде степени числа $3$:
$log_{27}9sqrt[7]{81}=log_{3^3}3^2 cdot 3^{frac{4}{7}}=log_{3^3}3^{frac{18}{7}}=$
теперь воспользуемся рассматриваемой формулой:
$=frac{frac{18}{7}}{3}=frac{18}{7 cdot 3}=frac{6}{7}$.
Ответ: $log_{27}9sqrt[7]{81}=frac{6}{7}$.
Пример 8
Вычислить $log_{sqrt[11]{8}}frac{x^3}{16}$, если $log_{sqrt[11]{8}}x=13$.
Решение.
Применим свойство логарифма дроби:
$log_{sqrt[11]{8}}frac{x^3}{16}=log_{sqrt[11]{8}}x^3-log_{sqrt[11]{8}}16=$
к первому логарифму применим свойство логарифма степени, а во втором в основании логарифма и подлогарифмическом выражении перейдем к степеням числа $2$:
$=3 log_{sqrt[11]{8}}x-log_{2^{frac{3}{11}}}2^4=$
подставим условие $log_{sqrt[11]{8}}x=13$ в первый логарифм и применим рассмотренное свойство для логарифма степени ко второму логарифму:
$=3 cdot 13-frac{4}{frac{3}{11}}=39-4 cdot frac{11}{3}=39-frac{44}{3}=frac{73}{3}=24 frac{1}{3}$.
Ответ: $log_{sqrt[11]{8}}frac{x^3}{16}=24 frac{1}{3}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 ((log_{2}(32))) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
$$ log_{2}(32)=5;$$
Аналогично, глядя в таблицу получим, что:
$$log_{2}(4)=2;$$
$$log_{2}(8)=3;$$
$$log_{2}(16)=4;$$
$$log_{2}(64)=6;$$
$$log_{2}(128)=7.$$
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа (b) по основанию положительно числа (a) называется степень (c), в которую нужно возвести число (a), чтобы получить (b)
$$log_{a}(b)=c;$$
$$a^{c}=b.$$
Будьте внимательны! В первое время обычно путают, что такое основание и то, что стоит под логарифмом (аргумент). Логарифм – это всегда функция, зависящая от двух переменных. Чтобы их не путать, помните определение логарифма – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
$$log_{2}(5)=???$$
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
$$log_{2}(5)=2,32192809…$$
Или логарифм шести по основанию 4:
$$log_{4}(6)= 1.2924812…$$
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм (log_{4}(6)). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6-ке:
$$ log_{4}(4) lt log_{4}(6) lt log_{4}(16);$$
$$ 1 lt log_{4}(6) lt 2. $$
Значит (log_{4}(6)) принадлежите промежутку от 1 до 2:
$$ log_{4}(6) in (1;2). $$
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма (log_{a}(b)) существует только при положительных значениях основания (a) и аргумента (b). И кроме этого на основание накладывается условие, что оно не должно быть равно (1).
$$ log_{a}(b) quad существует,;при quad a gt 0; ;b gt 0 ;a neq 1.$$
Почему так? Это следует из определения показательной функций. Показательная функция не может быть (0). А основание не равно (1), потому что тогда логарифм теряет смысл – ведь (1) в любой степени это будет (1).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
$$log_{3}(frac{1}{3})=-1;$$
Так как (вспоминайте определение отрицательной степени)
$$3^{-1}=frac{1}{3};$$
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться в какую степень (x) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
- (x) и будет искомым значением логарифма.
Давайте разберем на примерах.
Пример 1. Посчитать логарифм (9) по основанию (3): (log_{3}(9))
- Сначала представим аргумент и основание в виде степени тройки:
$$ 3=3^1, qquad 9=3^2;$$ - Теперь надо разобраться в какую степень (x) нужно возвести (3^1), чтобы получить (3^2)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2. Вычислить логарифм (frac{1}{125}) по основанию (5): (log_{5}(frac{1}{125}))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, qquad frac{1}{125}=frac{1}{5^3}=5^{-3};$$ - В какую степень (x) надо возвести (5^1), чтобы получить (5^{-3}):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(frac{1}{125})=-3.$$
Пример 3. Вычислить логарифм (4) по основанию (64): (log_{64}(4))
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, qquad 4=2^2;$$ - В какую степень (x) надо возвести (2^6), чтобы получить (2^{2}):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=frac{2}{6}=frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=frac{1}{3}.$$
Пример 4. Вычислить логарифм (1) по основанию (8): (log_{8}(1))
- Представим аргумент и основание в виде степени двойки:
$$ 8=2^3 qquad 1=2^0;$$ - В какую степень (x) надо возвести (2^3), чтобы получить (2^{0}):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5. Вычислить логарифм (15) по основанию (5): (log_{5}(15))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 qquad 15= ???;$$
(15) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число (a) не будет являться степенью другого числа (b). Это довольно просто – нужно разложить (a) на простые множители.
$$16=2*2*2*2=2^4,$$
(16) разложили, как произведение четырех двоек, значит (16) будет степенью двойки.
$$ 48=6*8=3*2*2*2*2,$$
Разложив (48) на простые множители, видно, что у нас есть два множителя (2) и (3), значит (48) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
На самом деле, все просто. Десятичный логарифм – это любой обыкновенный логарифм, но с основанием 10. Обозначается – (lg(a)).
Пример 6
$$ log_{10}(100)= lg(100)=2;$$
$$log_{10}(1000)=lg(1000)=3;$$
$$log_{10}(10)=lg(10)=1.$$
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию (e). Обозначение – (ln(x)). Что такое (e)? Так обозначают экспоненту, число-константу, равную, примерно, (2,718281828459…). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием (e) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.
Пример 7
$$ log_{e}(e^2)=ln(e^2)=2;$$
$$ log_{e}(e)=ln(e)=1;$$
$$ log_{e}(e^5)=ln(e^5)=5.$$
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
$$1. ; log_{a}(1)=0;$$
$$2. ; log_{a}(a)=1;$$
$$3. ; log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$4. ; log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$5. ; log_{a}(b^m)= m*log_{a}(b);$$
$$6. ; log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
$$ 7. ; log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0; ; c gt 0; ; c neq 1; $$
$$ 8. ; log_{a}(b)=frac{1}{log_{b}(a)};$$
$$ 9. ; a^{ log_{a}(b)}=b.$$
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой (3). Логарифм от произведения – это сумма логарифмов.
$$log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$ log_{3}(12)=log_{3}(3*4)=log_{3}(3)+log_{3}(4)=1+log_{3}(4);$$
$$ log_{3}(2.7)+log_{3}(10)=log_{3}(2.7*10)=log_{3}(27)=3;$$
Пример 9. Воспользоваться формулой (4). Логарифм от частного – это разность логарифмов.
$$ log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$ log_{7}(98)-log_{7}(2)=log_{7}(frac{98}{2})=log_{7}(49)=2;$$
Пример 10. Формула (5,6). Свойства степени.
$$log_{a}(b^m)= m*log_{a}(b);$$
$$log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
Логично, что будет выполняться и такое соотношение:
$$log_{a^m}(b^n)=frac{n}{m}* log_{a}(b);$$
И если (m=n), то:
$$log_{a^m}(b^m)=frac{m}{m}* log_{a}(b);=log_{a}(b)$$
$$log_{4}(9)=log_{2^2}(3^2)=log_{2}(3);$$
Пример 11. Формулы (7,8). Переход к другому основанию.
$$ log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0;c gt 0;c neq 1; $$
$$ log_{a}(b)=frac{1}{log_{b}(a)};$$
$$log_{4}(5)=frac{1}{log_{5}(4)};$$
$$log_{4}(5)=frac{log_{7}(5)}{log_{7}(4)};$$
#статьи
- 6 окт 2022
-
0
Стыдные вопросы о логарифмах: всё, что нужно знать программисту
Объясняем, почему не стоит бояться логарифмов и как их считать в Python.
Иллюстрация: Оля Ежак для Skillbox Media

Журналист, изучает Python. Любит разбираться в мелочах, общаться с людьми и понимать их.
Прежде чем начать обсуждение, давайте немного освежим знания и решим несколько стандартных задачек:
- Чему равен log3 81?
- А lg 2 × lb 10?
- А сумма log216 2 + log216 3?
Если вы легко прорешали все три примера в уме, не пользуясь калькулятором, — можете сразу переходить к заключительной главе. Для тех же, кто слегка подзабыл школьные годы чудесные, — буквально пять минут ликбеза.
По большому счёту, логарифм — это просто перевёрнутая степень. Рассмотрим выражение 23 = 8. В нём:
- 2 — основание степени;
- 3 — показатель степени;
- 8 — результат возведения в степень.
У возведения в степень существует два обратных выражения. В одном мы ищем основание (это извлечение корня), в другом — показатель (это логарифмирование).
Таким образом, выражение 23 = 8 можно превратить в log2 8 = 3.
Закрепляем знания: логарифм — это число, в которое нужно возвести 2 (основание степени), чтобы получить 8 (результат возведения в степень).
Форма записи неинтуитивна, и поначалу можно легко спутать основание со степенью. Чтобы избежать этого, можно использовать следующее правило:
Основание у логарифма, как и у возведения в степень, находится внизу.
Чтобы лучше запомнить структуру записи, посмотрите на эти выражения и постарайтесь понять их смысл:
- log3 9 = 2
- log4 64 = 3
- log5 625 = 4
- log7 343 = 3
- log10 100 = 2
- log2 128 = 7
- log2 0,25 = −2
- log625 125 = 0,75
В общем виде запись logAB читается так: логарифм B по основанию A.
Главная часть любого логарифма — его основание. Именно наличие общего основания у нескольких логарифмических функций позволяет проводить с ними различные операции.
Основанием натурального логарифма является число Эйлера (e) — иррациональное число, приблизительно равное 2,71828.
На всякий случай напомним, что такое иррациональные числа. Так называют числа, которые нельзя записать в виде обыкновенной дроби с целыми числителем и знаменателем. При этом знаменатель не должен быть равен нулю.
Например, 0,333… — рациональное число, потому что его можно записать как 1/3. А вот число Пи или корень из 2 — иррациональны.
Так как натуральные логарифмы часто используются, для них ввели особый способ записи: ln x — это то же самое, что loge x.
Представим кристалл, который весит 1 кг и растёт со скоростью 100% в год. Можно ожидать, что через год он будет весить 2 кг, но это не так.
Каждая новая выращенная часть начнёт растить свою собственную. Когда в кристалле будет 1,1 кг, он будет расти со скоростью 1,1 кг в год, а когда в нём будет 1,5 кг — со скоростью 1,5 кг в год. Математики подсчитали, что через год масса кристалла составит e, или ≈ 2,71828 кг.
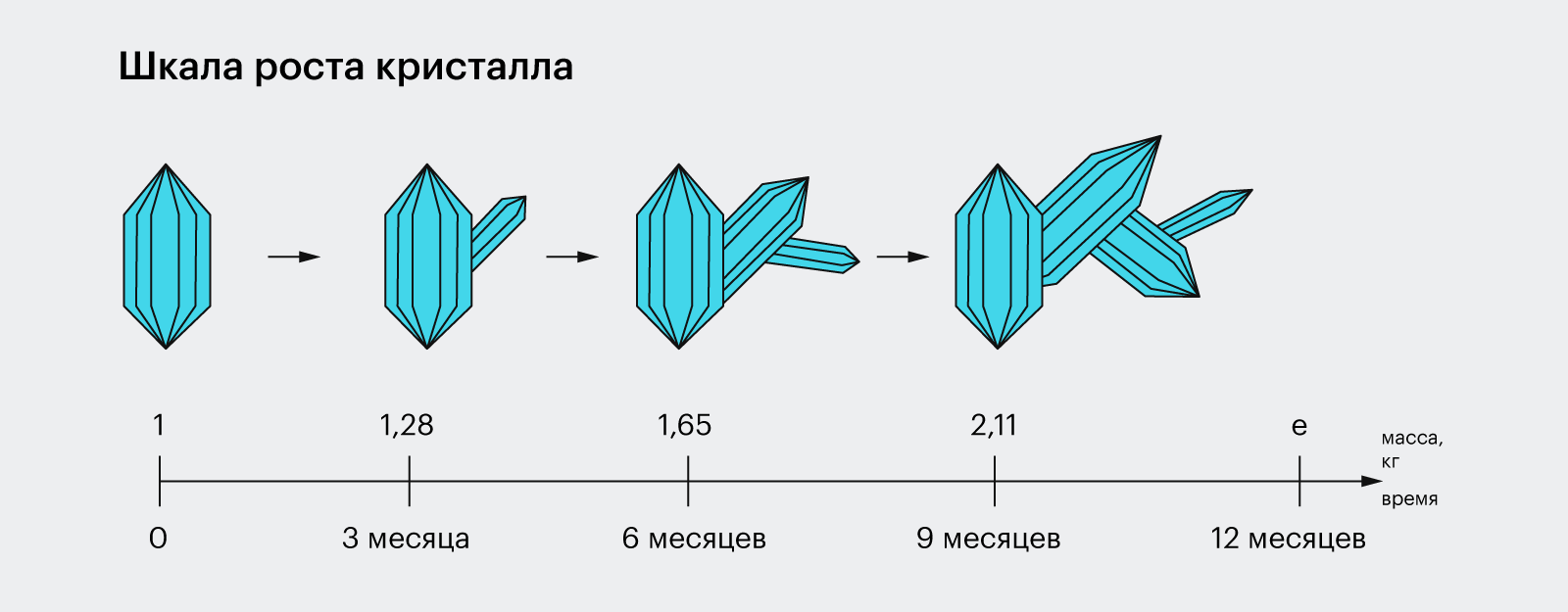
Такой рост называется экспоненциальным. По экспоненте размножаются бактерии, увеличиваются популяции, приумножаются доходы, растут снежные комья, распадается радиоактивное вещество и остывают напитки.
Чтобы узнать, какой массы достигнет кристалл через три, пять, десять лет, нужно возвести e в соответствующую степень.
e3 ≈ 20,0855 кг
e5 ≈ 148,4132 кг
e10 ≈ 22 026,4658 кг
Но как рассчитать, когда кристалл будет весить тонну? Составим уравнение:
ex = 1000
Нам известны основание степени и результат возведения в степень — осталось найти её показатель. Ничего не напоминает? Это ведь и есть логарифм x = loge 1000! Или, если использовать сокращённую запись, x = ln 1000.
Подставим в калькулятор и выясним, что x ≈ 6,9. Именно столько лет потребуется кристаллу, чтобы его масса достигла тонны.
Десятичный логарифм — логарифм, основание которого равно 10. Он обозначается lg x и очень удобен, потому что с ним легко вычислять круглые числа.

Двоичный логарифм — логарифм, основание которого равно 2. Он обозначается lb x и часто используется программистами, потому что компьютеры думают и считают в двоичной системе.

Список операций, которые можно совершать с логарифмами, ограничен. Если вы запомните все и научитесь их выполнять, то сможете щёлкать логарифмические задачки, как семечки.
У всех логарифмов есть ограничения. Их основание и аргумент должны быть больше нуля, при этом основание не может быть равно единице. На математическом языке это звучит так:

Перейдём к свойствам логарифмов. Они работают в обе стороны, и их применяют как слева направо, так и справа налево.
1. Логарифм единицы по любому основанию всегда равен нулю:
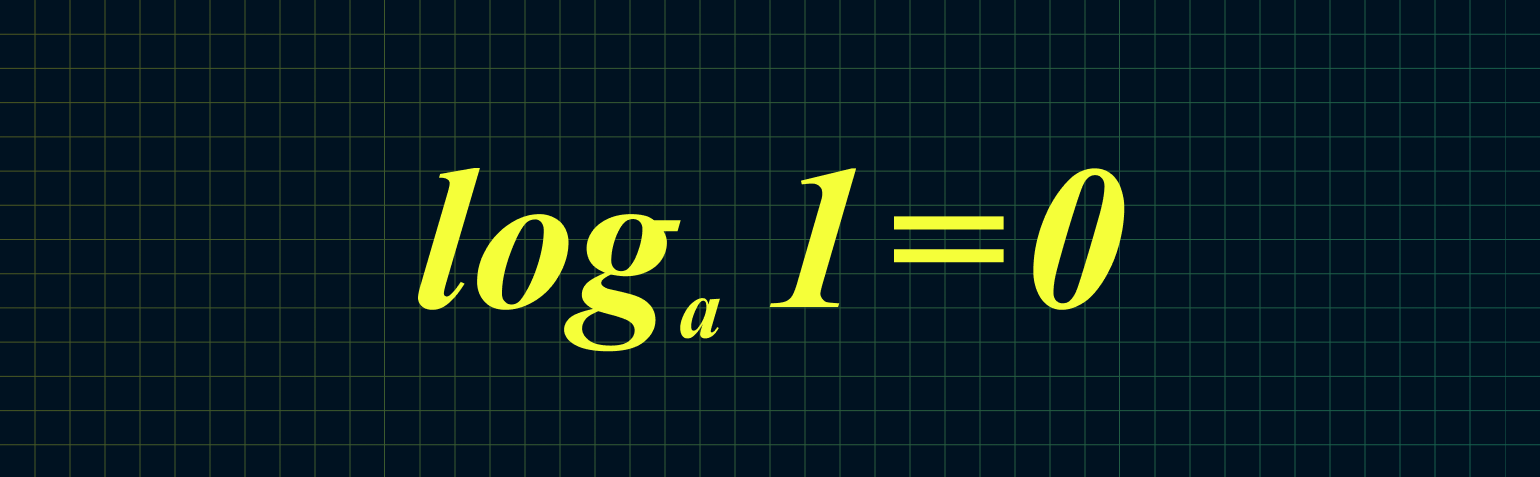
Например: log17 1 = 0
2. Логарифм, где число и основание совпадают, равен единице:
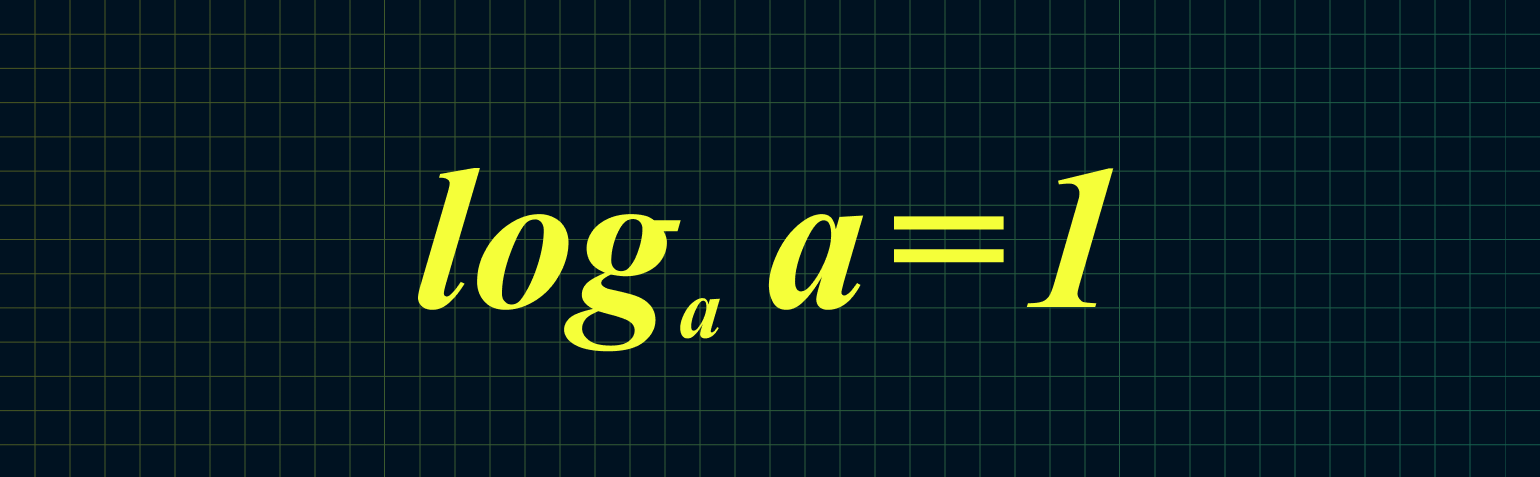
Например: log17 17 = 1
3. Основное логарифмическое тождество:
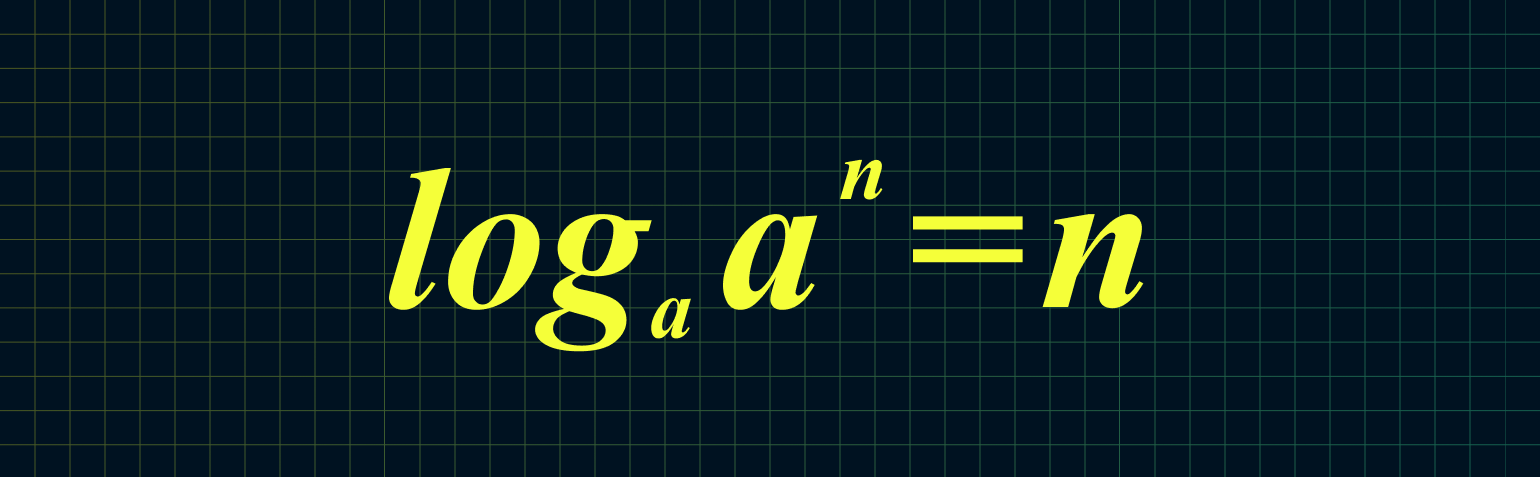
Например: log17 175 = 5
4. Логарифм произведения чисел равен сумме их логарифмов:
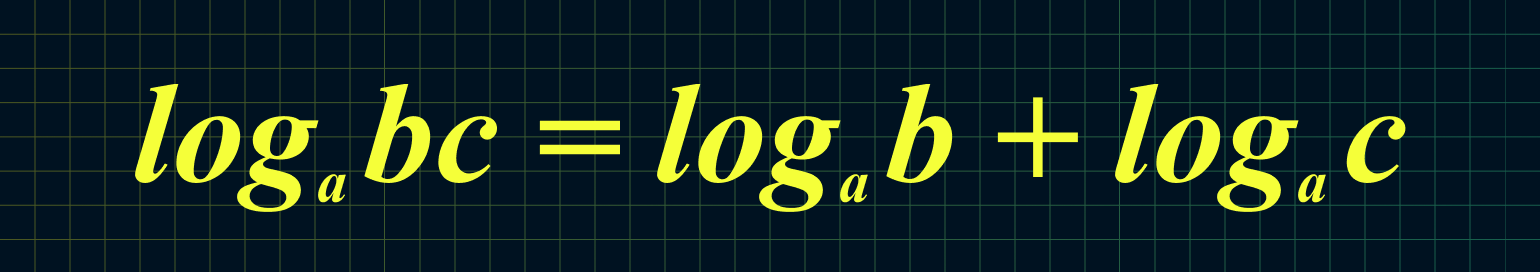
Например: log5 12,5 + log5 10 = log5 (12,5 × 10) = log5 125 = 3
5. Логарифм дроби равен разности логарифмов числителя и знаменателя:
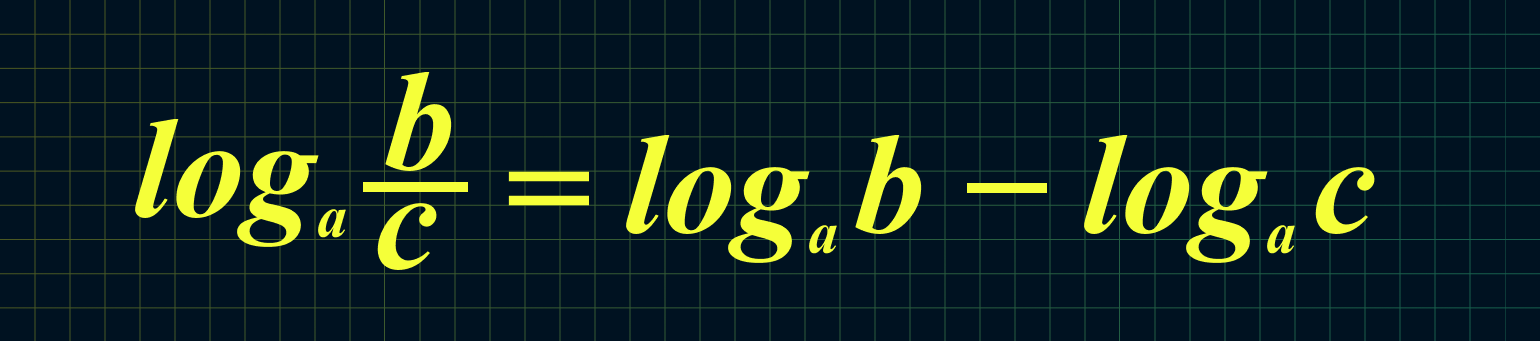
Например: log3 63 − log3 7 = log3 63/7 = log3 9 = 2
6. Если основание или аргумент возведены в степень, то их можно удобно выносить перед логарифмом:
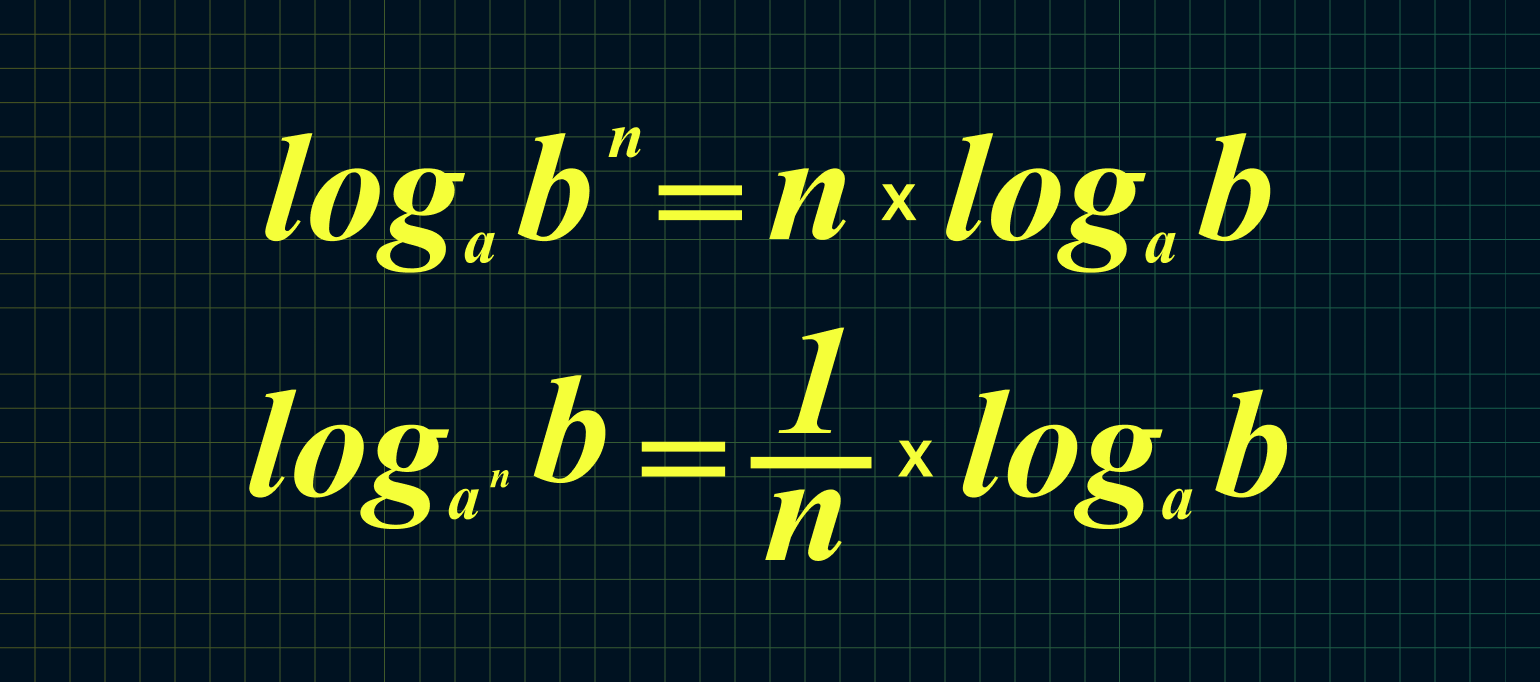
Из этих двух формул следует:
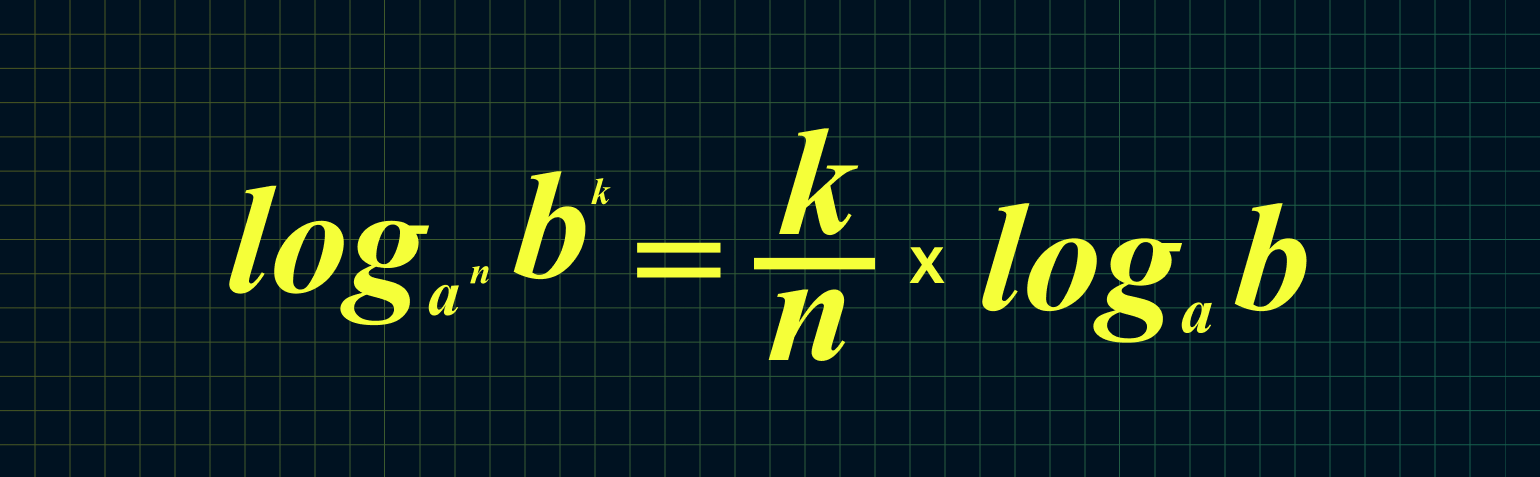
Например: log23 49 = 9/3 × log2 4 = 3 × 2 = 6
7. Если нам неудобно основание логарифма, то его можно изменить:
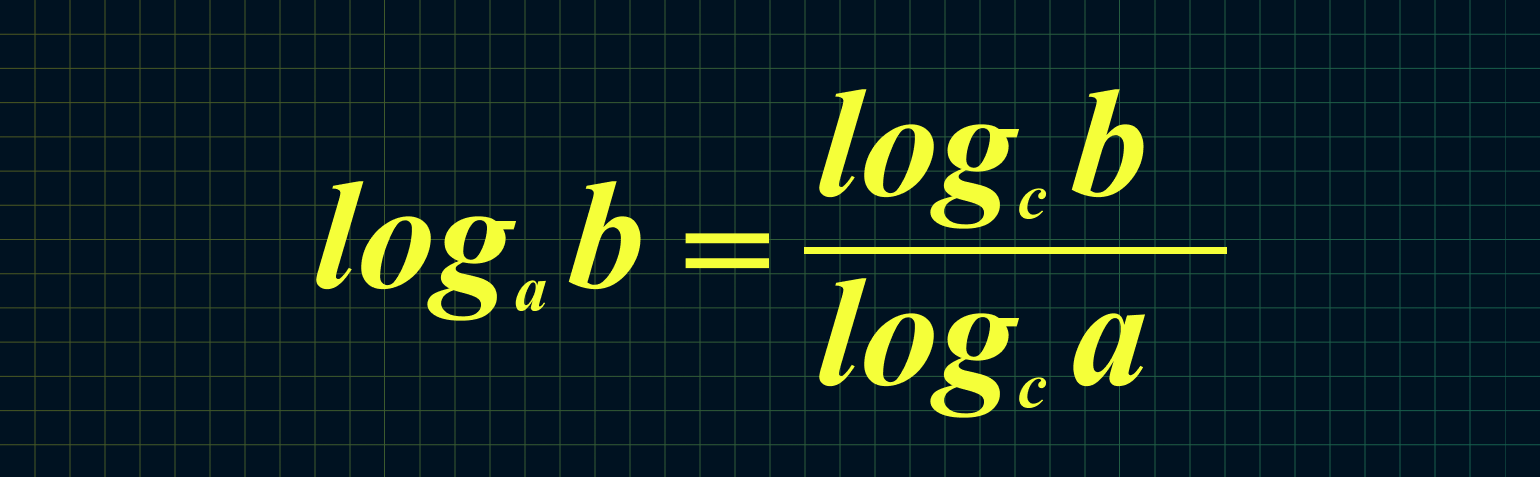
Например: log25 125 = log5 125/log5 25 = 3/2 = 1,5
Из этой формулы следует, что мы можем поменять местами основание и аргумент вот так:
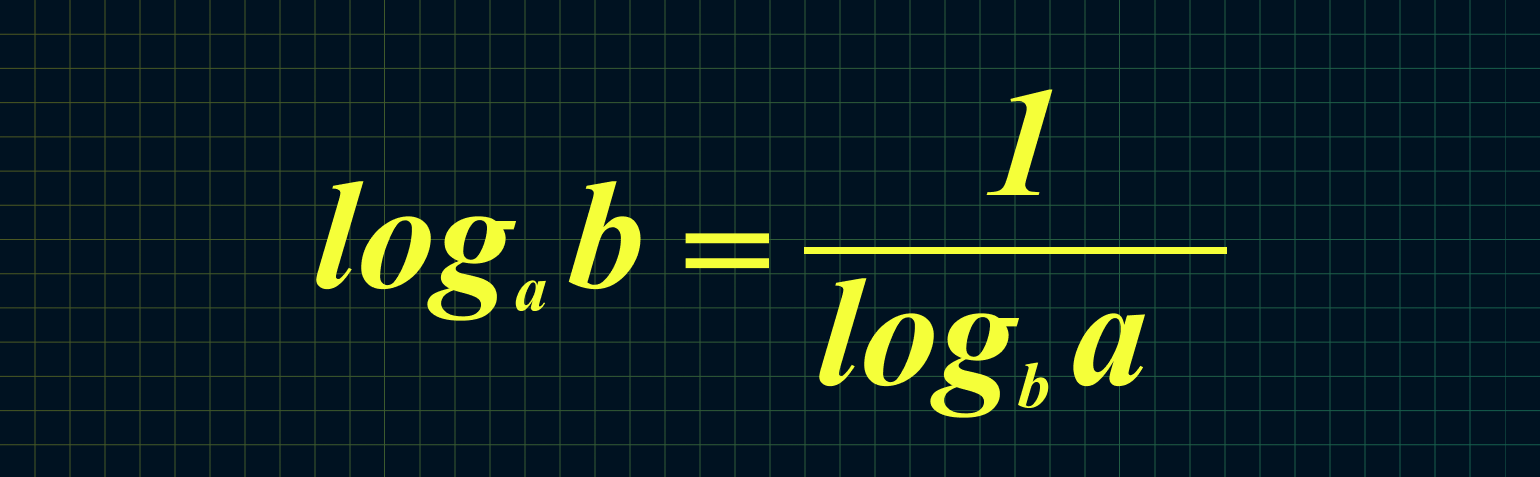
Например: log16 4 = 1/log4 16 = 1/2 = 0,5
А теперь возвращаемся к задачам, которые мы дали в начале статьи.
Пример 1
log3 81
Вспомните, что 81 — это 92. А 9 — это 32. Таким образом:
log3 81 = log3 92 = log3 32+2 = log3 34
Теперь логарифм не представляет для нас никаких сложностей. Воспользуемся свойством степени и вынесём четвёрку.
log3 34 = 4 × log3 3 = 4 × 1 =4
Ответ: 4.
Пример 2
lg 2 × lb 10
Переведём сокращённые записи в полный вид:
lg 2 × lb 10 = log10 2 × log2 10
Приведём оба логарифма к одному основанию.
log10 2 × log2 10 = 1/log2 10 × log2 10 = log2 10/log2 10 = 1
Ответ: 1.
Пример 3
log216 2 + log216 3
Воспользуемся свойством суммы.
log216 2 + log216 3 = log216 2 × 3 = log216 6
Представим 216 в виде степени числа 6 и вынесем с помощью свойства степени.
log216 6 = log63 6 = 1/3 × log6 6 = 1/3 × 1 = 1/3
Ответ: 1/3.
Чтобы работать с логарифмическими выражениями в Python, необходимо импортировать модуль math:
import math
И теперь посчитаем log2 8, используя метод math.log (b, a):
print (math.log (8, 2)) >>> 3.0
Обратите внимание на два момента. Во-первых, мы сначала передаём функции аргумент и только потом — основание. Во-вторых, функция всегда возвращает тип данных float, даже если результат целочисленный.
Если мы не передаём функции основание, то логарифм по умолчанию считается натуральным:
#math.e — метод для вызова числа Эйлера. print (math.log (math.e)) >>> 1.0
Для подсчёта десятичного и двоичного логарифма есть отдельные методы:
#Для десятичного. print (math.log10 (100)) >>> 2.0 #Для двоичного. print (math.log2 (512)) >>> 9.0
Ещё в Python есть специфичный метод, который прибавляет к аргументу единицу и считает натуральный логарифм от получившегося числа:
x = math.e print (math.log1p (x-1)) >>> 1.0
Когда х близок к нулю, этот метод даёт более точные результаты, чем math.log (1+x). Сравните:
x = 0.00001 print (math.log(x+1)) >>> 9.999950000398841e-06 print (math.log1p(x)) >>> 9.99995000033333e-06
Это все основные инструменты для работы с логарифмами в Python.

Научитесь: Профессия Python-разработчик
Узнать больше
Что такое логарифм?
Нагляднее всего понять это с помощью графического решения уравнений. Начертим график
и с его помощью решим уравнения:
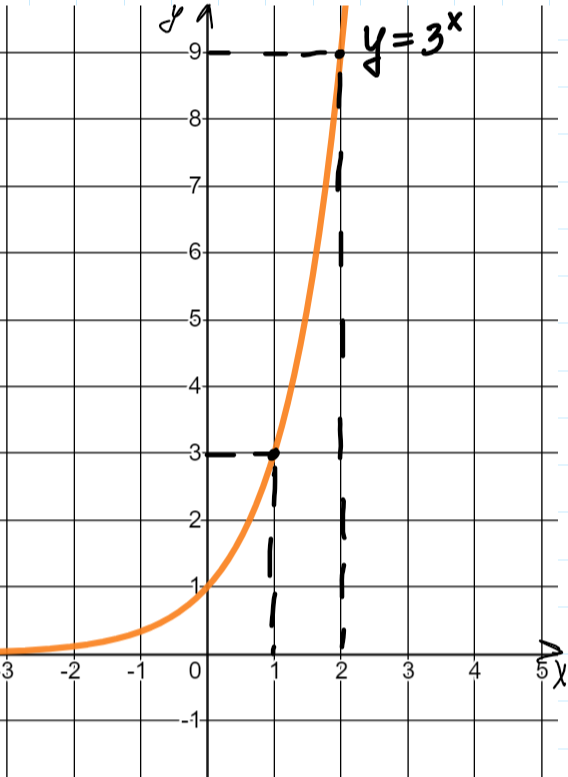
Отлично! А теперь решим уравнение
.
И в этом случае невозможно назвать точное значение, то есть мы понимаем, что корень больше одного и меньше двух, но более точных данных нет.
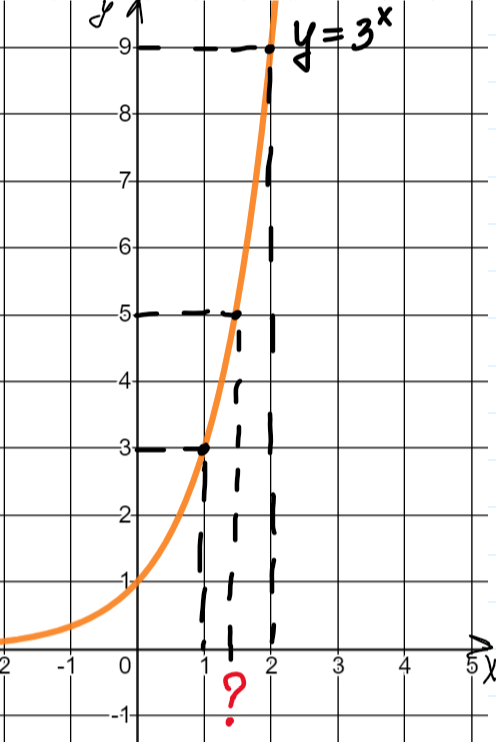
Вот такой корень и задается с помощью логарифма, а именно
(читается как «логарифм пяти по основанию три» или «логарифм по основанию три от пяти»).
Мы определили смысл — теперь перейдем к общему определению логарифма.
Логарифмом числа b по основанию a называют показатель степени с основанием a, равной b. То есть, попросту говоря, логарифм — это степень, в которую нужно возвести a для получения b. Однако у логарифма есть условия или ограничения, что основание а больше нуля и не равно единице, а также показатель b больше нуля.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Как решать примеры с логарифмами?
Рассмотрим пример, как решить логарифм:
Задаем вопрос: в какую степень нужно возвести 7, чтобы получить 49?
Ответ: во вторую степень. Значит,
.
Какие бывают виды логарифмов?
Логарифм по основанию 10 называется десятичным логарифмом и обозначается как
. Пример десятичного логарифма:
.
Логарифм по основанию e называется натуральным логарифмом и обозначается как
. Пример натурального логарифма:
.
Свойства и формулы логарифмов
-
Эта формула называется основным логарифмическим тождеством.
Пример:
.
-
Пример:
.
-
Пример:
.
-
Логарифм степени находится по формуле:
.
Видно, что показатель степени выносим перед логарифмом.
Пример:
.
-
Показатель степени основания также выносим перед логарифмом, но в виде обратного числа, то есть, например, вместо 5 будет
.
Пример:
.
-
Если нужно перейти к другому основанию, то можно сделать это по формуле:
. Свойство называется формулой перехода к новому основанию.
-
А частным случаем предыдущей формулы является формула, которая позволяет менять местами основание и аргумент логарифма:
.
Конечно, это не все свойства логарифмов, а только самые главные. Комбинируя свойства выше, можно получать все новые и новые формулы для логарифмов. Например, соединив 4-ю и 5-ю формулы, получим
. Но запоминать ее нет смысла, важно знать лишь базовые свойства логарифмов.
Применение логарифмических свойств в примерах
Пример 1
Найдите значение выражения
, если
.
Если видите частное в показателе логарифма, то распишите по 3-й формуле:
.
Решение
У каждого логарифма в показателе стоит степень, значит, поможет 4-я формула:
.
Первый логарифм можно вычислить по определению. И обратите внимание на второй логарифм: у него в основании стоит а, а в условии задачи дан логарифм с основанием b, значит, нужно а как-то заменить на b. Возможно ли это? Конечно, 7-я формула в помощь!
.
Подставьте числовое значение из условия, и все готово:
.
Отличный пример! Мы использовали практически все свойства логарифмов. А теперь попрактикуйтесь еще, но помните, что задача с подвохом!
Пример 2
Вычислите:
.
Получился ответ 27? Если да, то поздравляю: вы попались на удочку самых популярных ошибок! Какое бы задание вам ни встретилось, действия с логарифмами нужно производить только по определениям и правилам. В примере вы видите деление двух логарифмов. А есть ли какая-то формула, в которой записано деление двух логарифмов?
Конечно, это формула перехода к новому основанию, которую мы привели в пункте 6 выше. Применим ее к этому случаю и вычислим логарифм по определению, задав вопрос: в какую степень нужно возвести основание, чтобы получился показатель?
.
И получается ответ 4, а не 27.
Практическое применение логарифмов
Помните, выше мы говорили, что логарифм объединяет задания на ЕГЭ, галактики и рога горных козлов? И если с баллами на ЕГЭ все понятно, то про галактики и рога — интереснее.
Все дело в том, что существует логарифмическая спираль, которая задается по формуле:
. По этой логарифмической спирали растут рога горных козлов, закручены многие галактики (и даже та, в которой мы живем), а также раковины некоторых морских животных, усики растений, ураганы, смерчи и многое другое.

Как видите, логарифмы имеют большое значение для нашей жизни — не только баллы на ЕГЭ!
Вопросы для самопроверки
Чтобы информация точно усвоилась, вспомните:
-
Что такое логарифм?
-
Какие ограничения есть у логарифма?
-
Какие логарифмические свойства вы знаете?
-
Какие бывают способы преобразования выражений с логарифмом?
-
В чем практическое применение логарифмов?
На курсах по математике в онлайн-школе Skysmart мы всегда показываем, зачем нужны математические правила и формулы в реальной жизни — ведь так учиться гораздо интереснее! И подтянуть знания перед ЕГЭ тоже поможем: приходите на бесплатный вводный урок и все увидите сами.
