Восьмеричная система счисления

4.6
Средняя оценка: 4.6
Всего получено оценок: 121.
4.6
Средняя оценка: 4.6
Всего получено оценок: 121.
Числа можно представлять не только в десятичном формате, но и в системе счисления с основанием 8, которая использует для обозначения символы 0, 1, 2, 3, 4, 5, 6, 7. О том, как переводить в восьмеричную систему счисления числа из десятичной и двоичной системы и обратно, рассказано в данной статье.
Восьмеричная система счисления
Восьмеричная система счисления имеет вспомогательный характер, ее удобно использовать для сокращенной записи бинарных комбинаций чисел. Она более удобна в работе чем двоичная, так как использует меньшее количество разрядов. Восьмеричная система применялась в свое время для программирования на машинном языке, а также в устройствах подготовки данных, вышедших из употребления с появлением персональных компьютеров.
Алфавит восьмеричной системы составляют восемь цифр от 0 до 7, соответственно основание равно 8. Числовой ряд восьмеричных чисел: 1, 2, 3, 4, 5, 6, 7,10, 11, 12, 13, 14, 15, 16, 17, 20.
Следует обратить внимание, что после 7 в числовом ряду идет 10, а после 17 число 20.
Число 8 имеет символический смысл, является первым кубом двойки и отождествляется с трехмерным измерением. Для многих древних народов восьмёрка сакральное число. Внешне выглядит как символ бесконечности. В информатике один байт равен 8 битам.
Перевод 8 – 2
Перенос восьмеричного числа в двоичный формат – это самый простой способ перевода чисел. Каждой восьмеричной цифре ставится в соответствие группа двоичных цифр в количестве трех. Эта группа называется триадой.
И, наоборот, при переводе двоичного числа в восьмеричный формат производится замена трех двоичных цифр одной восьмеричной. Разбивка целого двоичного числа на трехзначные звенья производится справа налево. Когда крайняя триада получается неполной, то ее дополняют нулями.
Для более быстрого перевода чисел используется таблица записи восьмеричных чисел двоичным форматом.
Например, 348 = 0111002. Ноль впереди числа отбрасываем и получаем в итоге 111002.
И обратный перевод, например: 11011012 = (001)(101)(101) = 1558. В старшей триаде не хватило разрядов, она дополнилась слева двумя нулями.
Перевод 8 – 10
Преобразование чисел из восьмеричного формата в десятичную форму выполняется с использованием правила перевода: целая часть числа последовательно делится на основание новой системы счисления, то есть 8, и остатки от деления записываются начиная с последнего частного в обратном направлении. Например:
246 / 8 = 30 и в остатке 6
30 / 8 = 3 и в остатке 6
3 меньше 8, деление завершено.
Таким образом, 24610 = 3668.
Обратный перевод выполняется путем разложения числа в развернутую форму:
3668 = 3*82 + 6*81 + 6*80 = 3*64 + 6*8 + 6*1 = 192 + 48 + 6 = 24610
Арифметические действия
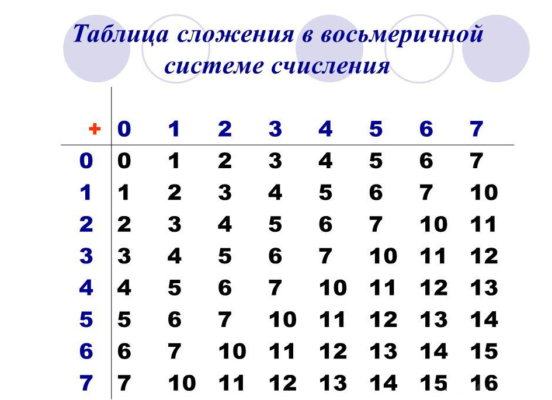
Арифметические действия в системе счисления с основанием 8 выполняются также как и в десятичной. Удобнее всего складывать и вычитать большие числа столбиком. Только следует помнить, что после 7 идет 10, то есть сумма восьмеричных чисел 3 + 5 = 10, а не восемь. Удобнее всего при вычислениях пользоваться таблицей сложения восьмеричных чисел.
Например, сумма 34 + 25 = 61. Это получилось следующим образом. Сначала складываются младшие разряды 4 + 5 = 11 (смотрят по таблице). Единица остается в младшем разряде, а вторая единица переносится в старший разряд и добавляется к сумме чисел 3 + 2 = 5. Итого получилось 61.
Что мы узнали?
Восьмеричная система счисления удобна для представления бинарных кодов и записи машинных команд в программировании. Основание этой системы равно 8. Для перевода чисел из двоичной системы счисления в восьмеричную и обратно используются триады. Перевод восьмеричных чисел в десятичную систему выполняется путем поочередного деления частного числа и записи остатков от деления. Обратный перевод выполняется через раскрытие числа в развернутую форму.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Елена Кетросан
10/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 121.
А какая ваша оценка?
Восьмеричная система счисления
Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Является одной из самых популярных в информатике, наряду с двоичной, десятичной и шестнадцатеричной.
Немного истории
Возникновение восьмеричной системы счисления связывают с техникой счета на пальцах. Однако, если классический счет на пальцах, подразумевает задействование всех десяти, то эта техника использует не пальцы, а промежутки между ними, которых — 8.
Основание и алфавит
Восьмеричная система является традиционной системой счисления с основанием 8. Алфавит состоит их цифр от 0 до 7.
Развернутая форма записи числа будет выглядеть следующим образом:
an-1an-2…a1a0 = an-1 ∙ 8n-1 + an-2 ∙ 8n-2 + ∙∙∙ + a0 ∙ 80
Например:
3678=3 ∙ 82 + 6 ∙ 81 + 7 ∙ 80 = 3 ∙ 64 + 6 ∙ 8 + 7 ∙ 1 = 192 + 48 + 7 = 24710
Применение восьмеричной системы счисления
Многие знают, что компьютеры используют двоичную систему счисления. Однако простому человеку использовать её не удобно, из-за больших вычислений и переводов. В этом случае, гораздо удобнее воспользоваться более емкими системами, такими как восьмеричная или шестнадцатеричная. Восьмеричная очень схожа с десятичной, за исключение двух цифр в алфавите (8,9). Благодаря этому – легка в восприятии. С её помощью можно легко переводить числа с одной системы счисления в другую и совершать арифметические действия.
Практическое применение восьмеричная система находила в программировании, однако с развитием компьютерных технологий, практически полностью уступила — шестнадцатеричной. На сегодняшний день, частичное использование можно встретить в Linux-системах.
Таблица десятичных чисел в восьмеричной системе
| Десятичное число | Восьмеричное число |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
| 16 | 20 |
| 17 | 21 |
| 18 | 22 |
| 19 | 23 |
| 20 | 24 |
Таблица восьмеричных чисел в двоичной системе
| Восьмеричное число | Двоичное число |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Оцените материал:
Загрузка…
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы,
для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и
):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Системы счисления. Перевод из одной системы в другую.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание:
Что такое восьмеричная система счисления
Как перевести целое десятичное число в восьмеричную систему счисления
Как перевести десятичную дробь в восьмеричную систему счисления
Как перевести число из восьмеричной системы счисления в десятичную
Как перевести дробное восьмеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
Что такое восьмеричная система счисления
Восьмеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа.
Для записи числа в восьмеричной системе счисления используется восемь цифр 0, 1, 2, 3, 4, 5, 6 и 7.
Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления.
Например, 72318 или 45568
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь
калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в восьмеричную систему счисления
Для того, чтобы перевести целое десятичное число в восьмеричную систему счисления нужно десятичное число делить на 8 до тех пор, пока неполное частное не будет равно нулю.
В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 36910 в восьмеричную систему счисления:
369 : 8 = 46 остаток: 1
46 : 8 = 5 остаток: 6
5 : 8 = 0 остаток: 5
36910 = 5618
Как перевести десятичную дробь в восьмеричную систему счисления
Для того чтобы перевести десятичную дробь в восьмеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в восьмеричную систему счисления,
а затем дробную часть, последовательно умножать на 8, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число)
или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Например, переведем десятичное число 0.210 в восьмеричную систему счисления:
Переведем целую часть
010 = 08
Переведем дробную часть
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.210 = 0.14631463148
Восьмеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной восьмеричной.
В данном примере получается бесконечная периодическая восьмеричная дробь, поэтому умножение на 8 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления.
К примеру, дробь 1.510 может быть представлена в восьмеричной системе счисления в виде конечной 2.510 = 1.48.
Как перевести число из восьмеричной системы счисления в десятичную
Для того, чтобы перевести число из восьмеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля.
Каждая позиция цифры будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на 8 в
степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем число 753108 в десятичную систему счисления:
| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | 7 | 5 | 3 | 1 | 0 |
753108 = 7 ⋅ 84 + 5 ⋅ 83 + 3 ⋅ 82 + 1 ⋅ 81 + 0 ⋅ 80 = 3143210
Как перевести дробное восьмеричное число в десятичное
Для того, чтобы перевести дробное восьмеричное число в десятичное, необходимо записать дробное восьмеричное число, убрав точку и затем сверху расставить индексы.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на
8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем дробное восьмеричное число 12.368 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 1 | 2 | 3 | 6 |
12.368 = 1 ⋅ 81 + 2 ⋅ 80 + 3 ⋅ 8-1 + 6 ⋅ 8-2 = 10.4687510
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 010 | 08 |
| 110 | 18 |
| 210 | 28 |
| 310 | 38 |
| 410 | 48 |
| 510 | 58 |
| 610 | 68 |
| 710 | 78 |
| 810 | 108 |
| 910 | 118 |
| 1010 | 128 |
| 1110 | 138 |
| 1210 | 148 |
| 1310 | 158 |
| 1410 | 168 |
| 1510 | 178 |
| 1610 | 208 |
| 1710 | 218 |
| 1810 | 228 |
| 1910 | 238 |
| 2010 | 248 |
| 2110 | 258 |
| 2210 | 268 |
| 2310 | 278 |
| 2410 | 308 |
| 2510 | 318 |
| 2610 | 328 |
| 2710 | 338 |
| 2810 | 348 |
| 2910 | 358 |
| 3010 | 368 |
| 3110 | 378 |
| 3210 | 408 |
| 3310 | 418 |
| 3410 | 428 |
| 3510 | 438 |
| 3610 | 448 |
| 3710 | 458 |
| 3810 | 468 |
| 3910 | 478 |
| 4010 | 508 |
| 4110 | 518 |
| 4210 | 528 |
| 4310 | 538 |
| 4410 | 548 |
| 4510 | 558 |
| 4610 | 568 |
| 4710 | 578 |
| 4810 | 608 |
| 4910 | 618 |
| 5010 | 628 |
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 5110 | 638 |
| 5210 | 648 |
| 5310 | 658 |
| 5410 | 668 |
| 5510 | 678 |
| 5610 | 708 |
| 5710 | 718 |
| 5810 | 728 |
| 5910 | 738 |
| 6010 | 748 |
| 6110 | 758 |
| 6210 | 768 |
| 6310 | 778 |
| 6410 | 1008 |
| 6510 | 1018 |
| 6610 | 1028 |
| 6710 | 1038 |
| 6810 | 1048 |
| 6910 | 1058 |
| 7010 | 1068 |
| 7110 | 1078 |
| 7210 | 1108 |
| 7310 | 1118 |
| 7410 | 1128 |
| 7510 | 1138 |
| 7610 | 1148 |
| 7710 | 1158 |
| 7810 | 1168 |
| 7910 | 1178 |
| 8010 | 1208 |
| 8110 | 1218 |
| 8210 | 1228 |
| 8310 | 1238 |
| 8410 | 1248 |
| 8510 | 1258 |
| 8610 | 1268 |
| 8710 | 1278 |
| 8810 | 1308 |
| 8910 | 1318 |
| 9010 | 1328 |
| 9110 | 1338 |
| 9210 | 1348 |
| 9310 | 1358 |
| 9410 | 1368 |
| 9510 | 1378 |
| 9610 | 1408 |
| 9710 | 1418 |
| 9810 | 1428 |
| 9910 | 1438 |
| 10010 | 1448 |
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская |
Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская |
Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая |
Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская |
Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) |
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.
Восьмеричная система применяется при выставлении прав доступа к файлам и прав исполнения для участников в Linux-системах[1][2].
Таблица перевода восьмеричных чисел в двоичные[править | править код]
08 = 0002 18 = 0012 28 = 0102 38 = 0112 48 = 1002 58 = 1012 68 = 1102 78 = 1112
Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например:
25418 = [ 28 | 58 | 48 | 18 ] = [ 0102 | 1012 | 1002 | 0012 ] = 0101011000012.
Использование в естественных языках[править | править код]
Языки юки[3] и паме[4] используют восьмеричную систему счисления.
В языках программирования[править | править код]
Ряд языков программирования, в частности, Си/C++, Ada, Perl, Java и Python (до 3.0), имеют специальный синтаксис (аналогичный использованию префикса “0x” для шестнадцатеричных констант) для записи восьмеричных констант с применением ведущего нуля, например, 0644 представляет собой запись литеральной константы с десятичным значением 42010.
По статистике, применение восьмеричных констант в программах на языке Си чрезвычайно низко (около 0,1 % от всех литеральных констант, без учета константы «0», технически также восьмеричной). Определенную популярность такие константы сохраняют в случае описания прав на файлы в Unix/POSIX стиле (0666, 0750), и при отдельных случаях работы с битовыми масками, когда программисту проще представлять битовое представление восьмеричных чисел, а не шестнадцатиричных или, тем более, десятичных[5].
Подобные правила указания системы счисления могут быть неочевидны для программистов и приводят к ошибкам. В некоторых языках существуют рекомендации не использовать такую запись[6], в других языках такая запись восьмеричных констант запрещена (например, в Python с версии 3 используется префикс 0o[7][8]) или не используется (например Rust и D[7]).
Некоторые версии языка Бейсик используют для записи восьмеричных констант префикс &O, например, &O644. Здесь O — это не ноль, а буква латинского алфавита, обозначающая английское слово Octal (восьмеричный).
Объединение двоичных разрядов в триплеты битов применялось системах команд и, как следствие, в языках ассемблера советских ЭВМ «Минск-22», БК-0010 и БК-0011, ДВК и других.
Источники[править | править код]
- ↑ Права доступа к файлам в ОС GNU/Linux (числовой способ записи). Дата обращения: 2 января 2015. Архивировано из оригинала 2 января 2015 года.
- ↑ Права доступа. Дата обращения: 2 января 2015. Архивировано 2 января 2015 года.
- ↑ Marcia Ascher. Ethnomathematics: A Multicultural View of Mathematical Ideas. The College Mathematics Journal. Дата обращения: 13 апреля 2007.
- ↑ Avelino, Heriberto. The typology of Pame number systems and the limits of Mesoamerica as a linguistic area (англ.) // Linguistic Typology : journal. — 2006. — Vol. 10, no. 1. — P. 41—60. — doi:10.1515/LINGTY.2006.002. Архивировано 4 июня 2011 года.
- ↑ 829 An octal constant consists of the prefix 0 Архивная копия от 11 июля 2018 на Wayback Machine / «The New C Standard: An Economic and Cultural Commentary» (version 1.2, 2009) (англ.)
- ↑ INT00-PL. Do not prepend leading zeroes to integer literals – SEI CERT Perl Coding Standard – Confluence. Дата обращения: 2 октября 2018. Архивировано 3 октября 2018 года.
- ↑ 1 2 Florian Weber. Octal Zero considered harmful (англ.) (8 апреля 2018). Дата обращения: 2 октября 2018. Архивировано 16 декабря 2018 года.
- ↑ Numbers — Conservative Python 3 Porting Guide 1.0 documentation. Дата обращения: 2 октября 2018. Архивировано 3 октября 2018 года.
Ссылки[править | править код]
- Octomatics: Статья о преимуществах восьмеричной системы, предложение специальных знаков и др. Архивная копия от 4 марта 2007 на Wayback Machine (англ.)