Посчитать ветви в цепи
Вовчик
Профи
(572),
закрыт
8 лет назад
Сколько ветвей в цепи и как их посчитать?
Valentin Ruchkin
Гуру
(3324)
11 лет назад
Здесь надо учитывать, что реально узлов всего три, а не шесть, поскольку между E2 и E1 фактически один узел, и внизу три узла также являются фактически одним (это называется «обобщённый узел») . Теперь посчитаем ветви:
1 ветвь: E1, R1;
2 ветвь: E2, R2;
3 ветвь: E3, R3;
4 ветвь: R4;
5 ветвь: R;
6 ветвь: J4.
На чтение 12 мин Просмотров 10 Опубликовано 8 апреля 2023 Обновлено 8 апреля 2023
Содержание
- Что такое электрическая схема, ветвь, узел, контур.
- Электрическая цепь
- Определение
- Графическое изображение электрической цепи и ее элементов
- Законы электрических цепей
- Законы электрических цепей
- Параметры электрических цепей
- Параметры электрических цепей
- Понятие о линейных и нелинейных электрических цепях
- Идеальные элементы электрической цепи
- Идеальные элементы электрической цепи
- Соотношение между током и напряжением в идеальных элементах цепи
- Основная задача анализа электрической цепи
Что такое электрическая схема, ветвь, узел, контур.

Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.

Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.

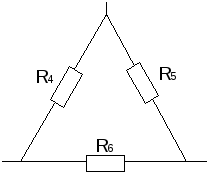
Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
Узел – место соединения трёх и  более ветвей.
более ветвей.
Точки К и Е не являются узлами.
Источник
Электрическая цепь
Определение
Электрической цепью называется совокупность электротехнических устройств, создающих замкнутый путь электрическому току. Она состоит из источников (генераторов) энергии, приемников энергии (нагрузки) и соединительных проводов. В цепи могут быть также различные преобразователи (играют роль как роль источников, так и приемников), защитная и коммутационная аппаратура.
В источниках неэлектрические виды энергии преобразуются (в соответствии с законом сохранения энергии) в энергию электромагнитного поля. Так, например, на гидроэлектростанциях энергия падающей воды (энергия гравитационного поля) преобразуется в энергию электромагнитного поля. В приемниках энергия электромагнитного поля преобразуется в тепловую и другие виды энергии. Кроме того, некоторая часть энергии запасается в электрических и магнитных полях цепи.
Электромагнитные процессы в электрической цепи описываются с помощью понятий о токе, напряжении, электродвижущей силе (ЭДС), сопротивлении, индуктивности и емкости. Буквенные обозначения этих, а также других величин, используемых в этом учебном пособии представлены в табл.1.1. Там же дана их русская транскрипция и единицы измерений. Заметим здесь, что ЭДС, токи и напряжения, изменяющиеся во времени, обозначаются строчными латинскими буквами е, i, u, а ЭДС, токи и напряжения, неизменные во времени, обозначаются заглавными латинскими буквами E, I, U.
Графическое изображение электрической цепи и ее элементов
Графическое изображение электрической цепи называется ее схемой. В схеме различают ветви, узлы и контуры. Ветвь – это часть схемы, состоящая только из последовательно соединенных источников и приемников. Узел – точка схемы, в которой сходятся не менее трех ветвей (ветви начинаются и заканчиваются на узлах цепи). Контур – часть схемы, образованная ветвями; число контуров определяется числом вариантов обходов по ветвям цепи. На рис.1.1 даны структурные схемы трех электрических цепей и указано количество ветвей узлов и контуров в каждой из них.

Принятые в настоящем учебном пособии графические обозначения основных элементов цепи, показаны на рис.1.2.

На этом рисунке : 1 — источник ЭДС; 2 — источник тока; 3 — соединительный провод; 4 — сопротивление R цепи; 5 — индуктивность L цепи; 6 — емкость С цепи; 7 — двухполюсник (цепь с неизвестной структурой, имеющая два входных зажима).

В цепях постоянного тока (рис.1.3,а) направление действия ЭДС источника принято указывать в сторону того зажима, на котором образуются положительные заряды. Направление тока во внешней цепи принято указывать от положительно заряженного полюса (зажима) источника к отрицательно заряженному. Направление действия напряжения в приемнике всегда указывают в ту же сторону, что и направление действия тока.
В цепях синусоидального тока (рис.1.3,б) принято обозначать направления ЭДС тока и напряжения, используя положительный полупериод тока, при котором ток не изменяет своего направления. При этом картина этих направлений получается аналогичной с цепью постоянного тока.


Законы электрических цепей
Законы электрических цепей
Ими являются первый и второй законы Кирхгофа.
Первый закон Кирхгофа относится к узлам цепи: в любой момент времени алгебраическая сумма токов в узле равна нулю

где К – число ветвей, подходящих к узлу (три и более).
Токи, подходящие к узлу, и токи, отходящие от узла, имеют противоположные знаки. Будем считать подходящие к узлу токи положительными и брать их в уравнениях первого закона Кирхгофа со знаком (+), а отходящие от узла, – отрицательными и брать их со знаком (−) . Первый закон Кирхгофа фактически является следствием известного из курса физики принципа непрерывности электрического тока, согласно которому линии тока всегда замкнуты и не имеют ни начала, ни конца.
Пример 1.1. На рис.1.4,а показан узел цепи с пятью подходящими к нему ветвями. Требуется составить для этого узла уравнение по первому закону Кирхгофа.
Решение. На основании формулы (1.1) имеем

Таким образом, всегда сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла.

Второй закон Кирхгофа относится к контурам цепи: в любой момент времени алгебраическая сумма ЭДС всех источников энергии контура равна алгебраической сумме напряжений на всех приемниках этого контура.

где Q – число источников ЭДС в контуре; N – число приемников контура.
Для составления уравнения по второму закону Кирхгофа необходимо предварительно (произвольно) выбрать направление обхода этого контура. Те ЭДС и напряжения, направления которых совпадают с выбранным 9
направлением обхода, считаются положительными и берутся в уравнении со знаком (+), а остальные − со знаком (−).
Пример 1.2. На рис.1.4,б показан один из контуров сложной электрической цепи. Направления действия ЭДС источников и напряжений на приемниках известны. Требуется составить для этого контура уравнение по второму закону Кирхгофа.
Решение. Для этого предварительно выбираем (произвольно) направление обхода контура и в соответствии с формулой (1.2) составляем следующее уравнение:

Здесь е2 и е3 , u1 и u2 взяты со знаком (−), так как их направление действия не совпадает с направлением обхода контура; е1, u4 и u3 взяты со знаком (+), так как их направление действия совпадает с направлением обхода контура.
Параметры электрических цепей
Параметры электрических цепей
Любая электрическая цепь и каждый ее элемент в отдельности обладают тремя параметрами: сопротивлением R, индуктивностью L и емкостью С.
Сопротивление R характеризует способность цепи преобразовывать электромагнитную энергию в тепловую. Количество тепловой энергии WТ , выделяющееся в сопротивлении R при протекании тока i в течение времени t, определяется соотношением (1.3) и измеряется в джоулях (Дж):

Величина сопротивления любого элемента цепи определяется как отношение постоянного напряжения на этом элементе к постоянному току в нем и измеряется в омах (Ом):
Индуктивность L характеризует способность цепи накапливать энергию магнитного поля. Такой способностью обладает любой проводник с током или система проводов. Количество этой энергии WM , накопленной в цепи, зависит от величины тока i и измеряется в джоулях (Дж):

Эта энергия не преобразуется в тепло, а существует в цепи в виде некоторого запаса. Когда ток в цепи равен нулю, запаса энергии магнитного поля в ней нет.
Величина индуктивности определяется как отношение потокосцепления цепи ψ к току i и измеряется в генри (Гн)

Потокосцеплением называется сумма магнитных потоков всех витков катушки. В простейшем случае для катушки на замкнутом стальном сердечнике можно считать, что ее потокосцепление есть магнитный поток Ф, умноженный на число витков w: Ψ = Ф w.
Емкость С характеризует способность цепи накапливать энергию электрического поля. Такой способностью обладают любые два провода, разделенные диэлектриком, например провод, висящий над землей, любые два провода линии передачи.
Количество энергии электрического поля W Э , накопленной в цепи с емкостью С , зависит от величины напряжения между проводами и измеряется в джоулях (Дж):

Эта энергия не может преобразовываться в тепловую, а существует в цепи в виде некоторого запаса. Если напряжение между проводами отсутствует, то и запаса энергии электрического поля в цепи нет.
Величина емкости С определяется как отношение электрического заряда q одного из проводов к напряжению u между ними и измеряется в фарадах (Ф):

В табл.1.2 представлены конструкции некоторых простейших электротехнических устройств и формулы для расчета их параметров. В этой табл.: γ − удельная электрическая проводимость провода (1/Ом⋅м); μ a − абсолютная магнитная проницаемость стали (Гн/м); ε a абсолютная диэлектрическая проницаемость диэлектрика (Ф/м); l −длина провода, средняя длина стального сердечника, расстояние между пластинами конденсатора (м); S – площадь поперечного сечения провода, площадь поперечного сечения стального сердечника, площадь пластины конденсатора (м 2 ); w – число витков обмотки; Ф – магнитный поток в сердечнике, измеряемый в веберах (Вб).
Понятие о линейных и нелинейных электрических цепях
Если γ, μa и εa (и следовательно R, L и С ) являются постоянными величинами и не зависят от тока (или напряжения), то такие устройства, называются линейными, а цепи, их содержащие, называются линейными цепями. Именно такие цепи рассматриваются в данном учебном пособии.
Существует, однако, целый ряд устройств, у которых γ, μa и εa зависят от величин токов (или напряжений). Таковыми, в частности, являются все полупроводниковые приборы, катушки на насыщенных стальных сердечниках, нагревательные устройства с большим диапазоном изменения температур (электрическая дуга, лампы накаливания), конденсаторы с сегнетодиэлектриками. Цепи, содержащие такие устройства, называются нелинейными.

Свойства нелинейного элемента электрической цепи не могут быть выражены одним постоянным числом и поэтому описываются его характеристикой. Для сопротивлений это зависимости напряжения от тока (вольтамперные характеристики); для индуктивностей это зависимости потокосцепления от тока (веберамперные характеристики); для емкостей это зависимости электрического заряда от напряжения (кулонвольтные характеристики). На рис.1.5 показаны примеры характеристик некоторых линейных (ЛЭ) и нелинейных (НЭ) элементов цепи. Заметим, что характеристики всех линейных элементов цепи являются прямыми линиями, а нелинейных элементов – кривыми.

Идеальные элементы электрической цепи
Идеальные элементы электрической цепи
Любое электротехническое устройство содержит все три параметра: сопротивление R , индуктивность L и емкость С. Рассмотрим (рис.1.6), катушку, выполненную из провода с конечной проводимостью (это может быть и нить лампы накаливания, и обмотка трансформатора или электродвигателя).
При подаче на ее зажимы напряжения u на концах катушки появляются разноименные заряды (+)q и (−)q и в обмотке начинает протекать ток i. При этом вокруг витков обмотки возникает магнитное поле, характеризуемое потокосцеплением ψ. Таким образом, в соответствии с формулами (1.4), (1.6) и (1.8) рассматриваемая катушка обладает всеми тремя вышеуказанными параметрами.

Для удобства анализа и расчета электрических цепей вводят в рассмотрение такие элементы, которые при всех условиях обладают только одним параметром: только сопротивлением, только индуктивностью, только емкостью. Они называются идеальными.
Графическое изображение идеальных элементов электрической цепи показано на рис.1.2 позициями 4, 5 и 6. В природе таких элементов не существует, но есть устройства, по своим свойствам близкие к идеальным. Реостат (резистор) при низких частотах обладает практически только сопротивлением R, а индуктивностью L и емкостью С этого устройства можно пренебречь. Катушка индуктивности на замкнутом ферромагнитном сердечнике с малыми тепловыми потерями в нем обладает на низких частотах практически только индуктивностью L, а сопротивлением R и емкостью С такой катушки можно пренебречь. Конденсатор с малыми внутренними тепловыми потерями обладает практически только емкостью С, а его активной проводимостью G и индуктивностью L можно пренебречь.
Заметим, что реостат, катушку индуктивности и конденсатор широко используют для имитации (моделирования) идеальных элементов при проведении лабораторного практикума по теории цепей.
Любое реальное электротехническое устройство можно изобразить в виде электрической схемы, состоящей из комбинации идеальных элементов и, следовательно, произвести его электрический расчет. В табл.1.3 приведено несколько примеров изображения реальных устройств в виде электрических схем.

Соотношение между током и напряжением в идеальных элементах цепи
Прежде чем приступать к расчету сколько-нибудь сложных электрических цепей, следует выяснить, каким образом связаны между собой ток и напряжение в каждом из идеальных элементов цепи. Эти соотношения, известные из курса физики, приведены в табл.1.4. Они имеют всеобщий характер и справедливы для цепей, у которых ток и напряжение изменяются во времени по любому закону. Это важнейшие формулы теории цепей, которые встретятся нам много раз в этом учебном пособии ∗. Заметим здесь, что формулы позиции 1 соответствуют закону Ома, формулы позиции 2 вытекают из закона электромагнитной индукции, а формулы позиции 3 следуют из определения электрической емкости.

Из табл.1.4 видно, что только в сопротивлении R ток и напряжение связаны между собой алгебраическим соотношением. Между током и напряжением в индуктивности и емкости имеют место интегро-дифференциальные соотношения.
Пример 1.3. В цепи с идеальной индуктивностью (рис.1.7,а) действует пилообразный периодический ток (рис.1.7,б). Требуется определить форму приложенного напряжения.

Решение. Для нахождения графика напряжения используем соотношение u = di/dt (поз.2 табл.1.4), из которого следует, что форма кривой напряжения соответствует производной от тока по времени. Из курса математики известно, что графически производная di/dt определяется в каждой точке кривой тока, как тангенс угла наклона касательной к этой кривой относительно оси t.
В нашем примере на участке от 0 до T/2 кривая тока представляет собой прямую, проходящую через начало координат под острым углом α 1 90°, и поэтому производная di/dt на этом участке есть постоянная и отрицательная величина. tgα 2 = tg(180 — α 1) = -tgα 1
Таким образом, график искомого напряжения представляет собой отрезки прямых, меняющих каждую половину периода свой знак, как это показано на рис.1.7,б.
Основная задача анализа электрической цепи
Анализ электрических цепей осуществляется с помощью законов Кирхгофа. При этом можно преследовать различные цели. Например, определять напряжения во всех ветвях цепи по их известным параметрам. Можно также определять необходимые ЭДС всех источников энергии по известным токам и параметрам приемников и источников. Для придания нашему курсу логической стройности основной задачей анализа (расчета) будем считать определение токов во всех ветвях цепи по известным параметрам всех источников и известным параметрам всех приемников. Научившись решать эту задачу, мы сможем решать и другие задачи, связанные с анализом и расчетом электрических цепей.
Источник
Методы расчета электрических цепей
Постановка
задачи: в известной схеме цепи с заданными
параметрами необходимо рассчитать
токи, напряжения, мощности на отдельных
участках. Для этого можно использовать
следующие методы:
-
преобразования цепи;
-
непосредственного применения законов
Кирхгофа; -
контурных токов;
-
узловых потенциалов;
-
наложения;
-
эквивалентного генератора.
Будем
рассматривать первых два метода.
-
Метод
преобразования цепи. Суть метода: если
несколько последовательно или (и)
параллельно включенных сопротивлений
заменить одним, то распределение токов
в электрической цепи не изменится.
а)
Последовательное соединение резисторов.
Сопротивления включены таким образом,
что начало следующего сопротивления
подключается к концу предыдущего (рис.
6).
Ток
во всех последовательно соединенных
элементах одинаков.
З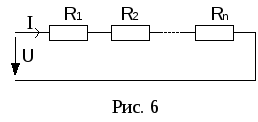
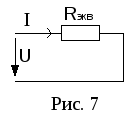 аменим
аменим
все последовательно соединенные
резисторы одним эквивалентным![]() (рис. 7.).
(рис. 7.).
По
IIзакону Кирхгофа:
![]() ;
;
![]() ;
;
т.е.
при последовательном соединении
резисторов эквивалентное сопротивление
участка цепи равно сумме всех
последовательно включенных сопротивлений.
б)
Параллельное соединение резисторов.
При этом соединении соединяются вместе
одноименные зажимы резисторов (рис. 8).
В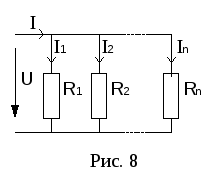 се
се
элементы присоединяются к одной паре
узлов. Поэтому ко всем элементам приложено
одно и тоже напряжениеU.
По Iзакону Кирхгофа:![]() .
.
По
закону Ома
![]() .
.
Тогда![]() .
.
Для
эквивалентной схемы (см рис. 7):
![]() ;
;
![]() .
.
Величина
![]() ,
,
обратная сопротивлению, называется
проводимостьюG.
![]() ;
;![]()
![]() =
=
Сименс (См).
Ч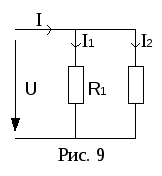 астный
астный
случай: параллельно соединены два
резистора (рис. 9).
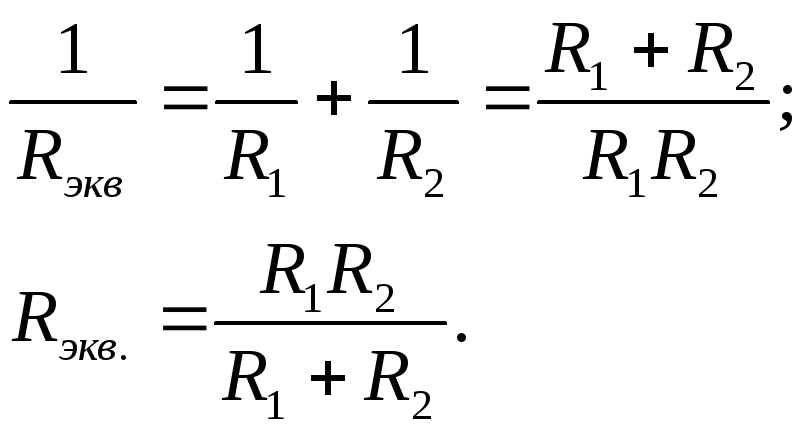
![]()
![]()
в)
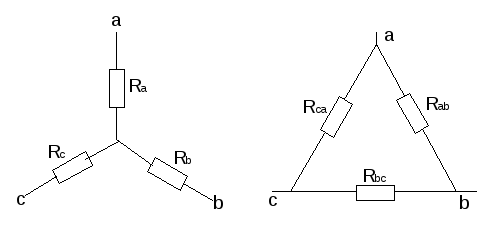
Взаимное преобразование звезды (рис.10а)
и треугольник сопротивлений (рис. 10б).
–
преобразование звезды сопротивлений
в треугольник:
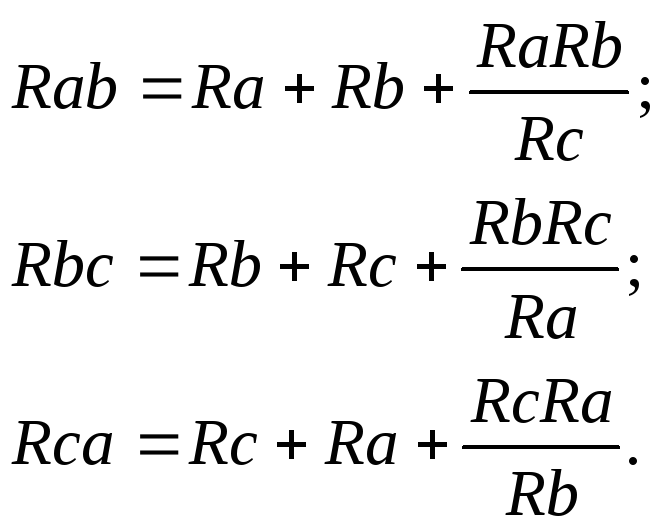
|
а) |
б) |
|
Рис. |
–
преобразование “треугольника”
сопротивлений в “звезду”:
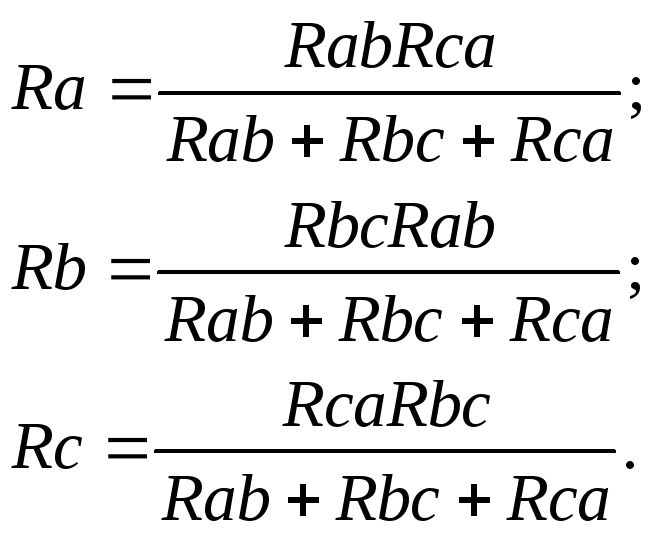
-
Метод
непосредственного применения законов
Кирхгофа. Порядок расчета:
-
Определить
число ветвей (т.е. токов) и узлов в схеме. -
Произвольно
выбрать условно-положительные направления
токов. Общее число уравнений должно
быть равно числу неизвестных токов. -
Определить,
сколько уравнений должно быть составлено
по Iзакону Кирхгофа, а
сколько – поIIзакону
Кирхгофа. -
Составить
уравнения для
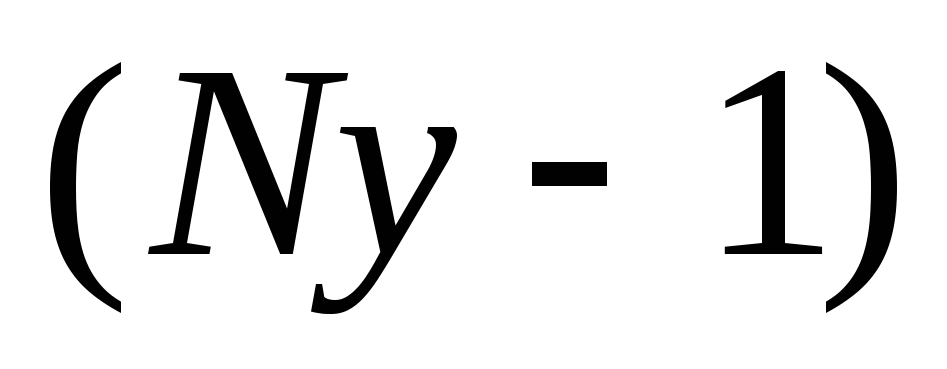 узлов
узлов
поIзакону Кирхгофа и
для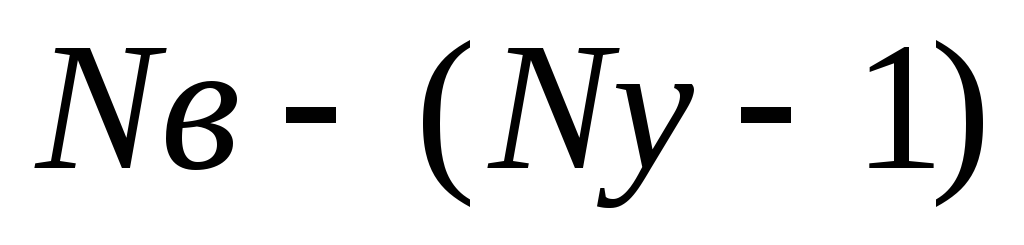 независимых
независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) – поIIзакону Кирхгофа. -
Решить
система уравнений относительно токов.
Если в результате ток получился
отрицательным, то его действительное
направление противоположно выбранному. -
Проверить
правильность решения задачи, составив
уравнение баланса мощности и смоделировав
электрическую цепь средствами
моделирующего пакета ElectronicsWorkbench.
Примечание:
если есть возможность, то перед
составлением системы уравнений по
законам Кирхгофа, следует преобразовать
“треугольник” сопротивлений в
соответствующую “звезду”.
Пример расчет электрических цепей постоянного тока
Расчет будем выполнять с применением
законов Кирхгофа, предварительно
преобразовав треугольник сопротивлений
в звезду.
П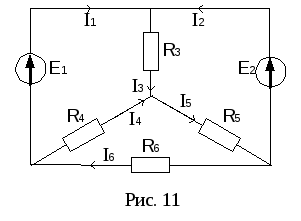 ример.
ример.
Определить токи в цепи рис. 11, еслиE1=160
В,E2=100 В,R3=100 Ом,R4=100 Ом,R5=150 Ом,R6=40
Ом.
Преобразуем
треугольник сопротивлений R4
R5 R6в звезду сопротивленийR45
R56 R64,
предварительно указав условные
положительные направления токов в цепи
(рис. 12).
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом.
Ом.
|
|
|
|
а) |
б) |
|
Рис. 12 |
После
преобразования электрическая цепь
примет вид рис. 13 (в непреобразованной
части электрической цепи направления
токов не изменятся).
В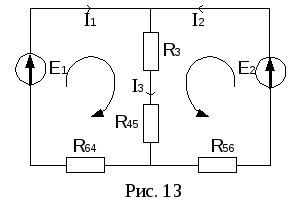 полученной электрической цепи 2 узла,
полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:
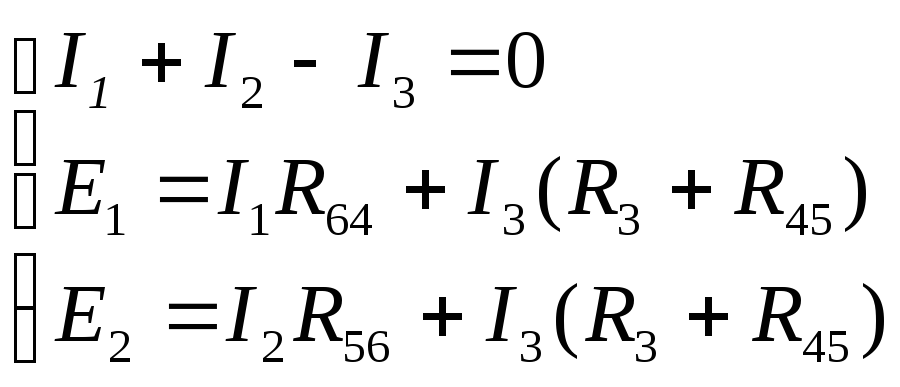
Подставим
в полученную систему уравнений известные
значения ЭДС и сопротивлений:

Решая
систему уравнений любым способом,
определяем токи схемы электрической
цепи рис. 13:
![]() А;
А;![]() А;
А;![]() А.
А.
Переходим
к исходной схеме (см. рис. 11). По IIзакону Кирхгофа:
![]() ;
;
![]() А.
А.
По Iзакону Кирхгофа:
![]() ;
;
![]() А;
А;
![]() ;
;
![]() А.
А.
Т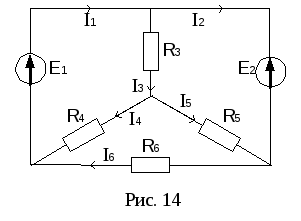 оки
оки![]() и
и![]() получились отрицательными, следовательно,
получились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).
Правильность
решения проверяем, составив уравнение
баланса мощности. Мощность источников
(учтем, что ЭДС источника E2направленно встречно токуI2,
протекающему через него):
![]() Вт.
Вт.
Мощность
потребителей:
![]()
Погрешность
вычислений в пределах допустимого
(меньше 5%).
Смоделируем
электрическую цепь рис. 11 средствами
моделирующего пакета ElectronicsWorkbench(рис. 15):
Р ис.
ис.
15
При
сравнении расчетных результатов и
результатов моделирования, можно
увидеть, что они отличаются (различия
не превышают 5%), т.к. измерительные
приборы имеют внутренние сопротивления,
которые моделирующая система учитывает
Соседние файлы в папке Все что скинул препод
- #
- #
- #
25.03.20169.01 Кб111Задача 1.xlsx
- #
25.03.201610.02 Кб63зАДАЧА 2.xlsx
- #
25.03.20168.97 Кб42Звезда с нулем.xlsx
- #
- #
- #
Уравнения Кирхгофа
Разберем на примере домашнего задания, как пользоваться уравнениями Кирхгофа при расчете электрических цепей.
Задается электрическая схема, в которой известны значения всех сопротивлений и ЭДС источников напряжения. То есть все R и E заданы.
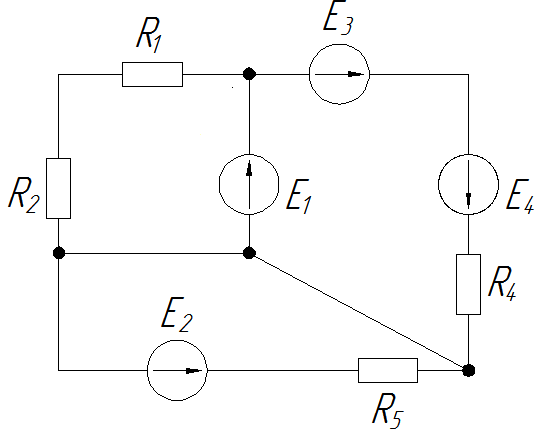
Первым делом, нужно определить, сколько в схеме узлов, независимых контуров и ветвей.
Узел — это просто точка, где сходится три и больше проводов. Иногда составители заданий хитрят и отмечают жирной точкой углы схем, не ведитесь, это провокация. Узлом считается только то место, где проводов не меньше трех. В нашем случае узлов 4. Нумеруем их в произвольном порядке.
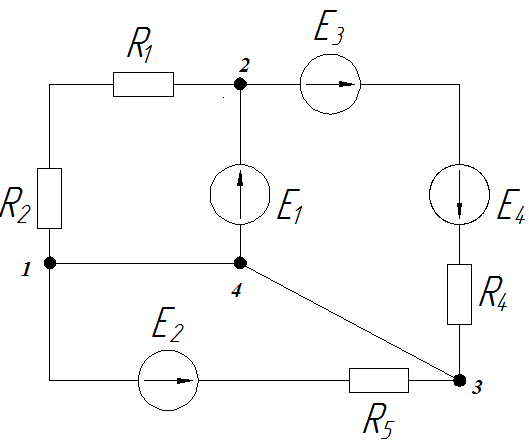
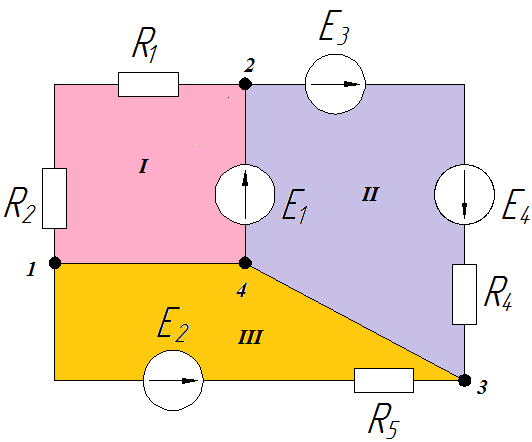
Число независимых контуров мы определяем по количеству геометрических фигур, составляющих схему. Обычно это не составляет труда, хотя встречаются и замороченные схемы, где не сразу становится очевидным количество контуров. То есть мысленно делаем заливку каждого участка схемы, и количество получившихся цветов соответствует количеству независимых контуров. Просим прощения за косноязычность, но стараемся объяснять, что называется, «на пальцах», чтобы было понятно. Вот контуры в нашей схеме.
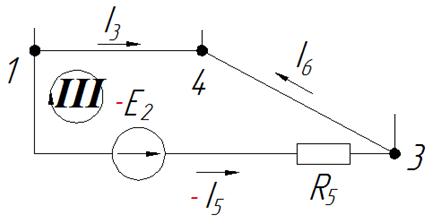
Ветвь — это участок провода между двумя узлами. Участки 1-2, 1-4, 1-3, 2-4, 2-3, 3-4 — это ветви нашей схемы. Всего получается 6 ветвей. В каждой из них течет свой ток, который надо обозначить на схеме. Направление стрелки, указывающей ток, выбираем произвольно (разве что, мы любим в ветвях с источниками напряжения выбирать направления токов туда же, куда указывают стрелки ЭДС). А вообще, направление стрелок ни на что не влияет, в результате расчета часть токов получится со знаком «плюс» (значит, направление соответствует выбранному), а часть токов — со знаком «минус» (значит, направление тока противоположно). Вот наши токи на схеме. Заодно выберем направление обхода в каждом контуре. Направление можно выбирать произвольно, но мы рекомендуем всегда брать направление по часовой стрелке во всех контурах. Меньше будете путаться.
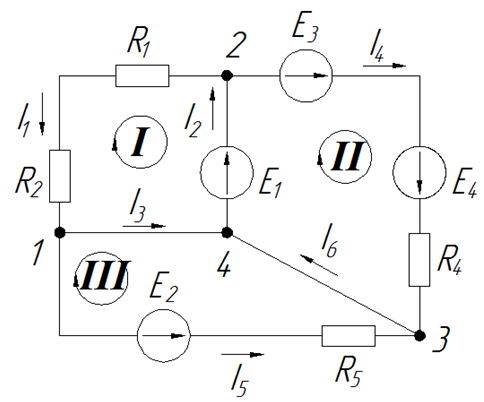
Подведем промежуточный итог. Мы изучили данную схему, посчитали количество узлов (четыре), количество независимых контуров (три), количество ветвей (шесть), пронумеровали узлы, контуры, выбрали направление обхода и расставили стрелки токов в ветвях (шесть токов в соответствии с количеством ветвей).
Перейдем непосредственно к уравнениям Кирхгофа.
Первый закон Кирхгофа гласит: сколько тока пришло в узел, столько и должно выйти. Напоминает закон сохранения чего-угодно и по сути им и является. То есть сумма токов, вошедших в узел, равна сумме токов вышедших из узла. На практике это выглядит так: смотрим на любой узел, записываем, какие токи текут в ветвях, составляющих этот узел (из определения узла понятно, что их должно быть не меньше трех), входящие токи берем с плюсом, исходящие — с минусом. В сумме должен получиться ноль. Число уравнений, записанных по первому закону Кирхгофа, должно быть на единицу меньше, чем количество узлов в схеме. То есть из четырех узлов выбираем любые три. Исключительно из любви к прекрасному возьмем подряд узлы 1, 2, 3.
Смотрим на узел 1. В нем сходятся ветви 1,3,5, ток I1 входит (+), ток I3 выходит (-), ток I5 выходит (-).
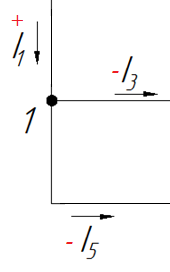
Получаем первое уравнение.
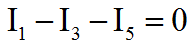
Узел 2. В нем сходятся ветви 1,2,4, ток I1 выходит (-), ток I2 входит (+), ток I4 выходит (-).
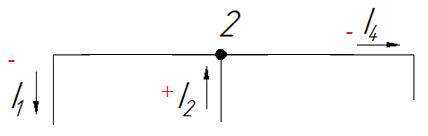
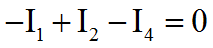
Узел 3. В нем сходятся ветви 4,5,6, ток I4 входит (+), ток I5 входит (+), ток I6 выходит (-).
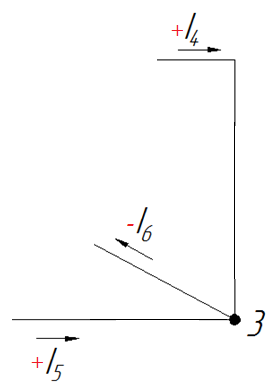
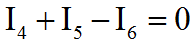
Аналогично можно записать уравнение по первому закону Кирхгофа для узла 4, но это уже будет избыточное уравнение. Нам нужно только три, но, подчеркиваем, что выбрать можно любые три узла.
Второй закон Кирхгофа простыми словами сводится к следующему: сумма напряжений на каждом резисторе внутри контура должна быть равна ЭДС этого контура. На практике это выглядит так: берем по очереди каждый контур, в левой части уравнения пишем напряжения на резисторах. Как мы помним из закона Ома U=IR, то есть напряжение на резисторе равно произведению силы тока в ветви на сопротивление резистора. ЭДС контура — это источники напряжения Е в нашей схеме. В общем, проще показать на примере, чем объяснить.
Уравнений пишем ровно столько, сколько в цепи независимых контуров, то есть три. Начинаем по порядку.
Контур I. Направление обхода мы выбрали по часовой стрелке. Ток I1 мы направили в другую сторону, поэтому падение напряжения на резисторе R1 берется с минусом. В резисторе R2 ток тот же и тоже берется с минусом. Ток I2 течет без сопротивления, игнорируем его, ток I3 — то же самое. ЭДС в контуре одна — E1, и направление также противоположно выбранному направлению обхода, значит, в правую часть уравнения записываем E1 со знаком минус.
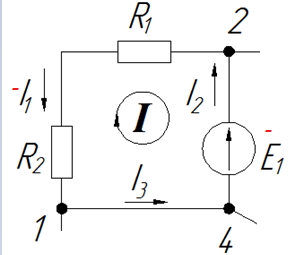
Для контура I уравнение Кирхгофа выглядит так:
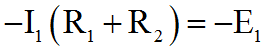
Контур II обходим тоже по часовой стрелке. Ток I4 течет через сопротивление R4 в направлении, совпадающем с направлением обхода. Токи I2 и I6 текут без сопротивлений, так что в уравнение не входят. ЭДС в правой части уравнения: E1 с плюсом, E3 с плюсом, E4 с плюсом.
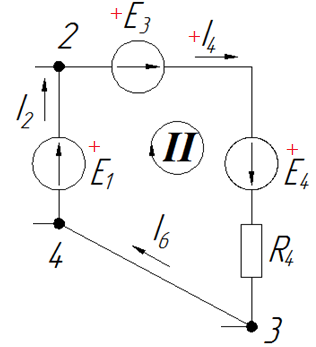
Уравнение получается таким:
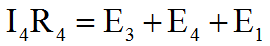
И наконец контур III. Ток I5 через резистор R5 с минусом, токи I3 и I6 не участвуют. ЭДС E2 с минусом.
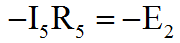 Окончательно получаем систему из шести уравнений (как раз столько, сколько у нас неизвестных токов в наших ветвях).
Окончательно получаем систему из шести уравнений (как раз столько, сколько у нас неизвестных токов в наших ветвях).
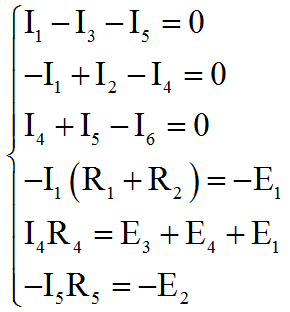
Эта система имеет одно решение, так что, решив ее любым доступным вам методом (мы предпочитаем решать в MathCad, поскольку меньше риск арифметической ошибки и проще вносить исправления, если понадобится), вы определите все неизвестные токи в цепи.
В следующих разделах мы обсудим методы проверки расчета электрической схемы, а также рассмотрим другие способы решения, такие как метод контурных токов, метод межузловых потенциалов, метод эквивалентного генератора.
Сколько ветвей и узлов
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3 . Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4 . Если между любой парой узлов графа существует связь, то граф называют связным.
3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.
Если граф содержит m узлов и n ветвей, то число ветвей любого дерева , а числа ветвей связи графа .
5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.
Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S 1 и S 2 . При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5 .
С понятием дерева связаны понятия главных контуров и сечений:
- главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;
- главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.
Топологические матрицы
Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.
1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.
Для графа на рис. 3 имеем число узлов m =4 и число ветвей n =6. Тогда запишем матрицу А Н , принимая, что элемент матрицы ( i –номер строки; j –номер столбца) равен 1 , если ветвь j соединена с узлом i и ориентирована от него, -1 , если ориентирована к нему, и 0 , если ветвь j не соединена с узлом i . Сориентировав ветви графа на рис. 3, получим
Данная матрица А Н записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы А Н всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1 , остальные нули.
Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы А Н путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим
Число строк матрицы А равно числу независимых уравнений для узлов , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А , перейдем к первому закону Кирхгофа.
Первый закон Кирхгофа
Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение
где — вектор плотности тока; — нормаль к участку dS замкнутой поверхности S .
Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S 2 графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать
Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:
т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.
При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.
Введем столбцовую матрицу токов ветвей
Тогда первый закон Кирхгофа в матричной форме записи имеет вид:
– где O — нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не А Н , т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.
В качестве примера запишем для схемы на рис. 3
Отсюда для первого узла получаем
что и должно иметь место.
2. Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы В соответствуют контурам, а столбцы – ветвям схемы.
Элемент b ij матрицы В равен 1 , если ветвь j входит в контур i и ее ориентация совпадает с направлением обхода контура, -1 , если не совпадает с направлением обхода контура, и 0 , если ветвь j не входит в контур i.
Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4 , запишем коэффициенты для матрицы В .
Перейдем теперь ко второму закону Кирхгофа.
Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.
Просуммируем напряжения на ветвях некоторого контура:
Поскольку при обходе контура потенциал каждой i -ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.
Таким образом, второй закон Кирхгофа математически записывается, как:
— и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
Введем столбцовую матрицу напряжений ветвей
Тогда второй закон Кирхгофа в матричной форме записи имеет вид
В качестве примера для схемы рис. 5 имеем
откуда, например, для первого контура получаем
что и должно иметь место.
Если ввести столбцовую матрицу узловых потенциалов
причем потенциал последнего узла , то матрица напряжений ветвей и узловых потенциалов связаны соотношением
где A Т — транспонированная узловая матрица.
Для определения матрицы В по известной матрице А=А Д А С , где А Д – подматрица, соответствующая ветвям некоторого дерева, А С— подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-А Т С А -1Т Д 1).
3. Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а столбцы – ветвям графа.
Матрица Q , составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Q равно числу независимых сечений.
Элемент q ij матрицы Q равен 1 , если ветвьвходит в i -е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него), -1 , если ориентирована противоположно направлению сечения, и 0 , если ветвь j не входит в i -е сечение.
В качестве примера составим матрицу Q главных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеем
В заключение отметим, что для топологических матриц А, В и Q , составленных для одного и того же графа, выполняются соотношения
которые, в частности, можно использовать для проверки правильности составления этих матриц. Здесь 0 – нулевая матрица порядка .
Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических матриц, по ее структуре можно восстановить остальные.
1. Теоретические основы электротехники. Т.1. Основы теории линейных цепей./Под ред. П.А.Ионкина. Учебник для электротехн. вузов. Изд.2-е , перераб. и доп. –М.: Высш. шк., 1976.-544с.
2. Матханов Х.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. и радиотехн. спец. 3-е изд. переработ. и доп. –М.: Высш. шк., 1990. –400с.
3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- Сформулируйте основные топологические понятия для электрических цепей.
- Что такое узловая матрица?
- Что такое контурная матрица?
- Что такое матрица сечений?
- Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе независимых уравнений:
Восстановив граф цепи, составить матрицы главных контуров и сечений, приняв, что ветвям дерева присвоены первые номера.
Что такое электрическая схема, ветвь, узел, контур.

Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.

Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.

Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.

Узел – место соединения трёх и более ветвей.