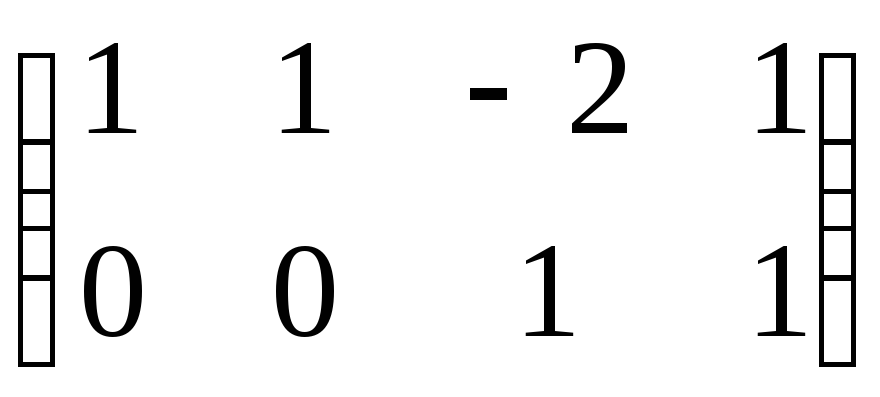Как найти число зависимых переменных

Содержание

Обозначим через $ mathbb A_{} $ любое из множеств $ mathbb Q_{}, mathbb R_{} $ или $ mathbb C_{} $.

Системой линейных (алгебраических) уравнений (СЛАУ или просто СЛУ) над $ mathbb A_{} $ называется совокупность (набор) из нескольких уравнений вида
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=b_1,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=b_2,\
dots & & & & dots \
a_{m1}x_1 &+a_{m2}x_2&+ ldots&+a_{mn}x_n &=b_m
end{array} right.
$$
от одного и того же набора переменных (неизвестных) $ x_{1},dots,x_n $.
Здесь числа $ left{a_{j k} right}_{j=1,dots,m atop k=1,dots,n } $ и $ { b_{j} }_{j=1,dots,m} $ — из $ mathbb A_{} $ ; они называются коэффициентами системы.
Первый индекс у коэффициента $ a_{j k} $ отвечает за номер уравнения, а второй — за номер переменной.

П

Примеры систем уравнений над $ mathbb R $.

$$
left{begin{array}{rrrr}
2,x & + y & + z &=1, \
x &+ 2, y &+ z & = 2.
end{array}
right.
$$
Допустимо, чтобы в системе были одинаковые уравнения; также формально не запрещается записывать взаимно противоречивые уравнения:
$$
left{begin{array}{rrrr}
x_1 & + x_2 & + x_3 &=1, \
x_1 & + x_2 & + x_3 &=1, \
x_1 & + x_2 & + x_3 &=2, \
x_1 & + x_2 & + x_3 &=3.
end{array}
right.
$$
Более того, подобные — очевидно «бессмысленные» — системы имеют право не только на формальное существование — см.

☞

ЗДЕСЬ. В следующей системе
$$
left{begin{array}{rrrrrr}
sqrt[3]{3}x_1 & & & + x_4 & + e^{pi} x_5 &=0, \
x_1 & & & -2, x_4 & &=3/9, \
-57,x_1 & & & & &=2, \
& & & & &0=1 \
end{array}
right.
$$
надо специально договариваться относительно каких переменных она рассматривается. Формально в ней присутствуют только переменные $ x_1, x_4 $ и $ x_5 $. Однако, возможно, что на самом деле в этой системе предполагается, что имеются еще и переменные $ x_2,x_3 $ с нулевыми коэффициентами при этих переменных. Последнее уравнение не содержит переменных вовсе; тем не менее, этот случай также формально допустим.

♦

Относительно числа $ m_{} $ уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных $ n_{} $. Если $ m_{}>n $ то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных
$ x_1=alpha_{1},dots, x_n = alpha_n $, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.

!

Можно доказать (см. результаты

☟

НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:

1.


система совместна и имеет единственное решение;

2.


cистема совместна и имеет бесконечное множество решений;

3.


cистема несовместна.

При этом все решения будут находиться в том же множестве $ mathbb A_{} $, что и коэффициенты системы.

Задача о существовании целочисленных решений системы уравнений с коэффициентами из $ mathbb Z_{} $ рассматривается отдельно, т.к. методы ее решения отличаются от здесь излагаемых.

метода достаточно проста.

П

Пример. Решить систему уравнений

$$
left{
begin{array}{rrrr}
2x_1&-3x_2&-x_3&=3 \
4x_1&-3x_2&-5x_3&=6 \
3x_1&+5x_2&+9x_3&=-8
end{array}
right.
$$

Решение. Выразим из первого уравнения $ x_{1} $
$$ x_1=frac{3}{2} x_2+frac{1}{2} x_3 + frac{3}{2} $$
и подставим в оставшиеся уравнения
$$ 4 left(frac{3}{2} x_2+frac{1}{2} x_3 + frac{3}{2}right) -3,x_2-5,x_3=6 {color{Red} iff } 3x_2-3x_3 = 0
$$
$$
{color{Red} iff } x_2-x_3=0 ;
$$
$$ 3 left(frac{3}{2} x_2+frac{1}{2} x_3 + frac{3}{2}right) +5x_2+9x_3=-8 {color{Red} iff } frac{19}{2} x_2 +frac{21}{2}x_3=-frac{25}{2}
$$
$$
{color{Red} iff } 19x_2 +21x_3=-25 .
$$
Два получившихся уравнения не зависят от неизвестной $ x_{1} $ — она оказалась исключенной из этих
уравнений. Иными словами, мы получили новую подсистему уравнений
$$
left{
begin{array}{rrl}
x_2&-x_3&=0 \
19x_2&+21x_3&=-25,
end{array}
right.
$$
которой должны удовлетворять неизвестные $ x_{2} $ и $ x_{3} $. Продолжаем действовать по аналогии:
выразим из первого уравнения $ x_{2} $ через $ x_{3} $:
$$x_2=x_3 $$
и подставим во второе:
$$ 40 x_3 =-25 {color{Red} iff } x_3=-frac{5}{8} . $$
Итак, значение одной компоненты решения получено. Для нахождения оставшихся подставим значение
$ x_{3} $ в полученные по ходу решения соотношения:
$$
x_2=x_3=-frac{5}{8} {color{Red} Rightarrow } x_1=frac{3}{2} x_2+frac{1}{2} x_3 + frac{3}{2}=frac{1}{4} .
$$

Ответ. $ x_{1}=1/4, x_2=-5/8, x_3=-5/8 $.

Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями —
те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.

Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:

1.

перестановка двух уравнений;

2.


умножение обеих частей уравнения на любое отличное от нуля число;

3.


прибавление к одному уравнению любого другого, умноженного на произвольное число: пара уравнений
$$
begin{array}{lcl}
a_{j1}x_1 +a_{j2}x_2+ ldots+a_{jn}x_n &=&b_j,\
a_{k1}x_1 +a_{k2}x_2+ ldots+a_{kn}x_n &=&b_k
end{array}
$$
заменяется парой
$$
begin{array}{rrrrcr}
(a_{j1}+ {color{RubineRed} lambda } a_{k1}) x_1 &+ (a_{j2}+ {color{RubineRed} lambda } a_{k2}) x_2 &+
ldots &+ (a_{jn}+ {color{RubineRed} lambda } a_{kn}) x_n &=&b_j + {color{RubineRed} lambda } b_k, , \
a_{k1}x_1 &+a_{k2}x_2&+ ldots &+a_{kn}x_n &=&b_k , .
end{array}
$$

Т

Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.

Задача. С помощью элементарных преобразований привести систему
л.у. к наиболее простому виду: такому, из которого легко было
бы установить множество решений.

Предположим, что первое уравнение системы содержит явно неизвестную $ x_{1} $, т.е. $ a_{11}^{} ne 0 $. Исключим эту неизвестную из всех оставшихся уравнений. С этой целью вычтем из второго уравнения первое, домноженное на $ a_{21}/a_{11}^{} $. Получим
$$left(a_{22}- frac{a_{21}}{a_{11}} a_{12} right)x_2 + dots +
left(a_{2n}- frac{a_{21}}{a_{11}} a_{1n} right)x_n =
b_2 – frac{a_{21}}{a_{11}} b_1 , $$
Аналогичное преобразование — вычитание из третьего уравнения системы первого,
умноженного на $ a_{31}/a_{11}^{} $, позволяет исключить $ x_{1} $ из этого
уравнения, т.е. заменить его на
$$left(a_{32}- frac{a_{31}}{a_{11}} a_{12} right)x_2 + dots +
left(a_{3n}- frac{a_{31}}{a_{11}} a_{1n} right)x_n =
b_3 – frac{a_{31}}{a_{11}} b_1 . $$
Продолжаем процесс далее. В конечном итоге исключаем $ x_{1} $ из всех уравнений
кроме первого:
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=b_1,\
&a_{22}^{[1]}x_2&+ ldots&+a_{2n}^{[1]}x_n &=b_2^{[1]},\
&dots & & & dots \
&a_{m2}^{[1]}x_2&+ ldots&+a_{mn}^{[1]}x_n &=b_m^{[1]}.
end{array} right.
npu
begin{array}{lcr}
a_{jk}^{[1]} &= & displaystyle a_{jk} – frac{a_{j1}a_{1k}}{a_{11}} ,\
b_j^{[1]} &= & displaystyle b_j – frac{a_{j1}b_1}{a_{11}} .
end{array}
$$
Полученная система эквивалентна исходной системе, однако она
имеет более простой вид: в ней выделилась подсиcтема
$$
left{
begin{array}{llll}
a_{22}^{[1]}x_2&+ ldots&+a_{2n}^{[1]}x_n &=b_2^{[1]},\
dots & & & dots \
a_{m2}^{[1]}x_2&+ ldots&+a_{mn}^{[1]}x_n &=b_m^{[1]},
end{array} right.
$$
которая не зависит от переменной $ x_{1} $. К этой новой подсистеме можно
применить те же рассуждения, что и к исходной системе,
поставив теперь целью исключение переменной $ x_{2} $.

Понятно, что процесс исключения может быть продолжен и далее. Теперь посмотрим,
где он может прерваться. Может так случиться, что очередная, $ ell_{} $-я
подсистема имеет коэффициент $ a_{ell ell}^{[ell-1]} $ равным нулю, что
не позволит алгоритму идти дальше — т.е. исключить переменную $ x_{ell}^{} $
из оставшихся уравнений (в принципе, такое могло случиться уже на первом
шаге, если бы коэффициент $ a_{11}^{} $ был бы равен нулю). Возможные варианты
дальнейших действий:

1.

если хотя бы один коэффициент при $ x_{ell}^{} $ в одном из оставшихся уравнений отличен от нуля: $ a_{j ell}^{[ell-1]}ne 0^{} $, то это уравнение переставляется с $ ell_{} $-м;

2.

если при всех $ jge ell^{} $ коэффициенты $ a_{j ell}^{[ell-1]} $ равны нулю, то переменная $ x_{ell}^{} $ не входит ни в одно оставшееся уравнение, и можно перейти к исключению переменной $ x_{ell+1}^{} $.

Поскольку число переменных конечно, то алгоритм исключения должен завершиться
за конечное число шагов. Чем он может завершиться? Окончательная система
должна иметь вид:
$$
left{
begin{array}{llllllrl}
a_{11}x_1 +&a_{12}x_2&+ ldots& +a_{1 {mathfrak r}}x_{mathfrak r}&
+a_{1 ,{mathfrak r} +1}x_{{mathfrak r}+1}&+ ldots + & a_{1n}x_n &=b_1,\
&a_{22}^{[1]}x_2&+ ldots& +a_{2 {mathfrak r}}^{[1]} x_{mathfrak r}&
+a_{2 ,{mathfrak r}+1}^{[1]} x_{{mathfrak r}+1}&+ ldots + & a_{2n}^{[1]} x_n &=b_2^{[1]},\
& & ddots & & & & & dots \
& & & a_{{mathfrak r} {mathfrak r}}^{[{mathfrak r}-1]}x_{mathfrak r} &
+ a_{{mathfrak r} ,{mathfrak r} +1}^{[{mathfrak r}-1]}x_{{mathfrak r}+1}& + ldots + &
a_{{mathfrak r} ,n}^{[{mathfrak r}-1]}x_n &=b_{mathfrak r}^{[{mathfrak r}-1]}, \
& & & & & & 0 &=b_{{mathfrak r}+1}^{[{mathfrak r}-1]}, \
& & & & & & dots & \
& & & & & & 0 &=b_{m}^{[{mathfrak r}-1]}, \
end{array} right.
$$
при $ {mathfrak r}le n_{} $. Заметим, что все коэффициенты этой системы будут
принадлежать тому же множеству, что и коэффициенты исходной
системы.

Предположение

. Мы будем считать, что каждое из первых $ {mathfrak r}_{} $ уравнений системы содержит в своей левой части хотя бы одну переменную с ненулевым коэффициентом.

Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.

И

Исторический комментарий о Гауссе

☞

ЗДЕСЬ.

Т

Теорема. Если хотя бы одно из чисел
$ b_{{mathfrak r}+1}^{[{mathfrak r}-1]},dots , b_{m}^{[{mathfrak r}-1]} $
отлично от нуля, то исходная система линейных уравнений будет несовместной.

Для простоты мы будем иллюстрировать наши рассуждения на системах л.у.
над $ mathbb R_{} $, в этом же множестве искать решения.
Каждое из преобразований метода Гаусса будем обозначать $ to_{} $.

П

Пример. Решить систему л.у.

$$
left{
begin{array}{rrrr}
x_1&+x_2&-3, x_3 =& -1 \
2,x_1&+x_2&-2, x_3 =& 1 \
x_1&+x_2&+ x_3 =& 3 \
x_1&+2,x_2&-3, x_3 =& 1.
end{array}
right.
$$

Решение.
$$
to
left{
begin{array}{rrrr}
x_1&+x_2&-3, x_3 =& -1 \
&-x_2&+4, x_3 =& 3 \
&&4, x_3 =& 4 \
&x_2&=& 2
end{array}
right.
to
left{
begin{array}{rrrr}
x_1&+x_2&-3, x_3 =& -1 \
&-x_2&+4, x_3 =& 3 \
&&4, x_3 =& 4 \
&&4, x_3=& 5
end{array}
right.
to
$$
$$
to
left{
begin{array}{rrrr}
x_1&+x_2&-3, x_3 =& -1 \
&-x_2&+4, x_3 =& 3 \
&&4, x_3 =& 4 \
&&0=& 1
end{array}
right.
$$
Последнее равенство абсолютно противоречиво.

Ответ. Система несовместна.

Пусть теперь $ b_{{mathfrak r}+1}^{[{mathfrak r}-1]}=0,{}dots, b_{m}^{[{mathfrak r}-1]}=0 $.
Возможны два случая: $ {mathfrak r}=n_{} $ и $ {mathfrak r}<n_{} $.
В случае $ {mathfrak r}=n_{} $ перепишем систему:
$$
left{
begin{array}{llllrl}
a_{11}x_1 +&a_{12}x_2&+ ldots& +a_{1,n-1}x_{n-1} &+a_{1, n}x_{n}&=b_1,\
&a_{22}^{[1]}x_2&+ ldots& +a_{2,n-1}^{[1]} x_{n-1}& +a_{2, n}^{[1]} x_{n}&=b_2^{[1]},\
& dots & & & dots & \
& & & a_{n-1,n-1}^{[n-2]}x_{n-1} &+a_{n-1, n}^{[n-2]}x_{n} &=b_{n-1}^{[n-2]},\
&&&& a_{nn}^{[n-1]} x_n &=b_n^{[n-1]}.
end{array} right.
$$
На основании

предположения

, имеем $ a_{nn}^{[n-1]} ne 0 $.
Но тогда, поскольку система является конечной
стадией прямого хода метода Гаусса, то
и все коэффициенты $ a_{n-1,n-1}^{[n-2]}, dots, a_{22}^{[1]}, a_{11} $
должны быть отличны от нуля — в противном случае метод Гаусса не остановился
бы на системе такого вида; он называется треугольным:

Из последнего уравнения системы можно однозначно установить
значение $ x_{n} $:
$$x_n=b_n^{[n-1]} big/ a_{nn}^{[n-1]} .$$
Далее, подставляя это значение в $ (n-1) $-е уравнение системы,
выражаем $ x_{n-1} $:
$$ x_{n-1}= frac{b_{n-1}^{[n-2]} – a_{n-1, n}^{[n-2]}x_{n}}{
a_{n-1,n-1}^{[n-2]}}= frac{ b_{n-1}^{[n-2]} –
a_{n-1, n}^{[n-2]} b_n^{[n-1]} Big/ a_{nn}^{[n-1]}}{
a_{n-1,n-1}^{[n-2]}} .
$$
Подставляем полученные значения для $ x_{n} $ и $ x_{n-1} $
в $ (n-2)_{} $-е уравнение системы, выражаем $ x_{n-2} $, и т.д.,
в конце концов приходим к первому уравнению, из которого выражаем $ x_{1} $
если ранее уже получены выражения для $ x_2,dots,x_{n} $.

Т

Теорема. Если прямой ход метода Гаусса заканчивается треугольной системой, т.е.
$ mathfrak r = n_{} $ и $ b_{{mathfrak r}+1}^{[{mathfrak r}-1]}=0,{}dots, b_{m}^{[{mathfrak r}-1]}=0 $, то исходная система линейных уравнений имеет единственное решение.

П

Пример. Решить систему л.у.

$$
left{
begin{array}{rrrr}
x_1&+3,x_2&+ x_3 =&5 \
2,x_1&+x_2&+ x_3 =& 2 \
x_1&+x_2&+ 5,x_3 =& -7 \
2,x_1&+3,x_2&-3, x_3 =& 14.
end{array}
right.
$$

Решение.
$$
to
left{
begin{array}{rrrr}
x_1&+3,x_2&+ x_3 =&5 \
&-5,x_2&- x_3 =& -8 \
&-2,x_2&+4, x_3 =& -12 \
&-3,x_2&-5, x_3 =& 4
end{array}
right.
to
left{
begin{array}{rrrr}
x_1&+3,x_2&+ x_3 =&5 \
&-5,x_2&- x_3 =& -8 \
&&22/5, x_3 =& -44/5 \
&&-22/5, x_3 =& 44/5 \
end{array}
right.
to
$$
$$
to
left{
begin{array}{rrrr}
x_1&+3,x_2&+ x_3 =&5 \
&-5,x_2&- x_3 =& -8 \
&&22/5, x_3 =& -44/5 \
&&0=& 0
end{array}
right.
$$
Из третьего уравнения определяем $ x_{3}=-2 $, подставляем во второе: $ x_{2}=2 $;
оба значения подставляем в первое: $ x_{1}=1 $.

Ответ. $ x_1=1,, x_{2}=2,, x_3=-2 $ .

Исследуем теперь случай $ {mathfrak r}<n_{} $, соответствующая форма системы называется трапециевидной или ступенчатой¹⁾:

На основании

предположения

, в $ {mathfrak r} $-м уравнении этой системы
имеется хотя бы один ненулевой коэффициент в левой части,
пусть $ a_{{mathfrak r} {mathfrak s}}^{[{mathfrak r}-1]}ne 0 $ — первый из них.
Если $ {mathfrak s}=n $, то из этого уравнения однозначно определится $ x_{n} $
$$
x_n=alpha_n = b_{mathfrak r}^{[{mathfrak r}-1]} big/ a_{{mathfrak r} n}^{[{mathfrak r}-1]}
.
$$
Если же $ {mathfrak s}<n_{} $, то из того же уравнения можно выразить
$ x_{mathfrak s}^{} $ через переменные $ x_{{mathfrak s}+1},dots,x_{n} $:
$$
x_{mathfrak s}= left( b_{mathfrak r}^{[{mathfrak r}-1]}
– a_{{mathfrak r} ,{mathfrak s} +1}^{[{mathfrak r}-1]}x_{{mathfrak s}+1} – dots –
a_{{mathfrak r} ,n}^{[{mathfrak r}-1]}x_n
right) big/ a_{{mathfrak r} {mathfrak s}}^{[{mathfrak r}-1]} .
$$
Придавая в этой формуле переменным $ x_{{mathfrak s}+1},dots,x_{n} $ любой набор
значений из $ mathbb A_{} $:
$$x_{{mathfrak s}+1} =alpha_{{mathfrak s}+1}, dots, x_n=alpha_n , $$
мы получим соответствующее значение для $ x_{mathfrak s}^{} $:
$$x_{mathfrak s}=alpha_{{mathfrak s}} =
left( b_{mathfrak r}^{[{mathfrak r}-1]}
– a_{{mathfrak r} ,{mathfrak s} +1}^{[{mathfrak r}-1]}alpha_{{mathfrak s}+1} – dots –
a_{{mathfrak r} ,n}^{[{mathfrak r}-1]}alpha_n
right) big/ a_{{mathfrak r} {mathfrak s}}^{[{mathfrak r}-1]}
.
$$
Рассмотрим теперь $ ({mathfrak r}-1) $-е уравнение системы.
На основании все того же

предположения

,
в этом уравнении имеется хотя бы один ненулевой коэффициент в левой части;
пусть $ a_{{mathfrak r}-1, {mathfrak k}}^{[{mathfrak r}-2]}ne 0_{} $ — первый из них.
Поскольку мы преположили, что система является конечной
стадией прямого хода метода Гаусса, то $ {mathfrak k}<{mathfrak s} $, и
переменная $ x_{mathfrak k} $ будет выражаться через переменные
$ x_{{mathfrak k}+1},dots,x_{n} $.
Снова различаются два случая. Если $ {mathfrak k}={mathfrak s}-1 $,
то по фиксированным ранее значениям
$$ x_{mathfrak s}=alpha_{{mathfrak s}}, x_{{mathfrak s}+1} =alpha_{{mathfrak s}+1},
dots, x_n=alpha_n $$
значение переменной $ x_{mathfrak k} $ установится однозначно. Если же
$ {mathfrak k}<{mathfrak s}-1 $, то переменным
$ x_{{mathfrak k}+1},dots,x_{{mathfrak s}-1} $ могут быть приданы произвольные
значения:
$$x_{{mathfrak k}+1}=alpha_{{mathfrak k}+1},dots,
x_{{mathfrak s}-1} =alpha_{{mathfrak s}-1} ,
$$
по которым величина $ x_{mathfrak k}^{} $ установится однозначно. Произведем
подстановку всех полученных значений переменных в
$ ({mathfrak r}-2) $-е уравнение системы, и т.д. Во всей
этой схеме нам на каком-то шаге обязательно встретится уравнение,
в котором будут содержаться по крайней мере две переменные,
значения которых еще не были зафиксированы на предыдущих шагах. Это
следует из предположения, что число уравнений $ {mathfrak r}_{} $ меньше
числа неизвестных $ n_{} $. Такое уравнение допускает бесконечное число
решений, любое из которых в ходе дальнейших шагов может быть «доделано»
до решения системы.

Т

Теорема. Если прямой ход метода Гаусса заканчивается трапециевидной системой, т.е.
$ mathfrak r < n_{} $ и $ b_{{mathfrak r}+1}^{[{mathfrak r}-1]}=0,dots, b_{m}^{[{mathfrak r}-1]}=0 $, то исходная система л.у. имеет бесконечное множество решений.

Процесс получения решения исходной системы из ее треугольной или трапециевидной формы называется обратным ходом метода Гаусса.

П

Пример. Решить систему л.у.

$$ left{
begin{array}{rrrrr}
x_1&-2,x_2&+3, x_3&-4, x_4 =& 4, \
&x_2&-x_3&+x_4 =& -3, \
x_1&+3,x_2 & &-3, x_4 =& 1, \
&-7,x_2&+3, x_3&+x_4 =& -3.
end{array}
right.
$$

Решение.
$$
to
left{
begin{array}{rrrrr}
x_1&-2,x_2&+3, x_3&-4, x_4 =& 4 \
&x_2&-x_3&+x_4 =& -3 \
&5,x_2 &-3, x_3 &+ x_4 =& -3 \
&-7,x_2&+3, x_3&+x_4 =& -3
end{array}
right.
to
left{
begin{array}{rrrrr}
x_1&-2,x_2&+3, x_3&-4, x_4 =& 4 \
&x_2&-x_3&+x_4 =& -3 \
& &2, x_3 &-4, x_4 =& 12 \
&&-4, x_3&+8,x_4 =& -24
end{array}
right.
to
$$
$$
to left{
begin{array}{rrrrr}
x_1&-2,x_2&+3, x_3&-4, x_4 =& 4 \
&x_2&-x_3&+x_4 =& -3 \
& &2, x_3 &-4, x_4 =& 12 \
&&&0=&0
end{array}
right.
$$
Придавая $ x_{4} $ любые значения, из полученных уравнений последовательно
выразим $ x_{3},x_2 $ и $ x_{1} $.

Ответ. Система имеет бесконечное множество решений, которое может быть
представлено формулами:
$$ x_1=-8, x_2=3+t, x_3=6+2,t, x_4=t npu forall, t in mathbb{R} . $$

П

Пример. Решить систему л.у.

$$
left{
begin{array}{rrrrr}
x_1&-2,x_2&-2, x_3&- x_4 =& -2 \
2, x_1&-4, x_2&+3,x_3&-2,x_4 =& 3 \
3,x_1&-6,x_2 &+5,x_3 &-3, x_4 =& 5 \
4,x_1&-8,x_2&-3, x_3&-4,x_4 =& -3.
end{array}
right.
$$

Решение.
$$
to
left{
begin{array}{rrrrr}
x_1&-2,x_2&-2, x_3&- x_4 =& -2 \
&&7,x_3& =& 7 \
& &11, x_3 & =& 11 \
&&5, x_3& =& 5
end{array}
right.
to
$$
$$
to
left{
begin{array}{rrrrr}
x_1&-2,x_2&-2, x_3&- x_4 =& -2 \
&& x_3& =& 1 \
&& { } & & \
&& { } & &
end{array}
right.
$$
Второе уравнение дает единственное значение для $ x_3 $: $ x_3=1 $, подставив
которое в первое, получим выражение для $ x_1 $ через переменные $ x_2 $ и $ x_4 $:
$$x_1=2, x_2 +x_4 .$$
Придавая $ x_2 $ и $ x_4 $ любые значения из $ mathbb{R}_{} $, получим соответствующие
значения для $ x_1 $.

Ответ. Система имеет бесконечное множество решений, которое может быть
представлено формулами:
$$ x_1=2,t+u , x_2=t, x_3=1, x_4=u npu forall, {t,u} subset mathbb{R} . $$

Применим метод Гаусса к системам уравнений общего вида (с символьными, т.е. буквенными коэффициентами) с целью получения общих формул решения. Ограничимся пока только случаем систем с числом уравнений равном числу неизвестных.

П

Пример. Решить систему уравнений

$$
left{
begin{array}{ll}
a_{11}x_1 +a_{12}x_2&=b_1,\
a_{21}x_1 +a_{22}x_2&=b_2.
end{array} right.
$$

Решение. Предположим, что $ a_{11}^{} ne 0 $. Тогда прямым ходом метода Гаусса систему уравнений можно привести к эквивалентной:
$$
left{
begin{array}{lrl}
a_{11}x_1 & +a_{12}x_2&=b_1,\
& & \
&left(a_{22}- frac{a_{21}}{a_{11}}a_{12}right)x_2&=b_2-frac{a_{21}}{a_{11}}b_1.
end{array} right.
$$
Если теперь выражение
$$ a_{11}a_{22}-a_{12}a_{21} $$
отлично от нуля, то последнее уравнение системы однозначно разрешимо относительно $ x_{2} $:
$$
x_2=frac{a_{11}b_2-a_{21}b_1}{a_{11}a_{22}-a_{12}a_{21}} .
$$
Подставляем найденное значение в первое уравнение, получаем:
$$
x_1=frac{a_{22}b_1-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}} .
$$

Ответ. При условиях $ a_{11}ne 0, a_{11}a_{22}-a_{12}a_{21} ne 0 $ система имеет единственное решение, которое представимо в виде
$$
x_1=frac{a_{22}b_1-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}},
x_2=frac{a_{11}b_2-a_{21}b_1}{a_{11}a_{22}-a_{12}a_{21}} .
$$

П

Пример. Решить систему уравнений:

$$
left{
begin{array}{rrrl}
a_{11}x_1 +&a_{12}x_2+&a_{13}x_3=&b_1 \
a_{21}x_1 +&a_{22}x_2+&a_{23}x_3=&b_2 \
a_{31}x_1 +&a_{32}x_2+&a_{33}x_3=&b_3.
end{array}
right.
$$

Решение. Начинаем действовать так же, как и в предыдущем примере. Пусть $ a_{11}^{} ne 0 $.
Тогда прямым ходом метода Гаусса исключаем из второго и третьего уравнений переменную $ x_{2} $:
$$
left{
begin{array}{rrrl}
a_{11}x_1 +&a_{12}x_2+&a_{13}x_3=&b_1 \
& & & \
&left(a_{22}- frac{a_{21}}{a_{11}}a_{12}right)x_2+&left(a_{23}- frac{a_{21}}{a_{11}}a_{13} right)x_3=&b_2 – b_1 frac{a_{21}}{a_{11}} \
& & & \
&left(a_{32}- frac{a_{31}}{a_{11}}a_{12} right)x_2+&left(a_{33} – frac{a_{31}}{a_{11}}a_{13} right)x_3=&b_3 – b_1 frac{a_{31}}{a_{11}}
end{array}
right.
$$
Коэффициент при $ x_{2} $ во втором уравнении был обозначен нами в предыдущем пункте через $ a_{22}^{[1]} $:
$$
a_{22}^{[1]}=frac{a_{11}a_{22}-a_{12}a_{21}}{a_{11}} .
$$
Если теперь $ a_{11}a_{22}-a_{12}a_{21}^{} ne 0 $, то можно исключить переменную $ x_{2} $ из последнего полученного уравнения:
$$
frac{a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}
-a_{31}a_{22}a_{13} -a_{21}a_{12}a_{33} -a_{11}a_{32}a_{23}}{a_{11}a_{22}-a_{12}a_{21}}, x_3=
$$
$$
=frac{a_{11}a_{22}b_{3}+a_{12}a_{31}b_2+a_{21}a_{32}b_1
-a_{31}a_{22}b_1 -a_{11}a_{32}b_{2} -a_{21}a_{12}b_3}{a_{11}a_{22}-a_{12}a_{21}} .
$$
Коэффициент при $ x_{3} $ в этом уравнении был обозначен в предыдущем пункте через $ a_{33}^{[2]} $. Если выражение
$$
a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}
-a_{31}a_{22}a_{13} -a_{21}a_{12}a_{33} -a_{11}a_{32}a_{23}
$$
отлично от нуля, то последнее уравнение системы однозначно разрешимо относительно $ x_{3} $:
$$
x_3=frac{a_{11}a_{22}b_{3}+a_{12}a_{31}b_2+a_{21}a_{32}b_1
-a_{31}a_{22}b_1 -a_{11}a_{32}b_{2} -a_{21}a_{12}b_3}{a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}
-a_{31}a_{22}a_{13} -a_{21}a_{12}a_{33} -a_{11}a_{32}a_{23}
} .
$$
Подставляем найденное значение в уравнение
$$
left(a_{22}- frac{a_{21}}{a_{11}}a_{12}right)x_2+left(a_{23}- frac{a_{21}}{a_{11}}a_{13} right)x_3=b_2 – b_1 frac{a_{21}}{a_{11}} ,
$$
получаем:
$$
x_2=frac{a_{11}a_{33}b_{2}+a_{21}a_{13}b_3+a_{31}a_{23}b_1
-a_{13}a_{31}b_2 -a_{11}a_{23}b_{3} -a_{21}a_{33}b_1}{a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}
-a_{31}a_{22}a_{13} -a_{21}a_{12}a_{33} -a_{11}a_{32}a_{23}
} .
$$
Наконец, подставляя найденные значения для $ x_{2} $ и $ x_{3} $ в первое уравнение системы, находим значение $ x_{1} $:
$$
x_1=frac{a_{22}a_{33}b_{1}+a_{12}a_{23}b_3+a_{32}a_{13}b_2
-a_{13}a_{22}b_3 -a_{32}a_{23}b_{1} -a_{12}a_{33}b_2}{a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}
-a_{31}a_{22}a_{13} -a_{21}a_{12}a_{33} -a_{11}a_{32}a_{23}
} .
$$

Ответ. При условиях
$$ a_{11}ne 0, a_{11}a_{22}-a_{12}a_{21} ne 0, $$
$$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}
-a_{31}a_{22}a_{13} -a_{21}a_{12}a_{33} -a_{11}a_{32}a_{23} ne 0
$$
система имеет единственное решение.

Итак, мы получили общие формулы решения системы уравнений. Правда, мы разобрали пока только случай единственности решения. Условия существования единственного решения получились в виде набора неравенств на коэффициенты $ a_{jk}^{} $ системы. Оказывается, что не все эти неравенства являются существенными для единственности, можно доказать, что необходимым и достаточным в каждом примере является последнее полученное неравенство: для системы
$$
left{
begin{array}{ll}
a_{11}x_1 +a_{12}x_2&=b_1,\
a_{21}x_1 +a_{22}x_2&=b_2
end{array} right.
$$
условие единственности решения заключается в выполнении
$$a_{11}a_{22}-a_{12}a_{21} ne 0 , $$
а для системы
$$
left{
begin{array}{rrrl}
a_{11}x_1 +&a_{12}x_2+&a_{13}x_3=&b_1 \
a_{21}x_1 +&a_{22}x_2+&a_{23}x_3=&b_2 \
a_{31}x_1 +&a_{32}x_2+&a_{33}x_3=&b_3
end{array}
right.
$$
– в выполнении
$$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}
-a_{31}a_{22}a_{13} -a_{21}a_{12}a_{33} -a_{11}a_{32}a_{23} ne 0 .
$$
Оба полученных выражения фактически являются функциями от элементов матрицы $ A_{} $ системы уравнений
$$
AX={mathcal B} ;
$$
эти функции имеют специальное название. Выражение
$$
det (A) = left|
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right|=a_{11}a_{22}-a_{12}a_{21} ;
$$
называется определителем матрицы $ A_{} $ (второго порядка); а выражение
$$
det (A) =
left|
begin{array}{lll}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right| =
$$
$$
=a_{11}a_{22}a_{33}+a_{12}a_{23} a_{31} +
a_{21}a_{32} a_{13} – a_{31} a_{22} a_{13} – a_{21}a_{12}a_{33} –
a_{11} a_{32} a_{23}
$$
— определителем²⁾ матрицы $ A_{} $ (третьего порядка). Понятие определителя распространяется и на квадратные матрицы бóльших порядков;
образно говоря, определитель — это функция элементов матрицы, отвечающая за единственность решения системы уравнений.

Оказывается, что введенные функции позволяют и записать это решение в компактной форме. Так, полученные в двух предыдущих примерах ответы можно переписать — для $ n_{}=2 $:
$$
x_1 = frac{left|
begin{array}{cc}
b_{1} & a_{12} \
b_{2} & a_{22}
end{array}
right|}{left|
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right|} , x_2=
frac{left|
begin{array}{cc}
a_{11} & b_{1} \
a_{21} & b_{2}
end{array}
right|}{left|
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right|} ;
$$
а для $ n_{}=3 $:
$$
x_1=frac{left|
begin{array}{lll}
b_{1} & a_{12} & a_{13}\
b_{2} & a_{22} & a_{23} \
b_{3} & a_{32} & a_{33}
end{array}
right|}{left|
begin{array}{lll}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right|} ,
x_2=frac{left|
begin{array}{lll}
a_{11} & b_{1} & a_{13}\
a_{21} & b_{2} & a_{23} \
a_{31} & b_{3} & a_{33}
end{array}
right|}{left|
begin{array}{lll}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right|} ,
x_3=frac{left|
begin{array}{lll}
a_{11} & a_{12} & b_{1} \
a_{21} & a_{22} & b_{2} \
a_{31} & a_{32} & b_{3}
end{array}
right|}{left|
begin{array}{lll}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right|} .
$$
Эти формулы, равно как и их обобщение на случай систем уравнений с $ n_{} $ неизвестными, называются формулами Крамера.

§

Дальнейший матричный анализ метода Гаусса

☞

ЗДЕСЬ.

Рассмотрим систему линейных уравнений с квадратной матрицей $ A_{} $, т.е. такую, у которой число уравнений совпадает с числом неизвестных.

Т

Теорема. Cистема

$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&b_1\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&b_2\
ldots& & ldots \
a_{n1}x_1 +a_{n2}x_2+ldots+a_{nn}x_n &=&b_n
end{array}right.
$$
имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля:
$$
left|
begin{array}{rrrr}
a_{11} & a_{12} & dots & a_{1n} \
a_{21} & a_{22} & dots & a_{2n} \
dots &&& dots \
a_{n1} & a_{n2} & dots & a_{nn}
end{array}
right|
ne 0 .
$$
В этом случае решение можно вычислить по формулами Крамера³⁾:
$$
x_k =frac{det left[ A_{[1]}|dots|A_{[k-1]}|{mathcal B}|A_{[k+1]}|dots|A_{[n]} right]}{det A} quad npu
quad kin { 1,dots,n } .
$$
Для получения значения $ x_{k} $ в числитель ставится определитель, получающийся из $ det A_{} $
заменой его $ k_{} $-го столбца на столбец правых частей ( здесь $ {} | $ означает конкатенацию).

Доказательство

☞

ЗДЕСЬ

П

Пример. Решить систему уравнений

$$
left{begin{array}{rrrrrr}
2x_1& +3x_2&+11x_3&+5x_4 &=& color{Red}2,\
x_1& +x_2&+5x_3&+2x_4 &=& color{Red}1 ,\
2x_1& +x_2&+3x_3&+2x_4 &=&color{Red}{-3},\
x_1& +x_2&+3x_3&+4x_4 &=&color{Red}{-3}.
end{array}right.
$$

Решение.
$$
x_1=frac{left|begin{array}{rrrr}
color{Red}2 & 3&11&5 \
color{Red}1 & 1&5&2 \
color{Red}{-3}& 1&3&2 \
color{Red}{-3} & 1&3&4
end{array}right|}
{left|begin{array}{rrrr}
2& 3&11&5 \
1& 1&5&2 \
2& 1&3&2 \
1& 1&3&4
end{array}right|}=frac{-28}{14}=-2,
x_2=frac{left|begin{array}{rrrr}
2& color{Red}2&11&5 \
1& color{Red}1&5&2 \
2& color{Red}{-3}&3&2 \
1& color{Red}{-3}&3&4
end{array}right|}
{left|begin{array}{rrrr}
2& 3&11&5 \
1& 1&5&2 \
2& 1&3&2 \
1& 1&3&4
end{array}right|}=frac{0}{14}=0, dots $$
Найдите оставшиеся компоненты решения.

♦

Формулы Крамера не представляют практического значения в случае систем с числовыми коэффициентами: вычислять по ним решения конкретных систем линейных уравнений неэффективно, поскольку они требуют вычисления $ (n+1)_{} $-го определителя порядка $ n_{} $, в то время как метод Гаусса фактически эквивалентен вычислению одного определителя порядка $ n_{} $. Тем не менее, теоретическое значение формул Крамера заключается в том, что они дают явное представление решения системы через ее коэффициенты. Например, с их помощью легко может быть доказан результат

=>

Решение системы линейных уравнений с квадратной матрицей $ A_{} $ является непрерывной функцией коэффициентов этой системы при условии, что $ det A_{} ne 0 $.

При фиксированной матрице $ A $ и вариации столбца $ mathcal B $ решение системы может меняться с разной скоростью в зависмости от «направления изменения» столбца $ mathcal B $. Отношение наибыстрейшей скорости изменения к самой медленной является характеристикой матрицы $ A $ известной под названием числа обусловленности матрицы.

Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее

☞

ЗДЕСЬ.

Еще один способ решения системы основан на построении обратной матрицы:
$$
AX={mathcal B} quad Rightarrow quad X=A^{-1}{mathcal B} .
$$
Этот способ малоэффективен при фиксированных числовых $ A_{} $ и $ {mathcal B}_{} $.

?

Найти достаточное условие существования общего решения систем уравнений:

$$ A_1 X = {mathcal B}_1 quad u quad A_2 Y = {mathcal B}_2 , $$
при квадратных матрицах $ A_1 $ и $ A_2 $ одинакового порядка.

Матрица, получающаяся конкатенацией матрицы $ A_{} $ и столбца правых частей $ {mathcal B}_{} $
$$
[ A|{mathcal B} ] =
left(
begin{array}{rrrrl}
a_{11} & a_{12} & dots & a_{1n} & b_1 \
a_{21} & a_{22} & dots & a_{2n} & b_2 \
dots &&& & dots \
a_{m1} & a_{m2} & dots & a_{mn} & b_m
end{array}
right)_{mtimes (n+1)}
$$
называется расширенной матрицей системы линейных уравнений $ AX={mathcal B} $.

Т

Теорема [Кронекер, Капелли]. Система $ AX={mathcal B} $ совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

$$ operatorname{rank}, A = operatorname{rank}, [ A|{mathcal B} ] . $$
При выполнении этого условия, система имеет единственное решение, если число неизвестных $ n_{} $ совпадает с общим значением ранга $ mathfrak r_{} $, и бесконечное множество решений, если $ n_{} $ больше этого значения.

Доказательство необходимости. Пусть существует решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы,
тогда $$alpha_1 A_{[1]}+dots+alpha_n A_{[n]}={mathcal B} ,$$
т.е. столбец $ {mathcal B} $ линейно выражается через столбцы $ A_{[1]},dots,A_{[n]} $.
Но тогда
$$ operatorname{rank} {A_{[1]},dots,A_{[n]}}=operatorname{rank} {A_{[1]},dots,A_{[n]},{mathcal B}} .$$
Следовательно $ operatorname{rank}, A = operatorname{rank}, [ A|{mathcal B} ] $.

Доказательство достаточности проводится в следующем пункте.

♦

Обозначение $ mathfrak r_{} $ для ранга матрицы $ A_{} $ соответствует по смыслу этому же обозначению в методе Гаусса: после приведения к трапециевидному (или треугольному) виду в системе л.у. должно остаться ровно $ mathfrak r_{} $ линейно независимых уравнений, явно содержащих неизвестные.
Это утверждение вытекает из способа вычисления ранга матрицы по методу элементарных преобразований.

П

Пример. Исследовать совместность системы уравнений

$$
left{ begin{array}{rrrrrcr}
{color{Red}{lambda}} x_1+&x_2+&x_3+&x_4&=&1, \
x_1+& {color{Red}{lambda}} x_2+&x_3+&x_4&=&1, \
x_1+&x_2+&{color{Red}{lambda}} x_3+&x_4&=&1, \
x_1+&x_2+&x_3+&{color{Red}{lambda}} x_4&=&1,
end{array}
right.
$$
в зависимости от значения параметра $ color{Red}{lambda} $.

Решение. В этом примере число уравнений совпадает с числом неизвестных. Это
обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта:
система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна.
Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность.
Оно, фактически, единственно: за все отвечает определитель системы $ det A_{} $. Если он отличен от нуля — система совместна.
$$det A =
left| begin{array}{cccc}{color{Red}{lambda}} &1&1&1 \
1&{color{Red}{lambda}}&1&1 \
1&1&{color{Red}{lambda}}&1 \
1&1&1&{color{Red}{lambda}}
end{array}
right|=
left| begin{array}{cccc}
({color{Red}{lambda}}-1) &(1-{color{Red}{lambda}})&0&0 \
0&({color{Red}{lambda}}-1)&(1-{color{Red}{lambda}})&0 \
0&0&({color{Red}{lambda}}-1)&(1-{color{Red}{lambda}}) \
1&1&1&{color{Red}{lambda}}
end{array}
right|=
$$
$$
=({color{Red}{lambda}}-1)^3
left| begin{array}{rrrr}
1 &-1&0&0 \
0&1&-1&0 \
0&0&1&-1 \
1&1&1&{color{Red}{lambda}}
end{array}
right|=
$$
$$ =({color{Red}{lambda}}-1)^3({color{Red}{lambda}}+3), .$$
По теореме Крамера при $ {color{Red}{lambda}}ne 1 $ и при $ {color{Red}{lambda}}ne -3 $ решение системы единственно:
$$x_1=x_2=x_3=x_4=1/({color{Red}{lambda}}+3) .$$

Осталось исследовать критические случаи: $ {color{Red}{lambda}}=1_{} $ и $ {color{Red}{lambda}}= -3 $: определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!).
При $ {color{Red}{lambda}}= 1_{} $ имеем
$$
operatorname{rank} left( begin{array}{cccc}
1 &1&1&1 \
1&1&1&1 \
1&1&1&1 \
1&1&1&1
end{array}
right)= operatorname{rank}
left( begin{array}{ccccc}
1&1&1&1&1 \
1&1&1&1&1 \
1&1&1&1&1 \
1&1&1&1&1
end{array}
right)=1 ,
$$
и система совместна. Она эквивалентна единственному уравнению
$$x_1+x_2+x_3+x_4=1 ,$$
которое имеет бесконечно много решений.

При $ {color{Red}{lambda}}= -3 $:
$$
operatorname{rank} left( begin{array}{rrrr}
-3 &1&1&1 \
1&-3&1&1 \
1&1&-3&1 \
1&1&1&-3
end{array}
right)=3,quad
operatorname{rank} left( begin{array}{rrrrr}
-3 &1&1&1&1 \
1&-3&1&1&1 \
1&1&-3&1&1 \
1&1&1&-3&1
end{array}
right)=4
$$
и система несовместна.

Ответ. Система несовместна при $ {color{Red}{lambda}} = -3 $; она имеет бесконечное множество решений при $ {color{Red}{lambda}} = 1_{} $ и единственное решение при $ {color{Red}{lambda}} notin {-3,1} $.

Что можно сказать о совместности или несовместности случайным образом составленной системы из $ m_{} $ линейных уравнений относительно $ n_{} $ неизвестных? При $ m_{}<n $ система, как правило, совместна и имеет бесконечное множество решений. В самом деле, если выбрать минор порядка $ m_{} $ в матрице системы $ A_{} $, элементы которой считаются случайными, то этот минор будет «с вероятностью 1» отличен от нуля (см. рассуждения в предыдущем пункте о совместности системы л.у. при $ m=n_{} $). Таким образом, $ operatorname{rank}, (A) = m $, и автоматически получаем, что $ operatorname{rank} (A | mathcal B) = m $ (поскольку ранг не может больше количества строк матрицы).
Если же $ m>n_{} $ то такая переопределенная система, как правило, несовместна. Рассуждения для доказательства правдоподобия этого утверждения могут быть следующими. Выберем произвольным образом в рассматриваемой системе какую-то подсистему, состоящую из $ n_{} $ уравнений. Она, как правило, будет иметь единственное решение. Теперь составим другую подсистему, хотя бы одним уравнением отличающуюся от предыдущей (поскольку $ m>n_{} $ такое всегда можно сделать). Новая подсистема снова, как правило, будет иметь единственное решение. Однако решения этих двух подсистем будут, как правило, различными и, следовательно, сама основная система не будет иметь решения. В этом последнем случае переопределенной системы имеется, однако, важный исключительный, который рассмотрим

☟

НИЖЕ.

=>

Система однородных уравнений

$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=0,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=0,\
dots & & & dots & \
a_{n1}x_1 &+a_{n2}x_2&+ ldots&+a_{nn}x_n &=0
end{array} right.
$$
всегда совместна: она имеет тривиальное решение $ x_1=0,dots,x_n=0 $. Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

П

Пример. Найти условие, при котором три точки плоскости с координатами $ (x_1,y_1), (x_2,y_2) $ и $ (x_3,y_{3}) $ лежат на одной прямой.

Решение. Будем искать уравнение прямой в виде $ ax+by+c=0 $ при неопределенных коэффициентах $ a,b,c_{} $. Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений:
$$
left{ begin{array}{cc}
ax_1+by_1+c & =0\
ax_2+by_2+c & =0\
ax_3+by_3+c & =0
end{array} right.
$$
Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора $ (a,b,c)_{} $ при хотя бы одном из чисел отличном от нуля):
$$
left|begin{array}{ccc}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|=0 .
$$

♦

?

Доказать, что для совместности системы

$$
left{
begin{array}{ccc}
a_{11}x_1+a_{12}x_2+a_{13}x_3 &=& b_1 \
a_{21}x_1+a_{22}x_2+a_{23}x_3 &=& b_2 \
a_{31}x_1+a_{32}x_2+a_{33}x_3 &=& b_3 \
a_{41}x_1+a_{42}x_2+a_{43}x_3 &=& b_4
end{array}
right.
$$
необходимо, чтобы было выполнено условие
$$
left|
begin{array}{cccc}
a_{11}&a_{12}& a_{13} & b_1 \
a_{21}&a_{22}& a_{23} & b_2 \
a_{31}&a_{32}& a_{33} & b_3 \
a_{41}&a_{42}& a_{43} & b_4
end{array}
right|=0 quad .
$$
Является ли это условие достаточным для совместности?

?

Додсон — один из самых знаменитых математиков мира. Назовите его псевдоним.

Ответ

☞

ЗДЕСЬ

Пусть выполнено условие теоремы Кронекера-Капелли: $ operatorname{rank} (A)=operatorname{rank}[Amid mathcal B ] =mathfrak{r} $. По определению ранга матрицы,
в матрице $ A $ существует минор порядка $ mathfrak{r} $, отличный от нуля; этот
же минор останется и минором расширенной матрицы $ [ Amid mathcal B ] $. Пусть, для определенности, ненулевой минор находится в левом верхнем углу матрицы⁴⁾:
$$
Delta = Aleft( begin{array}{llll}
1 & 2 & dots & mathfrak{r} \
1 & 2 & dots & mathfrak{r}
end{array}
right) = left|
begin{array}{llll}
a_{11} & a_{12} & dots & a_{1mathfrak{r}} \
a_{21} & a_{22} & dots & a_{2mathfrak{r}} \
dots &&& dots \
a_{mathfrak{r}1} & a_{mathfrak{r}2} & dots & a_{mathfrak{r} mathfrak{r}}
end{array}
right| ne 0 .
$$
Тогда первые $ mathfrak{r} $ строк матрицы $ A $ линейно независимы, а остальные будут линейно выражаться через них. Это же утверждение будет справедливо и для строк
матрицы $ [Amid mathcal B] $. Умножая первые $ mathfrak{r} $ уравнений системы на
соответствующие числа и складывая их, получим любое оставшееся уравнение.
Таким образом, система уравнений может быть заменена эквивалентной ей
системой из первых $ mathfrak{r} $ уравнений:
$$
left{ begin{array}{rrrr}
a_{11}x_1+dots+a_{1mathfrak{r}}x_{mathfrak{r}}&+a_{1,mathfrak{r}+1}x_{mathfrak{r}+1}+
dots +a_{1n}x_n&=&b_1, \
dots & & & dots \
a_{mathfrak{r}1}x_1+dots+a_{mathfrak{r}mathfrak{r}}x_{mathfrak{r}}&
+a_{mathfrak{r},mathfrak{r}+1}x_{mathfrak{r}+1}+dots
+a_{mathfrak{r}n}x_n&=&b_mathfrak{r}
end{array}
right.
quad iff quad A^{prime} X={mathcal B}^{prime}
$$
Если $ mathfrak{r}=n $, то матрица $ A^{prime} $ квадратная. По предположению
$ det A^{prime} ne 0 $. По теореме Крамера решение такой системы единственно.

Пусть теперь $ mathfrak{r}<n $. Перепишем получившиеся уравнения в виде
$$
left{ begin{array}{rrrr}
a_{11}x_1+dots+a_{1mathfrak{r}}x_{mathfrak{r}}&=&b_1-&
(a_{1,mathfrak{r}+1}x_{mathfrak{r}+1}+
dots +a_{1n}x_n), \
dots & & & \
a_{mathfrak{r}1}x_1+dots+a_{mathfrak{r}mathfrak{r}}x_{mathfrak{r}}
&=&b_mathfrak{r}-&(a_{mathfrak{r},mathfrak{r}+1}x_{mathfrak{r}+1}+dots +a_{mathfrak{r}n}x_n).
end{array}
right.
$$
По предположению, определитель матрицы, составленной из коэффициентов при $ x_1,dots,x_{mathfrak{r}} $, отличен от нуля. По теореме Крамера у этой системы
существует единственное решение относительно неизвестных
$ x_1,dots,x_{mathfrak{r}} $ при произвольных фиксированных значениях
$ x_{mathfrak{r}+1},dots,x_n $:
$$
x_j=frac{
left| begin{array}{lllllll}
a_{11} & dots &a_{1,j-1} &left[ b_1-(a_{1,mathfrak{r}+1}x_{mathfrak{r}+1}+dots +a_{1n}x_n)
right]
&a_{1,j+1}& dots &a_{1mathfrak{r}} \
dots &&&dots&&& dots \
a_{mathfrak{r}1} & dots &a_{mathfrak{r},j-1} & left[ b_{mathfrak{r}}-
(a_{mathfrak{r},mathfrak{r}+1}x_{mathfrak{r}+1}+dots +a_{mathfrak{r}n}x_n)
right]
&a_{mathfrak{r},j+1}& dots &a_{mathfrak{r}mathfrak{r}}
end{array}
right|
}{Delta}
$$
$$
mbox{при} jin {1,dots, mathfrak{r}} .
$$
Таким образом, в этом случае
система имеет бесконечное множество решений. Используя свойство линейности
определителя по столбцу (см. свойство

5

☞

ЗДЕСЬ ), формулы можно переписать в виде
$$
x_j=beta_j + gamma_{j,mathfrak{r}+1}x_{mathfrak{r}+1}+dots+gamma_{jn}x_n
npu jin {1,dots, mathfrak{r} } .
$$
Здесь
$$
beta_j =frac{1}{Delta}
left| begin{array}{lllllll}
a_{11} & dots &a_{1,j-1} & b_1 &a_{1,j+1}& dots &a_{1mathfrak{r}} \
vdots &&&vdots&&& vdots \
a_{mathfrak{r}1} & dots &a_{mathfrak{r},j-1} & b_{mathfrak{r}}
&a_{mathfrak{r},j+1}& dots &a_{mathfrak{r}mathfrak{r}}
end{array}
right|, ,
$$
$$
gamma_{jk} = -frac{1}{Delta}
left| begin{array}{lllllll}
a_{11} & dots &a_{1,j-1} & a_{1k} &a_{1,j+1}& dots &a_{1mathfrak{r}} \
vdots &&&vdots&&& vdots \
a_{mathfrak{r}1} & dots &a_{mathfrak{r},j-1} & a_{mathfrak{r}k}
&a_{mathfrak{r},j+1}& dots &a_{mathfrak{r}mathfrak{r}}
end{array}
right|
.
$$
Эти формулы называются общим решением системы $ A X=mathcal B $. Участвующие в них
переменные $ x_{mathfrak{r}+1},dots,x_n $ называются основными (или свободными), а
$ x_1,dots,x_{mathfrak{r}} $ — зависимыми. Решение, получающееся
из общего решения фиксированием значений основных переменных, называется
частным решением системы уравнений.

П

Пример. Исследовать совместность и найти общее решение системы уравнений:

$$
left{ begin{array}{rrrrrrcr}
{color{Red} 2}, x_1-&x_2+& {color{Red} 1}, x_3+&{color{Red} 2}, x_4+&3, x_5&=&2, \
{color{Red} 6} x_1-&3x_2+&{color{Red} 2}, x_3+&{color{Red} 4}, x_4+&5x_5&=&3, \
6x_1-&3x_2+&4x_3+&8x_4+&13x_5&=&9, \
{color{Red} 4} x_1-&2x_2+&{color{Red} 1}, x_3+&{color{Red} 1}, x_4+&2x_5&=&1.
end{array}
right.
$$

Решение проведем двумя способами, соответствующими двум способам вычисления ранга матрицы. Вычисляем сначала ранг матрицы $ A $ по методу окаймляющих миноров:
$$
|2| ne 0,quad left| begin{array}{rr} 2 & 1 \ 6 & 2 end{array} right| ne 0,
quad left| begin{array}{rrr} 2 & 1 & 2 \ 6 & 2 & 4 \ 4 & 1 & 1 end{array} right|=2 ne 0
,
$$
а все миноры, окаймляющие последний, равны нулю. Итак, $ operatorname{rank} (A) =3 $.
Для нахождения ранга расширенной матрицы $ [Amid mathcal B] $ достаточно проверить
окаймление найденного ненулевого минора третьего порядка с помощью
элементов взятых из столбца правых частей. Имеется всего один такой минор,
и он равен нулю. Следовательно $ operatorname{rank}[ Amid mathcal B ] =3 $, система совместна, и имеет бесконечное множество решений.

Ненулевой минор третьего порядка (базисный минор) находится в первой, второй и четвертых строках,
что означает линейную независимость соответствующих уравнений. Третье уравнение
линейно зависит от остальных, и может быть отброшено. Далее, указанный
базисный минор образован коэффициентами при $ x_1,x_3 $ и $ x_4 $.
Следовательно оставшиеся уравнения могут быть разрешены
относительно этих переменных, т.е. они — зависимые, а $ x_2 $ и $ x_5 $ —
основные. Использование формулы дает общее решение
$$
begin{array}{lll}
x_1&=&frac{left| begin{array}{rrr} 2 & 1 & 2 \ 3 & 2 & 4 \ 1 & 1 & 1
end{array}
right|}{displaystyle 2}
-x_2frac{left| begin{array}{rrr} -1 & 1 & 2 \ -3 & 2 & 4 \ -2 & 1 & 1
end{array}
right|}{displaystyle 2}
-x_5frac{left| begin{array}{rrr} 3 & 1 & 2 \ 5 & 2 & 4 \ 2 & 1 & 1
end{array}
right|}{displaystyle 2}
=-frac{1}{2}+frac{1}{2}x_2+frac{1}{2}x_5, \
& & \
x_3&=&frac{left| begin{array}{rrr} 2 & 2 & 2 \ 6 & 3 & 4 \ 4 & 1 & 1
end{array}
right|}{displaystyle 2}
-x_2frac{left| begin{array}{rrr} 2 & -1 & 2 \ 6 & -3 & 4 \ 4 & -2 & 1
end{array}
right|}{displaystyle 2}
-x_5frac{left| begin{array}{rrr} 2 & 3 & 2 \ 6 & 5 & 4 \ 4 & 2 & 1
end{array}
right|}{displaystyle 2}=3-4x_5, \
& & \
x_4 &=&frac{left| begin{array}{rrr} 2 & 1 & 2 \ 6 & 2 & 3 \ 4 & 1 & 1
end{array}
right|}{displaystyle 2}
-x_2frac{left| begin{array}{rrr} 2 & 1 & -1 \ 6 & 2 & -3 \ 4 & 1 & -2
end{array}
right|}{displaystyle 2}
-x_5frac{left| begin{array}{rrr} 2 & 1 & 3 \ 6 & 2 & 5 \ 4 & 1 & 2
end{array}
right|}{displaystyle 2}
= 0.
end{array}
$$
Решим теперь ту же задачу, воспользовавшись методом Гаусса исключения переменных в системе линейных уравнений:
$$
left{ begin{array}{rrrrrrcr}
2x_1&-x_2&+x_3&+2x_4&+3x_5&=&2, \
&&x_3&+2x_4&+4x_5&=&3, \
&&&x_4&&=&0
end{array}
right.
$$
Используя обратный ход метода Гаусса, снова приходим к полученным формулам.

Ответ. Общее решение системы:
$ x_1=1/2 (x_2+x_5-1), x_3=3-4,x_5, x_4=0 $.

Проанализируем теперь полученные общие формулы для общего решения. В этих формулах $ beta_j $ представляет решение системы, получаемое при $ x_{mathfrak{r}+1}=0,dots,x_n=0 $.
Величины же коэффициентов $ gamma_{jk} $ вовсе не зависят от правых частей системы и будут одинаковыми при любых значениях $ b_1,dots,b_m $. В частности, если
$ b_1=0,dots,b_m=0 $, то в формулах величины $ beta_j $ обращаются в нуль и эти формулы превращаются в
$$
x_j=gamma_{j,mathfrak{r}+1}x_{mathfrak{r}+1}+dots+gamma_{jn}x_n
npu jin {1,dots, mathfrak{r}} .
$$

Вывод. Формула общего решения системы $ A X=mathcal B $:
$$
x_j=beta_j + gamma_{j,mathfrak{r}+1}x_{mathfrak{r}+1}+dots+gamma_{jn}x_n
npu jin {1,dots, mathfrak{r} }
$$
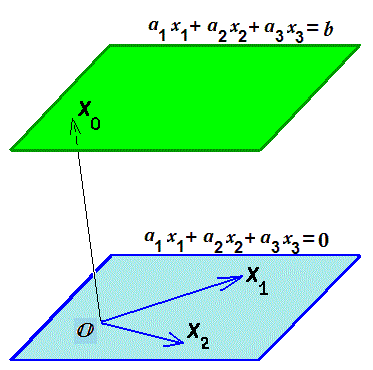
состоит из двух частей: слагаемые, не содержащие свободных переменных, определяют частное решение неоднородной системы:
$$ x_1= beta_1,dots, x_{mathfrak{r}}= beta_{mathfrak{r}},x_{mathfrak{r}+1}=0,dots,x_n=0 ; $$
оставшиеся после их отбрасывания формулы задают общее решение системы $ AX=mathbb O $. Этот результат обобщается в следующей теореме.

Т

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Доказательство тривиально если система $ A X=mathcal B $ имеет единственное решение. Если же решений бесконечно много, то выбрав какое-то одно частное $ X=X_1 $ мы получаем, что любое другое частное решение $ X=X_2 $ должно быть связано с первым соотношением
$$ A(X_2-X_1)=mathbb O , $$
т.е. разность частных решений неоднородной системы обязательно является решением однородной системы уравнений $ AX=mathbb O $.

♦

Теперь посмотрим как можно описать общее решение однородной системы.

Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю:
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=0,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=0,\
dots & & & dots & \
a_{m1}x_1 &+a_{m2}x_2&+ ldots&+a_{mn}x_n &=0.
end{array} right.
$$
или, в матричном виде:
$$
A_{mtimes n}X={mathbb O}_{mtimes 1}
$$

Однородная система всегда совместна: она имеет тривиальное решение:
$ x_{1}=0,dots,x_n=0 $.

Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру,
если матрица $ A_{} $ системы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет.
Теорема Кронекера-Капелли утверждает, что условие $ det (A_{}) = 0 $ является и достаточным для существования нетривиального решения.

Т

Теорема 1. Для того, чтобы система однородных уравнений с квадратной матрицей $ A_{} $ имела нетривиальное решение необходимо и достаточно, чтобы $ det (A_{}) = 0 $.

Для произвольной (не обязательно квадратной) матрицы $ A_{} $ имеет место следующий общий результат.

Т

Теорема 2. Если $ operatorname{rank} (A)=mathfrak r < n $ то у системы однородных уравнений имеется набор (система) из $ n- mathfrak r_{} $ решений

$$ X=X_1,dots, X=X_{n-mathfrak r} , $$
при линейно независимых столбцах $ {X_1,dots,X_{n-mathfrak r}} subset mathbb A^n $. Любое другое решение $ X= X_{*} $ системы линейно выражается через указанные столбцы:
$$ X_{*}=alpha_1X_1+dots+ alpha_{n-mathfrak r}X_{n-mathfrak r} . $$

Этот набор решений называется фундаментальной системой решений (ФСР) для системы однородных уравнений. Число $ n- mathfrak r $ иногда называется дефектом матрицы⁵⁾ $ A_{mtimes n}^{} $.

=>

Если $ m<n_{} $, то система однородных уравнений имеет нетривиальное решение.

Определение вместе с предшествующей ему теоремой можно переписать в терминах теории линейных пространств⁶⁾

Т

Теорема 3. Множество решений системы однородных уравнений образует линейное подпространство пространства $ mathbb A^{n} $. Размерность этого подпространства равна $ n-mathfrak r $, а фундаментальная система решений образует его базис.

?

Пусть матрица системы $ AX=mathbb O $ квадратная и

$$ operatorname{rank} (A) =n_{}-1 , .$$
Доказать, что если ненулевой минор матрицы порядка $ n_{}-1 $
соответствует какому-нибудь элементу $ j_{} $-й строки, то система алгебраических
дополнений к элементам $ a_{j1},dots,a_{jn}^{} $ этой строки составляет ФСР для $ AX=mathbb O_{} $.
Например, для системы
$$
left{
begin{array}{ll}
a_{11}x_1 +a_{12}x_2+a_{13}x_3&=0,\
a_{21}x_1 +a_{22}x_2+a_{23}x_3&=0
end{array} right.
$$
ФСР состоит из решения
$$
x_1=left|
begin{array}{ll}
a_{12} & a_{13} \
a_{22} & a_{23}
end{array}
right| ,
x_2=-left|
begin{array}{ll}
a_{11} & a_{13} \
a_{21} & a_{23}
end{array}
right| ,
x_3=left|
begin{array}{ll}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right| ,
$$
если только хотя бы один из миноров отличен от нуля.

Теперь обсудим способы нахождения ФСР.

1.

Первый из них получается из общего метода решения системы линейных уравнений, рассмотренного в предыдущем пункте. Так же, как и в том пункте, сделаем упрощающее обозначения предположение, что зависимыми переменными являются первые $ x_{1},dots,x_{mathfrak r} $,
т.е. общее решение задается формулами
$$
x_j=gamma_{j,mathfrak{r}+1}x_{mathfrak{r}+1}+dots+gamma_{jn}x_n
npu jin {1,dots, mathfrak{r}} .
$$
Иными словами, вектор столбец
$$
X=left(begin{array}{c}
gamma_{1,mathfrak{r}+1}x_{mathfrak{r}+1}+dots+gamma_{1n}x_n \
gamma_{2,mathfrak{r}+1}x_{mathfrak{r}+1}+dots+gamma_{2n}x_n \
vdots \
gamma_{mathfrak{r},mathfrak{r}+1}x_{mathfrak{r}+1}+dots+gamma_{mathfrak{r}n}x_n \
x_{mathfrak{r}+1} \
x_{mathfrak{r}+2} \
vdots \
x_{n}
end{array}right)
$$
будет решением однородной системы при любых наборах значений основных переменных $ x_{mathfrak{r}+1},dots,x_{n} $. Представим этот вектор в виде суммы векторов:
$$
=x_{mathfrak{r}+1} underbrace{
left(begin{array}{c}
gamma_{1,mathfrak{r}+1} \
gamma_{2,mathfrak{r}+1} \
vdots \
gamma_{mathfrak{r},mathfrak{r}+1} \
1 \
0 \
vdots \
0
end{array}right)}_{X_1} +
x_{mathfrak{r}+2}
underbrace{left(begin{array}{c}
gamma_{1,mathfrak{r}+2} \
gamma_{2,mathfrak{r}+2} \
vdots \
gamma_{mathfrak{r},mathfrak{r}+2} \
0 \
1 \
vdots \
0
end{array}right)}_{X_2}+dots+
x_{n}
underbrace{left(begin{array}{c}
gamma_{1n} \
gamma_{2n} \
vdots \
gamma_{mathfrak{r}n} \
0 \
0 \
vdots \
1
end{array}right)}_{X_{n-mathfrak r}} .
$$
Таким образом, любое решение однородной системы представимо в виде линейной комбинации $ n_{}- mathfrak r $ фиксированных решений. Именно эти решения и можно взять в качестве ФСР — их линейная независимость очевидна (единицы в нижних частях каждого вектора $ X_{j} $ расположены на разных местах, и ни какая линейная комбинация столбцов $ { X_1,dots,X_{n-mathfrak r} } $ не сможет обратить их одновременно в нуль).

Оформим этот способ построения ФСР в теорему:

Т

Теорема 4. Если система уравнений $ AX=mathbb O $ имеет структуру матрицы $ A_{} $ вида:

$$ A = left[ E_{mathfrak r} mid P_{mathfrak r times (n-mathfrak r)} right] , $$
то ее ФСР состоит из столбцов матрицы
$$ left[ begin{array}{r} – P^{top} \ hline E_{n-mathfrak r} end{array} right] . $$

Для одной и той же системы уравнений, фундаментальная система решений может быть построена разными способами и иметь разный вид. Как только мы смогли упростить систему линейных уравнений таким образом, чтобы выделить в ней основные и зависимые переменные, остается только зафиксировать несколько наборов значений для основных переменных.
$$
begin{array}{lll}
x_{{mathfrak r}+1}={mathbf x}_{1,{mathfrak r}+1} , & dots, &x_n={mathbf x}_{1n} \
dots & & dots \
x_{{mathfrak r}+1}={mathbf x}_{n-{mathfrak r},{mathfrak r}+1} , & dots, &
x_n={mathbf x}_{n-{mathfrak r},n}
end{array}
mbox{ чтобы }
det {mathbf D}= det
left[ begin{array}{lcl}
{mathbf x}_{1,{mathfrak r}+1} & dots & {mathbf x}_{1n} \
dots & & dots \
{mathbf x}_{n-{mathfrak r},{mathfrak r}+1} & dots & {mathbf x}_{n-{mathfrak r},n}
end{array}
right]
$$
был бы ненулевым.
Проще всего взять в качестве $ {mathbf D} $ единичную матрицу $ E_{n-{mathfrak r}} $, что и было сделано выше.

П

Пример. Найти ФСР для системы уравнений

$$
left{ begin{array}{rrrrcl}
x_1-&x_2+&x_3-&x_4&=&0, \
x_1-&x_2+&2x_3+&3x_4&=&0, \
x_1-&x_2-&x_3-&9x_4&=&0
end{array}
right.
$$

Решение. Приводим систему к трапециевидному виду:
$$
left{ begin{array}{rrrrl}
x_1-&x_2+&x_3-&x_4=&0, \
&&x_3+&4x_4=&0
end{array}
right.
$$
В качестве зависимых переменных можно взять, например, $ x_{1} $ и $ x_{3} $.
$$
begin{array}{cc|cc}
x_1 & x_3 & x_2 & x_4 \ hline
1 & 0 & 1 & 0 \
5 & -4 & 0 & 1
end{array}
$$

Ответ.⁷⁾ $ { [1,1,0,0]^{top}, [5,0,-4,1]^{top} } $.

2.

Этот способ напоминает вычисление обратной матрицы методом приписывания единичной матрицы. Транспонируем матрицу $ A_{} $ системы и припишем к ней справа единичную матрицу порядка $ n_{} $:
$$
left[ A^{top} | E_n right] = left(begin{array}{llllccccc}
a_{11} & a_{21} & dots & a_{m1} & 1 & 0 & 0 & dots & 0 \
a_{12} & a_{22} & dots & a_{m2} & 0 & 1 & 0 & dots & 0 \
a_{13} & a_{23} & dots & a_{m3} & 0 & 0 & 1 & dots & 0 \
vdots & & & vdots & vdots & & & ddots & vdots \
a_{1n} & a_{2n} & dots & a_{mn} & 0 & 0 & 0 & dots & 1
end{array}
right)
;
$$
здесь $ {} |_{} {} $ означает конкатенацию. Получившуюся матрицу элементарными преобразованиями строк приводим к форме:
$$
left(
begin{array}{cc}
hat A & K \
mathbb O & L
end{array}
right)
=
left(begin{array}{cccccccc|ccccc}
color{Red}{star} & * & * & dots & * & * & * & * & * & * & * & dots & * \
0 & color{Red}{star} & * & dots & * & * & * & * & * & * & * & dots & * \
0 & 0 & color{Red}{star} & dots & * & * & * & * & * & * & * & dots & * \
vdots & & & ddots & & vdots & & & vdots & & & & vdots \
0 & 0 & dots & & 0 & color{Red}{star} & * & * & * & * & * & dots & * \
hline
0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box \
vdots & & & & & vdots & & & vdots & & & & vdots \
0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box
end{array}
right)
begin{array}{l}
left.begin{array}{l}
\ \ \ \ \
end{array}right} mathfrak r
\
left. begin{array}{l}
\ \ \
end{array}right} n – mathfrak r
end{array} .
$$
Элементы трапециевидной матрицы $ hat A $, обозначенные $ color{Red}{star} $, могут быть равны нулю, но $ operatorname{rank}(hat A)= mathfrak r_{} $. В этом случае строки матрицы $ L_{} $, образовавшейся в правом нижнем углу (ее элементы обозначены $ Box $), составляют ФСР для системы $ AX=mathbb O $.

П

Пример. Найти ФСР для системы уравнений

$$
left{
begin{array}{rrrrrrl}
x_1 &+2,x_2&+ x_3&+3,x_4&-x_5&+2,x_6=&0,\
-3x_1 &-x_2&+ 2,x_3&-4,x_4&+x_5&-x_6=&0,\
x_1 &+x_2&+ 3,x_3&+2,x_4&+x_5&+3,x_6=&0,\
-8,x_1 &-7,x_2&+ 4,x_3&-15,x_4&+6,x_5&-5,x_6=&0,\
6x_1 &+5,x_2& +5,x_3&+11,x_4 &&+9,x_6=&0.
end{array} right.
$$
Решение. Преобразуем матрицу $ left[ A^{top} | E_6 right] $

$$
left(begin{array}{rrrrr|rrrrrr}
1 & -3 & 1 & -8 & 6 & 1 \
2 & -1 & 1 & -7 & 5 & & 1 \
1 & 2 & 3 & 4 & 5 & & & 1 \
3 & -4 & 2 & -15 & 11 &&&& 1 \
-1 & 1 & 1 & 6 & 0 &&&&& 1 \
2 & -1 & 3 & -5 & 9 &&&&&& 1
end{array}
right)_{6times 11}
$$
к трапециевидной форме с помощью элементарных преобразований строк:
$$
rightarrow left(begin{array}{rrrrr|rrrrrr}
1 & -3 & 1 & -8 & 6 & 1 \
0 & 5 & -1 & 9 & -7 &-2 & 1 \
0 & 5 & 2 & 12 & -1 &-1 &0 & 1 \
0 & 5 & -1 & 9 & -7 &-3&0&0& 1 \
0 & -2 & 2 & -2 & 6 &1&0&0&0& 1 \
0 & 5 & 1 & 11 & -3 &-2&0&0&0&0& 1
end{array}
right)rightarrow
$$
$$
rightarrow left(begin{array}{rrrrr|rrrrrr}
1 & -3 & 1 & -8 & 6 & 1 \
0 & 5 & -1 & 9 & -7 &-2 & 1 \
0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \
0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \
0 & 0 & 8/5 & 8/5 & 16/5 &1/5&2/5&0&0& 1 \
0 & 0 & 2 & 2 & 4 &0&-1&0&0&0& 1
end{array}
right)rightarrow
$$
$$
rightarrow left(begin{array}{rrrrr|rrrrrr}
1 & -3 & 1 & -8 & 6 & 1 \
0 & 5 & -1 & 9 & -7 &-2 & 1 \
0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \
0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \
0 & 0 & 0 & 0 & 0 &-1/3&14/15&-8/15&0& 1 \
0 & 0 & 0 & 0 & 0 &-2/3&-1/3&-2/3&0& 0 & 1
end{array}
right)
$$

Ответ.⁸⁾ $ { [-1,-1,0,1,0,0]^{top}, [-1/3,14/15,-8/15,0, 1,0]^{top},
[-2/3,-1/3,-2/3,0, 0, 1]^{top} } $.

§

Обоснование метода

☞

ЗДЕСЬ

3.

Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.

Т

Теорема. Пусть матрица системы $ AX=mathbb O $ квадратная и
$ operatorname{rank} (A) ={mathfrak r} $. Тогда характеристический полином матрицы $ A_{} $ имеет вид:

$$ det(A-lambda E)=(-1)^nlambda^{n-mathfrak r}(lambda^{mathfrak r}
+a_1lambda^{{mathfrak r}-1}+dots+a_{n-mathfrak r} ) $$
и ненулевые столбцы матрицы
$$
A^{{mathfrak r}}+a_1A^{{mathfrak r}-1}+dots+a_{n-mathfrak r}E
$$
составляют ФСР для $ AX=mathbb O $.

П

Пример. Найти ФСР для системы уравнений

$$
left{
begin{array}{rrrrr}
x_1&+x_2&-x_3&-x_4&=0 \
2x_1&+3x_2&+x_3&-2x_4&=0
end{array}
right.
$$

Решение. Здесь
$$
A=
left(
begin{array}{rrrr}
1 & 1 & -1 & -1 \
2 & 3 & 1 & -2 \
0 & 0 & 0 & 0 \
0 & 0 & 0 & 0
end{array}
right), quad det (A-lambda E) = lambda^2(lambda^2-4lambda+1),
$$
$$
A^2-4A+E=
left(
begin{array}{rrrrr}
0 & 0 & 4 & 1 \
0 & 0 & -3 & 0 \
0 & 0 & 1 & 0 \
0 & 0 & 0 & 1
end{array}
right)
$$

Ответ.⁹⁾ $ { [4_{},-3,1,0]^{top}, [1,0,0,1]^{top} } $.

§

Блок-схемы зависимости множества решений системы уравнений $ AX= mathcal B $ от комбинации чисел $ n, mathfrak r $

☞

ЗДЕСЬ.

Геометрический смысл введенных определений поясним на примере $ mathbb R^{3} $.
Уравнение
$$
a_1x_1+a_2x_2+a_3x_3=b
$$
— при фиксированных вещественных коэффициентах $ a_1,a_2,a_3 $ (хотя бы один из них считаем отличным от нуля) и $ b_{} $ — задает плоскость. Если, к примеру, $ a_1ne 0 $, то из уравнения получаем выражение для $ x_{1} $ как функции $ x_2,x_3 $:
$$
x_1=frac{b}{a_1}-frac{a_2}{a_1}x_2-frac{a_3}{a_1}x_3 .
$$
В этом представлении переменные $ x_{2} $ и $ x_{3} $ могут принимать любые вещественные значения независимо друг от друга, а вот переменная $ x_{1} $ полностью определяется заданием $ x_{2} $ и $ x_{3} $. С одной стороны, последняя формула определяет общее решения системы линейных уравнений (которая в нашем частном случае состоит из одного-единственного уравнения); переменные $ x_{2} $ и $ x_{3} $ выбраны основными, а $ x_{1} $ оказывается зависимой. Строго говоря, координаты любой точки плоскости можно представить формулами
$$x_1=frac{b}{a_1}-frac{a_2}{a_1}t-frac{a_3}{a_1}u, x_2=t, x_3=u quad npu quad {t,u} subset mathbb R , $$
которые называются параметрическим представлением плоскости. Таким образом, получили геометрическую интерпретацию общего решения системы уравнений. Идем далее: представим последние формулы в векторной форме:
$$
left(
begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=
left(
begin{array}{c}
b/a_1- t, a_2/a_1- u, a_3/a_1 \ t \ u
end{array}
right)=
left(
begin{array}{c}
b/a_1\ 0 \ 0
end{array}
right)+
t
left(
begin{array}{c}
-a_2/a_1\ 1 \ 0
end{array}
right)
+
u
left(
begin{array}{c}
-a_3/a_1\ 0 \ 1
end{array}
right) .
$$
Какой геометрический смысл имеет каждое из слагаемых? Первое слагаемое
$$ X_0=left(
begin{array}{c}
b/a_1\ 0 \ 0
end{array}
right)
$$
получается при задании $ t=0,u=0_{} $ в общем решении. Это — частное решение нашего уравнения и определяет точку, через которую проходит плоскость. Два оставшихся столбца
$$ X_1=left(
begin{array}{c}
-a_2/a_1\ 1 \ 0
end{array}
right) quad u quad
X_2=left(
begin{array}{c}
-a_3/a_1\ 0 \ 1
end{array}
right)
$$
не задают решения нашего уравнения — если только $ bne 0_{} $. Но оба удовлетворяют однородному уравнению
$$
a_1x_1+a_2x_2+a_3x_3=0 ,
$$
Последнее также определяет плоскость — параллельную исходной и проходящую через начало координат. Первая плоскость получается из второй сдвигом (параллельным переносом) на вектор
$ vec{OX_0} $: и этот факт составляет геометрическую интерпретацию теоремы, сформулированной в конце

☞

ПУНКТА:

Т

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Координаты произвольной точки плоскости $ a_1x_1+a_2x_2+a_3x_3=0 $ задаются соотношениями
$$
left(
begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=tX_1+uX_2 .
$$
Векторы пространства $ vec{OX_1} $ и $ vec{OX_2} $ являются базисными векторами плоскости — любой вектор $ vec{OX} $, лежащий в плоскости, через них выражается и они линейно независимы. Но $ X_{1} $ и $ X_{2} $ определяют фундаментальную систему решений однородного уравнения. Таким образом, мы получили геометрическую интерпретацию для ФСР: она задает базисные векторы плоскости, проходящей через начало координат.

Теперь рассмотрим систему из двух уравнений:
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+a_{13}x_3 &=&b_1,\
a_{21}x_1 +a_{22}x_2+a_{23}x_3 &=&b_2.
end{array}right.
$$
Ее можно интерпретировать как пересечение двух плоскостей в $ mathbb R^{3} $. Здесь уже возможны варианты: пересечение может оказаться как пустым так и непустым. От чего это зависит? — В соответствии с теоремой Кронекера-Капелли, надо сравнить два числа
$$
operatorname{rank}
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23}
end{array}
right)
quad u quad
operatorname{rank}
left(
begin{array}{cccc}
a_{11} & a_{12} & a_{13} & b_1 \
a_{21} & a_{22} & a_{23} & b_2
end{array}
right) .
$$
Очевидно, ни одно из них не может быть большим $ 2_{} $. Если оба равны $ 2_{} $ и этот факт обеспечен, например, условием
$$
left|
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right| ne 0,
$$
то решения системы определяют прямую в пространстве. Действительно, при таком условии систему можно разрешить относительно неизвестных $ x_{1} $ и $ x_{2} $ и представить общее решение в виде:
$$
x_1= frac{left|begin{array}{cc} b_1 & a_{12} \ b_2 & a_{22} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|}+
frac{left|begin{array}{cc} a_{12} & a_{13} \ a_{21} & a_{23} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|}x_3
,
quad
x_2= frac{left|begin{array}{cc} a_{11} & b_{1} \ a_{12} & b_{2} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|}-
frac{left|begin{array}{cc} a_{11} & a_{13} \ a_{21} & a_{23} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|}x_3 .
$$
В этих формулах переменная $ x_{3} $ принимает любое значение, а значения переменных $ x_{1} $ и $ x_{2} $ линейно выражаются через $ x_{3} $. Общее решение фактически задает прямую в параметрическом виде: координаты произвольной ее точки определяются формулами
$$
left(
begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=X_0+tX_1 ,
$$
где вектор
$$
quad X_0 = left(frac{left|begin{array}{cc} a_{11} & b_{1} \ a_{12} & b_{2} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|} , frac{left|begin{array}{cc} a_{11} & b_{1} \ a_{12} & b_{2} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|}, 0right)^{top}
$$
задает координаты точки, лежащей на прямой (т.е. принадлежащей пересечению плоскостей),
а вектор
$$
X_1= left(frac{left|begin{array}{cc} a_{12} & a_{13} \ a_{21} & a_{23} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|},
–
frac{left|begin{array}{cc} a_{11} & a_{13} \ a_{21} & a_{23} end{array} right|}{left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|}, 1
right)^{top}
$$
является направляющим для прямой. С тем же успехом мы могли бы взять в качестве направляющего вектор, получающийся растяжением $ X_{1} $:
$$
tilde X_1 =
left(left|begin{array}{cc} a_{12} & a_{13} \ a_{21} & a_{23} end{array} right|,
–
left|begin{array}{cc} a_{11} & a_{13} \ a_{21} & a_{23} end{array} right|, left|begin{array}{cc} a_{11} & a_{12} \ a_{21} & a_{22} end{array} right|
right)^{top} .
$$

Очевидно, что любой из векторов $ X_{1} $ или $ tilde X_1 $ задает фундаментальную систему решений однородной системы уравнений¹⁰⁾
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+a_{13}x_3 &=&0,\
a_{21}x_1 +a_{22}x_2+a_{23}x_3 &=&0.
end{array}right.
$$
Последняя определяет прямую в $ mathbb R^3 $, проходящую через начало координат. Мы снова получаем интерпретацию теоремы: общее решение неоднородной системы получается сдвигом (параллельным переносом) общего решения однородной системы на вектор $ vec{OX_0} $.

Мы рассмотрели пока только случай пересекающихся плоскостей в пространстве. Его можно считать общим, т.е. случаем «как правило»: две случайным образом выбранные плоскости в $ mathbb R^{3} $ пересекаться будут. Исследуем теперь исключительный случай — параллельности плоскостей. Исключительность этого случая может быть проверена и аналитикой. Для несовместности системы из двух уравнений необходимо, чтобы ранг ее матрицы
$$
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23}
end{array}
right)
$$
оказался меньшим $ 2_{} $. Это равносильно тому, что все миноры второго порядка этой матрицы обращаются в нуль:
$$
left|
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right|=0,
left|
begin{array}{cc}
a_{12} & a_{13} \
a_{22} & a_{23}
end{array}
right| =0,
left|
begin{array}{cc}
a_{11} & a_{13} \
a_{21} & a_{23}
end{array}
right|=0 .
$$
Эти условия можно переписать в виде
$$
frac{a_{11}}{a_{21}}=frac{a_{12}}{a_{22}}=frac{a_{13}}{a_{23}} ;
$$
и, если обозначить общую величину последний отношений через $ tau_{} $, то получаем:
$$
(a_{11},a_{12},a_{13})=tau (a_{21},a_{22},a_{23}) .
$$
Если вспомнить, что каждый из этих наборов коэффициентов задает вектор $ vec{OA^{[1]}} $ в $ mathbb R^{3} $, перпендикулярный соответствующей плоскости, то, в самом деле, плоскости, определяемые уравнениями, оказываются параллельными. Пересекаться они, как правило, не будут: для пересечения необходимо, чтобы
расширенная матрица системы
$$
left(
begin{array}{cccc}
a_{11} & a_{12} & a_{13} & b_1 \
a_{21} & a_{22} & a_{23} & b_2
end{array}
right)
$$
имела ранг меньший $ 2_{} $. Это возможно только при условии когда коэффициенты правых частей удовлетворяют соотношению
$$ b_1 = tau b_2 $$
при величине $ tau_{} $ определенной выше.
При выполнении этого условия второе уравнение получается из первого домножением на $ tau_{} $ и соответствующие плоскости попросту совпадают.

Перейдем теперь к системе из трех уравнений:
$$
left{
begin{array}{rrrl}
a_{11}x_1 +&a_{12}x_2+&a_{13}x_3=&b_1, \
a_{21}x_1 +&a_{22}x_2+&a_{23}x_3=&b_2, \
a_{31}x_1 +&a_{32}x_2+&a_{33}x_3=&b_3.
end{array}
right.
$$
Вариантов взаимного расположения трех плоскостей в $ mathbb R^{3} $ уже значительно больше.
Какой из них будет самым распространенным, то есть случаем «как правило»? Геометрически ответ очевиден:
если пересечение двух плоскостей определяет, как правило, прямую, то эта прямая пересекается с третьей плоскостью,
как правило, в одной-единственной точке. И алгебра подтверждает геометрию: в комментарии к теореме Крамера
говорится, что система, число уравнений которой совпадает с числом неизвестных, как правило, имеет единственное
решение. Условие для этого случая «как правило» дается той же теоремой Крамера:
$$
left|
begin{array}{lll}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right| ne 0 .
$$

Теорема Кронекера-Капелли в этом случае не нужна — нет, она остается справедливой! — но проверка условия на ранги матриц тривиальна: они оба равны $ 3_{} $. Если же указанный определитель обращается в нуль, то этот факт эквивалентен тому, что три строки определителя линейно зависимы. Например, возможно, что строка $ (a_{31},a_{32}, a_{33}) $ может быть представлена в виде линейной комбинации первых двух строк. Вспомним геометрический смысл этих строк: они задают координаты векторов, перпендикулярных соответствующим плоскостям. Если система уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+a_{13}x_3 &=&b_1,\
a_{21}x_1 +a_{22}x_2+a_{23}x_3 &=&b_2
end{array}right.
$$
определяет прямую в $ mathbb R^{3} $, то оба вектора $ vec{OA^{[1]}} $ и $ vec{OA^{[2]}} $ при $ A^{[1]}= (a_{11},a_{12}, a_{13}) $ и $ A^{[2]}= (a_{21},a_{22}, a_{23}) $ перпендикулярны этой прямой; любая их комбинация также перпендикулярна этой прямой, а, следовательно, плоскость
$$ a_{31}x_1 +a_{32}x_2+a_{33}x_3 =b_3 $$
будет ей параллельна.

Статья не закончена!

Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти

☞

ЗДЕСЬ.

Задача решения системы линейных уравнений
$$
left{
begin{array}{rrrr}
3x_1&+4x_2&-x_3&=2, \
x_1&-2x_2&+3x_3&=1
end{array}
right.
$$
может быть рассмотрена с двух точек зрения. С одной стороны, переписав систему в виде
$$
x_1left(begin{array}{r}
3 \ 1
end{array}
right)+
x_2left(begin{array}{r}
4 \ -2
end{array}
right)+
x_3left(begin{array}{r}
-1 \ 3
end{array}
right)=
left(begin{array}{r}
2 \ 1
end{array}
right) ,
$$
можно говорить о поиске линейной комбинации столбцов
$$
left(begin{array}{r}
3 \ 1
end{array}
right),
left(begin{array}{r}
4 \ -2
end{array}
right),
left(begin{array}{r}
-1 \ 3
end{array}
right)
$$
равной заданному столбцу
$$
left(begin{array}{r}
2 \ 1
end{array}
right) .
$$
В случае произвольной системы, записанной в матричном виде
$$ A_{mtimes n}X=mathcal B_{m times 1} $$
совместность системы интерпретировать в смысле принадлежности столбца $ mathcal B $ линейной оболочке столбцов $ A_{[1]},dots,A_{[n]} $:
$$ mathcal B=x_1 A_{[1]}+dots+x_nA_{[n]} quad iff quad mathcal B in mathcal L (A_{[1]},dots,A_{[n]}) . $$
В случае положительного ответа числа $ x_{1},dots,x_n $ интерпретируются как координаты столбца $ mathcal B $ в системе столбцов¹¹⁾ $ {A_{[1]},dots,A_{[n]}} $.

С другой стороны, к той же задаче решения системы уравнений, в предыдущем ПУНКТЕ мы подошли с другой стороны. Первое из уравнений системы
$$ 3,x_1+4,x_2-x_3=2 $$
можно интерпретировать так: скалярное произведение векторов $ vec{{mathbf OA}^{[1]}} $ и
$ vec{{mathbf OX}} $ равно фиксированному числу $ 2_{} $. Здесь вектора рассматриваются в пространстве строк $ mathbb R_{}^{3} $; считается, что каждый вектор имеет начало в начале координат $ mathbf O=[0,0,0] $, а конец — в точке с координатами $ [3,4,-1] $ или, соответственно, $ [x_1,x_2,x_3] $. Если скалярное произведение векторов обозначать скобками $ langle {} mbox{ } rangle $, то систему уравнений можно переписать в виде
$$ langle vec{{mathbf OA}^{[1]}} , vec{{mathbf OX}} rangle=2, langle vec{{mathbf OA}^{[2]}} , vec{{mathbf OX}} rangle=1 quad npu quad A^{[1]} = [3,4,-1], A^{[2]}=[1,-2,3] $$
— строках матрицы $ A_{} $. И задачу решения такой системы понимать в смысле: найти координаты всех векторов-строк $ [x_1,x_2,x_3] $ которые обеспечат нам заданные значения скалярных произведений с двумя фиксированными векторами.

Геометрическая интерпретация еще более упрощается если рассмотреть случай однородной системы уравнений. Так, решить систему уравнений
$$
left{
begin{array}{rrrr}
3x_1&+4x_2&-x_3&=0, \
x_1&-2x_2&+3x_3&=0
end{array}
right.
$$
означает подобрать вектор $ vec{{mathbf OX}} $ перпендикулярный (ортогональный) одновременно обоим векторам $ vec{{mathbf OA}^{[1]}} $ и $ vec{{mathbf OA}^{[2]}} $. Очевидно, что таких векторов в $ mathbb R^{3} $ бесконечно много — найдя хотя бы один такой вектор $ vec{{mathbf OX}} $, другие получим его растяжением: $ alpha cdot vec{{mathbf OX}} $ остается перпендикулярным векторам $ vec{{mathbf OA}^{[1]}} $ и $ vec{{mathbf OA}^{[2]}} $ при $ forall alpha in mathbb R $.

Все эти геометрические соображения обобщаются в произвольное пространство $ mathbb R_{}^{n} $ строк или столбцов, состоящих из $ n_{} $ вещественных чисел (компонент). Для этого приходится обобщать понятие скалярного произведения. В общем случае оно вводится аксиоматически (и, более того, в одном и том же множестве может быть определено разными способами, см.

☞

ЕВКЛИДОВО ПРОСТРАНСТВО ). Мы сейчас не будем залезать так глубоко в эту аксиоматику, а просто определим скалярное произведение двух строк $ X=[x_1,x_2,dots,x_n] $ и $ Y=[y_1,y_2,dots,y_n] $ формулой
$$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n $$
и продекларируем без обоснований, что все привычные нам по случаям $ mathbb R^{2} $ и $ mathbb R^{3} $ свойства скалярного произведения будут выполнены.

В терминах скалярного произведения, задачу решения системы линейных уравнений можно переформулировать как поиск строки $ X=[x_1,x_2,dots,x_n] $, ортогональной всем строкам матрицы $ A_{} $:
$$ langle A^{[1]},X rangle=0, langle A^{[2]},X rangle=0,dots, langle A^{[m]},X rangle=0 . $$
Множество таких строк образует линейное подпространство пространства $ mathbb R_{}^{n} $, это подпространство является ортогональным дополнением линейной оболочки
$ mathcal L ( A^{[1]}, A^{[2]},dots, A^{[m]} ) $ в пространстве $ mathbb R_{}^{n} $.
Это подпространство называется нуль-пространством матрицы или ядром матрицы $ A_{} $ и обозначается¹²⁾ $ {mathcal K}er (A) $.
Фундаментальная система решений системы $ AX=mathbb O $ составляет базис этого подпространства. Для произвольного линейного пространства количество векторов его базиса называется размерностью пространства и обозначается $ operatorname{dim} $. Во введенных обозначениях теорема из

☞

ПУНКТА переформулируется так:

Т

Теорема. $ operatorname{dim} left( {mathcal K}er (A) right)=n- mathfrak r $, где $ n_{} $ — количество столбцов матрицы $ A_{} $, а $ mathfrak r=operatorname{rank} (A) $ — ее ранг.

Здесь рассматриваются системы только с вещественными коэффициентами. Постановка задачи тесно увязана с основной задачей

☞

МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ.

В практических задачах часто бывает нужно найти решение, удовлетворяющее
большому числу возможно противоречивых требований. Если такая задача
сводится к системе линейных уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&b_1\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&b_2\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&b_m
end{array}right.
iff
AX={mathcal B}
$$
при числе уравнений $ m_{} $ большем числа неизвестных $ n_{} $, то такая переопределенная система, как правило, несовместна (см. рассуждения

☝

ВЫШЕ ). В этом случае задача может быть решена только путем выбора некоторого компромисса: все требования могут быть удовлетворены не полностью,
а лишь до некоторой степени.

Псевдорешением системы уравнений называется столбец $ X_{} $, обеспечивающий минимум величины
$$
sum_{j=1}^m [a_{j1}x_1 +a_{j2}x_2+dots+a_{jn}x_n-b_j]^2
$$
или, что то же, минимум квадрату евклидовой нормы вектора $ AX- mathcal B $:
$$ min_{Xin mathbb R^n} left| AX- mathcal B right|^2 . $$

Такому определению можно также соотнести вероятностную интерпретацию. Пусть для определения неизвестных величин $ x_{1},dots,x_n $ проводятся $ m_{} $ экспериментов, описываемых линейными уравнениями:
$$a_{j1}x_1 +a_{j2}x_2+dots+a_{jn}x_n =b_j npu jin {1,dots,m}
.$$
При этом величины $ a_{jk}^{} $ — известные постоянные, не подверженные погрешностям, сопутствующим экспериментам (наблюдениям), в то время как величины $ b_{j} $ этим
погрешностям подвержены. Формально каждое из равенств следует рассматривать как
приближенное.
Понятно, что при таких обстоятельствах не имеет смысла гоняться за
точным решением системы (его может и не
существовать вовсе!). Искать следует приближенное решение, оптимальное
в некотором смысле. Оказывается, что именно выбор критерия в виде cуммы квадратов разностей левых и правых частей системы обеспечивает то, что псевдорешение дает
максимально правдоподобные значения неизвестных величин $ x_{1},dots,x_n $.

?

На дубовой колоде лежит мелкая монетка. К колоде
по очереди подходят четыре рыцаря и каждый наносит удар мечом, стараясь
попасть по монетке. Все промахиваются. Расстроенные,
рыцари уходят в харчевню пропивать злосчастную монетку. Укажите
максимально правдоподобное ее расположение, имея перед глазами зарубки:

$$
begin{array}{rrcr}
3, x &- 2, y&=& 6,\
x &-3,y&=&-3,\
11,x& + 14,y&=& 154, \
4,x&+y&=&48.
end{array}
$$

Т

Теорема. Существует псевдорешение системы
$ AX= {mathcal B} $ и оно является решением системы

$$
left[A^{top}A right]X=A^{top} {mathcal B} .
$$
Это решение будет единственным тогда и только тогда, когда $ operatorname{rank} (A) =n $.

<note cert>
Образно говоря: как правило несовместная система $ AX={mathcal B} $ станет совместной если мы домножим обе ее части слева на матрицу $ A^{top} $.
<note>

Доказательство

☞

ЗДЕСЬ.

П

Пример. Найти псевдорешение системы

$$x_1+x_2 = 2, x_1-x_2 = 0, 2, x_1+x_2 = 2 .$$

Решение. Имеем:
$$A=left( begin{array}{rr}
1 & 1 \
1 & -1 \
2 & 1
end{array}
right),
operatorname{rank}(A) =2,
{mathcal B} =
left( begin{array}{r}
2 \ 0 \ 2
end{array}
right),
A^{top}A= left( begin{array}{rr}
6 & 2 \
2 & 3
end{array}
right),
A^{top} {mathcal B} =
left( begin{array}{r}
6 \ 4
end{array}
right).
$$

Ответ. $ x_1=5/7, x_2 =6/7 $.

[1]. Стренг Г. Линейная алгебра и ее применения. М.Мир.1980

[2]. Утешев А.Ю., Калинина Е.А. Лекции по высшей алгебре. Часть II. Учеб. пособие. СПб. «СОЛО». 2007. 279 c.