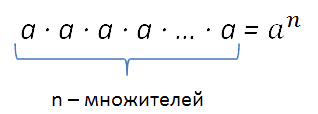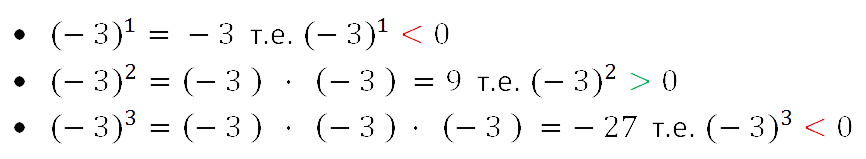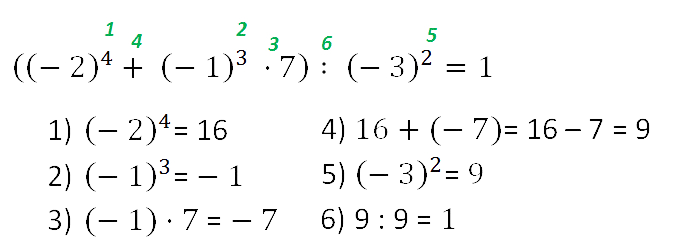Как найти число зная его степень

Действия со степенями

Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а. То есть а n =a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.

• 3 4 =3×3×3×3 число 3 берем 4 раза (показатель 4)
• 21 3 =21×21×21 число 21 берем 3 раза (показатель 3)

Свойства степени (применимы для степеней с одинаковым основанием)

При умножении степеней с одинаковым основанием основание оставляют тем же, а показатели складывают:

a n × a m =a n +m

а 2 ×а 8 =а 2+8 =а 10

5 5 ×5 3 ×5 4 =5 5+3+4 =5 12

При делении степеней с одинаковым основанием основание оставляют тем же, а показатели вычитают:

a n : a m =a n — m

с 12 :с 5 =с 12-5 = с 7

3 23 :3 20 =3 23-20 = 3 3

Возведение степени в степень

При возведении степени в степень основание оставляют тем же, а показатели умножают:

(a n ) m =a n×m

При возведении в степень произведения разных множителей необходимо возвести в эту степень каждый множитель:

(a×b×c) m =a m ×b m ×c m

(сmn) 5 =c 5 m 5 n 5

(3 2 5 4 ) 6 =3 12 5 24

Степень дроби (степень частного)

При возведении в степень обыкновенной дроби необходимо возвести в данную степень числитель и знаменатель дроби:

Источник

Как найти степень числа если известно

Степень — это краткая запись произведения одинаковых сомножителей. Основание степени — это число, которое нужно возвести в степень. А показатель степени — это число, в которое нужно возвести основание степени.

Основанием степени может быть любое целое число и десятичная дробь.

Возведению в степень обратны два действия:

• извлечение корня,
• нахождение логарифма.

Во-первых, сначала надо разобраться, что значит обратное действие. Так деление есть обратное действие умножению, а вычитание — сложению. Это вытекает из рассуждений, что произведение, получившееся от перемножения двух множителей, позволяет найти один из множителей, если известен другой. Например, 5 * 3 = 15. Если нам неизвестен второй множитель (5 * ? = 15), то его можно найти, выполнив деление: 15 : 5 = 3. Операция не меняется, если неизвестен первый множитель: ? * 3 = 15, 15 : 3 = 5. Это связано с тем, что умножение подчиняется переместительному закону (от перемены мест множителей произведение не меняется).

Аналогично и для вычитания: ? + 10 = 33, 33 — 10 = 23 или ? + 23 = 33, 33 — 23 = 10. Неважно, какое слагаемое неизвесто, его всегда находят вычитанием.

Но не все так просто с возведением в степень. Здесь от перестановки основания степени и показателя степени результат изменяется, т.е. возведение в степень не подчиняется переместительному закону: 4 3 = 64, но 3 4 = 81. (Хотя есть исключения: 2 4 = 16 и 4 2 = 16.)

Поэтому, если нам известен результат операции возведения в степень и показатель степени, то, чтобы найти основание степени, надо извлечь корень известной по показателю степени из результа возведения в степень:

? 3 = 125, следовательно 3 √125 = 5.

Если же известны основание степени и результат возведения в степень, а надо найти показатель степени, то используется такая операция как нахождение логарифма:

Самое разумное разложить число на простые множители, тогда можно найти и основание и показатель степени.
Если известно основание, то показатель можно найти логарифмированием, например,
2^x=8
Чтобы найти x нужно прологарифмировать обе части по основанию 2
x = log по основанию 2 от 8 = ln 8 / ln 2 (так можно на калькуляторе посчитать) = 3
Если известен показатель, то основание находится извлечением корня, например,
x^3=8
извлекаем корень кубический из обоих частей
x=корень кубический из 8 = 2

Если же неизвестно ни то ни другое разложи число на простые множители, это делается последовательным делением числа на простые множители
614656 / 2 = 307328
307328 / 2 = 153664
153664 / 2 = 76832
76832 / 2 = 38416
38416 / 2 = 19208
19208 / 2 = 9604
9604 / 2 = 4802
4802 / 2 = 2401
2401 не делится на 2, на 3, на 5 (последовательно перебираем простые числа)
2407 / 7 = 343
343 / 7 = 49
49 / 7 = 7
7 / 7 = 1
Итого мы делили на 2 восемь раз и на 7 четыре раза, следовательно
614656 = 2^8 * 7^4
Если мы хотим найти представление в виде a^b с натуральными a и b и b должно быть максимальным, то в качестве b нужно брать НОД степеней полученных в разложении на простые множители, то есть в данном случае b=НОД (8,4)=4
основанием степени a будет служить 2^(8/b) * 7^(4/b) = 2^2 * 7^1 = 4*7=28

Степень числа — это когда это число умножается само на себя, при этом столько раз, сколько в степени.
например:
2 в 5 степени — 2*2*2*2*2
если дано какое-нибудь число(допустим, 121) и нужно узнать, квадрат какого он числа, то нужно просто знать квадраты от 1 до 20(желательно). Например, 121 — квадрат 11

Источник

Свойства степеней. Действия со степенями

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

a — основание степени

n — показатель степени

Соответственно, a n = a·a·a·a. ·a

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:

2 — основание степени

3 — показатель степени

Действия, конечно, можно выполнять и на калькуляторе. Их выбор велик, а доступность иногда на расстоянии одного клика в онлайн. Всё это безусловно можно использовать, но сейчас нам важно подробно разобрать принцип работы, чтобы не упасть в грязь лицом на контрольной по математике.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

• 3·3·3·3 = 81. То есть получается, что три в степени четыре равно 81.

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Источник

Действия, обратные возведению в степень

7. В виду последней особенности действий возведения в степень для него можно составить 2 обратных задачи. Напр.:

1) Я задумал число, возвел его в третью степень (или: в куб), получилось 64; какое число я задумал?

Эту задачу можно записать в виде

2) Я взял число 3, возвел его в некоторую степень, – получилось 81. В какую степень было возведено число 3.

Эту задачу можно записать в виде:

Теперь уже, так как возведение в степень не обладает переместительным законом, эти две задачи следует считать совершенно различными.

Сначала решать их можно подбором: попробуем число 1, 1 3 = 1, а не 64, след., 1 не годится; 2 3 = 8, а не 64, след., 2 не годится, 3 3 = 27, а не 64, след., 3 не годится; 4 3 = 64, след., в 1 задаче было задумано число 4. Также выясним, что во второй задаче число 3 было возведено в 4-ую степень.

Так как таких задач можно составить очень много, то для их решения необходимо изобрести новые действия. Эти действия обратны возведению в степень. Итак, для возведения в степень существуют два обратных действия: первое из них называется извлечением корня и служит для решения вопросов, подобных первой из наших задач; второе называется нахождением логарифма и служит для решения вопросов, подобных второй задаче.

Если мы обратим внимание на то, что в первой задаче нам даны степень 64 и показатель степени 3, то мы установим определение:

Извлечением корня называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному показателю находят основание степени.

Также точно: во второй задаче даны степень (81) и основание степени (3), а надо найти показателя степени. Поэтому

нахождением логарифма называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному основанию находится показатель степени.

Источник

Возведению в степень обратны два действия:

• извлечение корня,
• нахождение логарифма.

Во-первых, сначала надо разобраться, что значит обратное действие. Так деление есть обратное действие умножению, а вычитание — сложению. Это вытекает из рассуждений, что произведение, получившееся от перемножения двух множителей, позволяет найти один из множителей, если известен другой. Например, 5 * 3 = 15. Если нам неизвестен второй множитель (5 * ? = 15), то его можно найти, выполнив деление: 15 : 5 = 3. Операция не меняется, если неизвестен первый множитель: ? * 3 = 15, 15 : 3 = 5. Это связано с тем, что умножение подчиняется переместительному закону (от перемены мест множителей произведение не меняется).

Аналогично и для вычитания: ? + 10 = 33, 33 — 10 = 23 или ? + 23 = 33, 33 — 23 = 10. Неважно, какое слагаемое неизвесто, его всегда находят вычитанием.

Но не все так просто с возведением в степень. Здесь от перестановки основания степени и показателя степени результат изменяется, т.е. возведение в степень не подчиняется переместительному закону: 4 3 = 64, но 3 4 = 81. (Хотя есть исключения: 2 4 = 16 и 4 2 = 16.)

Поэтому, если нам известен результат операции возведения в степень и показатель степени, то, чтобы найти основание степени, надо извлечь корень известной по показателю степени из результа возведения в степень:

? 3 = 125, следовательно 3 √125 = 5.

Если же известны основание степени и результат возведения в степень, а надо найти показатель степени, то используется такая операция как нахождение логарифма:

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

• 4 — основание степени;
• 6 — показатель степени.

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Степенью числа « a » с натуральным показателем « n », бóльшим 1 , называется произведение « n » одинаковых множителей, каждый из которых равен числу « a ».

Запись « a n » читается так: « а в степени n » или « n -ая степень числа a ».

Исключение составляют записи:

• a 2 — её можно произносить как « а в квадрате»;
• a 3 — её можно произносить как « а в кубе».

Конечно, выражения выше можно читать и по определению степени:

• a 2 — « а во второй степени»;
• a 3 — « а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0) .

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

• 5 3 = 5 · 5 · 5 = 125
• 2,5 2 = 2,5 · 2,5 = 6,25
• (

  ) 4 =

  ·

  ·

  ·

  =

  3 · 3 · 3 · 3

  4 · 4 · 4 · 4

  =

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Отрицательное число, возведённое в чётную степень, есть число положительное .

Отрицательное число, возведённое в нечётную степень, — число отрицательное .

Квадрат любого числа есть положительное число или нуль, то есть:

a 2 ≥ 0 при любом a .

• 2 · (−3) 2 = 2 · (−3) · (−3) = 2 · 9 = 18
• −5 · (−2) 3 = −5 · (−8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

1. Возвести в четвёртую степень положительное число 5 .
   5 4 = 5 · 5 · 5 · 5 = 625
2. Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
   −5 4 = −625

Пример. Вычислить: −6 2 − (−1) 4

1. 6 2 = 6 · 6 = 36
2. −6 2 = −36
3. (−1) 4 = (−1) · (−1) · (−1) · (−1) = 1
4. −(−1) 4 = −1
5. −36 − 1 = −37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление , а в конце сложение и вычитание .

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Логарифмом называется математическое введение, которое предназначено для того чтобы найти степень числа в уравнении. Если рассматривать степень числа, то число, возводимое в степень, называется основанием степени, а сама степень – показателем степени. Так, в числе 2 3 , 2 является основанием, а 3 – показателем. Для того чтобы понять суть логарифма, рассмотрим показательное тождество (равенство с использованием степени). В выражении 2 3 =8 взаимосвязаны три числа, основание степени, показатель и значение степени – 8 . Соответственно, каждое из этих чисел может быть заменено на переменную с тем, чтобы получить уравнение.
x 3 =8
2 3 =x
2 x =8

Если первые два уравнения считаются довольно стандартными, то третье уравнение становится в отдельный ряд показательных уравнений, и при усложнении его другими алгебраическими действиями появляется необходимость ввести дополнительный элемент для его решения. Этим элементом становится логарифм.
2 x =8
log₂8=x

Таким образом, чтобы найти неизвестную x , нужно вычислить логарифм от 8 по 2 . Названия чисел сохраняются те же самые, что и в степени, 2 остается основанием, но теперь уже не степени, а логарифма, 8 становится телом логарифма. Если обратить внимание, то они сохраняют и свое положение, и визуально легко запомнить, что для вычисления логарифма нужно узнать в какую степень нужно возвести 2 (число внизу, слева), чтобы получить 8 (число справа, вверху).

Чтобы вычислить логарифмы с различными основаниями и телами, можно воспользоваться приведенным ниже он-лайн калькулятором логарифмов.