Дифракцией
называется огибание волнами препятствий.
Дифракция наблюдается для волн различной
природы (звуковых, световых, волн на
воде и т. д.) Явление дифракции проявляется
сильнее, если размеры препятствий
соизмеримы с длиной волны.
Объяснить
дифракционные явления можно с помощью
принципа
Гюйгенса – Френеля, согласно которому
каждая точка фронта волны является
источником вторичных волн, которые
когерентны. Амплитуда и фаза волны в
любой точке пространства – есть результат
интерференции волн, излучаемых вторичными
источниками.
На
рис. 3.11 изображено препятствие
П в форме
щели шириной b,
размеры которого соизмеримы с длиной
волны λ.
На щель падает плоская монохроматическая
волна. Любая точка фронта волны S1
становится источником вторичных волн,
которые являются сферическими и огибающая
которых S2
дает положение фронта волны в следующий
момент времени.

Рис.3.11
Проходя через
щель, волны отклоняются от прямолинейного
распространения (дифрагируют). Если на
их пути поставить экран, то на нем будет
наблюдаться дифракционная картина,
причем интенсивность в любой точке
экрана наблюдения будет определяться
результатом интерференции вторичных
волн, пришедших в точку наблюдения.
Зоны Френеля.
Объяснить
и рассчитать распределение интенсивности
света в дифракционной картине можно,
применив вспомогательный прием – метод
зон Френеля. Зоны
Френеля
– это участки волновой поверхности,
построенные таким образом, что расстояние
от краев соседних зон до точки наблюдения
различается на половину волны (на
![]() ).
).
Известно, что разность хода и разность
фаз связаны соотношением (3.35)
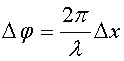 .
.
Следовательно,
если
![]() ,
,
то
![]() ,
,
т. е. колебания, создаваемые соседними
зонами Френеля находятся в противофазе
и попарно гасят друг друга. Тогда, если
отверстие щели открывает четное число
зон Френеля, то в точке наблюдения
находится минимум интенсивности, а,
если нечетное, то – максимум.
Применим метод
зон Френеля к рассмотрению дифракции
света на одной щели.
Пусть
на щель шириной b
нормально падает плоская монохроматическая
волна (рис. 3.12). Все точки волновой
поверхности, открытые щелью, являются
источниками вторичных волн, которые
когерентны и распространяются по всем
направлениям. Поставим между щелью и
экраном наблюдения линзу, которая
собирает параллельные лучи в одну точку.
Дифракция в параллельных лучах называется
дифракцией
Фраунгофера.
В результате интерференции вторичных
волн на экране получится дифракционная
картина. Распределение интенсивности
вдоль экрана изображено в нижней части
рис. 3.12 (кривая с максимумами и минимумами).
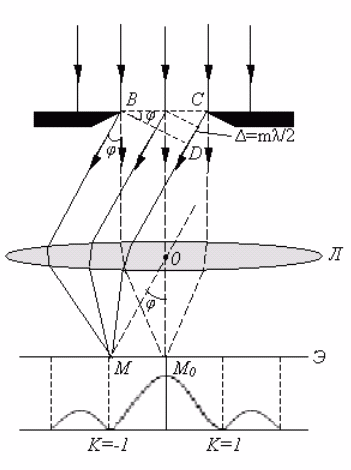
Рис.3.12
В
центре дифракционной картины будет
светлая полоса – центральный максимум,
так как при φ
= 0 все волны
придут на экран в точку М0
в одинаковой фазе и усилят друг друга.
Чтобы определить результат интерференции
вторичных волн при φ
≠ 0, разобьем
открытый участок волновой поверхности
на ряд зон Френеля. В данном случае они
будут представлять собой узкие полоски,
параллельные краям щели. Чтобы найти
число зон Френеля m1,
нужно разность хода крайних лучей
![]() поделить
поделить
на
![]()
 ,
,
тогда
 .
.
При
четном числе зон Френеля m1=
2k
будет наблюдаться
минимум интенсивности, при нечетном
m1=
2k
+1 – максимум.
Условие дифракционного минимума для
одной щели имеет вид
![]()
где
k
= 1, 2, 3, …
“Плюс-минус”
показывает, что картина симметрична
относительно центрального максимума.
Условие дифракционного
максимума от щели имеет следующий вид

k
называется порядком максимума или
минимума, k
= 1, 2, 3, …
10,
Пусть на щель шириной b
нормально падает плоская монохроматическая
волна (рис. 3.12). Все точки волновой
поверхности, открытые щелью, являются
источниками вторичных волн, которые
когерентны и распространяются по всем
направлениям. Поставим между щелью и
экраном наблюдения линзу, которая
собирает параллельные лучи в одну точку.
Дифракция в параллельных лучах называется
дифракцией
Фраунгофера.
В результате интерференции вторичных
волн на экране получится дифракционная
картина. Распределение интенсивности
вдоль экрана изображено в нижней части
рис. 3.12 (кривая с максимумами и минимумами).

Рис.3.12
В
центре дифракционной картины будет
светлая полоса – центральный максимум,
так как при φ
= 0 все волны
придут на экран в точку М0
в одинаковой фазе и усилят друг друга.
Чтобы определить результат интерференции
вторичных волн при φ
≠ 0, разобьем
открытый участок волновой поверхности
на ряд зон Френеля. В данном случае они
будут представлять собой узкие полоски,
параллельные краям щели. Чтобы найти
число зон Френеля m1,
нужно разность хода крайних лучей
![]() поделить
поделить
на
![]()
 ,
,
тогда
 .
.
При
четном числе зон Френеля m1=
2k
будет наблюдаться
минимум интенсивности, при нечетном
m1=
2k
+1 – максимум.
Условие дифракционного минимума для
одной щели имеет вид
![]()
где
k
= 1, 2, 3, …
“Плюс-минус”
показывает, что картина симметрична
относительно центрального максимума.
Условие дифракционного
максимума от щели имеет следующий вид

k
называется порядком максимума или
минимума, k
= 1, 2, 3, …
11, Дифракционная
решетка— оптический прибор, работающий
по принципудифракциисвета, представляет собой совокупность
большого числа регулярно расположенных
штрихов (щелей, выступов), нанесённых
на некоторую поверхность.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
Зона Френеля
Содержание:
- Что такое зона Френеля
- Расчет радиуса зоны Френеля
- Метод зон Френеля, основные принципы работы
- Принцип Гюйгенса-Френеля
Что такое зона Френеля
Определение
Зонами Френеля называют области, на которые можно разделить поверхность световой, либо звуковой волны с целью расчета результатов дифракции света или звука.
Методика анализа была впервые применена О. Френелем в 1815 – 1819 годах. Зону Френеля можно наглядно представить в виде объема радио-волнового канала между двумя передатчиками сигнала.
Максимальное значение объема канала отмечено центральной точкой, равноудаленной от двух антенн. Наиболее качественный сигнал обеспечивается путем подбора максимально чистой зоны, в которой отсутствуют физические и радио-волновые препятствия.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Расчет радиуса зоны Френеля
С помощью определенных характеристик можно выполнить корректный расчет. Для определения зоны Френеля в ее центре необходимо использовать формулу:
(Radius (mts.)=17.31times sqrt{frac{D (in km)}{4times f(in GHz)}})
Где D равно расстоянию в километрах, f является частотой в GHz.
Если необходимо рассчитать размер зоны Френеля в любой ее точке, к примеру, в месте, где обнаружено препятствие, следует воспользоваться формулой:
(r=17.3sqrt{frac{1}{f}frac{D_{1}D_{2}}{D_{1}+D_{2}}})
Где f — это частота в GHz, D1 является расстоянием от первой антенны до искомой точки в километрах, D2 равно расстоянию от второй антенны до искомой точки в километрах.
Знание характеристик зоны Френеля позволяет выполнить точные расчеты. В практическом применении представленные формулировки обеспечивают данные для стабильности параметров беспроводного моста и максимально возможной скорости передачи сигнала.
Метод зон Френеля, основные принципы работы
Опредление
С целью упрощения решений задач волновая поверхность S разбивается на отдельные зоны. Данный способ называют методом зон Френеля.
Точки поверхности S, которые являются границей первой или центральной зоны и удалены от точки М на расстояние:
(l+frac{lambda }{2})
Точки сферы S, которые находятся на расстоянии:
(l+frac{2lambda }{2})
(l+frac{3lambda }{2})
и так далее относительно точки М, образуют 2, 3 и так далее зоны Френеля.
В точке М образуются колебания. Они расположены между двумя соседними зонами, фазы которых противоположны по причине разности ходя от этих зон до точки М:
(Delta =frac{lambda }{2})
В процессе сложения колебания друг друга ослабляют:
(A=A_{1}-A_{2}+A_{3}-A_{4}+…+A_{i})
Где A является амплитудой результирующего колебания, Аi представляет собой амплитуду колебаний, возбуждаемую i-й зоной Френеля.
Значение Аi определяется площадью Si зоны и углом αi между нормалью к поверхности и прямой, направленной в точку M. Расчет площади одной зоны выглядит следующим образом:
(x = {-b pm sqrt{b^2-4ac} over 2a}Delta S_{i}=S_{i}-S_{i-1}=frac{pi Rllambda }{R+l}left(i-i+1 right)=frac{pi Rllambda }{R+l})
Исходя из представленного уравнения, можно сделать вывод о независимости площади зоны Френеля от номера зоны i. Данное утверждение позволяет сделать вывод о том, что при малых числах i соседние зоны будут обладать одинаковыми площадями. В то время, как номер зоны увеличивается, возрастает угол αi, а также снижается интенсивность излучения зоны по направлению к точке М, то есть уменьшается амплитуда Аi. Другой причиной данного явления служит увеличение расстояния до точки М:(x = {-b pm sqrt{b^2-4ac} over 2a})В целом количество зон Френеля, которые уменьшаются на части сферы, направленной к точке М, достаточно большое:
если радиус R=l=1 метр,
(lambda =-5times 10^{-7}) составляет 500 нм.
Количество зон (Napprox 3times 10^{5})
Радиус первой зоны (r_{1}approx 0.16) мм
Исходя из вышеизложенной информации, можно сделать вывод о равенстве углов соседних зон между нормалью к зоне и направлением на точку М. Таким образом, наблюдается примерное равенство амплитуд волн, которые приходят в точку М от соседних волн. При прямолинейном распространении световой волны фазы колебаний, которые образованы в соседних зонах, будут отличаться на π. Согласно этим данным, в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны рассчитывается, как среднее арифметическое от амплитуд зон, которые к ней примыкают:
(A_{m}=frac{A_{m-1}+A_{m+1}}{2})
В таком случае, исходное уравнение можно преобразовать следующим образом:
(A=frac{A_{1}}{2}+left(frac{A_{1}}{2}-A_{2}+frac{A_{3}}{2} right)+left(frac{A_{3}}{2}-A_{4}+frac{A_{5}}{2}right)+…=frac{A_{1}}{2})
Из равенства площадей, которыми обладают соседние зоны, вытекает нулевое значение выражения, заключенного в скобках. Тогда результирующая амплитуда будет равна:
(A=frac{A_{1}}{2})
Расчет интенсивности излучения имеет вид:
(Jsim A^{2})
Таким образом, результирующая амплитуда, которая образована в какой-либо точке М всей сферической поверхностью, определяется, как половина амплитуды, сформированной одной лишь центральной областью, а интенсивность составляет:
(J=frac{J_{1}}{4})
Радиус, которым характеризуется центральная зона, небольшой:
(r_{1}approx 0.16) мм
Тогда допустимо считать распространение света от точки Р до точки М прямолинейным. В условиях, когда путь волны преграждает непрозрачный экран, в котором есть отверстие, открывающее только центральную зону Френеля, то амплитуда в точке М составляет А1. Поэтому, интенсивность в точке М превышает в 4 раза тот же показатель, но в условиях без экрана. В случае, когда все зоны с четными номерами закрыты, интенсивность света будет увеличиваться.
Таким образом, объясняют прямолинейность распространения света в условиях однородной среды с помощью принципа Гюйгенса-Френеля. Справедливость деления волнового фронта на зоны Френеля нашла подтверждение в ходе эксперимента. Для опыта используют зонные пластинки, представляющие собой систему чередующихся прозрачных и непрозрачных колец. Эксперимент подтверждает возможность увеличения освещенности в точке М с помощью зонных пластинок по принципу собирающей линзы.
Принцип Гюйгенса-Френеля
Опредление
Дифракцией света в наиболее распространенном понятии называют огибание световыми лучами границы непрозрачных тел или экранов, то есть проникновение света в область с геометрической тенью.
Максимально рельефно дифракцию света можно наблюдать в зонах с резким изменением плотности потока лучей:
- около каустик;
- вблизи фокуса линзы;
- у границ геометрической тени.
Дифракция волн тесно связана с процессами, при которых волны распространяются и рассеиваются в неоднородных средах.
Определение
Дифракция — это комплекс явлений, которые можно наблюдать в процессе распространения света в среде, отличающейся резкими неоднородностями, габариты которых соотносимы с длиной волны и связаны с отклонениями от законов геометрической оптики.
Огибание препятствий звуковыми волнами, то есть дифракцию звуковых волн, можно заметить в повседневной жизни.
Пример
К примеру, за углом дома слышен звук. Для того чтобы наблюдать дифракцию световых лучей, требуются специальные условия, что является причиной небольшой длины световых волн. Интерференция не отличается существенно от дифракции. Данные явления зависят от перераспределения светового потока в результате суперпозиции волн.
Определение
Дифракция объясняется принципом Гюйгенса. Согласно данному утверждению, каждая точка, которую достигает волна, является центром вторичных волн, а огибающая этих волн определяет положение волнового фронта в следующий момент времени.
На рисунке изображен непрозрачный экран, на отверстие в котором нормально падает плоская волна.
Каждая точка области волнового фронта, выделенного отверстием, представляет собой источник вторичных волн. В условиях однородной среды они будут иметь сферическую форму. С помощью огибающих вторичных волн для некоторого момента времени можно увидеть, что фронт волны достигает области геометрической тени, то есть волна огибает края отверстия.
Благодаря принципу Гюйгенса, можно решить задачу, связанную с направлением, в котором распространяется волновой фронт. Но утверждение не касается вопроса о таких характеристиках разнонаправленных волн, как амплитуда и интенсивность. Решающая роль в определении волновой природы света отведена О. Френелю, который проводил данные исследования в начале XIX века. Ученый представил объяснение явлению дифракции и ее количественный расчет. В 1818 году Френель был удостоен премии Парижской академии за достижения в данной области.
Френель дополнил принцип Гюйгенса физическим смыслом с помощью идеи интерференции вторичных волн. Ученый рассматривал дифракцию по средствам нескольких ключевых положений, которые не требую доказательств. Комплекс данных утверждений называют принципом Гюйгенса-Френеля. Исходя из принципа Гюйгенса, каждая точка фронта волны рассматривается в качестве источника вторичных волн. Френель значительно развил это утверждение:
- Все вторичные источники фронта волны, которая исходит из одного источника, когерентны между собой.
- Участки волновой поверхности с разными площадями испускают равные интенсивности или мощности.
- Для каждого вторичного источника характерно излучение света в большей степени по направлению к внешней нормали к волновой поверхности в этой точке. Амплитуда вторичных волн в направлении, составляющем угол α с нормалью, тем меньше, чем больше угол α, и равна нулю при (alpha geq frac{pi }{2})
- Вторичные источники характеризуются принципом суперпозиции, то есть излучение одних областей волновой поверхности не оказывает влияние на излучение других участков. Это можно понять, когда часть волновой поверхности прикрыта непрозрачным экраном, а вторичные волны излучаются открытыми областями так, как если бы экран отсутствовал.
Благодаря данным положениям, Френелю удалось составить дифракционную картину. Используя справедливые утверждения, ученый выполнял количественные расчеты, характеризующие явление дифракции.
Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.
Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.
Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.
Принцип Гюйгенса-Френеля
Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.
Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.
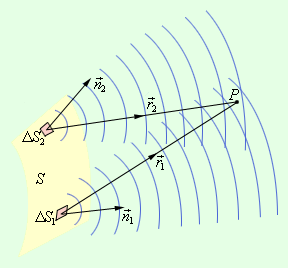
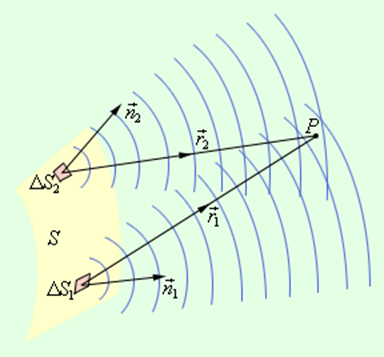
Рисунок 3.8.1 Принцип Гюйгенса-Френеля. ∆S1 и ∆S2 – элементы волнового фронта, n1→ и n2→ – заданные нормали.
Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.
Для определения колебания в заданной точке P, которое вызвано волной, используя принцип Френеля, находят колебания, которые вызваны в этой точке с помощью отдельных вторичных волн, которые приходят от элементов поверхности S (∆S1, ∆S2 и так далее). Далее следует произвести сложение колебаний, учитывая амплитуды и фазы. Элементы, загороженные препятствиями, не учитываются при решении.
Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.
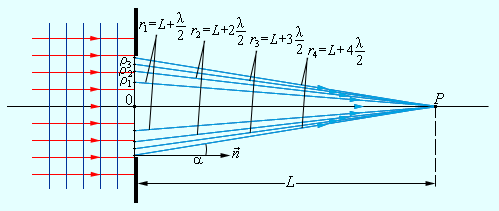
Рисунок 3.8.2 Дифракция плоской волны на экране, содержащем круглое отверстие.
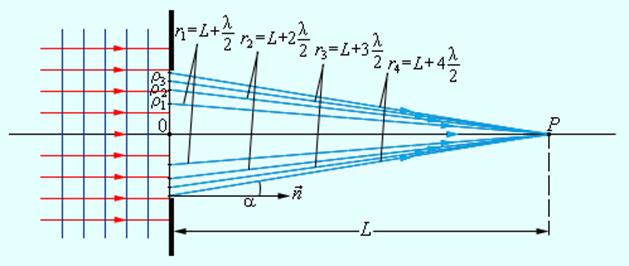
Р – точка наблюдения, находящаяся на оси симметрии, располагаемого на L расстоянии относительно экрана. По принципу Гюйгенса-Френеля распределить на волновой поверхности вторичные источники, совпадающие с плоскостью отверстия, где волны достигают точки Р. Интерференция волн в этой точке является причиной возникновения результирующего колебания, квадрат амплитуды которого определяется при наличии значений длин волн λ, амплитуды A0 падающей волны и расположением элементов.
Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.
Иначе говоря, r1=L+λ2, r2=L+2λ2, r3=L+3λ2…
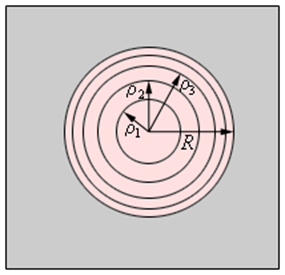
При рассмотрении волновой поверхности исходя из точки Р, тогда получим, что границы зон Френеля будут иметь вид концентрических окружностей. Наглядно это изображено на рисунке.
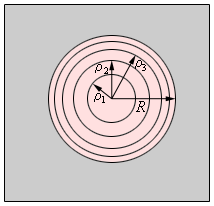
Рисунок 3.8.3 Границы зон Френеля в плоскости отверстия.
По рисунку 3.8.2 определяем радиусы ρm зон по формуле: ρm=ρm2-L2=mλL+m2λ24≈mλL.
Зоны Френеля. Интерференционный максимум
Из определений раздела оптики имеем, что λ<<L, тогда при решении можно пренебречь вторым подкоренным выражением. Для определения количества зон Френеля, которые укладываются на отверстии, используется формула, включающая в себя значение радиуса R: m=R2λL.
Значение m может быть любым числом. От него зависит результат интерференции вторичных волн, проходящих точку Р. Такие открытые зоны Френеля обладают одинаковым значением площади:
Sm=πρm2-πρm-21=πλL=S1.
По теории равные площади возбуждают колебания с одинаковой амплитудой в точке наблюдения. Но каждая последующая зона угла α, располагаемая между лучом, проводимым к точке наблюдения, и нормалью относительно волновой поверхности, возрастает. Предположения Френеля говорит о том, что при увеличении угла α происходит незначительное уменьшение колебаний, то есть:
A1>A2>A3>…>A1, где Am обозначает амплитуду колебаний, которые были вызваны при помощи m-ой зоны.
Используя приближение, видно, что амплитуда колебаний, которая вызвана определенной зоной, равняется среднему арифметическому соседних зон. Иначе это запишем как Am=Am-1+Am+12.
Отличие от двух соседних точек расстоянием λ2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:
A=A1–A2+A3–A4+…=A1–(A2–A3)–(A4–A5)–…<A1.
Отсюда делаем вывод, что суммарная амплитуда в точке меньше колебаний, вызванных только при помощи одной зоны Френеля. Если все имеющиеся зоны Френеля являлись открытыми, тогда к точке наблюдения двигалась волна с амплитудой A0, невозмущенная препятствием. Тогда запись принимает вид:
A=A0+A12-A2+A32+A32-A4+A52+…=A12.
Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.
Когда отверстие непрозрачного экрана дает возможность только одной зоне Френеля быть открытой, тогда наблюдается возрастание амплитуды колебаний в количестве 3 раз, а интенсивности – 4 раз. При открытии двух зон действие становится равным нулю. При наличии непрозрачного экрана с несколькими нечетными открытыми зонами, очевидно, что произойдет резкое возрастание амплитуды. При открытии 1, 3, 5 зон получим, что A=6·A0, I=36·I0.
Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.
Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:
A=Am+1-Am+2+Am+3-…=Am+12+Am+12-Am+2-Am+32+…
Иначе можно записать как A=Am+1 2, ибо выражения в скобках будут равняться нулю.
Когда диск может закрыть небольшие зоны, тогда Am + 1≈2A0 и A≈A0, можно наблюдать интерференционный максимум. Иначе его называют пятном Пуассона, которое окружается дифракционными кольцами светлого и темного цвета.
Чтобы углубиться в понятие, необходимо оценить зоны Френеля. Имеется дифракционная картина на экране с расстоянием равным L=1м, а значение длины волны света λ=600нм (красный). Отсюда получим, что радиусом первой зоны является ρ1=Lλ≈0,77мм.
Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.
Получим формулы вида:
m=R2Lλ≥1 или R2≥Lλ.
Название данного соотношения – критерий наблюдения дифракции.
Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:
m=R2Lλ>>1 или R2>>Lλ.
Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.
Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.
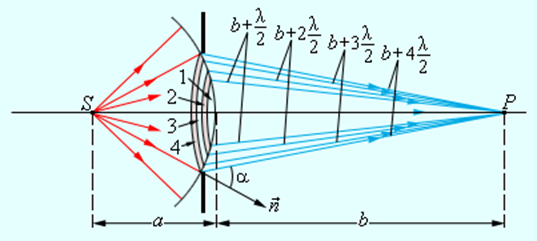
Выше рассмотренный случай относится к дифракции света с удаленным источником, располагаемом на препятствиях округлой формы. При расположении точечного источника света на конечном расстоянии сферически расходящаяся волна должна падать на препятствие. Данный случай усложняет задачу. Тогда построение зон Френеля необходимо выполнять на поверхности сферической формы, показанное на рисунке 3.8.4.
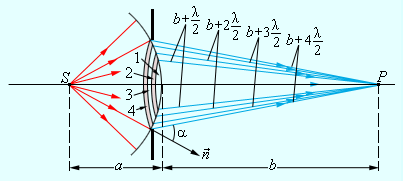
Рисунок 3.8.4 Зоны Френеля на сферическом фронте волны.
При расчете видно, что радиусы ρm зон Френеля на волне сферического фронта запишется, как
ρm=aba+bλ.
Выводы по теории Френеля справедливы.
Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.
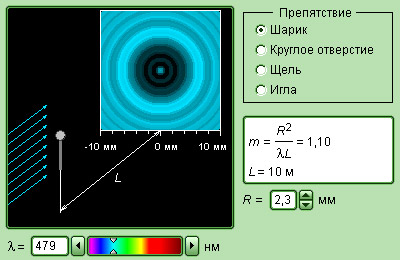
Рисунок 3.8.5 Модель дифракции света.
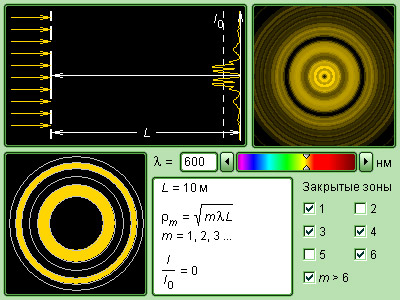
Рисунок 3.8.6 Модель зоны Френеля.
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.
Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т.Юнгом. Независимо от него в 1818 г. французский ученый О.Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающих вторичных волнах Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.
|
|
|
Рисунок 3.8.1. Принцип Гюйгенса–Френеля. ΔS1 и ΔS2 – элементы волнового фронта, |
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.
Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS1, ΔS2 и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.
Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране (рис. 3.8.2).
|
|
|
Рисунок 3.8.2. Дифракция плоской волны на экране с круглым отверстием |
Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A0 падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на половину длины волны, т. е.
![]() …
…
Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).
|
|
|
Рисунок 3.8.3. Границы зон Френеля в плоскости отверстия |
Из рис. 3.8.2 легко найти радиусы ρm зон Френеля:
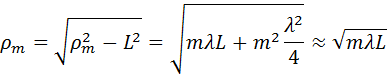
Так в оптике λ << L, вторым членом под корнем можно пренебречь. Количество зон Френеля, укладывающихся на отверстии, определяется его радиусом R:
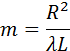
Здесь m – не обязательно целое число. Результат интерференции вторичных волн в точке P зависит от числа m открытых зон Френеля. Легко показать, что все зоны имеют одинаковую площадь:
![]()
Одинаковые по площади зоны должны были бы возбуждать в точке наблюдения колебания с одинаковой амплитудой. Однако у каждой последующей зоны угол α между лучом, проведенным в точку наблюдения, и нормалью к волновой поверхности возрастает. Френель высказал предположение (подтвержденное экспериментом), что с увеличением угла α амплитуда колебаний уменьшается, хотя и незначительно:
где Am – амплитуда колебаний, вызванных m-й зоной.
С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.
![]()
Так как расстояния от двух соседних зон до точки наблюдения отличаются на λ / 2, следовательно, возбуждаемые этими зонами колебания находится в противофазе. Поэтому волны от любых двух соседних зон почти гасят друг друга. Суммарная амплитуда в точке наблюдения есть
A = A1 – A2 + A3 – A4 + … = A1 – (A2 – A3) – (A4 – A5) – … < A1.
Таким образом, суммарная амплитуда колебаний в точке P всегда меньше амплитуды колебаний, которые вызвала бы одна первая зона Френеля. В частности, если бы были открыты все зоны Френеля, то до точки наблюдения дошла бы невозмущенная препятствием волна с амплитудой A0. В этом случае можно записать:
![]()
так как выражения, стоящие в скобках, равны нулю. Следовательно, действие (амплитуда), вызванное всем волновым фронтом, равно половине действия одной первой зоны.
Итак, если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность – в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастет. Например, если открыты 1, 3 и 5 зоны, то
Такие пластинки, обладающие свойством фокусировать свет, называются зонными пластинками.
При дифракции света на круглом диске закрытыми оказываются зоны Френеля первых номеров от 1 до m. Тогда амплитуда колебаний в точке наблюдения будет равна
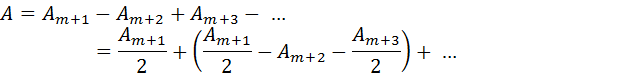
или A = Am + 1 / 2, так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не слишком больших номеров, то Am + 1 ≈ 2A0 и A ≈ A0, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.
Оценим размеры зон Френеля. Пусть, например, дифракционная картина наблюдается на экране, расположенном на расстоянии L = 1 м от препятствия. Длина волны света λ = 600 нм (красный свет). Тогда радиус первой зоны Френеля есть
![]()
Таким образом, в оптическом диапазоне вследствие малости длины волны размер зон Френеля оказывается достаточно малым. Дифракционные явления проявляются наиболее отчетливо, когда на препятствии укладывается лишь небольшое число зон:
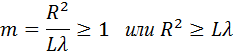
Это соотношение можно рассматривать как критерий наблюдения дифракции. Если число зон Френеля, укладывающихся на препятствии, становится очень большим, дифракционные явления практически незаметны:
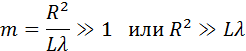
Это сильное неравенство определяет границу применимости геометрической оптики. Узкий пучок света, который в геометрической оптике называется лучом, может быть сформирован только при выполнении этого условия. Таким образом, геометрическая оптика является предельным случаем волновой оптики.
Выше был рассмотрен случай дифракции света от удаленного источника на препятствиях круглой формы. Если точечный источник света находится на конечном расстоянии, то на препятствие падает сферически расходящаяся волна. В этом случае геометрия задачи несколько усложняется, так как теперь зоны Френеля нужно строить не на плоской, а на сферической поверхности (рис. 3.8.4).
|
|
|
Рисунок 3.8.4. Зоны Френеля на сферическом фронте волны |
Расчет приводит к следующему выражению для радиусов ρm зон Френеля на сферическом фронте волны:
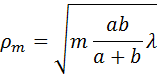
Все выводы изложенной выше теории Френеля остаются справедливыми и в этом случае.
Следует отметить, что теория дифракции (и интерференции) световых волн применима к волнам любой физической природы. В этом проявляется общность волновых закономерностей. Физическая природа света в начале XIX века, когда Т.Юнг, О.Френель и другие ученые развивали волновые представления, еще не была известна.
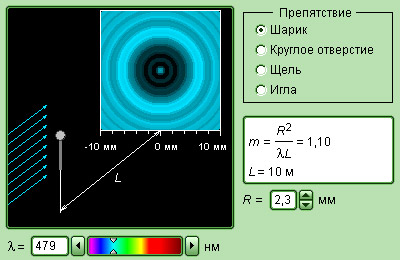 |
|
Модель. Дифракция света |
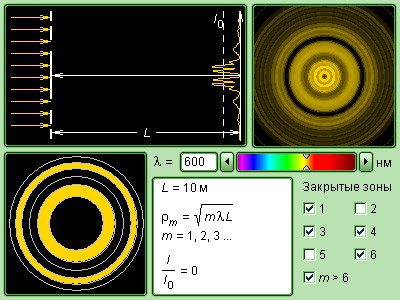 |
|
Модель. Зоны Френеля |
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Вычисление амплитуды световых колебаний с использованием аналитического выражения принципа Гюйгенса – Френеля является в общем случае сложной, нетривиальной задачей. Однако Френель показал, что в некоторых случаях при наличии симметрии найти амплитуду суммарных колебаний можно используя алгебраическое или геометрическое суммирование.
Пусть сферическая или плоская волна попадает на экран с отверстием. Необходимо определить, как распределяется интенсивность света за экраном. Для того чтобы решить эту задачу используя принцип Гюйгенса – Френеля делают предположения:
-
Непрозрачные части экрана не работают как источники вторичных волн.
-
В отверстии экрана точки волнового фронта служат источником вторичных волн, как будто нет экрана.
Пусть точка А является источником сферической волны, $S$ – волновой фронт в момент времени $t$.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
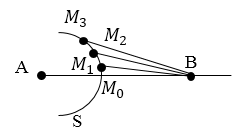
Рисунок 1.
Для того чтобы найти интенсивность волны в точке $В$, надо разбить поверхность $М$ на зоны – кольца, имеющие такие размеры, чтобы расстояния от краев зоны до точки $В$ были различны на величину $frac{lambda }{2}$. Границы зон на рис.1 обозначены как $M_0, M_1, M_2,dots $ Запишем вышеназванное условие как:
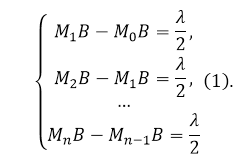
Рисунок 2.
Центральная зона носит название нулевой ($M_0$). Иногда центральную зону называют первой, при этом говорят, что $m=1,2,$ …
«Зоны Френеля» 👇
Радиусы и площади зон Френеля
Для определения радиусов зон рассмотрим рисунок (рис. 2). На этом рисунке: радиусы зон $r_1, r_2,dots ,r_m.$ $R$ – радиус кривизны сферического фронта волны. Точка $D$ обозначает место пересечения фронта волны с прямой $АВ$, $d_1, d_2,dots ,d_m-$ расстояния от точки $D$ до проекции границы соответствующей зоны на прямую $АВ$. Из рис.2 видно, что для радиуса $r_m$ будет справедливо уравнение:
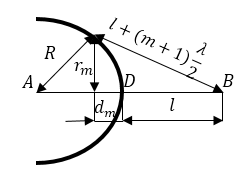
Рисунок 3.
Если ограничиться точностью величин до ${lambda }^2$ из уравнения (2) следует:
Используя второе выражение из (3) площадь нулевой зоны найдем как:
Найдем суммарную площадь первой и нулевой зон, получим:
Соответственно площадь первой зоны равна:
Получилось, что площадь первой зоны равна площади нулевой зоны. Выражение (6) определяет площади и всех остальных зон. Пренебрегая кривизной поверхности фронта волны считают, что площадь кольцевой зоны на поверхности волнового фронта равна ее проекции на плоскость, которая перпендикулярна прямой $АВ$. Если радиусы зон Френеля существенно меньше радиуса кривизны волнового фронта, то ошибка в таком допущении небольшая. Если длины волн малы, из формулы (3) можно сделать вывод, что данное условие хорошо выполнимо для большого количества зон Френеля.
Амплитуды колебаний
Амплитуды колебаний, которые возбуждаются в точке В зонами Френеля образуют монотонно убывающую последовательность. При этом фазы колебаний, которые возбуждают соседние зоны отличны на $pi $. Поэтому амплитуда результирующего колебания в точке В может быть записана как:
Запишем выражение (7) в ином виде:
Так как амплитуда ($A_m$) монотонно убывает, то приближенно можно положить, что:
В таком случае выражение (8) преобразуется до:
В соответствии с выражением (10) амплитуда волны в точке $В$ равна половине амплитуды волны, которая создается центральной зоной.
Пример 1
Задание: Длина волны, которую посылает точечный источник света, равна $lambda=500нм$. Источник находится на расстоянии $a=1м$ от непроницаемого для света экрана с круглым отверстием диаметр его, равен $d=1 мм$. Каким должно быть расстояние от экрана до точки, в которой ведутся наблюдения ($b$), если отверстие открывает три зоны Френеля?
Решение:
Будем считать, что центральная зона – первая, то есть $m=1,2,3$ …
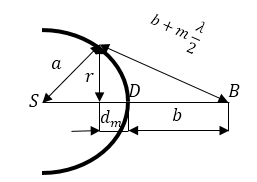
Рисунок 4.
Исходя из рис.4, можно записать:
[r^2=a^2-{left(a-d_mright)}^2left(1.1right).]
Из численных данных задачи имеем, что:
[lambda ll a, to lambda ll bleft(1.2right).]
Преобразуем выражение (1.1) к виду:
[r^2={(b+mfrac{lambda }{2})}^2-{left(b+d_mright)}^2left(1.3right).]
Выразим $d_m$, и $r^2$, учитывая, что выражение $frac{b^2}{4{(a+b)}^2}m^2{lambda }^2$мало, и им можно пренебречь, получим:
[d_m=frac{bmlambda }{2(a+b)}, r^2=frac{ab}{a+b}mlambda left(1.4right).]
Используя условие: $r=frac{d}{2}$, из формулы для $r^2$ (1.4) найдем расстояние $b$:
[b=frac{ar^2}{amlambda -r^2}to b=frac{ad^2}{4amlambda -d^2}.]
Проведем вычисления, получим:
[b=frac{1cdot {left({10}^{-3}right)}^2}{4cdot 1cdot 3cdot 500cdot {10}^{-9}-{left({10}^{-3}right)}^2}=0,2(м).]
Ответ: $0,2 м$.
Пример 2
Задание: Каким будет число зон Френеля, которые откроет отверстие радиусом r, если поле исследуется на расстоянии b от центра отверстия. Считать падающую волну плоской.
Решение:
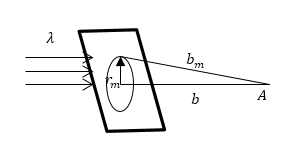
Рисунок 5.
Исходя из выражения, которое определяет зоны Френеля:
[b_m=b+mfrac{lambda }{2}(2.1)]
используя формулу для радиусов зон (рис.5):
[{r_m}^2={b_m}^2-b^2 left(2.2right)]
получим уравнение:
[{r_m}^2={left(b+mfrac{lambda}{2}right)}^2-b^2=b^2+2bmfrac{lambda}{2}+{left(mfrac{lambda}{2}right)}^2-b^2=bmlambda+{left(mfrac{lambda}{2}right)}^2left(2.3right).]
Так как длина волны видимого света мала, то ее квадратами можно пренебречь, то есть получаем:
[{r_m}^2approx bmlambda to m=frac{{r_m}^2}{blambda }left(2.4right).]
Если по условию задачи радиус отверстия равен r, то искомая величина:
[m=frac{r^2}{blambda }.]
Ответ: $m=frac{r^2}{blambda }.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме