Как найти число зубьев ведомого колеса

Определение чисел зубьев при одинаковом
модуле всех прямозубых колес одной
группы

 Для зубчатых колес, изготовленных
без смещения исходного контура, межосевое
расстояниеа_ω между осями ведущего
и ведомого валов является постоянной
величиной

.

В этом случае справедливо соотношение

,

(24)

где z_∑ – сумма чисел зубьев
сопряженных колес;

z_j1 и z_j2, – числа зубьев шестерен
и колес, входящих в рассматриваемую
группу передач; здесь j= 1, 2, 3, …, р
(количество зубчатых пар в данной группе)

.

Передаточное число этой пары

.

(25)

Из уравнений (24) и (25) следует:

(26)

Пользуясь этими уравнениями, находят
числа зубьев всех колес группы, задаваясь
z_∑ и зная необходимые значения
u_j на основе предварительно
составленного графика чисел оборотов.

Определение суммы зубьев z_∑
производится обычно методом наименьшего
кратного, если

 
,

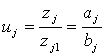
где а_j и b_j – взаимно простые
целые числа. Желательно, чтобы сумма
этих кратных чисел представляла числа,
разлагающиеся на простые множители.
Соотношение (26) тогда можно написать в
таком виде:                                              

(27)

Следовательно, чтобы числа зубьев Z_j
были целыми, число z_∑ должно быть
общим наименьшим кратным чисел

а₁
+ b₁, 
а₂
+ b₂, 
. . . , а_j
+ b_j.

С другой стороны, число z_∑ должно
быть не меньше суммы чисел зубьев либо
понижающей передачи с наибольшим
передаточным числом, либо повышающей
передачи c наименьшим передаточным
числом. Если

,
то должно быть соблюдено первое условие,
если

,
то должно быть соблюдено второе условие.

В первом случае
                                                           

(28)

во втором случае
(29)                                                           

(29)

где z_min – минимальное число зубьев,
ограниченное условиями подрезания.

Если z_∑, полученное как общее
наименьшее кратное, меньше числа зубьев,
определенного из выражений (28) или (29),
то его увеличивают в целое число раз, а
полученную сумму уточняют по нормали
Н21-5 с учетом межосевого расстояния и
модуля колес. Число зубьев z_∑
должно быть не больше 100 (в отдельных
случаях допускают его увеличение до
120), в противном случае чрезмерно
увеличиваются габариты коробки. К одним
из предпочтительных чисел зубьев z_∑
относится 72.

Рассмотрим конкретный пример определения
чисел зубьев:

и  

Пользуясь логарифмической линейкой,
выражаем передаточное число в виде
отношений простых чисел:

 

 

Соответственно

а₁
+ b₁
= 5 + 7 = 12;

а₂
+ b₂
= 7 + 5 = 12;

а₃
+ b₃
= 53 + 19 = 72

и z_∑,определяемое как общее
наименьшее кратное, равно 72. Так как

,

то по уравнению (28)

Принимаем z_∑ = 72.

Определяем числа зубьев

 

 

 

Передаточные числа, получаемые при
найденных расчетом числа зубьев, не
должны отклоняться от заданных
передаточных чисел больше чем на ±10(φ—1)
%. В данном случае наибольшее отклонение
имеет место у третьей передачи и
составляет +1,1 %. Для определения чисел
зубьев очень удобно пользоваться
таблицей Приложения
7.3.21, где по горизонтали отложена
сумма зубьев, а по вертикали — передаточные
числа, кратные 1,06. Пустые клетки означают,
что при данном z_∑ передаточное
число не может быть выдержано в требуемых
пределах ±10(φ—1) %, в остальных клетках
указано число зубьев меньшего зубчатого
колеса.

Пример. Определение чисел зубьев
трех пар зубчатых колес, которые должны
обеспечить передаточные числа:

u₁
= 1; u₂
= 1,26 и u₃ =
1,58; z_min
= 17.

Если по таблицам взять, например, z_∑
= 49, то при u =1,58 z₂: z₁= (49—19): 19
= 30 : 19, а при u =1,26 и u = 1 имеем пустые клетки.
Следовательно, надо найти такое значение
z_∑, которое удовлетворяло бы трем
передаточным числам.

Приемлемое решение будет при z_∑
= 52;

Здесь точное значение u₃ = 1,6
отличается от требуемого u = 1,58 всего на
1,25 %, что допустимо.

 Особенности определения чисел
зубьев при тройных блоках подвижных
зубчатых колес

 При перемещении подвижного блока
колеса, расположенные справа и слева
от среднего колеса, проходят мимо
среднего колеса неподвижного блока.
Чтобы зубцы этих колес не зацеплялись,
для колес без смещения должно быть
соблюдено условие

,

где z_ср – число зубьев среднего
колеса неподвижного блока;

z_кр – число зубьев крайнего колеса
подвижного блока.

Рисунок 2.8 – Варианты оформления
трехскоростных групповых передач при

z_кр
+ z_ср>z_Σ
– 4

В тех случаях, когда это условие не может
быть выполнено, что имеет место при
малой разнице в передаточных числах,
применяют конструктивную форму подвижного
блока, показанную на рисунке 2.8, а или
заменяют тройной подвижной блок двойным
подвижным блоком и одной подвижной
шестерней (рисунок 2.8, б).

При первом варианте увеличивается
осевая длина передачи, при втором
усложняется управление.

Определение чисел зубьев при различных
модулях зубчатых колес в одной группе
передач  

В данном случае в выражение (27) вместо
z_∑ следует подставить

и
соответственно 2_аω должно быть
общим наименьшим кратным выражений m
(a_j + b_j). Так
как модули могут быть не целыми числами,
то вместо них надо подставить кратные
им целые числа. Например, если m₁
= 2,5 мм, а m₂ = 3,5 мм, то при определении
величины 2_аω надо подставить 5 и
7. Однако при этом обычно получаются
весьма большие межосевые расстояния,
которые практически неприемлемы и
подбор приходится производить путем
ряда последовательных попыток, прибегая
в случае необходимости к применению
нарезания колес со смещением инструмента.

Например, если колесо с модулем 3,5 и
числом зубьев z = 59 теоретически
соответствует осевому расстоянию, но
не обеспечивает нужное передаточное
число, его можно заменить колесом в 58
зубьев при том же делительном диаметре.
Модуль такого колеса будет уже не 3,5, а
несколько больше; он определяется
следующим образом.

Делительный диаметр колеса

d =mz
= 3,5∙59 = 206,5 мм.

Если при этом диаметре на колесе нарезать
не 59, а 58 зубьев, то модуль будет

,

Этот модуль больше расчетного на

.
Колеса с таким видом смещения в тихоходных
передачах работают вполне удовлетворительно.
На рисунке 2.9 показаны схема и график
коробки подач, имеющей два передвижных
блока зубчатых колес. Первый блок из
трех зубчатых колес имеет модуль m₁
= 3,5, а второй, состоящий из двух колес,
имеет модуль m₂ = 2,75.

Из схемы и графика рисунка 2.9 имеем при
φ = 1,41

 

Межосевое расстояние

,

откуда

т. е. при сохранении постоянного расстояния
между валами можно принять для первой
группы колес m₁ = 3,5, для второй –
2,75;

Рисунок
2.9 – Схема двухваловой коробки подач с
зубчатыми колесами

различных
модулей

сумма чисел зубьев сопряженных колес
будет равна 88 для первой и 112 – для второй
группы.

Для первой группы колес числа зубьев
будут

; 

; 

; 

,

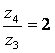
откуда

;  

; 

;  

.

Для сохранения более точного u₂ =
2 принимаем z₄ = 58 (смещение 1,7 %).

; 

; 

; 

.

Чтобы получить более точное значение

,
принимаем z₆ = 1,41 • 37 = 52 (смещение
1,9 %).

Расстояние между валами

Для второй группы колес m₂=2,75:

; 

;

;

;

;

;

.

Для получения более точного передаточного
отношения принимаем

(смещение
2,2 %).

Расстояние

В результате расчета находим, что
зубчатые пары

,  

 
и  

должны
иметь зубья со смещением, причем нарезанию
со смещением может подвергаться только
одно зубчатое колесо каждой пары. С
целью сокращения количества колес в
коробках скоростей передвижными блоками
применяются смещенные зубчатые колеса
для того, чтобы одно ведущее передвижное
зубчатое колесо могло входить в зацепление
с двумя постоянными колесами ведомого
вала. Например, на рисунке 2.10 передвижное
колесо z=24 может быть введено в зацепление
с любым из двух смещенных колес z = 30 и
z=32, обеспечивая передаточные числа

и

.
Эти значения удобны, например, для
подбора зубчатых колес коробки подач
при нарезании резьб.

Рисунок 2.10 – Схема переключения одной
шестерни с двумя колесами ведомого вала

 Определение чисел зубьев колес
при переборах  

Различные пары зубчатых колес перебора
обычно имеют неодинаковые модули, так
как действующие на них усилия сильно
различаются по величине. Соотношение
между модулями m₁ и m₂ и суммами
чисел зубьев зубчатых колес перебора
может быть найдено исходя из расстояния
между осями следующим образом:

откуда

На рисунке 2.11 показан одинарный перебор.
Две пары его колес имеют различные
модули. Знаменатель φ = 1,26.

Рисунок 2.11 – Схема одинарного зубчатого
перебора с графиком чисел оборотов

Передаточное число перебора

,

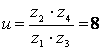
что позволяет иметь звено с увеличением
шага в 8 раз. Числа зубьев колес перебора,
согласно принятому графику, определятся
следующим образом:

;  

,

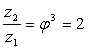
откуда

и

 Если
принять разность модулей обеих пар
колес перебора m₂—m₁ = 1, тогда
при m₁ = 4 и m₂ = 5 получим

 

откуда числа зубьев колес

z₁ = 50; z₂=100; z₃ = 24; z₄
= 96.  

Определение чисел зубьев при сменных
колесах 

Для сокращения количества сменных колес
они делаются обратимыми (т. е. одна пара
колес может давать две скорости
перестановкой их местами). Обычно
применяют набор из колес с числом зубьев,
кратным пяти (пятковый набор), т. е. z =
20, 25, 30 и т. д. до 120; набор колес с числом
зубьев, кратным четырем (четный набор),
т. е. z = 20, 24, 28, 32 и т. д. до 80. Кроме этого,
имеются специальные колеса для обоих
наборов с z = 47, 97, 127 и 157. Чтобы подобранные
сменные зубчатые колеса могли поместиться
на гитаре и не упирались во втулки
валиков зубчатых колес, необходимо
соблюдать следующие условия зацепляемости
сменных колес (рисунок 1.6):

а + b > с + (15÷20).

Для определения чисел зубьев сменных
колес существует несколько способов.
Рассмотрим некоторые из них.

Способ разложения на простые множители
применяют в том случае, если на них можно
разложить числитель и знаменатель
передаточного числа.

Пусть

,

где u – передаточное число сменных
зубчатых колес а, b, с и d.

Множители числителя и знаменателя
группируют в две группы

,

и каждую группу умножают на число, равное
или кратное 4 или 5 (в зависимости от
имеющегося набора)

Способ замены часто встречающихся
чисел приближенными дробями заключается
в том, что часто встречающиеся числа,
как-то 25,4; π; π/25,4; π∙25,4, заменяются
приближенными величинами (таблица 2.5),
дающими возможность с достаточной
точностью получить, передаточные числа,
в которых числа зубьев сменных колес
определяются известными способами.

Поясним это на примере. Пусть имеем

Из таблицы 2.5 значение 25,4 π можно заменить
приближенной дробью

Таблица 2.5 –
Заменяемые значения 25,4 и π

25,4	π	π /25,4	π  ∙ 25,4
* В скобках указаны неточности линейного перемещения в миллиметрах на 1 м длины.

 Логарифмический способ основан
на том, что находят логарифм передаточного
числа (если передаточное число имеет
вид неправильной дроби, берут логарифм
величины, обратной передаточному числу)
и по соответствующей таблице (универсальные
таблицы Н.Д. Левашова)  определяют
числа зубьев сменных зубчатых колес.
Они указываются рядом с логарифмом.

Способ подбора передаточных чисел по
логарифмической линейке состоит в
том, что с помощью логарифмической
линейки числитель передаточного числа,
выраженного в виде простой, неудобной
для разложения дроби, делят на знаменатель.
После этого движок оставляют в полученном
положении, а передвижением визира
находят риски, совпадающие на движке и
линейке. По полученным новым целым
числам, которые дают при делении то же
значение частного, подбирают числа
зубьев сменных зубчатых колес.

Например:.

Оставив движок в полученном положении,
передвигаем визир до тех пор, пока риски
на движке и на линейке не совпадут.

Тогда:

.

При однопарных гитарах числа зубьев
сменных колес определяют исходя из
межосевых расстояний, которые в
станкостроении принимаются трех значений
в зависимости от модуля 

; 

;  

.

Соответственно этим значениям сумма
чисел зубьев сменных колес будет

.

Числа зубьев сменных колес в станкостроении
нормализованы (Д11-20).

 Определение чисел зубьев при
связанных колесах  

При одном связанном колесе, входящем в
две группы передач, передаточные числа
определяются как обычно на основе
картины чисел оборотов. Числа зубьев
колес первой группы определяются на
основе приведенной выше методики.
Определив z_Σ-Ι для первой группы,
находят z_Σ-ΙΙ и для второй группы,
пользуясь тем, что снизанное колесо
является ведомым для первой группы и
ведущим для второй.

Числа зубьев связанного колеса как
ведомого колеса первой группы определяются
выражением:

.

Числа зубьев связанного колеса как
ведущего колеса второй группы определятся
выражением:

.

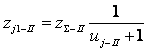
Приравнивая второе выражение первому,
находим

.

 Зная z_Σ-ΙΙ, определяем числа
зубьев колес второй группы. Числа зубьев,
полученные в результате расчета, должны
быть округлены до целых чисел, что
сопровождается большим или меньшим
отклонением фактических передаточных
чисел от заданных.  

Определение чисел зубьев косозубых
колес одной группы передач 

Если все передачи имеют одинаковый
нормальный модуль и одинаковый угол
наклона линии зубьев, то расчет ведется
так же, как и прямозубых колес.

С различным углом наклона линии зубьев
передачи выполняются для компенсации
отклонений в сумме зубьев z_Σ,
возникающих вследствие необходимости
точного подбора передаточных чисел или
применения передач с различным модулем.
В этом случае, установив межосевое
расстояние для одной пары зубчатых
колес, определяют угол наклона линии
зуба, необходимый для обеспечения
зацепления второй пары.

 Определение чисел зубьев червячных
передач  

Передаточное число червячной передачи

,

где z₂ – число зубьев червячного
колеса;

z₁ – число заходов червяка.

Зная передаточное число червячной
передачи и исходя из конструктивных
соображений, задаются числом зубьев
червячного колеса и определяют число
заходов червяка (можно и наоборот). При
этом придерживаются нормалей станкостроения
Н 21-5 , Н 24-2 и Н 24-5. Обычно число заходов
червяка не превышает 4.

Во всех рассмотренных случаях определения
чисел зубьев колес (Приложение
7.3.23) необходимо учитывать
следующие рекомендации:

1) не следует принимать слишком малые
значения чисел зубьев, так как при
небольшом модуле получается незначительный
диаметр колес и может оказаться
невозможным осуществление посадки их
на вал;

2) колеса большого диаметра работают
более плавно и износ их меньше, но при
этом увеличиваются размеры коробки;
при большом диаметре колес и высоких
числах оборотов на червяке могут
получаться недопустимо высокие окружные
скорости. Кроме того, с увеличением
окружной скорости должна быть понижена
шероховатость и повышена точность
обработки колес;

3) следует по возможности применять
нормализованные значения суммы чисел
зубьев и межосевых расстояний.

Расчет зубчатой передачи

Классификация передач. По форме различают цилиндрические, конические, реечные, эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В зависимости от взаимного расположения; зубчатых колес различают зубчатые передачи с внешним и внутренним зацеплением, а также разделяются на открытые и закрытые (рис. 81).

Назначение. Зубчатые передачи относятся к механическим передачам зацепления с непосредственным контактом и применяются для изменения скорости или направления вращения ведомого звена с соответствующим изменением крутящего момента, получения точных перемещений, при необходимости точного соответствия скоростей и положений ведущего и ведомого звеньев в произвольный момент времени. Зубчатая передача состоит из двух колес с зубьями, посредством которых они сцепляются между собой. Вращение ведущего зубчатого колеса преобразуется во вращение ведомого колеса путем нажатия зубьев первого на зубья второго. Меньшее зубчатое колесо передачи называется шестерней, большее – колесом. Зубчатые передачи могут преобразовывать вращательное движение между валами с параллельными, пересекающимися и перекрещивающимися осями.

а	б	в	г
д	е	ж	з
и	к	л	м

Рис. 81. Виды зубчатых передач: а – внешнего зацепления прямозубая, б – внешнего зацепления косозубая, в – внутреннего зацепления прямозубая, г – внешнего зацепления реечная, д – внешнего зацепления шевронная, е – коническая прямозубая, ж – коническая косозубая, з – коническая круговая, и – коническая круговая – гипоидная, к – внешнего зацепления винтовая, л – передача с круговыми зубьями, м – планетарная.

Преимущества. Важнейшие: компактность, высокий КПД, постоянство передаточного числа, большая долговечность и надежность в работе, возможность осуществления передачи практически любых мощностей при практически любых скоростях и передаточных отношениях, простота обслуживания. Высокая технологичность, которая обусловлена высокопроизводительным специальным оборудованием и технологиями.

Недостатки. Высокие требования к качеству изготовления и монтажа. Шум при больших скоростях. Концентрация напряжений в эвольвентных передачах при точечном контакте и чувствительность к ошибкам монтажа в передачах с линейным контактом. Поэтому для реализации преимуществ при изготовлении деталей необходимо применять высококачественные материалы и технологии изготовления.

Сферы применения. 3убчатые передачи нашли самое широкое распространение среди механических передач в машинах различных отраслей. Назначение и конструкции зубчатых передач разнообразны. Их применяют во многих приборах и почти во всех машинах, в том числе и самых тяжелых и мощных для передачи мощностей до 65 тыс.кВТ (65МВт), с диаметром колес от долей миллиметра до 6м и более. Окружная скорость зубьев может достигать 270м/с. Передаточные отношения для открытой передачи принимают 10, а для закрытой 25. КПД одной ступени зубчатой передачи при высоком качестве изготовления и монтажа может достигать 0,99.

Геометрический расчет. Передаточное отношение передачи

, (14.1)

где – число зубьев шестерни и колеса соответственно.

Номинальные значения передаточных чисел и зубчатых редукторов общего назначения, выполненных в виде самостоятельных агрегатов стандартизированы:

1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5.

2-й рад 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.

При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел не должны отличаться от расчетных не более чем на 3%.

Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:

, (14.2)

где и – начальные диаметры шестерни и колеса; знак плюс относится к передаче с внешним зацеплением, а минус – к передаче с внутренним зацеплением.

Стандартизированы номинальные значения межосевых расстояний aw, мм:

1-й ряд 40; 50; 63; 80100; 125; 160; 200; 250; 315; 400; 500; 630; 800

2-й ряд – – 71; 98; 112; 140; 180; 225; 280; 355; 450; 560; 710; 900.

Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров колеса d2 и шестерни при внешнем зацеплении или полуразности при внутреннем зацеплении, называется делительным межосевым расстоянием:

. (14.3)

Делительные диаметры для зубчатых колес прямозубой передачи

d = zm, (14.4)

для косозубой и шевронной

. (14.5)

где т – модуль зацепления основная характеристика размеров зубчатых и червячных колес. Для обеспечения взаимозаменяемости и унификации инструмента для изготовления модули цилиндрические и конические эвольвентных зубчатых колес стандартизованы: для цилиндрических колес – значения нормальных модулей, для конических – значения окружных делительных модулей в диапазоне 0,05..100мм.

1-й ряд 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25;

2-й ряд 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28.

Ширина венца цилиндрического зубчатого колеса определяется по одной из формул

, (14.6)

или

, (14.7)

где – коэффициент ширины зубчатого венца по межосевому расстоянию, а – коэффициент ширины зубчатого венца по диаметру шестерни.

Коэффициенты и связаны зависимостью:

. (14.8)

Значения коэффициентов ширины венца зубчатых колес по межосевому расстоянию выбираются из стандартного ряда: 0,1; 0,125; 0,16; 0,2; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,000; 1,25 и т. д.

Рис. 82. Обозначения  элементов зубчатого зацепления.

Для заданного числа зубьев и , коэффициентов смещения исходного контура и , угла наклона зубьев основные параметры эвольвентных цилиндрических колес внешнего зацепления, показанные на рис 82 в соответствии с ГОСТ 13755-81 определяются по расчетным формулам:

Параметр	Шестерня	Колесо
Делительный диаметр
Основной диаметр
Начальный диаметр
Диаметр вершин зубьев
Диаметр впадин зубьев
Межосевое расстояние
Делительный угол профиля в торцевом сечении
Коэффициент торцевого перекрытия
Рабочая ширина зубчатого венца
Коэффициент осевого перекрытия (при ширине венца )
Основной угол наклона

Кинематический и силовой расчет. Расчетная окружная скорость v цилиндрической передачи:

– шестерни ; (14.9)

– колеса ,

где – угловая скорость зубчатого колеса; п – частота вращения зубчатого колеса; – начальный диаметр цилиндрического зубчатого колеса.

Окружная сила цилиндрической зубчатой передачи Ft

, (14.10)

где – крутящий момент на шестерне.

Сила давления между зубьями в цилиндрической прямозубой передаче

. (14.11)

Составляющие этой силы: в цилиндрических прямозубых (рис. 83) и шевронных передачах – окружная сила , и радиальная сила , в конической прямозубой и цилиндрической косозубой передачах – окружная сила , радиальная сила , и осевая сила Fa.

Радиальная сила в цилиндрической передаче

, (14.12)

Осевая сила, действующая на колесо косозубой цилиндрической передачи

, (14.13)

Критерии работоспособности зубчатых передач. Учитывая виды повреждений критериями работоспособности зубчатых передач являются контактная и изгибная прочность зубьев. Проектный расчет закрытых передач малой и средней твердости выполняется на контактную выносливость. Расчет на изгибную прочность зубьев в этом случае выполняется как проверочный. Для зубчатых колес высокой прочности () размеры передачи определяются из расчета зубьев на изгиб, а проверочный расчет выполняется по контактным напряжениям. Для открытой передачи проектный расчет выполняется из условия предупреждения поломки зуба с учетом износа зубьев, проверочный расчет выполняется из условия обеспечения контактной прочности.

Проектные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. По зависимости для проектного расчета на контактную прочность зубьев определяется межосевое расстояние

, (14.14)

где – коэффициент для прямозубых передач Ка = 495, а для косозубых Ка= 430, – момент на зубчатом колесе передачи в , – коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев, который определяется по рис. 84; – допускаемое контактное напряжение в МПа.

Рис.84. Коэффициенты неравномерности распределения нагрузки по длине контактных линий  для расчета на контактную прочность.

Коэффициент ширины венца по межосевому расстоянию для редукторов принимают равным: для зубчатых колес из улучшенных сталей при несимметричном расположении = 0,315…0,4; для зубчатых колес из закаленных сталей = 0,25…0,315; при симметричном расположении зубчатых колес относительно опор = 0,4…0,5; для передвижных зубчатых колес коробок скоростей = 0,1…0,2. Принимаются стандартные значения .

Допускаемое контактное напряжение

, (14.15)

где – предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений (табл. 14.1); – коэффициент безопасности; ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; Zv – коэффициент, учитывающий окружную скорость передачи; KHL – коэффициент долговечности. Коэффициент безопасности зубчатых колес с однородной структурой материала sH = 1,1; с поверхностным упрочением зубьев sH = 1,2. Коэффициент ZR = 0,9…1; ZR =1,0 при мкм, ZR =0,95 при мкм и ZR =0,9 при мкм. Коэффициент Zv = 1…1.16; чем меньше скорость передачи и тверже зубья, тем меньше Zv. При v << 5м/с Zv = 1. При приближенном расчете можно принимать .

Коэффициент долговечности KHL определяют в зависимости от отношения – базового числа циклов нагружения при котором определяется предел контактной выносливости и – эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. Базовое число циклов напряжений в зубьях принимают в зависимости от твердости НВ рабочей поверхности зубьев либо по формуле

. (14.16)

При эквивалентном числе циклов нагужения зубьев колес больше базового коэффициент долговечности KHL =1. В случае когда эквивалентное число циклов

нагружения зубьев меньше базового то

. (14.17)

Если при расчете колес из нормализованной или улучшенной стали , то принимают .

Таблица 14.1. Предел контактной выносливости при базовом числе циклов

Термическая обработка	Твердость поверхностей зубьев	, Па
Нормализация или улучшение
Объемная закалка
Поверхностная закалка
Цементация или нитроцементация
Азотирование

Эквивалентное число циклов напряжений при работе передачи с постоянной нагрузкой

, (14.18)

где с – число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; – частота вращения рассчитываемого зубчатого колеса, ; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.

При работе передачи с переменными нагрузками

, (14.19)

где Tmax – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; – передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения .

Допускаемое контактное напряжение для зубьев прямозубых передач определяют раздельно для шестерни и колеса и в качестве расчетного принимают меньшее из них. При расчете зубьев косозубых передач, в которых зубья шестерни значительно превышают твердость зубьев колеса, расчетное контактное напряжение

, (14.20)

где и – допускаемые контактные напряжения зубьев шестерни и колеса, вычисляемые по формуле (14.15); – минимальное допускаемое напряжение из этих двух допускаемых напряжений.

Полученный по формуле (14.14) межосевое расстояние следует округлить до ближайшего большего стандартного значения. При проектировочном расчете числом зубьев шестерни задаются, а число зубьев колеса . Для зубчатых передач без смещения рекомендуется принимать зубьев для обеспечения отсутствия подрезание зубьев. Для уменьшения габаритных размеров тихоходных зубчатых передач допускается зубьев. В быстроходных передачах в целях уменьшения шума рекомендуется принимать зубьев.

Расчет зубьев на изгибную прочность. Предварительное значение модуля зубчатой передачи определяется из условия проектного расчета зубьев на изгиб.

, (14.21)

Рис. 85. Коэффициент формы зуба.

где – коэффициент для прямозубых передач =14, для косозубых и шевронных =11,2; – коэффициентом формы зуба, который определяется по рис.85; – коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, который определяется по рис.86; – момент на шестерне передачи в , – число зубьев шестерни; а – коэффициент ширины зубчатого венца по диаметру шестерни, который определяется по формуле (14.8), допускаемые напряжения при изгибе зубьев.

Для косых зубьев коэффициент YF определяют не по действительному числу зубьев z, а по эквивалентному по зависимости

. (14.22)

Допускаемое напряжение на изгиб для зубьев

, (14.23)

где – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений (табл.14.2); – коэффициент безопасности зубьев на изгиб; – коэффициент долговечности зубьев на изгиб; – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья; ; коэффициент безопасности =1,7…2,2 (большие значения для литых заготовок).

Рис. 86. Коэффициенты неравномерности распределения нагрузки по длине контактных линий для расчета на изгибную прочность. Схемы расположения колес показаны на рис.84.

Таблица 14.2 Пределы выносливости материалов зубчатых колес на изгиб

Вид термообработки и марка стали	Твердость зубьев	, МПа
на поверхности	в сердцевине
Цементация легированных сталей:
содержание Ni более 1% Cr 1% и менее (например, 20ХН2М, 12ХН2, 12ХН3А)	57-63	32-45	950
стали марок 18ХГТ, 30ХГТ, 12Х2Н4А и др.	57-63	32-45	800
Нитроцементация легированных сталей:
25ХГМ	57-63	32-45	1000
25ХГТ, 30ХГТ и др.	57-63	32-45	750
Заделка при нагреве ТВЧ по всему контуру:
стали пониженной прокаливаемости (например, 55ПП)	58-62	28-35	900
стали марок 60ХВ, 60ХН и др.	54-60	25-35	700
стали марок 35ХМА, 40ХН и др.	48-60	25-35	600
Нормализация или улучшение	НВ	180-350	1,35НВ+100
Азотирование легированных сталей	–	24-40	18HRCсерд+50

Коэффициент долговечности определяют в зависимости от отношения – базового числа циклов нагружения при котором определяется предел контактной выносливости и – эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. При эквивалентном числе циклов нагружения зубьев колес больше базового коэффициент долговечности =1.

В случае когда эквивалентное число циклов нагружения зубьев меньше базового, то

. (14.24)

Для зубчатых колес с твердостью поверхности зубьев , а также со шлифованной переходной поверхностью зубьев показатель корня т=6, для зубчатых колес с и нешлифованной переходной поверхностью т=9. Базовое число циклов нагружений зубьев изгибом .

Эквивалентное число циклов перемены напряжений NFE. при работе передачи с постоянной нагрузкой

, (14.25)

где с – число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; – частота вращения рассчитываемого зубчатого колеса, ; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.

При работе передачи с переменными нагрузками

, (14.26)

где Tmax – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; – передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения , показатель степени принимается согласно рекомендациям к формуле (14.24).

Значение коэффициента принимают: при односторонней нагрузке на зубья , а при двусторонней = 0,7…0,8 (большее значение при НВ > 350).

При известном межосевом расстоянии ориентировочное значение модуля передачи определяется по зависимости

, (14.27)

где – коэффициент для прямозубой передачи =1400, для косозубой и шевронной =850.

Значение модуля зацепления полученное по формуле (14.27) округляется до ближайшего стандартного значения. После определения значений межосевого расстояния и модуля определяются число зубьев и все геометрические параметры передачи по которым выполняется проверочные расчеты.

Проверочные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

– для прямозубых передач

; (14.28)

– для косозубых передач

, (14.29)

где , – коэффициент неравномерности распределения нагрузки между зубьями в зависимости от скорости и точности изготовления; – коэффициент динамической нагрузки, возникающей в зацеплении.

Таблица 14.3 Значения коэффициента динамических нагрузок

Степень точности	Твердость поверхностей зубьев	υ, м/с
1	2	4	6	8	10
6-я	а
б
7-я	а
б
8-я	а
б
9-я	а
б

Примечания: 1. Твердость поверхности зубьев: а) и или и ; б) и . 2. 3начения в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.

Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями : а – для расчета на контактную прочность, b – для расчета на изгибную прочность.

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят КНа = 1, а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.3.

Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями : а – для расчета на контактную прочность, b – для расчета на изгибную прочность.

При действии на зубья кратковременных перегрузок выполняется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:

, (14.30)

где – максимальное расчетное напряжение при перегрузке зубьев максимальным моментом ; – допускаемое максимальное контактное напряжение для зубьев; – расчетное контактное напряжение, вызываемое расчетным моментом и определяемое по формуле (14.27) или (14.28). Для зубьев зубчатых колес и термообработкой нормализацией, улучшением или объемной закалкой с отпуском , где – предел текучести материала зубьев при растяжении; для зубьев с термообработкой – цементация, контурная закалка после нагрева ТВЧ – ; для азотированных зубьев . Расчет зубьев по формуле (14.30) производится раздельно для колеса и для шестерни.

Расчет зубьев на изгибную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

, (14.31)

где – коэффициент учитывающий перекрытие зубьев; – коэффициент наклона зубьев; – коэффициент распределения нагрузки между зубьями; – коэффициент динамической нагрузки, возникающей в зацеплении при работе передачи, – коэффициент ширины венца зубчатого колеса по начальному диаметру шестерни.

При подстановке окружной силы по зависимости (14.10) формула (14.31) преобразуется к виду

.

Коэффициент, учитывающий перекрытие зубьев

.

При приближенных расчетах для для косозубых передач и прямозубых передач принимают .

Коэффициент наклона зубьев для прямозубых передач , для косозубых определяется по зависимости

, (14.32)

при .

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят , а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.4

Таблица 14.4 Значения коэффициента динамических нагрузок

Степень точности	Твердость поверхностей зубьев	υ, м/с
1	2	4	6	8	10
6-я	а
б
7-я	а
б
8-я	а
б
9-я	а
б

Примечания: 1. Твердость поверхности зубьев: а) и или и ; б) и . 2. 3начения в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.

Если материал зубчатых колес одинаковый, то расчет зубьев на изгиб производят по шестерне, у которой толщина зубьев у основания меньше и соответственно коэффициент формы зубьев YF больше, чем у зубьев колеса. Если материал зубьев шестерни более прочный по сравнению с материалом зубьев колеса, что обычно и принимается, то расчет зубьев на изгиб нужно производить по тому зубчатому колесу, для которого отношение имеет меньшее значение. Рекомендуется материал зубьев шестерни и колеса принимать таким, чтобы отношение для обоих зубчатых колес было примерно одинаковым.

Если известно напряжение изгиба для зуба шестерни, то для зуба колеса условие прочности на изгиб запишется в виде

. (14.33)

При действии кратковременных перегрузок зубья проверяют на пластическую деформацию или хрупкий излом при изгибе от максимальной нагрузки:

, (14.34)

где – максимальное расчетное напряжение на изгиб в зубьях при их перегрузке максимальным моментом ; – допускаемое максимальное напряжение на изгиб для зубьев; – расчетное напряжение на изгиб для зубьев, вызываемое расчетным моментом и определяемое по формуле (14.31).

Значение допускаемых максимальных напряжений

на изгиб для зубьев принимают: при твердости поверхности зубьев , где – предел текучести материала зубьев при растяжении; при твердости , где – предел прочности материала зубьев при растяжении. Расчет зубьев по формуле (14.34) производят для менее прочного колеса передачи.

Задача 14.1. Выполнить расчет зубчатой передачи. Выполнить проектный и проверочный расчеты (на контактную и изгибную прочность) косозубой зубчатой передачи быстроходной ступени двухступенчатого цилиндрического редуктора. Параметры циклограммы нагружения шестерни: момент на шестерне , продолжительность работы ; , ; , . Частота вращения шестерни . Передаточное число , передача нереверсивная. Марка стали колес – сталь 40ХН. Способ упрочнения – закалка при нагреве ТВЧ до твердости поверхности зубьев .

Решение. Проектный расчет зубчатой передачи.

Принимаем коэффициент ширины по межосевому расстоянию из стандартного ряда значений .

Коэффициент ширины по диаметру шестерни по формуле (14.8)

.

Ориентировочное значение коэффициента неравномерности распределения нагрузки определяем по рис.84. Твердость зубьев соответствует твердости , согласно зависимостям на рис.88. Для схемы ІІ, при твердости зубьев (рис.84.): .

Предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений определяем по таблице 14.1.

=

Рис.88. Зависимости для определения твердости в единицах

Коэффициент запаса прочности .

Базовое число нагружений для материала шестерни и колеса по формуле (14.16)

Эквивалентное число циклов нагружений зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.19) с учетом того, что частота вращения на всех режимах одинакова и равна . (При постоянном нагружении эквивалентное число циклов определяется по зависимости (14.18))

=

==

= циклов.

Эквивалентное число нагружений зубьев колеса

циклов.

Коэффициенты долговечности для зубьев шестерни и колеса по формуле (14.17)

,

.

Допустимые контактные напряжения по формуле (14.15), с учетом

– для шестерни

;

– для колеса

.

Так как твердость поверхности зубьев шестерни и колеса одинаковы, то в качестве расчетного допускаемого контактного напряжения принимаем меньшее значение

.

Расчетное межосевое расстояние определяем по формуле (14.14) для косозубой передачи

.

Принимаем наибольшее значение из стандартного ряда .

Находим предел усталости зубьев при изгибе по табл. 14.2. для стали 40ХН с упрочнением ТВЧ .

Базовое число циклов нагружений зубьев изгибом .

Эквивалентное число циклов нагружений изгибом зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.26) с учетом (14.24) и того, что частота вращения на всех режимах одинакова и равна :

=

=

= циклов.

Для зубьев колеса эквивалентное число циклов нагружений изгибом

циклов.

Коэффициенты долговечности для зубьев шестерни и колеса на изгиб с учетом того, что и , то .

Допускаемое напряжение на изгиб для зубьев шестерни определим по формуле (14.23) при и

.

Предварительно принимаем коэффициент формы зуба шестерни .

Расчетная ширина венца зубчатого колеса

.

Принимаем стандартный размер ширина венца .

Ширина зубчатого венца шестерни .

Принимаем .

По известному значению межосевого расстояния ориентировочно определяем модуль зацепления по зависимости (14.27) для косозубой передачи

мм.

Принимаем стандартное значение модуля зацепления мм.

Предварительное значение угла наклона зубьев принимаем из диапазона . Принимаем .

Число зубьев шестерни по межосевому расстоянию и модулю определим по зависимости:

.

Принимаем число зубьев шестерни .

Число зубьев колеса

.

Уточнение угла наклона зубьев по межосевому расстоянию и числу зубьев

0,96 и .

Принимаем коэффициент коррекции при изготовлении зубьев .

Расчет геометрических, кинематических и силовых параметров для выполнения проверочных расчетов.

Делительные диаметры колес зацепления:

– шестерни 166,67мм;

– колеса 333,33мм.

Начальные диаметры:

– шестерни 166,67мм;

– колеса 333,33мм.

Диаметр вершин зубьев:

– шестерни 176,67мм,

– колеса 343,33мм.

Диаметр впадин зубьев:

– шестерни 154,17мм,

– колеса 320,83мм.

Делительный угол профиля зуба в торцевом сечении

= 20,760.

Угол зацепления передачи при

.

Коэффициент торцевого перекрытия:

=

=1,66.

Коэффициент осевого перекрытия

=1,12.

Окружная скорость

Принимаем при такой скорости 8-ую степень точности (табл.14.5) с шероховатостью поверхности зубьев мкм.

Таблица 14.5 Степени точности зубчатых передач

Степень точности	Окружная скорость колес, м/с, не более	Область применения
прямозубых	косозубых
6 – я	15	30	Скоростные передачи, делительные механизмы
7 – я	10	15	Передачи при повышенных скоростях и умеренных нагрузках или наоборот
8 – я	6	10	Передачи общего машиностроения, не требующие особой точности
9 – я	2	4	Тихоходные передачи с пониженными требованиями к точности

Проверочные расчеты зубчатого зацепления на контактную прочность зубьев.

Определяем по графику на рис.87. а коэффициент неравномерности распределения нагрузки в зависимости от скорости и 8-ой степени точности изготовления

Определяем по таблице 14.3 коэффициент динамической нагрузки для твердости поверхности зубьев при скорости и 8-ой степени точности изготовления =1,045.

Коэффициент неравномерности

1,26.

Расчет зубьев на контактную прочность выполняем по зависимости (14.29)

Следовательно, условие контактной прочности зубьев выполнено. Допускается превышение над до 5%.

Проверочный расчет на изгибную прочность зубьев. Определяем по графику на рис.87 а коэффициент неравномерности распределения нагрузки на изгиб в зависимости от скорости и 8-ой степени точности изготовления .

Определяем по графику на рис.86 б коэффициент неравномерности распределения по длине контактных линий на изгиб в зависимости от схемы зацепления и твердости зубьев .

Определяем по таблице 14.3 коэффициент динамической нагрузки на изгиб для твердости поверхности зубьев при скорости и 8-ой степени точности изготовления =1,07.

Эквивалентное число зубьев косозубой передачи определяем по формуле (14.22)

– для шестерни ,

– для колеса .

Коэффициент формы зубьев колес принимаем по графику рис.85. в зависимости от эквивалентного числа зубьев:

– для шестерни 3,75,

– для колеса 3,62.

Коэффициент учитывающий угол наклона зубьев определяем по формуле (14.32)

==0,88.

Коэффициент, учитывающий перекрытие зубьев передачи

=0,6.

Окружную силу в зацеплении определим по формуле (14.10)

= 25200Н.

Расчетные напряжения изгиба в зубьях

– для шестерни

,

– для колеса

.

Следовательно, условие прочности зубьев на изгиб обеспечивается.

Задача 14.2. Определить размеры открытой конической зубчатой передачи. Передаваемая мощность N=3,5·103Вт. Передаточное числа i = 4.Частота вращения ведущего вала Передача нереверсивная.

Решение. Углы при вершинах начальных конусов

Выбираем материал зубчатых колес. Материал шестерни – сталь Ст.5, материал колеса – чугун СЧ 21–40 т. к. передача открытая расчет будет производится только из условия прочности зубьев на изгиб.

Допускаемые напряжения изгиба для шестерни

где ;

для колеса

где – предел прочности чугуна СЧ 21-40 на растяжение.

Задаемся числом зубьев шестерни Тогда

Сравнительная прочность зубьев шестерни и колеса на изгиб:

для шестерни

для колеса

Таким образом, расчет следует вести по колесу.

Задаемся:

Расчетный момент на ведущем валу

Здесь принято предварительно K=1,5.

Момент расчетный на ведомом валу (валу колеса) без учета потерь в зацеплении и подшипниках

Максимальный модуль зацепления при коэффициенте износа γ = 1,2

Принимаем из ряда стандартных значений модулей (по ГОСТ 9563-80).

По найденному определяем размеры колес:

Углы конусов выступов

Тогда

.

Длина зуба

Средний модуль

Расчет числа зубьев зубчатого колеса

Зубчатое колесо – это основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.

Формула расчета числа зубьев зубчатого колеса:

z – количество зубьев зубчатого колеса в мм;
d – диаметр делительной окружности в мм;
m – модуль зубчатого колеса.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета числа зубьев зубчатого колеса по простой математической формуле в зависимости от диаметра делительной окружности и числа зубьев. С помощью этого калькулятора вы в один клик сможете выполнить расчет числа зубьев зубчатого колеса.

Глава 8. зацепления зубчатые

Зацепления зубчатые относятся к передачам (подвиж­ным соединениям) и передают движение от двигателя к ис­полнитель­ным механизмам. К составным частям зубчатых передач отно­сятся зубчатые колеса (цилиндрические, кони­ческие), червяки, рейки.

Диаметр делительной ок­ружности d является од­ним из основных параметров, по кото­рому произ­водят расчет зубча­того ко­леса:

где z – число зубьев;

Модуль зацепления m – это часть диаметра делительной ок­ружности, приходящейся на один зуб:

где t – шаг зацепления.

где h _a – высота головки зуба, h _a = m ; h _f – высота ножки зуба, h _f = 1,25 m .

Диаметр окружности выступов зубьев :

Диаметр окружности впадин :

Служит для передачи вращения при параллельных осях валов.

ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2 .

Служит для преобразования вращательного движения в возвратно-посту­пательное.

ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращательного движения между валами со скрещивающимися осями.

ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).

Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …

Ряд 2: … 1,5; 3; 3,5; 6; 7 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращения при пересекающихся осях валов.

ГОСТ 9563-60 предусматривает два ряда модулей m  = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Как найти модуль зубчатого колеса?

История

Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.

В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.

Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.

Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес [4] .

Модуль зубьев зубчатого колеса

Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Чему равен модуль зубчатого колеса?

Модуль зубчатого колеса Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.

Для чего нужен модуль зубчатого колеса?

Что же такое модуль шестерни? это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Как определить параметры шестерни?

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр. Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

Как найти модуль шестерни?

Как определить модуль косозубой шестерни.

1. Диаметр окружности выступов (De) равен 28,6 мм.
2. Считаем количество зубьев. Z=25.
3. Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
4. Округляем до ближнего модуля. Получается модуль 1.

Как найти делительный диаметр шестерни?

Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.

Как найти модуль зуба?

Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2. Измеряем диаметр: Диаметр окружности выступов (De) равен 28,6 мм.

Какие бывают модули зубчатых колес?

Модуль — это линейная величина, в π раз меньшая шага зубьев p (окружного pt, осевого рx, нормального рn и других шагов) эвольвентного зубчатого колеса m = р/π. Соответственно различают модули: окружной mt, осевой mx, нормальный mn и др.

Цилиндрические зубчатые колёса

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

Параметры эвольвентного зубчатого колеса:

• m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

• • z — число зубьев колеса
  • p — шаг зубьев (отмечен сиреневым цветом)
  • d — диаметр делительной окружности (отмечена жёлтым цветом)
  • d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
  • d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
  • d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
  • h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

  Для целей стандартизации, удобства изготовления и замены зубчатых колёс в машиностроении приняты определённые значения модуля зубчатого колеса m, представляющие собой ряд из чисел на выбор: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 25; 32; 40; 50; 60; 80; 100.

  Зубчатые колеса могут быть изготовлены с различным смещением режущей рейки: без смещения (нулевое зубчатое колесо или «с нулевыми зубцами»), с положительным смещением (смещение в сторону увеличения материала), с отрицательным смещением (смещение в сторону уменьшения материала).

  Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае нулевого зубчатого колеса соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

  Отсюда получаем, что высота зуба h (на рисунке не обозначена):

  Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

Продольная линия зуба

Цилиндрические зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:

Прямозубые колёса

Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.

Косозубые колёса

Зубья располагаются под углом к оси вращения, а по форме образуют часть винтовой линии. Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. Также увеличена площадь контакта, что при тех же размерах с прямозубыми позволяет передавать больший крутящий момент. При работе косозубой пары зацепления возникает механическая осевая сила, направленная вдоль оси вращения каждого колеса и стремящаяся раздвинуть оба колеса в противоположные стороны от плоскости контакта, что обязательно требует применения упорных подшипников. Увеличенная площадь трения зубьев косозубого зацепления вызывает дополнительные потери мощности на нагрев. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.

Шевронные колеса

Изобретение шевронного профиля зуба часто приписывают Андре Ситроену, однако на самом деле он лишь выкупил патент на более совершенную схему, которую придумал польский механик-самоучка [6] . Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).

Колёса с круговыми зубьями

Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.

Винтовые шестерни

Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.

Секторные колёса

Секторное колесо представляет собой часть обычного цилиндрического колеса с зубьями любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.

Зубчатые колёса с внешним и внутренним зацеплением

Пара зубчатых колёс с ВНЕШНИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит противонаправлено.

Пара зубчатых колёс с ВНУТРЕННИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит сонаправленно.

Звездочка

Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.

Реечная передача (кремальера)

Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.

Также реечная передача применяется в зубчатой железной дороге.

Цевочная передача Коронная шестерня

Коронные колёса

Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо, как правило, стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах. Передачи с цевочным колесом — одни из самых ранних и просты в изготовлении, но характеризуются очень большими потерями на трение.

Конические зубчатые колёса

Во многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.

Зубчатые передачи

Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.

Типы зубчатых передач

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут из­готавливаться на одном оборудовании, не­зависимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и ко­нических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных пе­редач по DIN 780; модули шлицевых соедине­ний по DIN 5480; модули зубчатого зацепле­ния нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; чер­вячных передач — DIN 3975; шлицевых соеди­нений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регла­ментируется стандартом DIN 867. В допол­нение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы заце­пления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.

Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (из­менение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подреза­ния у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса произво­дится на одинаковую величину, но в противо­положных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для ше­стерни и зубчатого колеса производится независимо друг от друга, поэтому межосе­вое расстояние передачи может изменяться. Допускаемые отклонения линейных разме­ров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры за­цепления без зазора между зубьями. Для определения зазора между зубьями допу­скаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в за­висимости от требуемой степени точности зубчатой передачи.

Следует отметить, что не обязательно стремиться к нулевому за­зору между зубьями. Для компенсации имею­щихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.

Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.

Расчетные формулы для зубчатых передач

Основные параметры зубчатых цилиндрических передач

Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым

Межосевые расстояния

1 ряд	40	50	63	80	100	125	—	160	—	200	—	250	—	315	—	400
2 ряд	—	—	—	—	—	—	140	—	180	—	225	—	280	—	355	—
1 ряд	—	500	—	630	—	800	—	1000	—	1250	—	1600	—	2000	—	2500
2 ряд	450	—	560	—	710	—	900	—	1120	—	1400	—	1800	—	2240	—

1-й ряд следует предпочитать 2-му

Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200	225	250	280	315
Тихоходная ступень	63	80	100	125	160	200	225	250	280	315	355	400	450	500
Быстроходная ступень	355	400	450	500	560	630	710	800	900	1000	1120	1250	1400	1600
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600	1800	2000	2240	2500

Коэффициент запаса прочности при работе зуба двумя сторонами

Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах

Материал колес и термо- обработка	Отливки стальные и чугунные без термо- обработки	Отливки стальные и чугунные с термо- обработкой	Поковки стальные нормали- зованные или улучшенные	Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая)	Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой	Стальные с объемной закалкой	Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др.	Чугунные и пласт- массовые колеса
Коэфф.	1,9	1,7	1,5	2,2	1,4 — 1,6	1,8	1,2	1 — 1,2

Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200
Промежуточная ступень	63	80	100	125	160	200	225	250	280	315
Тихоходная ступень	100	125	160	200	250	315	355	400	450	500
Быстроходная ступень	225	250	280	315	355	400	450	500	560	630
Промежуточная ступень	355	400	450	500	560	630	710	800	900	1000
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600

Номинальные передаточные числа

1 ряд	1,0	—	1,25	—	1,6	—	2,0	—	2,5	—	3,15
2 ряд	—	1,12	—	1,4	—	1,8	—	2,24	—	2,8	—
1 ряд	—	4,0	—	5,0	—	6,3	—	8,0	—	10	—	12,5
2 ряд	3,55	—	4,5	—	5,6	—	7,1	—	9,0	—	11,2	—

1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5

Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25

Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.

При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.

Почему шестерни часто выполняют заодно с валом?

Несмотря на это, в редукторах шестерню часто выполняют заодно с валом и даже при толщине, значительно превышающей указанные нормы. Это объясняется большей жесткостью и прочностью, а также технологичностью вала-шестерни, что в конечном итоге оправдывает ее стоимость.

[spoiler title=”источники:”]

http://dgng.pstu.ru/sprav/8.htm

[/spoiler]