Одночлены
- Стандартный вид одночлена
- Коэффициент одночлена
- Приведение одночлена к стандартному виду
Одночлен — это алгебраическое выражение, представляющее собой число, переменную, их степени с натуральным показателем, а также любые произведения, составленные из них.
Пример. 12,  , m, (-2)3, a2, 5abc, a3x, 3,7c(-2ab2) — одночлены.
, m, (-2)3, a2, 5abc, a3x, 3,7c(-2ab2) — одночлены.
Выражения x + 2 или  не являются одночленами, так как представляют сумму или частное переменных и числа.
не являются одночленами, так как представляют сумму или частное переменных и числа.
Число 0 называют нулевым одночленом.
Буквы и числа одночлена, представляющего собой произведение, называют множителями данного одночлена. При этом числа называют числовыми множителями одночлена, а буквы — буквенными множителями одночлена.
Пример. Назовите числовые и буквенные множители одночлена 5abc.
Решение:
Множителями данного одночлена являются число 5 и буквы a, b, c:
Числовой множитель: 5.
Буквенные множители: a, b, c.
Стандартный вид одночлена
Стандартный вид одночлена — это запись одночлена, представляющая собой число, степень переменной или произведение, в котором только один числовой множитель, записанный на первом месте, а каждая его буква участвует в его записи лишь один раз, при этом буквы записаны в алфавитном порядке.
Пример. 7, a, -3xy2, 1abс — одночлены стандартного вида.
А вот следующие одночлены записаны не в стандартном виде:
12aa3b и 4cb(−2)y,
так как первый содержит одинаковые буквы, а во втором два числовых множителя и буквенные множители записаны не в алфавитном порядке.
Стандартный вид нулевого одночлена есть 0.
Коэффициент одночлена
Коэффициент одночлена — это числовой множитель в одночлене стандартного вида, который содержит хотя бы одну переменную. Понятие коэффициент также относят к одночленам стандартного вида, представляющим собой числа без буквенных множителей. Коэффициентами таких одночленов считаются сами числа.
Пример. Одночлены
-7ab3,  , -1x, 15
, -1x, 15
записаны в стандартном виде. Их коэффициенты соответственно равны числам -7,  , -1, 15.
, -1, 15.
Коэффициент одночлена, равный 1 или -1 обычно не пишут.
Если одночлен имеет только буквенные множители, то условились считать, что его коэффициент равен +1 или -1, в зависимости от знака, который стоит (или подразумевается) перед одночленом.
Пример. Одночлены
a, –xy
записаны в стандартном виде. Коэффициент первого из них равен 1, второго -1, так как
a = 1 · a, –xy = -1 · xy.
Целый положительный коэффициент означает, сколько раз повторяется слагаемым буквенное выражение, перед которым он стоит.
Пример.
3ab = (ab) · 3 = ab + ab + ab.
Дробный положительный коэффициент означает, какая часть берётся от буквенного выражения, к которому он относится.
Пример. В одночлене  коэффициент означает, что от x2 берётся
коэффициент означает, что от x2 берётся  , потому что
, потому что  , а умножить на
, а умножить на  значит взять
значит взять  от множимого.
от множимого.
Отрицательный коэффициент означает, что буквенное выражение, перед которым он стоит, умножается на абсолютную величину этого коэффициента и результат берётся с противоположным знаком.
Пример.
-4mn = -4 · mn = -(mn + mn + mn + mn).
Приведение одночлена к стандартному виду
С одночленами удобнее работать, когда они записаны в стандартном виде. Любой одночлен можно привести к стандартному виду путём тождественных преобразований. Процесс таких преобразований называют приведением одночлена к стандартному виду.
Привести одночлен к стандартному виду — значит выполнить с ним такие тождественные преобразования, чтобы он принял стандартный вид.
Чтобы привести одночлен к стандартному виду надо:
- Выполнить группировку числовых множителей (если их несколько), а также одинаковых буквенных множителей и их степеней.
- Вычислить произведение числовых множителей и по свойству степеней с одинаковыми основаниями перемножить буквенные множители.
- Поставить на первое место числовой множитель, а после него расположить буквенные множители в алфавитном порядке.
Пример 1. Запишите одночлен -2b(-3)x34ab2x2 в стандартном виде.
Решение:
Используя переместительное и сочетательное свойства умножения, сгруппируем по отдельности числовые и одинаковые буквенные множители. В результате исходный одночлен примет вид:
((-2) · (-3) · 4) · (b · b2) · (x3 · x2) · a.
Перемножаем числовые множители и степени с одинаковыми основаниями. Произведение числовых множителей равно 24. Произведение степеней b равно b · b2 = b3. Произведение степеней x равно x3 · x2 = x5:
24 · b3 · x5 · a.
Записываем на первом месте числовой множитель, а после него располагаем буквенные множители в алфавитном порядке. В итоге получаем одночлен стандартного вида:
24ab3x5.
Следовательно:
-2b(-3)x34ab2x2 = ((-2) · (-3) · 4) · (b · b2) · (x3 · x2) · a = 24 · b3 · x5 · a = 24ab3x5.
Пример 2. Представить одночлен -2a4c0b в стандартном виде.
Решение:
Среди своих множителей, данный одночлен имеет множитель 0, значит всё произведение в результате будет равно 0. Стандартный вид нулевого одночлена есть 0:
-2a4c0b = 0.
Часто при решении задач мы используем буквенные множители и числа вместе.
Выражение 5a2b — это произведение трёх множителей:
5a2b = 5 · a2 · b.
Подобные произведения буквенных и числовых множителей называют одночленами.
Запомните!
![]()
Произведение числовых и буквенных множителей называют одночленом.
Примеры одночленов: ac, 2xy2, −7xy, 0,5a3b.
Из чего состоит одночлен
Числовой множитель, который есть в одночлене, принято называть коэффициентом одночлена.
Буквенные множители иногда называют переменными.

Если в одночлене явно нет числового коэффициента, значит числовой коэффициент одночлена равен 1.
Например, для одночлена ab — числовой коэффициент равен 1.
Это связано с тем, что при умножении на 1 одночлен остаётся прежним, поэтому коэфффицент
1 не записывают перед одночленом.
1 · a · b = ab
Также не записывают явно коэффициент «−1».
Вместо этого ставят знак «−» перед одночленом.
При такой записи все понимают, что коэффициент одночлена равен «−1».
Например, у одночлена «−xyz» коэффициент равен
«−1».
Примеры одночленов и их коэффициентов
| Одночлен |
Коэффициент одночлена |
||||
|---|---|---|---|---|---|
| −8a2 | −8 | ||||
| xy2z | 1 | ||||
ab2 |
|
||||
| −tz2 | −1 | ||||
| 144x2 | 144 |
Приведение одночлена к стандартному виду
Запомните!
![]()
Одночлен, у которого единственный числовой множитель стоит на первом месте и буквенные множители в
различных степенях не повторяются, называется одночленом стандартного вида. Буквенные
множители следует располагать в алфавитном порядке.
Примеры одночленов стандартного вида:
2at, 16y3, −17pxy, 3d4
Примеры одночленов нестандартного вида:
2acа, 4xy2 · 3,
x4y · (−7).
Не забывайте, что одночлен — это произведение числовых и буквенных множителей, поэтому внутри
одночлена действуют все законы умножения, в том числе
переместительный закон умножения.
Чтобы привести одночлен к стандартному виду нужно сделать следующее.
Важно!

- Перемножить все числовые коэффициенты и поставить результат их умножения слева самым первым множителем.
- По свойствам степени перемножить буквы и поставить их в алфавитном порядке.
Пример. Привести к стандартному виду одночлен 3ada · 8.
- Перемножаем все числовые коэффициенты
3 · a · d · a · 8 =
3 · 8 · a · d · a
= 24 · a · d · a - Теперь, используя свойства степени,
перемножаем все буквенные множители.
24 · a · d · a =
24 · a · a · d = 24a2d
Что такое степень одночлена
Запомните!
![]()
Степень одночлена — это сумма всех степеней буквенных множителей.
Например, степень одночлена 9a2b
равна 3, т.к. у
a2 (вторая степень), у
b (первая степень): 2 + 1 = 3.
Примеры степеней одночленов
| Одночлен | Степень одночлена | ||
|---|---|---|---|
| −2a2b2 | 4 | ||
xy2 |
3 | ||
| −xyz | 3 |
Число «0» (ноль) называется нулевым одночленом. Степень нулевого одночлена не определена.
Но не путайте с одночленом нулевой степени!
Одночлен нулевой степени — это любое число (например, 123; 0,5; −324).
Любое число можно записать как произведение числа на буквенный множитель в нулевой степени. Т.е.
123 = 123 · a0 = 123 · 1 = 123 (одночлен нулевой степени).
Одночлен нулевой степени получил свое название, потому что любой буквенный множитель можно
представить как 1 через нулевую степень.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Одночлен — это произведение числовых и буквенных множителей, а также их степеней.
Например:
.
Одночленами являются также все числа, любые переменные и степени переменных.
Например:
Среди множества алгебраических выражений можно найти также такие, которые не могут быть названы одночленами.
Например:
— так как эти выражения представляют собой не произведение, а сумму или частное.
Обрати внимание!
Чтобы записать одночлен в стандартном виде, нужно:
1) на первое место записать результат произведения всех числовых множителей;
2) сгруппировать степени с одинаковым буквенным основанием и перемножить их;
3) сгруппировать степени с другим одинаковым буквенным основанием, перемножить их и т. д.
Коэффициентом одночлена называют числовой множитель одночлена, который записан в стандартном виде.
Например:
.
Коэффициент равен (-2).
.
Коэффициент равен (1), и этот коэффициент обычно не пишут, но подразумевают.
.
Коэффициент равен (-1), и этот коэффициент тоже обычно не пишут, но подразумевают.
Одночлены — это любое число, переменная, любая степень, а также произведение чисел, переменных и степеней, с которыми можно совершать разные математические действия. Примеры одночленов: 9, 52, x, 5a; 3ab2 ; −62aa2b3.
Приведение одночлена к стандартному виду
Приведение одночлена к стандартному виду заключается в умножении однотипных множителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему. Важно: в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.
Рассмотрим следующий одночлен: 3a25a3b2
— числа 3 и 5 перемножим и получим число 15,
— степени a2 и a3 имеют одинаковое основание a, поэтому мы можем записать результат a5,
— степень b2 остаётся без изменений.
Получили результат: 3a25a3b2 = 15a5b2
Для того, чтобы далее рассматривать одночлены и действия с ними, вспомним тему «Степень с натуральным показателем«
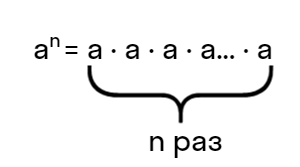
где: a — основание степени; n — показатель степени.
Коэффициент одночлена
- Числовой сомножитель (в примере 15) называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.
- Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице.
Например, для одночлена ab коэффициентом является 1, поскольку ab это произведение единицы и ab: abc = 1×ab. - Если перед одночленом стоит знак минуса, то коэффициент равен минус единице. Например, для одночлена —ab коэффициентом является -1, поскольку ab это произведение -1 и ab.
Степень одночлена
Степенью одночлена называют сумму показателей степеней всех переменных входящих в этот одночлен. Показатель числового множителя при этом не считается.
Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю.
Примеры:
- Степенью одночлена 15a5b2 является 7: переменная a имеет степень 5, а переменная b — 2. Отсюда 5 + 2 = 7. Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.
- Степенью одночлена 7ab2 является 3: переменная a имеет показатель 1, а переменная b — 2.
- Степень одночлена 11 равна нулю, так как это число.
Не следует путать степень одночлена и степень числа:
- Степень числа это произведение из нескольких одинаковых множителей.
- Степень одночлена это сумма показателей всех переменных входящих в этот одночлен.
Сложение и вычитание одночленов
Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.
Чтобы складывать и вычитать одночлены, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути представляет собой приведение подобных слагаемых.
Пример 1. Сложить одночлены 6a2b и 2a2b:
сложим коэффициенты 6 и 2, а буквенную часть 6a2b оставим без изменений.
Получим: 6a2b + 2a2b = 8a2b
Пример 2. Вычесть из одночлена 5a2b3 одночлен 2a2b3
Решение: 5a2b3 − 2a2b3 = 5a2b3 −2a2b3 = 3a2b3
Умножение одночленов
Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Пример 3. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности: 5x × 8y = (5 × 8) × (x × y) = 40xy
Пример 4. Перемножить одночлены 5x2y3 и 7x3y2c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c
Пример 5. Перемножить одночлены −5a2bc и 2a2b4
−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c
Деление одночленов
Для того, чтобы разделит один многочлен на другой, нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.
Пример 6. Разделить одночлен 8a2b2 на одночлен 4ab.
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2.
Теперь делим буквенную часть:
— в делимом содержится a2, в делителе — просто a. Делим a2 на a, получаем a, поскольку a2 : a = a2 − 1 = a.
— в делимом содержится b2, в делителе — просто b. Делим b2 на b, получаем b, поскольку b2 : b = b2 − 1 = b. Значит, при делении одночлена 8a2b2 на одночлен 4ab получается одночлен 2ab.
Если переменная есть только в одном многочлене:
Если в делителе окажется переменная, которой нет в делимом, то деление невозможно.
Например, одночлен 6xy2 нельзя разделить на одночлен 3xyz, так как в делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy2.
Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.
*сокращение дроби это деление числителя и знаменателя на одно и то же число.
Так, в примере нельзя разделить одночлен 6xy2 на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy.
Если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.
Например, при делении одночлена 4x2y2z на 2xy, получается 2xyz.
Если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя, то деление одночлена на одночлен также невозможно.
Например, разделить одночлен 2x на одночлен x2 нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x2, входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x2 даст в результате делимое 2x.
Возведение одночлена в степень
При возведении степень одночлена каждый из множителей возводится в степень. Затем полученные результаты перемножаются: (a × b)n = an × bn
Пример 7. Возвести одночлен xy во вторую степень.
Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый множитель этого одночлена: (xy)2 = x2y2
Пример 8. Возвести одночлен −a2bc3 в пятую степень.
В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:
(−a2bc3)5 = (−1)5 × (a2)5 × b5 × (c3)5 = −1a10b5c15 = −a10b5c15
Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные множители одночлена.
Пример 9. Представить одночлен 121a6 в виде одночлена, возведённого в квадрат.
— число 121 получается, если число 11 возвести в квадрат — это первый множитель.
— степень a6 получается, если возвести в квадрат степень a3 — это второй множитель.
Таким образом, если произведение 11a3 возвести во вторую степень, то получится 121a6
(11a3)2 = 112 × (a3)2 = 121a6
Разложение одночлена на множители
Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.
Пример 10. Разложить одночлен 3a3b2 на множители
Данный одночлен можно разложить на множители:
3a3b2 = 3×a×a×a× b×b = 3×a×a×a×b2 = 3×a3×b×b
Одночлен – это простейшее алгебраическое выражение, которое состоит из произведения чисел, переменных и их степеней. Никаких других действий одночлен не имеет. Числовой множитель у одночлена называется коэффициентом.
Пример №1. Рассмотрим примеры одночленов.
- 5ху это одночлен с коэффициентом, равным 5
- -2,76mn2 у этого одночлена коэффициент равен -2,7
- 15abc здесь коэффициент равен 15
- ¾xy5 у этого одночлена коэффициент равен ¾
Стандартный вид одночлена
Чтобы определить коэффициент у одночлена, он должен быть представлен в стандартном виде.
Что такое одночлен стандартного вида?
Одночлен стандартного вида – это одночлен, у которого на первом месте стоит коэффициент, а далее – буквенные множители (переменные).
Такие одночлены приведены в примере №1. Рассмотрим, как привести одночлен к стандартному виду.
Пример №2.
3х•у2(-2х3у4)=3(-2)х•х3у•у4= -6х4у5
Здесь выполняем умножение чисел 3 и (-2), затем степеней х и у (при умножении степеней с одинаковым основанием показатели складываем, а основание оставляем тем же); записываем на первом месте число (коэффициент одночлена), а затем уже степени. Получаем одночлен стандартного вида.
Пример №3.
-12a3b2(-4b7)=48a3b9
Данный ответ получен после умножения чисел и степеней с одинаковым основанием. Записан на первом месте коэффициент 48, а затем остальные множители.
Степень одночлена
Что такое степень одночлена?
Сумму показателей степени переменных называют степенью одночлена.
Рассмотрим, как найти степень одночлена.
Пример №4.
– 113с3х6
У переменных показатели степени равны 3 и 6, складываем их и получаем 9. Значит, степень одночлена равна 9.
Пример №5.
18ху
У этого одночлена степень равна 2, так как у переменных х и у первая степень, складывая 1 и 1, получаем 2.
Даниил Романович | Просмотров: 4.1k
