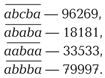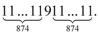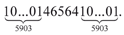Продолжаем разбирать задачки с сайта Leetcode. В прошлый раз было про массив и сумму чисел, теперь тоже необычное.
Условия
В переменной X лежит какое-то целое число
Задача — проверить, является ли это число палиндромом.
Задача со звёздочкой — проверить на наличие палиндрома, не используя строки.
Палиндром — это когда строка или число одинаково читается в прямом и обратном направлении:
121 — это палиндром.
А роза упала на лапу Азора — тоже палиндром (если не считать заглавных букв).
12321 — и это палиндром.
Решение, где используем строки
Самый простой способ проверить, число в переменной палиндром или нет, — преобразовать его в строку, выставить знаки задом наперёд и сравнить с оригиналом. Этим мы сразу решаем проблему отрицательных чисел, когда «−121»превращается в «121−» и сразу становится ясно, что это не палиндром.
Сначала решим это на Python. Тут вообще суть в одной строке:
X = 121
if str(X) == str(X)[::-1]:
print("Это палиндром")
else:
print("Это не палиндром")Здесь мы использовали трюк с переворачиванием строки без её изменения — применили конструкцию [::-1]. Работает это так:
- Первым параметром указывают начало, откуда начинать обработку строки. Раз ничего не указано, то начинаем с первого символа.
- Второй параметр — на каком по счёту символе надо остановиться. Здесь тоже ничего нет, поэтому алгоритм пройдёт до конца строки.
- Последний параметр — шаг и направление обработки. У нас указана минус единица, значит, алгоритм обработает строку справа налево, на каждом шаге считывая по символу.
- В итоге этот код вернёт нам строку, собранную в обратном порядке, при этом с оригинальной строкой ничего не случится — она останется неизменной.
Мы уже делали похожие штуки, когда писали свой генератор новых слов, но там было одно двоеточие, а здесь два.
Теперь решим это же, но на JavaScript:
var X = 121;
if (X.toString().split("").reverse().join("") == X.toString()) {
console.log("Это палиндром")
} else {
console.log("Это не палиндром")
}Здесь мы использовали другой метод пересборки:
- X.toString() — переводит число в строку.
- split(“”) — разбивает строку на массив из символов. В кавычках принцип разделения — если бы там была точка, то разделили бы на местах точек. А так как там пустота, то делится вообще по каждому из символов.
- reverse() — меняет элементы в массиве в обратном порядке.
- join(“”) — добавляет результат к пустой строке, чтобы на выходе получить строку в обратном порядке.
Решение без строк
Тем, кто справился с первой частью, предлагают задачу со звёздочкой — сделать то же самое, но не используя строки, а работая только с числами. Попробуем и мы.
Сделаем в JavaScript функцию, которая будет возвращать true, если в переменной лежит палиндром, и false — если нет. Всё остальное будем писать внутри этой функции:
function palindrome(x) {
}
Теперь обработаем три стандартные ситуации:
- Если в переменной лежит ноль, то это палиндром.
- Если переменная меньше ноля, то это не палиндром.
- Если переменная делится на 10 без остатка — это тоже не палиндром.
Запишем это на JavaScript:
function palindrome(x) {
// если перед нами ноль — это палиндром
if(x == 0) {
return true;
}
// если число меньше нуля или делится на 10 без остатка — это не палиндром
if(x < 0 || x%10 == 0){
return false;
}
}Чтобы проверить, является ли число палиндромом или нет, можно сделать так: отрезаем от числа цифры справа по одной, добавляем их в начало нового числа и постоянно сравниваем новое и старое значение. Если они станут равны — перед нами палиндром. Читайте комментарии, чтобы вникнуть в то, что происходит в коде:
function palindrome(x) {
// если перед нами ноль — это палиндром
if(x == 0) {
return true;
}
// если число меньше нуля или делится на 10 без остатка — это не палиндром
if(x < 0 || x%10 == 0){
return false;
}
// сюда будем собирать число в обратном порядке
temp = 0;
// а тут будем хранить промежуточные значения икса
preX = x;
// пока не дойдём до середины числа — повторяем цикл
while (x > temp) {
// берём самую правую цифру в числе — это остаток от деления на 10
pop = x%10;
// запоминаем старое значение переменной X
preX = x;
// и отрезаем от переменной последнюю цифру — делаем это через целую часть деления на 10
x /= 10;
// добавляем отрезанную цифру к обратной переменной
temp = temp*10 + pop;
}
// если обратная переменная совпала с оставшейся половиной исходной переменной — это палиндром
// мы добавляем сравнение с предыдущей версией исходной половины (которая на 1 цифру больше) на тот случай, если исходное число состояло из нечётного количества символов и его нельзя было бы разбить строго пополам
if(x == temp || preX == temp)
return true;
//
else
return false;
};Для запуска кода просто вызываем функцию и передаём её нашу переменную:
// запускаем код
var X = 121;
console.log(palindrome(X));
Чтобы попрактиковаться, попробуйте сделать такое же, но на Python и не подглядывая в наш код.
Вёрстка:
Кирилл Климентьев
Продолжая цикл статьей о числах (Ссылки на предыдущие статьи в конце материала), не могу не коснуться темы о числах-палиндромах.
Что же это за числа такие чудесные?
Числа-палиндромы читаются одинаково как слева направо, так и справа налево. Примерами таких чисел являются все однозначные числа, двузначные вида αα, такие как 11 и 99, трёхзначные числа вида αβα, например 535 и так далее.
Слово «палиндром» произошло от греческого слова palindromos, обозначающего «вновь бегущий назад». Пе́ревертень — число, буквосочетание, слово или текст, одинаково читающееся в обоих направлениях (Википедия).
Числа-палиндромы найти довольно легко, просто зная их определение. Но есть другой интересный способ их получения.
Возьмём любое число, переставим его цифры, и полученное новое число сложим с первоначальным.
Например, число 23.
- Число с переставленными цифрами — 32;
- Сложим их: 23+32=55;
- Получили число-палиндром!
Или: берём число, ну скажем, 142.
- Складываем его с числом, в котором цифры расположены в обратном порядке — 241;
- 142+241=383;
- 383 — Палиндром!
Продолжаем…
383+383=766+667=1433+3341=4774.
Снова палиндром!
Бывает так, что палиндром выходит не сразу, но если проделать с ним те же манипуляции ещё раз, то результат будет тот же:
359+953=1312+2131=3443.
Для многих чисел применение этой операции к результату предыдущего сложения от 1 до 6 раз ведёт в конце концов к образованию палиндрома. Существуют исключения. Для числа 89 сложение необходимо применить 24 раза.
ОДНАКО! Есть числа, которые палиндромов не дают.
196 — число, которое не даёт палиндромов!
Для числа 196 до сих пор так и не удалось найти числа-палиндрома, даже с привлечением компьютера и повторения сложения миллионы раз! Проблема 196 — условное название нерешённой математической задачи.
Число Лишрел
Есть такое понятие число Лишрел — это натуральное число, которое не может стать палиндромом с помощью итеративного процесса «перевернуть и сложить» в десятичной системе счисления. Этот процесс называется 196-алгоритмом.
Если вас заинтересовала эта тема — можно найти информацию о том, как в разные исторические периоды с помощью компьютерных программ пытались изучать числа Лишрел, есть даже такое понятие «КВЕСТ 196».
Другие кандидаты в числа Лишрел, которые подвергались такому же перебору, включают 879, 1997 и 7059: они были прослежены на протяжении миллионов итераций без обнаружения палиндрома.
Как было сказано выше, палиндромами могут быть не только числа, но также и слова, предложения и даже тексты. Я думаю, все помнят из начальной школы известный палиндром:
«А роза упала на лапу Азора»
© Афанасий Фет
Другие примеры палиндромов:
- Слово «топот» в русском языке;
- Финское слово «saippuakivikauppias» (продавец мыла; торговец щёлоком) — самое длинное слово-палиндром в мире;
- В английском языке фраза – «Madam, I’m Adam»;
- В биологии: в молекулах ДНК присутствует от 100 тыс. до 1 млн. коротких палиндромных последовательностей;
- В музыке: пьесу играют «как обычно», но после того, как она заканчивается, ноты переворачивают, и произведение играют заново, причём музыка не изменится (пример такого музыкального палиндрома: произведение «Застольная мелодия для двоих» Моцарта).
Вот такие они — ПАЛИНДРОМЫ…
#хакнем_математика 👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳
Автор: #ирина_чудневцева 42 года, город Ярославль, мама 16-летнего подростка.
Похожие материалы:
Основное
Задачи на сайтеЗадачи из сказкиЗадачи про числа – палиндромы |
Числа – палиндромы
|
Как определить число-палиндром
Главным образом курс программирования учит не правилам использования конкретных команд, а объясняет, как перекладывать простые повседневные задачи на понятный любой машине язык алгоритмов. Так, типичной задачей данного курса является написание программы по нахождению числа-палиндрома на языке C.
Инструкция
Согласно определению, число-палиндром является таковым, если его можно равнозначно прочитать слева направо и справа налево. Так, например, 2002 остается собой даже если зеркально отразить его в обратную сторону. К несчастью, компьютер не в состоянии рассмотреть число целиком. Решение задачи будет заключаться в том, что машина последовательно сравнит первую цифру с последней, вторую с предпоследней и далее.
Определите количество цифр в числе. Пусть пользователь вводит число в переменную X. Тогда для определения количества цифр в числе стоит написать цикл: for(n=0; N
Разбейте число на цифры. Сделать это можно при помощи обычного деления на 10: создав цикл, который последовательно делит X на 10 n раз и сохраняет остаток от деления в заранее подготовленный массив. Для удобства заполнять массив можно сразу по значению n. Во избежание проблем с делением убедитесь, что X задано целочисленно (int).for(n; n>0; n–){A[n]=X%10; X=X10;}
Проведите оценку. Создайте цикл, сравнивающий значения пар элементов до конца или до тех пор, пока не попадется различие: for(n=0; n
При написании кода не забудьте подключить библиотеку math.h для операции возведения в степень. Кроме того, добавьте в конце getch(); чтобы консоль не закрывалась сразу после завершения программы. Очевидно, что если вам нужно найти количество чисел-палиндромов в заданном диапазоне, то операцию проверки придется повторять циклически.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
ЗАДОМ НАПЕРЁД
Наука и жизнь // Иллюстрации
‹
›
Числовой палиндром — это натуральное число, которое читается слева направо и справа налево одинаково. Иначе говоря, отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным. Палиндромы встречаются в некоторых множествах чисел, удостоенных собственных названий: среди чисел Фибоначчи — 8, 55 (6-й и 10-й члены одноимённой последовательности); фигурных чисел — 676, 1001 (квадратное и пятиугольное соответственно); чисел Смита — 45454, 983389. Указанным свойством обладает также всякий репдиджит, например 2222222 и, в частности, репьюнит*.
Палиндром можно получить как результат операций над другими числами. Так, в книге «Есть идея!» известного популяризатора науки Мартина Гарднера в связи с этой задачей упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с обращённым числом, то есть записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не образуется палиндром. Иногда достаточно сделать всего один шаг (например, 312 + 213 = 525), но, как правило, требуется не менее двух. Скажем, число 96 порождает палиндром 4884 только на четвёртом шаге. В самом деле:
96 + 69 = 165,
165 + 561 = 726,
726 + 627 = 1353,
1353 + 3531 = 4884.
А суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.
Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:
ИГРЫ ЦИФР
До сих пор мы рассматривали в основном составные числа. Теперь обратимся к числам простым. В их бесконечном множестве имеются немало любопытных экземпляров и даже целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходятся на первую тысячу, из них четыре числа однозначные — 2, 3, 5, 7 и всего одно двузначное — 11. С такими числами связано немало интересных фактов и красивых закономерностей.
Во-первых, существует единственный простой палиндром с чётным числом цифр — 11. Другими словами, произвольный палиндром с чётным числом цифр, бóльшим двух, число составное, что нетрудно доказать на основе признака делимости на 11.
Во-вторых, первой и последней цифрами любого простого палиндрома могут быть только 1, 3, 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Любопытно, что все простые двузначные числа, записанные с помощью перечисленных цифр (за исключением 19), можно разбить на пары чисел-«перевёртышей» (взаимно обращённых чисел) вида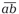 
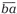
и 
, где цифры a и b различны. Каждая из них, независимо от того, какое число стоит на первом месте, читается одинаково слева направо и справа налево:
13 и 31, 17 и 71,
37 и 73, 79 и 97.
Заглянув в таблицу простых чисел, мы обнаружим аналогичные пары, в записи которых присутствуют и другие цифры, в частности, среди трёхзначных чисел подобных пар наберётся четырнадцать.
Кроме того, среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1:
181 и 191, 373 и 383,
787 и 797, 919 и 929.
Аналогичная картина наблюдается и у бо`льших простых чисел, например:
94849 и 94949,
1177711 и 1178711.
Простые числа-палиндромы могут «задаваться» разными симметричными формулами, которые отражают особенности их записи. Это хорошо видно на примере пятизначных чисел:
Кстати, простые многозначные числа вида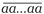 
встречаются, очевидно, только среди репьюнитов. Таких чисел известно пять. Примечательно, что у каждого из них количество цифр выражается простым числом: 2, 19, 23, 317, 1031. А вот среди простых чисел, у которых все цифры, кроме центральной, единицы, был обнаружен палиндром весьма внушительной длины — в нём 1749 цифр:
Вообще среди простых чисел-палиндромов встречаются удивительные экземпляры. Вот лишь один пример — числовой гигант
А интересен он тем, что содержит 11 811 цифр, которые можно разбить на три палидромические группы, причём в каждой группе количество цифр выражается простым числом (5903 или 5).
ПРИМЕЧАТЕЛЬНЫЕ ПАРЫ
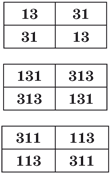
Любопытные палиндромические закономерности просматриваются и в группах простых чисел, в записи которых присутствуют определённые цифры. Скажем, только цифры 1 и 3, причём в каждом числе. Так, двузначные простые числа составляют упорядоченные пары 13 — 31 и 31 — 13, из шести трёхзначных простые сразу пять чисел, среди которых есть два палиндрома: 131 и 313, а ещё два числа образуют пары «перевёртышей» 311 — 113 и 113 — 311. Во всех этих случаях составленные пары наглядно представляются в виде числовых квадратов (рис. 1).
Рис. 1
Своими свойствами они напоминают магический и латинский квадраты. Например, у среднего квадрата сумма чисел, стоящих в каждой строке и в каждом столбце, равна 444, на диагоналях — 262 и 626. Сложив числа из всех клеток, получим 888. И что характерно, каждая сумма — палиндром. Даже просто выписывая без пробела несколько чисел из одной таблицы, получим новые палиндромы: 3113, 131313131 и т. д. Какое наибольшее число можно составить таким способом? Будет ли оно палиндромом?
Если в каждую из пар 311 — 113 и 113 — 311 добавить 131 или 313, образуются четыре палиндромические тройки. Запишем одну из них в столбик:
311
131
113
Как видим, и сами числа, и нужная их комбинация дают о себе знать при прочтении в разных направлениях. Кроме того, расположение цифр симметрично, а их сумма в каждой строке, каждом столбце и на одной из диагоналей выражается простым числом − 5.
Надо сказать, рассмотренные числа интересны и сами по себе. Например, палиндром 131 — простое циклическое число: при любых последовательных перестановках первой цифры на последнее место он порождает простые числа 311 и 113. Можете ли вы указать другие простые палиндромы, обладающие таким же свойством?
А вот пары чисел-«перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:
(1 + 3)2 = 1 + 6 + 9,
(1 + 1 + 3)2 = 1 + 2 + 7 + 6 + 9.
Добавим, что среди натуральных чисел имеются и другие пары «перевёртышей» с подобным свойством: 103 — 301, 1102 — 2011, 11113 — 31111 и др. Чем объясняется подмеченная закономерность? Чтобы ответить на этот вопрос, нужно понять, что особенного в записи указанных чисел, какие цифры и в каком количестве могут в ней присутствовать.
ЧИСЛОВОЙ КОНСТРУКТОР
Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1 и 3 (кроме первого, рис. 2). Особенность этого числового треугольника в том, что один и тот же фрагмент повторяется трижды, не нарушая симметрию рисунка.
Рис. 2
Легко видеть, что общее количество строк и столбцов — число простое (17). К тому же простые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, за исключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов (7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец, если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).
Рис. 3
Продолжая построение, можно сконструировать на основе данного треугольника более сложные фигуры. Так, ещё один треугольник с аналогичными свойствами нетрудно получить, двигаясь с конца, то есть начать с последнего числа, вычёркивая на каждом шаге две одинаковые симметрично расположенные цифры и переставляя или заменяя другие — 3 на 1 и наоборот. При этом сами цифры следует выбирать с таким расчётом, чтобы образующееся в итоге число оказалось простым. Объединив обе фигуры, получим ромб с характерным узором из цифр, скрывающим в себе немало простых чисел (рис. 4). В частности, сумма выделенных красным цветом цифр равна 37.
Рис. 4
Другой пример — треугольник, полученный из исходного после добавления к нему шести простых палиндромов (рис. 5). Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Её окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и ещё столько же — «боковые стороны» треугольника.
Рис. 5
Ещё несколько фигур
Можно составить также многоугольные фигуры из чисел, обладающие определёнными свойствами. Пусть требуется построить фигуру из простых палиндромов, записанных с помощью 1 и 3, у каждого из которых крайние цифры — единицы, а сумма всех цифр и общее количество единиц в строке — простые числа (исключение — однозначный палиндром). Кроме того, простым числом должно выражаться общее количество строк, а также цифр 1 либо 3, встречающихся в записи.
На рис. 6 приведено одно из решений задачи — «домик», сконструированный из 11 различных палиндромов.
Рис. 6
Конечно, не обязательно ограничиваться двумя цифрами и требовать наличия в записи каждого используемого числа всех указанных цифр. Скорее, наоборот: ведь именно их необычные сочетания придают своеобразие узору фигуры. В подтверждение этому приведём несколько примеров красивых палиндромических зависимостей (рис. 7−9).
Рис. 7
Рис. 8
Рис. 9
Теперь, вооружившись таблицей простых чисел, вы и сами сконструируете фигуры вроде предложенных нами.
А напоследок ещё одна диковинка — треугольник, буквально пронизанный вдоль и поперёк палиндромами (рис. 10). В нём 11 строк из простых чисел, а столбцы образованы репдиджитами. И главное: ограничивающий фигуру с боков палиндром 193111111323111111391 — число простое!
Рис. 10
Комментарии к статье
*Число Смита — составное число, сумма цифр которого равна сумме цифр его простых делителей.
Репдиджит — натуральное число, в записи которого все цифры одинаковые.
Репьюнит — натуральное число, записанное с помощью одних только единиц.
