Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
- названием;
- наличием обычного или двойного неравенства;
- обозначением;
- геометрическим изображением на координатой прямой.
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
- Открытый числовой луч. Название связано с тем, что его опускают, оставляя открытым.
Этот промежуток имеет соответствующие неравенства x<a или x>a, где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a – (x<a) или больше a – (x>a).
Множество чисел, которые будут удовлетворять неравенству вида x<a обозначается виде промежутка (−∞, a), а для x>a, как (a, +∞).
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x<a включает в себя точки, которые расположены левее, а для x>a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.


Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a. Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.
Рассмотрим несколько примеров.
При заданном строгом неравенстве x>−3 задается открытый луч. Эту запись можно представить в виде координат (−3, ∞) . То есть это все точки, лежащие правее, чем -3.
Если имеем неравенство вида x<2,3, то запись (−∞, 2,3) является аналогичной при задании открытого числового луча.

- Числовой луч. Геометрический смысл в том, что начало не отбрасывается, иначе говоря, луч оставляет за собой свою полноценность.
Его задание идет с помощью нестрогих неравенств вида x≤a или x≥a. Для такого вида приняты специальные обозначения вида (−∞, a] и [a, +∞), причем наличие квадратной скобки имеет значение того, что точка включена в решение или в множество. Рассмотрим рисунок, приведеный ниже.


Для наглядного примера зададим числовой луч.
Неравенство вида x≥5 соответствует записи [5, +∞), тогда получаем луч такого вида:

- Интервал. Задавание при помощи интервалов записывается при помощи двойных неравенств a<x<b, где а и b являются некоторыми действительными числами, где a меньше b, а x является переменной. На таком интервале имеется множество точек и чисел, которые больше a, но меньше b. Обозначение такого интервала принято записывать в виде (a, b). Наличие круглых скобок говорит о том, что число a и b не включены в это множество. Координатная прямая при изображении получает 2 выколотые точки.
Рассмотрим рисунок, приведенный ниже.

Пример интервала −1<x<3,5 говорит о том, что его можно записать в виде интервала (−1, 3,5). Изобразим на координатной прямой и рассмотрим.

- Числовой отрезок. Данный промежуток отличается тем, что он включает в себя граничные точки, тогда имеет запись вида a≤x≤b. Такое нестрогое неравенство говорит о том, что при записи в виде числового отрезка применяют квадратные скобки [a, b], значит, что точки включаются во множество и изображаются закрашенными.

Рассмотрев отрезок, получим , что его задание возможно при помощи двойного неравенства 2≤x≤3, которое изображаем в виде 2, 3. На координатной прямой данный точки будут включены в решение и закрашены.
- Полуинтервалы. Это промежуточные интервалы с включением приграничных точек. Они записываются при помощи двойных неравенств вида a<x≤b или a≤b<c, где (a, b] и [a, b). Изобразим на координатной прямой.


Если имеется полуинтервал (1, 3], тогда его обозначение можно в виде двойного неравенства 1<x≤3, при чем на координатной прямой изобразится с точками 1 и 3, где 1 будет исключена, то есть выколота на прямой.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
- открытого числового луча;
- числового луча;
- интервала;
- числового отрезка;
- полуинтервала.
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.
Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.
Виды числовых промежутков
На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.
Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.
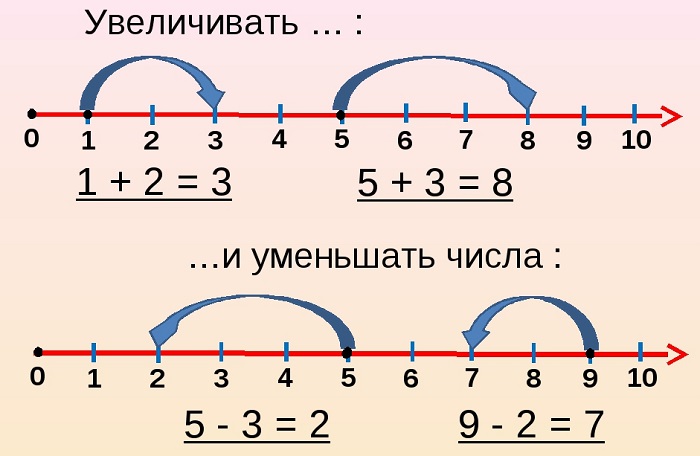
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.
На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.
Открытый числовой луч
Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.
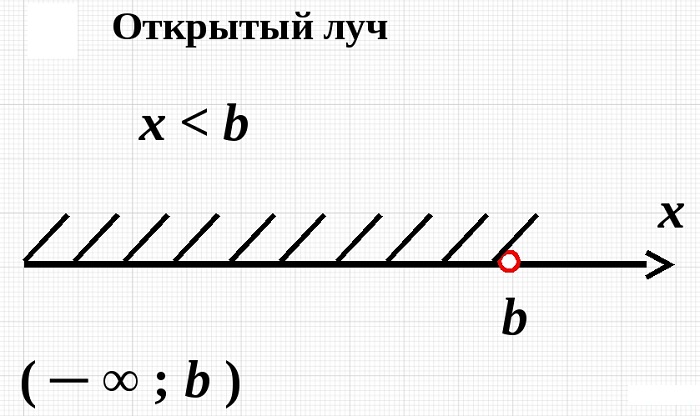
Точки расположены по одну сторону от определенной переменной, признанной началом координат.
Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:
-
(-∞; А);
-
(А; +∞).
Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».
Также можно охарактеризовать неравенством:
-
х < А;
-
х > А.
Знак зависит от расположения луча относительно А.
Замкнутый числовой луч
Замкнутый луч отличается от открытого тем, что к множеству относится А.

Также ему соответствует условие:
-
х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
-
х ≥ А (значение больше или равно А) или [А; +∞).
При графическом изображении А в этом случае закрашивается, на рисунке она черная.
Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.
Числовой отрезок
Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.
При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.
Обозначается отрезок, например, -7 ≤ х ≤ 3. Запись читается следующим образом: «отрезок от минус семи до трех».
Интервал
Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.
Обозначается, например, 5 < х < 13. Читается запись как «интервал от пяти до тринадцати».
Полуинтервал
Полуинтервал – интервал, при этом одна из точек, его ограничивающих, входит в него. То есть он закрыт с одной стороны. При этом неважно, какая из границ будет принадлежать интервалу, а какая нет.
Обозначаются с помощью двойных неравенств, при этом они называются нестрогими, так как используются знаки «больше или равно» или «меньше или равно». Одна из точек на графике не будет закрашена.
Обозначение может выглядеть, например, так -2 ≤ х < 9, «полуинтервал от минус двух до девяти».
Таблица числовых промежутков
Все промежутки имеют обозначения и неравенства. Данные об этом собраны в таблице. Каждому виду соответствует графическое изображение.
Наглядное изображение поможет восприятию и закреплению материала.

Границы представлены а и b, они так и называются, граничными точками. При этом знаки ≥ и ≤ обозначаются квадратной скобкой. При графическом изображении такая граница закрашивается, это означает, что она входит в множество. Строгие неравенства соответствуют выколотым точкам на графиках.
Промежутки знакомят школьников с простыми неравенствами, строгими и нестрогими, которые необходимы для решения сложных математических задач.
Числовые промежутки
- Виды числовых промежутков
- Открытый и замкнутый луч
- Отрезок
- Интервал и полуинтервал
Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.
Виды числовых промежутков
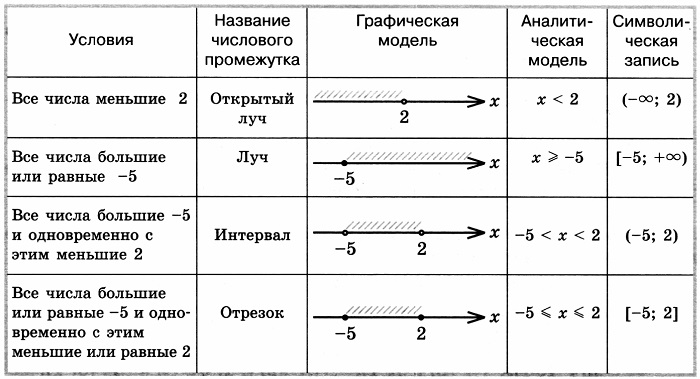
| Название | Изображение | Неравенство | Обозначение |
|---|---|---|---|
| Открытый луч |  |
x > a | (a; +∞) |
 |
x < a | (-∞; a) | |
| Замкнутый луч |  |
x ⩾ a | [a; +∞) |
 |
x ⩽ a | (-∞; a] | |
| Отрезок |  |
a ⩽ x ⩽ b | [a; b] |
| Интервал |  |
a < x < b | (a; b) |
| Полуинтервал |  |
a < x ⩽ b | (a; b] |
 |
a ⩽ x < b | [a; b) |
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Открытый и замкнутый луч
Открытый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, которая не входит в данное множество. Открытым луч называется именно из-за граничной точки, которая ему не принадлежит.
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:

Такое множество можно задать неравенством x > 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности
.
Множество, которому соответствует неравенство x < 2, можно обозначить (-∞; 2) или изобразить в виде луча, все точки которого лежат с левой стороны от точки 2:

Замкнутый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, принадлежащей данному множеству. На чертежах граничные точки, принадлежащие рассматриваемому множеству, обозначаются закрашенным кругом.
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:

Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности
и числовой луч от минус бесконечности до двух
. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх
.
Интервал и полуинтервал
Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 < x < 3 или обозначить (-2; 3). Такая запись читается так: интервал от минус двух до трёх
.
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:

Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3
, и полуинтервал от минус двух до трёх, включая минус два
.
Числовые промежутки. Геометрическая интерпретация числовых промежутков на координатной прямой. Системы и совокупности неравенств.
Числовые промежутки. Контекст. Определение
Равенство (уравнение) имеет одну точку на числовой прямой (хотя это точка зависит от проделанных преобразований и выбранного корня). Само решение уравнения будет числовым множеством (иногда состоящим из одного числа). Однако, всё это на числовой прямой (визуализации множества вещественных чисел) будет отображаться лишь точечно, но существуют также более обобщённые типы отношений между двумя числами – неравенства. В них числовая прямая разделяется некоторым числом и от неё отсекается определённая часть – значения выражения или числовой промежуток.
Тему числовых промежутков логично обсуждать вместе с неравенствами, но это отнюдь не означает, что она связана лишь с ними. Числовые промежутки (интервалы, отрезки, лучи) являются множеством значений переменной, удовлетворяющих некоему неравенству. То есть, по сути, это множество всех точек на числовой прямой, ограниченной какими-то рамками. Поэтому наиболее тесно связана тема числовых промежутков с понятием переменной. Там, где есть переменная, или произвольная точка x на числовой прямой, и её применяют, используют, есть и числовые промежутки, интервалы – значения x. Часто значение может быть любым, но это тоже числовой промежуток, охватывающий всю числовую прямую.
Введём понятие числового промежутка. Среди числовых множеств, то есть множеств, объектами которых являются числа, выделяют так называемые числовые промежутки. Их ценность в том, что очень легко вообразить множество, соответствующее указанному числовому промежутку, и наоборот. Поэтому с их помощью удобно записывать множество решений неравенства. Тогда как множеством решения уравнения будет не числовой промежуток, а просто несколько чисел на числовой прямой, с неравенствами, иначе говоря, любыми ограничениями значения переменной появляются числовые промежутки.
Числовой промежуток – это множество всех точек числовой прямой, ограниченное данным числом или числами (точками на числовой прямой).
Числовой промежуток любого вида (множество значений x, заключённых между некоторыми числами) всегда можно представить тремя видами математических обозначений: специальными обозначениями промежутков, цепочками неравенств (одним неравенством или двойным неравенством) или геометрически на числовой прямой. По сути, все эти обозначения имеют один смысл. Они дают ограничение(-я) для значений какого-то математического объекта, переменной величины (некоторой переменной, любого выражения с переменной, функции и т.д.).
Из вышесказанного можно понять, что так как можно по-разному ограничить область числовой прямой (есть разные типы неравенств), то и типы числовых промежутков бывают разные.
Виды числовых промежутков
Каждый тип числового промежутка имеет собственное название, особое обозначение. Для обозначения числовых промежутков используют круглую и квадратную скобку. Круглая скобка означает, что конечная, определяющая границу, точка на числовой прямой (конец) у этой скобки не входит во множество точек данного промежутка. Квадратная скобка означает, что конец входит в промежуток. С бесконечностью (с этой стороны промежуток не ограничен) используют круглую скобку. Иногда вместо круглых скобок можно писать квадратные, повёрнутые в обратную сторону: (a;b) ⇔]a;b[
| Вид промежутка (название) | Геометрическое изображение (на числовой прямой) | Обозначение | Запись с помощью неравенств (для краткости всегда цепочками) |
|---|---|---|---|
| Интервал (открытый) |
|
(a;b) | a < x < b |
| Сегмент (отрезок) |
|
[a;b] | a ≤ x ≤ b |
| Полуинтервал (полусегмент) |
|
[a;b) | a ≤ x < b |
| Полуинтервал (полусегмент) |
|
(a;b] | a < x ≤ b |
| Луч |
|
[a;+∞) | x ≥ a |
| Луч |
|
(-∞;b] | x ≤ b |
| Открытый луч |
|
(a;+∞) | x > a |
| Открытый луч |
|
(-∞;b) | x < b |
| Множество всех чисел (на координатной прямой) |
|
(-∞;+∞), хотя здесь следует указать конкретное множество-носитель алгебры, с которым производится работа; пример: ℝ | x ∈ ℝ (обычно говорят о множестве вещественных чисел, для представления комплексных чисел используют уже комплексную плоскость, а не прямую) |
| Равенство |
|
[a;a] или x=a | x = a (частный случай нестрогого неравенства: a ≤ x ≤ a – интервал длины 1, где оба конца совпадают – отрезок, состоящий из одной точки) |
| Пустое множество |
|
∅ | Пустое множество тоже является промежутком – у переменной x нет значений (пустое множество). Обозначение: x∈∅⇔x∈{ }. |
С названиями промежутков может возникнуть путаница: есть огромное количество вариантов. Поэтому лучше всегда точно их указывать. В англоязычной литературе используется только термин интервал (“interval”) – открытый, замкнутый, полуоткрытый (полузамкнутый). Вариаций много.
С помощью промежутков в математике обозначается очень большое количество вещей: есть промежутки изоляции при решении уравнений, промежутки интегрирования, промежутки сходимости рядов. Промежутками принято всегда обозначать при при исследовании функции её область значений и область определения. Промежутки очень важны, например, есть теорема Больцано — Коши (можно узнать больше в “Википедии”).
Системы и совокупности неравенств
Система неравенств
Итак, переменную x или значение некоторого выражения можно сравнить с какой-то постоянной величиной – это неравенство, но можно сравнивать это выражение с несколькими величинами – двойное неравенство, цепочка неравенств и т. д. Именно это было показано выше – как интервал и отрезок. И то, и то является системой неравенств.
Итак, если ставится задача найти множество общих решений двух или больше неравенств, то можно говорить о решении системы неравенств (также как с уравнениями — хотя можно сказать, что уравнения – это частный случай).
Тогда очевидно, что значение переменной, использованной в неравенствах, при котором каждое из них обращается в верное, называется решение системы неравенств.
Все неравенства, входящие в систему объединяют фигурной скобкой – “{“. Иногда их записывают в виде двойного неравенства (как показано выше) или даже цепочкой неравенств. Пример типичной записи:
f
x
≤
30
g
x
≥
5
.
Решение систем линейных неравенств с одной переменной в общем случае сводится к вот этим 4 видам:
x
>
a
x
>
b
(1)
x
>
a
x
<
b
(2)
x
<
a
x
>
b
(3)
x
<
a
x
<
b
(4)
. Здесь предполагается, что b > a.
Любую систему можно решать графически с использованием числовой прямой. Там, где решения составляющих систему неравенств пересекаются и будет решение самой системы.
Представим для каждого случая графическое решение.
Итак, что же получается? В случае (1) решением является промежуток (a;+∞). В случае (2) решение – промежуток (a;b). Случай (3) – это пример открытого луча (-∞;a). В случае (4) же решения отдельных неравенств не пересекаются – система не имеет решений.
Далее, системы неравенств можно классифицировать как равносильные, если они имеют общее множество решений. Отсюда (как можно видеть выше) следует, что более сложные системы можно упрощать (например, используя геометрическое решение).
Фигурную скобку можно условно, грубо говоря, назвать эквивалентом союза “И” для неравенств
Совокупность неравенств
Однако, бывают и другие случаи. Так кроме пересечения множеств решений бывает их объединение: если ставится задача найти множество всех таких значений переменной, каждое из которых является решением хотя бы одного из данных неравенств, то говорят, что надо решить совокупность неравенств.
Итак, все неравенства в совокупности объединяют скобкой совокупности “[“. Если значение переменной удовлетворяет хотя бы одному неравенству из совокупности, то оно принадлежит множеству решений всей совокупности. Также и с уравнениями (опять же их можно назвать частным случаем).
Если фигурная скобка – и, то скобка совокупности – это, условно, говоря простым языком, эквивалент союза “ИЛИ” для неравенств (хотя это, конечно, будет логическое или, включающее случай, удовлетворяющий обоим условиям).
Итак, решение совокупности неравенств – это значение переменной, при котором хотя бы одно неравенство, обращается в верное.
Множество решений, как совокупности, так и системы неравенств, можно определить через две основные бинарные операции для работы с множествами – пересечение и объединение. Множество решений системы неравенств – это пересечение множеств решений неравенств, её составляющих. Множество решений совокупности неравенств – это объединение множеств решений неравенств, её составляющих. Это тоже можно проиллюстрировать. Допустим у нас есть система и совокупность из двух неравенств. Множество решений первого обозначим A, а множество решений второго обозначим B. Прекрасной иллюстрацией будет диаграмма Эйлера-Венна.
Как вы уже знаете, любое число можно
отметить точкой на координатной прямой. Верно и обратное утверждение: каждой
точке на координатной прямой соответствует какое-то число.
Также на координатной прямой можно
отметить и множество чисел х, удовлетворяющих любому неравенству. Такое
множество называют числовым промежутком. И в зависимости
от типа неравенства выделяют виды числовых промежутков, которые имеют свои
названия, обозначения и изображения на координатной прямой.
Вспомним типы неравенств.
Рассмотрим виды числовых промежутков
на конкретных примерах.
Пусть есть два числа: и
.
Множество всех чисел,
удовлетворяющих условию называют интервалом.
Множество всех чисел,
удовлетворяющих условию называют числовым
отрезком.
Множества чисел , для которых
выполняются двойные неравенства или
, называют полуинтервалами.
На экране вы видите, как изображают
такие полуинтервалы на координатной прямой.
Как вы уже знаете, множество
действительных чисел изображается всей координатной прямой. Его называют числовой
прямой и обозначают так:
Рассмотрим другие виды числовых
промежутков.
Множество чисел, удовлетворяющих
условию называют числовым
лучом.
Множество чисел, удовлетворяющих
условию называют числовым
лучом.
Множества чисел, удовлетворяющих
условиям или
называют открытым
числовым лучом.
Заметим, что в обоих случаях число 3
не входит в множества.
Числовые отрезки, интервалы, полуинтервалы,
числовые лучи и открытые числовые лучи называют числовыми промежутками.
Замечание: Если
граничная точка в промежуток не входит, то на координатной прямой её изображают
пустой точкой и в обозначении промежутка её выделяют круглой скобкой. Если же
граничная точка входит в промежуток, то на координатной прямой её изображают
закрашенной точкой и в обозначении промежутка выделяют квадратной скобкой.
Запишем обозначения числовых
промежутков, их названия и изображение на координатной прямой для произвольных
чисел и
.
Задание: изобразить на
координатной прямой множество чисел, удовлетворяющих неравенствам, и записать
решение числовым промежутком.
Решение:
Задание: найдём все
целые числа, удовлетворяющие неравенствам.
Решение:
Имея представления о числовых
промежутках можно находить их пересечение и объединение.
Например: найдём
пересечение и объединение числовых промежутков:
Решение:
Итоги:
Интервал – это множество чисел,
удовлетворяющих условию 𝑎<𝒙<𝑏.
Отрезок – это множество чисел,
удовлетворяющих условию 𝑎≤𝒙≤𝑏.
Полуинтервал – это множество чисел,
удовлетворяющих условиям 𝑎≤𝒙<𝑏 или 𝑎<𝒙≤𝑏.
Числовой луч – это множество чисел,
удовлетворяющих условиям 𝒙≥𝑎 или 𝒙≤𝑎.
Открытый луч – это множество чисел,
удовлетворяющих условиям 𝒙>𝑎 или 𝒙<𝑎.
