Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 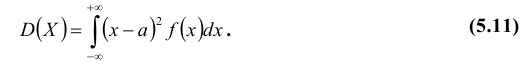
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
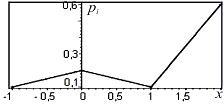
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 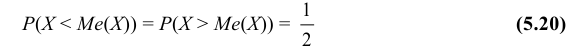
Пример №2
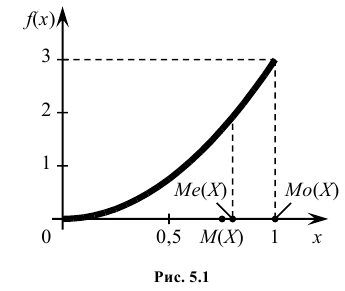
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 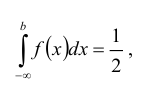
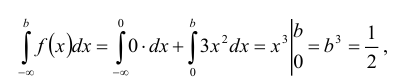
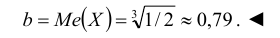
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 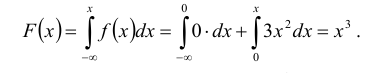
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
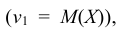
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
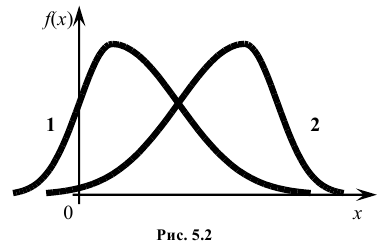
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 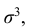
Полученная величина А называется коэффициентом асимметрии случайной величины: 
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
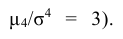
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 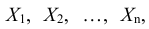
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 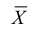
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
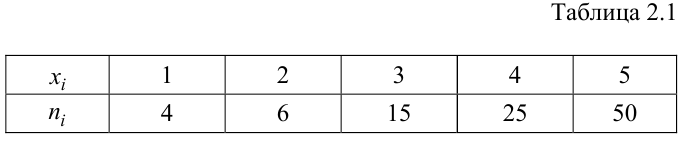
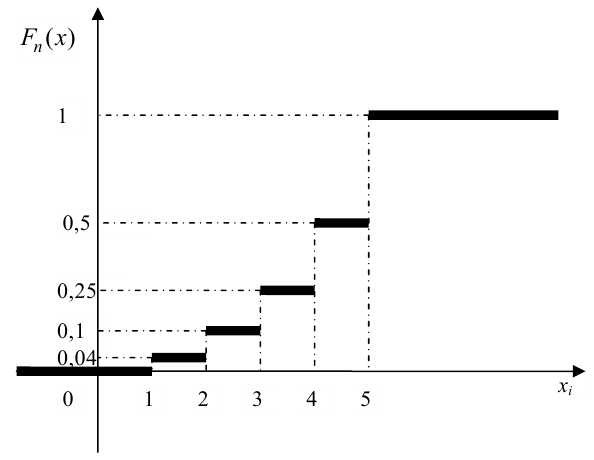
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
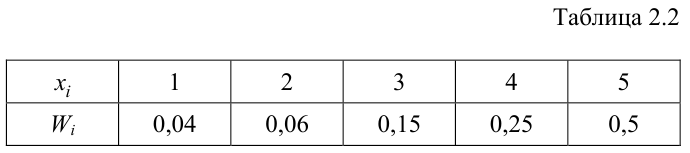
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 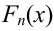
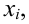
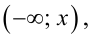
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Основные числовые характеристики случайных величин.
1.Математическое
ожидание и его свойства.
Математическим
ожиданием
случайной величины Х
называется число, равное сумме произведений
всех возможных значений случайной
величины на их вероятности.
Свойства
математического ожидания:
1)
,
где;
2)
3)
4)
5)
М
(М
(Х))
= М
(Х)
‒ следует из первого свойства и
определения математического ожидания.
2.Дисперсия
и её свойства
Дисперсией
случайной величины
называется математическое ожидание
квадрата отклонения случайной величины
от её математического ожидания.
D(X)=M(X
‒ M(
Дисперсия
показывает степень разброса случайной
величины относительно её математического
ожидания.
Преобразовав
формулу D(X)=M(X
‒ M(
D(X)=
‒ формула для вычисления дисперсии.
Свойства
дисперсии:
3.Среднее
квадратическое отклонение случайной
величины.
Средним
квадратическим отклонением
случайной величины X
называется корень квадратный из дисперсии
этой величины:
4.Мода
случайной величины.
Модой
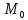
случайной величины называется наиболее
вероятное ее значение, то есть значение,
вероятность которого максимальна.
Если
максимальные вероятности принимают
несколько значений случайных величин,
то такое распределение называется
полимодальным.
Пример.
Дискретная
случайная величина X
задана законом распределения:
|
|
‒1 |
0 |
1 |
2 |
|
|
0,1 |
0,2 |
0,1 |
0,6 |
Найти:
числовые характеристики случайной
величины: M(X),
D(X),
Ϭ(X),
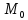
Решение:
Построим
многоугольник распределения данной
случайной величины.
1.
Математическое ожидание:
2.
Дисперсия:
3.
Средне
квадратическое откланение:
4.

как максимальная вероятность этого
значения равна 0,6.
5. Моменты случайных величин
Начальным
моментом k
‒
го порядка называется математическое
ожидание k
‒
й степени случайной величины:
при
k=1;
Центральным
моментом

называется математические ожидание
k‒й
степени отклонения случайной величины
(Х)
от ее математического ожидания:

при
k=2,
Функция
распределения случайной величины.
Функцией
распределения случайной величины (F(x))
– называется вероятность того, что
случайная величина X
примет значения меньше x.
Следовательно,

т.е.
геометрически значения X
будут левее x:
x
Так
как F(x)
– вероятность события X
< x,
то
Пример
|
xi |
1 |
4 |
5 |
7 |
|
pi |
0,4 |
0,1 |
0,3 |
0,2 |
Найти
функцию распределения F(x)
и построить график.
Решение:
1
4 5 7
1.
Если x
≤ 1,то F(x)
= 0.
2.
Если 1< x
≤ 4, например, x=2,
то F(2)
= P(X
< 2 ) = 0,4
3.
Если 4 < x
≤ 5, например, x
= 4,5, то F(4,5)
= P(X<4,5)
= P(X=1)+P(X=4)=0,4+0,1=0,5
4.Если
5 < x
≤ 7, например x=6,
то F(6)=P(X<6)=P(X=1)+P(X=4)+P(X=5)=0,4+0,1+0,3=0,8
5.
Если x
> 7, например x
=8, то F(8)=P(X<8)=P(X=1)+P(X=4)+P(X=5)+P(X=7)=
0,4+0,1+0,3+0,2=1
0; если x
≤ 1
0,4; если 1< x
≤ 4
F(x)
= 0,5 если 4 < x
≤ 5
0,8;
если 5
<
x≤ 7
1;
если
x > 7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Числовые характеристики дискретной случайной величины.
Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
2. Постоянную можно выносить за знак математического ожидания:
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
(для разности аналогично)
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Дисперсию удобно вычислять по формуле:
Свойства дисперсии:
1. Дисперсия постоянной равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:
4.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
Рассмотрим следующие задачи.
1. Математическое ожидание и дисперсия СВ Х соответственно равны 0,5 и 5. Найти математическое ожидание и дисперсию случайной величины .
Решение.
Согласно свойствам математического ожидания и дисперсии, получаем:
2. Случайные величины X и Y независимы, причем 



Решение.
На основании свойств дисперсии получаем:
3. Закон распределения ДСВ Х задан таблицей распределения
 |
1 | 2 | 3 | 4 |
 |
 |
Найти:
1) Так как , т.е.
, следовательно
Т.о. закон распределения примет вид
 |
1 | 2 | 3 | 4 |
 |
2) Для вычисления дисперсии воспользуемся формулой:
Сначала найдем математическое ожидание ДСВ Х2 для этого составим закон распределения этой СВ. Напоминаю, что для этого необходимо каждое значение ДСВ Х возвести в квадрат, а вероятности оставляем прежними. При одинаковых значениях ДСВ вероятности складываем.
3) Найдем среднее квадратическое отклонение:
4)
4. Функция распределения ДСВ Х имеет вид
Найти:
Решение.
Составляем закон распределения ДСВ Х (т.е. выполняем операцию обратную той, которую мы делали в предыдущей статье)
 |
0 | 1 | 2 | 3 |
 |
0,2 | 0,4 | 0,3 | 0,1 |
Составляем закон распределения ДСВ
 |
0 | 1 | 4 | 9 |
 |
0,2 | 0,4 | 0,3 | 0,1 |
5. Независимые случайные величины X и Y заданы таблицами распределения вероятностей
Найти двумя способами:
1. Составив предварительно таблицу распределения СВ ;
2. Используя правило сложения дисперсий.
Решение.
Составим таблицу распределения ДСВ .
Найдем
10+30=40 20+30=50
10+40=50 20+40=60
10+50=60 20+50=70
Т.о. значения ДСВ Z таковы:
Найдем соответствующие им вероятности:
Получаем ряд распределения СВ Z
| 40 | 50 | 60 | 70 | |
 |
0,1 | 0,46 | 0,28 | 0,16 |
2. Используя правило сложения дисперсий:
Случайной называют величину, которая в результате испытания примет одно и только одно
возможное значение, наперед не известное и зависящее от случайных причин,
которые заранее не могут быть учтены.
Случайные
величины обозначаются прописными буквами
, а их возможные значения – соответствующими строчными буквами
. Например, если случайная величина
имеет три возможных
значения, то они будут обозначены так:
.
Дискретной называют случайную
величину, которая принимает отдельные, изолированные возможные значения с
определенными вероятностями. Число возможных значений дискретной случайной
величины может быть конечным или бесконечным.
Законом распределения дискретной
случайной величины называют соответствие между возможными значениями и их
вероятностями; его можно задать таблично, аналитически (в виде формулы) и
графически.
При табличном задании закона
распределения дискретной случайной величины первая строка таблицы содержит
возможные значения, а вторая – их вероятности:
|
|
|
|
… |
|
|
|
|
|
… |
|
Приняв во внимание, что в одном
испытании случайная величина принимает одно и только одно возможное значение,
заключаем, что события
образуют полную
группу; следовательно, сумма вероятностей этих событий, то есть сумма
вероятностей второй строки таблицы, равна единице:
Если множество возможных значений
бесконечно
(счетно), то ряд
сходится и его
сумма равна единице.
Для наглядности закон распределения
дискретной случайной величины можно изобразить и графически. Для этого в
прямоугольной системе координат строят точки
, а затем соединяют их отрезками прямых. Полученную
фигуру называют многоугольником распределения.
Смежные темы решебника:
- Непрерывная случайная величина
- Функция распределения вероятностей
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Задача 1
В партии
из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Найти закон
распределения числа дефектных курток среди купленных. Построить многоугольник
распределения.
Задача 2
Устройство
состоит из пяти независимых элементов. Вероятность безотказной работы каждого
элемента в одном опыте равна p=0,7. Для случайной
величины X элементов, безотказно работавших в одном опыте,
построить закон распределения, их графики, найти ее числовые характеристики.
Задача 3
С
вероятностью попадания при явном выстреле p=0.88 охотник стреляет по
дичи до первого попадания, но успевает сделать не более n=6
выстрелов.
ДСВ X – число
промахов:
а) Найти
закон распределения X.
б)
Построить многоугольник распределения.
в) Найти
вероятность событий: X<2, X<3,
1<X<3.
Задача 4
Составьте
закон распределения дискретной случайной величины ξ, вычислите ее
математическое ожидание, медиану, дисперсию, среднее квадратическое отклонение,
коэффициенты асимметрии и эксцесса, все моменты, а также начертите ее
многоугольник распределения и график функции распределения. Сделайте выводы по
результатам расчетов.
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор окажется надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8.
ξ – число испытаний, после которых закончится проверка.
Задача 5
В первой урне
6 шаров – 3 белых и 3 черных. Во второй 5 шаров –3 белых и 2 черных. Из первой
урны наудачу переложили во вторую 2 шара, после чего, из второй в первую
переложили 1 шар. Найти закон распределения случайной величины Х – числа белых
шаров в первой урне, после всех перекладываний шаров. Какова вероятность того,
что число белых шаров не больше, чем первоначально. Построить многоугольник
распределения.
Задача 6
В коробке
N=9 карандашей, из которых M=6 красных. Из этой коробки
наудачу извлекается n=5 карандашей.
а) Найти
закон распределения случайной величины X равной числу красных
карандашей в выборке.
б)
Построить многоугольник распределения.
в) Найти
вероятность события: 0<X<4.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Производятся
последовательные испытания 5 приборов, причем испытания прекращаются сразу
после того, как проверяемый прибор оказался надежным. Вероятность выдержать
испытание для каждого прибора равна 0,8. X – число испытаний, после
которых закончится проверка. Составьте закон распределения случайной величины X,
вычислите ее математическое ожидание, дисперсию, среднее квадратическое
отклонение, а также начертите ее многоугольник распределения и график функции
распределения.
Задача 8
Проведено
n=5 независимых опытов. Вероятность взрыва в каждом опыте равна p=2/7.
Составить закон распределения числа взрывов, вычислить математическое ожидание,
дисперсию, среднеквадратическое отклонение и построить многоугольник
распределения.
Задача 9
Найти закон
распределения указанной дискретной СВ X и ее функции. распределения
F(x). Вычислить математическое ожидание М(Х), дисперсию D(X) и
среднее квадратичное отклонение σ(Х). Построить график
функции распределения F(x).
Вероятность отказа прибора за время испытания
на надежность равна 0,2; СВ Х – число приборов, отказавших в работе, среди 5
испытываемых.
Задача 10
В интернет-магазине
приобретается смартфон. Курьер приносит на дом покупателю 5 одинаковых
смартфонов, среди которых три (заранее неизвестно какие) бракованные.
Покупатель проверяет один за другим, пока не найдет хороший прибор, но делает
не более трех попыток.
Составить
закон распределения случайной величины – числа произведенных попыток.
Найти ее
математическое ожидание, дисперсию, среднее квадратическое отклонение.
Построить
функцию распределения.
Задача 11
В команде
9 спортсменов, из них 4 – первого разряда и 5 – второго. Наудачу отобраны 3
спортсмена. Найти ряд распределения дискретной случайной величины Х – числа
спортсменов второго разряда среди отобранных.
Задача 12
К контролеру с конвейера поступили 4 детали.
Вероятность брака для каждой детали равна 0,1. Детали проверяют одну за другой,
пока не наберут 2 доброкачественные.
Найти закон распределения вероятностей для числа проверенных деталей.
Задача 13
Двое рабочих,
выпускающих однотипную продукцию, допускают производство изделий второго сорта
с вероятностями соответственно равными 0,4 и 0,3. У каждого рабочего взято по 2
изделия. Для случайной величины Х –
числа изделий второго сорта среди отобранных для проверки четырех найти закон
распределения, математическое ожидание и дисперсию.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
На викторине
задаются 3 вопроса. Вероятность правильно ответить на первый – p, на
второй – r, на третий – s. После неправильного
ответа игрок выбывает из игры. Найти распределение числа правильных ответов.
Вычислить математическое ожидание. Решить задачу, если:
а) p=0.7; r=0.6; s=0.3;
б)
p=0.8; r=0.4; s=0.1.
Задача 15
На
некоторой остановке автобус останавливается только по требованию. Вероятность
остановки равна 0,2. За смену автобус проходит мимо этой остановки 5 раз.
Составить закон распределения числа остановки за смену, найти математическое
ожидание и дисперсию этой случайной величины.
Задача 16
Вероятность
того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3.
Аудитору на заключение представлено 3 баланса предприятия. Составить закон
распределения числа положительных заключений на проверяемые балансы.
Задача 17
Два товароведа
проверяют партию изделий. Производительность их труда соотносится как 5:4.
Вероятность определения брака первым товароведом составляет 85%, вторым – 90%.
Из проверенных изделий отбирают четыре. Найти а) математическое ожидание и б)
дисперсию числа годных изделий среди отобранных.
Задача 18
Два
станка выпускают детали с вероятностями брака 0,01 и 0,05 соответственно. В
выборке одна деталь выпущена первым станком и две – вторым. Найти распределение числа бракованных деталей
в выборке.
Задача 19
Монета
подбрасывается до тех пор, пока герб не выпадет 2 раза, но при этом делается не
более 4 бросаний. Найти распределение числа подбрасываний.
Задача 20
Вероятность
сдачи данного экзамена для каждого из n=5 студентов равна p=0.6.
Случайная величина X (СВ X) – число студентов, сдавших экзамен. Найти закон
распределения указанной дискретной СВ X и ее функцию распределения F(x).
Вычислить математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x). Построить график функции распределения F(x).
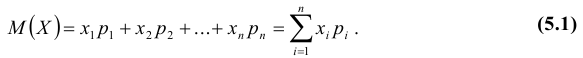
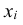
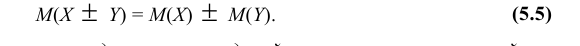


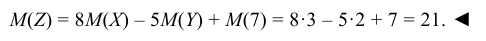







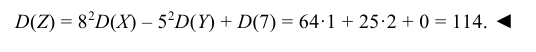
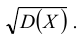

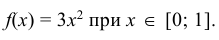

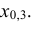
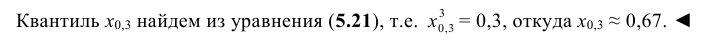



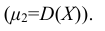
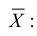
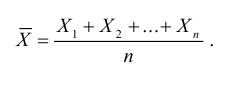

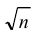 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: 

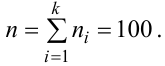
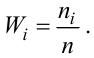
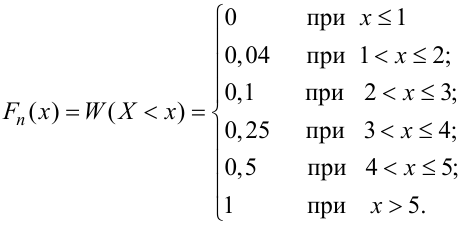

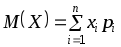



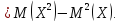




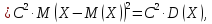

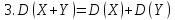






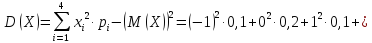











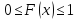













![Rendered by QuickLaTeX.com [M(C)=C]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-471b40041b6933f0801951cd2c46c645_l3.png)
![Rendered by QuickLaTeX.com [M(CX)=CM(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ded777e15e9adcf8796eeaac76336930_l3.png)
![Rendered by QuickLaTeX.com [M(X_1 cdot X_2 cdot ... cdot X_n)=M(X_1)cdot M(X_2)cdot ... cdot M(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6b30f00123a46fe5905869e2348bdd02_l3.png)
![Rendered by QuickLaTeX.com [M(X_1 + X_2 + ... + X_n)=M(X_1) + M(X_2) + ... + M(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c7b91ac649ba7364f862a40bf8faa91d_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M{[X-M(X)]}^2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-85d713b45963c5757fd071259ac6010f_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M(X^2)-{[M(X)]}^2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0d17db045a4e914ee13c4f6d75c27ea3_l3.png)
![Rendered by QuickLaTeX.com [D(C)=0]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6d535643c4c0b9772d8010dd2bc73943_l3.png)
![Rendered by QuickLaTeX.com [D(CX)=C^2D(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cce0e2900dab2027e7e321a4a122b4a9_l3.png)
![Rendered by QuickLaTeX.com [D(X_1 pm X_2 pm ... pm X_n)=D(X_1) + D(X_2) + ... + D(X_n)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-08c51f96c711f2b69dd776944a864ee3_l3.png)
![Rendered by QuickLaTeX.com [D(X+C)=D(X)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-a915073dccca53c6e5527d0241d183e6_l3.png)
![Rendered by QuickLaTeX.com [sigma (X) =sqrt{D(X)}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-bcacf00d61c4a3f0f69c6d6cfed60d51_l3.png)
![Rendered by QuickLaTeX.com [M(2X-3)=M(2X)+M(-3)=2M(X)-3=2cdot frac12-3=1-3=-2]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-010184719e61abad64efd1f6bf166096_l3.png)
![Rendered by QuickLaTeX.com [D(2X-3)=4cdot D(X)=4cdot 5=20]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2a326d2cfcb9cfa50fdee69fe551cee4_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=D(4cdot X- 5 cdot Y +3)=16cdot D(X)+25cdot D(Y)=16cdot 3+25cdot 5=48+125=173]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-72cc99dbd22855f093a923bfe7693994_l3.png)
![Rendered by QuickLaTeX.com [c=1-frac18 -frac14 -frac13=frac{24-3-6-8}{24}=frac{7}{24}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-01420ef852ee1007bd45d93fcbe0b95b_l3.png)
![Rendered by QuickLaTeX.com [M(X)=sum_{i=1}^4 x_i cdot p_i=1cdot frac18+2cdot frac14+3cdot frac13+4cdot frac{7}{24}=frac18+frac12+1+frac76=]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-42c69ea716d0d80a5cc1caa69ef11227_l3.png)
![Rendered by QuickLaTeX.com [M(X^2)=1cdot frac18+4cdot frac14+9cdot frac13+16cdot frac{7}{24}=frac18+1+3+frac{14}{3}=frac{3+96+112}{24}=frac{211}{24};]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-99d6101975deac0f6dbe962de43e23a1_l3.png)
![Rendered by QuickLaTeX.com [D(X)=frac{211}{24}-{left(frac{67}{24}right)}^2=frac{24cdot 211-{67}^2}{{24}^2}=frac{5064-4489}{576}=frac{575}{576};]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cc6b23de18058d53a5ed1fdc11cd9921_l3.png)
![Rendered by QuickLaTeX.com [sigma (X) =sqrt{D(X)}=sqrt{frac{575}{576}}=frac{5sqrt{23}}{24}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-f779e760519df59d8651da0aaa8c2e4b_l3.png)
![Rendered by QuickLaTeX.com [P{X<3}=P{X=1}+P{X=2}=frac18+frac14=frac38]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-65e7c06bd40f6f6cbc44912a49eefda2_l3.png)
![Rendered by QuickLaTeX.com [F(x)={ 0, qquad qquad xle 0 \ 0,2, qquad 0< x le 1, \ 0,6, qquad qquad 1< x le 2 \ 0,9, qquad qquad 2< x le 3 \ 1, qquad qquad x>3]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0947abc5c1ed52fd612642b5b73df2aa_l3.png)
![Rendered by QuickLaTeX.com [M(X), quad M(X^2) quad D(X), quad sigma (X).]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-e2e328ddbafd8e7412cee6e6b7013e8e_l3.png)
![Rendered by QuickLaTeX.com [M(X)=0cdot 0,2+1cdot 0,4+2cdot 0,3+3cdot 0,1=0,4+0,6+0,3=1,3]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-7b7b00dc6dd7147605a5d00f6e4ba120_l3.png)

![Rendered by QuickLaTeX.com [M(X^2)=0cdot 0,2+1cdot 0,4+4cdot 0,3+9cdot 0,1=0,4+1,2+0,9=2,5]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-d3aee42db306199c080afa80f72b3b92_l3.png)
![Rendered by QuickLaTeX.com [D(X)=M(X^2)-{[M(X)]}^2=2,5-{1,3}^2=2,5-1,69=0,81]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-cf146049246b3e3f395117bc29116db0_l3.png)
![Rendered by QuickLaTeX.com [sigma (X)=sqrt{0,81}=0,9]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ac025cd6cccf0e250723d48aad978616_l3.png)
![Rendered by QuickLaTeX.com [p_1=P{Z=40}=P{X=10, Y=30}=0,2cdot 0,5=0,1]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-7e1ae4f8b0462f0e7f531d90b468f792_l3.png)
![Rendered by QuickLaTeX.com [p_4=P{Z=70}=P{X=20, Y=50}=0,8cdot 0,2=0,16]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c4ec8e48db0ba1e5f8772cd6e498ea7e_l3.png)
![Rendered by QuickLaTeX.com [M(Z)=sum_{i=1}^4 z_i cdot p_i=40cdot 0,1+50cdot 0,46+60cdot 0,28+70cdot 0,16=4+23+16,8+11,2=55;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ac4878cee852a38e8245022d95b24e00_l3.png)
![Rendered by QuickLaTeX.com [M(Z^2)=sum_{i=1}^4 z_i^2 cdot p_i=1600cdot 0,1+2500cdot 0,46+3600cdot 0,28+4900cdot 0,16=]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ec5b2451d92ebf30458b26e4926d5f63_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=M(Z^2)-{[M(Z)]}^2=3102-3025=77]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-451663c9d742fa3e5fb04afdd7766522_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=D(X+Y)=D(X)+D(Y)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-448a698e43900414c039e2e1e624b053_l3.png)
![Rendered by QuickLaTeX.com [M(X)=10cdot 0,2+20cdot 0,8=2+16=18;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-1ebf2d8b6e0fe85428901ac0b008f5dd_l3.png)
![Rendered by QuickLaTeX.com [M(X^2)=100cdot 0,2+400cdot 0,8=20+320=340;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-32cfe37c5de52468e58eeeadf3e2f766_l3.png)
![Rendered by QuickLaTeX.com [M(Y)=30cdot 0,5+40cdot 0,3+50cdot 0,2=15+12+10=37]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0a5b2478301af6479cd142fcd67c4146_l3.png)
![Rendered by QuickLaTeX.com [M(Y^2)=900cdot 0,5+1600cdot 0,3+2500cdot 0,2=450+480+500=1430]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6b21d4279e597b4488766bf66dc5ec57_l3.png)
![Rendered by QuickLaTeX.com [D(Y)=1430-1369=61]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-641d0e807ce0687edbf79f037574635d_l3.png)
![Rendered by QuickLaTeX.com [D(Z)=16+61=77]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c0e8e4fe96eb97d5374b249328fd738f_l3.png)
