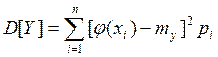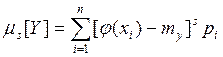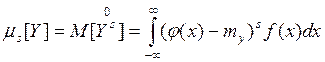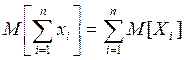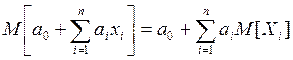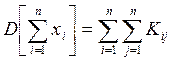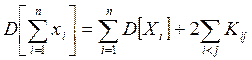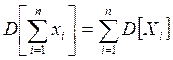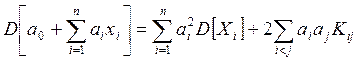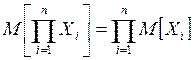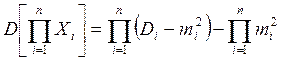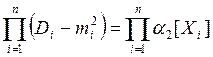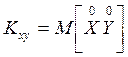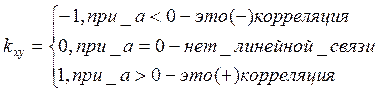Как найти числовые характеристики функции

Как найти числовые характеристики функции

Пусть случайная
величина Z
является функцией двух случайных
величин, образующих систему (Х,
У), т.е.
.
Для непрерывной системы (Х,У)
с известной плотностью распределения
вероятностей
,
закон распределения Z
следует определять, начиная с построения
интегральной функции
:

,
(7.2)

величина z
содержится в этом выражении неявно в
пределах интегрирования.

Плотность
распределения Z
можно
 найти,
дифференцируя G(z)
по z:

.
(7.3)

При известном
законе распределения случайной величины
Z
ее числовые характеристики можно
вычислить по обычным правилам, но можно
их определить и не прибегая к нахождению
закона распределения Z.

Для дискретных
Х
и Y:

; . (7.4)

Для непрерывных
Х
и Y:

;

. (7.5)

Пример
7.7. Система
(Х1,Х2)
задана плотностью распределения
;
величинаZ
есть произведение случайных величин
и
;
.
Найти плотность распределения величиныZ.

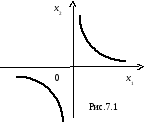
 Графиком функции
является гипербола.
(Рис. 7.1).

Функция распределения
имеет вид:

+.

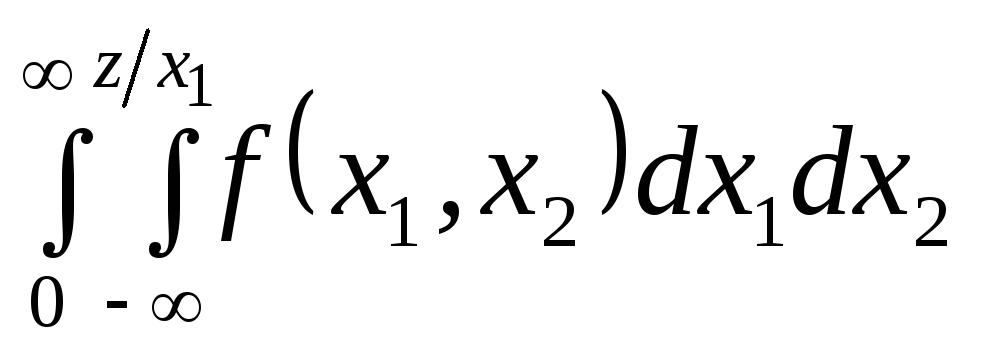
Дифференцируя по
z,
получим:

.

Пример 7.8. Система
(Х,У)
задана законом распределения

ХУ

0

1

2

3

-1

0,01

0,06

0,05

0,04

0

0,04

0,24

0,15

0,07

1

0,05

0,10

0,10

0,09

Найти закон
распределения случайной величины Z
=Х+У.

 Находим значения
xi+yj:
-1, 0, 1, 2, 0, 1,2 , 3, 1, 2, 3, 4. Объединяя одинаковые
и располагая их в порядке возрастания,
получим возможные значения Z
: –1, 0, 1, 2, 3, 4. Вычисляем соответствующие
вероятности:
;

;
и т.д.

Z

-1

0

1

2

3

4

P

0,01

0,1

0,34

0,29

0,17

0,09

Искомый закон распределения
Z
имеет вид:

Контроль:
0,01+0,1+0,34+0,29+0,17+0,09=1. 

Пример 7.9. Система
(Х,У)
задана плотностью распределения
,
где.
Вычислить числовые характеристикиислучайной величины.

 Воспользуемся
формулами (7.5)

Получим:
=

====,

.

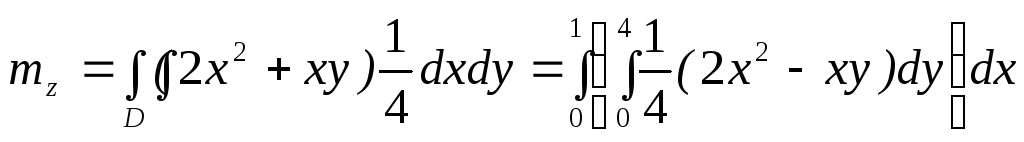
Пример 7.10.
Система (Х,
У) задана
законом распределения

ХУ

1

2

0

0,3

0,1

1

0,2

0,4

Вычислить
математическое ожидание и дисперсию
случайной величины
.

 Не определяя
закон распределения случайной величины
Z,
воспользуемся формулами

=

=

7.3. Теоремы о числовых характеристиках и их применение

Процесс вычисления
числовых характеристик функций случайных
аргументов значительно упрощается,
если
использовать
теоремі
о свойствах числовых характеристик,
особенно в тех случаях, когда функции
– линейны.

Теоремы о
математических ожиданиях.

1.

2.

3.

4.

5. Если случайные
величины
независимы,
то

Теоремы о
дисперсиях

1.

2.

3.
,
где
–
корреляционный момент пары случайных
величини.

4.

Пример 7.11.
Случайная величина Х
– число автомобилей, реализуемых в
течение одного дня автомобильным
салоном, задана законом распределения

Х

1

2

4

5

Р

0,4

0,3

0,2

0,1

Номинальная
стоимость одного автомобиля 3тыс. усл.
ед. и за каждый день салон имеет 0,2 тыс.
усл. ед. прибыли за счет дополнительных
услуг. Указать среднюю выручку, получаемую
салоном ежедневно и ее разброс.

 Ежедневная
выручка автомобильного салона есть
случайная величина
,
и для решения задачи требуется определитьи.
Вначале найдем числовые характеристикиХ:

–
в среднем продается 2 автомобиля в день;
,

-разброс
продажи составляет 1 автомобиль в день.

На основании теорем
о числовых характеристиках будем иметь:

тыс.усл.ден.ед. –
средняя ежедневная выручка; тыс.усл.ден.ед. – разброс от средней
выручки.

Пример 7.12.
Случайная величина Х
задана плотностью распределения
вероятностей
.
Найти математическое ожидание и дисперсию
случайной величины.

 Функция
представляет собой плотность показательного
закона распределения, а это значит, чтои.
Тогда согласно теоремам о числовых
характеристикахи.

Пример 7.13.
Случайные
величины Х
и У,
характеризующие соответственно
расширение ассортимента выпускаемой
продукции и изменение ее качества,
заданы своими числовыми характеристиками
Вычислить числовые характеристикиислучайной величины,
характеризующей колебания прибыли
предприятия.

 Согласно теоремам
о числовых характеристиках, будем иметь:

;
.

Пример 7.14.
Плотности распределения вероятностей
независимых случайных величин Х и У
заданы формулами:

.

Определить
математическое ожидание и дисперсию
случайной величины
.

 Случайная
величина Х
распределена равномерно в интервале
,
это значит, чтоСлучайная величина У подчинена
показательному закону распределения,
следовательно.
Так какХ
и У
независимы, то
и согласно теоремам о числовых
характеристиках, получим

;
.

Задачи

  1. Случайная величина
    Х задана законом распределения

хi

-2

-1

0

1

2

pi

0,1

0,2

0,3

0,3

0,1

Составить закон
распределения случайной величины У=X
вычислить

Ответ:

Y

0

1

4

P

0,3

0,5

0,2

=1,45

Система (Х,У) задана
законом распределения:

ХiУi

-2

-1

0

-1

0,1

0,05

0,1

0

0,15

0,1

0,2

1

0,15

0,05

0,1

Найти закон
распределения и числовые характеристики
случайной величины
:
а)Z=X+Y;
б) Z=XY;
в) Z=2X-3Y;
г).

Ответ: а) б)

;

=1,07. ;

в) г)

  1. Случайная величина
    Х
    задана плотностью вероятности
    .
    Найти математическое ожиданиеслучайной
    величины
    .

Ответ:
М=1.

  1. Дискретная
    случайная величина Х
    задана законом распределения:

Найти функцию
распределения F(y),
построить ее график и вычислить
вероятность события (Y≤4),
если
.

Frame20

Ответ:
Р(Y≤4)=0,4

  1. В партии из 10
    деталей содержится 4 нестандартных.
    Наугад отобраны 2 детали. Записать
    законы распределения случайных величин
    Х={число
    стандартных деталей среди отобранных}
    и
    .

Ответ:

Х

0

1

2

Р

2/15

8/15

5/15

У

1/3

1/2

1

Р

5/15

8/15

2/15

,

Случайная величина
Х
задана плотностью распределения:

.

Найти математическое
ожидание, дисперсию и среднее квадратичное
отклонение величины
.

Ответ:

  1. Случайная величина
    Х задана функцией распределения
    .Найти
    плотность распределенияg(y)
    случайной величины
    .

Ответ:

  1. Найти математическое
    ожидание, дисперсию и среднее квадратичное
    отклонение случайной величины Y=sinX,
    если случайная величина Х
    задана законом распределения:

xi

-

-/2

0

/2

pi

0,1

0,3

0,4

0,2

Ответ:

  1. Партия из 10 деталей
    содержит 8 стандартных. Наугад отобраны
    2 детали. Составить законы распределения
    случайной величины Х={число
    стандартных деталей среди двух
    отобранных} и случайной величины
    .
    Определить вероятность того, что Y>4.

Ответ:

Х

0

1

2

Р

1/45

16/45

28/45

У

3

4

5

Р

1/45

16/45

28/45

Р(Y>4)=28/45.

  1. Найти математическое
    ожидание случайной величины Y=eX,
    если случайная величина Х
    задана функцией распределения:

.

Ответ:
М= 0,5( е
+1 ).

  1. Дискретная
    случайная величина Х
    имеет возможные значения Х={-2,0,3}.
    Известно, что математическое ожидание
    величины Х равно 1.0; а дисперсия равна
    1.4. Найти законы распределения случайной
    величины Х
    и случайной величины Y=X2.

Ответ:

Х

-2

0

3

Р

1/130

85/130

44/130

У

0

3

4

Р

85/130

44/130

1/130

    1. Дана плотность
      вероятности случайной величины:
      .
      Найти коэффициента
      и плотность вероятности случайной
      величиной Y=
      eX
      .

Ответ:
а= 2;

  1. Случайная величина
    Х задана функцией распределения Рэлея:
    .Найти
    плотность распределенияслучайной величиныY=eX.

Ответ:

  1. Партия из 5 изделий
    проверяется на стандартность. Вероятность
    того, что изделие стандартно, равна
    0.8. Определить математическое ожидание
    и дисперсию случайной величины Х={число
    стандартных изделий в партии}, а также
    математическое ожидание и дисперсию
    случайной величины Y=3X-1.

Ответ:

  1. Плотность
    распределения случайной величины Х:
    .
    Найти коэффициента
    и плотность вероятности величины Y=X2.

Ответ:
а
= 1/;

  1. Дискретная
    случайная величина Х
    задана законом распределения:

xi

-

-/2

0

/2

pi

0,1

0,3

0,3

0,2

0,1

Вычислить
математическое ожидание, дисперсию и
среднее квадратичное отклонение
случайной величины
=cos
X.

Ответ:

  1. Задана функция
    распределения случайной величины Х:
    .
    Определить вероятность того, что0.2≤Y≤0.5,
    если Y=.

Ответ:
Р =
0,00195.

  1. Случайная величина
    Х
    может принимать значения: Х={-1,0,1}.
    Известно, что математическое ожидание
    величины Х
    равно 0, а
    дисперсия равна 0.08. Составить законы
    распределения случайных величин Х
    и Y=X2.

Ответ:

Х

-1

0

1

Р

0,2

0,6

0,2

У

0

1

Р

0,6

0,4

  1. Случайная величина
    Х задана рядом распределения:

xi

-1

0

1

2

pi

0,25

0,3

0,2

0,25

Найти функцию
распределения F(y),
построить ее график и вычислить
вероятность события (Y3),
если Y=X2.

Ответ:

У

0

1

2

Р

0,3

0,45

0,25

.

Р(У3)=Р(У3)=1.

  1. Случайная величина
    Х
    имеет плотность вероятностей:
    .

Найти математическое
ожидание и дисперсию случайной величины
Y=eX.

Ответ: Му=0,5е;Dy
=(e
–1)/16.

  1. Производится два
    выстрела с вероятностями попадания в
    цель при каждом выстреле соответственно
    0.6. Составить законы распределений
    случайной величины Х={
    число попаданий при двух выстрелах} и
    величины Y=2X+2.

Ответ:

Х

0

1

2

Р

0,16

0,48

0,36

У

2

4

6

Р

0,16

0,48

0,36

  1. Случайная величина
    Х
    имеет плотность распределения
    вероятностей:
    .
    Найти математическое ожидание, дисперсию
    и среднее квадратичное отклонение
    величиныY=.

Ответ:

    1. Определить
      математическое ожидание и дисперсию
      случайной величины Z=4X+Y,
      если X
      и Y
      – независимые нормально распределенные
      случайные величины с плотностями
      распределений:

,
.

Ответ:

    1. Определить
      математическое ожидание случайной
      величины Z=
      XY+X,
      если X
      и Y
      – случайные величины с
      известными mx=2,
      my=
      ‑2 и Kxy=
      ‑3.

Ответ:

    1. Заданы две
      независимые случайные величины X
      и Y.
      Величина Х
      распределена по показательному закону
      с параметром
      ;
      величина Y
      распределена по тому же закону с
      параметром
      .
      Определить математическое ожидание
      и дисперсию случайной величины Z=‑3X+2Y.

Ответ:

    1. Определить
      математическое ожидание и дисперсию
      случайной величины Z=4X–2Y,
      если X
      и Y
      – случайные величины с известными
      характеристиками mx=2,
       my=-1,
      Dx=4,
      Dy=2,
      Kxy=2.

Ответ:

    1. Случайная величина
      Х
      распределена равномерно в интервале
      .
      Найти математическое ожидание и
      дисперсию случайной величины.

Ответ:

    1. Случайная величина
      Х
      равномерно распределена в интервале
      (0,3). Найти математическое ожидание,
      дисперсию и среднее квадратичное
      отклонение случайной величины
      .

Ответ:

    1. Заданы две
      независимые случайные величины X
      и Y.
      Величина Х
      распределена равномерно на интервале
      (‑3, 1), величина Y
      распределена по показательному закону
      с параметром
      .
      Определить математическое ожидание
      случайной величины Z=
      5XY–3X.

Ответ:

    1. Определить
      математическое ожидание и дисперсию
      случайной величины Z=3X+4Y,
      если X
      и Y
      – случайные величины с известными
      характеристиками mx=‑2,
      my=1,
      Dx=3,
      Dy=1,
      Kxy=4.

Ответ:

    1. Определить
      математическое ожидание и дисперсию
      случайной величины Z=
      ‑      X+3Y,
      если X
      и Y
      – случайные величины с известными
      характеристиками mx=
      ‑1, my=2,
      Dx=1,
      Dy=3,
      Kxy=
      ‑2

Ответ:

    1. Заданы две
      независимые случайные величины X
      и Y.
      Величина Х
      распределена нормально с плотностью
      вероятности
      ,
      величинаY
      распределена равномерно на интервале
      (‑5, 1). Определить математическое
      ожидание случайной величины Z=
      -2XY-10.

Ответ:

Соседние файлы в папке ФУБ 4 семестр ТВ

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Функции случайных величин

Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей и плотности для функции двух случайных аргументов.

Закон распределения вероятностей функции одной случайной величины

При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др., часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции также являются случайными величинами. Поэтому при решении задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно известны закон распределения системы случайных аргументов и функциональная зависимость.

Таким образом, возникает задача, которую можно сформулировать так.

Дана система случайных величин (X_1,X_2,ldots,X_n), закон распределения которой известен. Рассматривается некоторая случайная величина Y как функция данных случайных величин:

Y=varphi(X_1,X_2,ldots,X_n).

(6.1)

Требуется определить закон распределения случайной величины Y, зная вид функций (6.1) и закон совместного распределения ее аргументов.

Рассмотрим задачу о законе распределения функции одного случайного аргумента

Y=varphi(X).

Пусть X — дискретная случайная величина, имеющая ряд распределения

begin{array}{|c|c|c|c|c|}hline{X}&x_1&x_2&cdots&x_n\hline{P}&p_1&p_2&cdots&p_n\hlineend{array}

Тогда Y=varphi(X) также дискретная случайная величина с возможными значениями y_1=varphi(x_1),y_2=varphi(x_2),ldots,y_n=varphi(x_n). Если все значения y_1,y_2,ldots,y_n различны, то для каждого k=1,2,ldots,n события {X=x_k} и {Y=y_k=varphi(x_k)} тождественны. Следовательно,

P{Y=y_k}=P{X=x_k}=p_k

и искомый ряд распределения имеет вид

begin{array}{|c|c|c|c|c|}hline{Y}&y_1=varphi(x_1)&y_2=varphi(x_2)&cdots&y_n=varphi(x_n)\hline{P}&p_1&p_2&cdots&p_n\hlineend{array}

Если же среди чисел y_1=varphi(x_1),y_2=varphi(x_2),ldots,y_n=varphi(x_n) есть одинаковые, то каждой группе одинаковых значений y_k=varphi(x_k) нужно отвести в таблице один столбец и соответствующие вероятности сложить.

Для непрерывных случайных величин задача ставится так: зная плотность распределения f(x) случайной величины X, найти плотность распределения g(y) случайной величины Y=varphi(X). При решении поставленной задачи рассмотрим два случая.

Предположим сначала, что функция y=varphi(x) является монотонно возрастающей, непрерывной и дифференцируемой на интервале (a;b), на котором лежат все возможные значения величины X. Тогда обратная функция x=psi(y) существует, при этом являясь также монотонно возрастающей, непрерывной и дифференцируемой. В этом случае получаем

g(y)=fbigl(psi(y)bigr)cdot |psi'(y)|.

(6.2)

Пример 1. Случайная величина X распределена с плотностью

f(x)=frac{1}{sqrt{2pi}}e^{-x^2/2}

Найти закон распределения случайной величины Y, связанной с величиной X зависимостью Y=X^3.

Решение. Так как функция y=x^3 монотонна на промежутке (-infty;+infty), то можно применить формулу (6.2). Обратная функция по отношению к функции varphi(x)=x^3 есть psi(y)=sqrt[LARGE{LARGE{3}}]{y}, ее производная psi'(y)=frac{1}{3sqrt[LARGE{LARGE{3}}]{y^2}}. Следовательно,

g(y)=frac{1}{3sqrt{2pi}}e^{-sqrt[LARGE{LARGE{3}}]{y^2}/2}frac{1}{sqrt[LARGE{LARGE{3}}]{y^2}}

Рассмотрим случай немонотонной функции. Пусть функция y=varphi(x) такова, что обратная функция x=psi(y) неоднозначна, т. е. одному значению величины y соответствует несколько значений аргумента x, которые обозначим x_1=psi_1(y),x_2=psi_2(y),ldots,x_n=psi_n(y), где n — число участков, на которых функция y=varphi(x) изменяется монотонно. Тогда

g(y)=sumlimits_{k=1}^{n}fbigl(psi_k(y)bigr)cdot |psi'_k(y)|.

(6.3)

Пример 2. В условиях примера 1 найти распределение случайной величины Y=X^2.

Решение. Обратная функция x=psi(y) неоднозначна. Одному значению аргумента y соответствуют два значения функции x

begin{gathered}x_1=psi_1(y)=+sqrt{y};\x_2=psi_2(y)=-sqrt{y}.end{gathered}

Применяя формулу (6.3), получаем:

begin{gathered}g(y)=f(psi_1(y))|psi'_1(y)|+f(psi_2(y))|psi'_2(y)|=\\=frac{1}{sqrt{2pi}},e^{-left(-sqrt{y^2}right)^2/2}!left|-frac{1}{2sqrt{y}}right|+frac{1}{sqrt{2pi}},e^{-left(sqrt{y^2}right)^2/2}!left|frac{1}{2sqrt{y}}right|=frac{1}{sqrt{2pi{y}}},e^{-y/2}.end{gathered}

Закон распределения функции двух случайных величин

Пусть случайная величина Y является функцией двух случайных величин, образующих систему (X_1;X_2), т. е. Y=varphi(X_1;X_2). Задача состоит в том, чтобы по известному распределению системы (X_1;X_2) найти распределение случайной величины Y.

Пусть f(x_1;x_2) — плотность распределения системы случайных величин (X_1;X_2). Введем в рассмотрение новую величину Y_1, равную X_1, и рассмотрим систему уравнений

left{!begin{gathered}y=varphi(x_1;x_2);hfill\y_1=x_1.hfillend{gathered}right.

Будем полагать, что эта система однозначно разрешима относительно x_1,x_2

left{!begin{gathered}x_2=psi(y;y_2);hfill\x_1=y_1.hfillend{gathered}right.

и удовлетворяет условиям дифференцируемости.

Плотность распределения случайной величины Y

g_1(y)=intlimits_{-infty}^{+infty}f(x_1;psi(y;x_1))!left|frac{partialpsi(y;x_1)}{partial{y}}right|dx_1.

Заметим, что рассуждения не изменяются, если введенную новую величину Y_1 положить равной X_2.

Математическое ожидание функции случайных величин

На практике часто встречаются случаи, когда нет особой надобности полностью определять закон распределения функции случайных величин, а достаточно только указать его числовые характеристики. Таким образом, возникает задача определения числовых характеристик функций случайных величин помимо законов распределения этих функций.

Пусть случайная величина Y является функцией случайного аргумента X с заданным законом распределения

Y=varphi(X).

Требуется, не находя закона распределения величины Y, определить ее математическое ожидание

M(Y)=M[varphi(X)].

Пусть X — дискретная случайная величина, имеющая ряд распределения

begin{array}{|c|c|c|c|c|}hline{x_i}&x_1&x_2&cdots&x_n\hline{p_i}&p_1&p_2&cdots&p_n\hlineend{array}

Составим таблицу значений величины Y и вероятностей этих значений:

begin{array}{|c|c|c|c|c|}hline{y_i=varphi(x_i)}&y_1=varphi(x_1)&y_2=varphi(x_2)&cdots&y_n=varphi(x_n)\hline{p_i}&p_1&p_2&cdots&p_n\hlineend{array}

Эта таблица не является рядом распределения случайной величины Y, так как в общем случае некоторые из значений могут совпадать между собой и значения в верхней строке не обязательно идут в возрастающем порядке. Однако математическое ожидание случайной величины Y можно определить по формуле

M[varphi(X)]=sumlimits_{i=1}^{n}varphi(x_i)p_i,

(6.4)

так как величина, определяемая формулой (6.4), не может измениться от того, что под знаком суммы некоторые члены будут заранее объединены, а порядок членов изменен.

Формула (6.4) не содержит в явном виде закон распределения самой функции varphi(X), а содержит только закон распределения аргумента X. Таким образом, для определения математического ожидания функции Y=varphi(X) вовсе не требуется знать закон распределения функции varphi(X), а достаточно знать закон распределения аргумента X.

Для непрерывной случайной величины математическое ожидание вычисляется по формуле

M[varphi(X)]=intlimits_{-infty}^{+infty}varphi(x)f(x),dx,

где f(x) — плотность распределения вероятностей случайной величины X.

Рассмотрим случаи, когда для нахождения математического ожидания функции случайных аргументов не требуется знание даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики. Сформулируем эти случаи в виде теорем.

Теорема 6.1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин:

M(X+Y)=M(X)+M(Y).

Теорема 6.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:

M(XY)=M(X)M(Y)+mu_{xy}.

Следствие 6.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.

Следствие 6.2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Дисперсия функции случайных величин

По определению дисперсии имеем D[Y]=M[(Y-M(Y))^2].. Следовательно,

D[varphi(x)]=M[(varphi(x)-M(varphi(x)))^2], где M(varphi(x))=M[varphi(X)].

Приведем расчетные формулы только для случая непрерывных случайных аргументов. Для функции одного случайного аргумента Y=varphi(X) дисперсия выражается формулой

D[varphi(x)]=intlimits_{-infty}^{+infty}(varphi(x)-M(varphi(x)))^2f(x),dx,

(6.5)

где M(varphi(x))=M[varphi(X)] — математическое ожидание функции varphi(X); f(x) — плотность распределения величины X.

Формулу (6.5) можно заменить на следующую:

D[varphi(x)]=intlimits_{-infty}^{+infty}varphi^2(x)f(x),dx-M^2(X)

Рассмотрим теоремы о дисперсиях, которые играют важную роль в теории вероятностей и ее приложениях.

Теорема 6.3. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими:

D!left[sumlimits_{i=1}^{n}X_iright]=sumlimits_{i=1}^{n}D[X_i]+2sumlimits_{i<j}mu_{x_ix_j}

Следствие 6.3. Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых:

D!left[sumlimits_{i=1}^{n}X_iright]=sumlimits_{i=1}^{n}D[X_i]

Теорема 6.4. Дисперсия произведения двух независимых случайных величин вычисляется по формуле

D[XY]=D[X]D[Y]+M^2(X)D[Y]+M^2(Y)D[X].

Корреляционный момент функций случайных величин

Согласно определению корреляционного момента двух случайных величин X и Y, имеем

mu_{xy}=M[(X-M(X))(Y-M(Y))].

Раскрывая скобки и применяя свойства математического ожидания, получаем

mu_{xy}=M(XY)-M(X)M(Y).

(6.6)

Рассмотрим две функции случайной величины X

Y_1=varphi_1(X);qquad Y_2=varphi_2(X).

Согласно формуле (6.6)

mu_{y_1y_2}= M(Y_1Y_2)-M(Y_1)M(Y_2).

отсюда

mu_{y_1y_2}=M(varphi_1(X)varphi_2(X))-M(varphi_1(X))M(varphi_2(X)).

т.е. корреляционный момент двух функций случайных величин равен математическому ожиданию произведения этих функций минус произведение из математических ожиданий.

Рассмотрим основные свойства корреляционного момента и коэффициента корреляции.

Свойство 1. От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не изменяются.

Свойство 2. Для любых случайных величин X и Y абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий данных величин:

|mu_{xy}|leqslantsqrt{D[X]cdot D[Y]}=sigma_xcdot sigma_y,

где sigma_x,sigma_y — средние квадратические отклонения величин X и Y.

Следствие 6.5. Для любых случайных величин X и Y абсолютная величина коэффициента корреляции не превосходит единицы:

|r_{xy}|leqslant1.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Случайные функции

Случайные процессы – довольно редкая тема в курсе теории вероятностей (не все до нее доходят), но все-таки приведем несколько примеров решений типовых задач.

Обычно в заданиях требуется найти характеристики случайной функции: математическое ожидание, корреляционную функцию, дисперсию. Также нужно уметь находить характеристики процесса, который зависит от другого (чаще всего зависимость выражается интегралом, производной или задается дифференциальным уравнением).

Далее: Примеры решений для стационарных случайных процессов.

Спасибо за ваши закладки и рекомендации

Примеры решений

Задача 1. Найти $m_X(t), K_X(t_1,t_2), D_X(t)$, если $X(t)=U cdot e^{-t^2}$, где $U$ – случайная величина с характеристиками $m_U=5, D_U=0,001$.

Задача 2. На вход интегрирующего устройства поступает случайный процесс $X(t)$ с характеристиками:
$$m_X(t)=t^2-5, K_X(t_1,t_2)=2sin 3t_1 sin 3t_2.$$

Найти $m_Y(t), K_Y(t_1,t_2), D_Y(t)$, если $$Y(t)=t^2 int_0^t X(tau)dtau +3t.$$

Задача 3. Найти числовые характеристики производной случайной функции, если

$$
m_{xi}(t)=cos 7t, quad K_{xi}(t_1, t_2) = 7t_1 t_2 +1/7 t_1^4 t_2^4.
$$

Задача 4. Случайная функция $X(t)$ задана каноническим разложением $X(t)=t^2+t+Zcos 3t +V e^2t$, где $D_Z=1$, $D_V=3$. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции $Y(t)=frac{dX(t)}{dt}+2-t$.

Задача 5. Дан случайный процесс $Y(t)=X cos(t)$, $t gt 0$, где $X$ – нормально распределенная величина с параметрами $m_x$ и $sigma_x$. Найти корреляционную функцию и нормированную корреляционную функцию случайного процесса.

Задача 6. Найти взаимную корреляционную функцию $R_{xy}(t_1, t_2)$ и взаимную нормированную корреляционную функцию $rho_{xy}(t_1, t_2)$ двух случайных функций $X(t)=Asin t + B cos t$ и $Y(t)=A e^t +Be^{-t}$, если известно, что дисперсии случайных величин $A$ и $B$ равны: $DA=4$, $DB=4$, коэффициент ковариации $cov(A,B)=-4$.

Задача 7. Случайная функция $X(t)$ имеет автоковариационную функцию $K_x(t,t’)=e^{t-2t’}$. Найти автоковариационную функцию случайной функции $Y(t) = int_0^t X(tau) d tau$.

Мы отлично умеем решать задачи по теории вероятностей

Источник

10.1. Математическое ожидание функции. Дисперсия функции

При решении различных задач,
связанных со случайными явлениями, современная теория вероятностей широко
пользуется аппаратом случайных величин. Для того чтобы пользоваться этим
аппаратом, необходимо знать законы распределения фигурирующих в задаче
случайных величии. Вообще говоря, эти законы могут быть определены из опыта, но
обычно опыт, целью которого является определение закона распределения случайной
величины или системы случайных величин (особенно в области военной техники),
оказывается и сложным и дорогостоящим. Естественно возникает задача – свести
объем эксперимента к минимуму и составлять суждение о законах распределения
случайных величин косвенным образом, на основании уже известных законов
распределения других случайных величин. Такие косвенные методы исследования
случайных величин играют весьма большую роль в теории вероятностей. При этом
обычно интересующая нас случайная величина представляется как функция других
случайных величин; зная законы распределения аргументов, часто удается
установить закон распределения функции. С рядом задач такого типа мы встретимся
в дальнейшем (см. главу 12).

Однако на практике часто
встречаются случаи, когда нет особой надобности полностью определять закон
распределения функции случайных величин, а достаточно только указать его
числовые характеристики: математическое ожидание, дисперсию, иногда – некоторые
из высших моментов. К тому же очень часто самые законы распределения аргументов
бывают известны недостаточно хорошо. В связи с этим часто возникает задача об
определении только числовых характеристик функций случайных величин.

Рассмотрим такую задачу:
случайная величина  есть
функция нескольких случайных величин :

.

Пусть нам известен закон
распределения системы аргументов ; требуется найти числовые характеристики
величины , в
первую очередь – математическое ожидание и дисперсию.

Представим себе, что нам удалось
тем или иным способом найти закон распределения  величины . Тогда задача об определении числовых
характеристик становится тривиальной; они находятся по формулам:

;

и т.д.

Однако самая задача нахождения
закона распределения  величины
 часто
оказывается довольно сложной. К тому же для решения поставленной нами задачи
нахождение закона распределения величины  как такового вовсе и не нужно: чтобы
найти только числовые характеристики величины , нет надобности знать ее закон
распределения; достаточно знать закон распределения аргументов . Более того, в
некоторых случаях, для того чтобы найти числовые характеристики функции, не
требуется даже знать закона распределения ее аргументов; достаточно бывает
знать лишь некоторые числовые характеристики аргументов.

Таким образом, возникает задача
определения числовых характеристик функций случайных величин помимо законов
распределения этих функций.

Рассмотрим задачу об определении
числовых характеристик функции при заданном законе распределения аргументов.
Начнем с самого простого случая – функции одного аргумента – и поставим
следующую задачу.

Имеется случайная величина  с заданным законом
распределения; другая случайная величина  связана с  функциональной зависимостью:

.

Требуется, не находя закона
распределения величины , определить ее математическое ожидание:

.                    (10.1.1)

Рассмотрим сначала случай, когда  есть прерывная
случайная величина с рядом распределения:

Выпишем возможные значения
величины  и
вероятности этих значений:

 

(10.1.2)

Таблица (10.1.2) не является в
строгом смысле слова рядом распределения величины , так как в общем случае некоторые из
значений

                        (10.1.3)

могут
совпадать между собой; к тому же эти значения в верхнем столбце таблицы
(10.1.2) не обязательно идут в возрастающем порядке. Для того чтобы от таблицы
(10.1.2) перейти к подлинному ряду распределения величины , нужно было бы расположить
значения (10.1.3) в порядке возрастания, объединить столбцы, соответствующие
равным между собой значениям , и сложить соответствующие вероятности.
Но в данном случае нас не интересует закон распределения величины  как таковой; для наших
целей – определения математического ожидания – достаточно такой
«неупорядоченной» формы ряда распределения, как (10.1.2). Математическое
ожидание величины  можно
определить по формуле

                                 (10.1.4)

Очевидно,
величина ,
определяемая по формуле (10.1.4), не может измениться от того, что под знаком
суммы некоторые члены будут объединены заранее, а порядок членов изменен.

В формуле (10.1.4) для
математического ожидания функции не содержится в явном виде закона
распределения самой функции, а содержится только закон распределения аргумента.
Таким образом, для определения математического ожидания функции вовсе не
требуется знать закон распределения этой функции, а достаточно знать закон
распределения аргумента.

Заменяя в формуле (10.1.4) сумму
интегралом, а вероятность  – элементом вероятности, получим
аналогичную формулу для непрерывной случайной величины:

.             (10.1.5)

где
 – плотность
распределения величины .

Аналогично может быть определено
математическое ожидание функции  от двух случайных аргументов  и . Для прерывных величин

,                (10.1.6)

где
 –
вероятность того, что система  примет значения .

Для непрерывных величин

,                   (10.1.7)

где
 – плотность
распределения системы .

Совершенно аналогично
определяется математическое ожидание функции от произвольного числа случайных
аргументов. Приведем соответствующую формулу только для непрерывных величин:

,                    (10.1.8)

где
 – плотность
распределения системы .

Формулы типа (10.1.8) весьма часто
встречаются в практическом применении теории вероятностей, когда речь идет об
осреднении каких-либо величин, зависящих от ряда случайных аргументов.

Таким образом, математическое
ожидание функции любого числа случайных аргументов может быть найдено помимо
закона распределения функции. Аналогично могут быть найдены и другие числовые
характеристики функции – моменты различных порядков. Так как каждый момент
представляет собой математическое ожидание некоторой функции исследуемой
случайной величины, то вычисление любого момента может быть осуществлено
приемами, совершенно аналогичными вышеизложенным. Здесь мы приведем расчетные
формулы только для дисперсии, причем лишь для случая непрерывных случайных аргументов.

Дисперсия функции одного
случайного аргумента выражается формулой

,                       (10.1.9)

где
 –
математическое ожидание функции ;  – плотность распределения величины .

Аналогично выражается дисперсия
функции двух аргументов:

,                 (10.1.10)

где
 –
математическое ожидание функции ;  – плотность распределения системы .

Наконец, в случае произвольного
числа аргументов, в аналогичных обозначениях:

.                 (10.1.11)

Заметим, что часто при вычислении
дисперсии бывает удобно пользоваться соотношением между начальным и центральным
моментами второго порядка (см. главу 5) и писать:

;            (10.1.12)

;                  (10.1.13)

.                    (10.1.14)

Формулы (10.1.12) – (10.1.14)
можно рекомендовать тогда, когда они не приводят к разностям близких чисел, т.
е. когда  сравнительно
невелико.

Рассмотрим несколько примеров,
иллюстрирующих применение изложенных выше методов для решения практических
задач.

Пример 1. На плоскости задан
отрезок длины  (рис.
10.1.1), вращающийся случайным образом так, что все направления его одинаково
вероятны. Отрезок проектируется на неподвижную ось . Определить среднее значение
длины проекции отрезка.

image1

Рис. 10.1.1

Решение. Длина проекции равна:

,

где
угол  –
случайная величина, распределенная с равномерной плотностью на участке .

По формуле (10.1.5) имеем:

.

Пример 2. Удлиненный осколок
снаряда, который можно схематически изобразить отрезком длины , летит, вращаясь вокруг
центра массы таким образом, что все его ориентации в пространстве одинаково
вероятны. На своем пути осколок встречает плоский экран, перпендикулярный к
направлению его движения, и оставляет в нем пробоину. Найти математическое
ожидание длины этой пробоины.

Решение. Прежде всего дадим
математическую формулировку утверждения, заключающегося в том, что «все ориентации
осколка в пространстве одинаково вероятны». Направление отрезка  будем характеризовать единичным
вектором  (рис.
10.1.2).

image2

Рис. 10.1.2

Направление
вектора  в
сферической системе координат, связанной с плоскостью , на которую производится проектирование,
определяется двумя углами: углом , лежащим в плоскости , и углом , лежащим в плоскости,
перпендикулярной к .
При равной вероятности всех направлений вектора  все положения его конца на поверхности
сферы единичного радиуса  должны обладать одинаковой плотностью
вероятности; следовательно, элемент вероятности

,

где
 – плотность
распределения углов ,
должен быть пропорционален элементарной площадке  на сфере ; эта элементарная площадка равна

,

откуда

;
,

где
 –
коэффициент пропорциональности.

Значение коэффициента  найдем из соотношения

,

откуда

.

Таким образом, плотность
распределения углов  выражается
формулой

 при
                    (10.1.15)

Спроектируем отрезок па плоскость
; длина
проекции равна:

.

Рассматривая  как функцию двух аргументов  и  и применяя формулу (10.1.7),
получим:

.

Таким образом, средняя длина
пробоины, оставляемой осколком в экране, равна  длины осколка.

Пример 3. Плоская фигура площади  беспорядочно вращается
в пространстве так, что все ориентации этой фигуры одинаково вероятны. Найти
среднюю площадь проекции фигуры  на неподвижную плоскость  (рис. 10.1.3).

image3

Рис. 10.1.3

Решение. Направление плоскости
фигуры  в
пространстве будем характеризовать направлением нормали  к этой плоскости. С плоскостью  свяжем ту же
сферическую систему координат, что в предыдущем примере. Направление нормали  к площадке  характеризуется
случайными углами  и
 распределенными
с плотностью (10.1.5). Площадь  проекции фигуры  на плоскость  равна

,

а
средняя площадь проекции

.

Таким образом, средняя площадь
проекции произвольно ориентированной плоской фигуры на неподвижную плоскость
равна половине площади этой фигуры.

Пример 4. В процессе слежения
радиолокатором за определенным объектом пятно, изображающее объект, все время
удерживается в пределах экрана. Экран представляет собой круг  радиуса . Пятно занимает на
экране случайное положение с постоянной плотностью вероятности. Найти среднее
расстояние от пятна до центра экрана.

Решение. Обозначая расстояние , имеем , где  – координаты пятна;  в пределах круга  и равна нулю за его
пределами. Применяя формулу (10.1.7) и переходя в интеграле к полярным
координатам, имеем:

.

Пример 5. Надежность (вероятность
безотказной работы) технического устройства есть определенная функция  трех параметров
характеризующих работу регулятора. Параметры  представляют собой случайные величины с
известной плотностью распределения  . Найти среднее значение (математическое
ожидание) надежности устройства и среднее квадратическое отклонение,
характеризующее ее устойчивость.

Решение. Надежность устройства  есть функция трех
случайных величин (параметров) . Ее среднее значение (математическое ожидание)
найдется по формуле (10.1.8):

.                (10.1.16)

По формуле (10.1.14) имеем:

,

.

Формула (10.1.16), выражающая
среднюю (полную) вероятность безотказной работы устройства с учетом случайных
величии, от которых зависит эта вероятность в каждом конкретном случае,
предоставляет собой частный случай так называемой интегральной формулы
полной вероятности, обобщающей обычную формулу полной вероятности на случай
бесконечного (несчетного) числа гипотез.

Выведем здесь эту формулу в общем
виде.

Предположим, что опыт, в котором
может появиться или не появиться интересующее нас событие , протекает в случайных, заранее
неизвестных условиях. Пусть эти условия характеризуются непрерывными случайными
величинами

,                       (10.1.17)

плотность
распределения которых

.

Вероятность  появления события  есть некоторая функция
случайных величин (10.1.17):

.               (10.1.18)

Нам нужно найти среднее значение
этой вероятности или, другими словами, полную вероятность события :

.

Применяя формулу (10.1.8) для
математического ожидания функции, найдем:

.               (10.1.19)

Формула (10.1.19) называется интегральной
формулой полной вероятности. Нетрудно заметить, что по своей структуре она
сходна с формулой полной вероятности, если заменить дискретный ряд гипотез
непрерывной гаммой, сумму – интегралом, вероятность гипотезы – элементом
вероятности:

,

а
условную вероятность события при данной гипотезе – условной вероятностью
события при фиксированных значениях случайных величин:

.

Не менее часто, чем интегральной
формулой полной вероятности пользуются интегральной формулой полного
математического ожидания. Эта формула выражает среднее (полное)
математическое ожидание случайной величины , значение которой принимается в опыте,
условия которого заранее неизвестны (случайны). Если эти условия
характеризуются непрерывными случайными величинами

с
плотностью распределения

,

а
математическое ожидание величины  есть функция от величин :

,

то
полное математическое ожидание величины  вычисляется по формуле

,              (10.1.20)

которая
называется интегральной формулой полного математического ожидания.

Пример 6. Математическое ожидание
расстояния ,
на котором будет обнаружен объект с помощью четырех радиолокационных станций,
зависит от некоторых технических параметров этих станций:

,

которые
представляют собой независимые случайные величины с плотностью распределения

                                            .

При фиксированных значениях
параметров  математическое
ожидание дальности обнаружения равно

.

Найти среднее (полное)
математическое ожидание дальности обнаружения.

Решение. По формуле (10.1.20)
имеем:

.

Источник

Числовые характеристики функций случайных величин

Страницы работы

Содержание работы

Тема 6. Числовые
характеристики функций случайных величин.

В практических задачах часто встречаются вопросы, требующие
оценки числовых характеристик функций СВ. Простейший случай нам
встречался, например, вычисление значения начального момента порядка 2 (α2).
Известно, что 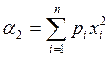, где ,
а X – дискретная СВ, заданная своим рядом
распределения. Напомним, что в этом случае значения  имели
ряд значений вероятностей pi, эквивалентных
для соответствующих xi, , т.е. вероятности самих СВ и функций
совпадали.

Другого типа задача: на вход технического устройства
поступает случайное воздействие X, которое
преобразуется по некоторому закону φ и на выходе мы имеем СВ вида Y=φ(X). При известном законе
распределения СВ X необходимо найти числовые
характеристики СВ Y. См. Схемы:

В описанных случаях могут возникнуть три типа задач:

1. Зная закон
распределения СВ X, найти закон распределения СВ Y, естественно это можно обобщить на системы СВ.

2. Зная закон
распределения СВ X, найти числовые характеристики СВ Y (или системы).

3. Зная
числовые характеристики СВ X, найти числовые
характеристики СВ Y.

Рассмотрим методы решения задач типа 2 и 3.

Пусть СВ Y зависит функционально
от СВ X, т.е.

Y=φ(X).

Схема решения такой задачи такова:

Для дискретного случая :

Дано:

X:

x1

x2

…

xi

…

xn

p1

p2

…

pi

…

pn

Это ряд распределения для СВ X

где      ,

 и

При X=xi
имеем Y=φ(xi) и
вероятность этого события равна pi. Можно
записать таблицу вида:

φ(x1)

φ(x2)

…

φ(xi)

…

φ(xn)

(6.1)

p1

p2

…

pi

…

pn

Но это еще не ряд распределения для СВ Y.

Необходимо построить ΣY={y1, y2,…} и
объединить одинаковые значения на совокупности функций
φ(xi), присваивая им вероятность как
сумму составляющих.

Но если речь идёт о расчёте M[Y] и D[Y], то можно воспользоваться таблицей в виде (6.1).
Действительно, имеем

,

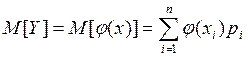
, где

или в координатной форме

Аналогично определяются начальные и центральные
моменты s-го порядка:

 и

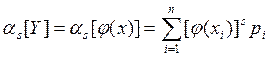
Для непрерывного случая при известной плотности f(x) имеем:

;

;

;

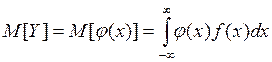
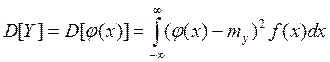
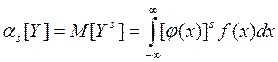
Таким образом, по закону распределения аргумента X есть возможность найти числовые характеристики функции вида
Y=φ(X).

Расчётные формулы, аналогичные приведённым, можно
привести и для функции нескольких случайных аргументов.

Пусть Y=φ(X1, X2, …, Xn) и известна совместная плотность вида f(x1, x2,…,
xn). Для расчётов используем формулы вида:

                   (6.2)

       (6.3)

                 (6.4)

      (6.5)

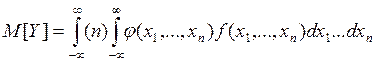
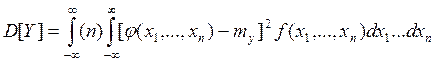
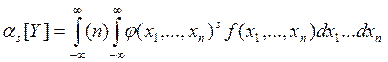
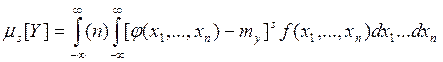
Очевидно, что с ростом размерности системы НСВ
появляются сложности аналитического и вычислительного направлений.

Идею упрощения покажем на примере системы НСВ размерности
2.

Известно, что совместная плотность пары случайных величин X1 и X2,
непрерывных по своей природе, выражается в общем виде как

, где

 – условная плотность СВ X1 при условии, что СВ X2
приняла значение x2.

Мы можем записать симметричную форму в виде

с той же интерпретацией.

Замечание. Это правило строго называют
теоремой умножения плотностей (в схеме непрерывных случайных величин).

Если сейчас попытаться, например, оценить значение M[Y], где Y=φ(X1, X2), то
необходимо использовать формулу

   (6.6)

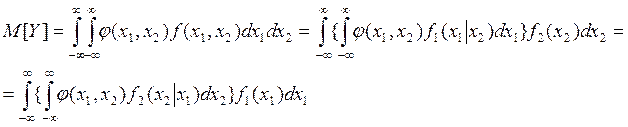
где внутренний интеграл представляет собой условное
математическое ожидание, которое затем преобразуется в безусловное. Такое
преобразование называют интегральной формулой полного математического
ожидания.

Можно обобщить такую формулу на систему n>2
случайных величин. Например, формула (6.2) принимает вид:

(6.7)

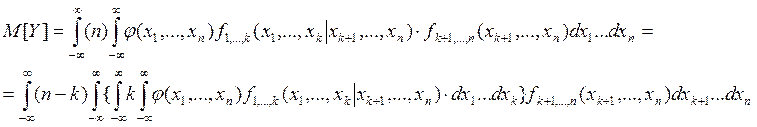
Эта формула построена как и (6.6), называется она
интегральная формула полного математического ожидания для системы НСВ, заданных
своей совместной плотностью f(x1,…,xn).

Запись формул для D[Y], αs[Y],
μs[Y] в виде (6.7)
требует только аккуратности.

Во многих прикладных задачах числовые характеристики СВ Y=φ(X1,…,Xn)
можно определить как функции числовых характеристик системы СВ (X1,…,Xn).
Главное – при этом нет необходимости знать законы распределения для системы,
достаточно знать лишь числовые характеристики системы.

Перечислим именно такие случаи, (частично они нам
знакомы).

  1. Математическое ожидание неслучайной величины c равно c,
    т.е

M[c]=c

  1. Дисперсия неслучайной величины c
    равна 0, т.е

D[c]=0

  1. Обобщение 1 и 2 можно представить так:

M[cX]=cM[X] и D[cX]=c2D[X]

Для доказательства последнего
следует представить D[cX] в
виде

  1. Правило сложения математических ожиданий для 2-х СВ
    представляют обычно в виде:

и его обобщение

  1. Математическое ожидание линейной функции определяют по
    правилу:

где ,  – неслучайные величины.

  1. Дисперсия суммы СВ равна сумме всех элементов
    корреляционной матрицы ||Kij|| этих СВ:

или, в силу симметрии матрицы ||Kij|| относительно главной диагонали, имеем

Замечание. Если СВ X1,…,Xn некоррелированы, т.е. Kij=0
при i≠j, то

  1. Дисперсия линейной функции случайных величин определяется
    по формуле:

где a0,a1,…,an – неслучайные величины.

  1. Математическое ожидание произведения 2-х СВ вычисляют
    по формуле:

, где

Для некоррелированных СВ X1 и X2, т.е.
при K12=0

Обобщение следует непосредственно
при некоррелированности

Оказывается, независимость
системы упрощает все вычисления, т.к. независимость влечёт некоррелированность.

  1. Дисперсия произведения независимых СВ X1,…,Xn
    выражается в виде

где Di=D[Xi], mi=M[Xi].

Напомним, что

  1. О коэффициенте корреляции для линейно зависимых случайных
    величин X и Y, т.е. для случая

Y=aX+b, a и b – неслучайные величины

Имеем по определению

. Тогда

, что
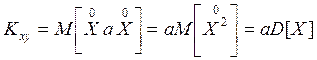
и следовало ожидать.

Для нормирования Kxy необходимо знать σy и σx.

, т.е.

Тогда 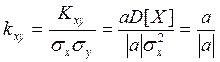, т.е.

Таким образом, в общем случае

 –
это нам уже встречалось.

Похожие материалы

  • Условие устойчивости. Исследования методов теории вероятностей
  • Подмножества из пространства элементарных событий
  • Методы многокритериальной оптимизации для линейного непрерывного случая (Лабораторная работа № 1)

Информация о работе

Источник

Добавить комментарий