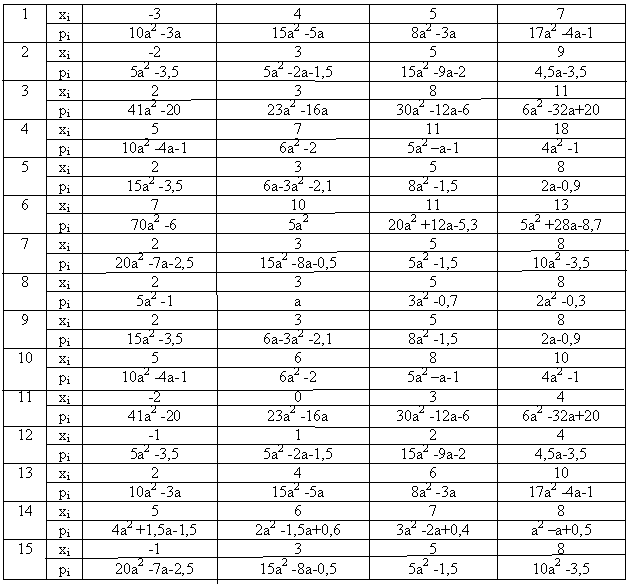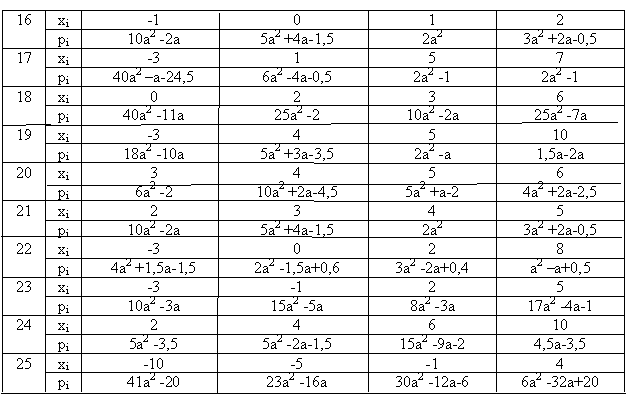Как найти числовые характеристики таблица

Как найти числовые характеристики таблица

Числовые характеристики случайной величины (Таблица)

Числовые характеристики случайной величины таблица

Числовые характеристики 

Дискретная случайная величина

Непрерывная случайная величина

Математическое ожидание

mat 14 12

 mat 14 13

Дисперсия

mat 14 17

mat 14 14

mat 14 15

Среднее квадратическое отклонение

mat 14 16

Свойства числовых характеристик

Математическое ожидание

Дисперсия

1. MC=C, где C – константа;

2. M(CX)=CMX;

3. M(X+Y)=MX+MY;

4. M(X·Y)=MX·MY – для независимых случайных величин

1. DC=0, где C – константа;

2. D(CX)=C2DX;

3. D(X±Y)=DX+DY для независимых случайных величин

Моменты случайных величин

Моменты

Дискретная случайная величина

Непрерывная случайная величина

Начальный момент порядка k

mat 14 18

mat 14 19

mat 14 20

Центральный момент порядка k

Коэффициент асимметрии:

mat 14 21

Коэффициент экцесса (островершинности):

mat 14 22

mat 14 23

mat 14 24
Источник


Числовые характеристики дискретной случайной величины.

Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.

Характеристикой среднего значения случайной величины служит математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

sum_{i=1}^n x_{i} cdot p_{i}=x_{1} cdot p_{1}+x_{2} cdot p_{2}+cdots +x_{n} cdot p_{n}

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной:

    [M(C)=C]

2. Постоянную можно выносить за знак математического ожидания:

    [M(CX)=CM(X)]

3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

    [M(X_1 cdot X_2 cdot ... cdot X_n)=M(X_1)cdot M(X_2)cdot ... cdot M(X_n)]

4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

    [M(X_1 + X_2 + ... + X_n)=M(X_1) + M(X_2) + ... + M(X_n)]

(для разности аналогично)

Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.

Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

    [D(X)=M{[X-M(X)]}^2]

Дисперсию удобно вычислять по формуле:

    [D(X)=M(X^2)-{[M(X)]}^2]

Свойства дисперсии:

1. Дисперсия постоянной равна нулю:

    [D(C)=0]

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

    [D(CX)=C^2D(X)]

3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:

    [D(X_1 pm X_2 pm ... pm X_n)=D(X_1) + D(X_2) + ... + D(X_n)]

4.

    [D(X+C)=D(X)]

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

    [sigma (X) =sqrt{D(X)}]

Рассмотрим следующие задачи.

1. Математическое ожидание и дисперсия СВ Х соответственно равны 0,5 и 5. Найти математическое ожидание и дисперсию случайной величины 2X-3.

Решение.

Согласно свойствам математического ожидания и дисперсии, получаем:

    [M(2X-3)=M(2X)+M(-3)=2M(X)-3=2cdot frac12-3=1-3=-2]

    [D(2X-3)=4cdot D(X)=4cdot 5=20]

2. Случайные величины X и Y независимы, причем D(X)=3 и D(Y)=5. Найти D(Z), если Z=4cdot X- 5 cdot Y +3.

Решение.

На основании свойств дисперсии получаем:

    [D(Z)=D(4cdot X- 5 cdot Y +3)=16cdot D(X)+25cdot D(Y)=16cdot 3+25cdot 5=48+125=173]

3. Закон распределения ДСВ Х задан таблицей распределения

x_i 1 2 3 4
p_i frac18 frac14 frac13 c

Найти: c,quad M(X), quad D(X), quad sigma (X), quad P{X<3}.

1) Так как sum_{i=1}^4 p_i =1, т.е. frac18 +frac14 +frac13+c=1, следовательно

    [c=1-frac18 -frac14 -frac13=frac{24-3-6-8}{24}=frac{7}{24}]

Т.о. закон распределения примет вид

x_i 1 2 3 4
p_i frac18 frac14 frac13 frac{7}{24}

    [M(X)=sum_{i=1}^4 x_i cdot p_i=1cdot frac18+2cdot frac14+3cdot frac13+4cdot frac{7}{24}=frac18+frac12+1+frac76=]

    [=frac{3+12+24+28}{24}=frac{67}{24};]

2) Для вычисления дисперсии воспользуемся формулой:

    [D(X)=M(X^2)-{[M(X)]}^2]

Сначала найдем математическое ожидание ДСВ Х2 для этого составим закон распределения этой СВ. Напоминаю, что для этого необходимо каждое значение ДСВ Х возвести в квадрат, а вероятности оставляем прежними. При одинаковых значениях ДСВ вероятности складываем.

    [M(X^2)=1cdot frac18+4cdot frac14+9cdot frac13+16cdot frac{7}{24}=frac18+1+3+frac{14}{3}=frac{3+96+112}{24}=frac{211}{24};]

    [D(X)=frac{211}{24}-{left(frac{67}{24}right)}^2=frac{24cdot 211-{67}^2}{{24}^2}=frac{5064-4489}{576}=frac{575}{576};]

3) Найдем среднее квадратическое отклонение:

    [sigma (X) =sqrt{D(X)}=sqrt{frac{575}{576}}=frac{5sqrt{23}}{24}]

4)

    [P{X<3}=P{X=1}+P{X=2}=frac18+frac14=frac38]

4. Функция распределения ДСВ Х имеет вид

    [F(x)={ 0, qquad qquad xle 0 \ 0,2, qquad 0< x le 1, \ 0,6, qquad qquad 1< x le 2 \ 0,9, qquad qquad 2< x le 3 \ 1, qquad qquad x>3]

Найти:

    [M(X), quad M(X^2) quad D(X), quad sigma (X).]

Решение.

Составляем закон распределения ДСВ Х (т.е. выполняем операцию обратную той, которую мы делали в предыдущей статье)

x_i 0 1 2 3
p_i 0,2 0,4 0,3 0,1

    [M(X)=0cdot 0,2+1cdot 0,4+2cdot 0,3+3cdot 0,1=0,4+0,6+0,3=1,3]

Составляем закон распределения ДСВ X^2

x_i^2 0 1 4 9
p_i 0,2 0,4 0,3 0,1

    [M(X^2)=0cdot 0,2+1cdot 0,4+4cdot 0,3+9cdot 0,1=0,4+1,2+0,9=2,5]

    [D(X)=M(X^2)-{[M(X)]}^2=2,5-{1,3}^2=2,5-1,69=0,81]

    [sigma (X)=sqrt{0,81}=0,9]

5. Независимые случайные величины X и Y заданы таблицами распределения вероятностей

Найти D(X+Y) двумя способами:

1. Составив предварительно таблицу распределения СВ Z=X+Y;

2. Используя правило сложения дисперсий.

Решение.

Составим таблицу распределения ДСВ Z=X+Y.

Найдем z_{ij}=x_i+y_{j}

10+30=40 20+30=50
10+40=50 20+40=60
10+50=60 20+50=70
Т.о. значения ДСВ Z таковы: z_1=40,quad z_2=50,quad z_3=60,quad z_4=70

Найдем соответствующие им вероятности:

    [p_1=P{Z=40}=P{X=10, Y=30}=0,2cdot 0,5=0,1]

    [p_2=P{Z=50}=P{X=10, Y=40}+P{X=20, Y=30}=]

    [=0,2cdot 0,3+0,8cdot 0,5=0,06+0,4=0,46]

    [p_3=P{Z=60}=P{X=10, Y=50}+P{X=20, Y=40}=]

    [=0,2cdot 0,2+0,8cdot 0,3=0,04+0,24=0,28]

    [p_4=P{Z=70}=P{X=20, Y=50}=0,8cdot 0,2=0,16]

Получаем ряд распределения СВ Z

z_i^2 40 50 60 70
p_i 0,1 0,46 0,28 0,16

    [M(Z)=sum_{i=1}^4 z_i cdot p_i=40cdot 0,1+50cdot 0,46+60cdot 0,28+70cdot 0,16=4+23+16,8+11,2=55;]

    [M(Z^2)=sum_{i=1}^4 z_i^2 cdot p_i=1600cdot 0,1+2500cdot 0,46+3600cdot 0,28+4900cdot 0,16=]

    [=160+1150+1008+784=3102;]

    [D(Z)=M(Z^2)-{[M(Z)]}^2=3102-3025=77]

2. Используя правило сложения дисперсий:

    [D(Z)=D(X+Y)=D(X)+D(Y)]

    [D(X)=M(X^2)-{[M(X)]}^2]

    [M(X)=10cdot 0,2+20cdot 0,8=2+16=18;]

    [M(X^2)=100cdot 0,2+400cdot 0,8=20+320=340;]

    [M(Y)=30cdot 0,5+40cdot 0,3+50cdot 0,2=15+12+10=37]

    [M(Y^2)=900cdot 0,5+1600cdot 0,3+2500cdot 0,2=450+480+500=1430]

    [D(Y)=1430-1369=61]

    [D(Z)=16+61=77]

Источник

Числовые характеристики случайных величин таблица

Числовые характеристики Дискретная случайная величина Непрерывная случайная величина
Математическое ожидание
Дисперсия
Среднее квадратическое отклонение

Свойства числовых характеристик

Математическое ожидание Дисперсия
1. MC=C, где C — константа;

2. M(CX)=CMX;

3. M(X+Y)=MX+MY;

4. M(X·Y)=MX·MY — для независимых случайных величин

 1. DC=0, где C — константа;

2. D(CX)=C2DX;

3. D(X±Y)=DX+DY для независимых случайных величин

Моменты случайных величин

Моменты Дискретная случайная величина Непрерывная случайная величина
Начальный момент порядка k
Центральный момент порядка k Коэффициент асимметрии:

Коэффициент экцесса (островершинности):
Источник

1. Цели работы:

1.1. Развивать аналитическое мышление
через постоянное обращение к имеющимся знаниям
учащихся, настойчивость, умение доводить начатое
дело до конца.

1.2. Проверить уровень
сформированности вычислительных навыков
учащихся, их умение применять свои знания при
выполнении заданий различного уровня сложности.

1.3. Научиться находить математическое
ожидание, дисперсию и среднее квадратичное
отклонение дискретной случайной величины.

2. Теоретические обоснования:

Математическим ожиданием дискретной
случайной величины называется число, равное
сумме произведений всех значений случайной
величины на вероятности этих значений.

Если случайная величина Х принимает значения x1,
x2, … , xn с вероятностями
соответственно p1, p2,… pn , то
математическое ожидание находится по формуле:

М(x) = xipi = x1p1+ x2p2
+ … + xnpn (1)

Математическое ожидание иначе называют
средним значением случайной величины, так как
оно указывает некоторое среднее число, около
которого группируются все значения случайной
величины.

Дисперсией дискретной случайной величины
называется математическое ожидание квадрата
отклонения случайной величины от её
математического ожидания: D(x) = M(x – M(x))2
(2)

Пусть случайная величина Х принимает значения x1,
x2, … , xn с вероятностями
соответственно p1, p2,… pn , тогда
квадрат отклонения случайной величины Х от её
математического ожидания есть случайная
величина, принимающая значения (Х1 – М(Х)), (Х2
– М(Х)), …, (Хn – М(Х) с вероятностями Р1 , Р2
, …, Рn. Поэтому математическое ожидание так
распределенной случайной величины, то есть
дисперсию Х, можно вычислять по формуле: D(X) = (xi
– M(x))2pi (3)

Преобразуем эту формулу:

D(x) = (xi – M(x))2pi = (xi2
– 2(M(x))2)pi = xi2pi –
2(M(x))xipi
+ (M(x))2pi

Учитывая, что pi = 1, a xipi = M(x),
получим равенство

D(x) = M(x2) – (M(x))2 (4)

Дисперсия случайной величины характеризует
степень разброса значений случайной величины
относительно её математического ожидания.

Средним квадратичным отклонением
дискретной случайной величины называется
квадратный корень из дисперсии:

(x)
= D(x)
(5)

Пример 1.

Найти числовые характеристики случайной
величины Х, имеющей закон распределения,
представленный в таблице 1.

Таблица 1. Закон распределения случайной
величины Х.

Xi – 2 – 1 1 2 3
Pi 0.3 0.1 0.2 0.1 0.3

Решение:

1. Найдём математическое ожидание.

По формуле (1): M(x) = –2 . 0.3 +
(–1) . 0.1 + 1 . 0.2 + 2 .
0.1 + 3 . 0.3 = – 0.6 – 0.1 + 0.2 + 0.2 + 0.9 = 0.6

2. Найдём дисперсию.

  • Воспользуемся формулой (2):

случайная величина (Х – М(Х)) имеет
распределение, представленное в таблице 2

Таблица 2. Закон распределения случайной
величины (Х – М(Х))

Xi – М(х) – 2.6 – 1.6 0.4 1.4 2.4
Pi 0.3 0.1 0.2 0.1 0.3

Тогда:

D(X) = M(x – M(x))2 = (–2.6)2 .
0.3 + (–1.6)2 . 0.1 + 0.42 .
0.2 + 1.42 . 0.1 + 2.42 .
0.3 = 2.028 + 0.256 + 0.032 + 0.196 + 1.728 = 4.24

  • Воспользуемся формулой (4):

случайная величина x2 имеет
распределение, представленное в таблице 3

Таблица 3. Закон распределения случайной
величины х2

Тогда M(x2) = 1 . 0.3 + 4 .
0.4 + 9 . 0.3 = 0.3 + 1.6 + 2.7 = 4.6

  • По формуле (4):

D(x) = M(x2) – (M(x))2 = 4.6 – 0.62
= 4.6 – 0.36 = 4.24

3. Найдём среднее квадратичное отклонение по
формуле (5)

(x)
= D(x)
= 4.24 ~2.059

Пример 2.

Найти значение параметра а для закона
распределения.

Таблица 4. Закон распределения
дискретной случайной величины

xi

0

3

5

8
pi 40a2 – 11a 25a2 – 2 10a2 – 2a 25a2 – 7a

Решение:

Так как ,то

100а2 – 20а – 3 = 0

а1 = – 0,1
а2 = 0,3

а1= – 0,1 – посторонний корень , так
как 0 Р(xi)1. Подставив
значение 0,3 вместо а, получим закон
распределения (таблица 5).

Таблица 5. Закон распределения ДСВ


xi 0 3 5 8
pi 0.3 0.25 0.3 0.15

3. Порядок выполнения работы:

3.1. Проработать теоретический
материал по теме.

3.2. Ответить на контрольные вопросы.

3.3. Получить вариант задания.

3.4. Найти математическое ожидание,
дисперсию и среднее квадратичное отклонение
дискретной случайной величины для задания 1
(воспользоваться формулами (1), (3), (5)).

3.5. В заданиях 2 и 3 составить законы
распределения случайной величины.

3.6. Вычислить М(x), Д(x), (x) в
заданиях 1, 2, 3.

3.7. Сделать вывод по работе.

4. Контрольные вопросы:

4.1. Дать определение дискретной
случайной величины.

4.2. Что такое математическое ожидание?

4.3. Что такое дисперсия?

4.4. Что такое среднее квадратичное
отклонение?

4.5. Дать определение закона
распределения дискретной случайной величины.

5. Рекомендации по оформлению отчёта

Отчёт по работе должен содержать:

5.1. Вид работы.

5.2. Точное наименование.

5.3. Цель.

5.4. Ход работы.

5.5. Условие задания (свой вариант
задания смотри в приложениях А, Б, В).

5.6. Вывод.

5.7. Законы распределений для заданий 2
и 3.

5.8. В выводе отразить полученные
значения числовых характеристик.

6. Методические рекомендации

6.1. При составлении законов
распределений помните, что:

6.2. При решении уравнения старайтесь
не допускать вычислительной ошибки, иначе весь
дальнейший ваш труд будет насмарку.

6.3. Лучше меньше, да лучше!

Учащимся предлагаются следующие задания.

Задание 1. Составить закон
распределения случайной величины Х .

Для заданного закона распределения найти М(x),
Д(x), (x).

п – порядковый номер учащегося по списку в
журнале.

xi п – 10 п – 6 п – 2 п п + 1 п + 3 п + 5 п + 8
pi 0,17 0,03 0,16 0,07 0,12 0,4 0,04 0,01

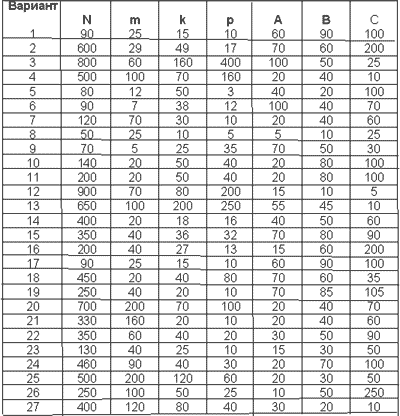
Задание 2. Составить закон
распределения случайной величины Х. Найти
числовые характеристики случайной величины x (x –
выигрыш владельца одного лотерейного билета).

  • В лотерее разыгрываются N билетов;
  • m из них выигрывают по А рублей;
  • k из них выигрывают по В рублей;
  • p из них выигрывают по С рублей.

Задания по вариантам смотрите на рисунке:

Задание 3. Найти числовые
характеристики случайной величины “х”.
Варианты:


Источник

Непрерывные распределения вероятностей и их параметры

  1. Общие свойства непрерывного распределения
  2. Функция распределения непрерывной случайной величины
  3. Числовые характеристики непрерывного распределения
  4. Таблица непрерывных распределений, их параметров и числовых характеристик
  5. Примеры

п.1. Общие свойства непрерывного распределения

Если случайная величина x может принимать любые значения в интервале (a;b), она называется непрерывной случайной величиной.
Функция (p(x)) от значения случайной величины, равная вероятности получения этого значения в испытании, называется плотностью распределения.
Свойства плотности распределения: begin{gather*} p(x)geq 0\ int_{-infty}^{+infty}p(x)dx=1 text{(условие нормировки)} end{gather*}

Например:
Пусть случайная величина равномерно распределена на отрезке (xin [a;b]), т.е. (p(x)=c=const). Из условия нормировки получаем: $$ int_{-infty}^{+infty}p(x)dx=int_{a}^{b}ccdot dx=ccdot x|_{a}^{b}=c(b-a)=1Rightarrow c=frac{1}{b-a} $$ Плотность равномерного непрерывного распределения: $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$

п.2. Функция распределения непрерывной случайной величины

Функцией распределения непрерывной случайной величины называют функцию, которая определяет вероятность, что значение случайной величины x не превышает граничное значение t: $$ F(t)=P(xleq t)=int_{-infty}^t p(x)dx $$ Вероятность для случайной величины попасть в интервал (cleq xleq d) определяется интегралом от плотности вероятности: $$ P(cleq xleq d)=int_{c}^d p(x)dx=F(d)-F(c) $$ и равна разности значений функции распределения на концах интервала.

Для непрерывной случайной величины график (F(x)) является монотонно возрастающей гладкой кривой. Область значений (F(x)in [0;1]).
Предел (F(x)) слева равен 0, предел справа равен 1: $$ lim_{xrightarrow -infty}F(x)=0; lim_{xrightarrow +infty}F(x)=1 $$ Например:
Найдем функцию распределения для равномерного распределения с плотностью: $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$ Для всех (xlt a) $$ F(x)=int_{-infty}^a p(x)dx=int_{-infty}^acdot dx=0 $$ Для всех (aleq xleq b) begin{gather*} F(t)=0+int_{a}^t p(x)dx=int_{a}^tfrac{1}{b-a}cdot dx=frac{1}{b-a}cdot x|_{a}^t=frac{t-a}{b-a}\ F(x)=frac{x-a}{b-a} end{gather*} Для всех (xgt b) begin{gather*} F(x)=F(b)+int_{b}^{+infty} p(x)dx=1+0=1 end{gather*} Получаем: $$ F(x)= begin{cases} 0, xlt a\ frac{x-a}{b-a}, xin [a;b]\ 1, xgt b end{cases} $$ Графики плотности распределения и функции распределения для равномерно распределенной непрерывной величины:
Функция распределения непрерывной случайной величины

п.3. Числовые характеристики непрерывного распределения

Числовыми характеристиками непрерывного распределения являются математическое ожидание, дисперсия и среднее квадратичное отклонение (СКО).
Если для дискретных распределений числовые характеристики определяются через суммы (см. §62 данного справочника), то для непрерывных распределений для этого используются интегралы.

Математическое ожидание непрерывной случайной величины (x) с плотностью распределения (p(x)) равно интегралу: $$ M(X)=int_{-infty}^{+infty}xcdot p(x)dx $$

Дисперсия непрерывной случайной величины (x) с плотностью распределения (p(x)) равна интегралу: $$ D(X)=int_{-infty}^{+infty}(x-M(x))^2cdot p(x)dx=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x) $$

Среднее квадратичное отклонение (СКО) непрерывной случайной величины – это корень квадратный от дисперсии: $$ sigma(X)=sqrt{D(X)} $$

Например:
Найдем числовые характеристики равномерного распределения. $$ p(x)= begin{cases} frac{1}{b-a}, xin [a;b]\ 0, xnotin [a;b] end{cases} $$ Мат. ожидание: begin{gather*} M(x)=int_{-infty}^{+infty} xcdot p(x)dx=int_{a}^{b} xcdotfrac{1}{b-a}dx=frac{1}{b-a}cdotfrac{x^2}{2}|_{a}^{b}=frac{b^2-a^2}{2(b-a)}=\ =frac{(b-a)(b+a)}{2(b-a)}=frac{a+b}{2} end{gather*} Т.е., среднее значение (центр тяжести) равномерного распределения – это середина отрезка.
Дисперсия: begin{gather*} D(x)=D(X)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=D(X)=int_{a}^{b}x^2cdotfrac{1}{b-a}dx-left(frac{a+b}{2}right)^2=\ =frac{1}{b-a}cdotfrac{x^3}{3}|_{a}^{b}-left(frac{a+b}{2}right)^2=frac{b^3-a^3}{3(b-a)}-frac{b^3-a^3}{3(b-a)}-frac{(a+b)^2}{4}=frac{a^2+ab+b^2}{3}-frac{a^2+2ab+b^2}{4}=\ =frac{a^2-2ab+b^2}{12}=frac{(b-a)^2}{12} end{gather*} СКО: $$ sigma(x)=sqrt{D(x)}=frac{b-a}{2sqrt{3}} $$

п.4. Таблица непрерывных распределений, их параметров и числовых характеристик

Название Принятое
обозначение		 Плотность
распределения		 Мат.
ожидание		 Дисперсия
Непрерывное равномерное (U(a,b)) begin{gather*} p(x)=frac{1}{b-a}\ xinleft[a;bright] end{gather*} (frac{a+b}{2}) (frac{(b-a)^2}{12})
Нормальное (Гаусса) (N(mu,sigma^2)) begin{gather*} p(x)=frac{1}{sqrt{2pisigma^2}}e^{-frac{(x-mu)^2}{2sigma^2}}\ xinmathbb{R} end{gather*} (mu) (sigma^2)
Экспоненциальное (Exp(lambda)) begin{gather*} p(x)=lambda e^{-lambda x}\ lambdagt 0, xgeq 0 end{gather*} (frac1lambda) (frac{1}{lambda^2})

п.5. Примеры

Пример 1. Непрерывная случайная величина x задана плотностью распределения: $$ p(x)= begin{cases} Ax^2, xin [0;2]\ 0, xnotin [0;2] end{cases} $$ Найдите множитель A, функцию распределения, мат. ожидание, дисперсию и СКО случайной величины x. Постройте графики плотности распределения и функции распределения. Чему равна вероятность, что случайная величина окажется в интервале (frac12leq xleq 1)?

Находим множитель A из условия нормировки: begin{gather*} int_{-infty}^{+infty}p(x)dx=int_{0}^{2}Ax^2dx=1\ Acdotfrac{x^3}{3}|_{0}^{2}=frac{A}{3}(2^3-0)=frac{8A}{3}=1Rightarrow A=frac38\ p(x)= begin{cases} frac38 x^2, xin [0;2]\ 0, xnotin [0;2] end{cases} end{gather*} График плотности распределения:
Пример 1
Функция распределения (F(x)) для (xlt 0) равна 0, для (xgt 2) равна 1.
Найдем (F(x)) в интервале (xinleft[0;2right]): begin{gather*} F(t)=int_{0}^{t}p(x)dx=frac38int_{0}^{t}x^2dx=frac38cdotfrac{x^3}{3}|_{0}^{t}=frac{t^3}{8}Rightarrow F(x)=frac{x^3}{8}\ F(x)= begin{cases} 0, xlt 0\ frac{x^3}{8}, xin [0;2]\ 1, xgt 2 end{cases} end{gather*} График функции распределения:
Пример 1
Найдем математическое ожидание: begin{gather*} M(x)=int_{-infty}^{+infty}xcdot p(x)dx=int_{0}^{2}xcdotfrac38 x^2dx=frac38int_{0}^{2}x^3dx=frac38cdotfrac{x^4}{4}|_{0}^{2}=frac{3}{32}cdot 2^4=1,5 end{gather*} Найдем дисперсию: begin{gather*} D(x)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=int_{0}^{2}x^2cdotfrac38 x^2dx-1,5^2=frac38int_{0}^{2}x^4dx-1,5^2=\ =frac38cdotfrac{x^5}{5}|_{0}^{2}-1,5^2=frac{3}{40}cdot 2^5-1,5^2=2,4-2,25=0,15 end{gather*} Найдем СКО: $$ sigma(x)=sqrt{D(x)}=sqrt{0,15}approx 0,387 $$ Вероятность для x оказаться в интервале (frac12leq xleq 1) равна: $$ Pleft(frac12leq xleq 1right)=F(1)-Fleft(frac12right)=frac{1^3}{8}-frac{left(frac12right)^3}{8}=frac{7}{64} $$

Пример 2. Непрерывная случайная величина x задана функцией распределения: $$ F(x)= begin{cases} 0, xlt c\ frac{(x+2)^2}{4}, cleq xleq d\ 1, xgt d end{cases} $$ Найдите границы интервала c и d, плотность распределения, мат. ожидание, дисперсию и СКО случайной величины x. Постройте графики плотности распределения и функции распределения. Чему равна вероятность, что случайная величина окажется в интервале (-1leq xleq -frac12)

Границы интервала ищем из условий: begin{gather*} F(c)=frac{(c+2)^2}{4}=0Rightarrow c=-2\ F(d)=frac{(d+2)^2}{4}=1Rightarrow d=0 end{gather*} Получаем: begin{gather*} F(x)= begin{cases} 0, xlt -2\ frac{(x+2)^2}{4}, -2leq xleq 0\ 1, xgt 0 end{cases} end{gather*} График функции распределения:
Пример 2
Плотность распределения равна производной от функции распределения: $$ p(x)=F'(x) $$ Для (xlt -2cup xgt 0) получим (p(x)=0), т.к. производная от постоянной равна 0.
На значащем интервале: $$ p(x)=left(frac{(x+2)^2}{4}right)=frac{2(x+2)}{4}=frac{x+2}{2} $$ Получаем: begin{gather*} p(x)= begin{cases} frac{x+2}{2}, -2leq xleq 0\ 0, xlt -2cup xgt 0 end{cases} end{gather*} График плотности распределения:
Пример 2
Найдем математическое ожидание: begin{gather*} M(x)=int_{-infty}^{+infty}xcdot p(x)dx=int_{-2}^{0}xcdotfrac{x+2}{2}dx=frac12int_{-2}^{0}(x^2+2x)dx=frac12cdotleft(frac{x^3}{3}+x^2right)|_{-2}^{0}=\ =frac12left(0-left(frac{-8}{3}+4right)right)=-frac23 end{gather*} Найдем дисперсию: begin{gather*} D(x)=int_{-infty}^{+infty}x^2cdot p(x)dx-M^2(x)=int_{-2}^{0}x^2cdotfrac{x+2}{2}dx-left(-frac23right)^2=\ =frac12int_{-2}^{0}(x^3+2x^2)dx-frac49=frac12cdotleft(frac{x^4}{4}+frac{2x^3}{3}right)|_{-2}^{0}-frac49=frac12left(0-left(frac{16}{4}-frac{2cdot 8}{3}right)right)-frac49=\ =frac23-frac49=frac29 end{gather*} Найдем СКО: $$ sigma(x)=sqrt{D(x)}=frac{sqrt{2}}{3} $$ Вероятность для x оказаться в интервале (-1leq xleq -frac12) равна: $$ Pleft(-1leq xleq -frac12right)=Fleft(-frac12right)-F(-1)=frac{left(-frac12+2right)^2}{4}-frac{(-1+2)^2}{4}=frac{1,5^2-1^2}{4}=frac{9}{16} $$

Источник

Добавить комментарий