На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
Для записи неравенств используют знаки > , < , ≥ , ≤ .
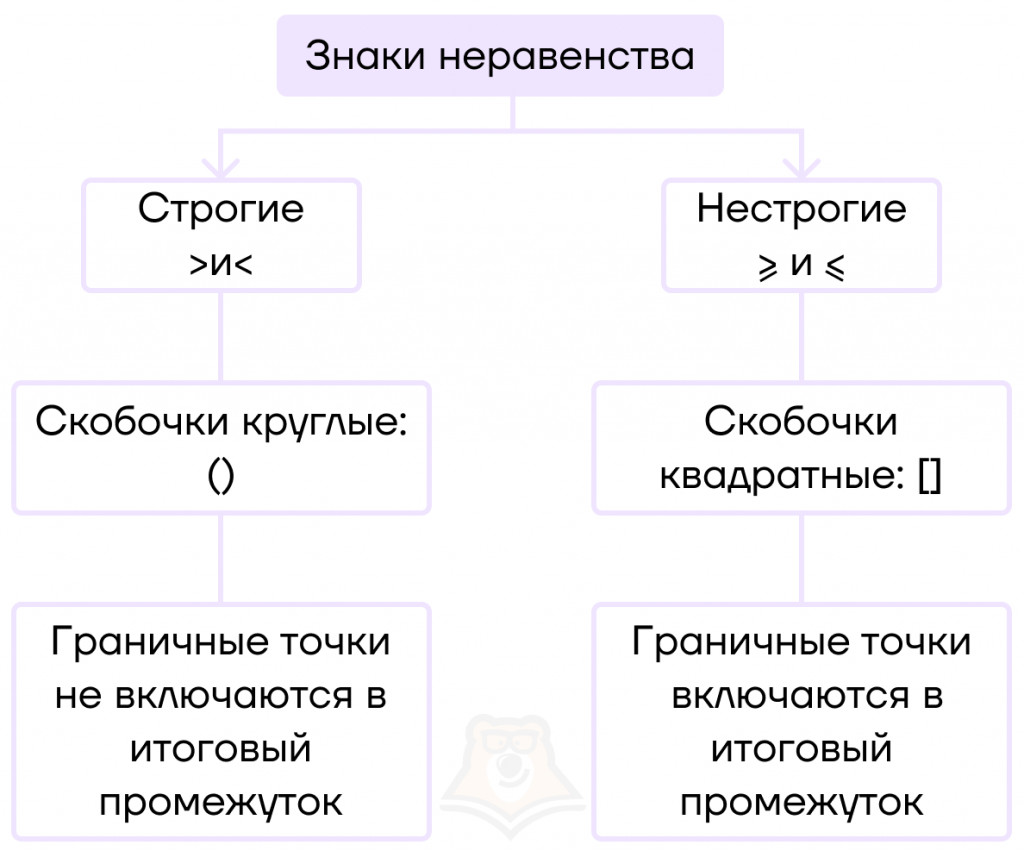
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
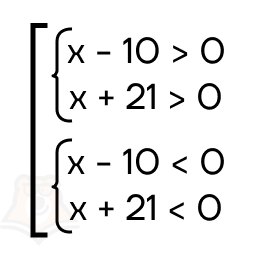
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
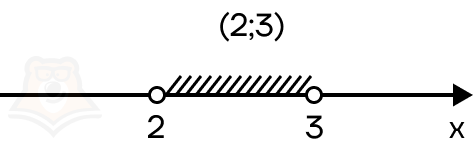
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
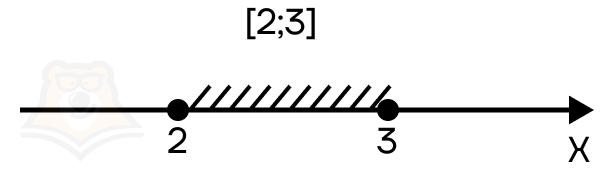
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
В случае сомнений мы всегда можем проверить себя по простой схеме.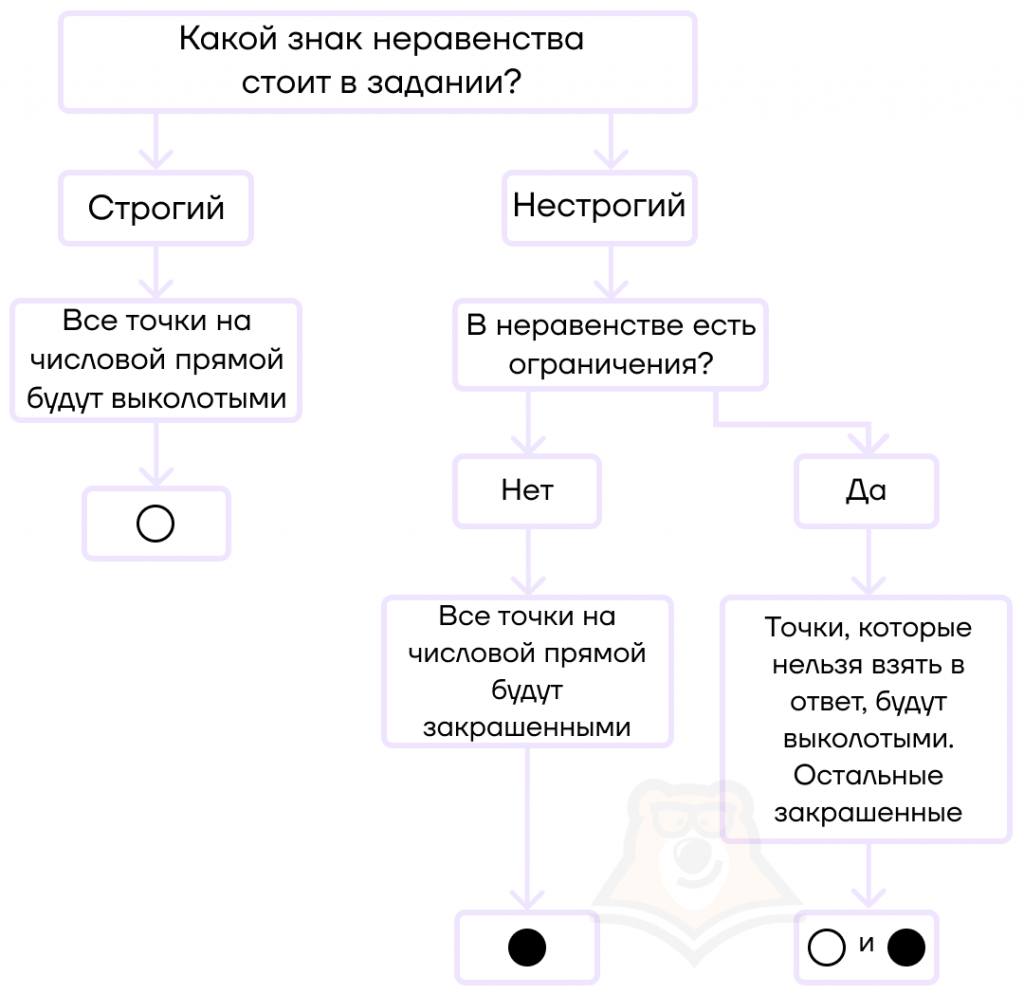
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков. 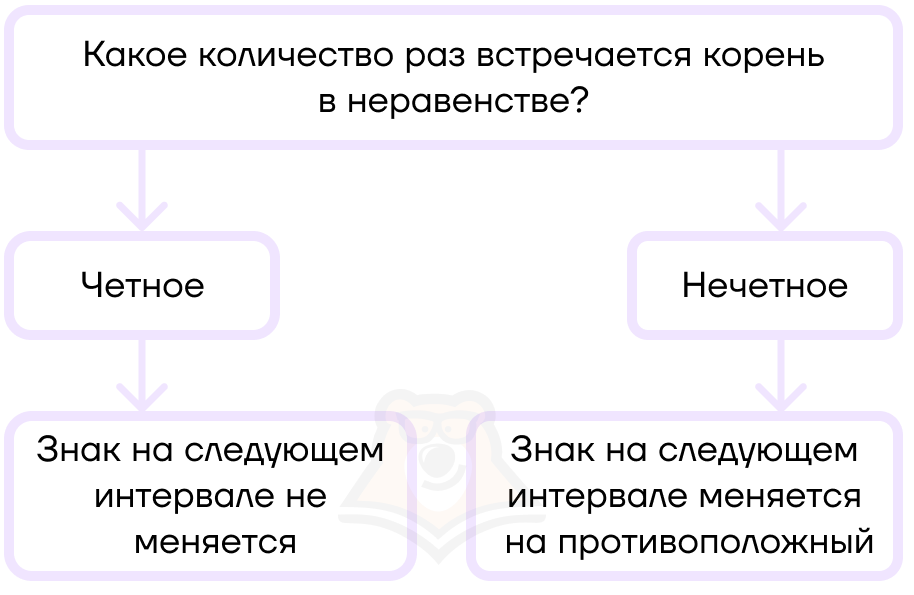
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
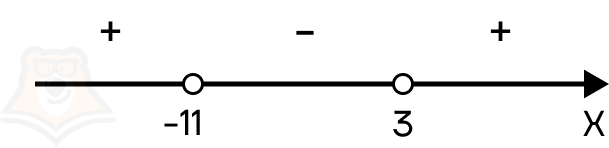
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.
Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.
Виды числовых промежутков
На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.
Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.
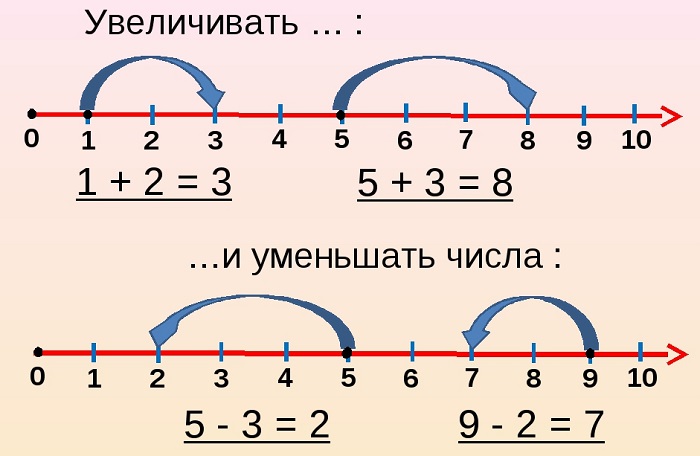
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.
На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.
Открытый числовой луч
Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.
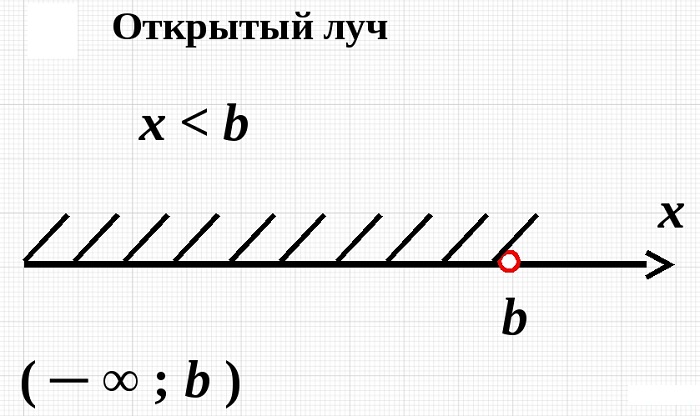
Точки расположены по одну сторону от определенной переменной, признанной началом координат.
Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:
-
(-∞; А);
-
(А; +∞).
Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».
Также можно охарактеризовать неравенством:
-
х < А;
-
х > А.
Знак зависит от расположения луча относительно А.
Замкнутый числовой луч
Замкнутый луч отличается от открытого тем, что к множеству относится А.

Также ему соответствует условие:
-
х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
-
х ≥ А (значение больше или равно А) или [А; +∞).
При графическом изображении А в этом случае закрашивается, на рисунке она черная.
Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.
Числовой отрезок
Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.
При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.
Обозначается отрезок, например, -7 ≤ х ≤ 3. Запись читается следующим образом: «отрезок от минус семи до трех».
Интервал
Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.
Обозначается, например, 5 < х < 13. Читается запись как «интервал от пяти до тринадцати».
Полуинтервал
Полуинтервал – интервал, при этом одна из точек, его ограничивающих, входит в него. То есть он закрыт с одной стороны. При этом неважно, какая из границ будет принадлежать интервалу, а какая нет.
Обозначаются с помощью двойных неравенств, при этом они называются нестрогими, так как используются знаки «больше или равно» или «меньше или равно». Одна из точек на графике не будет закрашена.
Обозначение может выглядеть, например, так -2 ≤ х < 9, «полуинтервал от минус двух до девяти».
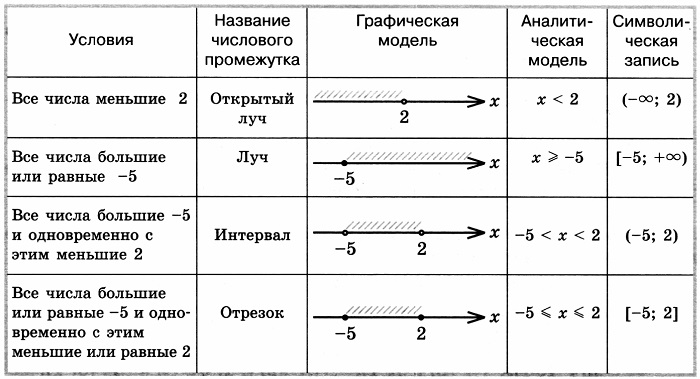
Таблица числовых промежутков
Все промежутки имеют обозначения и неравенства. Данные об этом собраны в таблице. Каждому виду соответствует графическое изображение.
Наглядное изображение поможет восприятию и закреплению материала.

Границы представлены а и b, они так и называются, граничными точками. При этом знаки ≥ и ≤ обозначаются квадратной скобкой. При графическом изображении такая граница закрашивается, это означает, что она входит в множество. Строгие неравенства соответствуют выколотым точкам на графиках.
Промежутки знакомят школьников с простыми неравенствами, строгими и нестрогими, которые необходимы для решения сложных математических задач.
Как вы уже знаете, любое число можно
отметить точкой на координатной прямой. Верно и обратное утверждение: каждой
точке на координатной прямой соответствует какое-то число.
Также на координатной прямой можно
отметить и множество чисел х, удовлетворяющих любому неравенству. Такое
множество называют числовым промежутком. И в зависимости
от типа неравенства выделяют виды числовых промежутков, которые имеют свои
названия, обозначения и изображения на координатной прямой.
Вспомним типы неравенств.
Рассмотрим виды числовых промежутков
на конкретных примерах.
Пусть есть два числа: и
.
Множество всех чисел,
удовлетворяющих условию называют интервалом.
Множество всех чисел,
удовлетворяющих условию называют числовым
отрезком.
Множества чисел , для которых
выполняются двойные неравенства или
, называют полуинтервалами.
На экране вы видите, как изображают
такие полуинтервалы на координатной прямой.
Как вы уже знаете, множество
действительных чисел изображается всей координатной прямой. Его называют числовой
прямой и обозначают так:
Рассмотрим другие виды числовых
промежутков.
Множество чисел, удовлетворяющих
условию называют числовым
лучом.
Множество чисел, удовлетворяющих
условию называют числовым
лучом.
Множества чисел, удовлетворяющих
условиям или
называют открытым
числовым лучом.
Заметим, что в обоих случаях число 3
не входит в множества.
Числовые отрезки, интервалы, полуинтервалы,
числовые лучи и открытые числовые лучи называют числовыми промежутками.
Замечание: Если
граничная точка в промежуток не входит, то на координатной прямой её изображают
пустой точкой и в обозначении промежутка её выделяют круглой скобкой. Если же
граничная точка входит в промежуток, то на координатной прямой её изображают
закрашенной точкой и в обозначении промежутка выделяют квадратной скобкой.
Запишем обозначения числовых
промежутков, их названия и изображение на координатной прямой для произвольных
чисел и
.
Задание: изобразить на
координатной прямой множество чисел, удовлетворяющих неравенствам, и записать
решение числовым промежутком.
Решение:
Задание: найдём все
целые числа, удовлетворяющие неравенствам.
Решение:
Имея представления о числовых
промежутках можно находить их пересечение и объединение.
Например: найдём
пересечение и объединение числовых промежутков:
Решение:
Итоги:
Интервал – это множество чисел,
удовлетворяющих условию 𝑎<𝒙<𝑏.
Отрезок – это множество чисел,
удовлетворяющих условию 𝑎≤𝒙≤𝑏.
Полуинтервал – это множество чисел,
удовлетворяющих условиям 𝑎≤𝒙<𝑏 или 𝑎<𝒙≤𝑏.
Числовой луч – это множество чисел,
удовлетворяющих условиям 𝒙≥𝑎 или 𝒙≤𝑎.
Открытый луч – это множество чисел,
удовлетворяющих условиям 𝒙>𝑎 или 𝒙<𝑎.
Числовые промежутки
- Виды числовых промежутков
- Открытый и замкнутый луч
- Отрезок
- Интервал и полуинтервал
Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.
Виды числовых промежутков
| Название | Изображение | Неравенство | Обозначение |
|---|---|---|---|
| Открытый луч |  |
x > a | (a; +∞) |
 |
x < a | (-∞; a) | |
| Замкнутый луч |  |
x ⩾ a | [a; +∞) |
 |
x ⩽ a | (-∞; a] | |
| Отрезок |  |
a ⩽ x ⩽ b | [a; b] |
| Интервал |  |
a < x < b | (a; b) |
| Полуинтервал |  |
a < x ⩽ b | (a; b] |
 |
a ⩽ x < b | [a; b) |
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Открытый и замкнутый луч
Открытый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, которая не входит в данное множество. Открытым луч называется именно из-за граничной точки, которая ему не принадлежит.
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:

Такое множество можно задать неравенством x > 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности
.
Множество, которому соответствует неравенство x < 2, можно обозначить (-∞; 2) или изобразить в виде луча, все точки которого лежат с левой стороны от точки 2:

Замкнутый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, принадлежащей данному множеству. На чертежах граничные точки, принадлежащие рассматриваемому множеству, обозначаются закрашенным кругом.
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:

Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности
и числовой луч от минус бесконечности до двух
. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх
.
Интервал и полуинтервал
Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 < x < 3 или обозначить (-2; 3). Такая запись читается так: интервал от минус двух до трёх
.
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:

Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3
, и полуинтервал от минус двух до трёх, включая минус два
.
Числовые промежутки. Пересечение и объединение числовых промежутков
Отметим на координатной прямой точки с координатами -3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше -3 и меньше 2. Верно и обратное: если число х удовлетворяет условию -3<x<2 , то оно изображается точкой, лежащей между точками с координатами -3 и 2.
Множество всех чисел, удовлетворяющих условию -3<x<2, называется числовым промежутком или просто промежутком от -3 до 2 и обозначается так: (-3;2).
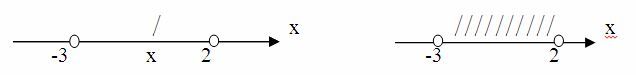
На рисунках изображены множество чисел х, для которых выполняется неравенство х<10 и х≤10. Эти множества представляют собой промежутки, обозначаемые соответственно (-∞; 10) и (-∞; 10]. Читается так: число х принадлежит промежутку от минус бесконечности (-∞) до 10 (х<10) и число х принадлежит промежутку от минус бесконечности (-∞) до 10, включая число 10 (х≤10). Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В. Промежуток [3;5] является пересечением промежутков [-1;5] и [3;7]. Это можно записать так: [-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.
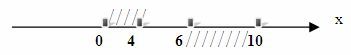
Объединение числовых промежутков
Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим.
Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают AB.
Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так:
![]()
Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество не является промежутком.
![]()
- Числовым промежутком называется множество всех чисел, удовлетворяющих неравенству.
- Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.
- Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В.
- Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают .
Вопросы к конспектам
Найдите объединение промежутков [-5; 9] и [7; 12]
Найдите пересечение отрезков [-3;5] и [-1;9]
Запишите двойное неравенство -2 < y ≤ 0 в виде промежутка:
Количество целых решений неравенства: 10 < x ≤ 14
Найдите разницу наибольшего и наименьшего целых чисел в промежутке [-10;8)
Числовой промежуток, удовлетворяющий неравенству: х ≥ -2
