| … (выделенный фрагмент повторяется бесконечно) |
| i−3 = i |
| i−2 = −1 |
| i−1 = −i |
| i0 = 1 |
| i1 = i |
| i2 = −1 |
| i3 = −i |
| i4 = 1 |
| i5 = i |
| i6 = −1 |
| in = im где m ≡ n mod 4 |
Чи́сто мни́мое число́ — комплексное число с нулевой действительной частью. Иногда только такие числа называются мнимыми числами, но этот термин также используется для обозначения произвольных комплексных чисел с ненулевой мнимой частью[1]. Термин «мнимое число» предложил в XVII веке французский математик Рене Декарт[2], изначально этот термин носил уничижительный смысл, поскольку такие числа считались вымышленными или бесполезными, и лишь после работ Леонарда Эйлера и Карла Гаусса это понятие получило признание в научном сообществе.
Определения[править | править код]
Пусть 







История[править | править код]

Размещение мнимых чисел на комплексной плоскости. Мнимые числа расположены на вертикальной оси.
Впервые мнимые числа упоминает в своих трудах древнегреческий математик и инженер Герон Александрийский[3][4], но правила осуществления арифметических операций (в частности, умножения) над ними ввёл Рафаэль Бомбелли в 1572 году. Концепция Бомбелли появилась раньше аналогичных работ Джероламо Кардано. В XVI—XVII веках мнимые числа рассматривались большей частью научного сообщества как фиктивные или бесполезные (аналогично тому, как воспринималось в свое время понятие нуля). В частности, Рене Декарт, упоминая о мнимых числах в своём фундаментальном труде «Геометрия», использовал термин «мнимый» в уничижительном смысле[5][6]. Использование мнимых чисел не было широко распространено до появления работ Леонарда Эйлера (1707—1783) и Карла Фридриха Гаусса (1777—1855). Геометрическое значение комплексных чисел как точек на плоскости было впервые описано Каспаром Весселем (1745—1818)[7].
В 1843 году ирландский математик Уильям Гамильтон расширил идею оси мнимых чисел на плоскости до четырёхмерного пространства кватернионов, в котором три измерения аналогичны мнимым числам в комплексном поле.
С развитием в теории факторколец концепции кольца многочленов понятие мнимого числа стало более содержательным и получило дальнейшее развитие в понятии j — бикомплексных чисел[en], у которых квадрат равен +1. Эта идея появилась в статье английского математика Джеймса Кокла[en] 1848 года[8].
Геометрическая интерпретация[править | править код]

Поворот на 90 градусов на комплексной плоскости
На плоскости комплексных чисел мнимые числа находятся на вертикальной оси, перпендикулярной оси действительных чисел. Один из способов геометрической интерпретации мнимых чисел — рассмотреть стандартную числовую ось, где положительные числа находятся справа, а отрицательные — слева. Через точку 0 на оси x может быть проведена ось y с «положительным» направлением, идущим вверх; «положительные» мнимые числа увеличиваются по величине вверх, а «отрицательные» мнимые числа увеличиваются по величине вниз. Эта вертикальная ось часто называется «мнимой осью» и обозначается iℝ,
В этом представлении умножение на –1 соответствует повороту на 180 градусов относительно начала координат. Умножение на i соответствует повороту на 90 градусов в «положительном» направлении (то есть против часовой стрелки), а уравнение i2 = −1 интерпретируется как говорящее о том, что если мы применим два поворота на 90 градусов относительно начала координат, результатом будет один поворот на 180 градусов. При этом поворот на 90 градусов в «отрицательном» направлении (то есть по часовой стрелке) также удовлетворяет этой интерпретации. Это отражает тот факт, что −i также является решением уравнения x2 = −1. Как правило, умножение на комплексное число аналогично вращению вокруг начала координат аргумента[en] комплексного числа с последующим масштабированием по его величине.
Квадратные корни из отрицательных чисел[править | править код]
Необходимо соблюдать осторожность при работе с мнимыми числами, являющимися главными значениями[en] квадратных корней отрицательных чисел. Например, такой математический софизм:
[9]
Иногда это записывается так:
Подобный математический софизм возникает в случае, когда в равенстве 
где и x и y — неотрицательные действительные числа.
См. также[править | править код]
- Вещественное число
- Мнимая единица
- Формула Муавра
Примечания[править | править код]
- ↑ Комплексное число // «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — : «Советская энциклопедия», 1982. — Т. 3. — С. 708. — 1183 с. — (51[03] М34).
- ↑ Giaquinta, Mariano; Modica, Giuseppe. Mathematical Analysis: Approximation and Discrete Processes (англ.). — illustrated. — Springer Science & Business Media, 2004. — P. 121. — ISBN 978-0-8176-4337-9. Extract of page 121
- ↑ Hargittai, István. Fivefold symmetry (неопр.). — 2nd. — World Scientific, 1992. — С. 153. — ISBN 981-02-0600-3.
- ↑ Roy, Stephen Campbell. Complex numbers: lattice simulation and zeta function applications (англ.). — Horwood, 2007. — P. 1. — ISBN 1-904275-25-7.
- ↑ René Descartes, Discourse de la Méthode … (Leiden, (Netherlands): Jan Maire, 1637), цитируемая книга: Геометрия, книга 3, p. 380. From page 380: «Au reste tant les vrayes racines que les fausses ne sont pas tousjours reelles; mais quelquefois seulement imaginaires; c’est a dire qu’on peut bien tousjours en imaginer autant que jay dit en chasque Equation; mais qu’il n’y a quelquefois aucune quantité, qui corresponde a celles qu’on imagine, comme encore qu’on en puisse imaginer trois en celle cy, x3 — 6xx + 13x — 10 = 0, il n’y en a toutefois qu’une reelle, qui est 2, & pour les deux autres, quoy qu’on les augmente, ou diminue, ou multiplie en la façon que je viens d’expliquer, on ne sçauroit les rendre autres qu’imaginaires.» («Более того, как истинные корни, так и ложные [корни] не всегда реальны; но иногда имеются только мнимые [числа]; то есть, в каждом уравнении всегда можно представить их столько, сколько я сказал; но иногда нет такой величины, которая соответствует тому, что можно себе представить, точно так же, как в этом [уравнении], x3 — 6xx + 13x — 10 = 0, где только один корень реальный и равен 2, а в отношении двух других, хотя одно увеличивает, или уменьшает, или умножает их так, как я только что объяснил, никто не сможет сделать их отличными от мнимых [величин].»)
- ↑ Martinez, Albert A. (2006), Negative Math: How Mathematical Rules Can Be Positively Bent, Princeton: Princeton University Press, ISBN 0-691-12309-8.
- ↑ Rozenfeld, Boris Abramovich. Chapter 10 // A history of non-euclidean geometry: evolution of the concept of a geometric space (англ.). — Springer, 1988. — P. 382. — ISBN 0-387-96458-4.
- ↑ Cockle, James (1848) «On Certain Functions Resembling Quaternions and on a New Imaginary in Algebra», London-Dublin-Edinburgh Philosophical Magazine, series 3, 33:435-9 and Cockle (1849) «On a New Imaginary in Algebra», Philosophical Magazine 34:37-47
- ↑ Nahin, Paul J. An Imaginary Tale: The Story of “i” [the square root of minus one] (англ.). — Princeton University Press, 2010. — P. 12. — ISBN 978-1-4008-3029-9. Extract of page 12
Литература[править | править код]
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. — М.: Физматлит, 2003. — Т. 2. — 810 с.
- Nahin, Paul. An Imaginary Tale: the Story of the Square Root of −1 (англ.). — Princeton: Princeton University Press, 1998. — ISBN 0-691-02795-1.
Ссылки[править | править код]
- How can one show that imaginary numbers really do exist? (англ.)
- In our time: Imaginary numbers (англ.)
- 5Numbers programme 4 (англ.)
- Why Use Imaginary Numbers? (англ.)
Развитие понятия числа является
важнейшей сквозной методико-содержательной
линией школьного курса математики, проходящий в
той или иной степени через все классы средней
школы. В приложении «Математика» неоднократно
публиковались статьи о методике изучения
различных числовых систем в школе. В частности, в
1995–96 гг. были опубликованы три лекции академика
РАО, профессора Г. Глейзера:
Лекция 1. Натуральные числа,
1995, № 47.
Лекция 2. Рациональные числа, 1995, № 48.
Лекция 3. Действительные числа, 1996, № 3.
Публикуемая ниже статья завершает цикл этих
лекций.
Введение
Начнем с нескольких
напоминаний.
Одна из причин введения
рациональных чисел обусловлена требованием,
чтобы всякое линейное уравнение ax = b (где a № 0) было
разрешимо. В области целых чисел линейное
уравнение разрешимо лишь в том случае, когда b
делится нацело на a.
Одна из причин расширения
множества рациональных чисел до множества
действительных чисел была связана с
разрешимостью квадратных уравнений, например,
уравнения вида x2 = 2. На множестве
рациональных чисел это уравнение не разрешимо,
так как среди рациональных нет числа, квадрат
которого равен двум. Как известно, ![]() – число иррациональное. На
– число иррациональное. На
множестве же действительных чисел уравнение x2
= 2 разрешимо, оно имеет два решения x1 = ![]() и x2 = –
и x2 = – ![]() .
.
И все же нельзя считать, что на
множестве действительных чисел разрешимы все
квадратные уравнения. Например, квадратное
уравнение x2 = – 1 на множестве
действительных чисел решений не имеет, так как
среди действительных чисел нет такого числа,
квадрат которого отрицателен.
Таким образом, действительных
чисел явно недостаточно, чтобы построить такую
теорию квадратных уравнений, в рамках которой
каждое квадратное уравнение было бы разрешимо.
Это соображение приводит к необходимости
вводить новые числа и расширять множество
действительных чисел до множества комплексных
чисел, в котором было бы разрешимо любое
квадратное уравнение.
Вспомним о едином принципе
расширения числовых систем и поступим в
соответствии с этим принципом.
Если множество А расширяется
до множества В, то должны быть выполнены
следующие условия:
1. Множество А есть
подмножество В.
2. Отношения элементов множества А (в частности,
операции над ними) определяются также и для
элементов множества В; смысл этих отношений для
элементов множества А, рассматриваемых уже как
элементы множества В, должен совпадать с тем,
какой они имели в А до расширения.
3. В множестве В должна выполняться операция,
которая в А была невыполнима или не всегда
выполнима.
4. Расширение В должно быть минимальным из всех
расширений данного множества А, обладающих
первыми тремя свойствами, причем это расширение
В должно определяться множеством А однозначно (с
точностью до изоморфизма).
Итак, расширяя множество
действительных чисел до множества новых чисел,
названных комплексными, необходимо, чтобы:
а) комплексные числа
подчинялись основным свойствам действительных
чисел, в частности, коммутативному,
ассоциативному и дистрибутивному законам;
б) в новом числовом множестве были разрешимы
любые квадратные уравнения.
Множество действительных
чисел недостаточно обширно, чтобы в нем были бы
разрешимы все квадратные уравнения. Поэтому,
расширяя множество действительных чисел до
множества комплексных чисел, мы потребуем, чтобы
в нем можно было бы построить полную и
законченную теорию квадратных уравнений.
Другими словами, мы расширим множество
действительных чисел до такого множества, в
котором можно будет решить любое квадратное
уравнение. Так, уравнение x2 = – 1 не имеет
решений во множестве действительных чисел
потому, что квадрат действительного числа не
может быть отрицательным. В новом числовом
множестве оно должно иметь решение. Для этого
вводится такой специальный символ i, называемый
мнимой единицей, квадрат которого равен – 1.
Ниже будет показано, что
введение этого символа позволит осуществить
расширение множества действительных чисел,
пополнив его мнимыми числами вида bi (где b –
действительное число) таким образом, чтобы в
новом числовом множестве (множестве комплексных
чисел) при сохранении основных законов
действительных чисел были разрешимы любые
квадратные уравнения.
Основные
определения. Операции над комплексными числами
1. Существует элемент i (мнимая
единица) такой, что i2 = – 1.
2. Символ a + bi называют
комплексным числом с действительной частью a и
мнимой частью bi, где a и b – действительные числа, b
– коэффициент мнимой части.
Комплексное число a + 0i
отождествляется с действительным числом a, т.е. a +
0i = a, в частности, 0 + 0i = 0. Числа вида bi (b № 0) называют чисто
мнимыми.
Например, комплексное число 2 +
3i имеет действительную часть – действительное
число 2 и мнимую часть 3i, действительное число 3 –
коэффициент мнимой части.
Комплексное число 2 – 3i имеет
действительную часть число 2, мнимую часть – 3i,
число – 3 – коэффициент при мнимой части.
3. Правило равенства. Два
комплексных числа равны тогда и только тогда,
когда равны их действительные части и равны
коэффициенты мнимых частей.
Т.е., если a + bi = c +di, то a = c, b = d: и,
обратно, если a = c, b = d, то a + bi = c +di.
4. Правило сложения и
вычитания комплексных чисел.
(a + bi) + (c + di) = (a + c) + (b +
d)i.
Например:
(2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i
= 7 + 4i;
(– 2 + 3i) + (1 – 8i) = (– 2 + 1)
+ (3 + (– 8))i = – 1 – 5i;
(– 2 + 3i) + (1 – 3i) = (– 2 + 1)
+ (3 + (– 3))i =
= – 1 + 0i = – 1.
Вычитание комплексных чисел
определяется как операция, обратная сложению, и
выполняется по формуле:
(a + bi) – (c + di) = (a – c) + (b
– d)i.
Например:
(5 – 8i) – (2 + 3i) = (3 – 2) +
(– 8 – 3)i = 1 – 11i;
(3 – 2i) – (1 – 2i) = (3 – 1) +
((– 2) – (– 2))i = 2 + 0i = 2.
5. Правило умножения
комплексных чисел.
(a + bi)(c + di) = (aс + bd) + (ad +
bc)i.
Из определений 4 и 5 следует,
что операции сложения, вычитания и умножения над
комплексными числами осуществляются так, как
будто мы выполняем операции над многочленами,
однако с условием, что i2 = – 1.
Действительно: (a + bi)(c + di) = ac + adi
+ bdi2 = (ac – bd) + (ad + bc)i.
Например, (– 1 + 3i)(2 + 5i) = – 2 – 5i +
6i + 15i2 = – 2 – 5i + 6i – 15 = – 17 + i; (2 + 3i)(2 – 3i) = 4
– 6i + 6i – 9i2 = 4 + 9 = 13.
Из второго примера следует,
что результатом сложения, вычитания,
произведения двух комплексных чисел может быть
число действительное. В частности, при умножении
двух комплексных чисел a + bi и a – bi, называемых
сопряженными комплексными числами, в результате
получается действительное число, равное сумме
квадратов действительной части и коэффициента
при мнимой части. Действительно:
(a + bi)(a – bi) = a2 –
abi + abi – b2i2 = a2 + b2.
Произведение двух чисто
мнимых чисел – действительное число.
Например: 5i•3i = 15i2 = –
15; – 2i•3i = – 6i2 = 6, и вообще bi•di = bdi2
= – bd.
6. Деление комплексного числа a
+ bi на комплексное число c + di № 0 определяется как операция
обратная умножению и выполняется по формуле:
![]() .
.
Формула теряет смысл, если c + di
= 0, так как тогда c2 + d2 = 0, т. е. деление
на нуль и во множестве комплексных чисел
исключается.
Обычно деление комплексных
чисел выполняют путем умножения делимого и
делителя на число, сопряженное делителю.
Например,
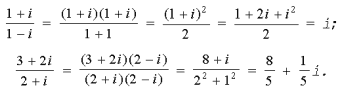
Опираясь на введенные
определения нетрудно проверить, что для
комплексных чисел справедливы коммутативный,
ассоциативный и дистрибудивный законы. Кроме
того, применение операций сложения, умножения,
вычитания и деления к двум комплексным числам
снова приводит к комплексным числам. Тем самым
можно утверждать, что множество комплексных
чисел образует поле. При этом, так как
комплексное число a + bi при b = 0 отождествляется с
действительным числом a = a + 0i, то поле комплексных
чисел включает поле действительных чисел в
качестве подмножества.
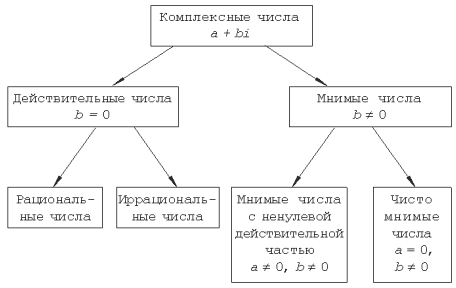
Приведем классификацию
комплексных чисел:
Решение квадратных
уравнений
Одна из причин введения
комплексных чисел состояла в том, чтобы добиться
разрешимости любого квадратного уравнения, в
частности уравнения
x2 = – 1.
Покажем, что расширив поле
действительных чисел до поля комплексных чисел,
мы получили поле, в котором каждое квадратное
уравнение разрешимо, т.е. имеет решение. Так,
уравнение x2 = – 1 имеет два решения: x1
= i, x2 = – i.
Это нетрудно установить
проверкой: i•i = i2 = – 1, (– i)•(– i) = i2
= – 1.
Перейдем теперь к вопросу о
решении полного квадратного уравнения.
Квадратным уравнением называют уравнение вида:
ax2 + bx + c = 0 (a № 0),
где x – неизвестная, a, b, c –
действительные числа, соответственно первый,
второй коэффициенты и свободный член, причем a № 0. Решим это
уравнение, выполнив над ним ряд несложных
преобразований.
· Разделим все члены
уравнения на a № 0 и перенесем свободный член в
правую часть уравнения: ![]()
Теперь можно исследовать
полученное решение. Оно зависит от значения
подкоренного выражения, называемого
дискриминантом квадратного уравнения. Если b2
– 4ac > 0, то ![]()
есть действительное число и квадратное
уравнение имеет действительные корни. Если же ![]() – мнимое число,
– мнимое число,
квадратное уравнение имеет мнимые корни.
Результаты
исследования представлены ниже в таблице:

Итак, введение комплексных
чисел позволяет разработать полную теорию
квадратных уравнений. В поле комплексных чисел
разрешимо любое квадратное уравнение.
Примеры.
1. Решите уравнение x2 – 2x
– 8 = 0.
Решение. Найдем
дискриминант D = b2 – 4ac = (– 2)2 –
4•1•(– 8) = 36 > 0.
Уравнение имеет два
действительных корня: 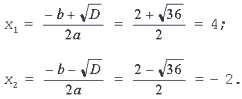
2. Решите уравнение x2 + 6x +
9 = 0.
Решение. D = 62 – 4•1•9 = 0,
уравнение имеет два равных действительных корня:
![]()
3. Решите уравнение x2 – 4x
+ 5 = 0.
Решение. D = 16 – 4•1•5 = – 4 < 0,
уравнение имеет мнимые корни: 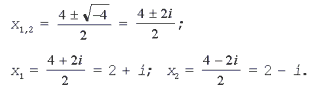
Геометрическая
интерпретация комплексных чисел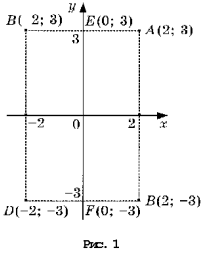
Известно, что отрицательные
числа были введены в связи с решением линейных
уравнений с одной переменной. В конкретных
задачах отрицательный ответ истолковывался как
значение направленной величины (положительные и
отрицательные температуры, передвижения в
противоположных направлениях, прибыль и долг и
т.п.). Однако еще в ХVI веке многие математики не
признавали отрицательных чисел. Только с
введением координатной прямой и координатной
плоскости отчетливо проявился смысл
отрицательных чисел, и они стали такими же
«равноправными» и понятными, как и натуральные
числа. Аналогично обстоит дело с комплексными
числами. Смысл их отчетливо проявляется при
введении их геометрической интерпретации.
 Геометрическая
Геометрическая
интерпретация комплексных чисел состоит в том,
что каждому комплексному числу z = x + yi ставится в
соответствие точка (x, y) координатной плоскости
таким образом, что действительная часть
комплексного числа представляет собой абсциссу,
а коэффициент при мнимой части – ординату точки.
Таким образом,
устанавливается взаимно однозначное
соответствие между множеством комплексных чисел
и множеством точек координатной плоскости.
Подобным образом было установлено соответствие
между множеством действительных чисел и
множеством точек числовой прямой.
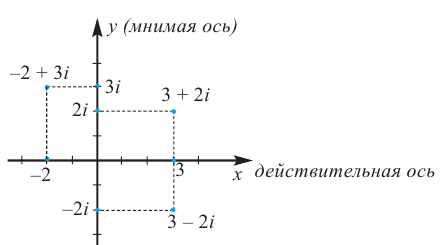
На рисунке 1 изображена
координатная плоскость. Числу 2 + 3i соответствует
точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3);
числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка
D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а
числу – 3i – точка F(0, – 3). Итак, каждому
комплексному числу соответствует единственная
точка координатной плоскости и, обратно, каждой
точке координатной плоскости соответствует
единственное комплексное число, при этом двум
различным комплексным числам соответствуют две
различные точки координатной плоскости. Ясно,
что действительным числам x + 0i соответствуют
точки оси абсцисс, а чисто мнимым числам 0 + yi, где y
№ 0 –
точки оси ординат. Поэтому ось Oy называют мнимой,
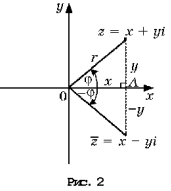
а ось Ox – действительной. Сопряженным
комплексным числам ![]() соответствуют точки, симметричные
соответствуют точки, симметричные
относительно оси абсцисс (рис. 2).
Тригонометрическая
форма комплексного числа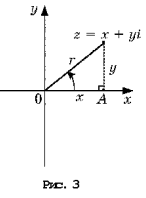
Точка координатной плоскости,
соответствующая комплексному числу z = x + yi, может
быть указана по-другому: ее координатами могут
быть расстояние r от начала координат и величина
угла j между положительной полуосью Ox и лучом Oz
(рис. 3).
Расстояние r от начала системы
координат до точки, соответствующей
комплексному числу z, называют модулем этого
числа. Тогда по теореме Пифагора (рис. 2)
имеем: r2 = x2 + y2 = (x + yi)(x – yi)
= z•z.
Отсюда найдем модуль
комплексного числа как арифметическое
(неотрицательное) значение корня: ![]()
Если комплексное число z
изображается точкой оси абсцисс (т.е. является
действительным числом), то его модуль совпадает с
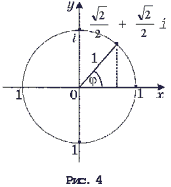
абсолютным значением. Все комплексные числа,
имеющие модуль 1, изображаются точками единичной
окружности – окружности с центром в начале
системы координат, радиуса 1 (рис. 4).
 Угол j между положительной полуосью Ox и
Угол j между положительной полуосью Ox и
лучом Oz называют аргументом комплексного числа z
= x + yi (рис. 3).
Сопряженные комплексные
числа ![]() имеют
имеют
один и тот же модуль ![]() и аргументы, отличающиеся знаком: j = – j.
и аргументы, отличающиеся знаком: j = – j.
В отличие от модуля аргумент
комплексного числа определяется неоднозначно.
Аргумент одного и того же комплексного числа
может иметь бесконечно много значений,
отличающихся друг от друга на число, кратное 360°.
Например, число z (рис. 3) имеет модуль r, аргумент
же этого числа может принимать значения j; j + 360°; j + 720°; j + 1080°; … или
значения j – 360°; j –720°; j – 1080°; … Данное значение модуля r и любое из
приведенных выше значений аргумента определяют
одну и ту же точку плоскости, соответствующую
числу z.
Пусть точке с координатами (x;
y) соответствует комплексное число z = x + yi. Запишем
это комплексное число через его модуль и
аргумент. Воспользуемся определением
тригонометрических функций синуса и косинуса
(рис. 3):
x = r cos j; y = r sin j.
Тогда число z выражается через
модуль и аргумент следующим образом: z = x + yi =
r(cos j + i sin
j).
Выражение z = r(cos j + i sin j) называют
тригонометрической формой комплексного числа, в
отличии от выражения z = x + yi, называемого
алгебраической формой комплексного числа.
Приведем примеры обращения
комплексных чисел из алгебраической формы в
тригонометрическую:
Для числа i имеем r = 1, j = 90°, поэтому
i = 1(cos 90° + i sin 90°);
Для числа – 1 имеем r = 1, j = 180°,
поэтому – 1 = 1(cos 180° + i sin 180°);
Для числа 1 + i имеем ![]() поэтому
поэтому ![]()
Для числа ![]() имеем r = 1, j = 45°, поэтому
имеем r = 1, j = 45°, поэтому ![]()
Для числа ![]() имеем r = 2, j = 120°, поэтому
имеем r = 2, j = 120°, поэтому ![]()
Справедливость приведенных
равенств нетрудно проверить путем подстановки в
их правой части числовых значений
тригонометрических функций. Итак, для того, чтобы
комплексное число, заданное в алгебраической
форме, обратить в тригонометрическую форму,
необходимо найти его модуль r и аргумент j,
пользуясь формулами:
![]()
Комплексные числа и
векторы
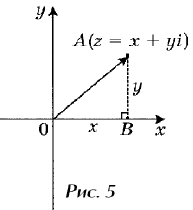 Существует и другой способ
Существует и другой способ
геометрической интерпретации комплексных чисел.
Каждой точке (x , y) координатной плоскости,
изображающей комплексное число
z = x + yi, соответствует единственный вектор,
отложенный от начала системы координат и обратно
(рис. 5). При этом двум различным точкам
координатной плоскости будут соответствовать
два таких различных вектора.
Таким образом, может быть
установлено взаимно однозначное соответствие
между множеством точек координатной плоскости
(комплексными числами) и множеством векторов,
отложенных от начала системы координат.
Если z = x + yi (рис. 5), то вектор![]() , отложенный от
, отложенный от
начала системы координат до точки, изображающей
число z, будет иметь координаты (x; y). Известно, что
равные векторы имеют равные координаты.
Итак, мы рассмотрели два
способа интерпретации комплексных чисел: их
можно изображать либо точками координатной
плоскости, либо векторами, отложенными от начала
системы координат. При этом любые два равных
вектора (имеющих одно и то же направление и
равные длины) изображают одно и то же комплексное
число, а векторы, отличные либо длиной, либо
направлением, изображают разные числа. На
рисунке 6 с помощью векторов изображены
различные комплексные числа: ![]() изображает число 2 + 0i;
изображает число 2 + 0i; ![]() – число – 3 + 0i;
– число – 3 + 0i;![]() – число 0 + i;
– число 0 + i; ![]() – число 0 + 2i;
– число 0 + 2i;![]() – число 0 – 3i;
– число 0 – 3i;![]() – число 3 + 2i;
– число 3 + 2i;![]() – число – 1 – 2i.
– число – 1 – 2i.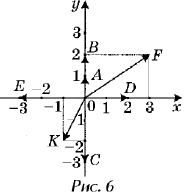
Ясно, что любой ненулевой
вектор, лежащий на оси Oy (или параллельный ей),
изображает чисто мнимое число yi, причем y > 0,
если направление вектора совпадает с
направлением оси, y < 0, если направление вектора
противоположно направлению оси. Вследствие
этого ось Oy называют мнимой. Все векторы, лежащие
на оси Ox (или параллельные ей) изображают
действительные числа, поэтому ее называют
действительной осью.
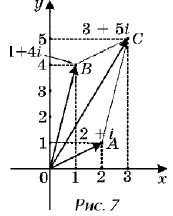
Векторная интерпретация
комплексных чисел позволяет уяснить
геометрический смысл операций над комплексными
числами. Например, сумма двух комплексных чисел 2
+ i и 1 + 4i равна 3 + 5i. Каждое из слагаемых изображает
соответствующий вектор, отложенный от начала O
координат (рис. 7):
![]() = 2 + i;
= 2 + i; ![]() = 1 + 4i.
= 1 + 4i.
Сумма этих векторов – вектор ![]() = 3 + 5i, изображается
= 3 + 5i, изображается
диагональю параллелограмма, построенного на
векторах и .
 Для того, чтобы лучше уяснить
Для того, чтобы лучше уяснить
себе геометрический смысл умножения двух
комплексных чисел, воспользуемся их
тригонометрической формой. Пусть векторы![]() изображают
изображают
соответственно комплексные числа:
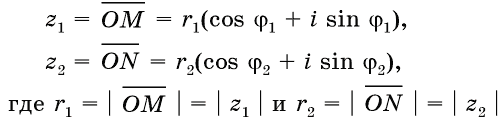
соответственно модули этих
чисел, а j1
и j2
– их аргументы. Найдем произведение этих чисел:
z1z2 = r1r2(cosj1 + i sin j1)(cos j2 + i sin j2) = r1r2(cos
j1cos
j2
– sin j1
sin j2)
+ i = (cos j1sin
j2 +
sin j1cos
j2).
 Воспользуемся известными из
Воспользуемся известными из
школы теоремами сложения синуса и косинуса:
cos j1cos j2 – sin j1 sin j2 = cos(j1 + j2);
cos j1sin j2 + sin j1cos j2 = sin(j1 + j2).
Тогда произведение данных
комплексных чисел равно комплексному числу:
z1z2 = r1r2(cos(j1 + j2) + isin(j1 + j2)).
Последнее соотношение
позволяет сформулировать правило умножения
комплексных чисел: при умножении двух
комплексных чисел их модули перемножаются, а их
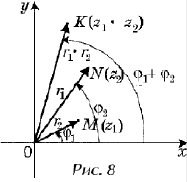
аргументы складываются. Это проиллюстрировано
на рисунке 8.
 Ясно, что произведение
Ясно, что произведение
комплексных чисел связано с поворотом
(вращением). Так, произведение z1z2
изображается вектором ![]() представляющим собой образ вектора
представляющим собой образ вектора ![]() , повернутого на
, повернутого на
угол j2
(или образ вектора ![]() , повернутого на угол j1), при этом модуль вектора
, повернутого на угол j1), при этом модуль вектора
равен произведению модулей данных векторов.
Связь произведения
комплексных чисел с вращением становится более
наглядной, если рассматривать произведение
различных комплексных чисел (векторов) на
комплексное число i, у которого модуль равен 1, а
аргумент 90°. Например, найдем произведение
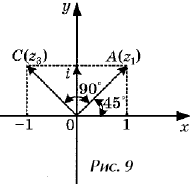
комплексных чисел z1 = 1 + i и z2 = i.
z = z1z2 = (1 +
i)i = i + i2 = – 1 + i.
Числа z1 и z2
соответственно изображают векторы и (рис.9). Мы
видим, что модуль комплексного числа z равен
модулю числа z1:
![]()
Аргумент же комплексного
числа z равен 45° + 90° = 135°, в то время, как аргумент
комплексного числа z1 равен 45°. Т.е. вектор ,
изображающий число z, есть образ вектора ,
изображающего число z1 при повороте на 90°.
Содержание:
Хроника возникновения комплексных чисел:

Исследование.
1) Подтвердите примерами справедливость следующих высказываний. Если высказывание ложно, то сделайте так, чтобы оно стало истинным.
- а) Если а и b – натуральные числа, то корень уравнения х + а = b также является натуральным числом.
- б) Если а и b -целые числа, то корень уравнения ах = b также является целым числом
- в) Если а неотрицательное рациональное число, то корень уравнения х1 = а также является рациональным числом.
- г) Если а неотрицательное действительное число, то корень уравнения х2 = а также является действительным числом.
2) Существует ли действительное число квадрат которого равен -1?
3)
- а) Существуют ли действительные корни уравнения х2 = а при
- б) Можно ли решить эту задачу расширив множество действительных чисел?
4) Существует ли однозначное соответствие между множеством действительных чисел и множеством точек на числовой оси? А какие числа соответствуют точкам на координатной плоскости?
На множестве действительных чисел уравнение х2 = -1 не имеет решений. Значит, мы должны расширить множество действительных чисел так, чтобы корни этого уравнения входили в него. Для этого введём новое число и примем, что оно является корнем уравнения х2 + 1 = 0, т.е. 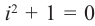 . Отсюда
. Отсюда 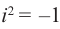 . После этого, корнями уравнения х2 + 1 = 0 являются числа
. После этого, корнями уравнения х2 + 1 = 0 являются числа 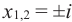 . Число
. Число 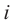 называется мнимой единицей.
называется мнимой единицей.
Расширим множество действительных чисел так, чтобы в него входили все действительные числа и число 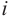 , и были справедливы все свойства сложения и умножения. Для произвольных действительных чисел а и b введём “произведение”
, и были справедливы все свойства сложения и умножения. Для произвольных действительных чисел а и b введём “произведение” 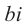 и “сумму”
и “сумму”  , и назовём комплексным числом следующее выражение
, и назовём комплексным числом следующее выражение 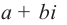 . Выражение вида
. Выражение вида 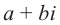 называется комплексным числом, где а и b – действительные числа,
называется комплексным числом, где а и b – действительные числа, 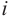 мнимая единица.Комплексные числа можно обозначать через
мнимая единица.Комплексные числа можно обозначать через 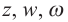 и т.д.Например,
и т.д.Например, 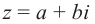 . Запись
. Запись 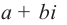 называется алгебраической формой комплексного числа, а является действительной частью, b – мнимой частью комплексного числа
называется алгебраической формой комплексного числа, а является действительной частью, b – мнимой частью комплексного числа 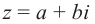 , и записывается так:
, и записывается так: 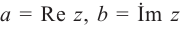 . При а = 0 получается число вида
. При а = 0 получается число вида  . Эти числа называются чисто мнимыми числами. При а = 0, b = 0 комплексное число равно нулю и наоборот, если а +
. Эти числа называются чисто мнимыми числами. При а = 0, b = 0 комплексное число равно нулю и наоборот, если а +  = 0, то а = 0 и b = 0.
= 0, то а = 0 и b = 0.
Следствие: для комплексных чисел а +  и с +
и с +  равенство
равенство
а +  = с +
= с +  справедливо тогда и только тогда, если а = с, b = d.
справедливо тогда и только тогда, если а = с, b = d.
Пример. Из равенства 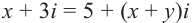 найдите х и у.
найдите х и у.
Решение: Из равенства действительных и мнимых частей получаем: х = 5
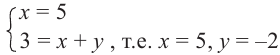 .
.
Суммой комплексных чисел 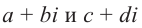 называется комплексное число
называется комплексное число 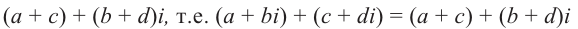
Действия над комплексными числами
Произведением комплексных чисел 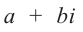 и
и  называется число
называется число 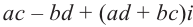 , т.е.
, т.е.
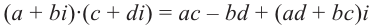
Значит, два комплексных числа умножаются по правилу умножения многочленов при условии, что 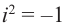 .
.
Пример №1
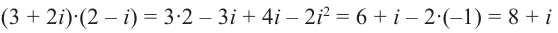
Рассмотрим частные случаи степеней мнимых единиц: 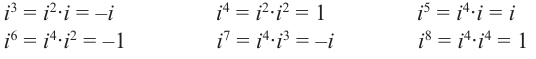
Как видно, натуральные степени мнимой единицы 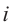 равны
равны 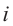 , -1, –
, -1, –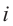 ‘, 1 и повторяются через каждые четыре шага, т.е.справедливо равенство
‘, 1 и повторяются через каждые четыре шага, т.е.справедливо равенство 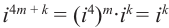
Пример №2
Вычислите: а) 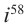 б)
б) 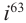
Решение: а) 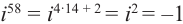 б)
б) 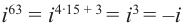
Число  называется сопряжённым для числа
называется сопряжённым для числа  и обозначается как :
и обозначается как : 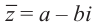 . Ясно, что если число
. Ясно, что если число  является сопряжённым для числа
является сопряжённым для числа  , то число
, то число  является сопряжённым для числа
является сопряжённым для числа  . Поэтому, числа
. Поэтому, числа 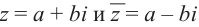 называются взаимно сопряжёнными комплексными числами. Действительные части взаимно сопряжённых чисел равны, а мнимые части являются противоположными числами.
называются взаимно сопряжёнными комплексными числами. Действительные части взаимно сопряжённых чисел равны, а мнимые части являются противоположными числами.
Произведение взаимно сопряжённых комплексных чисел является действительным числом: 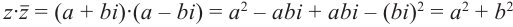 .
.
В частном случае, сопряжённым для действительного числа является само число, для мнимого – произведение числа и (-1).
Для каждого комплексного числа 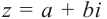 существует противоположное число
существует противоположное число 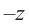 и
и 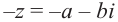 . Для каждого, отличного от нуля, комплексного числа
. Для каждого, отличного от нуля, комплексного числа 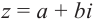 существует противоположное.
существует противоположное. 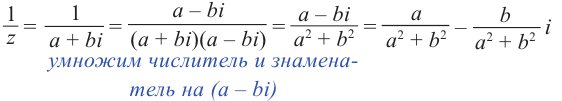
Вычитание и частное комплексных чисел определяется равенствами:
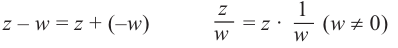
Для нахождения отношения комплексных чисел, удобнее числитель и знаменатель умножить на число, сопряжённое для знаменателя .
Пример №3
Найдём разность и отношение чисел 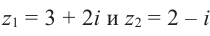 .
.
Решение: 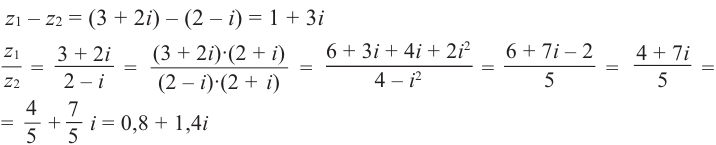
Все свойства арифметических операций для действительных чисел, справедливы для комплексных чисел. Как следствие, получаем, что любые алгебраические тождества справедливы для множества комплексных чисел. Например, для комплексных чисел 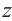 и
и 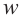 справедливы тождества
справедливы тождества
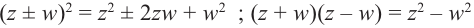
Квадратный корень комплексного числа
Число, квадрат которого равен 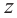 называется квадратным корнем комплексного числа
называется квадратным корнем комплексного числа 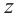 и обозначается как
и обозначается как 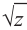 .
.
Пример №4
Найдём квадратный корень комплексного числа 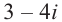
Решение: Пусть 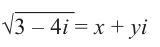 . Возведём обе части равенства в квадрат:
. Возведём обе части равенства в квадрат: 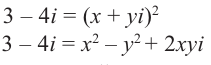
Из равенства действительных и мнимых частей имеем:
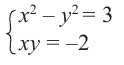
Отсюда получаем решение (2; -1) и (-2; 1). Значит, 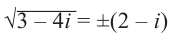
Примечание: В отличии от действительных чисел, говоря о квадратном корне комплексного числа, имеется в виду каждое из двух значений, различающихся знаками. Корни квадратного уравнения 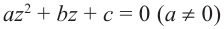 для множества комплексных чисел находится по тому же правилу, что и для действительных чисел.
для множества комплексных чисел находится по тому же правилу, что и для действительных чисел. 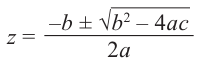
Пример №5
Решим уравнение 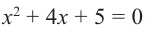 .
.
Решение:
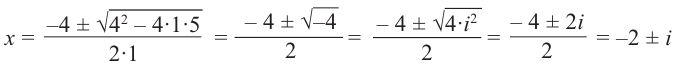 .
.

Легко можно проверить, что также в силе остаётся и теорема Виета. Для квадратного уравнения с действительными коэффициентами комплексные корни являются сопряжёнными числами. Комплексное число 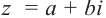 задаётся парой действительных чисел (а; b) и эта пара соответствует определённым точкам на координатной плоскости. Поставим в соответствие числу
задаётся парой действительных чисел (а; b) и эта пара соответствует определённым точкам на координатной плоскости. Поставим в соответствие числу 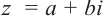 точку А (а; b) и обозначим её через
точку А (а; b) и обозначим её через  . Каждая точка на координатной плоскости изображает комплексное число и наоборот, каждое комплексное число на координатной плоскости, соответствует одной точке. Действительные числа располагаются на оси абсцисс, чисто мнимые числа на оси ординат. Поэтому ось абсцисс называется действительной осью, ось ординат – мнимой, а плоскость – комплексной плоскостью.
. Каждая точка на координатной плоскости изображает комплексное число и наоборот, каждое комплексное число на координатной плоскости, соответствует одной точке. Действительные числа располагаются на оси абсцисс, чисто мнимые числа на оси ординат. Поэтому ось абсцисс называется действительной осью, ось ординат – мнимой, а плоскость – комплексной плоскостью.
Пример:
Точки, соответствующие комплексно сопряжённым числам располагаются симметрично оси абсцисс.
Модуль и аргумент комплексного числа
Тригонометрическая форма комплексного числа
Пусть на комплексной плоскости комплексному числу 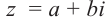 соответствует точка М(а; b). Обозначим расстояние ОМ через R, угол между лучом ОМ и положительным направлением оси абсцисс через
соответствует точка М(а; b). Обозначим расстояние ОМ через R, угол между лучом ОМ и положительным направлением оси абсцисс через  . Из
. Из 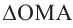 по теореме Пифагора имеем:
по теореме Пифагора имеем: 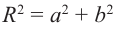
Отсюда: 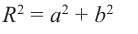
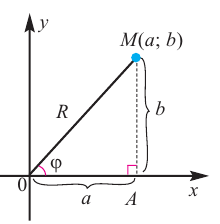
Расстояние, от начала координат до точки соответствующей комплексному числу, называется модулем комплексного числа и обозначается как:  .
.
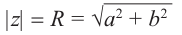
Угол, образованный конечной стороной угла поворота луча ОМ,
называется аргументом  комплексного числа
комплексного числа 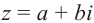 .
.
Из  :
: 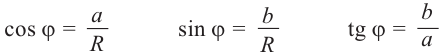
Модуль числа 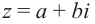 имеет единственное значение, а аргумент
имеет единственное значение, а аргумент  находится с точностью
находится с точностью 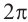 . То есть, если одно из значений аргумента равно
. То есть, если одно из значений аргумента равно  , то другое будет иметь вид
, то другое будет иметь вид 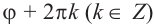 .
.
Для аргумента комплексного числа, обычно берётся угол принадлежащий промежутку [0; 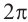 ).
).
Пример №6
Найдём модуль и аргумент комплексного числа 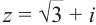
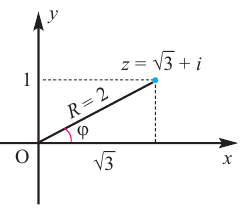
Решение: Из того, что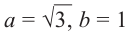 следует,что
следует,что 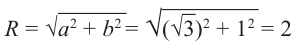
и принимая внимание, что угол 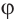 расположен в I четверти,
расположен в I четверти,
получим: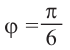
Из формул 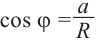 ,
, 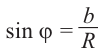 получаем:
получаем: 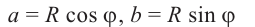
Тогда 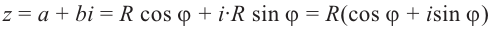
Для комплексного числа 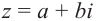 число
число 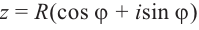 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
В частном случае для модуля и аргумента числа 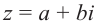 имеем:
имеем:
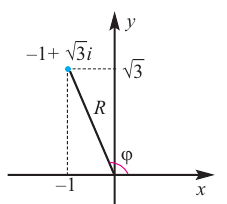
Пример №7
Запишем комплексное число 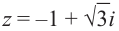
в тригонометрической форме.
Решение: 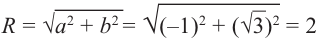
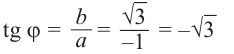
Так как угол 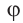 принадлежит II четверги, то
принадлежит II четверги, то
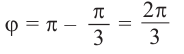
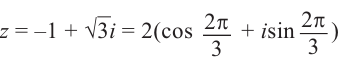
Действия над комплексными числами, заданными в тригонометрической форме
Найдём произведение комплексных чисел, заданных в тригонометрической форме 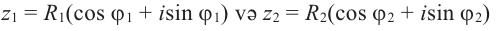 .
.
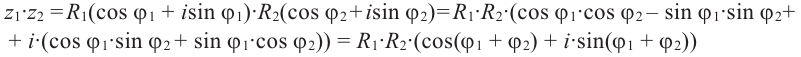
Чтобы найти произведение комплексных чисел, заданных в тригонометрической форме, надо перемножить их модули и сложить их аргументы.
Пример:
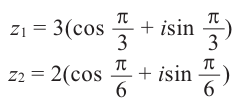
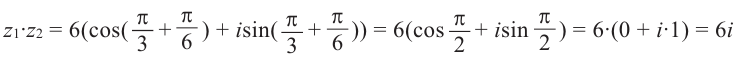
Теперь найдём отношение 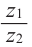
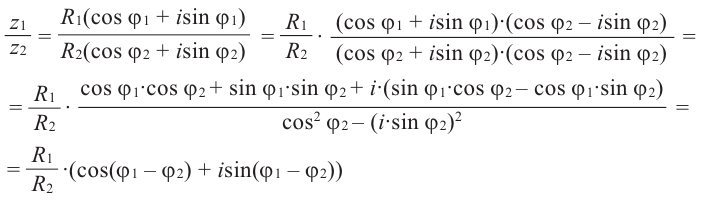
Модуль отношение равен отношению модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.
Пример:
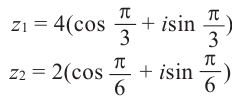
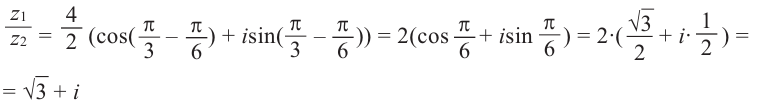
Возвести число 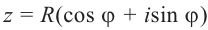 в степень с натуральным показателем n можно умножив n раз число
в степень с натуральным показателем n можно умножив n раз число 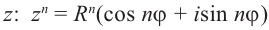
Модуль степени комплексного числа с натуральным показателем равен степени модуля основания, а аргумент равен аргументу основания умноженному на показатель степени n.
Пример:
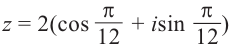
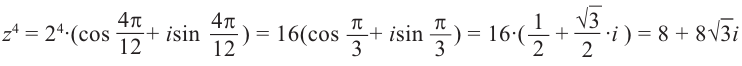
Формулу 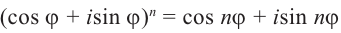 называют формулой Муавра. При помощи этой формулы можно найти синус и косинус n кратных углов через синус и косинус одинарных углов. Например, при n = 2 имеем:
называют формулой Муавра. При помощи этой формулы можно найти синус и косинус n кратных углов через синус и косинус одинарных углов. Например, при n = 2 имеем:
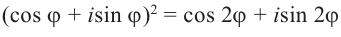
Отсюда
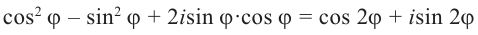
Из равенства двух комплексных чисел имеем:
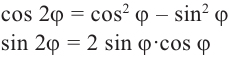
Аналогичным образом можно написать формулы для 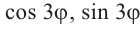 .
.
Корень n-ой степени комплексного числа
Найдём значение выражения 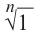 .
.
Запишем в виде 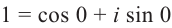 и найдём корень n – ой степени
и найдём корень n – ой степени
виде 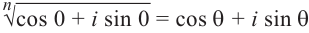 .
.
Возведём каждую из двух сторон в n-ую степень:
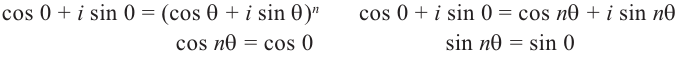
Если два комплексных числа, заданных в тригонометрической форме равны, то их модули равны, а аргументы отличаются на 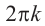 .
.
Это значит,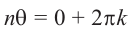
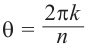
Таким образом, 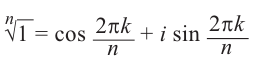
Отсюда при 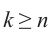 для первых
для первых 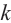 значений полученного числа равны значениям, полученным при
значений полученного числа равны значениям, полученным при  .
.
Обозначим корни  – ой степени единицы через
– ой степени единицы через 
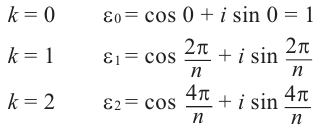
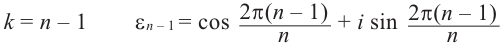
Как видно, модули корней  -ой степени равны 1, аргументы отличаются друг от друга в
-ой степени равны 1, аргументы отличаются друг от друга в 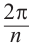 раз. То есть, эти числа расположены внутри единичной окружности, центр которой совпадает с началом координат, и соответствуют комплексным числам, являющимися вершинами правильного
раз. То есть, эти числа расположены внутри единичной окружности, центр которой совпадает с началом координат, и соответствуют комплексным числам, являющимися вершинами правильного  -угольника.
-угольника.
Корнем  -ой степени комплексного числа
-ой степени комплексного числа 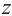 называется такое число
называется такое число 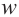 , что
, что 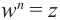 . Если
. Если 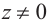 , то для корня
, то для корня  -ой степени существуют
-ой степени существуют  различных значений.
различных значений.
Запишем 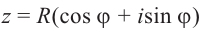 в виде
в виде
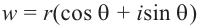 .
.
Для 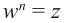 получим:
получим:
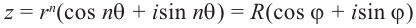
Из равенства двух комплексных чисел получим:
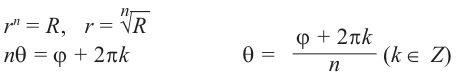
Значения при 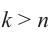 отличаются от первых
отличаются от первых  значений на
значений на 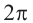
Поэтому, должно соблюдаться следующее: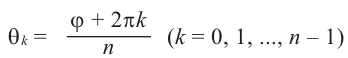
Формула корни n-ой степени комплексного числа
Если 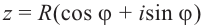 , то
, то
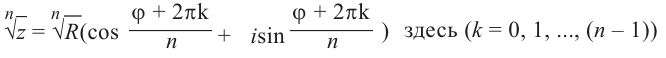
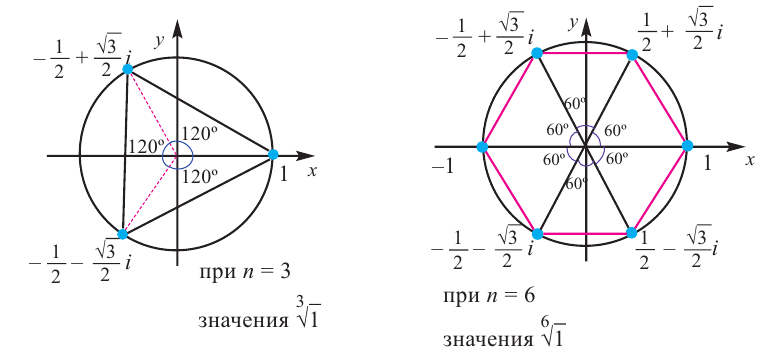
Пример №8
Найдём все значения 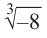
Решение: пусть 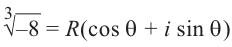
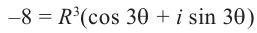
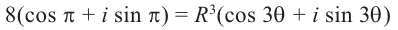
Отсюда 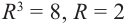
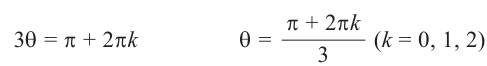
При 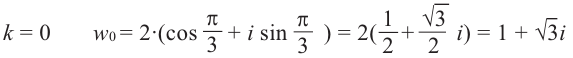
При 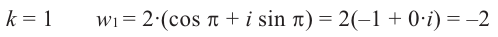
При 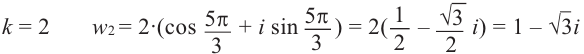
Для чего нужны комплексные числа
Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Арифметические операции над комплексными числами
Комплексным числом называется выражение вида  где
где  — действительные числа,
— действительные числа, 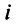 — мнимая единица.
— мнимая единица.
Число 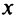 называется действительной частью числа
называется действительной частью числа 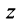 и обозначается
и обозначается 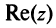 (от франц. reele — «действительный»), а число
(от франц. reele — «действительный»), а число 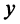 — мнимой частью числа
— мнимой частью числа 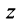 и обозначается
и обозначается 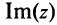 (от франц. imaginaire — «мнимый»), т.е.
(от франц. imaginaire — «мнимый»), т.е. 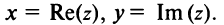
Действительное число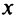 является частным случаем комплексного
является частным случаем комплексного 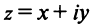 при
при 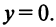 Комплексные числа вида
Комплексные числа вида 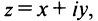 не являющиеся действительными, т.е. при
не являющиеся действительными, т.е. при 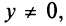 называются мнимыми, а при
называются мнимыми, а при 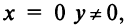 т.е. числа вида
т.е. числа вида 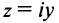 — чисто мнимыми.
— чисто мнимыми.
Числа 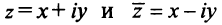 называются сопряженными.
называются сопряженными.
Два комплексных числа 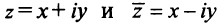 называются равными, если равны их действительные и мнимые части, т.е.
называются равными, если равны их действительные и мнимые части, т.е. 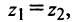 если
если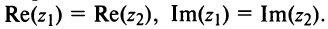 В частности,
В частности, 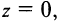 если
если 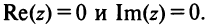
Арифметические операции на множестве комплексных чисел определяются следующим образом.
1.Сложение (вычитание) комплексных чисел
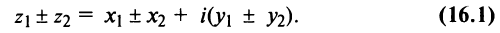
2. Умножение комплексных чисел
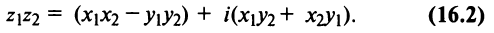
В частности,
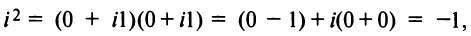
т.е. мнимая единица есть число, квадрат которого равен — 1.
3. Деление двух комплексных чисел
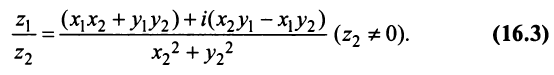
Нетрудно убедиться в том, что все арифметические операции (16.1)-(16.3) над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 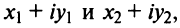 если считать
если считать 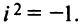 Например, произведение комплексных чисел (16.2) есть
Например, произведение комплексных чисел (16.2) есть
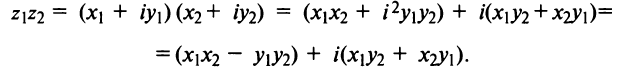
Пример №9
Даны комплексные числа 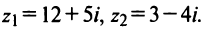
Найти 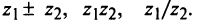
Решение:
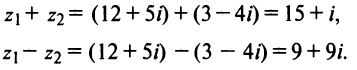
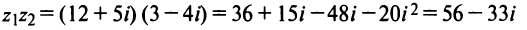 (учли, что
(учли, что 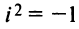 ).
).
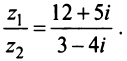 Умножая числитель и знаменатель на сопряженное делителю комплексное число
Умножая числитель и знаменатель на сопряженное делителю комплексное число 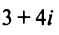 , получим
, получим
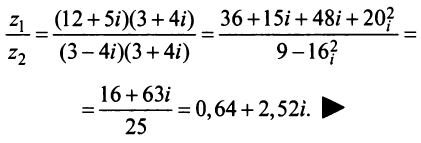
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости 
Плоскость называется комплексной, если каждому комплексному числу 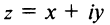 ставится в соответствие точка плоскости
ставится в соответствие точка плоскости 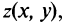 причем это соответствие взаимно однозначное (рис. 16.1).
причем это соответствие взаимно однозначное (рис. 16.1).
Оси 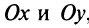 , на которых расположены действительные числа
, на которых расположены действительные числа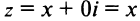 и чисто мнимые числа
и чисто мнимые числа 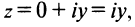 называются соответственно действительной и мнимой осями.
называются соответственно действительной и мнимой осями.
Тригонометрическая и показательная формы комплексного числа
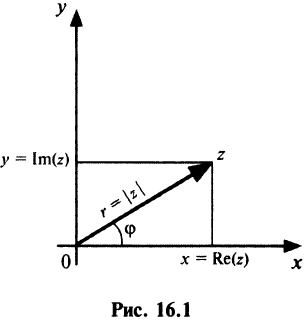
С каждой точкой 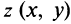 комплексной плоскости связан радиус-вектор этой точки
комплексной плоскости связан радиус-вектор этой точки 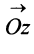 , длина которого
, длина которого 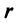 называется модулем комплексного числа
называется модулем комплексного числа 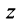 и обозначается
и обозначается 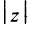 (см. рис. 16.1):
(см. рис. 16.1):

Угол 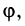 образованный радиусом-вектором
образованный радиусом-вектором 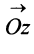 с осью
с осью 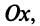 называется аргументом комплексного числа
называется аргументом комплексного числа 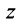 и обозначается
и обозначается 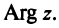 Из значений
Из значений 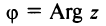 выделяется главное значение
выделяется главное значение 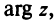 удовлетворяющее условию
удовлетворяющее условию 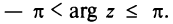 Например,
Например, 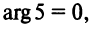
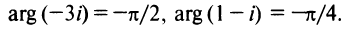
Очевидно (см. рис. 16.1), что
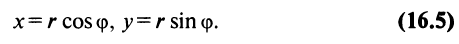
Следовательно, комплексное число можно представить как
можно представить как

Представление комплексного числа в виде (16.6), где 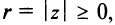
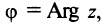 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
Сформулируем некоторые свойства арифметических операций над комплексными числами.
1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
На рис. 16.2 показаны радиусы-векторы комплексных чисел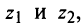 их суммы
их суммы 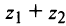 и разности
и разности 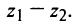
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
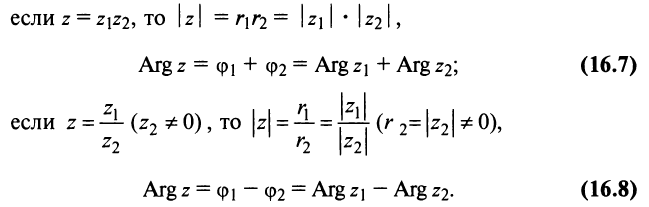
Геометрически умножение числа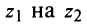 означает изменение длины радиуса-вектора
означает изменение длины радиуса-вектора 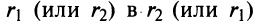 раз и его поворот вокруг точки
раз и его поворот вокруг точки 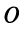 против часовой стрелки на угол
против часовой стрелки на угол 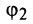
Пример №10
Комплексные числа 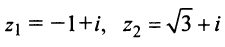 представить в тригонометрической форме и найти
представить в тригонометрической форме и найти 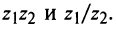
Решение:
По формуле (16.4) найдем модуль комплексного числа 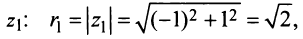 а из соотношений (16.5)
а из соотношений (16.5) 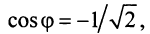
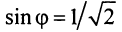 получим аргумент числа
получим аргумент числа 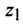 (берем его главное значение):
(берем его главное значение): 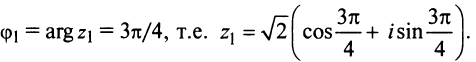
Аналогично 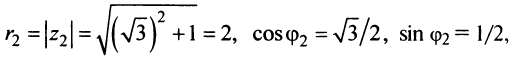 т.е.
т.е. 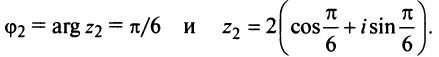
Теперь по формулам (16.7) и (16.8)
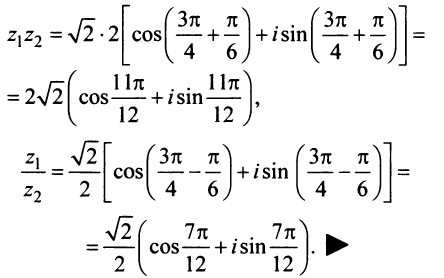
Так как в соответствии с формулами (16.7) и (16.8) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 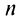 , известную как формула Муавра:
, известную как формула Муавра:
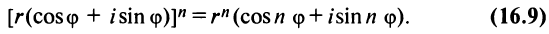
Пример №11
Найти 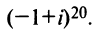
Решение:
По формуле Муавра (16.9)
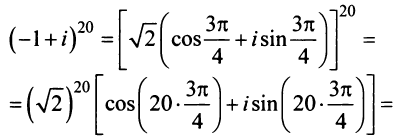
 Обратимся к извлечению корня из комплексного числа.
Обратимся к извлечению корня из комплексного числа.
Пусть

Тогда, используя определение корня и формулу Муавра (16.9), получим
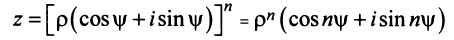
или
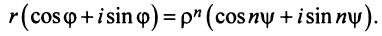
Отсюда следует, что
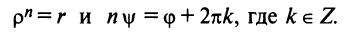
Итак,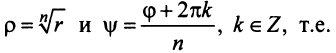
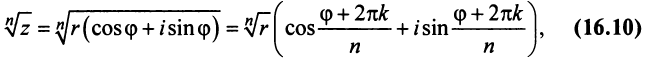
где 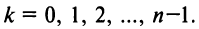
При 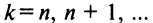 значения корня уже будут повторяться.
значения корня уже будут повторяться.
Таким образом, корень 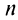 -й степени из комплексного числа (не равного нулю) имеет
-й степени из комплексного числа (не равного нулю) имеет 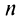 различных значений.
различных значений.
Пример №12
Найти 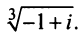
Решение:
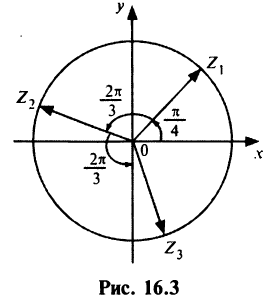
В примере 16.2 было получено
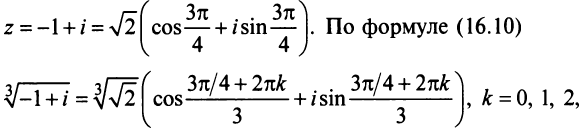
откуда получаем три значения корня
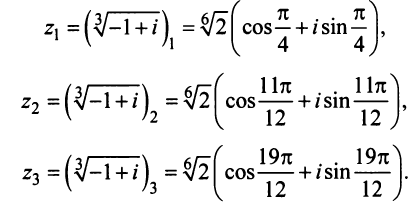
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки 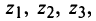 расположенные на окружности радиуса
расположенные на окружности радиуса 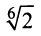 (рис. 16.3). ►
(рис. 16.3). ►
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера.
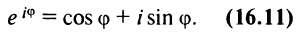
Отсюда следует показательная форма комплексного числа. 
где 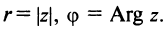
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.
Формы записи комплексного числа
Решение простейшего квадратного уравнения 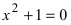 невозможно в области вещественных чисел. Однако, если выполнить решение формально, то получим
невозможно в области вещественных чисел. Однако, если выполнить решение формально, то получим 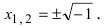
Определение: Выражение 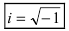 называется мнимой единицей.
называется мнимой единицей.
Определение: Комплексным числом называется выражение вида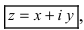 где х,у
где х,у
Определение: Приведенная форма записи комплексного числа называется алгебраической.
Определение: Два комплексных числа 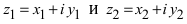 называются равными, если равны их вещественные и мнимые части, т.е.
называются равными, если равны их вещественные и мнимые части, т.е. 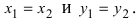
Определение: Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.
Определение: Комплексно-сопряженным к комплексному числу 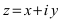 называется комплексное число
называется комплексное число 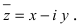
Пример №13
Записать комплексно-сопряженное число к комплексному числу 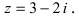
Решение:
Согласно определению комплексно-сопряженного числа получаем 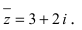
Замечание: Двойное комплексное сопряжение приводит к исходному комплекс- ному числу, т.е. 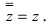
Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.
Пример №14
Решить квадратное уравнение 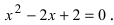
Решение:
Вычислим дискриминант уравнения 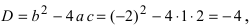 таким образом,
таким образом, 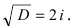 Следовательно,
Следовательно, 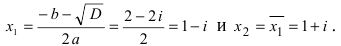
Замечание: Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.
Комплексное число 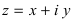 изобретается на комплексной плоскости
изобретается на комплексной плоскости  в виде вектора, соединяющего начало координат с точкой М(х; у) (Рис. 2):
в виде вектора, соединяющего начало координат с точкой М(х; у) (Рис. 2): 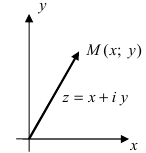
Рис. 2. Изображение комплексного числа на комплексной плоскости.
Пример №15
Изобразить на комплексной плоскости число z = 2-3i (Рис. 3). 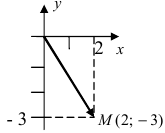
Решение:
Рис. 3. Изображение комплексного 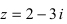 на комплексной плоскости. Если перейти от декартовой системы координат к полярной системе отсчета, т.е.
на комплексной плоскости. Если перейти от декартовой системы координат к полярной системе отсчета, т.е. 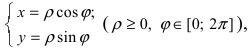 то комплексное число
то комплексное число 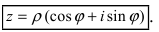
Определение: Полученная форма записи комплексного числа называется тригонометрической.
Обратный переход от полярной системы отсчета к декартовой системе координат осуществляется по формулам: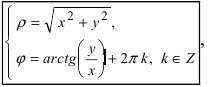 при этом
при этом 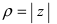 является модулем, а
является модулем, а 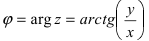 – аргументом комплексного числа z .
– аргументом комплексного числа z .
Замечание: Аргумент комплексного числа 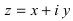 определяется в зависимости от знаков вещественной и мнимой частей:
определяется в зависимости от знаков вещественной и мнимой частей:
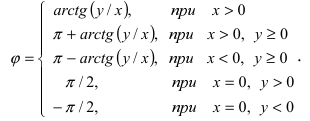
Действия с комплексными числами
1. Для того чтобы сложить (найти разность) два комплексных числа 
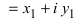 и
и 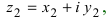 сложить (найти разность) отдельно действительные и мнимые части,
сложить (найти разность) отдельно действительные и мнимые части, 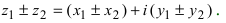
Пример №16
Найти сумму и разность чисел 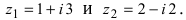 Изобразить все числа на комплексной плоскости.
Изобразить все числа на комплексной плоскости.
Решение:
Найдем сумму заданных комплексных чисел 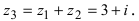 Вычислим разность данных чисел
Вычислим разность данных чисел 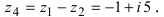 Изобразим заданные и полученные числа на комплексной плоскости (Рис. 4):
Изобразим заданные и полученные числа на комплексной плоскости (Рис. 4):
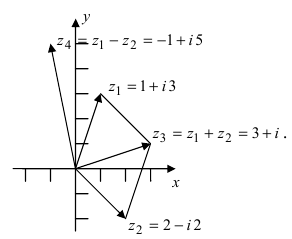
Рис. 4. Изображение комплексных чисел на комплексной плоскости.
Замечание: Отметим, что 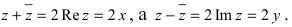
2. Для того чтобы найти произведение двух комплексных чисел 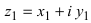 и
и 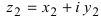 надо их перемножить, как два выражения с учетом того, что
надо их перемножить, как два выражения с учетом того, что 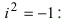
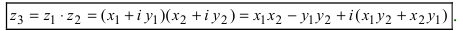
Замечание: Отметим, что 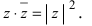
Замечание: Произведение комплексных чисел в тригонометрической форме записи имеет вид 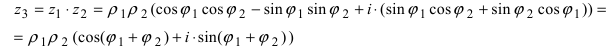 Из полученной формулы видно, что модули комплексных чисел перемножаются, а аргументы складываются. Следовательно, n-ая степень любого комплексного числа будет иметь вид
Из полученной формулы видно, что модули комплексных чисел перемножаются, а аргументы складываются. Следовательно, n-ая степень любого комплексного числа будет иметь вид 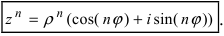 При извлечении корня п -ой степени применяют формулу Муавра
При извлечении корня п -ой степени применяют формулу Муавра 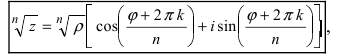 где величина
где величина 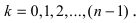
3. Деление комплексного числа 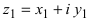 на комплексное число
на комплексное число 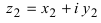 осуществляется так
осуществляется так 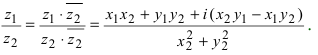
Замечание: Деление этих чисел в тригонометрической форме записи имеет вид: 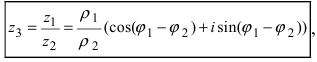 т.е. при делении комплексных чисел берут отношение модулей этих чисел, а из аргумента первого числа вычитают аргумент второго комплексного числа.
т.е. при делении комплексных чисел берут отношение модулей этих чисел, а из аргумента первого числа вычитают аргумент второго комплексного числа.
Показательная форма записи комплексного числа
Известно, что любую дифференцируемую функцию можно представить по формуле Тейлора-Маклорена (см. Лекцию № 22, Первый семестр), например, 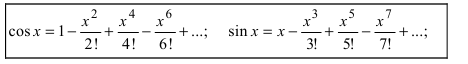
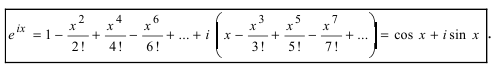
Последняя формула называется формулой Эйлера. Используя эту формулу,
запишем комплексное число 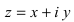 в показательной форме:
в показательной форме: 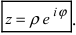 Отсюда видно, что при нахождении произведения и отношения комплексных чисел получаем
Отсюда видно, что при нахождении произведения и отношения комплексных чисел получаем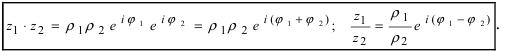
Комплексные числа и арифметические операции
Как известно, под комплексным числом понимается выражение вида
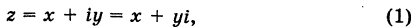
где х и у — действительные числа, a i — мнимая единица.
Числа вида  отождествляются с действительными числами; в частности,
отождествляются с действительными числами; в частности, 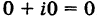 . Числа вида 0 + iy = iy называются чисто мнимыми.
. Числа вида 0 + iy = iy называются чисто мнимыми.
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
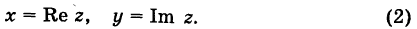
Под модулем комплексного числа z понимается неотрицательное число
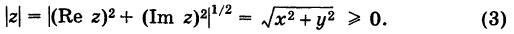
Сопряженным числом 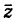 к числу (1) называется комплексное число
к числу (1) называется комплексное число
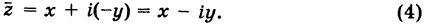
Таким образом,
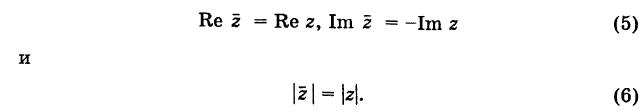
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
I. Пусть z1=x1+iy1 и z2=x2+iy2.Тогда
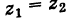
 Rez1 = Re z2, Im z1 = Im z2
Rez1 = Re z2, Im z1 = Im z2
В частности, z = 0 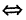 Re z = 0, Im z = 0.
Re z = 0, Im z = 0.
II. z1±z2= (x1± x2) + i(y1 ± y2)-
Отсюда следует, что
Re (z1 ± z2) – Re z1 ± Re z2,
Im (z1 ± z2) – Imz1 ± 1mz2
III. z1z2 = (x1x2 – y1y2) + i(x1y2+x2y1).
Отсюда, в частности, получаем важное соотношение
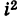 =
=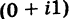
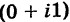 =
=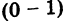 +
+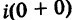 =-1
=-1
Заметим, что правило умножения III получается формально путем умножения двучленов 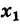 +
+ 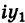 и
и 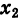 +
+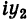 с учетом (7).
с учетом (7).
Очевидно также, что для 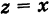
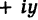
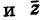
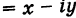 имеем
имеем
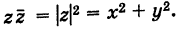
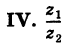 =
=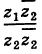 =
=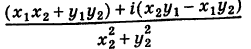
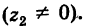
Легко проверить следующие свойства:
1)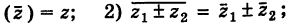
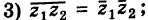
- Заказать решение задач по высшей математике
Комплексная плоскость
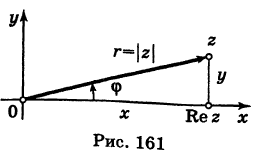
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу z = х + iy может быть поставлена в соответствие точка плоскости z(x, у) (рис. 161), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
На оси Ох расположены действительные числа: z =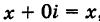 :, поэтому она называется действительной осью. На оси Оу расположены чисто мнимые числа z = 0 + iy = iy, она носит название мнимой оси.
:, поэтому она называется действительной осью. На оси Оу расположены чисто мнимые числа z = 0 + iy = iy, она носит название мнимой оси.
Заметим, что г = |z| представляет собой расстояние точки г от начала координат.
С каждой точкой z связан радиус-вектор этой точки Oz; угол, образованный радиусом-вектором точки z с осью Ох, называется аргументом ф = Arg z этой точки. Здесь 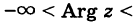
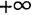 . Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение Arg z называется главным значением его и обозначается через arg z:
. Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение Arg z называется главным значением его и обозначается через arg z:

Для аргумента ср имеем (рис. 161)
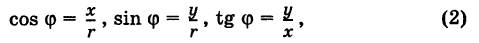
где 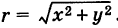
Примеры: 1) arg 2 = 0; 2) arg (-1) = 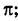 ; 3) arg i =
; 3) arg i = 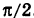 .
.
Модуль г и аргумент ф комплексного числа z можно рассматривать (рис. 161) как полярные координаты точки z. Отсюда получаем
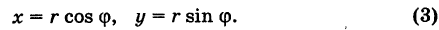
Таким образом, имеем тригонометрическую форму комплексного числа
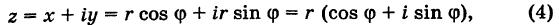
где 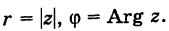
Теорема: При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).
Действительно, если число 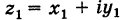 соответствует точке с координатами
соответствует точке с координатами 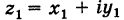 , а число
, а число 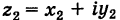 — точке с координатами
— точке с координатами 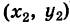 то числу
то числу 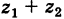 отвечает точка
отвечает точка 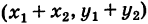 Так как (рис. 162) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами 0,
Так как (рис. 162) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами 0, 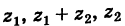 есть параллелограмм. Следовательно, радиус-вектор точки
есть параллелограмм. Следовательно, радиус-вектор точки 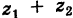 является суммой радиусов-векторов точек
является суммой радиусов-векторов точек 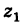 и
и 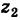 .
.
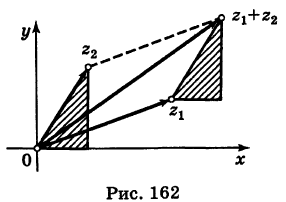
Следствие. Так как 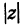 есть длина вектора
есть длина вектора 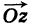 , то
, то
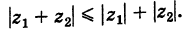
Теорема: При вычитании комплексных чисел их радиусы-векторы вычитаются. Так как 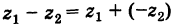 , то
, то  равен второй диагонали параллелограмма, построенного на векторах
равен второй диагонали параллелограмма, построенного на векторах 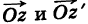 (рис. 163), т. е. равен разности радиусов-векторов точек
(рис. 163), т. е. равен разности радиусов-векторов точек 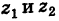 .
.
Следствие. Расстояние между двумя точками 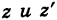 равно
равно
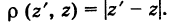
Теоремы о модуле и аргументе
Теорема: Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей. Действительно, если
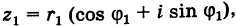
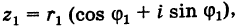
то имеем
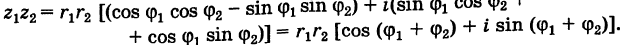
Отсюда
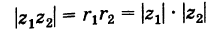
и
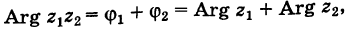
где значения многозначной функции Arg, стоящие в левой и правой частях равенства (1), следует подбирать соответствующим образом. Это замечание надо иметь в виду и для дальнейшего.
Следствие. Модуль целой положительной степени комплексного числа равен такой же степени модуля этого числа, а аргумент степени равен аргументу числа, умноженному на показатель степени, т. е.
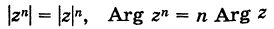
( — целое положительное число).
— целое положительное число).
Доказательство непосредственно вытекает из рассмотрения произведения равных сомножителей.
Пример №17
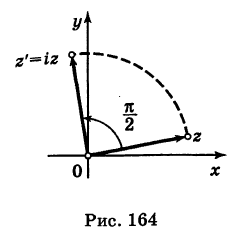
Построить точку 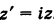 .
.
Решение:
Имеем
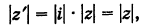
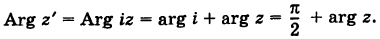
Следовательно, при умножении на i вектор  поворачивается на прямой угол против хода часовой стрелки (рис. 164).
поворачивается на прямой угол против хода часовой стрелки (рис. 164).
Теорема: Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя. Пусть
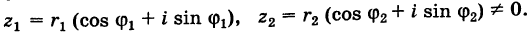
Так как
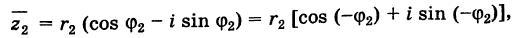
то на основании теоремы 1 имеем
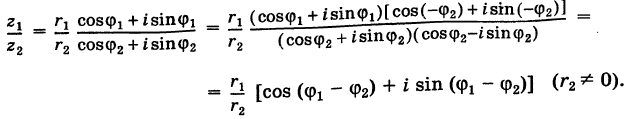
Отсюда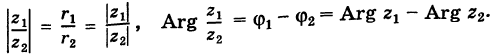
Извлечение корня из комплексного числа
Пусть
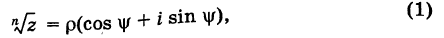
где 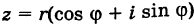 . Тогда на основании имеем
. Тогда на основании имеем
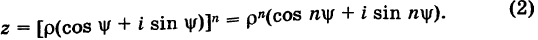
Отсюда получаем
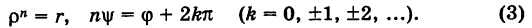
Таким образом,
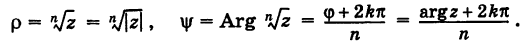
Заметим, что здесь под 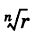 понимается арифметическое значение корня.
понимается арифметическое значение корня.
Здесь в качестве числа k достаточно брать лишь значения 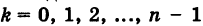 , так как при всех прочих значениях k получаются повторения уже найденных значений корня. Следовательно, окончательно имеем
, так как при всех прочих значениях k получаются повторения уже найденных значений корня. Следовательно, окончательно имеем
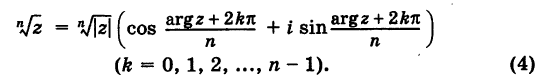
Из формулы (4) следует, что корень 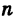 -й степени из любого комплексного числа
-й степени из любого комплексного числа 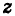 =0 имеет точно л значений.
=0 имеет точно л значений.
Пример №18
Найти 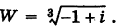
Решение:
Так как 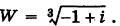 , то на основании формулы (4) имеем
, то на основании формулы (4) имеем
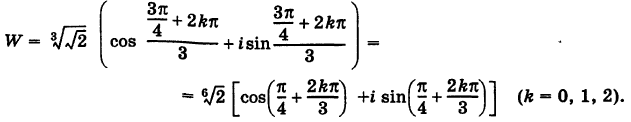
Отсюда
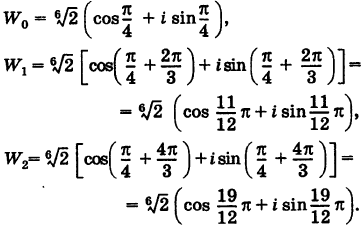
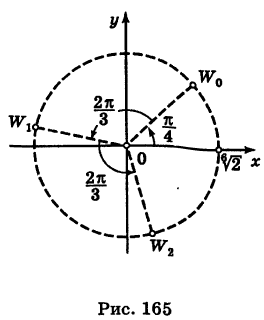
Точки 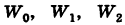 представляют собой равноотстоящие друг от друга точки, расположенные на окружности радиуса
представляют собой равноотстоящие друг от друга точки, расположенные на окружности радиуса 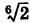 (рис. 165).
(рис. 165).
Понятие функции комплексной переменной
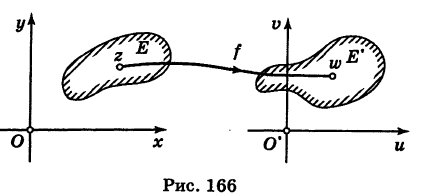
Пусть даны две комплексные плоскости Оху (плоскость г) и O’uv (плоскость w).
Определение: Если каждой точке z  Е (Е — множество точек плоскости z) по некоторому закону f ставится в соответствие единственная точка w
Е (Е — множество точек плоскости z) по некоторому закону f ставится в соответствие единственная точка w  Е’ (Е’ — множество точек плоскости w), то говорят, что w есть функция от z (однозначная)
Е’ (Е’ — множество точек плоскости w), то говорят, что w есть функция от z (однозначная)

с областью определения Е, значения которой принадлежат множеству Е’ (рис. 166). Если множество значений функции f(z) исчерпывает все множество Е то Е’ называется множеством значений (областью изменения) функции f(z). В этом случае пишут

Множества Е и Е’ можно изображать на одной комплексной плоскости.
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
Пример:
Во что переходит сектор Е
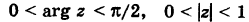
(рис. 167, а) при отображении 
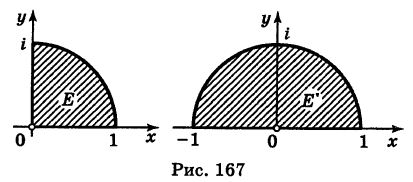
Решение:
Имеем
Поэтому отображенная область E’ представляет собой полукруг (рис. 167, б).
Определение комплексных чисел
Определение комплексного числа и основные функции комплексной переменной
Определение 7.1. Множеством комплексных чисел 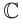 называется множество пар действительных чисел
называется множество пар действительных чисел 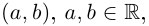 на котором введены операции сложения и умножения следующим образом. Если
на котором введены операции сложения и умножения следующим образом. Если 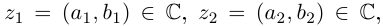 то
то 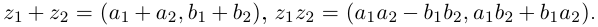 Элементы множества
Элементы множества  называются комплексными числами. Два комплексных числа
называются комплексными числами. Два комплексных числа 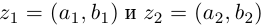 называются равными, если
называются равными, если 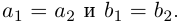
Операции сложения и умножения на множестве 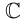 обладают привычными свойствами (коммутативность сложения и умножения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения).
обладают привычными свойствами (коммутативность сложения и умножения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения).
Лемма 7.1. Для любых комплексных чисел 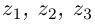 выполняются равенства
выполняются равенства
- 1)
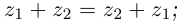
- 2)
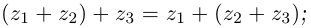
- 3)
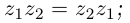
- 4)
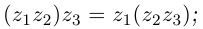
- 5)
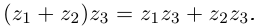
□ Докажем, например, свойство 4 (свойство 5 доказывается аналогично, свойства 1, 2, 3 очевидны).
Пусть 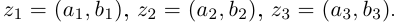 Тогда
Тогда
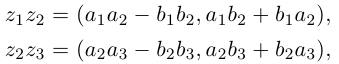
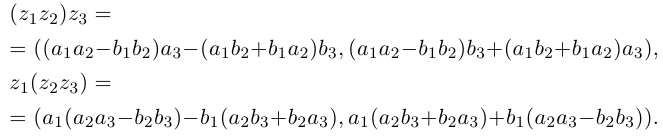
Два последних комплексных числа совпадают. После раскрытия скобок оказывается, что оба они равны
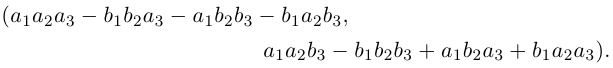 ■
■
Определение 7.2. Комплексное число 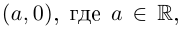 отождествляется с действительным числом а.
отождествляется с действительным числом а.
Это определение оправдывается тем, что установлено взаимно однозначное соответствие между множеством пар 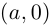 и множеством действительных чисел, сохраняющее операции сложения и умножения:
и множеством действительных чисел, сохраняющее операции сложения и умножения:
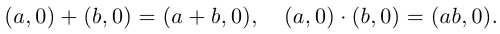
Такое соответствие в высшей алгебре называется изоморфизмом.
Определение 7.3. Комплексное число (0,1) обозначается буквой 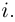
Легко видеть, что 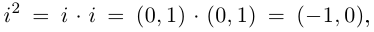 т.е.
т.е. 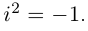
Далее, так как 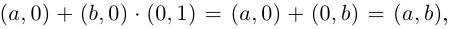 то пару
то пару 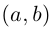 можно записать в виде
можно записать в виде 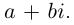 В дальнейшем комплексное число так и будем записывать:
В дальнейшем комплексное число так и будем записывать: 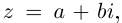 где
где 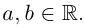 Определения операций при этом запишутся так:
Определения операций при этом запишутся так:
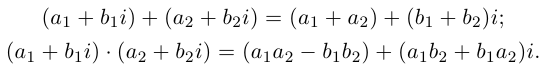
Иными словами, комплексные числа можно складывать и умножать, пользуясь известными законами сложения и умножения (лемма 7.1), имея в виду, что 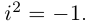
Определение 7.4. Разностью двух комплексных чисел  и
и 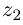 называется такое комплексное число
называется такое комплексное число 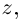 что
что 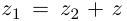 (обозначается
(обозначается 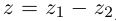 ). Частным двух комплексных чисел
). Частным двух комплексных чисел 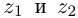 (
(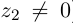 ) называется такое комплексное число z, что
) называется такое комплексное число z, что 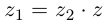 (обозначается
(обозначается 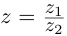 ).
).
Проверим, что эти операции однозначно определены.
□ Пусть 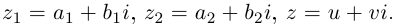 Для разности имеем:
Для разности имеем: 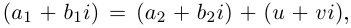 откуда
откуда 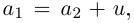
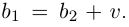 Тогда
Тогда 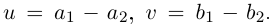 Разность двух комплексных чисел
Разность двух комплексных чисел 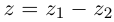 определяется однозначно:
определяется однозначно: 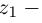
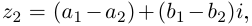 т.е. вычитание можно осуществлять непосредственно.
т.е. вычитание можно осуществлять непосредственно.
Для частного имеем: 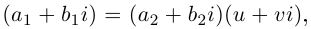 откуда
откуда 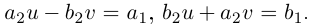 Так как
Так как 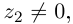 то определитель этой системы
то определитель этой системы 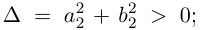 решая систему по правилу Крамера, получим:
решая систему по правилу Крамера, получим: 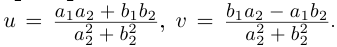 Частное двух комплексных чисел
Частное двух комплексных чисел 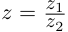 определено однозначно:
определено однозначно:
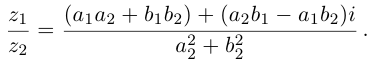
Такое деление можно осуществлять непосредственно:
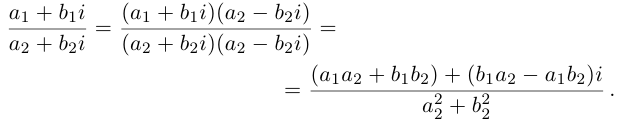
Комплексное число 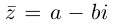 называется сопряжённым к числу
называется сопряжённым к числу 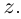 Мы воспользовались тем, что
Мы воспользовались тем, что 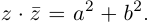 Произведённые действия аналогичны домножению числителя и знаменателя дроби со знаменателем вида
Произведённые действия аналогичны домножению числителя и знаменателя дроби со знаменателем вида 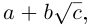 где
где 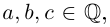
 на число
на число 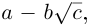 сопряжённое к знаменателю (такие действия применяются для избавления от иррациональности в знаменателе).
сопряжённое к знаменателю (такие действия применяются для избавления от иррациональности в знаменателе).
Определение 7.5. Пусть 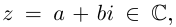 где
где 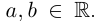 Тогда числа
Тогда числа 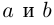 называются соответственно действительной и мнимой частью числа
называются соответственно действительной и мнимой частью числа 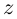 (
(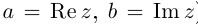 ). Комплексное число
). Комплексное число 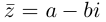 называется числом, сопряжённым к
называется числом, сопряжённым к 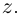 Действительное неотрицательное число
Действительное неотрицательное число 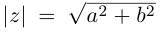 называется модулем числа
называется модулем числа 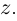
Лемма 7.2. Для любых комплексных чисел 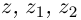 имеют место следующие соотношения:
имеют место следующие соотношения:
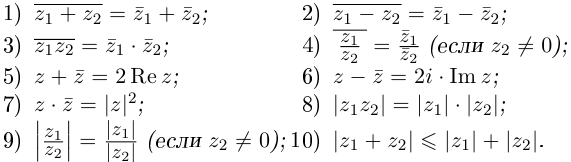
Доказать эти утверждения будет предложено самостоятельно в качестве упражнения.
Множество комплексных чисел  геометрически интерпретируется как множество точек плоскости (комплексная плоскость
геометрически интерпретируется как множество точек плоскости (комплексная плоскость  ). Если координаты точек заданы в прямоугольной системе координат 0,
). Если координаты точек заданы в прямоугольной системе координат 0,  (кратчайший поворот от
(кратчайший поворот от 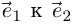 осуществляется против часовой стрелки), то комплексное число
осуществляется против часовой стрелки), то комплексное число 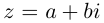 соответствует точке
соответствует точке 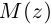 с координатами
с координатами 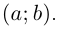 Такое соответствие является взаимно однозначным. Точка
Такое соответствие является взаимно однозначным. Точка 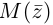 симметрична точке
симметрична точке 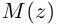 относительно оси абсцисс, которая называется действительной осью, ось ординат называется мнимой осью. Расстояние от точки
относительно оси абсцисс, которая называется действительной осью, ось ординат называется мнимой осью. Расстояние от точки 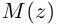 до начала координат равно
до начала координат равно 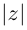 (см. рис. 7.1).
(см. рис. 7.1).
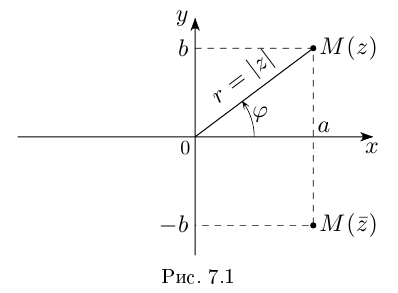
Аргументом числа 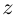 называется угол
называется угол 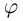 поворота от положительного луча действительной оси к лучу
поворота от положительного луча действительной оси к лучу 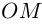 (против часовой стрелки). Этот угол определён с точностью до
(против часовой стрелки). Этот угол определён с точностью до 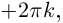
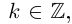 и обозначается
и обозначается 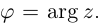 Аргумент нулевого комплексного числа не определён. Фактически мы ввели полярные координаты на комплексной плоскости:
Аргумент нулевого комплексного числа не определён. Фактически мы ввели полярные координаты на комплексной плоскости: 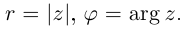 При этом
При этом 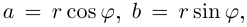 и комплексное число
и комплексное число 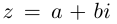 можно записать в тригонометрической форме:
можно записать в тригонометрической форме:
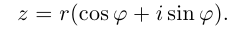
Пример:
Записать в тригонометрической форме числа 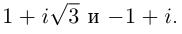
□ 1) 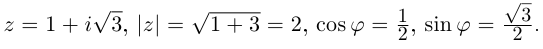
При записи комплексного числа в тригонометрической форме обычно берут одно фиксированное («наиболее простое») значение аргумента. Возьмём 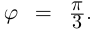 Тогда
Тогда 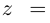
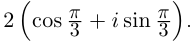
2) 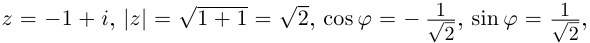
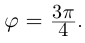 Тогда
Тогда 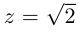 (
(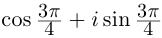 ).
).
Комплексные числа, записанные в тригонометрической форме, удобно умножать и делить. При умножении модули чисел перемножаются, аргументы складываются. При делении модули делятся, аргументы вычитаются.
Лемма 7.3. Пусть 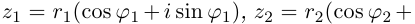
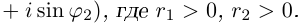 Тогда
Тогда
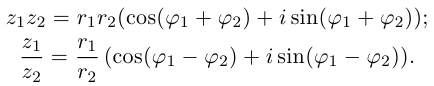
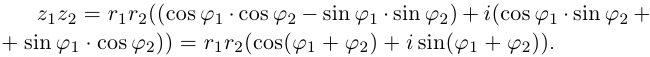
Если 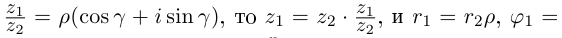
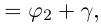 откуда следует, что
откуда следует, что 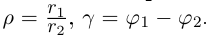
Степень с целым показателем для комплексных чисел определяется так же, как и для действительных. Поэтому мы можем сформулировать
Следствие (формула Муавра). Если 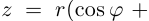
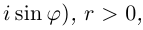 то при любом целом
то при любом целом 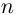 имеет место равенство
имеет место равенство
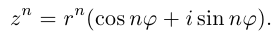
Иными словами, при возведении комплексного числа в целую степень модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Пример:
Применяя формулу Муавра, получить известные формулы тригонометрии для 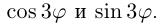
□ Имеем: 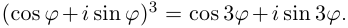 Возводя двучлен в куб, получим:
Возводя двучлен в куб, получим: 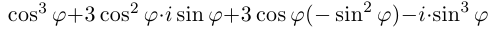 (мы воспользовались тем, что
(мы воспользовались тем, что 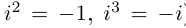 ). Приравнивая действительные и мнимые части двух равных выражений, имеем
). Приравнивая действительные и мнимые части двух равных выражений, имеем
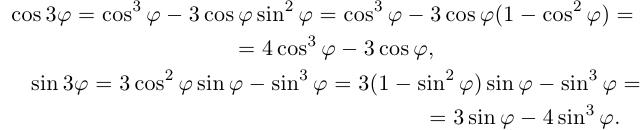
Определение 7.6. Пусть 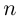 — натуральное число,
— натуральное число, 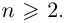 Корнем
Корнем 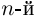 степени из комплексного числа
степени из комплексного числа 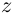 называется комплексное число
называется комплексное число 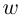 такое, что
такое, что 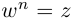 (обозначение:
(обозначение: 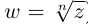 ).
).
Лемма 7.4. Если 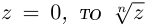 принимает единственное значение 0 при любом
принимает единственное значение 0 при любом 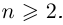 Если
Если 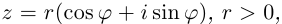 то
то 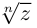 принимает ровно
принимает ровно 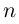 комплексных значений, имеющих одинаковый модуль
комплексных значений, имеющих одинаковый модуль 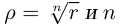 различных значений аргумента
различных значений аргумента 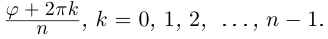
□ Правая часть леммы очевидна, так как  и если
и если 
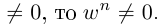 Пусть теперь
Пусть теперь 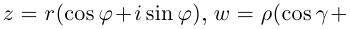
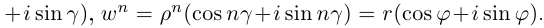 Комплексные числа, записанные в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на
Комплексные числа, записанные в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на 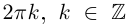 (пока значение
(пока значение 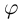 стояло только под знаком косинуса и синуса, неоднозначность определения
стояло только под знаком косинуса и синуса, неоднозначность определения 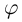 можно было не учитывать, если сравнивать сами углы — эту неоднозначность учитывать необходимо). Итак,
можно было не учитывать, если сравнивать сами углы — эту неоднозначность учитывать необходимо). Итак, 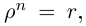
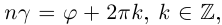 откуда
откуда 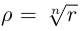 (арифметический корень
(арифметический корень 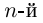 степени из положительного числа),
степени из положительного числа), 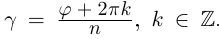
При замене 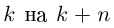 получим тот же угол, увеличенный на
получим тот же угол, увеличенный на 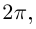 поэтому существенно различные значения
поэтому существенно различные значения 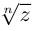 дают лишь
дают лишь 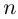 значений
значений 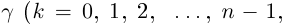 далее значения корня повторяются).
далее значения корня повторяются).
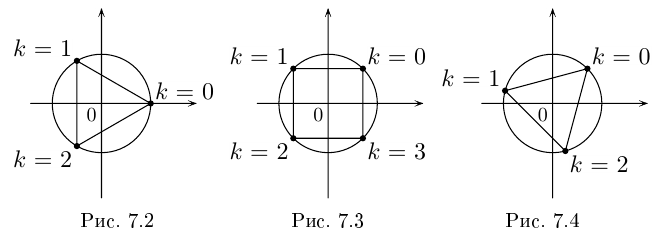
Замечание. 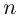 значений
значений 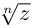 на комплексной плоскости соответствуют
на комплексной плоскости соответствуют 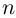 точкам, лежащим в вершинах правильного
точкам, лежащим в вершинах правильного 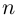 -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса 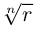 с центром в начале координат.
с центром в начале координат.
Пример №19
Найти все значения 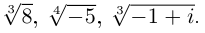
□ 1) 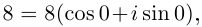 поэтому
поэтому 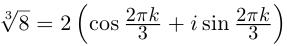
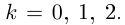 Получим 3 значения:
Получим 3 значения: 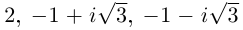 (см. рис. 7.2).
(см. рис. 7.2).
Первое из них — арифметическое значение кубического корня из положительного числа 8.
2) 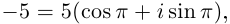 поэтому
поэтому
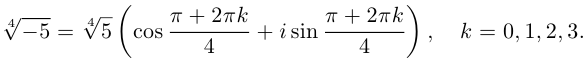
Получим 4 значения:
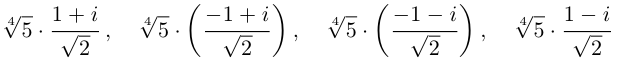
(см. рис. 7.3). 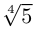 здесь — арифметическое значение корня 4-й степени из положительного числа 5.
здесь — арифметическое значение корня 4-й степени из положительного числа 5.
3) 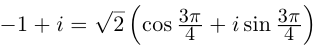 , поэтому
, поэтому
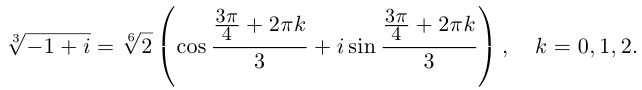
Получим 3 значения:
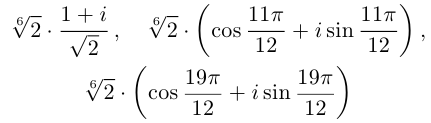
(см. рис. 7.4). ■
Определение 7.7. Пусть 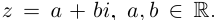 Тогда
Тогда 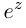 определяется как комплексное число
определяется как комплексное число 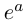
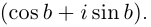
Если 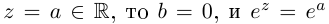 (при
(при 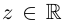 получаем обычное действительное значение
получаем обычное действительное значение 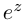 ). Отмстим, что
). Отмстим, что 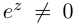 при любых
при любых 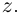
Лемма 7.5. Для любых 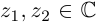 имеют место равенства
имеют место равенства 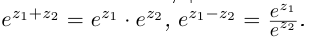
□ Пусть 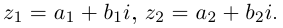 Тогда
Тогда
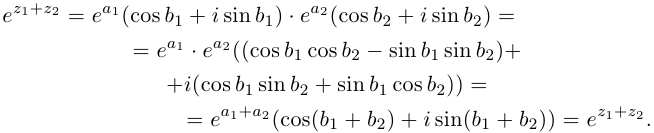
Далее, так как 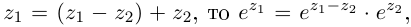 откуда следует второе утверждение леммы.
откуда следует второе утверждение леммы.
Пример №20
Вычислить 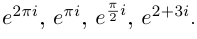
□ Имеем: 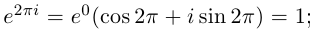
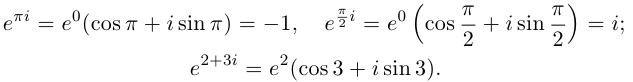
Так как при всех 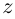 выполняются равенства
выполняются равенства 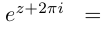
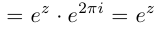 , то функция комплексной переменной
, то функция комплексной переменной 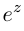 имеет мнимый период
имеет мнимый период 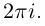 Привычной взаимной однозначности отображения при помощи функции
Привычной взаимной однозначности отображения при помощи функции 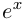 уже нет.
уже нет.
Определение 7.8. Логарифмом комплексного числа 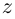 называется комплексное число
называется комплексное число 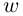 такое, что
такое, что 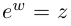 (обозначение:
(обозначение: 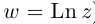 ).
).
Лемма 7.6. Если 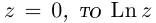 не определен. Если
не определен. Если 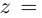
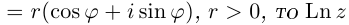 принимает бесконечно много значений, имеющих одинаковую действительную часть
принимает бесконечно много значений, имеющих одинаковую действительную часть 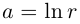 (обычный натуральный логарифм положительного числа) и бесконечное число значений мнимой части
(обычный натуральный логарифм положительного числа) и бесконечное число значений мнимой части 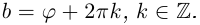
□ Первая часть леммы следует из того, что 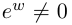 при любых
при любых 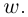 Пусть теперь
Пусть теперь 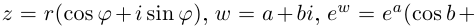
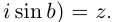 Тогда
Тогда 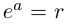 (откуда
(откуда 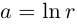 ),
), 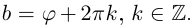
Таким образом, множество значений функции 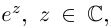 есть вся комплексная плоскость, кроме точки 0.
есть вся комплексная плоскость, кроме точки 0.
Пример №21
Найти все значения 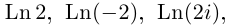
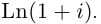
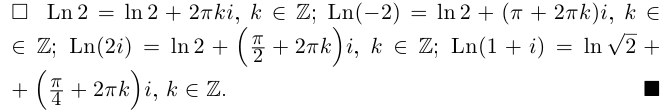
Определение 7.9. Для любых  определим
определим 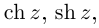
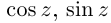 так:
так:
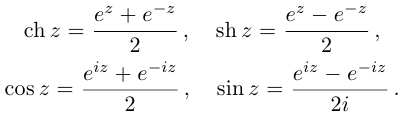
Если 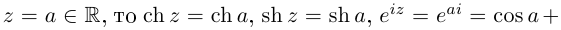
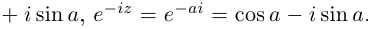 Поэтому
Поэтому
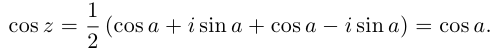
Аналогично, 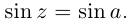
Отметим также, что все известные формулы тригонометрии сохраняются для комплексных значений аргументов (при этом 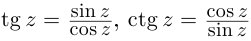 ). Например, для всех
). Например, для всех 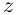
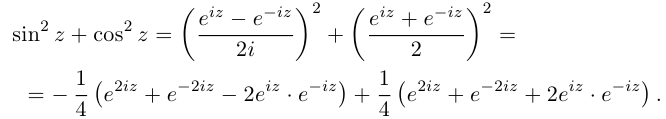
Так как 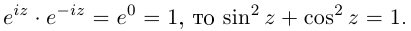
Легко видеть, что 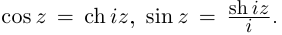 Косинус на действительной оси соответствует гиперболическому косинусу на мнимой оси и наоборот: аналогично для синусов. Поэтому формально все операции для тригонометрических и гиперболических функций проводятся одинаково с точностью до некоторых степеней числа
Косинус на действительной оси соответствует гиперболическому косинусу на мнимой оси и наоборот: аналогично для синусов. Поэтому формально все операции для тригонометрических и гиперболических функций проводятся одинаково с точностью до некоторых степеней числа 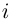 (если работать только с действительными числами, то всё будет происходить одинаково с точностью до степеней числа —1). Этим и объясняется сходство формул тригонометрии с соответствующими формулами для гиперболических функций, включая формулы для производных и разложения по формуле Тейлора.
(если работать только с действительными числами, то всё будет происходить одинаково с точностью до степеней числа —1). Этим и объясняется сходство формул тригонометрии с соответствующими формулами для гиперболических функций, включая формулы для производных и разложения по формуле Тейлора.
Комплекснозначные функции действительной переменной
Рассмотрим функцию  такую, что
такую, что 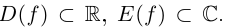 Тогда при всех
Тогда при всех  можно рассмотреть
можно рассмотреть 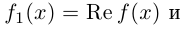
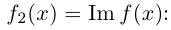
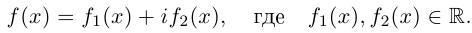
Так как  можно интерпретировать как плоскость
можно интерпретировать как плоскость  , то комплекснозначная функция действительной переменной фактически есть двумерная вектор-функция, значения которой записываются как комплексные числа.
, то комплекснозначная функция действительной переменной фактически есть двумерная вектор-функция, значения которой записываются как комплексные числа.
Определение 7.10. Комплекснозначная функция действительной переменной  называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) в точке или на промежутке, если таковыми же являются обе функции
называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) в точке или на промежутке, если таковыми же являются обе функции 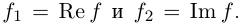 Для дифференцируемой функции по определению
Для дифференцируемой функции по определению 
Для комплекснозначных функций сохраняются формулы производной суммы, произведения и частного.
Лемма 7.7. Если комплекснозначные функции действительной переменной  дифференцируемы в точке
дифференцируемы в точке 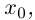 то функции
то функции  также дифференцируемы в этой точке, причем
также дифференцируемы в этой точке, причем
в точке  (в последнем случае нужно требовать, чтобы
(в последнем случае нужно требовать, чтобы 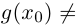
□ Докажем лемму для случая производной произведения. Утверждение для производной суммы доказывается проще, а для производной частного — несколько сложнее, но, по сути дела, аналогично.
Пусть 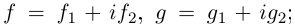 функции
функции  дифференцируемы в точке
дифференцируемы в точке 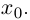 Тогда
Тогда
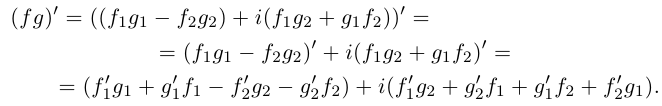
Функция  дифференцируема в точке
дифференцируема в точке  так как существуют и конечны все производные в последнем выражении. Далее,
так как существуют и конечны все производные в последнем выражении. Далее,
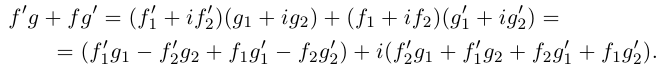
Легко видеть, что это выражение совпадает с 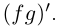
Пример №22
Доказать, что при любом  имеет место равенство
имеет место равенство
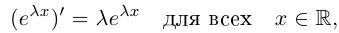
т.е. привычная для действительных 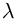 формула сохраняется и при комплексных
формула сохраняется и при комплексных 
□ Пусть 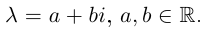
Тогда 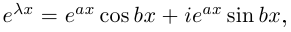
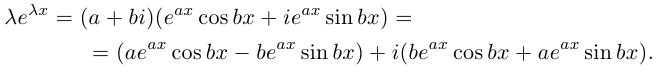
С другой стороны, 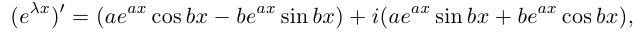
что совпадает с 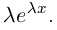
Отметим, что производная комплекснозначной функции берётся по действительной переменной. Принципиально иная ситуация возникает при рассмотрении комплекснозначных функций комплексной переменной и при дифференцировании их по комплексной переменной. Здесь имеют место совершенно неожиданные эффекты (например, если функция дифференцируема в окрестности точки, то она имеет производные всех порядков в этой окрестности), которые студенты обычно изучают на III курсе (курс ТФКП — теория функций комплексной переменной).
Многочлены
Функция комплексной переменной 
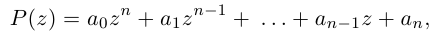
где  называется многочленом степени
называется многочленом степени 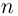 от переменной
от переменной 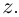 Многочлен степени 0 — это постоянная функция
Многочлен степени 0 — это постоянная функция 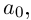 где
где 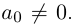 Нулевому многочлену не приписывается никакая степень (иногда удобно считать, что его степень равна
Нулевому многочлену не приписывается никакая степень (иногда удобно считать, что его степень равна  ). Если все
). Если все 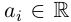 , то говорят о многочлене с действительными коэффициентами (
, то говорят о многочлене с действительными коэффициентами (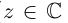 или
или 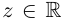 по смыслу задачи). Если все
по смыслу задачи). Если все 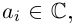 то говорят о многочлене с комплексными коэффициентами
то говорят о многочлене с комплексными коэффициентами 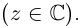
Если 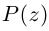 — многочлен степени
— многочлен степени 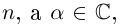 то многочлен
то многочлен 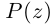 можно разделить с остатком на
можно разделить с остатком на 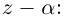
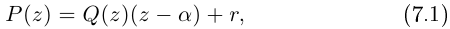
где 
Теорема 7.1 (Безу). Остаток от деления многочлена  на двучлен
на двучлен  равен
равен 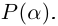
□ Из (7.1) имеем при 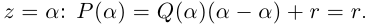
Следствие. Многочлен  делится без остатка на
делится без остатка на  тогда и только тогда, когда число
тогда и только тогда, когда число  является корнем многочлена
является корнем многочлена 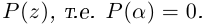
□ Утверждение немедленно следует из теоремы Безу.
Таким образом, число  является корнем многочлена
является корнем многочлена  тогда и только тогда, когда
тогда и только тогда, когда  где степень многочлена
где степень многочлена 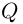 на единицу меньше степени Р.
на единицу меньше степени Р.
Теорема 7.2 (основная теорема алгебры). Любой многочлен степени  с комплексными коэффициентами имеет комплексный корень.
с комплексными коэффициентами имеет комплексный корень.
В настоящее время мы не располагаем математическим аппаратом для доказательства этой теоремы, поэтому примем её без доказательства. Доказана она будет очень просто в курсе ТФКП (и даже двумя способами — как простое следствие из теоремы Лиувилля или теоремы Руше).
Теорема 7.3. Многочлен с комплексными коэффициентами
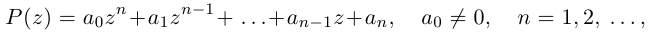
раскладывается в произведение линейных множителей
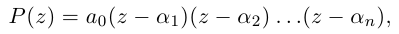
где 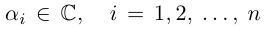 (среди чисел
(среди чисел  возможно, есть равные).
возможно, есть равные).
□ По основной теореме алгебры  где
где  — многочлен степени
— многочлен степени 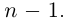 Применяя такую же процедуру к
Применяя такую же процедуру к  получим:
получим:  — многочлен степени
— многочлен степени  и т.д. В конце концов дойдём до многочлена степени 0.
и т.д. В конце концов дойдём до многочлена степени 0.
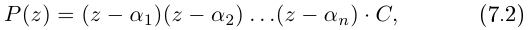
где 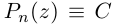 (комплексная постоянная). Здесь
(комплексная постоянная). Здесь 
 — комплексные числа, среди которых могут быть равные.
— комплексные числа, среди которых могут быть равные.
Если раскрыть скобки в правой части (7.2), то коэффициент при 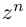 будет равен С, т.е.
будет равен С, т.е. 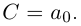
Определение 7.11. Комплексное число  называется корнем кратности
называется корнем кратности  многочлена
многочлена 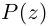 степени
степени  если
если  — многочлен такой, что
— многочлен такой, что  При
При 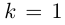 корень называется простым, при
корень называется простым, при 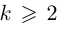 — кратным.
— кратным.
Если 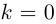 , то число
, то число  не является корнем многочлена
не является корнем многочлена 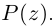
В общем случае, учитывая кратность корней, многочлен  степени
степени  раскладывается на линейные множители:
раскладывается на линейные множители:
где все комплексные числа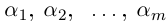 различны, корень
различны, корень 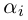 имеет кратность
имеет кратность 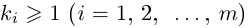 , при этом степень многочлена равна
, при этом степень многочлена равна 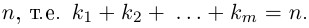
Лемма 7.8. Пусть 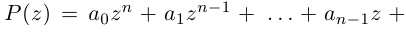
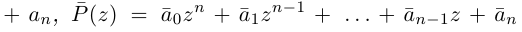 (многочлен, сопряжённый к P). Число
(многочлен, сопряжённый к P). Число  является корнем многочлена Р кратности
является корнем многочлена Р кратности  тогда и только тогда, когда число а является корнем многочлена
тогда и только тогда, когда число а является корнем многочлена 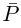 той же кратности
той же кратности 
□ Так как  то утверждение достаточно доказать лишь в одну сторону. Пусть
то утверждение достаточно доказать лишь в одну сторону. Пусть 
 Тогда
Тогда 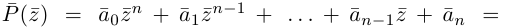
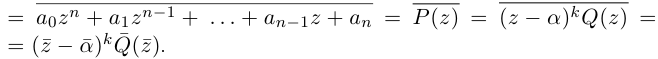
Так как  — любое комплексное число, то в последней записи можно заменить
— любое комплексное число, то в последней записи можно заменить 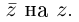 Получим
Получим
Это и означает, что  — корень многочлена
— корень многочлена  кратности
кратности 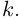
Следствие. Если 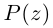 — многочлен с действительными коэффициентами, то числа
— многочлен с действительными коэффициентами, то числа  одновременно являются его корнями, причем кратности их совпадают (т.е. недействительные корни появляются «парочками» — взаимно сопряжённые корни одинаковой кратности).
одновременно являются его корнями, причем кратности их совпадают (т.е. недействительные корни появляются «парочками» — взаимно сопряжённые корни одинаковой кратности).
□ Это очевидно из леммы 7.8, так как 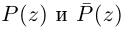 — один и тот же многочлен.
— один и тот же многочлен.
Теорема 7.4. Многочлен степени 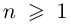 с действительными коэффициентами
с действительными коэффициентами 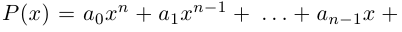
 раскладывается в произведение линейных и неприводимых квадратичных множителей:
раскладывается в произведение линейных и неприводимых квадратичных множителей:
□ По теореме 7.3 и лемме 7.8
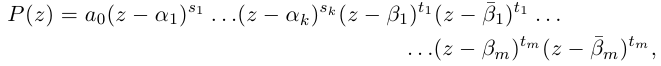
где  — действительные корни многочлена
— действительные корни многочлена  кратностей
кратностей  соответственно, a
соответственно, a  — оставшиеся корни (
— оставшиеся корни ( имеют одинаковую кратность
имеют одинаковую кратность 
 ). Очевидно, что степень многочлена равна
). Очевидно, что степень многочлена равна 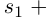
 т.е. эта сумма равна
т.е. эта сумма равна 
Пусть 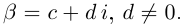 Тогда
Тогда 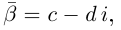
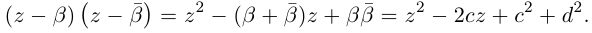
Получили квадратный трёхчлен с действительными коэффициентами 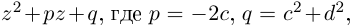 который имеет отрицательный дискриминант
который имеет отрицательный дискриминант 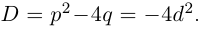 Остаётся символически заменить
Остаётся символически заменить 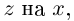 подчёркивая этим, что нас интересуют лишь действительные значения
подчёркивая этим, что нас интересуют лишь действительные значения  и мы получим нужное равенство.
и мы получим нужное равенство.
Теорема 7.4 является примером утверждения, в формулировке которого отсутствуют комплексные числа (чисто действительное утверждение), а естественное доказательство его получается с выходом во множество комплексных чисел. Таких утверждений можно встретить немало в различных математических курсах и прикладных науках.
Кстати, квадратный трехчлен с комплексными коэффициентами имеет такой же вид разложения на линейные множители, как и квадратный трёхчлен с действительными корнями в элементарной алгебре:
Корни 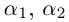 — комплексные, и они обязательно существуют. Роль дискриминанта
— комплексные, и они обязательно существуют. Роль дискриминанта 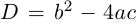 сводится только к определению того, различны ли корни
сводится только к определению того, различны ли корни 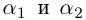 или они совпадают (т.е. квадратный трёхчлен имеет один корень
или они совпадают (т.е. квадратный трёхчлен имеет один корень  кратности 2). Если
кратности 2). Если 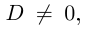 то квадратный трёхчлен имеет два различных простых корня, если
то квадратный трёхчлен имеет два различных простых корня, если 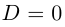 — один корень кратности 2. В самом деле, решая квадратное уравнение
— один корень кратности 2. В самом деле, решая квадратное уравнение 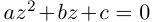 методом выделения полного квадрата, получим, как и в элементарной алгебре:
методом выделения полного квадрата, получим, как и в элементарной алгебре:
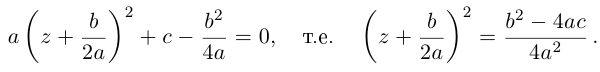
Если 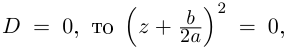 и уравнение имеет один корень
и уравнение имеет один корень 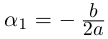 кратности 2
кратности 2 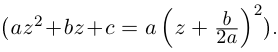 Если
Если 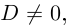 то
то 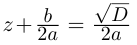 (писать ± не имеет смысла, так как
(писать ± не имеет смысла, так как 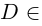
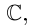 и под
и под 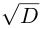 понимаются оба значения квадратного корня из ненулевого комплексного числа). Окончательно получим привычную формулу корней квадратного уравнения:
понимаются оба значения квадратного корня из ненулевого комплексного числа). Окончательно получим привычную формулу корней квадратного уравнения:
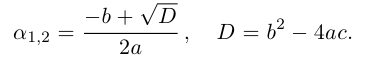
Пример №23
Решить уравнение 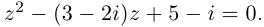
□ 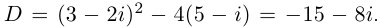 Найдём оба значения
Найдём оба значения 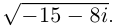 Пусть
Пусть 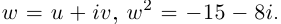 Тогда
Тогда 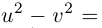
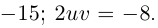 Решая эту систему, получим:
Решая эту систему, получим: 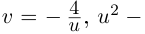
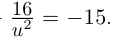 Полученное биквадратное уравнение
Полученное биквадратное уравнение 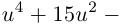
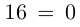 решается при помощи замены
решается при помощи замены 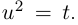 Квадратное уравнение
Квадратное уравнение 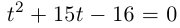 имеет корни
имеет корни 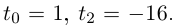 Так как
Так как 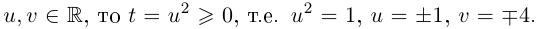 Получили два значения квадратного корня:
Получили два значения квадратного корня: 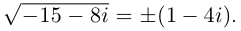 Тогда корни данного уравнения равны
Тогда корни данного уравнения равны
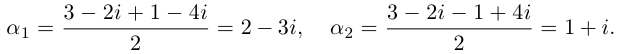
Пример №24
Найти все значения 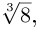 решая уравнение
решая уравнение 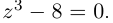
□ Левая часть раскладывается на множители:
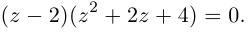
Поэтому один из корней равен 2. Квадратный трёхчлен 
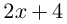 не имеет действительных корней
не имеет действительных корней 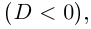 поэтому
поэтому 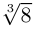 имеет всего одно действительное значение 2. Найдём оставшиеся два комплексно-сопряжённых значения. Решаем квадратное уравнение
имеет всего одно действительное значение 2. Найдём оставшиеся два комплексно-сопряжённых значения. Решаем квадратное уравнение 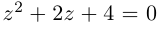 по формуле чётного коэффициента:
по формуле чётного коэффициента:
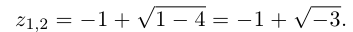
Во множестве комплексных чисел 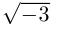 имеет два значения
имеет два значения 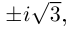 поэтому
поэтому  имеет 3 комплексных значения:
имеет 3 комплексных значения: 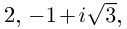
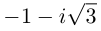 (такой же результат был получен в примере 7.3 другим способом). ■
(такой же результат был получен в примере 7.3 другим способом). ■
Разложение правильной дроби в сумму простейших дробей
Мы будем рассматривать действительные дробно-рациональные функции 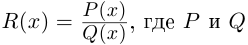 — многочлены степеней соответственно
— многочлены степеней соответственно 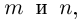 где
где 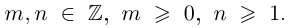 Дробь называется правильной, если
Дробь называется правильной, если 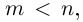 и неправильной, если
и неправильной, если 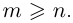
Лемма 7.9. Если 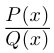 правильная дробь и
правильная дробь и 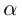 —действительный корень многочлена
—действительный корень многочлена  кратности
кратности  то
то
где 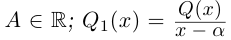 — многочлен, для которого
— многочлен, для которого 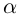 является корнем кратности
является корнем кратности  a
a  — такой многочлен, что дробь
— такой многочлен, что дробь 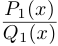 является правильной.
является правильной.
□ Так как 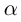 — корень
— корень 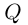 кратности
кратности  то
то 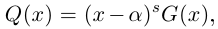 где
где  — многочлен такой, что
— многочлен такой, что  Рассмотрим число
Рассмотрим число 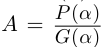 и многочлен
и многочлен 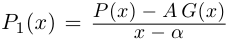 (это многочлен, так как
(это многочлен, так как  и числитель делится нацело на
и числитель делится нацело на  ).
).
Так как степень G меньше степени Q и степень Р меньше степени Q, то степень числителя последней дроби меньше степени Q; значит, степень  меньше степени
меньше степени 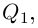 т.е. дробь
т.е. дробь  правильная. Далее,
правильная. Далее,  откуда
откуда 
Утверждение леммы, очевидно, сохраняется, если все числа и многочлены считать комплексными.
Лемма 7.10. Пусть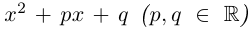 — неприводимый квадратный трёхчлен, входящий в разложение многочлена
— неприводимый квадратный трёхчлен, входящий в разложение многочлена  на множители в степени
на множители в степени  Тогда правильная дробь
Тогда правильная дробь  представляется в виде
представляется в виде
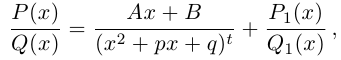
где 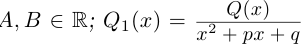 — многочлен, в разложение которого
— многочлен, в разложение которого 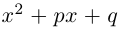 входит в степени
входит в степени 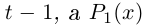 — такой многочлен, что дробь
— такой многочлен, что дробь 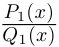 является правильной.
является правильной.
□ Пусть  где
где  и
и  комплексно-сопряжённые корни квадратного трёхчлена
комплексно-сопряжённые корни квадратного трёхчлена 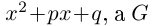 — действительный многочлен такой, что
— действительный многочлен такой, что 
 Рассмотрим действительные числа А и В такие, что
Рассмотрим действительные числа А и В такие, что
Такие числа А и В определены единственным образом, так как если 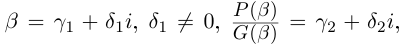 то равенство (7.3) перепишется так:
то равенство (7.3) перепишется так:
и числа А, В находятся из системы  очевидно, имеющей единственное решение. Из (7.3) следует также, что
очевидно, имеющей единственное решение. Из (7.3) следует также, что  так как
так как  — многочлены с действительными коэффициентами.
— многочлены с действительными коэффициентами.
Рассмотрим многочлен 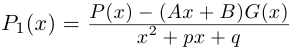 (это — многочлен, так как
(это — многочлен, так как 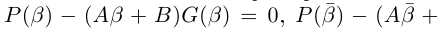
 значит, числитель делится нацело на
значит, числитель делится нацело на 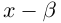 и на
и на 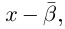 следовательно, делится на
следовательно, делится на 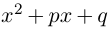 ). Пусть степень Q равна
). Пусть степень Q равна  Так как степень G не превосходит
Так как степень G не превосходит 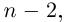 то степень многочлена
то степень многочлена  не превосходит
не превосходит  т.е. меньше степени Q. Степень Р также меньше степени Q, поэтому степень числителя последней дроби меньше степени Q.
т.е. меньше степени Q. Степень Р также меньше степени Q, поэтому степень числителя последней дроби меньше степени Q.
Значит, степень  меньше, чем
меньше, чем 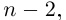 , т.е. меньше степени
, т.е. меньше степени  и дробь
и дробь  правильная. Далее,
правильная. Далее,
откуда
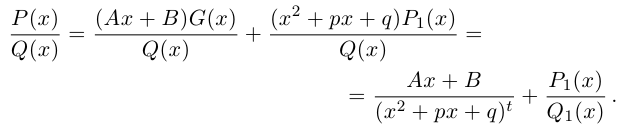
Последовательно выделяя из многочлена  линейные, а затем неприводимые квадратичные множители, и применяя соответственно леммы 7.9 и 7.10, получим разложение
линейные, а затем неприводимые квадратичные множители, и применяя соответственно леммы 7.9 и 7.10, получим разложение  в сумму правильных дробей вида
в сумму правильных дробей вида

(здесь 
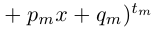 — как разложение многочлена в теореме 7.4).
— как разложение многочлена в теореме 7.4).
Все слагаемые последней суммы называются простейшими дробями. Все коэффициенты, обозначенные символом  , являются действительными числами (вообще говоря, различными). Всего их
, являются действительными числами (вообще говоря, различными). Всего их  штук. Можно доказать, что они определены единственным образом. Процесс выделения слагаемых по леммам 7.9 и 7.10 прекратится, когда в знаменателе останется ровно один множитель вида
штук. Можно доказать, что они определены единственным образом. Процесс выделения слагаемых по леммам 7.9 и 7.10 прекратится, когда в знаменателе останется ровно один множитель вида  Но такая правильная дробь сама будет простейшей. Таким образом, доказана
Но такая правильная дробь сама будет простейшей. Таким образом, доказана
Теорема 7.5. Любая правильная рациональная дробь с действительными коэффициентами раскладывается в сумму простейших дробей.
Пример №25
Разложить в сумму простейших дробей:
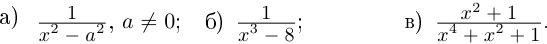
а) 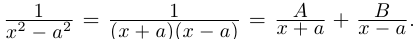 Приводя к общему знаменателю, имеем:
Приводя к общему знаменателю, имеем: 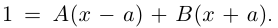 При
При 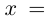
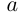 получим
получим 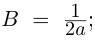 при
при 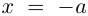 получим
получим 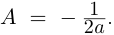 Окончательно имеем:
Окончательно имеем: 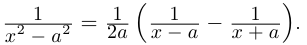
б)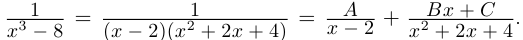 Приводя в общему знаменателю, имеем:
Приводя в общему знаменателю, имеем: 
 При
При  получим
получим 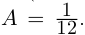 Приравнивая коэффициенты при
Приравнивая коэффициенты при  получим
получим 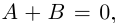 т.е.
т.е.  Приравнивая свободные члены, получим
Приравнивая свободные члены, получим 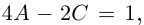 откуда
откуда 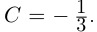 Окончательно имеем
Окончательно имеем
в) 
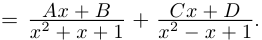 Приводя к общему знаменателю, имеем:
Приводя к общему знаменателю, имеем: 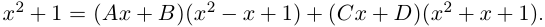 Приравнивая коэффициенты при
Приравнивая коэффициенты при 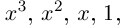 получим:
получим: 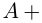
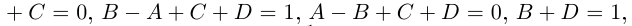 откуда
откуда  Окончательно имеем
Окончательно имеем
Вычисление комплексного числа
Определение 1.1. Многочленом (полиномом) степени n с действительными коэффициентами называется любое выражение вида
где 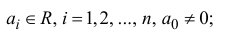
х – переменная.
Корнем многочлена (1.1) называется любое число 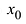 такое, что
такое, что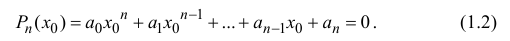
Нетрудно заметить, что некоторые многочлены вообще не имеют
действительных корней, например: 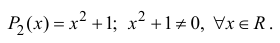
Расширим множество действительных чисел. Добавим к этому
множеству символ i , такой что 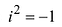 ( i называется мнимой единицей).
( i называется мнимой единицей).
Тогда ±i – два корня уравнения 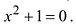
Определение 1.2. Множеством комплексных чисел называется множество
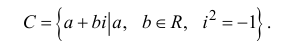
Суммой двух комплексных чисел 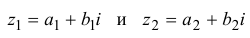 называется число
называется число
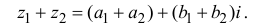 .
.
Произведением двух комплексных чисел 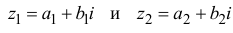 называется число
называется число
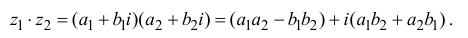
Для числа z= a +bi число а называется действительной частью,
число b – мнимой частью. Обозначения: 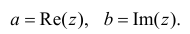
Относительно операций «+» и « · » комплексные числа С обладают
такими же свойствами, как и действительные числа. Эти операции
коммутативны и ассоциативны; для них существуют обратные операции:
вычитание и деление (кроме деления на 0).
Пример №26
Найти 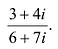
Решение:
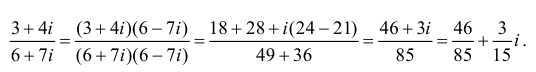
Теорема 1.1 (основная теорема алгебры). Любое уравнение вида (1.2)
имеет решение во множестве С.
Пример №27
Решить уравнение
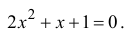
Решение:
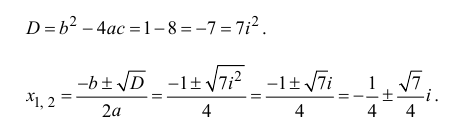
Определение 1.3. Для комплексного числа z =a +bi число z =a -bi называется комплексно-сопряженным, число 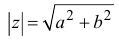 называется модулем z.
называется модулем z.
Если рассмотреть плоскость с декартовой системой координат ( O,x,y ) и на оси Ох отложить а – действительную часть z, а на оси Oy – b – мнимую часть z, то получим взаимно однозначное соответствие между множеством С всех
комплексных чисел и множеством точек плоскости.
Такая плоскость называется комплексной плоскостью, рис. 1.1.
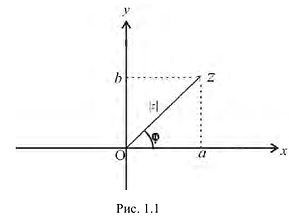
При этом 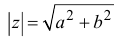 – длина радиуса-вектора точки z.
– длина радиуса-вектора точки z.
Определение 1.4. Аргументом комплексного числа z =a +bi называется
угол 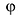 , который образует радиус-вектор точки z с положительным
, который образует радиус-вектор точки z с положительным
направлением оси Ох Аргумент будем обозначать Argz . Аргумент
определен с точностью до 2 πn. При этом значение 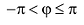 называется
называется
главным и обозначается argz.
Замечание. 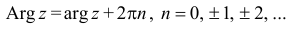
При этом
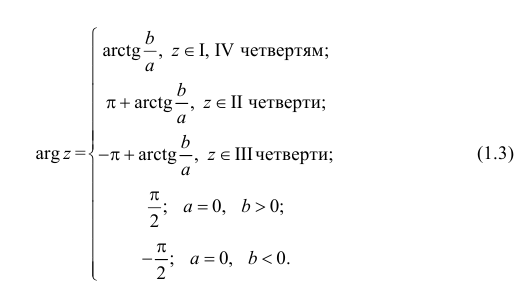
Если  – аргумент z, то z представляется в виде
– аргумент z, то z представляется в виде 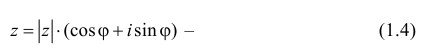
тригонометрическая форма комплексного числа.
Теорема 1.2. Пусть 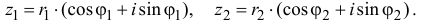
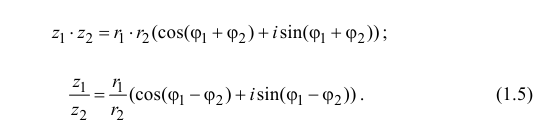
Доказательство
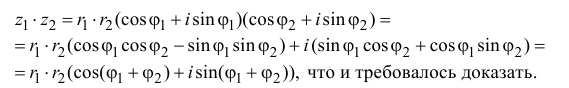
Из формул (1.5) следует, в частности, что 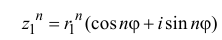 – формула Муавра. (1.6)
– формула Муавра. (1.6)
Пример №28
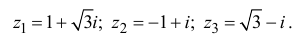 Представить числа
Представить числа  в тригонометрической форме.
в тригонометрической форме.
Решение:
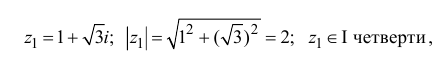
поэтому по формуле (1.3)
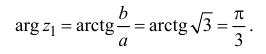
Тогда по формуле (1.4)
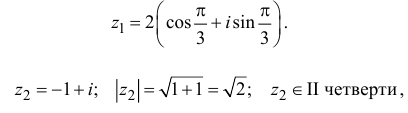
поэтому по формуле (1.3)
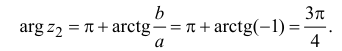
Тогда 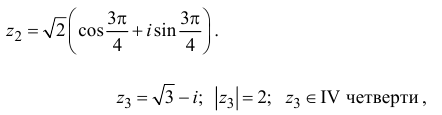
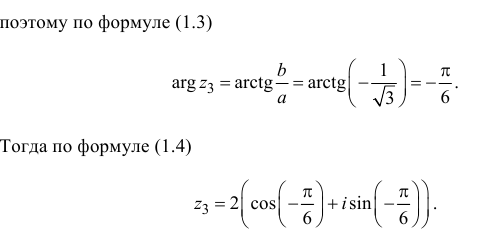
Из формул (1.5), (1.6) видно, что аргумент 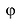 комплексного числа z при
комплексного числа z при
умножении, делении, возведении в степень ведет себя как показатель
степени. Обозначим 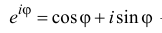 – формула Эйлера. (1.7)
– формула Эйлера. (1.7)
Тогда из теоремы 1.2 следует, что
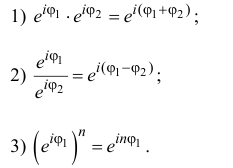
Учитывая (1.7), формулу (1.4) для z можно переписать в виде 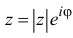 показательная форма комплексного числа.
показательная форма комплексного числа.
Пример №29
Вычислить 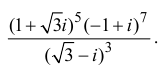
Решение:
Согласно примеру 1.3 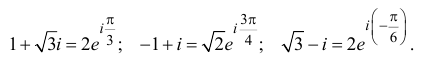
Поэтому
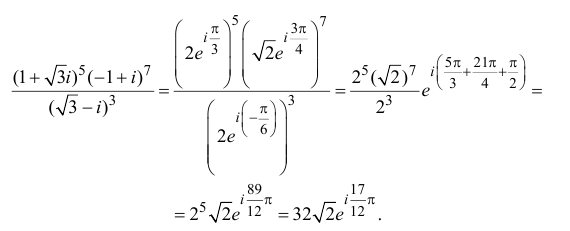
Определение 1.5. Корнем n-й степени из числа z  C называется такое
C называется такое
число  , что
, что  , при этом обозначается
, при этом обозначается 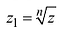 . Таким образом
. Таким образом

Из формулы (1.8) видно что  корней n-й степени из числа z, при этом,
корней n-й степени из числа z, при этом,
если 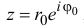 , то
, то

Пример №30
Найти 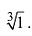
Решение:
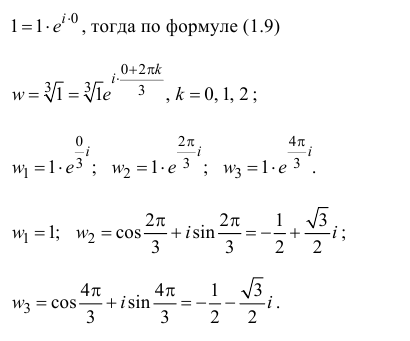
- Координаты на прямой
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
7
Лекция
Комплексные
числа.
Определение.
Комплексным
числом z
называется
выражение
![]() ,
,
где a
и b
– действительные числа, i
– мнимая единица, которая определяется
соотношением:
![]()
При
этом число a
называется действительной
частью числа
z
(a
= Re
z),
а b–
мнимой частью
(b
= Im
z).
Если
a
=Re
z
=0, то число
z
будет чисто
мнимым, если
b
= Im
z
= 0, то число
z
будет действительным.
Определение.
Числа
![]()
и
![]() называются
называются
комплексно
– сопряженными.
Определение.
Два комплексных числа
![]()
и
![]()
называются равными, если соответственно
равны их действительные и мнимые части:
![]()
Определение.
Комплексное число равно нулю, если
соответственно равны нулю действительная
и мнимая части.
![]()
Понятие
комплексного числа имеет геометрическое
истолкование. Множество комплексных
чисел является расширением множества
действительных чисел за счет включения
множества мнимых чисел. Комплексные
числа включают в себя все множества
чисел, которые изучались ранее. Так
натуральные, целые, рациональные,
иррациональные, действительные числа
являются, вообще говоря, частными
случаями комплексных чисел.
Если
любое действительное число может быть
геометрически представлено в виде точки
на числовой прямой, то комплексное число
представляется точкой на плоскости,
координатами которой будут соответственно
действительная и мнимая части комплексного
числа. При этом горизонтальная ось будет
являться действительной числовой осью,
а вертикальная – мнимой осью.
у
A(a,
b)
r b
0 a
x
Таким
образом, на оси Оx
располагаются действительные числа, а
на оси Оy
– чисто мнимые.
С
помощью подобного геометрического
представления можно представлять числа
в так называемой тригонометрической
форме.
Тригонометрическая
форма комплексного числа.
Из
геометрических соображений видно, что
![]() .
.
Тогда комплексное число можно представить
в виде:
![]()
Такая
форма записи называется тригонометрической
формой записи комплексного числа.
При
этом величина r
называется модулем
комплексного
числа, а угол
– аргументом
комплексного
числа.
![]() .
.
Из
геометрических соображений видно:
![]()
Очевидно,
что комплексно – сопряженные числа
имеют одинаковые модули и противоположные
аргументы.
![]()
Действия с
комплексными числами.
Основные
действия с комплексными числами вытекают
из действий с многочленами.
1)
Сложение и
вычитание.
![]()
![]()
2)
Умножение.
![]()
![]()
В
тригонометрической форме:
![]() ,
,
![]()
![]()
С
случае комплексно – сопряженных чисел:
![]()
3)
Деление.
![]()
![]()
![]()
В
тригонометрической форме:
![]()
4)
Возведение
в степень.
Из
операции умножения комплексных чисел
следует, что
![]()
В
общем случае получим:
![]() ,
,
где
n
– целое
положительное число.
Это
выражение называется формулой
Муавра. (Абрахам
де Муавр (1667 – 1754) – английский математик)
Формулу
Муавра можно использовать для нахождения
тригонометрических функций двойного,
тройного и т.д. углов.
Пример.
Найти формулы sin2
и cos2.
Рассмотрим
некоторое комплексное число
![]()
Тогда
с одной стороны
![]() .
.
По
формуле Муавра:
![]()
Приравнивая,
получим
![]()
Т.к.
два комплексных числа равны, если равны
их действительные и мнимые части, то
![]()
![]()
Получили
известные формулы двойного угла.
5)
Извлечение
корня из комплексного числа.
![]()
Возводя
в степень, получим:
![]()
Отсюда:
![]()
![]()
Таким
образом, корень n
– ой степени из комплексного числа
имеет n
различных значений для k=0,1,…,n-1.
Показательная
форма комплексного числа.
Рассмотрим
показательную функцию
![]()
Можно
показать, что функция w
может быть записана в виде:
![]()
Данное
равенство называется уравнением
Эйлера. Вывод
этого уравнения будет рассмотрен
позднее.
Для
комплексных чисел будут справедливы
следующие свойства:
1)
![]()
2)
![]()
3)
![]()
где m
– целое число.
Если
в уравнении Эйлера показатель степени
принять за чисто мнимое число (х=0),
то получаем:
![]()
Для
комплексно – сопряженного числа
получаем:
![]()
Из
этих двух уравнений получаем:
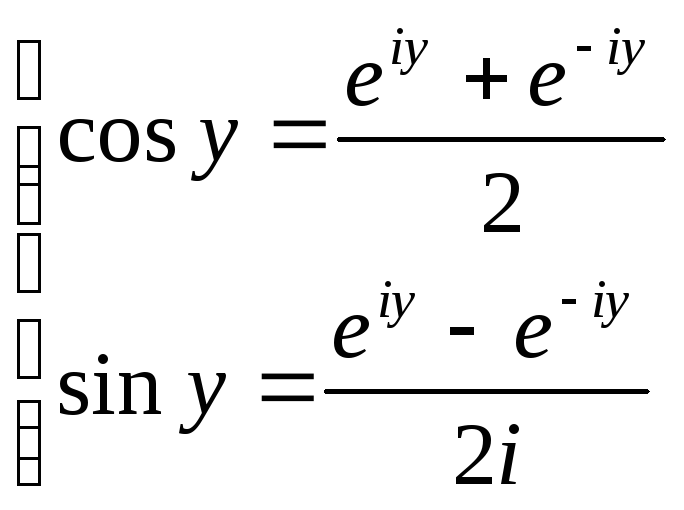
Этими
формулами пользуются для нахождения
значений степеней тригонометрических
функций через функции кратных углов.
Если
представить комплексное число в
тригонометрической форме:
![]()
и
воспользуемся формулой Эйлера:
![]()
![]()
Полученное
равенство и есть показательная
форма комплексного числа.
Разложение
многочлена на множители.
Определение.
Функция вида f(x)![]()
называется целой
рациональной
функцией от х.
Теорема
Безу.
(Этьенн Безу (1730 – 1783) – французский
математик)
При
делении многочлена f(x)
на разность x
– a
получается остаток, равный f(a).
Доказательство.
При делении многочлена f(x)
на разность x
– a
частным
будет многочлен f1(x)
степени на
единицу меньшей, чем f(x),
а остатком
– постоянное число R.
![]()
Переходя
к пределу при х
a,
получаем
f(a)
= R.
Следствие.
Если, а – корень многочлена, т.е. f(a)
= 0, то многочлен f(x)
делится на (х – а) без остатка.
Определение.
Если уравнение имеет вид Р(х)
= 0, где Р(х)
– многочлен степени n,
то это уравнение называется алгебраическим
уравнением степени n.
Теорема.
(Основная теорема алгебры) Всякая целая
рациональная функция f(x)
имеет, по крайней мере, один корень,
действительный или комплексный.
Теорема.
Всякий многочлен n
– ой степени разлагается на n
линейных множителей вида (x
– a)
и множитель, равный коэффициенту при
xn.
Теорема.
Если два многочлена тождественно равны
друг другу, то коэффициенты одного
многочлена равны соответствующим
коэффициентам другого.
Если среди корней
многочлена встречаются кратные корни,
то разложение на множители имеет вид:
![]()
![]()
ki
– кратность соответствующего корня.
Отсюда
следует, что любой
многочлен n
– ой степени имеет ровно n
корней (действительных или комплексных).
Это
свойство имеет большое значение для
решения алгебраических уравнений,
дифференциальных уравнений и играет
важную роль в анализе функций.
Рассмотрим
несколько примеров действий с комплексными
числами.
Пример.
Даны два комплексных числа
![]() .
.
Требуется а) найти значение выражения
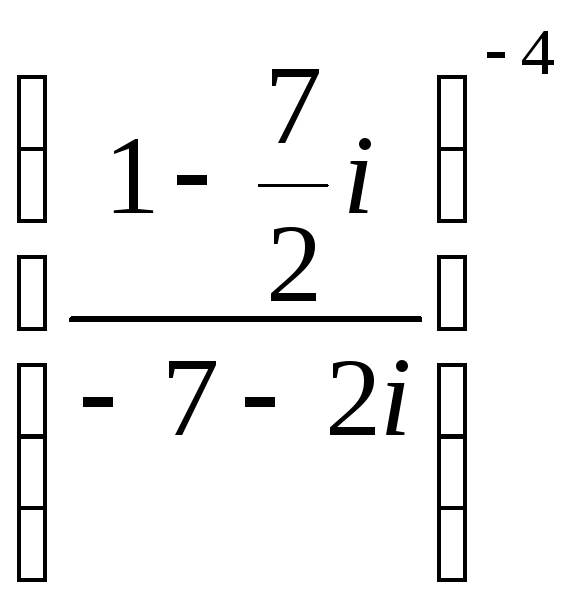 в
в
алгебраической форме, б) для числа
![]()
найти тригонометрическую форму, найти
z20,
найти корни уравнения
![]()
-
Очевидно,
справедливо следующее преобразование:
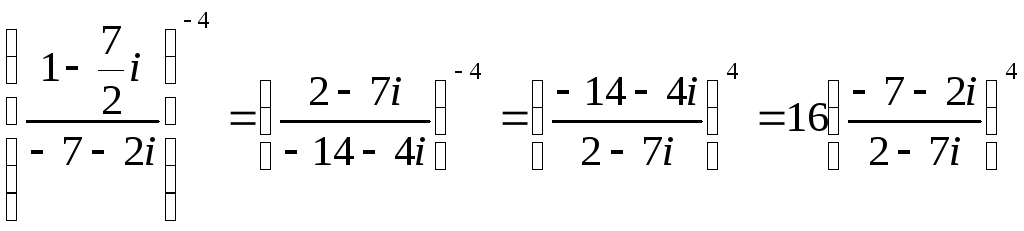
Далее
производим деление двух комплексных
чисел:
![]()
Получаем
значение заданного выражения: 16(-i)4
= 16i4
=16.
б)
Число
![]()
представим в виде
![]() ,
,
где
![]()
Тогда
![]() .
.
Для
нахождения
![]()
воспльзуемся формулой Муавра.
![]()
![]()
Если
![]() ,
,
то
![]()
![]()
Подставляя
последовательно k=0,
k=1
и k=2
и производя вычисления получим 3 значения
корня кубического.
Содержание:
- Действительная и мнимая часть комплексного числа
- Мнимая единица
- Равные комплексные числа
Определение
Комплексным числом называется выражение вида
$z=a+b i$
Например. $z=3-7 i$
Действительная и мнимая часть комплексного числа
Определение
Действительное число $a$ называется
действительной частью комплексного числа $z=a+b i$ и
обозначается $a=operatorname{Re} z$
(От французского слова reel – действительный).
Действительное число
$b$ называется мнимой частью числа
$z=a+b i$ и обозначается
$b=operatorname{Im} z$ (От французского слова imaginaire – мнимый).
Например. Для комплексного числа
$z=3-7 i$ действительная часть
$a=operatorname{Re} z=3$, а мнимая –
$b=operatorname{Im} z=-7$ .
Если действительная часть комплексного числа $z=a+b i$
равна нулю ( $a=operatorname{Re} z=0$ ), то комплексное число
называется чисто мнимым.
Например. $z=-2 i$
Мнимая единица
Величина $i$ называется мнимой единицей и
удовлетворяет соотношению:
Равные комплексные числа
Два комплексных числа $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$ называются равными, если равны их
действительные и мнимые части соответственно:
$z_{1}=z_{2} Leftrightarrow a_{1}=a_{2} wedge b_{1}=b_{2}$
Пример
Задание. Определить при каких значениях
$x$ и
$y$ числа
$z_{1}=2-x i$ и
$z_{2}=y+2 i$ будут равными.
Решение. Согласно определению $z_{1}=z_{2}$ тогда и только тогда, когда
$2=y wedge-x=2 Rightarrow y=2, x=-2$
Ответ. $x=-2, y=2$
Число $overline{z}=a-b i$ называется
комплексно сопряженным числом к числу
$z=a+b i$ .
То есть комплексно сопряженные числа отличаются лишь знаком мнимой части.
Например. Для комплексного числа
$z_{1}=2+3 i$ комплексно сопряженным есть число
$overline{z}_{1}=2-3 i$ ; для
$z_{2}=i$ комплексно сопряженное
$overline{z}_{2}=-i$ и для
$z_{3}=-2$ имеем, что
$overline{z}_{3}=-2$ .
Комплексное число
$-z=-a-b i$ называется противоположным к комплексному числу
$z=a+b i$ .
Например. Противоположным к числу
$z=2+i$ есть число:
$-z=-(2+i)=-2-i$ .
Читать дальше: геометрическая интерпретация комплексного числа.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!



