Чистый дисконтированный доход — показатель, позволяющий оценить инвестиционную привлекательность проекта. Основываясь на величине чистого дисконтированного дохода, инвестор может понять, насколько обоснованными являются его первоначальные капиталовложения с учетом запланированного уровня доходности проекта, не дожидаясь его завершения.
Чистый дисконтированный доход: формула
В общем порядке величина чистого дисконтированного дохода определяется как сумма всех дисконтированных значений потоков будущих платежей, приведенных к сегодняшнему дню, и определяется следующим образом:
NPV = – IC + Ʃ CFt/ (1 + r)ᵗ,
где:
NPV — величина чистого дисконтированного дохода;
IC — первоначальные инвестиции;
CFt — потоки денежных средств в конкретный период срока окупаемости проекта, которые представляют собой суммы притоков и оттоков денежных средств в каждом конкретном периоде t (t = 1…n);
r — ставка дисконтирования.
В зависимости от значения данного показателя инвестор оценивает привлекательность проекта. В случае, если:
1. NPV > 0, то инвестиционный проект выгоден, инвестор получит прибыль;
2. NPV = 0, то проект не принесет ни прибыли, ни убытка;
3. NPV < 0, проект невыгоден и сулит инвестору убытки.
Также для анализа инвестиционной привлекательности проекта инвесты изучают чистый денежный поток предприятия. Существует 2 метода определения величины чистого денежного потока: прямой и косвенный.
Денежный поток рассчитывается по специальной формуле, которую можно найти в материале от КонсультантПлюс. Если у вас нет доступа к системе К+, получите пробный онлайн-доступ бесплатно.
Учет инфляции при расчете чистого дисконтированного дохода
В связи с тем, что в некоторых ситуациях инфляционные колебания невозможно нивелировать на практике, возникает вопрос о том, каким образом отразить влияние инфляции на показатель чистого дисконтированного дохода. Наиболее распространенным решением данной проблемы является корректировка дисконта на прогнозируемый уровень инфляции.
При этом процентная ставка будет рассчитываться следующим образом:
R = (1 + r) × J,
где:
R — дисконтная ставка с учетом инфляции;
r — дисконт;
J — уровень инфляции.
Таким образом, чем выше уровень инфляции, прогнозируемый на время реализации проекта, тем ниже должна быть доходность проекта, чтобы после дисконтирования проект не стал убыточным.
Чистый дисконтированный доход: пример расчета
Предположим, что инвестор хочет модернизировать систему автоматизации производственного процесса. Предполагается, что сумма затрат на перевооружение конвейера составит 50 000,00 руб. При этом планируется увеличение объемов производства за счет нового оборудования, как следствие — увеличение объемов продаж в течение ближайших 5 лет. Приток денежных средств за 1-й год составит 45 000,00 руб., за 2-й год — 40 000,00 руб., за 3-й год — 35 000,00 руб., за 4-й год — 30 000,00 руб., за 5-й год — 25 000,00 руб. Необходимая норма прибыли — 10%. Расчет приведенной стоимости проекта представлен в таблице.
|
Период (t),год |
Денежный поток (CF) |
Дисконт (r) |
Чистая приведенная стоимость (CFt) |
|
0 |
–50 000,00 |
10% |
–50 000,00 |
|
1 |
45 000,00 |
10% |
40 909,09 |
|
2 |
40 000,00 |
10% |
33 057,85 |
|
3 |
35 000,00 |
10% |
26 296,02 |
|
4 |
30 000,00 |
10% |
20 490,40 |
|
5 |
25 000,00 |
10% |
15 523,03 |
|
Чистый дисконтированный доход (NPV)м |
86 276,40 |
Исходя из того, что показатель NPV положительный, можно сделать вывод о том, что данный проект рентабелен.
Однако ситуация изменится в худшую сторону, если предположить, что инфляция на протяжении всех пяти лет будет держаться на уровне 8%.
|
Период (t),год |
Денежный поток (CF) |
Дисконт (r) |
Уровень инфляции, (J) |
Чистая приведенная стоимость (CFt) c учетом инфляции |
|
0 |
–50 000,00 |
10% |
8% |
–46 296,30 |
|
1 |
45 000,00 |
10% |
8% |
34 435,26 |
|
2 |
40 000,00 |
10% |
8% |
25 296,79 |
|
3 |
35 000,00 |
10% |
8% |
18 293,14 |
|
4 |
30 000,00 |
10% |
8% |
12 958,54 |
|
5 |
25 000,00 |
10% |
8% |
8 924,61 |
|
Чистый дисконтированный доход (NPV) |
53 612,05 |
В целом чистый дисконтированный доход остался в пределах положительных значений, значит, проект все также принесет инвесторам прибыль. Однако по сравнению с первым вариантом, где инфляция не была учтена, отдача от первоначальных вложений с учетом дисконтированной стоимости поступлений от продажи новой продукции стала значительно ниже.
Итоги
Принимая решение о выгодном вложении денежных средств, высвобожденных из делового оборота, инвестор должен сделать выбор в пользу наиболее доходного проекта. На основании расчета чистого дисконтированного дохода сравнивать несколько вариантов с разными сроками окупаемости становится удобнее.
Если вам нужно рассчитать чистую прибыль, см. наш материал «Расчет чистой прибыли по балансу – формула».
О том, как провести анализ чистой прибыли, вы можете узнать из материала «Порядок проведения анализа чистой прибыли предприятия».
Чистая приведённая стоимость (ЧПС, чистый приведённый эффект, чистая текущая стоимость, чистый дисконтированный доход, ЧДД, англ. net present value, NPV) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню. Показатель NPV представляет собой разность между всеми денежными притоками и оттоками, приведёнными к текущему моменту времени (моменту оценки инвестиционного проекта). Он показывает величину денежных средств, которую инвестор ожидает получить от проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением проекта. Поскольку денежные платежи оцениваются с учётом их временно́й стоимости и рисков, NPV можно интерпретировать как стоимость, добавляемую проектом. Её также можно интерпретировать как общую прибыль инвестора.
Определение[править | править код]
Согласно американскому профессору Энтони Аткинсону чистая приведённая стоимость — сумма всех дисконтированных денежных потоков (притоков и оттоков), связанных с инвестиционным проектом[1].
Для потока платежей CF (Cash Flow), где 




,
- где
— ставка дисконтирования.
В обобщённом варианте, инвестиции также должны дисконтироваться, так как в реальных проектах они осуществляются не одномоментно (в нулевом периоде), а растягиваются на несколько периодов.
Расчёт ЧПС — стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведённую к настоящему моменту времени с учётом разной временно́й стоимости денег. Если ЧПС больше 0, то инвестиция экономически эффективна, а если ЧПС меньше 0, то инвестиция экономически невыгодна (то есть альтернативный проект, доходность которого принята в качестве ставки дисконтирования требует меньших инвестиций для получения аналогичного потока доходов).
С помощью ЧПС можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выгоден проект с наибольшим ЧПС). Но всё же для сравнительного анализа более применимыми являются относительные показатели. Применительно к анализу инвестиционных проектов таким показателем является внутренняя норма доходности.
В отличие от показателя дисконтированной стоимости при расчёте чистого дисконтированного дохода учитывается начальная инвестиция. Поэтому формула чистого дисконтированного дохода отличается от формулы дисконтированной стоимости на величину начальной инвестиции 
Достоинства и недостатки[править | править код]
Положительные свойства ЧПС:
- Чёткие критерии принятия решений.
- Показатель учитывает стоимость денег во времени (используется коэффициент дисконтирования в формулах).
- Показатель учитывает риски проекта посредством различных ставок дисконтирования. Бо́льшая ставка дисконтирования соответствует бо́льшим рискам, меньшая — меньшим.
Отрицательные свойства ЧПС:
- В руководстве ЮНИДО критикуется использование NPV для сравнения эффективности альтернативных проектов (Беренс, Хавранек, 1995, стр.240). Для устранения этого недостатка NPV был разработан индекс скорости удельного прироста стоимости (Коган, 2012).
- Во многих случаях корректный расчёт ставки дисконтирования является проблематичным, что особенно характерно для многопрофильных проектов, которые оцениваются с использованием NPV.
- Хотя все денежные потоки (коэффициент дисконтирования может включать в себя инфляцию, однако зачастую это всего лишь норма прибыли, которая закладывается в расчётный проект) являются прогнозными значениями, формула не учитывает вероятность исхода события.
Для того чтобы оценить проект с учётом вероятности исхода событий поступают следующим образом:
Выделяют ключевые исходные параметры. Каждому параметру устанавливают ряд значений с указанием вероятности наступления события. Для каждой совокупности параметров рассчитывается вероятность наступления и NPV. Дальше идёт расчёт математического ожидания. В итоге получаем наиболее вероятное NPV.
Пример[править | править код]
Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет.
Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере $ 100 000 (которые могут включать в себя механизмы, а также расходы на обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30 000 за каждый год 1-6. Как только компания получает прибыль от реализации проекта (например, $ 25 000 после первого года), она кладёт их в банк под 10 % годовых на оставшееся до конца проекта время (то есть на оставшиеся 5 лет для первых $ 25 000). Все денежные потоки после уплаты налогов, и на 7 год никаких денежных потоков не планируется. Ставка дисконтирования составляет 10 %.
Таким образом, требуется оценить, какая сумма больше:
, где
— прибыль от проекта, полученный в i-й год реализации проекта, t — общая длительность проекта. Поделим обе части на
:
.
Каждое слагаемое в правой части неравенства — это приведённая стоимость денег по годам. Например, $ 25 000, полученные от реализации проекта после первого года и положенные в банк на 5 лет, дадут такой же доход, как $ 22 727, положенные в банк в начальный момент времени на 6 лет. Таким образом, приведённая стоимость (PV) может быть рассчитана по каждому году:
| Год | Денежный поток | Приведённая стоимость |
|---|---|---|
| T=0 |  |
– $ 100 000 |
| T=1 |  |
$ 22 727 |
| T=2 |  |
$ 20 661 |
| T=3 |  |
$ 18 783 |
| T=4 |  |
$ 17 075 |
| T=5 |  |
$ 15 523 |
| T=6 |  |
$ 14 112 |
Сумма всех этих значений является настоящей чистой приведённой стоимостью, которая равна $ 8881.52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк (под 10 % годовых с капитализацией процентов), и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Тот же пример с формулами в Excel:
- NPV (ставка, net_inflow) + initial_investment
- PV (ставка, year_number, yearly_net_inflow)
При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативных возможностей для инвестиций.
Кроме того, если мы будем использовать формулы, упомянутые выше, для расчёта NPV — то мы видим, что входящие потоки (притоки) денежных средств являются непрерывными и имеют такую же сумму; и подставив значения в формулу
мы получим
.
И если умножить полученное значение на денежные потоки (CF), и учесть первоначальные затраты, то в итоге вычислим чистую приведённую стоимость (NPV):
Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Сравнение эффективности альтернативных проектов[править | править код]
Использование NPV может привести к ошибке при сравнении эффективности разнопараметрических инвестиционных проектов и при формировании портфеля инвестиционных проектов. Под разнопараметрическими понимаются такие проекты, у которых одновременно отличаются три инвестиционных параметра: сумма инвестиций, расчётный период и ежегодные финансовые результаты (Коган, 2012).
Покажем это на следующем примере. Сравним эффективность покупки векселя А и векселя В. Эти сделки можно рассматривать как простейшие инвестиционные проекты с единственным оттоком и единственным притоком. Вексель А стоит 100 тыс.р., его выкупят через три года, заплатив при этом 150 тыс.р. Вексель В стоит 50 тыс.р., его выкупят через два года, заплатив при этом 70 тыс. р. При ставке дисконта 10 %, 

Таким образом, по NPV, проект А эффективнее проекта В. Казалось бы, инвестору выгоднее покупать векселя типа А. Однако, представим, что этот инвестор купит два векселя В. При этом он потратит те же 100 тыс.р., что и для покупки векселя А, но выгод получит больше: 
Эти два проекта отличаются не только по суммам инвестиций, но и по расчётным периодам: покупка векселя А — трёхлетний проект, покупка векселя В — двухлетний проект. Если добавить в анализ и этот фактор, то покупка векселя А выглядит ещё менее выгодной. Так, инвестор, имеющий только 100 тыс.р., за шесть лет сможет только дважды купить вексель типа А (NPV этих двух сделок составит 22,24 тыс.р.), но трижды по два векселя типа В (NPV этих шести сделок составит 39,4 тыс.р.). Таким образом, в результате включения в анализ суммы инвестиций и расчётного периода проектов, векселя типа В выглядят ещё более эффективными, чем векселя типа А.
Из данного примера следует вывод, что для корректного анализа эффективности инвестиций, необходимо учитывать три фактора: NPV, сумму инвестиций и расчётный период проекта. Все эти факторы объединены в индекс скорости удельного прироста стоимости, поэтому при использовании этого показателя не возникают вышеуказанные проблемы.
См. также[править | править код]
- Индекс скорости удельного прироста стоимости
- Стоимость денег с учётом фактора времени
- Дисконтированная стоимость
- Внутренняя норма доходности
- Срок окупаемости
- Индекс рентабельности
- Коэффициент эффективности инвестиций
Ссылки[править | править код]
- NPV — Чистая текущая стоимость Пример расчёта, определение, характеристика, формула, условия сравнения, критерий приемлемости, недостатки.
Примечания[править | править код]
- ↑ Аткинсон Э.А., Банкер Р.Д., Каплан Р.С., Юнг М.С. Управленческий учёт. — СПб.: ООО «Диалектика», 2019. — С. 504—505. — 880 с. — ISBN 978-5-907144-70-5.
Зачем нужен инвестпроект
Инвестиционные проект составляют, чтобы привлечь инвестиции для реализации идеи. При этом инвестиции должны быть целесообразными, иметь конкретные сроки и установленные объёмы.
Когда инвесторы рассматривают проекты, они хотят найти способ сохранить или приумножить капитал. Чтобы сделать грамотный выбор, они оценивают потенциальный доход, сроки и риски.
В статье мы разберём, какие существуют методы для оценки инвестпроектов, какие показатели рассматривают инвесторы и как их рассчитать.
Основные показатели оценки инвестпроектов
Существуют два типа современных методов оценки инвестиционных показателей: статистические и методы, основанные на дисконтировании.
Главное отличие статистических от методов дисконтирования в том, что они не учитывают временную стоимость денег.
В 1999 г. ученые Грэм и Харви попытались выяснить, какие методы используют в практике финансовые директоры американских компаний. Они отправили анкету 4440 компаниям, в которой просили указать наиболее часто используемые методы оценки проектов. Ответы были получены от 392 респондентов.
Результаты исследования показали, что крупные фирмы (с уровнем продаж до 1 млрд $) предпочитают показатели внутренней нормы доходности (IRR) и чистой дисконтированной стоимости (NPV), не всегда принимая в расчёт срок окупаемости (PBP) и дисконтированный срок окупаемости (DPP) в отличие от маленьких предприятий (с уровнем продаж до 100 млн $) [Graham, Harvey, 2001].
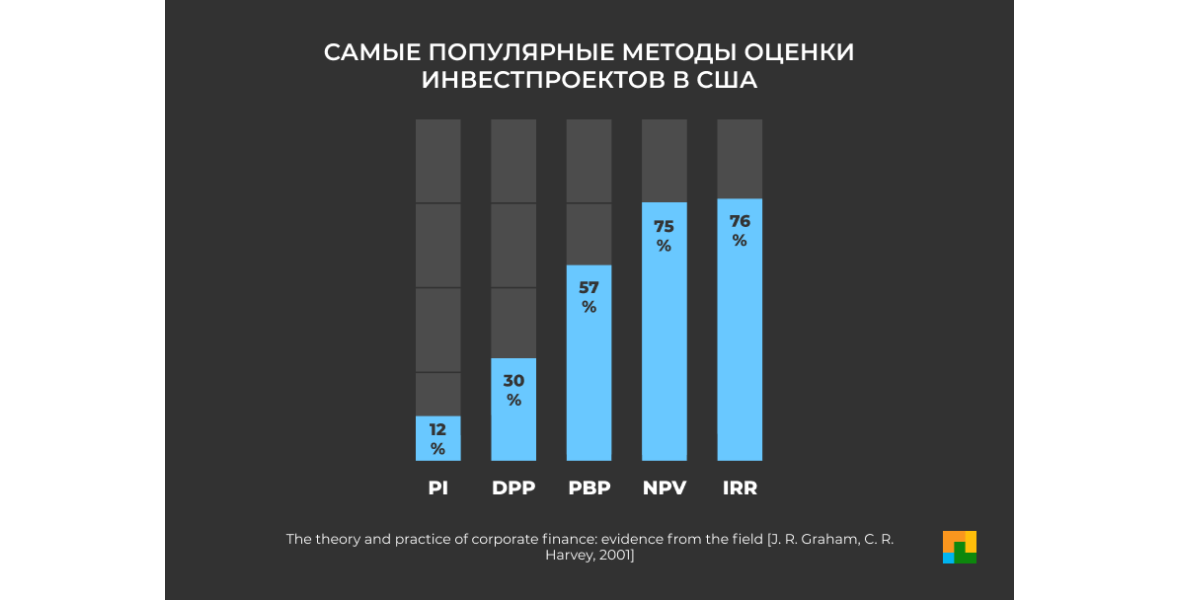
Самые популярные показатели инвестпроектов. США, 2001
Деньги сегодня — ценнее, чем завтра
Правило основано на концепции временной стоимости денег, когда иметь 100 рублей сегодня — выгоднее, чем 100 рублей завтра.
Есть два проекта с одинаковыми вложениями и отдачей, но в разное время. Согласно концепции — предпочтительнее тот, который вернёт деньги быстрее — проект Б, так как полученные за два года возврат и проценты можно инвестировать в другие проекты.
|
Период |
Проект А |
Проект Б |
|
0 |
-100 |
-100 |
|
1 |
30 |
75 |
|
2 |
30 |
75 |
|
3 |
30 |
|
|
4 |
30 |
|
|
5 |
30 |
Выше риски — больше отдача
Вложения в менее надёжный проект увеличивают риск потерять деньги. Есть два варианта: положить деньги в банк под 10% годовых или инвестировать в стартап под 20%. На первый взгляд, вложения в стартап принесут больший доход, но стоит учитывать более высокий риск потерять деньги.
Если сравнивать проекты:
- с одинаковым доходом, то предпочтительнее проекты с меньшим риском;
- с одинаковыми рисками, то предпочтительнее проекты с более высоким доходом.
Срок окупаемости
Период, в течение которого проект окупает инвестиции.
Есть два проекта с разными вложениями и доходом.
|
Период |
Проект А |
Проект Б |
|
0 |
-100 |
-10 |
|
1 |
50 |
15 |
|
2 |
50 |
15 |
|
3 |
50 |
15 |
|
Итого |
150 |
45 |
Проект А принесёт больше, чем Проект Б, но он требует более высокую сумму инвестиций для возврата. Кроме того, проект Б вернёт вложенные деньги быстрее и больше на каждый вложенный рубль. Какой выбрать — зависит от стратегии инвесторов. Некоторые инвесторы устанавливают лимит на срок окупаемости, например, не принимают проекты, которые окупаются больше года. В таком случае проект Б является более привлекательным, несмотря на меньшую прибыль.
Чтобы высчитать срок окупаемости, нужно разделить инвестиции на среднегодовую прибыль. Для проекта А средняя ежегодная прибыль равна 50, поэтому 100/50 = 2 года — срок, за который окупится проект. Среднегодовая прибыль проекта Б — 15, значит 10/15 = 2/3 года = 8 месяцев — срок окупаемости проекта Б.
Срок окупаемости ещё не говорит о прибыльности проекта, потому что не учитывает риски. Чтобы учесть все факторы оценки инвестиционных показателей в экономической теории появились понятия дисконтирования и NPV.
Дисконтирование и NPV
Допустим, что инвесторы вкладывают деньги в проект под 10% годовых.
|
Сегодня |
Через год |
Через 2 года |
|
|
Инвестиции |
100 ₽ |
110 ₽ |
121 ₽ |
Возврат 110₽ через год равен возврату 121₽ через два года. В случае если владельцы проектов отказажутся от проекта до старта, им придётся вернуть инвестору 100₽ без процентов. Из этого следует, что 100₽ сегодня, 110₽ через год и 121₽ через два года — эквивалентны.
Дисконтирование основывается на приведении к подобной эквивалентности — мы пытаемся увидеть, сколько стоят будущие деньги в «сегодняшних деньгах».
Для дисконтирования денежных потоков используют формулу:

Дисконтированные денежные потоки, формула расчета
n, t — количество временных периодов;
CF — денежный поток;
i — ставка дисконтирования или процент, при котором инвесторы готовы инвестировать деньги в проект.
Чтобы получить чистую дисконтированную стоимость (Net Present Value — NPV) — стоимость проекта в «сегодняшних деньгах», нужно сложить все дисконтированные денежные потоки и вычесть первоначальные инвестиции.
- Если NPV >0 — проект стоит принять, он принесёт больше, чем требуется инвесторам.
- При NPV <0 мы получаем сумму, которую владельцы проекта должны компенсировать инвестору сегодня, чтобы он принял участие в проекте.
Рассчитаем NPV для проекта: сумма инвестиций — 500, срок денежных потоков — 4 года, ставка дисконтирования — 12%.
Рассчитаем денежные потоки к текущей стоимости:
DCF1 = 100 / (1+0,12) = 89,29
DCF2 = 100 / (1+0,12)² = 100 / 0,7972 = 159,44
DCF3 = 300 / (1+0,12)³ = 300 / 0,7118 = 213,54
DCF4 = 400 / (1+0,12)⁴ = 400 / 0,6355 = 254,20
Сумма дисконтированных денежных потоков равна 716,47
|
Период |
CF |
R |
DCF |
|
0 |
-500 |
0 |
|
|
1 год |
100 |
0,8929 |
89,29 |
|
2 год |
200 |
0,7972 |
159,44 |
|
3 год |
300 |
0,7118 |
213,54 |
|
4 год |
400 |
0,6355 |
254,2 |
|
Всего |
1000 |
716,47 |
NPV = PV-I, где I — сумма первоначальных инвестиций.
NPV = 716,47-500 = 216,47
По сути NPV — это дополнительная прибыль сверх требуемой суммы, которую инвестор должен заплатить, чтобы получить долю в бизнесе. Если же NPV отрицательный, то это сумма, которую организаторы проекта должны возместить инвестору, чтобы он захотел вложить свои деньги.
Если рассматривается два проекта с одинаковыми затратами, то не всегда принимается проект с большим NPV. Проект с меньшим NPV, но с меньшим сроком окупаемости может быть выгоднее проекта с большим NPV.
Рассчитать все показатели можно в нашей таблице.
Внутренняя норма доходности
(Internal Rate of Return — IRR) — значение ставки дисконтирования, при которой чистый приведённый доход (NPV) равен нулю. Показатель отражает максимальную процентную ставку, под которую можно инвестировать в проект.
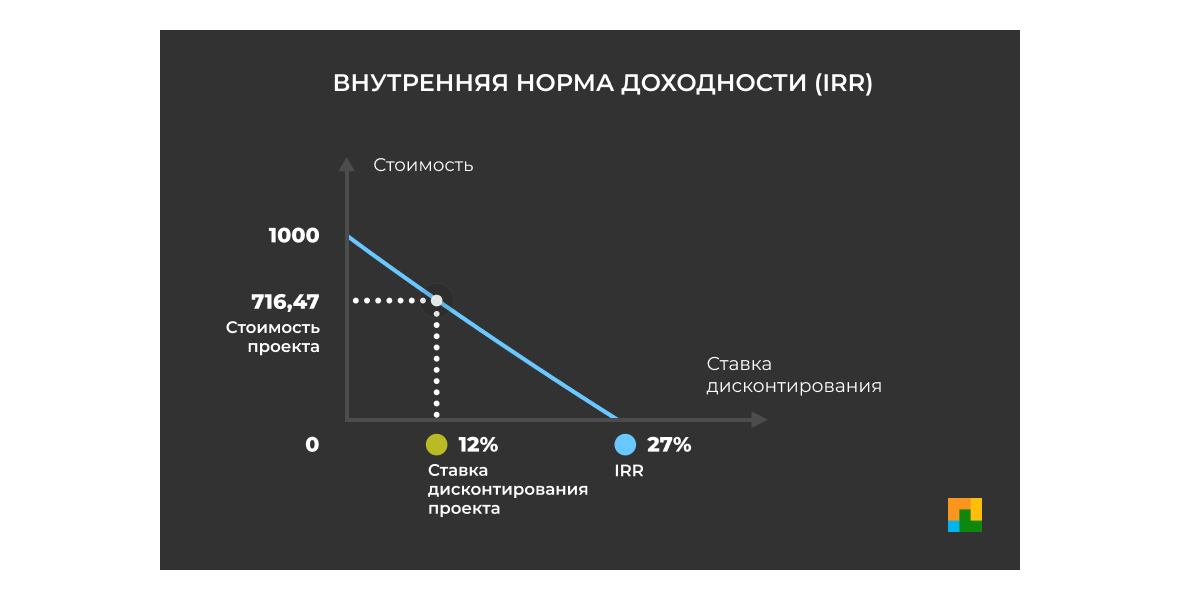
Внутренняя норма доходности, IRR
Ось x — ставка дисконтирования в процентах, y — NPV проекта. По мере увеличения ставки дисконтирования чистый приведенный доход стремится к нулю. Там, где кривая пересекает ось x, и будет искомое значение IRR.
При значениях:
- IRR > r — требуемый инвесторами доход меньше IRR, значит проект стоит принять.
- IRR < r — отказаться, потому что проект не принесёт требуемого дохода инвесторам.
Когда мы сравниваем несколько проектов или финансовых инструментов с одинаковой ставкой дисконтирования, предпочтительнее те, чьи показатели IRR выше.
Воспользуемся формулой «ВСД» в Excel. Она нужна, чтобы рассчитывать показатель IRR.
|
Период |
CF |
|
0 |
-500 |
|
1 |
100 |
|
2 |
200 |
|
3 |
300 |
|
4 |
400 |
|
IRR = 27% |
Показатель IRR составляет 27%. При ставке дисконтирования 12%, IRR> r, поэтому проект стоит рассматривать.
Дисконтированный срок окупаемости
Дисконтированный срок окупаемости (Discounted Payback Period = DPP) показывает за какой период времени сумма дисконтированных денежных потоков покроет все дисконтированные инвестиционные затраты. То есть, с какого момента инвестор окупит затраты и начнет получать дополнительную прибыль.
При использовании этого метода в сравнении нескольких проектов, стоит выбирать тот, который имеет меньшее значение DPP.
Формула для расчёта:
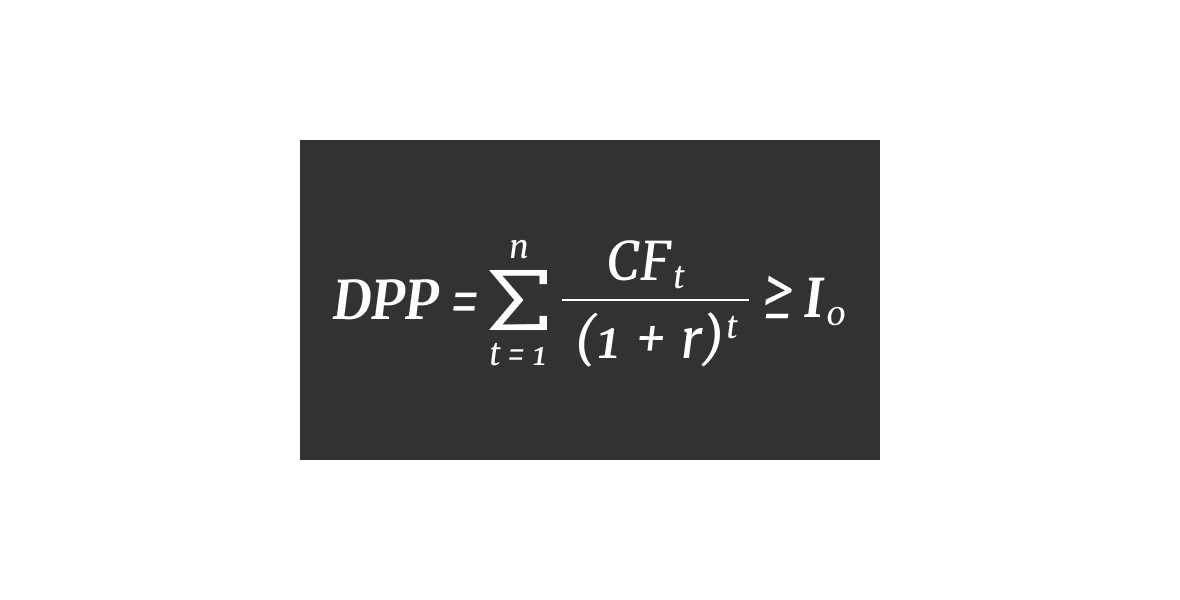
Дисконтированный срок окупаемости, формула расчета
Рассчитаем дисконтированный срок окупаемости для проекта: сумма инвестиций — 500 руб., срок денежных потоков — 4 лет, ставка дисконтирования — 12%
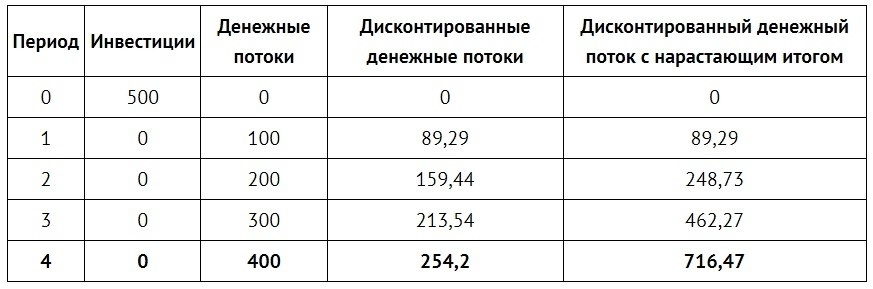
Срок окупаемости проекта составит 3 года, так как именно в этот период сумма денежных потоков превысит сумму первоначальных инвестиций.
Дисконтированный срок окупаемости проекта — 4 года.
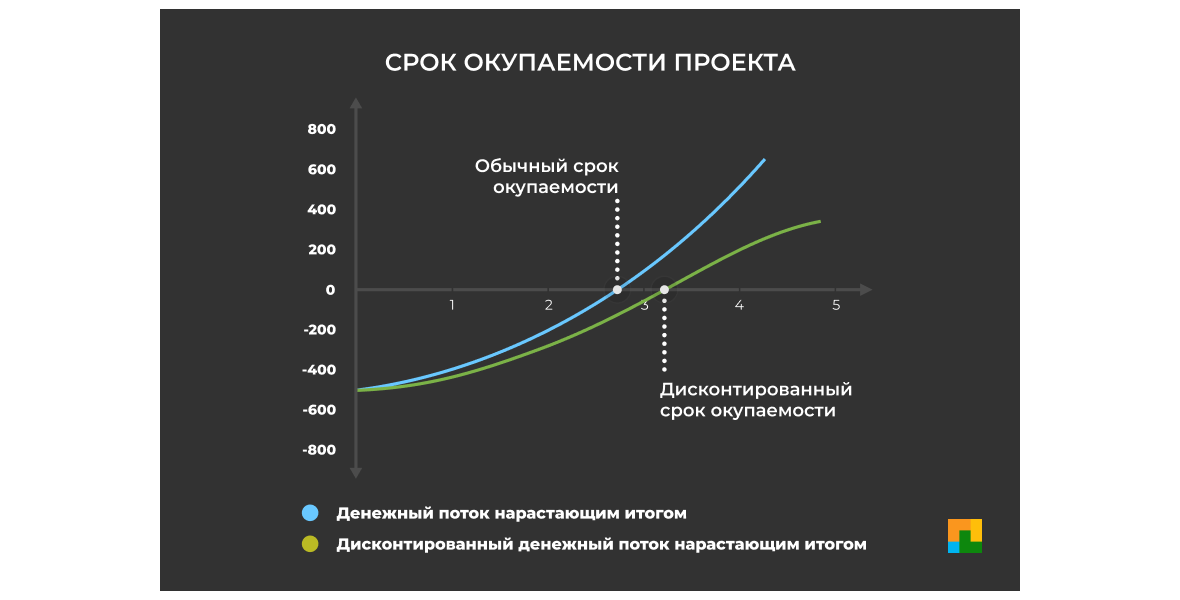
Разница обычного и дисконтированного срока окупаемости
Если для оценки проектов используется только этот метод, то из нескольких альтернативных проектов при равных условиях принимается тот проект, который имеет меньшее значение DPP. Недостаток метода в том, что он не учитывает денежные потоки, которые могут быть получены после завершения периода окупаемости.
Индекс прибыльности
Индекс прибыльности (Profitability Index — PI) — это отношение NPV к дисконтированному объему инвестиций. Он показывает сколько дополнительных рублей получит инвестор на каждый вложенный рубль.
Индекс считают по формуле:
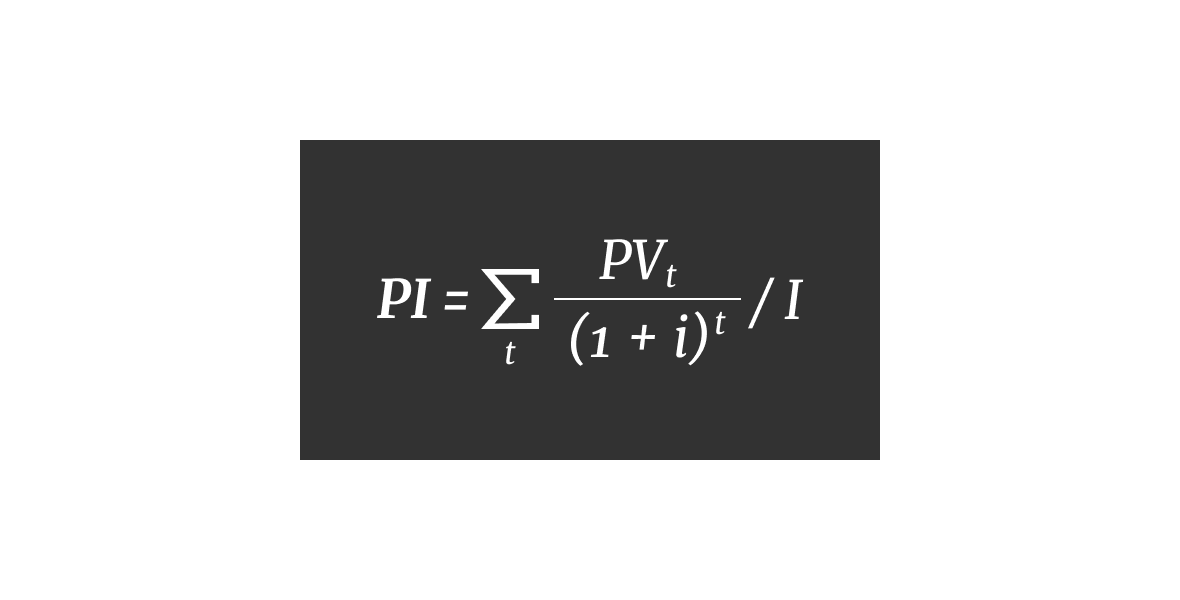
Индекс прибыльности, формула расчета.
где I — первоначальные инвестиции,
PV — дисконтированный доход за период времени t,
R — ставка дисконтирования.
В нашем примере PV = 716,47. Чтобы рассчитать PI, нужно разделить PV на I (сумму первоначальных инвестиций: 716,47/500 = 1,43.
PI — показатель, который покажет сколько прибыли принесёт проект при требуемой ставке дисконтирования на каждый вложенный рубль.
Подробнее по теме:
Герасименко А.В., Финансовый менеджмент — это просто. — Москва: Альпина Паблишер, 2019.
Сайт: «Корпоративный менеджмент», https://www.cfin.ru/finanalysis/invest
Сайт: «Финансы и МСФО: теория и практика», http://msfo-dipifr.ru/
Данная статья посвящена расчетам основных показателей эффективности инвестиционных проектов, рассчитываемых с учетом фактора времени, а также вопросам, возникающим при расчете показателей. Статья ориентирована на специалистов финансово-экономических служб, перед которыми, может быть впервые, стоит задача оценки инвестиционного проекта, с целью предоставления результатов владельцу компании, привлечения сторонних инвесторов, либо кредиторов.
Для оценки инвестиционных проектов используется две группы показателей: показатели, рассчитываемые без учета фактора времени и показатели, рассчитываемые с учетом фактора времени.
Первая группа показателей более проста в расчете, но она не учитывает того, что сегодняшние и завтрашние деньги для инвестора стоят по-разному, то есть расчеты этих показателей осуществляются без приведения денежных потоков к единому моменту времени.
Вторая группа показателей, о которых и пойдет речь в статье, в отличие от показателей первой группы учитывают разную стоимость денег в разные моменты времени (теория временной стоимости денег). Эти показатели являются более интересными для владельцев, инвесторов и банков, так как более корректно отражают эффективность проекта (не завышают ее, как показатели первой группы), то есть являются более надежным (лучшим) гарантом успешности проекта. Суть их расчета заключается в приведении будущих денежных потоков (стоимости денег) к «сегодняшнему» дню, вернее, к моменту начала инвестиций в проект (предполагается, что инвестиции будут осуществлены в этом году). Приведение денежных потоков называется дисконтированием, суть которого состоит в том, что нам «сегодня» нужно принять решение о том, следует ли инвестировать средства в проект, либо стоит проблема выбора более эффективного проекта из нескольких, для этого необходимо знать: насколько выгоден, либо не выгоден проект; либо какой проект более эффективен (выгоден)? Для этого мы составляем бизнес-план – моделируем деятельность на несколько лет вперед, чтобы рассчитать эффективность, а моделируем, исходя из «сегодняшних» цен, расходов, предполагаемых доходов (а соответственно, исходя из «сегодняшних» платежей и поступлений). Следовало бы еще учесть альтернативные безрисковые вложения, которые могли бы принести нам определенный доход наверняка, риски неблагополучного исхода проекта, требуемую норму доходности от вложенного капитала. Предполагается, что как раз дисконтирование планируемых денежных потоков и приводит их к текущему моменту с учетом инфляции, безрисковых вложений, рисков конкретного проекта, либо требуемой нормы доходности от вложенного капитала в зависимости от выбранного подхода к определению ставки дисконтирования, используемой при дисконтировании денежных потоков. Результаты дисконтирования и оценки эффективности проекта во многом зависят от ставки дисконтирования, которая в свою очередь зависит от метода ее определения (расчета).
Управленческий учет: с нуля до настройки в 1С, Excel и Google-таблицах
Уметь настраивать и вести управленку — значит быть полезным для руководителей. Научитесь понимать, откуда приходят и куда уходят деньги компании на курсе повышения квалификации от «Клерка».
Выбор варианта определения (расчета) ставки дисконтирования – это отдельная большая тема, не раз описанная в различных источниках – Интернет, учебниках, книгах, в профильных журналах. Поэтому не будем останавливаться на ней подробно, отмечу только, что существует несколько подходов к определению ставки дисконтирования, такие как:
-
Определение стоимости собственного капитала (модель оценки долгосрочных активов CAMP);
-
Средневзвешенной стоимости капитала (WACC);
-
Кумулятивного построения – наиболее часто используемый подход, основанный на экспертной оценке рисков.
Более подробно остановимся на расчете самих показателей эффективности проекта, рассчитываемых с учетом фактора времени:
-
NPV – чистый дисконтированный доход (чистая приведенная стоимость проекта);
-
IRR – внутренняя норма доходности (прибыли/ рентабельности) инвестиций;
-
DPBP – дисконтированный срок окупаемости инвестиций
Расчет каждого показателя и подготовка денежных потоков к расчету имеет нюансы, которые неизбежно вызывают вопросы при расчете их впервые, которые мы и постараемся разобрать.
Расчет показателей осуществляется на основе данных из плана движения денежных средств инвестиционного проекта, который в свою очередь строится на основе плана доходов и расходов проекта и графика поступлений и платежей. Таким образом, важно, чтобы первоначальная информация для моделирования деятельности в пределах горизонта планирования (рассматриваемого срока проекта), а также сами планы движения денежных средств, доходов и расходов были как можно более проработанными, точными и корректными, в целях минимизации погрешности результатов расчетов и рисков проекта. Здесь возникает вопрос: а учитывать ли инфляцию при моделировании деятельности и как это сделать? Существует два способа учета инфляции в расчетах:
-
Дефлирование денежных потоков до осуществления дисконтирования, то есть путем моделирования денежных потоков с учетом инфляции по периодам проекта, например, с поправкой сумм на инфляционный коэффициент;
-
Учет инфляционной составляющей при расчете ставки дисконтирования
В первом случае не нужно учитывать инфляционную составляющую в ставке дисконтирования, а во втором соответственно – не учитывать инфляцию при моделировании денежных потоков (то есть следует формировать план движения денежных средств в текущих ценах). Отмечу, что в случае, когда инфляция по разным составляющим плана существенно различается, следует ее учитывать способом дефлирования денежных потоков.
Часто возникает вопрос: а что же такое срок проекта (горизонт планирования/ исследования проекта) и как его определить, ведь чем больший срок мы рассматриваем, тем больше значение основного показателя эффективности проекта (NPV)? Теоретически, период планирования проекта должен быть равен жизненному циклу проекта, то есть интервалу времени от момента его появления (начала инвестиций) до его ликвидации/ полного износа. Но представьте, если рассматривается проект, жизненный цикл которого более 10 лет. Это значит, что мы должны моделировать деятельность на более 10 лет вперед? Это довольно сложно в сегодняшних условиях экономики. Поэтому следует моделировать деятельность на срок, позволяющий более точно и уверенно спланировать потоки денежных средств, доходы и расходы проекта (несколько лет), но срок должен быть не менее простого срока окупаемости проекта, чтоб была возможность просчитать дисконтированный срок окупаемости проекта. Если рассматривается проект со 100% кредитным финансированием, рекомендуется рассматривать срок проекта равный сроку погашения кредита (количество лет). Срок планирования можно понять непосредственно в процессе моделирования – формирования плана движения денежных средств. Однако, распространенная ошибка при оценке инвестиционных проектов, когда планируемый срок меньше жизненного цикла проекта и в расчетах показателей не учитывается остаточная/ ликвидационная стоимость проекта, что значительно может уменьшить значение показателей эффективности. Остаточную/ ликвидационную стоимость проекта необходимо учитывать при расчетах с целью их корректности.
Период проекта – обычно, это год, так как традиционная формула дисконтирования подразумевает дисконтирование денежных потоков по годам, таким образом, в случае, когда период проекта не год, потребуется корректировка формулы дисконтирования, либо сама ставка дисконтирования должна отражать не годовую, а месячную разницу стоимости денег.
Теперь перейдем непосредственно к показателям эффективности инвестиционного проекта, рассчитываемым с учетом фактора времени. Для наглядности, методику расчетов рассмотрим на примере. В качестве примера возьмем проект строительства нежилого объекта недвижимости под 100% привлеченных средств (кредитная линия). Планируется получение дохода от продажи и сдачи в аренду площадей данного объекта недвижимости.
В таблице 1 представлен смоделированный план движения денежных средств по данному проекту. Рассматриваемый срок проекта – 7 лет, в который более точно можно спланировать доходы и расходы и, который больше простого срока окупаемости проекта. В 7-ом году проекта отражен предполагаемый ликвидационный денежный поток (остаточная стоимость объекта за вычетом налога на прибыль) со знаком «+» от моделируемой продажи объекта недвижимости в конце рассматриваемого срока проекта.
Таблица 1
|
1 год |
2 год |
3 год |
4 год |
5 год |
6 год |
7 год |
|
|
Остаток на начало периода |
0 |
3 784 778 |
29 157 938 |
70 496 191 |
106 072 147 |
141 618 389 |
257 390 934 |
|
Поступления |
590 833 375 |
479 124 033 |
434 469 792 |
392 763 800 |
470 343 200 |
476 512 400 |
476 434 800 |
|
Кредитные средства |
566 800 000 |
177 700 000 |
0 |
0 |
0 |
0 |
0 |
|
Доходы от продажи, аренды |
24 033 375 |
301 424 033 |
434 469 792 |
392 763 800 |
470 343 200 |
476 512 400 |
476 434 800 |
|
Доход от продажи объекта недвижимости (ликвидационный CF) |
0 |
0 |
0 |
0 |
0 |
0 |
485 346 090 |
|
Платежи |
587 048 597 |
453 750 873 |
393 131 538 |
357 187 844 |
434 796 958 |
360 739 855 |
209 351 247 |
|
Платежи за проектные, СМР, покупка ОС (инвестиции, без учета оборотных средств) |
516 923 255 |
224 997 745 |
0 |
0 |
0 |
0 |
0 |
|
Платежи по текущей деятельности |
13 354 092 |
84 974 378 |
109 391 538 |
125 960 344 |
187 744 458 |
206 367 355 |
209 351 247 |
|
% по кредиту (15% год) |
56 771 250 |
105 278 750 |
95 240 000 |
65 227 500 |
40 652 500 |
9 272 500 |
0 |
|
Погашение “тела кредита” |
0 |
38 500 000 |
188 500 000 |
166 000 000 |
206 400 000 |
145 100 000 |
0 |
|
Остаток на конец периода |
3 784 778 |
29 157 938 |
70 496 191 |
106 072 147 |
141 618 389 |
257 390 934 |
524 474 487 |
Традиционно приводятся примеры, где в период инвестиций отсутствуют платежи по текущим расходам и поступление дохода. В нашем примере в период инвестиций появляются и доходы, и текущие расходы, причем, инвестиции осуществляются в течение первых двух периодов проекта.
Итак, показатели, рассчитываемые с учетом фактора времени, подразумевают предварительное дисконтирование (приведение) чистого денежного потока. Чистый денежный поток NCF (Net cash flow) – разность между суммами поступлений и выплат денежных средств компании за определенный период времени; рассчитывается с учетом выплат, дивидендов и налогов. Из определения следует, что мы должны из поступлений вычесть платежи по годам проекта и дисконтировать этот поток, но существует много разных мнений о том, что же включать или не включать в состав дисконтируемого чистого денежного потока. Дискуссии в основном касаются движения денежных средств по кредитам, то есть поступлений денежных средств по кредиту, возврата «тела кредита» (основной суммы кредита) и процентов по нему. Дело в том, что получение и возврат кредита, в том числе процентов по кредиту относятся к финансовой деятельности, а для оценки эффективности инвестиционного проекта используются только сумма инвестиций в проект и данные текущей деятельности. Поэтому мы не включаем в дисконтируемые денежные потоки поступления и выплаты по кредитам (в том числе проценты), относящиеся к финансовой деятельности.
Под инвестициями в данном случае подразумеваем сумму денежных средств, необходимую на проектные работы и строительство объекта недвижимости, покупку основных средств для его дальнейшей эксплуатации, а также начальный оборотный капитал, необходимый для покрытия текущих затрат при начальной эксплуатации объекта до тех пор, пока выручка не будет покрывать текущие расходы.
Нулевым периодом проекта будет первый год проекта, далее – по порядку (1-6 период). В таблице 2 приведен расчет чистого денежного потока (NCF) нашего проекта, где NCF разность поступлений и платежей, в том числе инвестиций.
Справочно: Вопрос о включении в расчет потоков денежных средств амортизации возникает при косвенном определении величины денежного потока, то есть через план доходов и расходов.
Таблица 2
|
Период проекта |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Поступления |
24 033 375 |
301 424 033 |
434 469 792 |
392 763 800 |
470 343 200 |
476 512 400 |
961 780 890 |
|
Доходы от продажи, аренды |
24 033 375 |
301 424 033 |
434 469 792 |
392 763 800 |
470 343 200 |
476 512 400 |
476 434 800 |
|
Доход от продажи объекта недвижимости (ликвидационный CF) |
0 |
0 |
0 |
0 |
0 |
0 |
485 346 090 |
|
Платежи |
530 277 347 |
309 972 123 |
109 391 538 |
125 960 344 |
187 744 458 |
206 367 355 |
209 351 247 |
|
Платежи за проектные, СМР, покупка ОС (инвестиции, без учета оборотных средств) |
516 923 255 |
224 997 745 |
0 |
0 |
0 |
0 |
0 |
|
Платежи по текущей деятельности |
13 354 092 |
84 974 378 |
109 391 538 |
125 960 344 |
187 744 458 |
206 367 355 |
209 351 247 |
|
Чистый денежный поток (NCF) |
-506 243 972 |
-8 548 090 |
325 078 254 |
266 803 456 |
282 598 742 |
270 145 045 |
752 429 643 |
Теперь можно дисконтировать чистый денежный поток (NCF). Формула дисконтирования выглядит следующим образом:
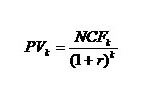
где
PVk — приведенная (текущая) стоимость денежного потока k-го периода проекта
NCFk – чистый денежный поток k-го периода проекта
k – период проекта
r – ставка дисконтирования (в десятичном выражении)
По правилу дисконтирования нулевой период проекта (первый год) является периодом инвестиций, перед нами стоит задача привести чистые денежные потоки проекта к периоду первых инвестиций в проект, то есть к нулевому периоду, поэтому чистый денежный поток нулевого периода не дисконтируется. Следует обратить внимание, что помимо инвестиций, как уже говорилось выше, в нулевом периоде проекта мы имеем текущие расходы и доходы, которые также не дисконтируем. Ликвидационный денежный поток от продажи объекта недвижимости в конце рассматриваемого срока проекта дисконтируется в составе NCF 6-го периода, моделируя тем самым продажу объекта недвижимости в шестом периоде проекта.
Справочно: нет разницы – дисконтировать сначала по отдельности поступления и платежи, а затем высчитать дисконтированный чистый денежный поток (NPV) путем вычитания дисконтированных платежей из дисконтированных поступлений по годам, либо сначала высчитать чистый денежный поток (NCF = поступления – платежи по годам), а затем осуществить дисконтирование чистого денежного потока по годам, результат будет одинаковым.
Предположим, что определенная кумулятивным методом ставка дисконтирования нашего проекта составляет 20%, то есть r = 0.2. Дисконтируем чистый денежный поток (NCF) 1-6 периодов из таблицы 2. Подставляя в формулу дисконтирования соответствующие значения, получаем:
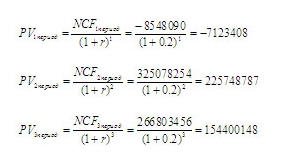
И так далее (аналогично за 4-6 периоды). Значения дисконтированных чистых денежных потоков по годам представлены в таблице 3.
Таблица 3
|
Период проекта |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Чистый денежный поток нулевого периода (NCF0) |
-506 243 972 |
||||||
|
Дисконтированный чистый денежный поток (PV) |
-7 123 408 |
225 748 787 |
154 400 148 |
136 284 115 |
108 565 235 |
251 987 165 |
|
|
Накопленный дисконтированный чистый денежный поток |
-506 243 972 |
-513 367 380 |
-287 618 593 |
-133 218 445 |
3 065 670 |
111 630 905 |
363 618 070 |
В случае дисконтирования денежных потоков «вручную» с помощью Excel, можно использовать формулу, созданную «вручную»:
=ссылка на ячейку NCF/СТЕПЕНЬ(1+r в десятичном выражении;k)*
Теперь рассчитаем первый показатель эффективности инвестиционного проекта – NPV (Net Present Value) – чистая приведенная стоимость проекта. Классическая формула для расчета NPV выглядит следующим образом:
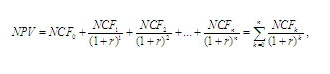
где
NPV — чистый приведенный денежный поток
NCF – чистый денежный поток соответствующего периода проекта
n – горизонт исследования, выраженный в интервалах планирования (срок проекта)
k – период проекта
r – ставка дисконтирования (в десятичном выражении)
В случае осуществления расчета NPV с помощью Excel можно использовать специально предназначенную для этого формулу:
=ЧПС(r в %; ссылка на ячейку NCF1период;NCF2период;NCF3период; …; NCFn период) + NCF0 период*
Показатель NPV заключается в суммировании дисконтированных чистых денежных потоков (PV) c 1 по n-ый период проекта и прибавлении к нему отрицательного денежного потока 0-го периода (инвестиций). То есть за счет положительного, либо отрицательного знака чистого денежного потока каждого периода при расчете NPV у нас осуществляется сложение, либо вычитание соответственно дисконтированного денежного потока каждого следующего периода.
По данным из таблицы 3 рассматриваемого примера получаем:
NPV = PV1период+ PV2период+…+ PV6период + NCF0 = – 7 123 408 + 225 748 787 + 154 400 148 +
+ 136 284 115 + 108 565 235 + 251 987 165 – 506 243 972 = 363 618 070 (см. сумму накопленного чистого денежного потока в 6-м периоде таблицы 3)
По общему правилу, если NPV > 0, то проект принимается. Положительное значение NPV значит, что денежный поток проекта за рассматриваемый срок при установленной ставке дисконтирования покрыл своими поступлениями инвестиции и текущие затраты, то есть обеспечил min доход заданный ставкой дисконтирования (r), равный доходу от альтернативных безрисковых вложений и доход равный значению NPV.
Когда NPV = 0 – проект не является ни прибыльным, ни убыточным, он только покрыл свои инвестиции и текущие затраты, обеспечил min доход заданный ставкой дисконтирования (r) при указанных рисках. В данном случае при реализации проекта доход собственников не изменится, но стоимость компании увеличится на сумму инвестиций.
Если NPV
При рассмотрении нескольких проектов выбирают тот, у которого NPV больше.
В нашем случае показатель NPV>0, то есть проект должен быть принят, но прежде чем делать выводы об эффективности рассматриваемого проекта следует рассчитать остальные показатели и рассматривать их в совокупности.
Рассмотрим следующий показатель эффективности инвестиционного проекта, рассчитываемого с учетом фактора времени – IRR (Internal Rate of Return) – внутренняя норма доходности. Данный показатель отражает в отличие от NPV доходность проекта в относительном выражении (в процентах), поэтому является более понятным. IRR – это такое значение ставки дисконтирования (r), при котором NPV = 0, то есть при котором текущая стоимость поступлений равна текущей стоимости инвестиций и текущих затрат. IRR отражает безубыточную норму доходности проекта, то есть когда проект становится ни прибыльным, ни убыточным.
Для расчета данного показателя можно применить технически сложные математические расчеты, используя формулу NPV:
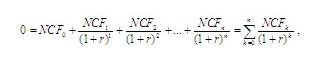
где
NCF– чистый денежный поток соответствующего периода
r – ставка дисконтирования (в десятичном выражении)
n – горизонт исследования, выраженный в интервалах планирования (срок проекта)
k – период проекта
В данном случае ставка дисконтирования (r) отражает внутреннюю норму доходности (IRR).
Можно вычислить значение IRR «вручную» методом подбора (подстановки) ставки дисконтирования (r) в формуле NPV, пока не будет достигнуто значение NPV=0,
Рассматривая наш пример, при ставке дисконтирования (r) равной 20% значение NPV имеет довольно неплохое значение (363 618 070), поэтому, чтобы найти значение IRR, попробуем увеличить ставку дисконтирования до 30%. Соответственно, при (r) равной 0,3, используя те же формулы, что при расчете NPV со ставкой дисконтирования 20%, получаем значение NPV =128 563 580. Значение NPV получилось больше нуля, но уже гораздо меньше, соответственно попробуем еще увеличить ставку дисконтирования до 40%, получаем NPV = -25 539 469. Значение NPV получилось отрицательным, соответственно значение IRR данного проекта находится между 30% и 40%, ближе к 40%. Таким образом, продолжая подбор ставки дисконтирования (r), мы нашли значение (r), при котором NPV равно нулю – значение IRR рассматриваемого проекта = 38%.
При расчете показателей с помощью Excel, можно воспользоваться специально предназначенной формулой для расчета IRR:
=ВСД(ссылка на массив NCF0:NCFn; предполагаемое значение IRR в %, либо любое значение в %>r)*
Проект принимается, когда значение показателя IRR>ставки дисконтирования (r). В данном случае проект окупает затраты, обеспечивает прибыль, заданную ставкой дисконтирования и обеспечивает запас прибыли в абсолютной величине, равной NPV, а в относительной – равной (IRR-r). Когда IRR
Уже второй показатель удовлетворяет установленным требованиям, но не стоит торопиться с выводами, рассчитаем следующий показатель.
Рассчитаем дисконтированный срок окупаемости инвестиций нашего проекта – DPBP (Discount Payback Period), который учитывает различную стоимость денег во времени. Дисконтированный срок окупаемости проекта рассчитывается аналогично обычному сроку окупаемости, разница лишь в том, что для расчета дисконтированного срока окупаемости используется не простой, а дисконтированный чистый денежный поток. Показатель DPBP отражает, за какой период времени доходы проекта окупят инвестиции и будут покрывать текущие затраты, то есть когда накопленный по периодам (годам) проекта дисконтированный чистый денежный поток сменит знак с минуса на плюс и больше не будет изменяться. Соответственно, дисконтированный срок окупаемости проекта будет всегда больше обычного срока окупаемости. В нашем примере, накопленный дисконтированный денежный поток (см.таблицу 3) имеет последнее отрицательное значение в третьем периоде проекта. Обычно в рассматриваемых инвестиционных проектах получение доходов начинается после нулевого периода проекта – в первом, поэтому отсчет срока окупаемости начинается с первого периода проекта. В нашем случае получение дохода и текущие расходы присутствуют уже в нулевом периоде проекта, поэтому отсчет срока окупаемости мы начнем с нулевого периода проекта, то есть период проекта+1 год. Таким образом, дисконтированный срок окупаемости нашего проекта равен (3период+1) четырем полным годам. Чтобы более точно просчитать дисконтированный срок окупаемости нам необходимо понять: за какую часть следующего (за 4-м годом проекта, то есть за 3-м периодом) года проект выйдет на ноль, то есть инвестиции полностью окупятся. Для этого мы делим отрицательный остаток третьего периода (133 218 445) на значение дисконтированного чистого денежного потока следующего периода (PV4 = 136 284 115), получаем значение равное 0,98 – это соответствует 11,7 месяцам. Соответственно, дисконтированный срок окупаемости нашего проекта равен почти пяти годам, точнее – 4 годам 11,7 месяцам.
Обязательным в оценке инвестиционного проекта является анализ его чувствительности. Понятие чувствительности говорит само за себя, суть его в том, что необходимо понять: как проект реагирует на изменения тех или иных первоначальных данных, то есть, насколько изменятся наши показатели эффективности, при изменении условий проекта. Чувствительность показывает прочность проекта. Для этого необходимо выбрать несколько основополагающих факторов, обеспечивающих успех проекта, например:
-
Спрос (план продаж);
-
Сроки строительства и сдачи объекта в эксплуатацию;
-
Стоимость проектных и строительно-монтажных работ (СМР) и т.д.
По сути, это факторы, влияющие на риски проекта, которые выражены при расчете в ставке дисконтирования (r). Таким образом, чувствительность проекта можно оценить, изменяя ставку дисконтирования. Но, если необходимо знать, какой именно фактор (параметр) и насколько влияет на успешность проекта, следует изменять поочередно сами первоначальные данные для расчетов, осуществлять пересчет показателей, наблюдая за тем, как они изменяются при этом. Изменяем поочередно:
-
спрос в плане продаж, соответственно изменятся доходы, суммы поступлений денежных средств и сумма требующихся инвестиций;
-
сроки строительства и сдачи объекта в эксплуатацию, соответственно изменится график реализации проекта – сдвинутся во времени расходы, доходы, платежи и поступления, а также потребность в инвестиционных средствах;
-
стоимость проектных и СМР, соответственно изменятся расходы, суммы платежей и сумма необходимых инвестиционных средств и т.д.
Изменение данных следует осуществлять в процентах к первоначальным. В таком случае анализ чувствительности будет описывать: как изменились значения показателей проекта при изменении, например, спроса (плана продаж) на 10% от первоначального плана.
В нашем примере мы будем изменять ставку дисконтирования (r). Имеет смысл изменять ставку дисконтирования в пределах значения IRR. Таким образом, анализ чувствительности проекта выглядит следующим образом:
|
r |
NPV |
IRR |
DPBP |
|
20% |
363 618 070 |
38% |
5 лет |
|
25% |
233 089 497 |
38% |
5 лет 6 мес |
|
30% |
128 563 580 |
38% |
6 лет |
|
35% |
43 858 930 |
38% |
6 лет 8 мес |
Рассматриваемые показатели близки по своей сути, поэтому для одного проекта выполняются их соотношения:
когда NPV>0, то IRR>r;
когда NPV
когда NPV=0, то IRR=r;
Теперь можно сравнить все рассчитанные показатели и, используя анализ чувствительности проекта, сделать выводы об его эффективности.
Проект имеет очень хорошие показатели NPV и IRR. Проект достаточно рискован, на это указывает высокая ставка дисконтирования (r), но не смотря на это имеет хороший запас прочности, то есть даже при увеличении ставки дисконтирования до 38% мы имеем положительный NPV. Срок окупаемости проекта равен пяти годам, то есть это долгосрочные вложения. В случае, если данный проект рассматривается в качестве долгосрочного вложения, то данный проект следует принять. Если же проект рассматривается с целью быстрого получения прибыли с последующим ее вложением в другой проект, то есть в качестве «толчкового» проекта, то срок окупаемости довольно большой, то есть проект не достигает своих целей. В таком случае предлагается попробовать уменьшить масштаб проекта, то есть уменьшить первоначальные площади строительства, соответственно изменятся потребность в инвестициях и текущие расходы, но и доходы также уменьшатся. Не смотря на это, возможно, уменьшение масштаба проекта удовлетворит его целям.
Если рассматривается несколько альтернативных проектов, следует сравнить показатели проектов для выбора лучшего. В любом случае необходимо их соотнести с условиями проекта – условиями финансирования, рисками, отраслью, целями и задачами проекта.
* Серые поля в формуле следует заменить на соответствующие значения, либо на ссылки на ячейки с соответствующими значениями
Метод дисконтирования основан на известном экономическом законе, который заключается в убывающей стоимости денег. Деньги со временем обесцениваются — это заметно даже тем, кто не знаком с экономической теорией. При растущих ценах реальная стоимость денег уменьшается, то есть на условные 1000 руб. завтра мы сможем купить меньше, чем сегодня, и меньше, чем вчера. Чтобы ответить на вопрос, сколько в будущем будут стоить сегодняшние 1000 руб., используется метод дисконтирования денежных потоков. Пример расчета и наглядное объяснение данного метода вы найдете в статье ниже.
Расчет дисконтированного денежного потока
Стоимость денег может изменяться не только под влиянием инфляции, но и за счет других факторов. Например, деньги в форме депозита в банке могут принести прибыль, а при выдаче денег в кредит всегда существует риск недополучения предполагаемой возвратной суммы. Точка отсчета в методе дисконтирования — настоящий момент. Именно на текущую дату определяется стоимость будущих денежных потоков.
Дисконтирование денежных потоков— это приведение размера денежных средств, полученных в разные интервалы времени в соответствие с их реальной стоимостью на текущий момент. Метод применяется при оценке бизнеса и анализе экономической эффективности инвестиционных проектов, расчете их окупаемости и составлении бизнес-планов. Рассчитывая экономическую целесообразность будущего бизнес-проекта, инвестор приводит в соответствие планируемый объем будущих денежных потоков к их текущей реальной стоимости.
Формулы сложных процентов и дисконтирования
Смысл операции дисконтирования легко объяснить на небольшом примере. Например, в наличии сумма S0 = 1000 руб. Если положить эту сумму в банк под 7% годовых с ежегодной капитализацией процентов, т.е. зачислением их во вклад в конце года, мы получим через год:
S1 =1000 + 0,07 х 1000 = (1 + 0,07) х 1000 = 1070 руб.
Через 2 года: S2 = (1 + 0,07) х (1 + 0,07) х 1000 = (1+ 0,07)2 х 1000 = 1144,90 руб.
Через 3 года: S3 = (1+0,07)3 х 1000 = 1225,04 руб.
Через n-лет: Sn = (1+0,07)n х 1000, и таким образом формула сложных процентов выглядит так:
Sn = (1+P)n х S0, где
Sn — сумма денег через n-периодов начисления процентов;
S0 — первоначальная сумма денег;
P — процентная ставка по депозиту за период.
Подведем итог: при размещении денег на депозите сумма в размере 1000 руб., которая имеется в наличии сейчас, будет равняться по стоимости 1070 рублям, полученным через 1 год, и сумме 1225,04 руб., выплаченной через 3 года и т. д.
Расчет дисконтированного денежного потока – задание, обратное предыдущему: необходимо вычислить сумму S0 на текущий момент времени, равную по стоимости сумме Snчерез n-количество лет. Другими словами,величина Sn нам известна, нужно рассчитать S0.
Формула дисконтирования после простых математических преобразований расчета сложных процентов будет выглядеть так:
S0 = Sn / (1+P)n.
Величина P в этом расчете не процентная ставка, а ставка дисконтирования.
S0 — это продисконтированный денежный поток;
Sn — денежный поток каждого расчетного периода. Число n в формуле обозначает количество расчетных периодов, как правило, расчетным периодом в экономических расчетах считают год, иногда квартал или месяц.
Таким образом, если вернуться к предыдущему примеру, при ставке дисконтирования 7% деньги в сумме 1070 руб., выплаченные через 1 год, будут равняться 1000 руб. в настоящем: 1070 / (1+ 0,07) = 1000.
Инструменты дисконтирования: денежные потоки и ставка
В начале расчетов денежные потоки группируют в разрезе некоторых временных интервалов: год, квартал, месяц, а затем суммируют. Полученные величины могут быть с плюсом (поступления больше оттоков) или с минусом, убыточными (отток превышает сумму поступлений). В качестве денежного потока в расчетах могут считать:
-
чистый доход, равный поступившим доходам за вычетом расходов;
-
прибыль, рассчитываемая до исчисления налогов;
-
чистый поток наличности, из которого исключаются текущие затраты на содержание и реконструкцию объекта.
Вычисление ставки дисконтирования — наиболее ответственный момент в расчетах. В самом простом варианте, когда инвестор планирует разместить деньги на депозите, защитив их от инфляции, в качестве основы для расчета ставки применяют прогнозируемый индекс инфляции. Если кроме сбережения финансов планируется еще и получение дополнительной прибыли, то к ставке инфляции добавляется желаемый процент дохода. При инвестициях, особенно долгосрочных, необходимо учитывать не только инфляцию и норму ожидаемой прибыли, но различные сопутствующие риски. Поэтому в ставку дисконтирования закладываются еще и так называемые премии за риск, а при пользовании заемными средствами для реализации инвестиционного проекта к ставке добавляют еще процент по банковским кредитам, выпуску облигаций и т. п.
Чаще всего при анализе окупаемости дисконтная ставка складывается из безрисковой базовой доходности, приравненной к ключевой ставке ЦБ РФ или средневзвешенному проценту по банковским депозитам с добавлением премии за риск.
Дисконтирование денежных потоков: пример расчета
Проведем расчет дисконтированных денежных потоков для инвестиционных вложений сроком на 3 года. В нашем примере дисконтная ставка равна 15%, из них 8% — средневзвешенная ставка банковских депозитов и 7% — премия за риск. Период дисконтирования равен 1 году.
1. Выпишем для каждого годового периода ожидаемую сумму дохода и расходов в рублях. Будем считать, что расходы каждый год будут неизменными, а размер поступлений будет меняться.
2. Рассчитаем разность между доходами и расходами на каждый год.
Таблица расчета:
|
Период |
Доходы |
Расходы |
Чистый доход |
|
1 год |
80 000 |
90 000 |
-10 000 |
|
2 год |
120 000 |
90 000 |
+30 000 |
|
3 год |
150 000 |
90 000 |
+ 60 000 |
3. Приводим финансовые потоки в соответствие к текущему моменту, используя ставку дисконтирования 15%. Применяем коэффициент дисконтирования (1 + 0,15)n, дисконтирующий каждый поток, где n — число каждого года, для которого делаем расчет. Итак:
1 год: -10 000 / (1 + 0,15) = -8 695,65 руб.
2 год: +30 000 / (1 + 0,15)2 = 22 727,27 руб.
3 год: +60 000 / (1 + 0,15)3 = 39 473,68 руб.
4. Полученные суммы складываем:
-8 695,65 + 22 727,27 + 39 473,68 = 53 505,30 руб.
Сумма 53 505,30 – это дисконтированный денежный поток. Положительная величина свидетельствует о привлекательности данного проекта для инвесторов и возможности последующего анализа его перспективности.








![{displaystyle [4.3553,(30,000-5000)]-100,000=$,8,881.52}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b2dcb959b33b3f5f5874b88dec320d9455385c)
