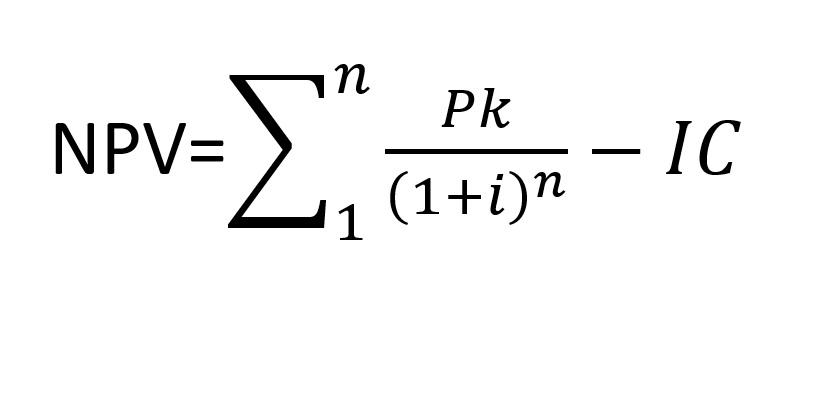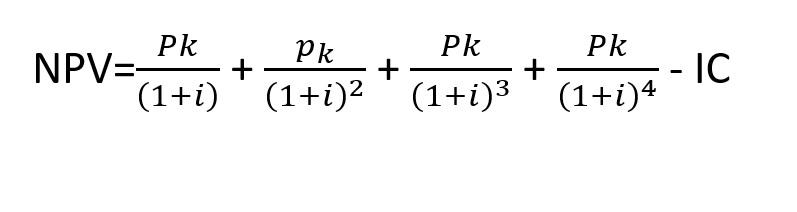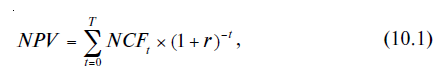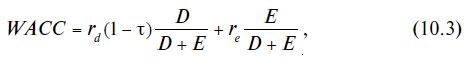Чистый дисконтированный доход — показатель, позволяющий оценить инвестиционную привлекательность проекта. Основываясь на величине чистого дисконтированного дохода, инвестор может понять, насколько обоснованными являются его первоначальные капиталовложения с учетом запланированного уровня доходности проекта, не дожидаясь его завершения.
Чистый дисконтированный доход: формула
В общем порядке величина чистого дисконтированного дохода определяется как сумма всех дисконтированных значений потоков будущих платежей, приведенных к сегодняшнему дню, и определяется следующим образом:
NPV = – IC + Ʃ CFt/ (1 + r)ᵗ,
где:
NPV — величина чистого дисконтированного дохода;
IC — первоначальные инвестиции;
CFt — потоки денежных средств в конкретный период срока окупаемости проекта, которые представляют собой суммы притоков и оттоков денежных средств в каждом конкретном периоде t (t = 1…n);
r — ставка дисконтирования.
В зависимости от значения данного показателя инвестор оценивает привлекательность проекта. В случае, если:
1. NPV > 0, то инвестиционный проект выгоден, инвестор получит прибыль;
2. NPV = 0, то проект не принесет ни прибыли, ни убытка;
3. NPV < 0, проект невыгоден и сулит инвестору убытки.
Также для анализа инвестиционной привлекательности проекта инвесты изучают чистый денежный поток предприятия. Существует 2 метода определения величины чистого денежного потока: прямой и косвенный.
Денежный поток рассчитывается по специальной формуле, которую можно найти в материале от КонсультантПлюс. Если у вас нет доступа к системе К+, получите пробный онлайн-доступ бесплатно.
Учет инфляции при расчете чистого дисконтированного дохода
В связи с тем, что в некоторых ситуациях инфляционные колебания невозможно нивелировать на практике, возникает вопрос о том, каким образом отразить влияние инфляции на показатель чистого дисконтированного дохода. Наиболее распространенным решением данной проблемы является корректировка дисконта на прогнозируемый уровень инфляции.
При этом процентная ставка будет рассчитываться следующим образом:
R = (1 + r) × J,
где:
R — дисконтная ставка с учетом инфляции;
r — дисконт;
J — уровень инфляции.
Таким образом, чем выше уровень инфляции, прогнозируемый на время реализации проекта, тем ниже должна быть доходность проекта, чтобы после дисконтирования проект не стал убыточным.
Чистый дисконтированный доход: пример расчета
Предположим, что инвестор хочет модернизировать систему автоматизации производственного процесса. Предполагается, что сумма затрат на перевооружение конвейера составит 50 000,00 руб. При этом планируется увеличение объемов производства за счет нового оборудования, как следствие — увеличение объемов продаж в течение ближайших 5 лет. Приток денежных средств за 1-й год составит 45 000,00 руб., за 2-й год — 40 000,00 руб., за 3-й год — 35 000,00 руб., за 4-й год — 30 000,00 руб., за 5-й год — 25 000,00 руб. Необходимая норма прибыли — 10%. Расчет приведенной стоимости проекта представлен в таблице.
|
Период (t),год |
Денежный поток (CF) |
Дисконт (r) |
Чистая приведенная стоимость (CFt) |
|
0 |
–50 000,00 |
10% |
–50 000,00 |
|
1 |
45 000,00 |
10% |
40 909,09 |
|
2 |
40 000,00 |
10% |
33 057,85 |
|
3 |
35 000,00 |
10% |
26 296,02 |
|
4 |
30 000,00 |
10% |
20 490,40 |
|
5 |
25 000,00 |
10% |
15 523,03 |
|
Чистый дисконтированный доход (NPV)м |
86 276,40 |
Исходя из того, что показатель NPV положительный, можно сделать вывод о том, что данный проект рентабелен.
Однако ситуация изменится в худшую сторону, если предположить, что инфляция на протяжении всех пяти лет будет держаться на уровне 8%.
|
Период (t),год |
Денежный поток (CF) |
Дисконт (r) |
Уровень инфляции, (J) |
Чистая приведенная стоимость (CFt) c учетом инфляции |
|
0 |
–50 000,00 |
10% |
8% |
–46 296,30 |
|
1 |
45 000,00 |
10% |
8% |
34 435,26 |
|
2 |
40 000,00 |
10% |
8% |
25 296,79 |
|
3 |
35 000,00 |
10% |
8% |
18 293,14 |
|
4 |
30 000,00 |
10% |
8% |
12 958,54 |
|
5 |
25 000,00 |
10% |
8% |
8 924,61 |
|
Чистый дисконтированный доход (NPV) |
53 612,05 |
В целом чистый дисконтированный доход остался в пределах положительных значений, значит, проект все также принесет инвесторам прибыль. Однако по сравнению с первым вариантом, где инфляция не была учтена, отдача от первоначальных вложений с учетом дисконтированной стоимости поступлений от продажи новой продукции стала значительно ниже.
Итоги
Принимая решение о выгодном вложении денежных средств, высвобожденных из делового оборота, инвестор должен сделать выбор в пользу наиболее доходного проекта. На основании расчета чистого дисконтированного дохода сравнивать несколько вариантов с разными сроками окупаемости становится удобнее.
Если вам нужно рассчитать чистую прибыль, см. наш материал «Расчет чистой прибыли по балансу – формула».
О том, как провести анализ чистой прибыли, вы можете узнать из материала «Порядок проведения анализа чистой прибыли предприятия».


Содержание
Инвестирование позволяет получать стабильный доход. Можно вкладывать деньги в финансовые проекты, в новый бизнес или в расширение уже существующей компании.
Чтобы не ошибиться с выбором объекта капиталовложения, люди используют инструменты, предназначенные для быстрого определения эффективности инвестиционного проекта. Один из них – расчет NPV.
Что такое NPV
Net Present Value дословно переводится как «чистая приведенная стоимость». Обычно этот показатель используют, чтобы понять, стоит ли вкладывать деньги в проект. Иногда с его помощью рассчитывают финансовые характеристики за определенный период времени.
Например, инвестор хочет вложить 5 миллионов рублей. Его интересуют сроки окупаемости проекта и возможный заработок. Показатель NPV позволит понять, каким будет размер чистой прибыли через год, 5 или 10 лет. От результатов его расчета часто зависит окончательное решение – насколько целесообразно вкладывать деньги в конкретный проект.
Зачем нужно считать NPV
В первую очередь NPV проекта показывает, когда и в каком количестве вернутся вложения и вернутся ли они вообще. Инвесторы часто сравнивают несколько проектов, чтобы определить, какой из них окажется наиболее прибыльным. В этом случае формула тоже работает.
Существуют 3 цели, для которых используют расчет NPV:
- определение размера первоначальных вложений;
- вычисление сроков окупаемости;
- оценка размеров дохода, необходимого для окупаемости.
Преимущества и недостатки подсчета NPV
Если результат подсчета NPV проекта оказывается положительным, значит, проект экономически эффективен, и потенциальные инвесторы обратят на него больше внимания. При расчете NPV можно учитывать разные сроки, складывать показатели отдельных проектов и принимать во внимание дополнительные риски. Все это – неоспоримые преимущества расчета NPV.
Главные недостатки – сложность и сравнительно низкая точность расчета NPV, а речь идет о размере будущей прибыли. Ее невозможно точно предсказать, так как темпы роста, инфляция и курс валют постоянно меняются. Если учитывать в формуле много дополнительных рисков, сложность подсчета увеличивается и растет вероятность допустить ошибку.
Формула расчета
Стандартная NPV-формула выглядит следующим образом:
n – период расчета;
Pk – денежные потоки за выбранный период времени;
i – ставка дисконтирования;
IC – размер первоначальных вложений.
Важно учесть все составляющие, и здесь многое зависит от конкретного проекта. Вложения нужны для того, чтобы увеличить прибыль, но для небольшого магазина и крупной фабрики эти суммы будут совершенно разными. Определение срока окупаемости тоже зависит от множества факторов. Хотя сложнее всего – рассчитать денежные потоки и ставку дисконтирования.
Денежные потоки
Под денежными потоками понимают все финансовые поступления и расходы. Под поступлениями чаще всего подразумеваются продажи, хотя встречаются и другие их виды – например, проценты от проведенных сделок. Расходы включают в себя выплату заработной платы сотрудникам, коммунальные платежи, закупку сырья, аренду помещений, обустройство рабочих мест, налоги.
Существуют также предположительные потоки, и рассчитать их гораздо сложнее – например, грядущее повышение арендной ставки или затраты на запуск на рынок нового продукта. В качестве аналитической базы используют экономические показатели, данные мониторинга конкурентов, ожидаемый эффект от рекламы и другие данные.
Чтобы оценить прибыльность рекламных кампаний, подключите сквозную аналитику Calltouch. Сервис посчитает прибыль, продемонстрирует эффективность рекламы и позволит спрогнозировать результативность кампаний.
Сквозная аналитика Calltouch
- Анализируйте воронку продаж от показов до денег в кассе
- Автоматический сбор данных, удобные отчеты и бесплатные интеграции
Узнать подробнее
Ставка дисконтирования
Узнать NPV проекта невозможно без ставки дисконтирования. Далеко не все инвесторы вкладывают собственные средства – иногда выгоднее взять кредит, чем использовать внутренние ресурсы. Или можно продать акции, если потенциальная прибыль у проекта выше, чем их доходность.
Посчитать ставку в случае с кредитом проще. Достаточно ориентироваться на годовой процент. Если же инвестор планирует использовать деньги с продаж акций, придется сравнивать прогнозы по доходам. И все равно это будет только приблизительная информация.
Как рассчитать NPV
Предположим, что в проект инвестировали 1 000 000 рублей. В качестве периода расчета NPV выбрали 1 год. Ставка дисконтирования равна 15%. Обычно ее переводят в коэффициент, то есть, делят на 100. Если размер денежных поступлений составит 900 000 рублей, получится:
900 000 / (1 + 0,15) – 1 000 000= -217 391
Эта сумма и будет чистой стоимостью, приведенной за год. Так как она отрицательная, проект считается убыточным на выбранном периоде. Но это не значит, что вложения не окупятся – просто увеличьте временной отрезок и используйте формулу:
С каждым годом коэффициент дисконтирования уменьшается, поэтому его нужно возводить в степень. Если взять предыдущий пример, за 3 года получится следующий результат:
900 000 / (1 + 0,15) + 900 000 / (1 + 0,15)² + 900 000 / (1 + 0,15)³ – 1 000 000 = 1 054 902
Так как сумма положительная, проект на этом промежутке времени оказывается прибыльным.
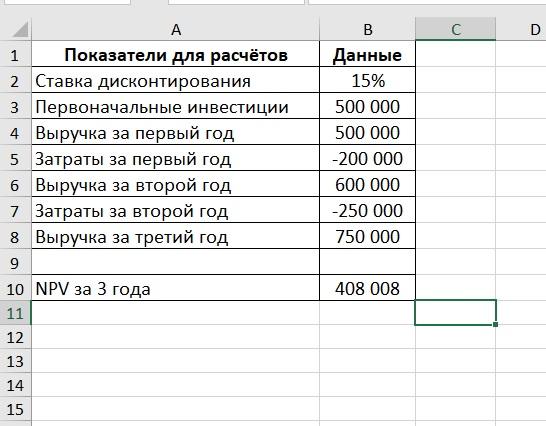
Пример расчета в Excel
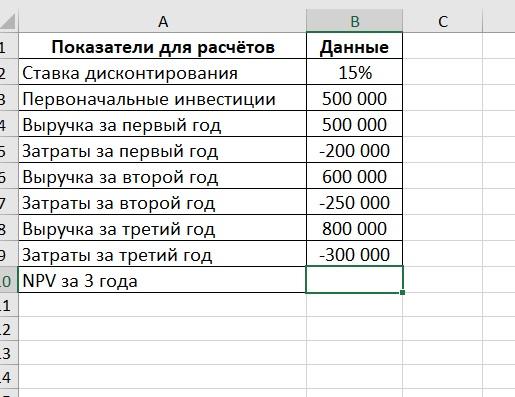
Чтобы считать было удобнее, лучше составить таблицу в MS Excel. Преимущество этого способа в том, что можно менять различные показатели, не высчитывая их вручную, и сравнивать несколько проектов. Также в MS Excel предусмотрена функция расчета чистой приведенной стоимости – ЧПС.
Таблица с показателями выглядит так:
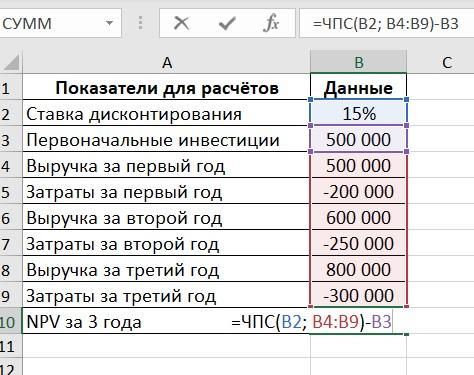
Для расчета в ячейку B10 нужно добавить формулу:
При изменении показателей NPV проекта будет рассчитываться автоматически.
Стоит помнить, что поступления должны быть положительными, а затраты – отрицательными.
Сложности, которые могут возникнуть при расчете
Иногда инвесторы составляют слишком оптимистичный прогноз, но как раз из-за него и возникают трудности с расчетом NPV. Ошибки в вычислении приводят к тому, что инвестиции не приносят ожидаемого дохода.
Здесь можно выделить 4 причины:
- Ошибка в вычислении ставки дисконтирования. Проценты в банках по текущим кредитам обычно не меняются, а вот рост инфляции и изменения курса акций предугадать невозможно.
- Отсутствие учета непредвиденных расходов. Например, инвестор вкладывает значительные средства в покупку коммерческой недвижимости и ожидает прибыли от аренды, но не учитывает затраты на ремонт и благоустройство.
- Искаженное представление о доходах. Ни один бизнес не может гарантировать бесперебойность потока покупателей. Например, в период пандемии многим владельцам бизнеса пришлось приостановить деятельность, а кто-то и вовсе объявил себя банкротом.
- Нереалистичные и некорректные прогнозы. Любые расчеты следует проверять несколько раз, и в каждом прогнозе инвестор должен быть уверен.
В отличие от суммы инвестиций, рассчитать окупаемость рекламных вложений гораздо проще – для этого существуют специальные сервисы. Чтобы рассчитать доходность рекламы и увеличить прибыльность онлайн-магазина, установите E-commerce Calltouch. На основе результатов отчетов сопоставьте рекламный бюджет и прибыль и скорректируйте рекламную стратегию.
Аналитика для интернет-магазина
- Отслеживайте корзины, звонки, заявки и продажи с них с привязкой к источнику
- Постройте воронку продаж и оптимизируйте маркетинг
Узнать подробнее
Коротко о главном
- NPV инвестиционного проекта позволяет определить сроки окупаемости и будущую прибыль.
- Стандартная формула включает в себя размер первоначальных инвестиций, денежные потоки, период и ставку дисконтирования.
- Для более точного результата лучше учитывать максимум рисков.
Для предстоящих вложений в новый проект инвесторы всегда рассчитывают показатели его эффективности, сопоставляя сумму вложений с ожидаемым доходом. Эти величины чаще всего сильно разнесены во времени, поэтому для их оценки применяют понятие «чистый дисконтированный доход». Для сокращения обычно используют аббревиатуру ЧДД или NPV. Разберем подробнее этот показатель.
Содержание статьи
- 1 Что такое чистый дисконтированный доход
- 2 Назначение показателя NPV
- 3 Как рассчитать чистый дисконтированный доход
- 3.1 Формула NPV
- 3.2 Учет инфляции при расчете NPV
- 3.3 Пример расчета
- 3.4 Сложности при расчетах
- 4 Анализ результата расчета
- 5 Модификация чистого дисконтированного дохода
- 6 Чистая терминальная стоимость
- 7 Плюсы и минусы показателя
Что такое чистый дисконтированный доход
Чистый дисконтированный доход (NPV) – это показатель, с помощью которого инвестор может оценить вероятность и объем дохода от предполагаемых вложений. Для расчета используются несколько величин – прежде всего, сумма вложений и величина финансового потока от инвестиций. Кроме того, этот показатель учитывает изменение стоимости денег во времени – только так достигается относительная точная позиция рентабельности инвестиций.
Простыми словами, NPV – это оценочная характеристика возможности инвестирования и оценка предстоящей рентабельности, проводимая с учетом разной стоимости денег сейчас и к концу срока реализации проекта.
Чистым дисконтированным доходом называют разницу между объемом инвестиций и той денежной массой, которая в итоге вернется инвестору. Его альтернативные названия: «дисконтированная стоимость», «чистая приведенная стоимость», «чистая текущая стоимость», а англоязычный аналог – это Net Present Value, что и дает сокращенную аббревиатуру NPV.
Назначение показателя NPV
Показатель чистого дисконтированного дохода позволяет определить ценность инвестиций в момент времени, давая представление о том, сколько вложенные инвестиции будут стоить завтра. Изучая NPV, можно предположить целесообразность вложений и сравнивать проекты, выбрать самый оптимальный.
В основе показателя лежит тот факт, что стоимость денег меняется во времени в силу различных факторов:
- Один из самых простых и понятных – инфляция, из-за роста цен меняется покупательная способность денег.
- Доходность от альтернативных инвестиций – например, инвестор может на старте не вкладываться в проект, а купить государственные облигации. Тогда доходность по этим облигациям и будет базой для сравнения (нет смысла рисковать, если можно получить гарантированную отдачу от бумаги).
- Отдача от инвестиций у конкурентов – если проект будет приносить меньше прибыли, чем у других компаний этой отрасли, это поставит бизнес в менее выгодное положение.
Соответственно, NPV – суммарный доход от инвестиций, из которого вычтена определенная часть. И эта часть соответствует тому, сколько стоимости потеряли вложенные деньги за срок реализации проекта.
Благодаря проводимым расчетам инвестор получает более полную картину и возможность оценить рентабельность проекта в данный момент времени.
Как рассчитать чистый дисконтированный доход
Для расчета нужно знать сумму первоначальных инвестиций в проект, а также определить период времени, за который оценивается ЧДД. Рассмотрим подробнее, как рассчитать NPV.
Формула NPV
Так как ценность денег меняется каждый год, в формулу введен специальный коэффициент, рассчитываемый от ставки дисконтирования.
Сама формула NPV выглядит так:
где:
- NPV – показатель чистого дисконтированного дохода;
- IC – первоначальная сумма инвестиций;
- CFt – чистый денежный поток за период времени t, в котором оценивают ЧДД (то есть, разница доходов и расходов);
- i – ставка дисконтирования.
Иногда показатель инвестиций включают в основной блок формулы – но тогда нужно учесть, что это 0-й год реализации проекта (и делиться инвестиции будут на 1).
Говоря проще, нужно просуммировать значения чистого денежного потока за каждый год реализации инвестиционного проекта. Например, для проекта с 3-летним сроком реализации формула чистого дисконтированного дохода будет такой:
Таким образом, в зависимости от полученных данных можно оценить инвестиционную привлекательность проекта.
Учет инфляции при расчете NPV
Так как в расчете учитывается изменение ценности денег, обычно в расчет берется инфляция. Ставка дисконтирования из формулы – это показатель стоимости капитала, безрисковая ставка доходности или просто инфляция. Безрисковая ставка дисконтирования актуальна для облигаций федерального займа или срочных рублевых депозитов. Кроме того, ставку можно посчитать, используя показатели рентабельности, объема капитала и инвестиционных возможностей имеющихся активов.
А чтобы учесть как безрисковую доходность, так и инфляцию, ставку дисконтирования рассчитывают по формуле:
- R = (1 + r) * j, где:
- R – ставка дисконтирования;
- r – дисконт или норма прибыли, которую закладывают в проект;
- j – показатель инфляции.
Рентабельность инвестиционного проекта с учетом инфляции может быть представлена меньшей цифрой – но она все равно должна быть достаточной, чтобы инвестор получал прибыль.
Как правило, многие краткосрочные инвестиционные проекты предлагают к сравнению уже подсчитанные показатели, сведенные в специальные таблицы. Например, можно найти нужные данные на сайте Росстата или профильных исследовательских агентств.
Пример расчета
Для примера рассмотрим инвестиционный проект сроком на 4 года. Вложения составят 150 тысяч рублей, ставку дисконтирования примем равной 12% (это сейчас – максимально возможная безрисковая доходность), а предполагаемый объем денежных потоков оценим в 30, 70, 70 и 45 тысяч рублей на первый, второй, третий и четвертый годы соответственно.
Используем приведенную выше формулу расчета NPV. Стартуя с отрицательной цифры в 150 тысяч, прибавляем данные за каждый год последовательно:
В итоге получим показатель ЧДД, равный 11 012 рублей. NPV инвестиционного проекта выше нуля, а значит, в него можно вкладываться.
Сложности при расчетах
Особых математических сложностей при расчете NPV не возникает. Однако, чтобы избежать вычислений вручную, используют программы, причем достаточно даже возможностей таблиц Excel. Для этого нужно заполнить ячейки показателями ставки дисконтирования и суммы денежного потока. Важно, что данные первоначальных вложений нужно вносить со знаком «минус». Результат расчетов покажет сумму приведенных к данному моменту платежей в итоговой ячейке.
Пример расчета (по данным выше) и формула выглядят так:
Разница с расчетом выше связана с тем, что Excel в расчете чистой приведенной стоимости (ЧПС) считает год инвестирования первым, тогда как обычно экономисты считают его нулевым. С другой стороны, в ряде источников встречается и такой подход, когда первый год в расчете уже считается вторым.
Вместе с тем, существуют сложности подсчета, с математикой никак не связанные. Дело в том, что на практике достоверно оценить показатели денежных потоков и ставки дисконтирования довольно сложно. Для первого из них проводят масштабный анализ, изучая эластичность спроса, конъюнктуру рынка, другие макро- и микроэкономические факторы.
Анализ результата расчета
Для анализа результата расчетов рассматривают показатели чистого денежного потока дисконта в границах изучаемого периода. Возможны 3 варианта результата:
- NPV меньше нуля – в этом случае вложения не принесут желаемого дохода в сравнении с аналогичными или подобными, рекомендуется искать другой проект.
- NPV равен нулю. Нулевой показатель ЧДД говорит о том, что денежные потоки будут поступать в объеме, не позволяющем нарастить капитал.
- NPV больше нуля. Этот тот вариант, при котором инвестиции окупаются и капитал нарастает.
Есть и обратный расчет – когда нужно рассчитать ставку дисконтирования, при которой чистая текущая стоимость будет нулевой. То есть, это та номинальная доходность, которую обеспечит проект с заданными параметрами инвестиций и чистого потока (это – внутренняя норма доходности).
Модификация чистого дисконтированного дохода
Классическая формула ЧДД предполагает, что бизнесмен сначала вкладывает деньги в проект, а потом получает от него отдачу. Но в реальности обычно часть получаемых средств реинвестируется обратно в проект.
Чтобы учесть это, используется модификация чистого дисконтированного дохода (MNPV):
где:
- MNPV – модифицированный ЧДД;
- IC – сумма оттока за период t;
- d – показатель реинвестирования – это процент доходности от той суммы, которую получит и реинвестирует владелец бизнеса;
- n – количество периодов анализа.
В качестве доходности от реинвестирования можно взять, например, доходность по депозитам или облигациям. Эта формула позволит учесть дополнительные доходы от задействования полученной от проекта прибыли (которую инвестор и так куда-то бы направил).
Интерпретация полученного результата – такая же, как и у NPV: если он выше нуля, проект можно рассматривать, если ниже нуля – его стоит отклонить.
Чистая терминальная стоимость
Расчет показателей ЧДД по формуле всегда связан с допуском некоторых погрешностей. Чтобы их устранить, применяют показатель чистой терминальной стоимости (NTV). Для его расчета все составляющие денежного потока приводят к моменту окончания проекта, используя наращение (процесс, обратный дисконтированию).
Формула выглядит следующим образом:
где:
- g – показатель темпа роста;
- WACC – средняя стоимость капитала с учетом удельного веса каждого источника поступлений.
Условия применения показателя NTV те же: проект может считаться успешным при уровне выше нуля.
Плюсы и минусы показателя
Главное преимущество показателя чистого дисконтированного дохода – это возможность оценки доходности инвестиционного проекта на протяжении всего срока реализации с учетом постепенного обесценения денег.
С помощью ЧДД инвестору проще анализировать график поступлений. Такой метод учитывает в том числе и процентную ставку, которая со временем может меняться. Суммируя чистый дисконтированный доход различных проектов, можно сформировать инвестиционный портфель с оптимальными показателями роста.
Недостаток показателя кроется в его абсолютности – NPV не учитывает возможные риски. Таким образом, картина рентабельности может сложиться неверной.
В целом, показатель чистого дисконтированного дохода является ключевым для анализа эффективности. Пусть его формула имеет некоторые допуски и погрешности, а также требует взвешенного всестороннего анализа различных составляющих, все же именно ЧДД определяет решение инвестора о возможности вложений.
Основные
методы оценки венчурных проектов
Ключевые
понятия:
Чистая
дисконтированная стоимость
Норма
доходности проекта
Внутренняя
норма доходности
Рентабельность
инвестиций
Стратегическая
ценность управленческих решений
Экономическая
добавленная стоимость
Технологический
аудит
10.1. Метод чистой дисконтированной стоимости
Чистая
дисконтированная (текущая) стоимость
(NPV, net present value of cash flows) – это разница
между рыночной стоимостью проекта и
затратами на его реализацию. Она
представляет собой сумму дисконтированных
по годам денежных потоков за все периоды
реализации проекта:
где NCFt
– чистый денежный поток для года I
(см. главу 9); г – процентная ставка,
использующаяся для данного проекта
(норма дисконтирования); Т
—
период реализации проекта; Т
=
0 – период осуществления первоначальных
инвестиций в проект.
Нетрудно
заметить, что соответствующее значение
чистой дисконтированной стоимости
может быть получено путем умножения
чистых денежных потоков за каждый период
на соответствующий коэффициент
дисконтирования.
Чистая
дисконтированная стоимость показывает
настоящую стоимость разновременных
результатов от реализации конкретного
проекта. Другими словами, чистая
дисконтированная стоимость – это мера
той добавочной или вновь создаваемой
стоимости, которую мы получим, финансируя
сегодня первоначальные затраты проекта.
Инвестиционное
предложение следует рассматривать,
если чистая дисконтированная стоимость
проекта положительная.
Если чистая текущая стоимость проекта
меньше 0, проект должен быть отклонен.
Из нескольких альтернативных проектов
следует выбирать тот, у которого, при
прочих равных условиях, больше чистая
текущая стоимость.
Положительная
величина чистой текущей стоимости
свидетельствует не только о полном
возмещении затрат на инвестиционный
проект при прогнозируемом уровне
доходности капитала, но и о получении
дополнительного дохода, т. е. об
увеличении активов предприятия вследствие
принятия проекта.
При расчете
дисконтированной стоимости принято
делать некоторые допущения,
которые значительно упрощают инвестиционные
расчеты.
• Капитал
можно привлечь и разместить под один и
тот же процент.
• Денежные
притоки и оттоки происходят в начале
или конце каждого периода, а не возникают
в течение всего периода.
• Денежные
потоки точно определены и нет необходимости
делать поправку на риск.
• В
качестве стратегической цели принимается
максимизация благосостояния фирмы.
Если не
учитывать фактор налогообложения,
чистую текущую стоимость инвестиционного
проекта можно определить как максимальную
сумму, которую может заплатить фирма
за возможность инвестировать капитал
без ухудшения своего финансового
положения. Ожидаемая чистая текущая
стоимость является нереализованным
приростом капитала в части, превышающей
расчетные затраты на инвестиционный
проект. Реализованным этот прирост
капитала станет в том случае, если
ожидаемые денежные доходы станут
реальными денежными доходами.
С точки
зрения инвестора, чистая дисконтированная
стоимость является сверхприбылью,
поскольку положительная ее величина
свидетельствует не только о полном
возмещении затрат на инвестиционный
проект при прогнозируемом уровне
доходности капитала, но и о получении
дополнительного дохода.
В условиях
совершенной конкуренции не существует
возможностей для получения какого-либо
дохода сверх нормальной величины,
поэтому величина чистой текущей стоимости
не должна превышать нуля. Однако в
условиях реальной рыночной экономики
существуют некоторые возможности для
максимизации прибыли (новые рынки, новые
продуктовые ниши, новые технологические
решения и т. п.).
Пример
10.1
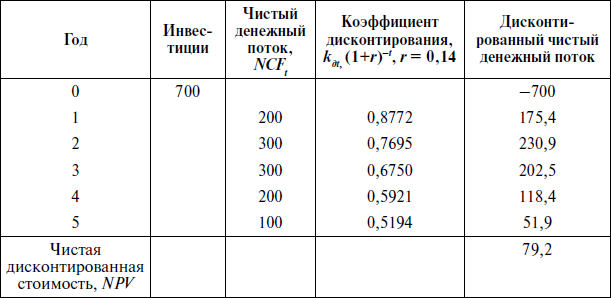
Предприятие
рассматривает инвестиционный проект,
объем инвестируемого капитала по
которому составляет 700 тыс. д.е., при
этом за последующие пять лет ожидаются
следующие чистые денежные потоки от
реализации проекта: в первый год –
200 тыс. д.е., во второй год – 300 тыс.
д.е., в третий год – 300 тыс. д.е., в
четвертый год – 200 тыс. д.е., в пятый
год – 100 тыс. д.е. Требуется найти
чистую дисконтированную стоимость
инвестиционного проекта при условии,
что норма дисконтирования составляет
14 %. Решение приводится в таблице.
Расчет
чистой дисконтированной стоимости по
проекту
Метод
чистой дисконтированной стоимости
рассматривается в теории инвестиционного
менеджмента как наиболее правильно
отражающий влияние инвестиционного
проекта на рыночную стоимость предприятия
[Брейли, 1997; Бригхем, 1997] по следующим
причинам.
Во-первых,
он учитывает изменение ценности денег
во времени, а следовательно, является
корректным с точки зрения экономической
теории.
Во-вторых,
показатель NPV
определяется
исключительно величиной генерируемых
проектом чистых денежных потоков и
альтернативными издержками, указывающими
на возможную ставку дисконтирования.
Он свободен от влияния таких факторов,
как предпочтения менеджеров, выбранные
предприятием принципы учетной политики,
рентабельность уже осуществляемой
деятельности, рентабельность независимых
от данного инвестиционных проектов и
т. д.
В-трегьих,
критерий является аддитивным (можно
складывать дисконтированные денежные
потоки по различным элементам проекта).
Это позволяет оценивать эффективность
комбинированных инвестиций (а венчурные
проекты, как правило, являются комплексными,
состоящими из различных подпроектов,
о чем подробнее сказано в главе 6). Другие
аналогичные NPV
критерии
(например, срок окупаемости, рентабельность
инвестиций или внутренняя норма
доходности) имеют ограничения при
использовании в сложных случаях и могут
привести к ошибочному результату. Однако
этот теоретически безупречный критерий
не всегда может быть использован на
практике, особенно при оценке инноваций.
Можно
выделить три основные проблемы, связанные
с использованием показателя чистой
дисконтированной стоимости для оценки
инвестиций в новые технологии.
1. Правильность
оценки генерируемых проектом денежных
потоков.
Оценка денежных потоков является одним
из самых важных элементов управления
инвестиционным процессом. Прогноз
денежных потоков должен составляться
на несколько лет вперед, что вызывает
неизбежные ошибки в оценках. На самом
деле прогнозы денежных потоков не лишены
смещений в оценках. Менеджеры в своих
прогнозах склонны к чрезмерному
оптимизму, и в результате доходы имеют
тенденцию к завышению, а издержки – к
занижению. В результате происходит
смещение чистых операционных денежных
потоков вверх и, следовательно, смещение
вверх оценочных NPV.
Часто это случается потому, что заработная
плата менеджеров зависит от размеров
компании, поэтому они заинтересованы
в максимизации размеров фирмы, а не в
ее прибыльности. Кроме того, менеджеры
часто эмоционально привязываются к
проекту и, таким образом, не могут
объективно оценить его потенциальные
риски. Последний фактор имеет большое
значение для инноваторов, что может
привести к их завышенным ожиданиям и
стать препятствием для осуществления
венчурных инвестиций.
2. Критерий
чистой дисконтированной стоимости
«пассивен»
по отношению к стратегическим
управленческим решениям.
Использование критерия NPVдля
оценки инвестиционных решений не
учитывает управленческих возможностей,
заложенных в тех или иных активах
предприятия. Эти возможности, при условии
их использования, могут принести
предприятию существенные преимущества,
например:
– разработку
новых продуктов в русле начатого проекта;
– расширение
рынков сбыта продукции;
– расширение
или переоснащение производства;
– прекращение
проекта и т. д.
Некоторые
управленческие возможности сопряжены
со стратегическим выходом компании на
новые рынки. Ценность такой возможности
часто называется стратегической
ценностью [Бригхем, 1997]. Так как
управленческие возможности многочисленны
и многообразны, а время их использования
неопределенно, обычно нецелесообразно
включать их непосредственно в оценки
денежных потоков проекта. Однако
концептуально можно представить реальную
стоимость проекта как сумму дисконтированных
чистых денежных потоков и ценности
заключенных в проекте управленческих
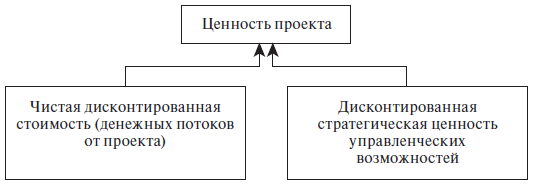
возможностей (рис. 10.1):
Рис. 10.1.
Стоимость инвестиционного проекта с
учетом стратегической ценности
управленческих возможностей
В некоторых
случаях стратегическую ценность
управленческих возможностей можно
выразить количественно, на основе теории
оценки реальных опционов.
3. Существуют
мнения, что
с помощью чистой приведенной стоимости
невозможно учесть фактор риска
[Волков, 1998]. Для анализа инвестиционного
проекта в качестве дополнения метода
NPV
предлагается
использовать различные методы анализа:
анализ чувствительности, анализ
безубыточности, модель Монте-Карло и
«дерево решений». Эти методы позволяют
оценить влияние факторов риска на
денежные потоки, генерируемые проектом,
и определить границы, в которых может
находиться бюджет противорисковых
мероприятий.
4. Одна
из важнейших проблем при использовании
критерия чистой дисконтированной
стоимости – выбор
ставки дисконтирования.
С теоретической точки зрения она
представляет собой стоимость капитала
предприятия, т. е. те альтернативные
издержки, которые связаны с инвестированием
в данный проект. «Альтернативные издержки
осуществления проекта представляют
собой доход, который могли бы получить
акционеры, если бы инвестировали свои
средства по собственному усмотрению.
Когда мы дисконтируем потоки денежных
средств по ожидаемой норме доходности
сопоставимых финансовых активов, мы
определяем, сколько инвесторы были бы
готовы заплатить за ваш проект» [Брейли,
1997, с. 77]. Сопоставимость активов означает,
что им присуща та же степень риска, что
и инвестициям в проекты предприятия.
Такая теоретическая концепция представлена
на рис. 10.2.
В качестве
распространенных методов определения
ставки доходности используются следующие
модели:
– модель
оценки капитальных активов (Capital Asset
Pricing Model – САРМ);
– метод
кумулятивного построения (Build-up Approach);
– метод
средневзвешенной стоимости капитала
(Weighted Average Cost of Capital – IVACC).
Все эти
модели опираются на ряд общих допущений,
которые не могут быть осуществлены на
практике (например, предполагается
существование эффективного рынка и
отсутствие трансакционных издержек).
Кроме того, каждая из них может
использоваться в российских условиях
с существенными ограничениями.
Рис. 10.2.
Интерпретация нормы доходности как
альтернативных издержек, которые
акционеры могли бы получить, самостоятельно
инвестируя средства в финансовые активы
Модель
оценки капитальных активов
исходит из того, что требуемая инвестором
норма доходности капитала г определяется
следующими факторами – безрисковой
ставкой доходности rf;
премией за риск rm
–
rf
(rт
– среднерыночная ставка доходности);
уровнем систематического риска проекта
(предприятия) ?i:
ri = rf
+ ?i(rm-rf).
(10.2)
Теоретически
безрисковая ставка равна доходности
ценной бумаги или портфеля ценных бумаг,
ни при каких обстоятельствах не
подверженных риску невыполнения
обязательств. Эта ставка не коррелирует
с иными ставками доходов. Экономисты
США рекомендуют использовать процентную
ставку десятилетних казначейских
облигаций и достаточно убедительно
аргументируют такой выбор. Надежность
и объективность использования ставок
по государственным долговым обязательствам
в России затруднена по известным
причинам. Вопрос выбора безрисковой
ставки дохода дискутируется. Рекомендуемые
значения безрисковой ставки по ряду
стран (с учетом коэффициента странового
риска) представлены в табл. 10.1.
Таблица
10.1.
Безрисковая ставка с премией за страновые
риски (псевдобезрисковые уровни
доходности)[36]
Рыночная
премия за риск (цена риска) представляет
собой разницу между ожидаемой доходностью
рыночного портфеля и безрисковой
процентной ставкой. Применительно к
инвестициям в США рекомендовано исходить
из 5–6 % рыночной премии за риск.
Обоснование этой величины получено при
анализе доходности рыночного индекса
S&P по сравнению с доходностью
долгосрочных государственных ценных
бумаг за период с 1926 по 1992 г. [Сычева,
2002]. В отечественных условиях провести
такого рода расчеты затруднительно в
силу недолговечности существования
фондового рынка и его подверженности
существенным рискам несистематического
характера невозможно. По данным Российской
торговой системы (РТС) уровень средней
рыночной доходности диверсифицированного
портфеля акций, рассчитанный по изменению
индекса РТС за период с 1995 по 2000 г.,
составлял приблизительно 18 %.
Приблизительные рекомендуемые данные
для расчета ставки доходности на основе
модели оценки капитальных активов
приведены в табл. 10.2 [Лимитовский, 2003].
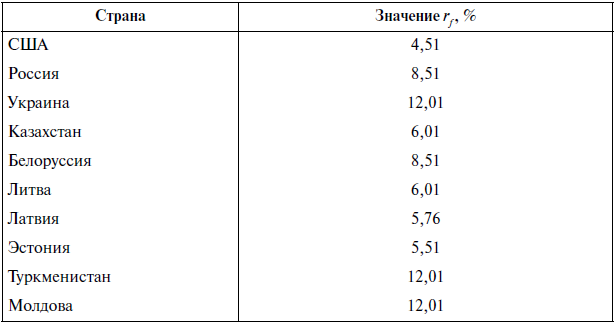
Таблица
10.2.
Безрисковый уровень доходности и
рыночные премии по странам бывшего СССР
(номинальная оценка в долл. США)
Коэффициент
р отражает уровень систематического
риска, который невозможно устранить
путем диверсификации. Выбор метода
оценки ? зависит оттого, обращаются
ли акции компании на открытом рынке.
Если да, то можно воспользоваться
публикуемыми показателями. Так, в США
BARRA ежеквартально обновляет свои прогнозы
значений [5 для 7 тыс. компаний, акции
которых котируются на Нью-Йоркской
фондовой бирже, Американской фондовой
бирже и NASDAQ. Эти показатели систематического
риска основаны на финансовых коэффициентах
каждой компании, изменяются по мере
изменения этих коэффициентов и отражают
актуальные рыночные оценки риска акций.
Также случается, что оценки ?, выполненные
разными организациями, различаются
между собой. Примеры таких различий
показаны в табл. 10.3. В России получить
данные для расчета величины этого
коэффициента можно, например, у известных
информационных агентств, таких как АК&М
или РБК.
Если
компания является закрытой, данные,
публикуемые организациями, должны быть
скорректированы. Тоже самое должно
происходить и в том случае, если проект
является инновационным, так как иначе
трудно подобрать базу для сравнения.
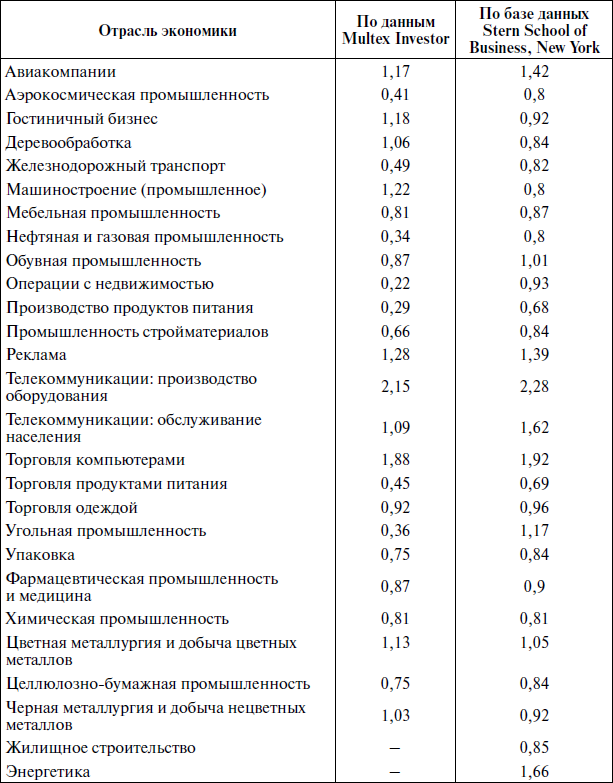
Таблица
10.3.
Коэффициенты систематического риска
(р) по отраслям экономики
В результате
практической проверки достоверности
расчетов ставки дисконтирования с
помощью модели САРМ западные экономисты
пришли к выводу, что модель оценки
долгосрочных активов следует дополнить
таким многофакторным методом, как модель
арбитражного ценообразования. В этой
модели систематический риск измеряется
не один раз, а некоторое количество раз.
Каждая рассчитанная величина [5 отражает
чувствительность доходности акций
компании к изменению некоторых основных
экономических факторов, таких как:
индекс промышленного производства,
краткосрочная реальная процентная
ставка, краткосрочные темпы инфляции,
долгосрочные темпы инфляции, риск
невыполнения обязательств.
В случае,
если невозможно применить данные
фондового рынка, в условиях развивающегося
рынка для расчета ставки дисконтирования
используют метод
кумулятивного построения.
Согласно этому методу к безрисковой
ставке доходности прибавляются премии,
отражающие риски инвестирования в
конкретный бизнес (табл. 10.4) [Коупленд,
2008].
Отметим,
что данному методу присуща значительная
субъективность оценок, так как часть
информации о состоянии исследуемого
бизнеса и его перспективах собирается
путем опроса менеджеров компании. Кроме
того, субъективная интерпретация
получаемых результатов со стороны
аналитика усиливает погрешность
результата. Тем не менее это наиболее
распространенный способ расчета ставки
дисконтирования в российской экономике.
Кроме вышеперечисленных рисков в ставке
дисконтирования учитываются риски
инвестирования в малые компании и риски
инвестирования в экономику конкретной
страны.
Средневзвешенная
стоимость капитала
представляет собой требуемую доходность
для фирмы в целом и является усредненным
показателем. Сторонники этого метода
рекомендуют принять инвестиционный
проект, если ожидаемая доходность его
больше или равна стоимости капитала
фирмы. Применение средневзвешенной
стоимости капитала оправданно, если
предприятие активно использует заемный
капитал, что нередко встречается в
проектах, связанных с технологическими
инновациями.
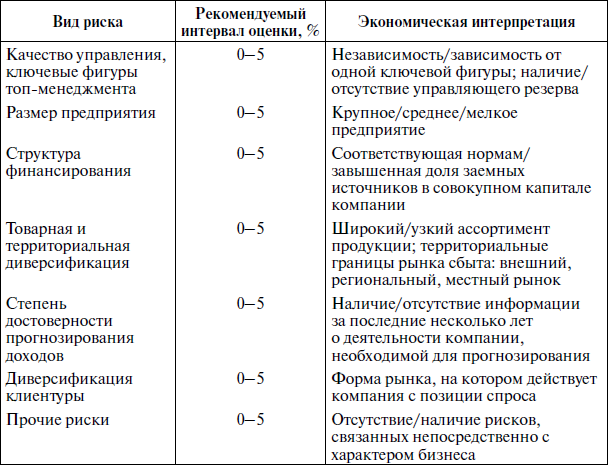
Таблица
10.4.
Виды риска, учитываемые в методе
кумулятивного построения ставки
дисконтирования
Значение
средневзвешенной стоимости капитала
определяется исходя из структуры
капитала инвестора, т. е. соотношения
собственных (E) и заемных (D)
средств, используемых им для формирования
портфеля или конкретного проекта.
Использование заемного капитала приводит
к увеличению денежного потока, однако
ввиду большего риска одновременно
должна возрасти ставка доходности.
Поэтому процентная ставка, требуемая
кредиторами фирмы (гd), отличается от
той доходности, которая устроила бы
собственника капитала (rе).
Общая
формула для расчета средневзвешенной
стоимости капитала выглядит следующим
образом:
где ?
– ставка налога на прибыль (выполняется
условие налоговой защиты).
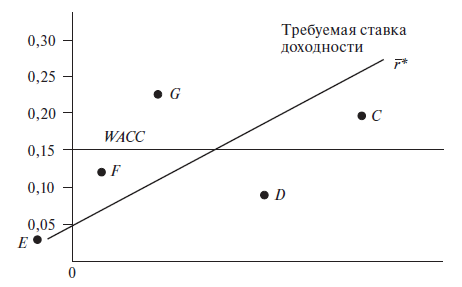
На рис. 10.3
показаны графики средневзвешенной
стоимости капитала (WACC)
и линии рынка ценных бумаг (отражающей
построение ставки доходности по модели
оценки капитальных активов). Каждый из
показателей подразумевает свой критерий,
в обоих случаях линия – это граница
между областями приемлемых (выше линии)
и неприемлемых (ниже линии) проектов
[Рогова, 2001].
Рис. 10.3.
Графики средневзвешенной стоимости
капитала и модели оценки капитальных
активов
График
показывает различия в управленческих
решениях относительно принятия проектов.
Одинаковые решения, исходя из обеих
моделей, могут быть приняты для проектов D
и G.
Инвестиционные проекты F и E будут
отвергнуты, если применяется критерий
средневзвешенной стоимости капитала,
но они будут приняты, если используется
модель САРМ (несмотря на низкую доходность
проекта Е).
Инвестиционный проект С
приемлем при использовании средневзвешенной
стоимости капитала, но использование
метода САРМ заставит инвестора отказаться
от него.
График,
представленный на рис. 10.3, иллюстрирует
серьезное ограничение, свойственное
методу средневзвешенной стоимости
капитала: он не учитывает различий в
уровнях риска различных проектов.
Корректные оценки по данному методу
возможны только в том случае, если
структура капитала проекта и уровень
его риска совпадают со структурой
капитала и уровнем риска предприятия
на протяжении всего его жизненного
цикла. В остальных случаях ответ
получается лишь приблизительно верным,
и формула WACC
может использоваться только в качестве
некоего исходного ориентира. Учитывая
то, что риск технологических инноваций,
как правило, высок, а при венчурном
финансировании структура капитала
проекта подвержена изменениям,
использование данной модели затруднено.
Однако в качестве исходного пункта для
расчета средневзвешенная стоимость
капитала предприятия может применяться
на практике.
Таким
образом, использование критерия чистой
дисконтированной стоимости при оценке
экономической эффективности инновационных
проектов связано с определенными
трудностями. Пути преодоления этих
трудностей показаны в табл. 10.5.
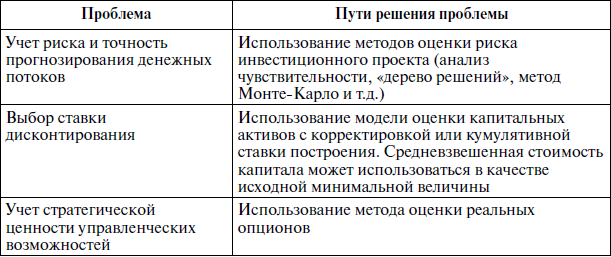
Таблица
10.5.
Проблемы использования критерия NPV
и
пути их преодоления
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
NPV (аббревиатура, на английском языке – Net Present Value), по-русски этот показатель имеет несколько вариаций названия, среди них:
- чистая приведенная стоимость (сокращенно ЧПС) – наиболее часто встречающееся название и аббревиатура, даже формула в Excel именно так и называется;
- чистый дисконтированный доход (сокращенно ЧДС) – название связано с тем, что денежный потоки дисконтируются и только потом суммируются;
- чистая текущая стоимость (сокращенно ЧТС) – название связано с тем, что все доходы и убытки от деятельности за счет дисконтирования как бы приводятся к текущей стоимости денег (ведь с точки зрения экономики, если мы заработаем 1 000 руб. и получим потом на самом деле меньше, чем если бы мы получили ту же сумму, но сейчас).
NPV – это показатель прибыли, которую получат участники инвестиционного проекта. Математически этот показатель находится путем дисконтирования значений чистого денежного потока (вне зависимости от того отрицательный он или положительный).
Чистый дисконтированный доход может быть найден за любой период времени проекта начиная с его начала (за 5 лет, за 7 лет, за 10 лет и так далее) в зависимости от потребности расчета.
Для чего нужен
NPV – один из показателей эффективности проекта, наряду с IRR, простым и дисконтированным сроком окупаемости. Он нужен, чтобы:
- понимать какой доход принесет проект, окупится ли он в принципе или он убыточен, когда он сможет окупиться и сколько денег принесет в конкретный момент времени;
- для сравнения инвестиционных проектов (если имеется ряд проектов, но денег на всех не хватает, то берутся проекты с наибольшей возможностью заработать, т.е. наибольшим NPV).
Формула расчета
Для расчета показателя используется следующая формула:

- CF – сумма чистого денежного потока в период времени (месяц, квартал, год и т.д.);
- t – период времени, за который берется чистый денежный поток;
- N – количество периодов, за который рассчитывается инвестиционный проект;
- i – ставка дисконтирования, принятая в расчет в этом проекте.
Пример расчета
Для рассмотрения примера расчета показателя NPV возьмем упрощенный проект по строительству небольшого офисного здания. Согласно проекту инвестиций планируются следующие денежные потоки (тыс. руб.):
| Статья | 1 год | 2 год | 3 год | 4 год | 5 год |
| Инвестиции в проект | 100 000 | ||||
| Операционные доходы | 35 000 | 37 000 | 38 000 | 40 000 | |
| Операционные расходы | 4 000 | 4 500 | 5 000 | 5 500 | |
| Чистый денежный поток | – 100 000 | 31 000 | 32 500 | 33 000 | 34 500 |
Коэффициент дисконтирования проекта – 10%.
Подставляя в формулу значения чистого денежного потока за каждый период (там где получается отрицательный денежный поток ставим со знаком минус) и корректируя их с учетом ставки дисконтирования получим следующий результат:
NPV = – 100 000 / 1.1 + 31 000 / 1.12 + 32 500 / 1.13 + 33 000 / 1.14 + 34 500 / 1.15 = 3 089.70
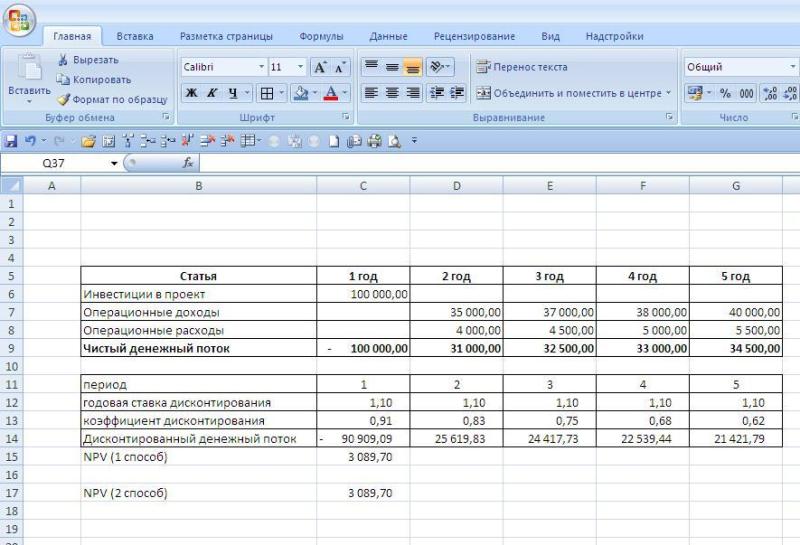
Чтобы проиллюстрировать как рассчитывается NPV в Excel, рассмотрим предыдущий пример заведя его в таблицы. Расчет можно произвести двумя способами
- В Excel имеется формула ЧПС, которая рассчитывает чистую приведенную стоимость, для этого вам необходимо указать ставку дисконтирования (без знака проценты) и выделить диапазон чистого денежного потока. Вид формулы такой: = ЧПС (процент; диапазон чистого денежного потока).
- Можно самим составить дополнительную таблицу, где продисконтировать денежный поток и просуммировать его.
Ниже на рисунке мы привели оба расчета (первый показывает формулы, второй результаты вычислений):
Как вы видите, оба метода вычисления приводят к одному и тому же результату, что говорит о том, что в зависимости от того, чем вам удобнее пользоваться вы можете использовать любой из представленных вариантов расчета.
Примеры расчета NPV в бизнес-планах
Увидеть как рассчитан показатель на конкретном примере бизнес-плана вы можете выбрав соответствующий документ в форме поиска или перейдя по ссылке ниже: