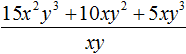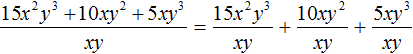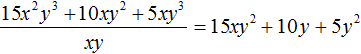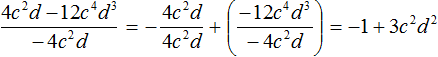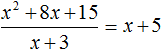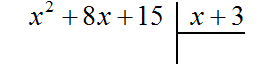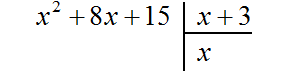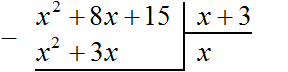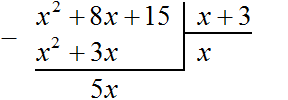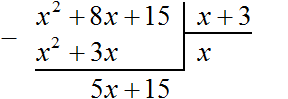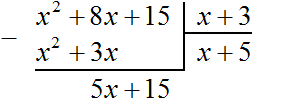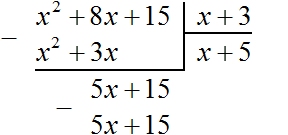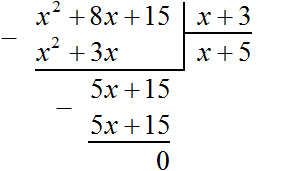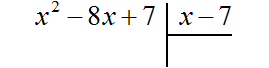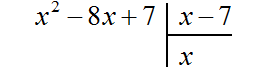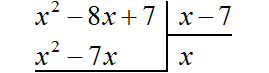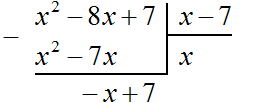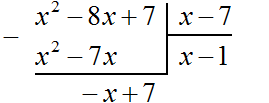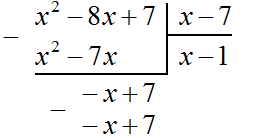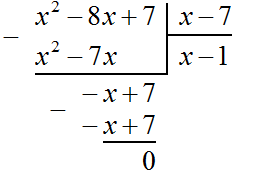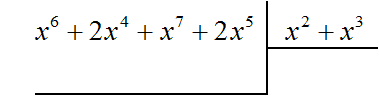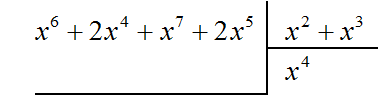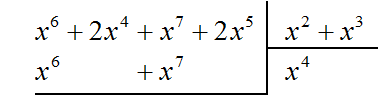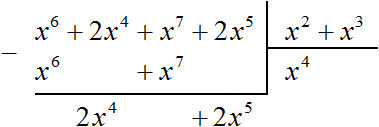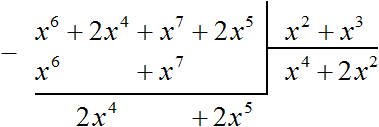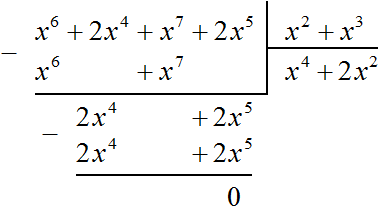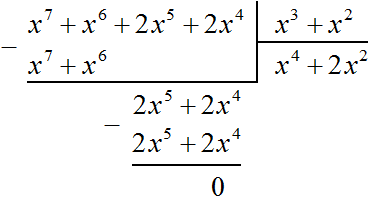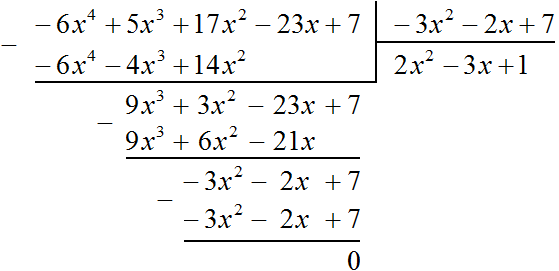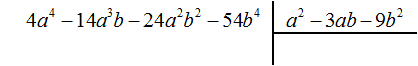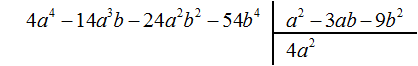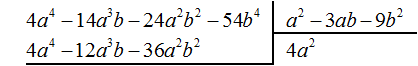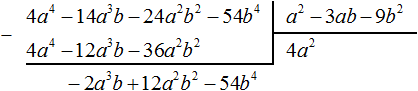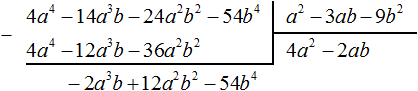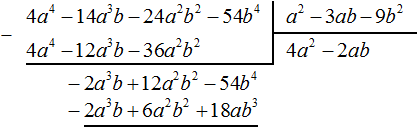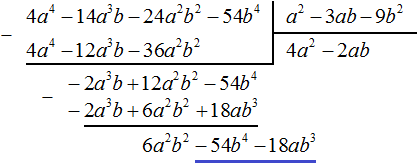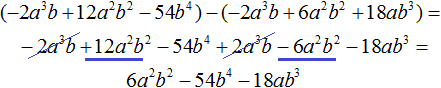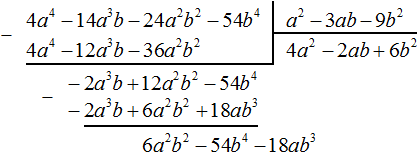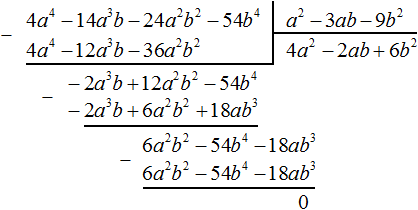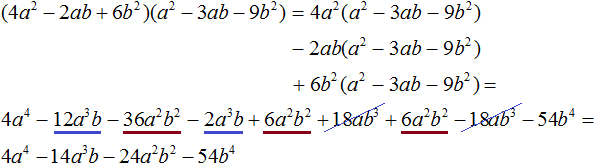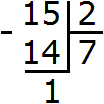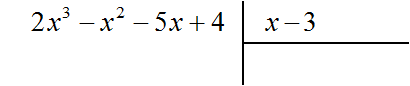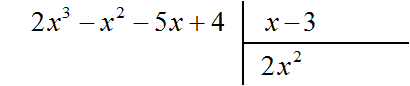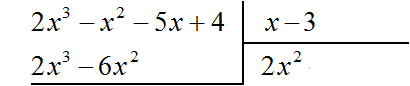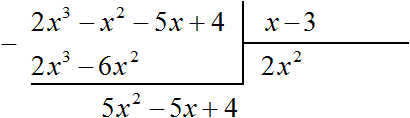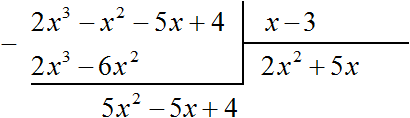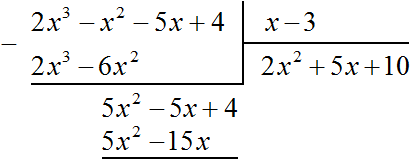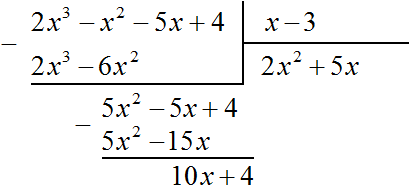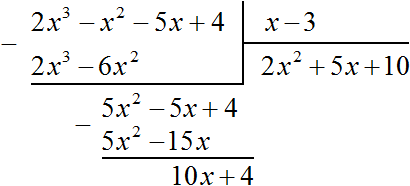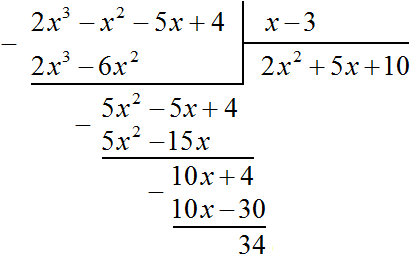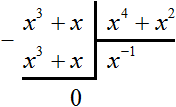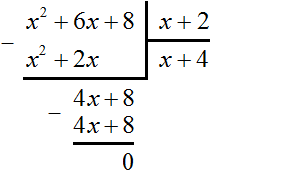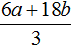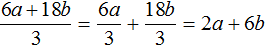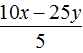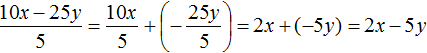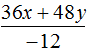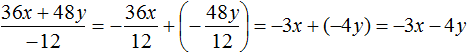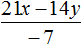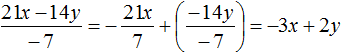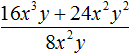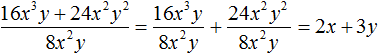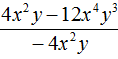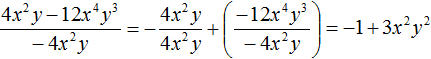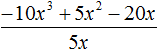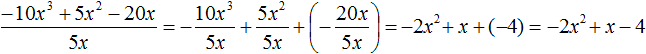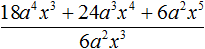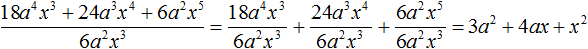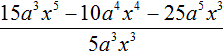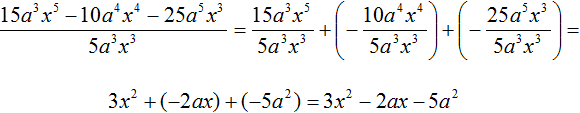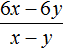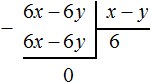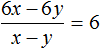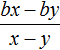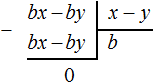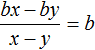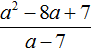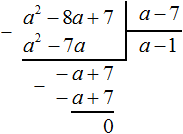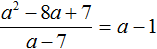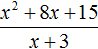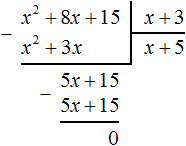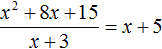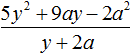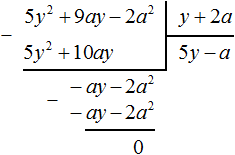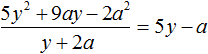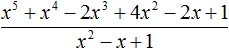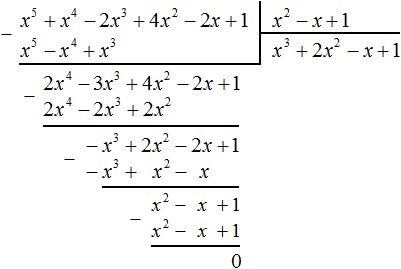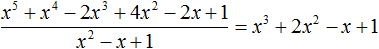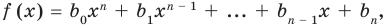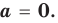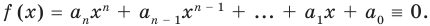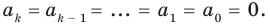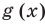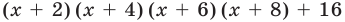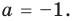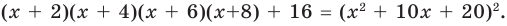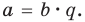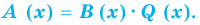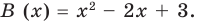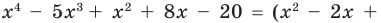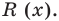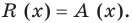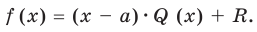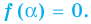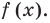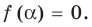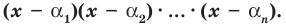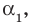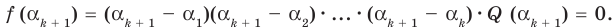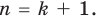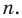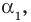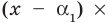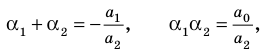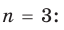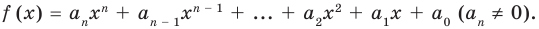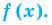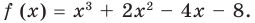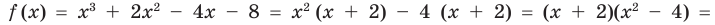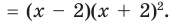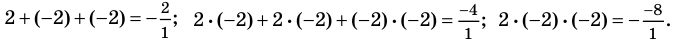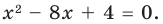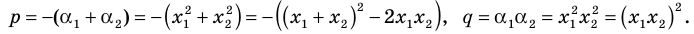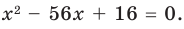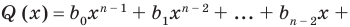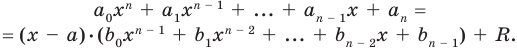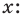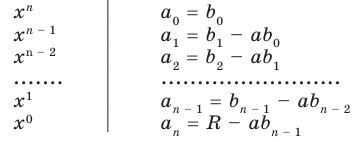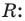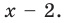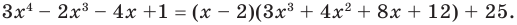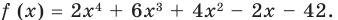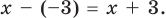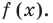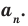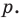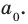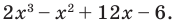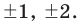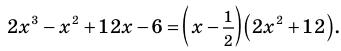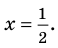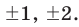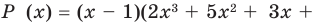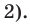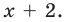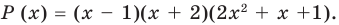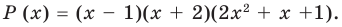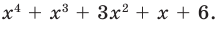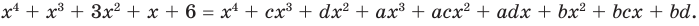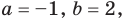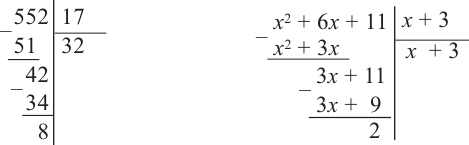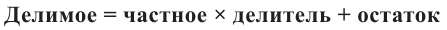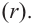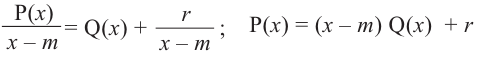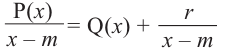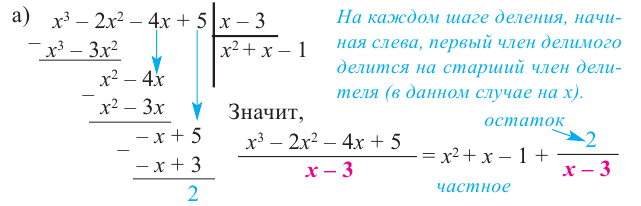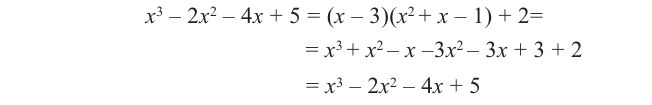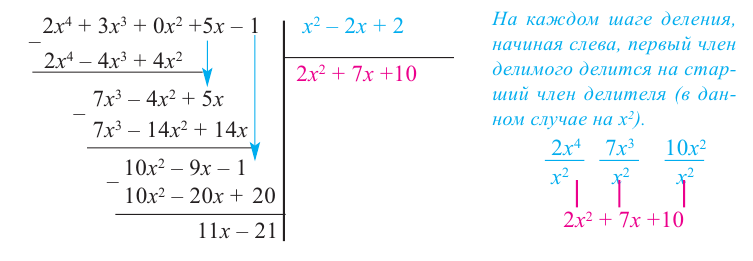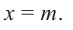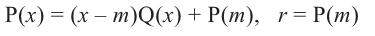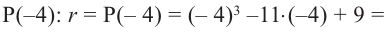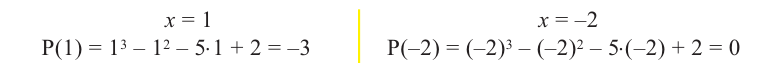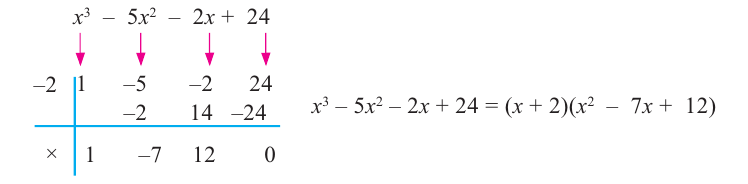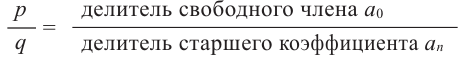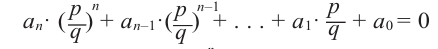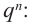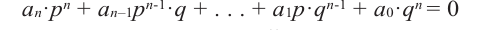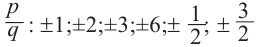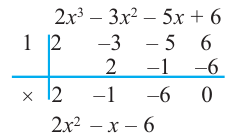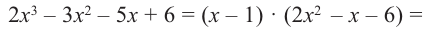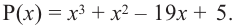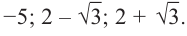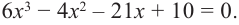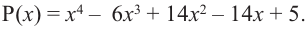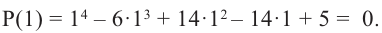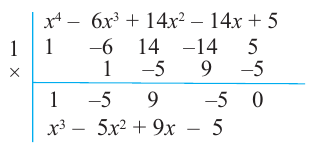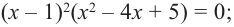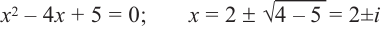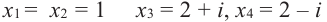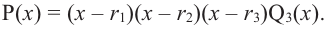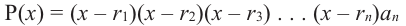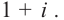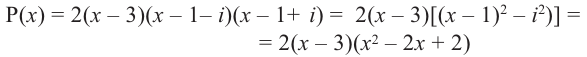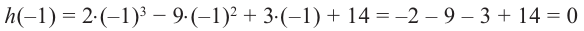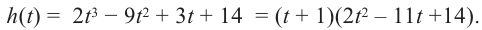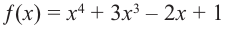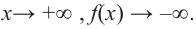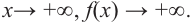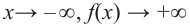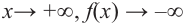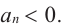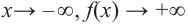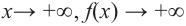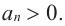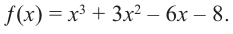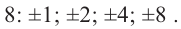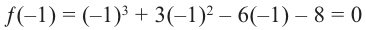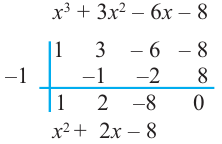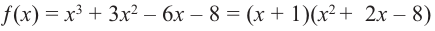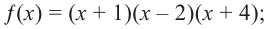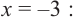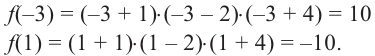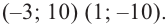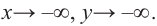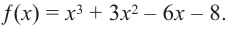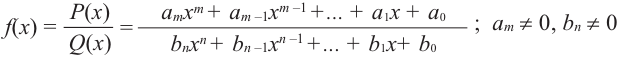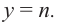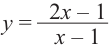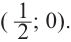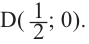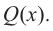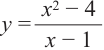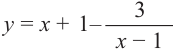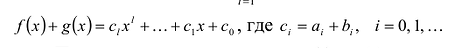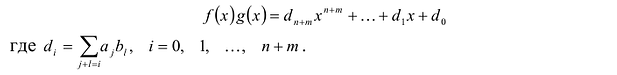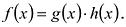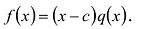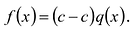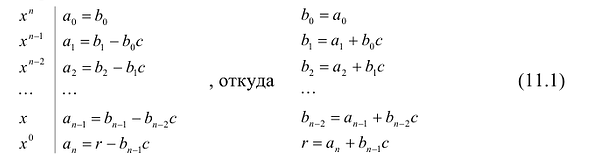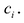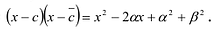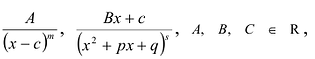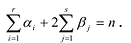Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!
Содержание статьи:
Частное чисел в математике: что это такое
Однажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:
Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Полное и неполное частное
А потом было замечательное представление.
В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?
Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.
— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:
7:3=2(1)
Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).
- Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
- Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).
Как найти делитель
Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:
— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).
— Всего было трое ребят, — ответил Бом.
— Верно! — вспомнил Бим.
Для того чтобы найти делитель, надо делимое разделить на частное.
6:2=3
Здесь 6 – делимое, 2 – частное, а 3 – делитель.
Как найти делимое
— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.
— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.
Бом и говорит:
— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.
Для того чтобы найти делимое, надо делитель умножить на частное.
Запишем это цифрами:
3*2=6.
3 — наш делитель, 2 — частное, а 6 — делимое.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Заключение
А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:
Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
- Деление — действие, обратное умножению;
- умножение проверяет правильность математического действия — деления;
- для того чтобы найти делимое, надо делитель умножить на частное;
- для того чтобы найти делитель, надо делимое разделить на частное.
Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Продолжаем изучать многочлены. В данном уроке мы научимся их делить.
Деление многочлена на одночлен
Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Запишем это деление в виде дроби:
Теперь делим каждый член многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Получающиеся частные будем складывать:
Получили привычное для нас деление одночленов. Выполним это деление:
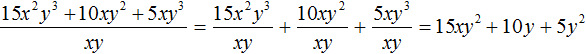
При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.
В нашем примере произведение полученного многочлена 15xy2 + 10y + 5y2 и делителя xy должно быть равно многочлену 15x2y3 + 10xy2 + 5xy3, то есть исходному делимому. Проверим так ли это:
(15xy2 + 10y + 5y2)xy = 15x2y3 + 10xy2 + 5xy3
Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.
Например, чтобы сложить дроби ,
и
нужно записать следующее выражение:
Если мы вычислим выражение , то получим дробь
, значение которой равно 1,5.
При этом выражение мы можем вернуть в исходное состояние
, и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5
Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x
Вычисление каждой дроби даст в результате многочлен a + b + c
Пример 2. Разделить многочлен 8m3n + 24m2n2 на одночлен 8m2n
Пример 3. Разделить многочлен 4c2d − 12c4d3 на одночлен −4c2d
Деление одночлена на многочлен
Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.
Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.
Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy. Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy, поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.
Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.
Например, найдём значение выражения при x = 2.
Выражение представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:
Деление многочлена на многочлен
Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3, получается многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
(x + 5)(x + 3) = x2 + 8x + 15
Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.
Тогда согласно этому правилу, деление полученного нами многочлена x2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.
Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Выполним уголком деление многочлена x2 + 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.
В данном случае результат нам известен заранее. Это будет многочлен x + 5. Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.
Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.
Сейчас наша задача найти первый член нового многочлена. Как это сделать?
Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:
Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.
Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.
Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.
Если первый член делимого (в нашем случае это x2) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:
Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3, получается x2 + 3x. Записываем этот многочлен под делимым x2+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:
Теперь из делимого x2 + 8x + 15 вычитаем x2 + 3x. Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:
Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)
Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15. Записываем этот многочлен под делимым 5x + 15
Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.
На этом деление завершено.
После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3, должен получаться многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
Пример 2. Разделить многочлен x2 − 8x + 7 на многочлен x − 7
Записываем уголком данное деление:
Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:
Умножаем x на x − 7, получаем x2 − 7x. Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Вычитаем из x2 − 8x + 7 многочлен x2 − 7x. При вычитании x2 из x2 получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7
Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:
Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:
Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7
Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0
Деление завершено. Таким образом, частное от деления многочлена x2 − 8x + 7 на многочлен x − 7 равно x − 1
Выполним проверку. Умножим частное x − 1 на делитель x − 7. У нас должен получиться многочлен x2 − 8x + 7
(x − 1)(x − 7) = x2 − x − 7x + 7 = x2 − 8x + 7
Пример 3. Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3
Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x4
Умножаем x4 на делитель x2 + x3 и полученный результат записываем под делимым. Если x4 умножить на x2 + x3 получится x6 + x7. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:
Теперь из делимого вычитаем многочлен x6 + x7. Вычитание x6 из x6 даст в результате 0. Вычитание x7 из x7 тоже даст в результате 0. Оставшиеся члены 2x4 и 2x5 снесём:
Получилось новое делимое 2x4 + 2x5. Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7
Разделим многочлен 2x4 + 2x5 на делитель x2 + x3. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x2. Записываем этот член в частном:
Умножаем 2x2 на делитель x2 + x3 и полученный результат записываем под делимым. Если 2x2 умножить на x2 + x3 получится 2x4 + 2x5. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:
Вычитание многочлена 2x4 + 2x5 из многочлена 2x4 + 2x5 дало в результате 0, поэтому деление успешно завершилось.
В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.
Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.
Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x6 + 2x4 + x7 + 2x5 упорядочить в порядке убывания степеней, то получим многочлен x7 + x6 + 2x5 + 2x4. А если члены многочлена x2 + x3 упорядочить в порядке убывания степеней, то получим многочлен x3 + x2
Тогда деление уголком многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 примет следующий вид:
Деление завершено. Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2
Выполним проверку. Умножим частное x4 + 2x2 на делитель x2 + x3. У нас должен получиться многочлен x6 + 2x4 + x7 + 2x5
(x4 + 2x2)(x2 + x3) = x4 (x2 + x3) + 2x2(x2 + x3) = x6 + 2x4 + x7 + 2x5
При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Перепишем умножение (x4 + 2x2)(x2 + x3) упорядочив члены многочленов в порядке убывания степеней.
(x4 + 2x2)(x3 + x2) = x4(x3 + x2) + 2x2(x3 + x2) = x7 + x6 + 2x5 + 2x4
Пример 4. Разделить многочлен 17x2 − 6x4 + 5x3 − 23x + 7 на многочлен 7 − 3x2 − 2x
Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:
Значит,
Пример 5. Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a2. Записываем 4a2 в частном:
Умножим 4a2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 4a4 − 12a3b − 36a2b2
Теперь делим −2a3b + 12a2b2 − 54b4 на делитель a2 − 3ab − 9b2. Разделим первый член делимого на первый член делителя, получим −2ab. Записываем −2ab в частном:
Умножим −2ab на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым −2a3b + 12a2b2 − 54b4
Вычтем из многочлена −2a3b + 12a2b2 − 54b4 многочлен −2a3b + 12a2b2 − 18ab3. При вычитании подобных членов обнаруживаем, что члены −54b4 и 18ab3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a3b из −2a3b и 6a2b2 из 12a2b2, а вычитание 18ab3 из −54b4 запишем в виде разности −54b4 − (+18ab3) или −54b4 − 18ab3
Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:
Вернёмся к нашей задаче. Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
Умножим 6b2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым 6a2b2 − 54b4 − 18ab3. Сразу вычтем этот полученный результат из делимого 6a2b2 − 54b4 − 18ab3
Деление завершено. Таким образом, частное от деления многочлена 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2 равно 4a2 − 2ab + 6b2.
Выполним проверку. Умножим частное 4a2 − 2ab + 6b2 на делитель a2 − 3ab − 9b2. У нас должен получиться многочлен 4a4 − 14a3b − 24a2b2 − 54b4
Деление многочлена на многочлен с остатком
Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.
Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:
То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:
Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.
Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:
Например, разделим многочлен 2x3 − x2 − 5x + 4 на многочлен x − 3
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:
Умножим 2x2 на делитель x − 3 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 2x3 − 6x2
Теперь делим 5x2 − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x2 − 5x + 4
Вычтем из многочлена 5x2 − 5x + 4 многочлен 5x2 − 15x
Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:
Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4
Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.
Поэтому при делении многочлена 2x3 − 2x2 − 5x + 4 на многочлен x − 3 получается 2x2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:
Когда деление многочленов невозможно
Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.
Например, нельзя разделить многочлен x3 + x на многочлен x4 + x2, поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.
Вопреки этому запрету можно попробовать разделить многочлен x3 + x на многочлен x4 + x2, и даже получить частное x−1, которое при перемножении с делителем будет давать делимое:
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x−1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x−1 это дробь , которая не является произведением.
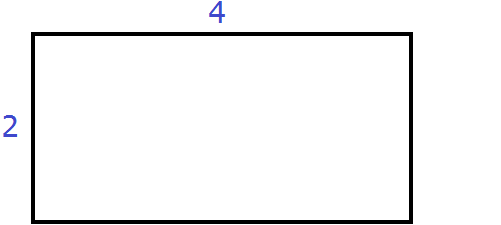
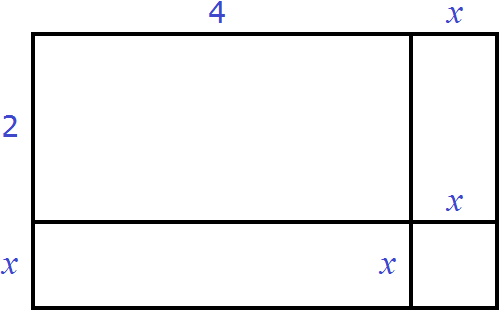
Пусть имеется прямоугольник со сторонами 4 и 2
Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.
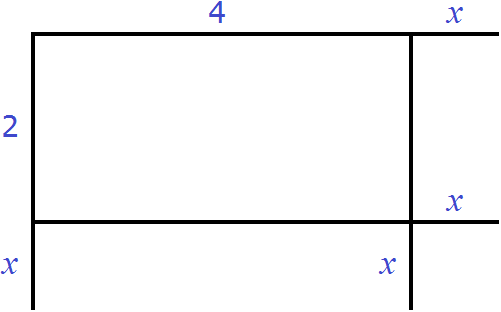
Увеличим длину и ширину этого прямоугольника на x
Достроим отсутствующие стороны:
Теперь прямоугольник имеет длину x + 4 и ширину x + 2. Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x2 + 6x + 8
(x + 4)(x + 2) = x2 + 4x + 2x + 8 = x2 + 6x + 8
При этом мы можем выполнить обратную операцию, а именно разделить площадь x2 + 6x + 8 на ширину x + 2 и получить длину x + 4.
Степень многочлена x2 + 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2, а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.
Задания для самостоятельного решения
Задание 1. Выполните деление:
Решение:
Задание 2. Выполните деление:
Решение:
Задание 3. Выполните деление:
Решение:
Задание 4. Выполните деление:
Решение:
Задание 5. Выполните деление:
Решение:
Задание 6. Выполните деление:
Решение:
Задание 7. Выполните деление:
Решение:
Задание 8. Выполните деление:
Решение:
Задание 9. Выполните деление:
Решение:
Задание 10. Выполните деление:
Решение:
Задание 11. Выполните деление:
Решение:
Задание 12. Выполните деление:
Решение:
Задание 13. Выполните деление:
Решение:
Задание 14. Выполните деление:
Решение:
Задание 15. Выполните деление:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Содержание:
Многочлен – это сумма одночленов, причем сам одночлен – это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 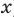
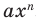
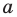
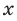
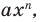
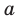
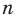
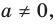
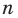
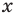
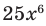
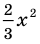
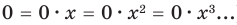
По определению многочлен от одной переменной 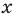
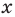
многочленом от одной переменной 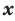
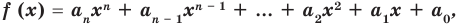
где коэффициенты 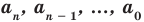
Если 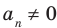
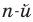
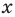
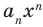
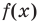
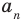
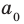
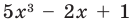
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 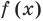
где 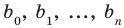
Теорема 1. Одночлены 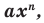
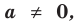
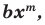
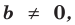
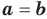
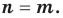
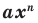
Поскольку равенство одночленов
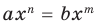
выполняется при всех значениях 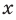
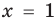
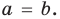
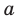
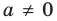
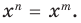
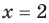
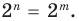
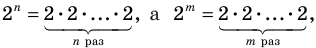
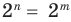
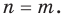
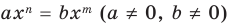
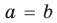
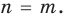
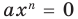
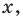
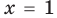
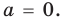
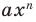
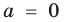
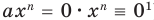
Далее любой одночлен вида 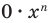
Теорема 2. Если многочлен 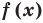
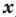
Для доказательства используем метод математической индукции. Пусть
При 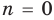
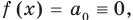
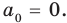
Предположим, что при 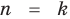
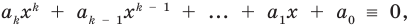
Докажем, что данное утверждение выполняется и при 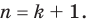
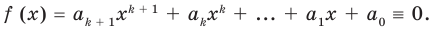
Поскольку равенство (3) выполняется при всех значениях 
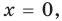
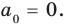
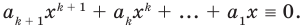

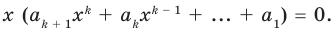
Равенство (4) должно выполняться при всех значениях 
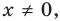
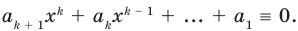
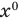
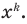
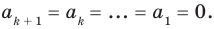
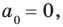
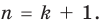
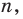
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 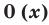
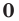
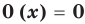
Теорема 3. Если два многочлена 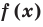
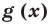
Пусть многочлен 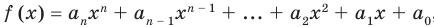
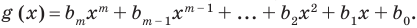
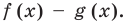
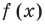
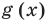
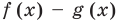
Но 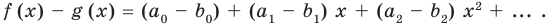
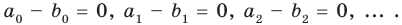
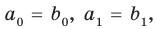
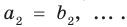
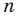
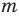
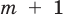
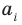
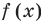
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
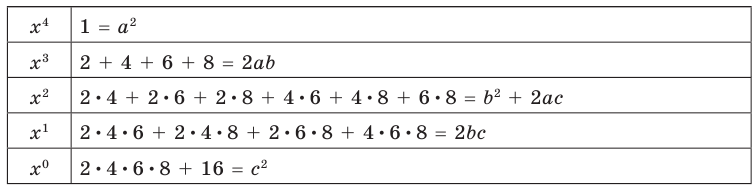
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 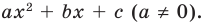
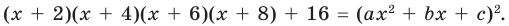
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 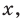
Из первого равенства получаем 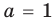
При 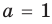
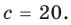
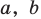
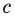
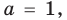
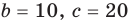
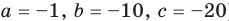
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 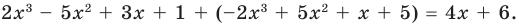
Например, 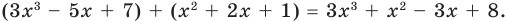
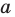
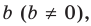
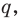
Определение: Многочлен 
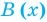
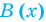

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 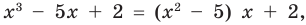
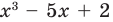
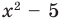
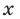
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 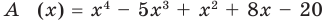
Решение:
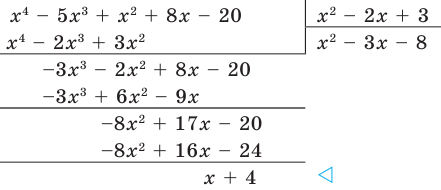
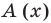
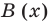
Если обозначить результат выполнения первого шага алгоритма через 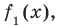
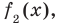
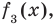
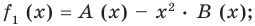
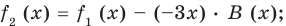
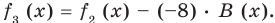
Сложим почленно равенства (1), (2), (3) и получим
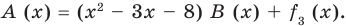
Учитывая, что степень многочлена 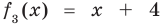
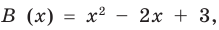
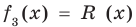
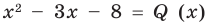
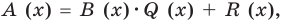
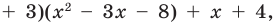
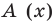
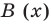
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 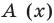
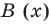
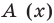
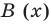
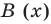
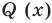
Отметим, что в случае, когда степень делимого 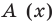
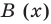
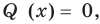
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 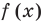
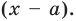
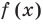
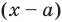
Это равенство выполняется тождественно, то есть при любом значении 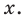
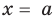
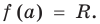
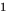
Теорема 1 (теорема Безу). Остаток от деления многочлена 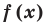
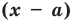
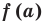
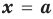
Пример №2
Докажите, что 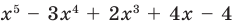
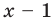
Решение:
► Подставив в 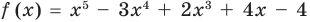
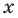
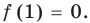
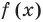

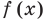

Определение: Число 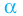
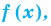
Если многочлен 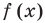

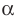
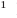
Действительно, если 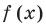
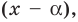

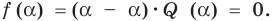
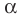
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 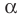
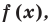
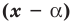
По теореме Безу остаток от деления 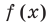

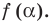
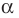
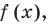
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 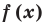
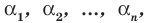
Для доказательства используем метод математической индукции.
При 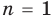
Допустим, что утверждение справедливо при 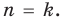
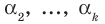
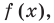
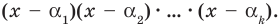
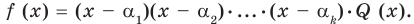
Докажем, что утверждение теоремы справедливо и при 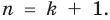
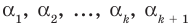
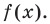
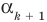
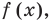
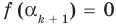
По условию все корни 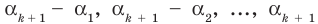
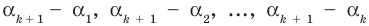
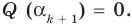
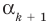
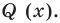
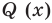
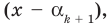
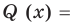
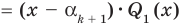
Это означает, что 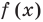
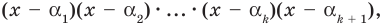
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 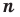
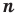
Допустим, что многочлен 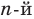
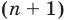
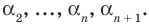
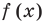
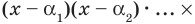
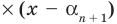
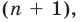
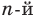
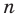
Пусть теперь многочлен 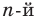
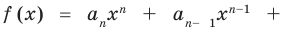
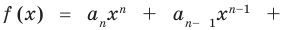
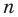
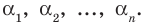
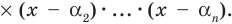
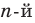
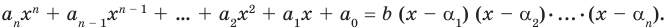
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 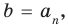
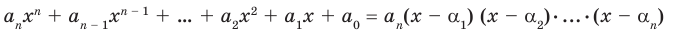
Сравнивая коэффициенты при одинаковых степенях 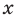
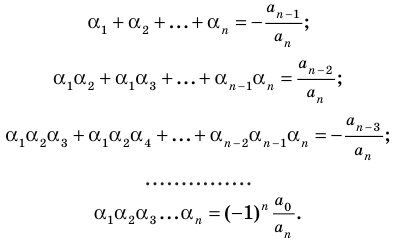
Например, при 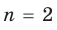
а при
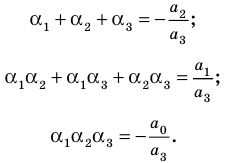
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 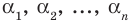
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 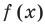
Если многочлен 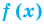
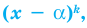
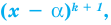


Например, если произведение 
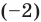
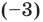
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
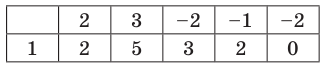
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 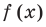
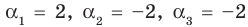
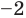
Проверим справедливость формулы (5). В нашем случае: 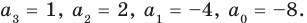
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 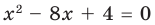
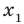
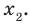
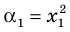
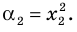
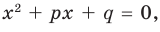
По формулам Виета имеем 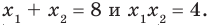
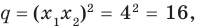
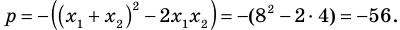
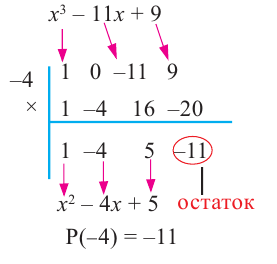
Схема Горнера
Делить многочлен 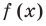
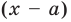
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 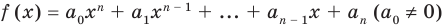
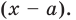
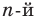
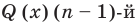
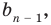
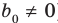
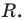
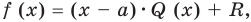
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 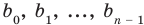
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 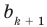
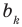
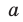
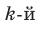
Пример №5
Разделите по схеме Горнера многочлен 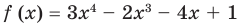
Решение:
► Запишем сначала все коэффициенты многочлена 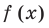
Таким образом,
Пример №6
Проверьте, является ли 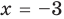
Решение:
► По теореме Безу остаток от деления многочлена 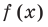
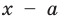
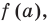
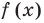
Поскольку 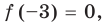
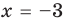
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 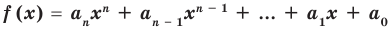
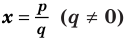
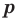
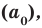
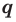
Если 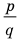
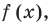
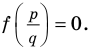
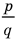
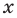
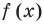
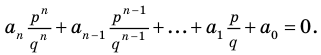
Умножим обе части равенства (1) на 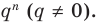
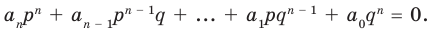
В равенстве (2) все слагаемые, кроме последнего, делятся на 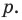
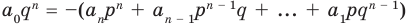
Но когда мы записываем рациональное число в виде 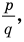
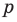
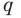
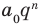
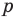
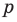
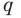
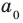
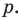
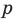
Аналогично все слагаемые равенства (2), кроме первого, делятся на 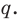
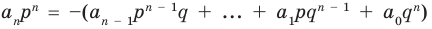
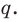
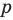
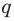
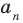
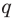
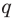
Отметим два следствия из этой теоремы. Если взять 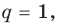
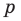
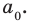
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 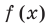
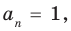
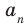
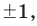
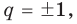
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 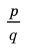
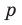
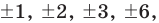
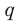
Таким образом, рациональные корни многочлена необходимо искать среди чисел 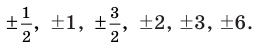
При 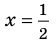
Кроме того, по схеме Горнера можно записать, что
Многочлен 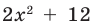
Пример №8
Разложите многочлен 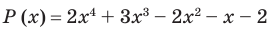
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 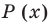

Тогда
Ищем целые корни кубического многочлена 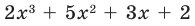
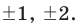
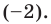
Имеем
Квадратный трехчлен 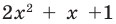
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 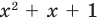
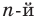
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
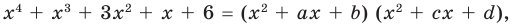
где 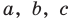
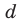
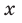
Получаем систему
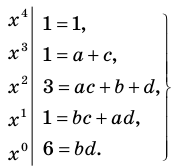
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 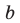
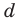
Коэффициенты 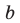
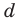
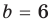
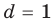
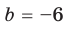
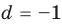
Для каждой пары значений 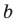
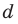
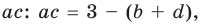
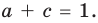
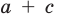
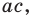
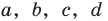
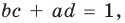
Как видим, системе (4) удовлетворяет набор целых чисел 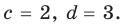
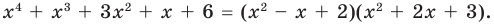
Поскольку квадратные трехчлены 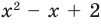
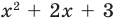
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 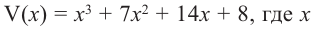
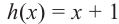
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 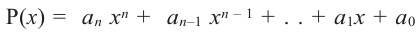
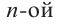
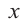
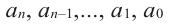
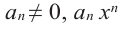
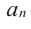
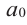
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 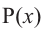
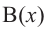
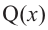
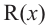
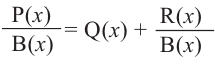
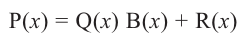
Здесь, степень многочлена 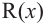
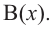
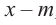
В этом случае:
Пример №10
а) Разделите многочлен 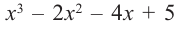
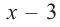
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 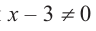
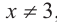
c) Должно выполняться тождество
Пример №11
Разделите 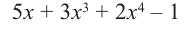
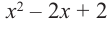
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 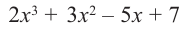
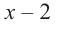
2) На каждом шаге деления делимое делится на старший член делителя, на 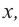
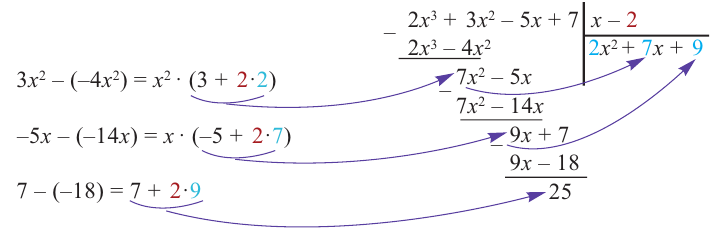
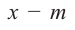
При делении многочлена на двучлен вида 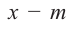
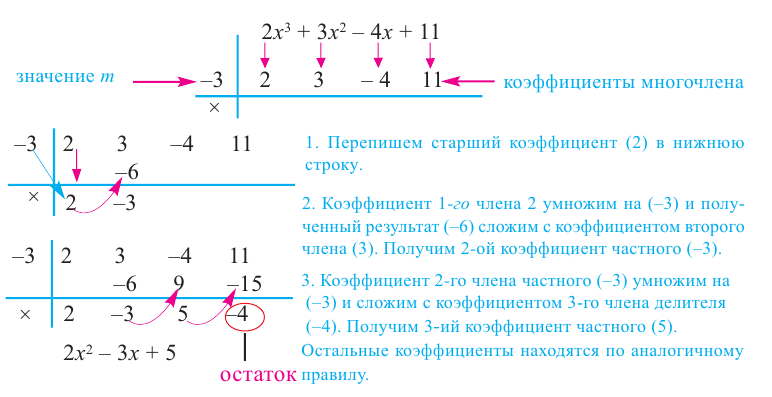
Пример №13
Разделите многочлен 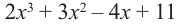
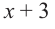
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 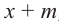
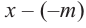
Запишем двучлен 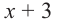
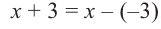
Таким образом, для делимого 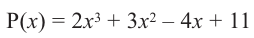
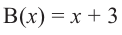
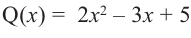
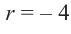
Деление можно записать в виде: 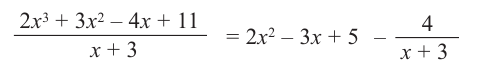
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 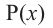
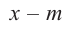
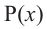
Доказательство: В равенстве 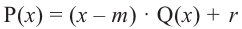
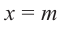
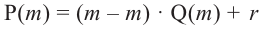
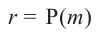
Пример №14
Найдите остаток от деления многочлена 
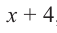
Решение: запишем делитель в виде 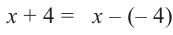
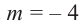
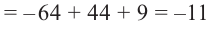
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 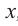
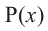
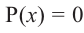
Теорема. Если число 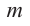
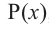
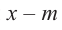
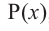
Действительно, если 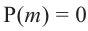
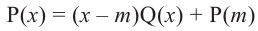
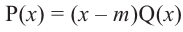
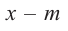
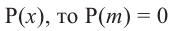
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 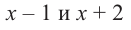
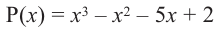
Решение: вычислим значение многочлена 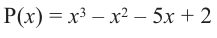
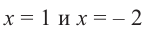
Значит, 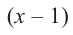
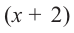
Пример №16
Зная, что 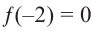
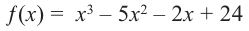
Решение: так как 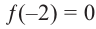
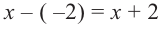
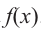
Учитывая, что 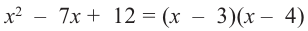
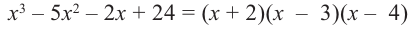
Отсюда получаем, что 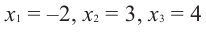
Примечание: Если многочлен задан в виде 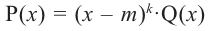
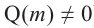
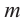
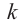
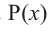
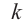
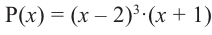
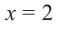
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 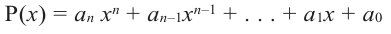
Доказательство. Пусть несократимая дробь 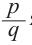
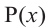
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 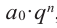
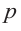
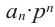
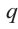
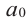
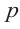
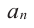
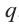
Пример №17
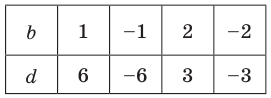
Найдите рациональные корни многочлена 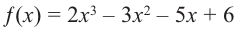
Решение: свободный член 6, старший коэффициент 2.
Для 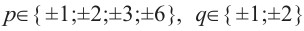
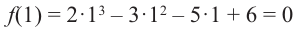
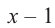
Так как, 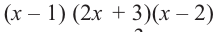
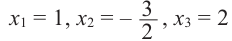
Следствие 1. Если старший коэффициент 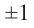
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
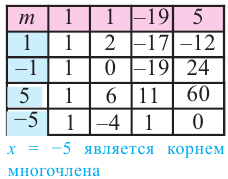
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
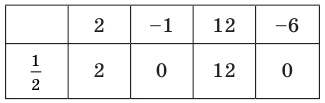
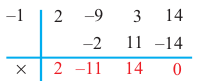
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 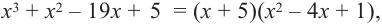
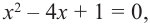
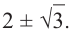
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 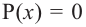
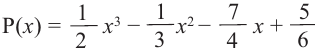
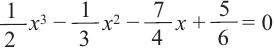
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 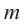
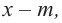
3. Для данного многочлена при помощи синтетического деления на двучлен 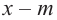
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 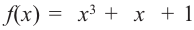
Проверим: 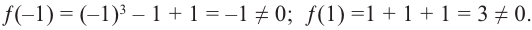
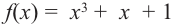
Основная теорема алгебры
Покажем на примере, что многочлен 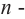
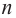
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 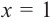
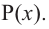
В выражении 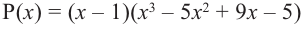
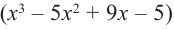
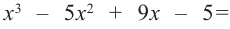
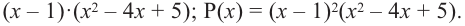
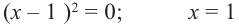
Корни:
Во всех рассмотренных нами примерах уравнение 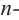
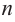
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 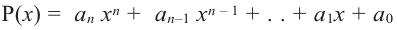
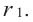
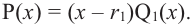
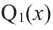
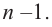
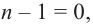
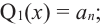
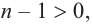
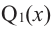
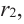
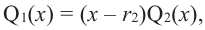
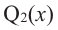
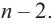
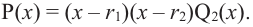
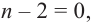
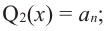
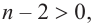
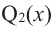
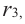
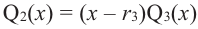
Продолжая процесс 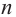
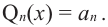
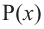
здесь числа 
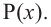
Следствие. Многочлен 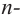
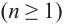
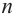
Отметим, что если комплексное число 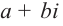
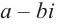
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 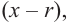
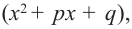
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 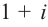
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 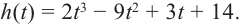
Решение: во всех случаях, кроме значений 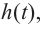
1. Проверим, является ли число 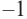
2. Число 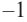
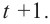
Учитывая, что 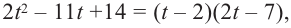
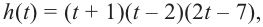
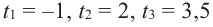
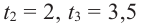
Функция-многочлен
График функции-многочлен
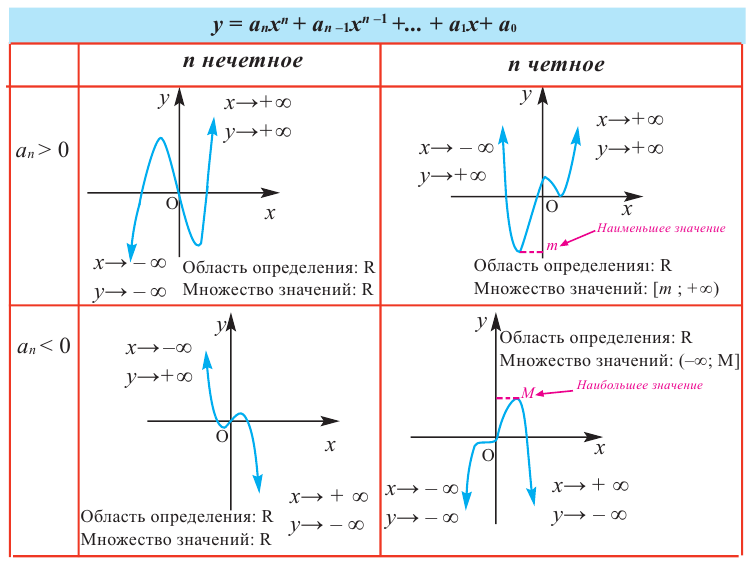
В стандартном виде функция – многочлен записывается как 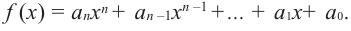
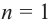
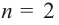
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 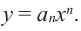
Пример №22
Определите характер поведения функции – многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 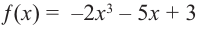
Решение: а) степень многочлена 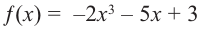
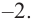
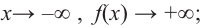
b) степень многочлена 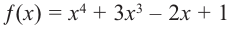
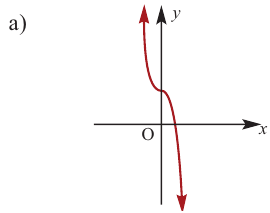
Пример №23
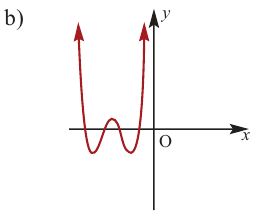
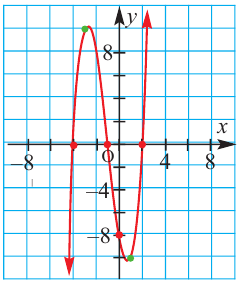
По графику определите как ведет себя функция – многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 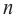
Алгоритм построения эскиза графика функции – многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
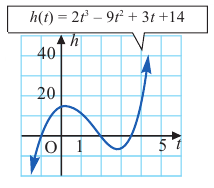
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 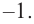
Значит, двучлен 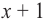
Зная, что 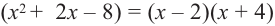
Отсюда находим нули 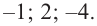
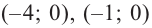
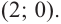
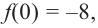
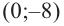
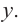
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 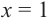
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 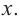
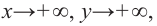
4. Соединим отмеченные точки и получим схематический график функции
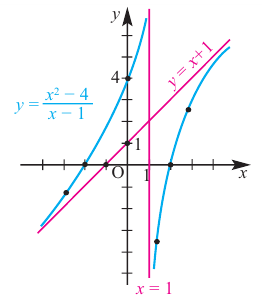
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
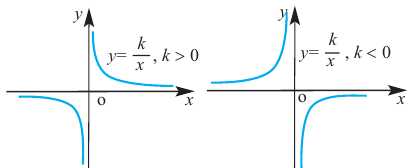
Самым простым примером рациональной функции является функция
График функции 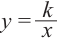
При стремлении значений 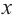
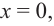
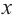
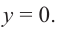
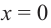
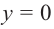
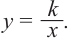
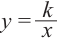
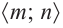
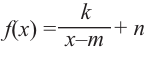
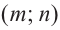
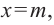
Пример №25
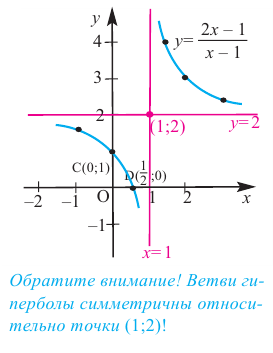
Постройте график функции
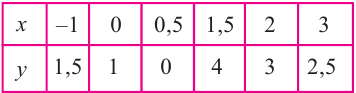
Решение: точки пересечения с осью 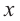
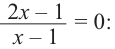
При 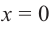
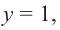
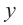
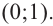
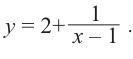
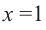
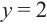
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 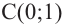
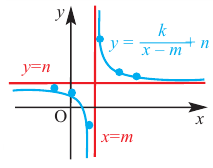
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 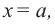
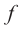
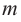
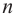
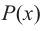
Для 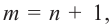
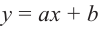
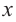
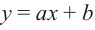
Пример №26
Найдите асимптоты и схематично изобразите график функции
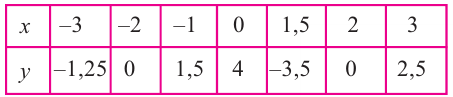
Решение: Точки пересечения с осью 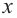
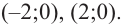
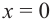
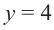
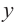
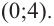
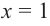
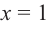
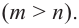
Для больших, но модулю, значений 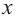
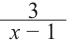
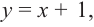
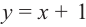
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
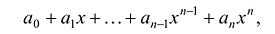
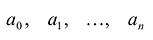
Если коэффициент 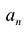
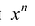
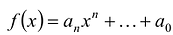
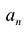
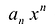
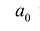
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 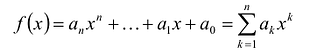
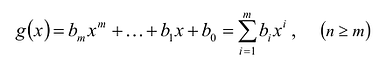
Произведением многочленов 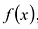
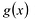
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 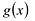
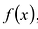
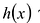
Теорема о делении с остатком
Для любых многочленов 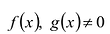
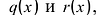
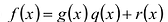
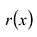
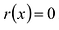
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
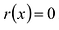
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с – корень многочлена 


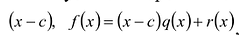
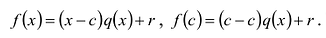

Обратно, пусть (х-с) делит 
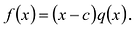
Следствие. Остаток от деления многочлена 
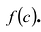
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 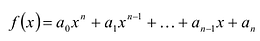
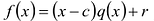
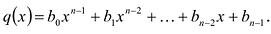
Число с-называется корнем кратности к многочлена 
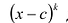

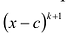

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 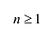
где 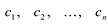

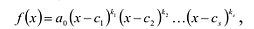
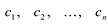

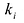
Если многочлен 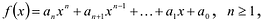
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 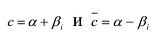


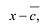
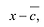

Утверждение 2. Многочлен с действительными коэффициентами степени 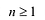
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где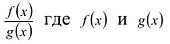
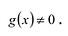

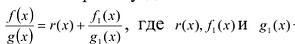
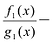
Лемма 1, Если 
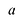
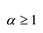
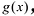
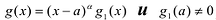
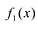
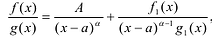
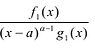
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
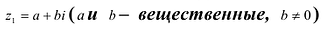
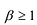
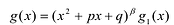
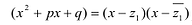
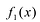
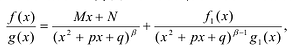
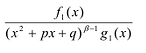
Рациональные дроби вида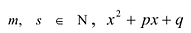
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 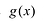
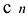
Число неизвестных 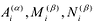
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
Загрузить PDF
Загрузить PDF
Многочлены можно разделить так же, как числа: либо разложением на множители, либо делением в столбик. Используемый метод зависит от вида многочлена и вида делителя.
-
1
Определите вид делителя. Делитель (многочлен, на который вы делите) сравнивается с делимым (многочленом, который вы делите) и определяется подходящий метод деления.
- Если делитель одночлен, представляющий собой коэффициент при переменной или свободный член (коэффициент без переменной), вероятно, вы сможете разложить делимое на множители и сократить один из множителей и делитель. Смотрите раздел «Разложение делимого на множители».
- Если делитель двучлен (многочлен с двумя членами), вероятно, вы сможете разложить делимое на множители и сократить один из множителей и делитель.
- Если делитель трехчлен (многочлен с тремя членами), вероятно, вы сможете разложить на множители как делимое, так и делитель, а затем сократить общий множитель или поделить в столбик.
- Если делитель многочлен с более чем тремя членами, скорее всего, придется использовать деление в столбик. Смотрите раздел «Деление в столбик».
-
2
Определите вид делимого. Если вид делителя не подсказывает вам метод деления, определите вид делимого.
- Если делимое содержит три или менее члена, вероятно, вы сможете разложить делимое на множители и сократить один из множителей и делитель.
- Если делимое содержит более трех членов, скорее всего, придется использовать деление в столбик.
Реклама
-
1
Определите общий множитель у делителя и делимого. Если он существует, вы можете вынести его за скобки и сократить.
- Пример. При делении 3x – 9 на 3 в двучлене вынесите 3 за скобки: 3(х – 3). Затем сократите вынесенную за скобки 3 и делитель (3). Ответ: х – 3.
- Пример: При делении 24x3 – 18x2 на 6x в двучлене вынесите 6х за скоби: 6x(4x2 – 3). Затем сократите вынесенные за скобки 6х и делитель (6х). Ответ: 4x2 – 3.
-
2
Определите, может ли делимое быть разложено на множители по формулам сокращенного умножения. Если один из множителей равен делителю, то вы можете их сократить. Вот некоторые формулы сокращенного умножения:
- Разность квадратов. Это двучлен вида a2x2 – b2, где значения a2 и b2 являются полными квадратами (то есть из этих чисел можно извлечь квадратный корень). Этот двучлен можно разложить на два множителя: (ax + b)(ax – b).
- Полный квадрат. Это трехчлен вида a2x2 + 2abx + b2, который можно разложить на два множителя: (ax + b)(ax + b) или записать как (ax + b)2. Если перед вторым членом стоит минус, этот трехчлен раскладывается как: (ax – b)(ax – b).
- Сумма или разность кубов. Это двучлен вида a3x3 + b3 или a3x3 – b3, где значения a 3 и b 3 являются полными кубами (то есть из этих чисел можно извлечь кубический корень). Сумма кубов раскладывается на: (ax + b)(a2x2 – abx + b2). Разность кубов раскладывается на: (ax – b)(a2x2 + abx + b2).
-
3
Используйте метод проб и ошибок для разложения делимого на множители. Если вы видите, что к делимому нельзя применить формулу сокращенного умножения, попробуйте разложить делимое другими способами. Для начала найдите множители свободного члена, учтя коэффициента второго члена делимого.
- Пример. Если делимое имеет вид x2 – 3x – 10, найдите множители свободного члена 10, учтя коэффициент 3.
- Число 10 может быть разбито на следующие множители: 1 и 10 или 2 и 5. Так как перед 10 стоит минус, перед одним из множителей числа 10 тоже должен стоять минус.
- Коэффициент 3 равен 5-2, поэтому выбираем множители 5 и 2. Так как перед 3 стоит минус, перед 5 должен тоже стоять минус. Таким образом, делимое раскладывается на множители: (х – 5)(х + 2). Если делитель равен одному из этих двух множителей, то их можно сократить.
Реклама
-
1
Запишите делимое и делитель так, как вы записываете обычные числа при их делении в столбик.
- Пример. Разделим x2 + 11 x + 10 на x +1.
-
2
Разделите первый член делимого на первый член делителя. Запишите результат.
- Пример. Разделите x2 (первый член делимого) на х (первый член делителя). Запишите результат: х.
-
3
Умножьте результат из предыдущего шага (х) на делитель. Запишите результат умножения соответственно под первым и вторым членами делимого.
- Пример. Умножьте х на х + 1 и получите x2 + x. Запишите этот двучлен соответственно под первым и вторым членами делимого.
-
4
Вычтите результат (из предыдущего шага) из делимого. В первую очередь из делимого вычтите результат умножения (полученный в предыдущем шаге), а затем снесите свободный член.
- Поменяйте знаки у двучлена x2 + x и запишите его как – x2 – x. Вычитая этот двучлен из первых двух членов делимого, получите 10x. После сноса свободного члена делимого вы получите двучлен 10х + 10 (промежуточный двучлен).
-
5
Повторите предыдущие три шага с промежуточным двучленом (полученным в предыдущем шаге). Вы разделите его первый член на первый член делителя и запишите результат рядом с результатом первого деления. Затем умножьте этот результат второго деления на делитель и вычтите результат умножения из промежуточного двучлена.
- Так как 10х / х = 10, запишите «+10» после результата первого делениях (х).
- Умножив 10 на х +1, получите двучлен 10х + 10. Поменяйте знаки этого двучлена (- 10x – 10) и соответственно запишите его под промежуточным двучленом.
- Вычтите двучлен, полученный в предыдущем шаге, из промежуточного двучлена и получите 0. Таким образом, x2 + 11 x + 10 делить на x +1 равно x + 10 (возможно, вы получите тот же результат, разложив трехчлен на множители, но этот трехчлен был выбран в качестве простейшего примера).
Реклама
Советы
- Если при делении в столбик у вас получился остаток, вы можете записать его в виде дробного члена, у которого в числителе находится остаток, а в знаменателе – делитель.[3]
Например, если вместо x2 + 11 x + 10 вам дано x2 + 11 x + 12, то при делении этого трехчлена на х+1 вы получите остаток 2. Поэтому запишите ответ (частное) в виде: х + 10 + (2/(х +1)). - Если в данном многочлене нет члена с переменной соответствующего порядка, например, в 3x3+9x2+18 нет члена с переменной первого порядка, вы можете добавить недостающий член с коэффициентом 0 (в нашем примере это 0x), чтобы правильно расположить члены во время деления. Этот ход не изменит значения данного многочлена.
Реклама
Предупреждения
- При делении в столбик правильно записывайте члены (члены одного порядка записывайте друг под другом), чтобы избежать ошибок при вычитании членов.
- При написании результата деления, который включает дробный член, перед дробным членом всегда ставьте знак плюс.
Реклама
Об этой статье
Эту страницу просматривали 19 853 раза.
Была ли эта статья полезной?
Содержание:
- Деление многочлена на многочлен
- Задача пример №1
- Задача пример №2
- Задача пример №3
- Задача пример №4
Деление многочлена на многочлен
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена 
Схематическую запись правила деления многочлена на двучлены впервые ввел итальянский математик Паоло Руффини.
Полиномография – вид искусства, который является результатом синтеза изобразительного искусства, математики и компьютерной науки. Основой полиномографии является визуализация корней многочлена при помощи компьютерных программ.
Задача пример №1
Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 



Исследование:
Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились, что каждое из двух делений выполнено правильно?
Выражение вида 





Деление целого числа на целое число можно проверить равенством
Делимое = частное х делитель + остаток
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 









В этом случае: 
Задача пример №2
а) Разделите многочлен 

Ответ запишите в виде –
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение: а)
b) При этом 

c) Должно выполняться тождество
Задача пример №3
Разделите 

Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Практическая работа:
1) Исследуйте деление столбиком многочлена 

2) На каждом шаге деления делимое делится на старший член делителя, на 
Правило синтетического деления многочлена на двучлен 
При делении многочлена на двучлен вида 
Задача пример №4
Разделите многочлен 

Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 

Запишем двучлен 






Деление можно записать в виде:
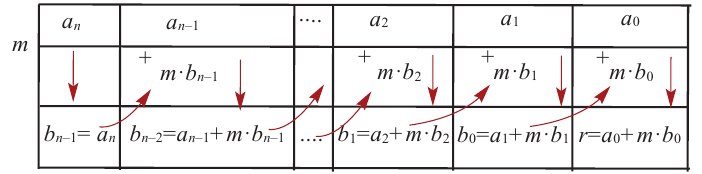
В общем случае, правило синтетического деления (или схема Горнера) многочлена n-ой степени на двучлен 
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Правила дифференцирования
- Теорема Пифагора
- Производная экспоненты
- Как решать дробные уравнения
- Собственные значения матрицы
- Матанализ для чайников
- Производные некоторых элементарных функций
- Векторы
- Объем конуса
- Разложение на множители