Обновлено: 18.05.2023
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
- цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
- буквы латинского и греческого алфавитов ((a, b, c, d, α, β, γ, δ) и т.д.)
- знаки математических действий ( (+, -, times , div), и т.д.);
- скобки (), [], >.
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
- 258 – конкретное числодвести пятьдесят восемь;
- (a + b) – сумма любых двух чисел;
- (x + 24 = 78) – уравнение с неизвестным первым слагаемым икс.
- числа, обозначенные цифрами или буквами,
- знаки математических действий, которые связывают эти числа математическими действиями;
- вспомогательные знаки – скобки.
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
- x;
- 74;
- (2cdot3)
- (adiv (25+38))
- (374+(48cdot 2))
- (ac + bc)
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
- запись только знака;
- запись, не обозначающая математического действия над числами (когда знаки не связывают собой числа и не указывают на последовательность действий);
- запись, в которой присутствуют знаки сравнения (в этом случае запись является уравнением или неравенством, сравнивающем два и более выражений).
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
- между числовым и буквенным множителем: (5cdot x = 5x)
- между буквенными множителями: (acdot b = ab)
- между числовым множителем и скобкой: (3cdot (d+c)=3(d+c))
- между буквенным множителем и скобкой: (acdot (b+c)=a(b+c))
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
- (2+3) – суммачисел 2 и 3
- (5cdot 4) – произведение чисел 5 и 4
- (24div 6) – частноечисел 24 и 6
- (35-5) – разность чисел 35 и 5
Более сложные выражения, называют по последнему выполняемому действию:
- ((a+b)-c) – разность суммы чисел a и b и числа c
- ((a+b)cdot (a-b)) – произведение суммы чисел a и b и разности чисел a и b
- (adiv (ccdot d)) – частное числа a и произведения чисел c и d
- Сумма первых пяти натуральных чисел – (1+2+3+4+5)
- Произведение всех однозначных чисел – (1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7cdot 8cdot 9)
- Сумма всех двузначных чётных чисел – (10+12+14+…+94+96+98)
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
- Определить порядок действий в выражении
- Прочитать, начиная с последнего действия
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью (v_) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: (v_=3cdot v_);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: (v_
= v_-15).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения – это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения – это 76.
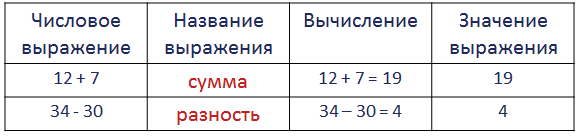
Чтение числовых выражений
49 – 20 – разность
34 – (8 + 21) – из 34 вычесть сумму чисел 8 и 21
13 + (26 – 8) – к 13 прибавить разность чисел 26 и 8
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 – 6 и 18 – 9.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением .
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
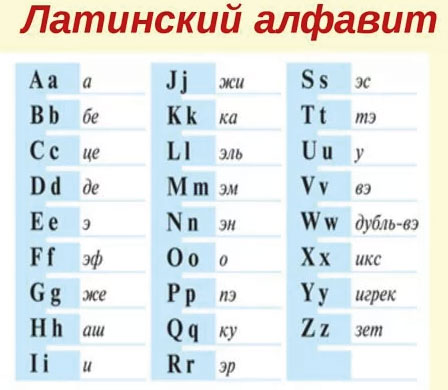
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм – значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2. Дать несколько выражений и предложить прочитать эти выражения разными способами. Один ученик читает выражение, а другие проверяют. Полезно давать столько выражений, сколько формулировок знают дети к этому времени.
3. Учитель диктует выражения разными способами, а дети записывают сами выражения, не вычисляя их значение. Такие задания направлены на то, чтобы проверить знание детьми математической терминологии, а именно: умение записывать выражения или вычислительные упражнения разными способами.
Для проверки сформированности вычислительного навыка полезно читать выражения или вычислительные упражнения, только теми формулировками, которые хорошо усвоены, не заботясь об их разнообразии, а детям предложить записывать только результаты вычислений, сами выражения не записывать.
Требования к проведению диктантов.
1. темп – прочитать выразительно, делая паузу перед числом, логическое ударение ставить на то слово, которое определяет выбор действия. Читаем один раз, а скорость можно определить так: прочитали и про себя повторили с такой же скоростью как прочли детям, а затем читаем новое выражение.
2. скорость – 1кл – 8 – 10 выражений за 5 минут
– 2кл – 18 – 20 выражений (устно) 8 -10 выражений (письменно).
Программа Истоминой.
Требование к уроку – научность математического языка.
Слово выражение дается, отрабатываются существенные признаки. Дается несколько математических записей и сказано, что они называются выражением.
Большинство заданий в математике связано с вычислением значения выражения. Если значение выражения найдено, то результат выполнения вычислительного действия записывают в виде равенства. Например, 3+1=4. Если значение выражения вычислили верно, то равенство называют верным, если неверно, то записанное равенство считают неверным.
Равенство, содержащее переменную величину, называют уравнением. Решить уравнение – значит, найти такое значение переменной величины (корень уравнения), при котором уравнение преобразуется в верное числовое равенство. Значение переменной, при котором уравнение преобразуется в верное равенство, называют корнем уравнения.
В большинстве программ и систем обучения в начальной школе рассматривают два способа решения уравнения.
Первый способ называют способом подбора, что вполне отражает действия производимые ребенком при его использовании. При этом способе значение неизвестного числа подбирается либо из произвольного множества чисел, либо из заданной их совокупности. После каждого выбора значения осуществляется проверка правильности решения. Сущность проверки вытекает из определения уравнения и сводится к выполнению четырех взаимосвязанных действий:
1. В заданное уравнение вместо неизвестного числа подставляется найденное значение.
2. Вычисляется значение левой и правой части уравнения (значение одной из частей может быть элементарным выражением, т.е. числом).
3. Сравнивается значение левой и правой части полученного равенства.
4. Делается вывод о верности или неверности полученного равенства и далее, является ли найденное число решением (корнем) уравнения.
На первых порах практически выполняется только первое действие, а остальные проговариваются. Этот алгоритм проверки сохраняется для каждого способа решения уравнения.
Ряд авторов программ и систем обучения (М.П.,М.Д.) для решения простых уравнений используют зависимость между частью и целым.
Задание: реши уравнение 8+х=11
В данном уравнении неизвестно второе слагаемое. Мы знаем, чтобы найти второе слагаемое можно из значения суммы вычесть второе слагаемое. Значит надо из 11 вычесть 8. Записываю: Х=11-8 Вычисляю, 11 минус 8 равно 3, пишу Х=3
Далее делается проверка по выше указанному алгоритму.
Полная запись решения с проверкой будет иметь следующий вид:
Названным выше способом решаются уравнения с двумя и более действиями со скобками и без них. В этом случае нужно определить порядок действий в составном выражении и, называя компоненты в составном выражении по последнему действию, следует выделить неизвестное, которое в свою очередь может быть выражением на сложение, вычитание, умножение или деление (выражено суммой, разностью, произведением или частным). Затем применяют правило для нахождения неизвестного компонента, выраженного суммой, разностью, произведением или частным, учитывая названия компонентов по последнему действию в составном выражении. Выполнив вычисления в соответствии с этим правилом, получают простое уравнение (или снова составное, если первоначально в выражении было три или более знаков действий). Его решение проводится по уже описанному выше алгоритму. Например.
Задание: реши уравнение (х+2):3=8
В данном уравнении неизвестно делимое, выраженное суммой чисел Х и 2. ( В соответствии с правилами порядка действий в выражении, записанном справа от знака равенства, действие деления выполняют последним).
Чтобы найти неизвестное делимое, можно значение частного умножить на делитель: Х+2=8*3
Вычисляем значение выражения справа от знака равенства, получаем: Х+2=24.
Далее получаем уравнение на нахождение неизвестного слагаемого и рассуждаем как в предыдущем примере.
Полная запись имеет вид: (х+2):3=8
В программе Л.Г.Петерсон, в связи с широким использованием алгоритмов и их видов, дается алгоритм (блок – схема) решения таких уравнений (М.3.П.).
Найти последнее действие
Выделить неизвестный компонент
Применить правило нахождения неизвестного компонента
Упростить правую часть
Корень уравнения найден?
Второй способ решения уравнений достаточно громоздкий, особенно для составных уравнений, где правило взаимосвязи между компонентами и результатом действия применяется многократно. В связи с этим, многие методисты, авторы программ (М.М., М.И.) не включают в программу начальных классов знакомство с уравнениями сложной структуры и ограничиваются изучением уравнений следующих видов:
Х+2=6; 5+Х=8 – уравнения на нахождение неизвестного слагаемого;
Х-2=6; 5-Х=3 – уравнения на нахождение неизвестного уменьшаемого и вычитаемого соответственно;
Х*5=20, 5*Х=35- уравнения на нахождение неизвестного множителя;
Х:3=8, 6:Х=2 – уравнения на нахождение неизвестного делимого и делителя соответственно.
Ряд альтернативных программ обучения математике в начальных классах (М.П.; М.З.) практикуют знакомство детей с более сложными уравнениями, где правило взаимосвязи между компонентами и результатом действия приходится применять многократно и, нередко, требуют выполнения действий по преобразованию одной из частей уравнений на основе свойств математических действий. Например, в программе (М.3.П., М.3.З.) для решения предлагаются такие уравнения:
3х-(20+х)=70 или 2*х-8+5*х=97.
Из данной теоремы вытекают следствия, которые и используются при решении уравнений.
Следствие 1. Если к обеим частям уравнения прибавить одно и то же число, то получим новое уравнение равносильное данному.
Следствие 2. Если в уравнении одно из слагаемых (числовое выражение или выражение с переменной) перенести из одной части в другую, поменяв знак слагаемого на противоположный, то получим уравнение равносильное данному.
Таким образом, процесс решения уравнения сводится к замене данного уравнения, равносильным, причем эта замена (преобразование) может осуществляться только с учетом теорем о равносильности уравнений или следствий из них. Этот способ решения уравнений является универсальным, с ним детей знакомят в системе обучения Л.В. Занкова (М. А.) и в старших классах.
В методике работы над уравнениями накоплено большое число творческих заданий:
· на выбор уравнений по заданному признаку из ряда предложенных;
· на сравнение уравнений и способов их решений;
· на составление уравнений по заданным числам;
· на изменение в уравнении одного из известных чисел так, чтобы значение переменной стало больше, чем (меньше; чем) первоначально найденное значение;
· на подбор известного числа в уравнении;
· на составление алгоритмов решения с опорой на блок схемы решения уравнений или без них;
· составление уравнений по текстам задач.
Технологии изучения геометрического материала в курсе математики начальных классов
1. Цель и задачи введения геометрического материала в курс математики
2. Содержание ГМ в начальных классах.
3. Уровни развития мышления в области геометрии
4. Подходы к изучению ГМ в начальных классах
5. Виды геометрических заданий и методика работы над геометрическим заданием определенного вида.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Папиллярные узоры пальцев рук – маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Подготовила: Рябова Я.Н., Студентка 49 группы ТПК Проверила: Киреева И.А. Алгоритмы чтения произведения и деления

Алгоритм чтения выражения на умножение: 15 умножить на 4, получится 60. Первый множитель 15, второй множитель 4, произведение 60. Произведение чисел 15 и 4 равно 60. Если 15 увеличить в 4 раза получится 60. По 15 взять 4 раза, получится 60. Четырежды пятнадцать – шестьдесят. = 60 Примеры на умножение читаются по разному. 15 4 I Множ. II Множ. Произв. 15 60 15 15 15 15 60

Алгоритм чтения выражения на деление: Если 84 разделить на 42 получится 2. Если 84 уменьшить в 42 раза получится 2. Делимое 84, делитель 42, частное 2. Частное 84-ти и 42-х равно двум. Примеры на деление читаются по разному. 84 : 42 = 2 Дел-ое Дел-ль Частное
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Дистанционные курсы для педагогов
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 592 753 материала в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
Свидетельство и скидка на обучение каждому участнику
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
- 19.12.2020 893
- PPTX 141.7 кбайт
- 12 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Рябова Яна Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
40%
- Подготовка к ЕГЭ/ОГЭ и ВПР
- Для учеников 1-11 классов
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей
Время чтения: 1 минута
Студенты российских вузов смогут получить 1 млн рублей на создание стартапов
Время чтения: 3 минуты
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
РДШ организовало сбор гуманитарной помощи для детей из ДНР
Время чтения: 1 минута
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Читайте также:
- Конкурс семейных рецептов в доу
- Физика эксперименты для средней школы и колледжа
- Внеклассное чтение сказки и рассказы для детей хрестоматия начальной школы
- Родительское собрание по толерантности в школе 6 класс
- Тришкин кафтан краткое содержание
Как читать математику
Математика — это «язык, который ни читать, ни понять невозможно без инициации» (Эдвард Ротштейн, «Эмблемы ума»)
Протокол чтения — набор стратегий, которые должен использовать читатель для получения всех преимуществ от чтения текста. Набор стратегий для поэзии отличается от художественной литературы, а стратегии чтения художественной литературы отличаются от научных статей. Будет нелепо читать художественную книгу и задаваться вопросом, какие источники позволили автору утверждать, что главный герой — загорелый блондин; но будет неправильно читать научную литературу и не задать такой вопрос. Этот протокол чтения расширяется на протоколы просмотра и прослушивания в живописи и музыке. На самом деле большинство вводных курсов по литературе, музыке и искусству посвящено изучению этих протоколов.
Для математики существует особый протокол чтения. Как мы учимся читать литературу, так и математику мы должны научиться читать. Школьникам следует изучать протокол чтения для математики так же, как они учатся правилам чтения романа или стихотворения, учатся понимать музыку и живопись. Замечательная книга «Эмблемы ума» Эдварда Ротштейна выявляет взаимосвязь между математикой и музыкой, неявно затрагивая протоколы чтения для математики.
Когда мы читаем роман, нас поглощает сюжет и персонажи. Мы пытаемся следовать различным сюжетным линиям и тому, как каждая из них влияет на развитие героев. Сами персонажи должны стать для нас реальными людьми — и те, которые нас восхищают, и те, которых мы презираем. Мы не останавливаемся на каждом слове, а представляем слова как мазки на картине. Даже если конкретное слово неизвестно, общая картина всё равно ясна. Мы редко прерываемся поразмыслить над конкретной фразой или предложением. Вместо этого мы позволяем произведению увлечь нас в своём потоке и быстро донести до конца. Это полезное и расслабляющее занятие, оно даёт пищу для размышлений.
Писатели часто характеризуют персонажей, вовлекая их в тщательно подобранные эпизоды действий, а не описывая тщательно подобранными прилагательными. Они изображают один аспект, затем другой, потом снова первый в новом свете и так далее. По мере этого общая картина растёт, становится всё более ясной. Таков способ передать сложные мысли, которые не поддаются точному определению.
Математические идеи по своей сути точны и хорошо определены, так что можно дать чёткое и очень краткое описание. И математическая статья, и художественный роман рассказывают некую историю и развивают сложные идеи, но математическая статья делает это с гораздо меньшим количеством слов и символов, чем в книге. Красота книги — в эстетическом способе использования языка для пробуждения эмоций и представления вещей, которые не поддаются точному определению. Красота математической статьи — в элегантности и эффективности лаконичного выражения чётких идей огромной сложности.
Какие типичные ошибки делают люди, которые пытаются прочитать математику? Как эти ошибки можно исправить?
Не теряй большой картины
«Чтение математики вообще не линейно… Для понимания текста нужны перекрёстные ссылки, быстрое сканирование, паузы и повторное чтение» (оттуда же)
Не думайте, что понимание каждой фразы в отдельности позволит вам понять идею целиком. Это как пытаться увидеть портрет, разглядывая в упор каждый квадратный сантиметр картины. Вы увидите детали, текстуру и цвет, но совершенно упустите портрет. Математическая статья рассказывает историю. Попробуйте понять, что это за история, прежде чем углубиться в детали. Взглянуть поближе можно позже, когда построите фреймворк понимания. Сделайте это так же, как вы могли бы перечитать художественную книгу.
Не будь пассивным читателем
«Трёхстрочное доказательство скромной теоремы — это квинтэссенция лет работы. Чтение математики… предусматривает возвращение к мыслительному процессу, который происходил во время её записи» (оттуда же)
Исследуйте примеры на предмет шаблонов. Попробуйте особые случаи.
Математическая статья обычно рассказывает только малую часть большой и протяжённой истории. Как правило, автор месяцами блуждает в темноте, пытаясь открыть что-то новое. В конце концов он организует своё открытие в виде статьи, где скрывает все ошибки (и их причины) и представляет законченную идею в виде чистого аккуратного потока. Чтобы по-настоящему понять идею и воссоздать, что скрыл автор, читайте между строк.
Математики очень лаконичны, но многое скрывается за этим немногословием. Читатель должен участвовать. На каждом этапе он/она Должен решать, насколько ясна представленная идея. Задавайте себе следующие вопросы:
- Почему эта идея верна?
- Действительно ли я верю в неё?
- Могу я убедить кого-нибудь, что она верна?
- Почему автор не использовал иной аргумент?
- Есть ли у меня лучший аргумент или метод, объясняющий идею?
- Почему автор не объяснил её понятным мне способом?
- Мой способ неверен?
- Я в самом деле понял идею?
- Я упускаю какой-то нюанс?
- Автор упускает какой-то нюанс?
- Если я не могу понять смысл, может мне будет понятнее похожая, но более простая идея?
- Действительно ли так необходимо понимание этой идеи?
- Могу ли я принять эту идею без понимания деталей, почему она верна?
- Пострадает ли моё понимание большой картины от того, что я не понимаю доказательства этой конкретной идеи?
Если потратить слишком мало усилий на подобное участие, то это как читать книгу без концентрации внимания. Через полчаса вы внезапно понимаете, что просто переворачивали страницы, думая о своём, и не запомнили ничего из того, что читали.
Не читай слишком быстро
Слишком быстрое чтение математики приводит к разочарованию. Полчаса концентрации внимания над художественной книгой позволит среднему читателю прочитать 20-60 страниц с полным пониманием текста, в зависимости от книги и опыта чтения. Те же полчаса над математической статьёй дадут 0-10 строчек, в зависимости от статьи и опыта чтения математики. Работу и время ничем нельзя заменить. Вы можете ускорить математическое чтение с помощью практики, но будьте осторожны. Как и в любом навыке, попытка сделать слишком многое слишком быстро может отбросить вас назад и уничтожить мотивацию. Представьте, что вы в течение часа энергично занимаетесь физическими упражнениями, если до этого не занимались два года. Может вы и пройдёте через первый этап, но вряд ли продолжите дальше. Разочарование от постоянного наблюдения, как опытные ребята без устали выполняют вдвое больше вашего, в то время как у вас на следующий день всё тело ноет от усталости — это слишком трудно принять.
Например, возьмём такую теорему из трактата «Дело вычислителя» Леви бен Гершома, написанного в 1321 году.
«Когда вы складываете последовательные числа, начиная с 1, и количество слагаемых нечётное, то результат равен произведению среднего числа на последнее». Для современной математики естественно будет записать теорему следующим образом:
Читателю понадобится примерно столько же времени, чтобы распутать эту небольшую формулу, сколько ему нужно на понимание двух строчек текстовой версии теоремы. Пример теоремы Леви:
Сделай идею свой собственной
Лучший способ понять прочитанное — сделать идею своей собственной. Это означает отследить идею к её корням и самостоятельно заново открыть её. Математики часто говорят, что для понимания чего-либо вы должны сначала прочитать это, затем записать собственными словами, а потом научить кого-то другого. У каждого разный инструментарий и разный уровень «усвоения» сложных идей. Нужно приспособить идею к собственному ви́дению и опыту.
«Когда я беру слово, оно означает то, что я хочу»
(Шалтай-Болтай из книги «Алиса в Зазеркалье» Льюиса Кэролла)
«Значение редко будет полностью понятным, потому что каждый символ или слово уже представляют собой экстраординарную конденсацию концепции и ссылки» (оттуда же)
Хорошо написанный математический текст будет аккуратно использовать слово только в одном смысле, делая различие, скажем, между комбинацией и перестановкой (или расстановкой). Чёткое математическое определение может подразумевать, что «жёлтая бешеная собака» и «бешеная жёлтая собака» — это разная расстановка слов, но одинаковая комбинация. Большинство англоязычных читателей не согласятся с этим. Исключительная точность совершенно чужда большей части художественной литературы и поэзии, где хорошим тоном считается использование разнообразных слов, синонимов и изменчивых описаний.
Со стороны читателя ожидается понимание, что абсолютное значение — это не какое-то произвольное значение, которое оказалось абсолютным, а функция не имеет отношения ни к чему функциональному.
Особенно печально известный пример — использование фразы «из этого легко следует, что…» и тому подобных конструкций. Они означают примерно следующее:
Теперь можно проверить справедливость следующего утверждения. Проверка потребует определённого количества по существу механической, хотя, возможно, и трудной работы. Я как автор мог бы её провести, но она займёт много места и, возможно, не приведёт к хорошим результатам, поскольку в ваших же интересах самостоятельно сделать вычисления и прояснить, что здесь происходит. Обещаю, что никакие новые идеи не участвуют. Хотя, конечно, вам может понадобиться немного подумать, чтобы найти правильную комбинацию хороших идей для применения.
Другими словами, эта фраза при правильном применении — сигнал автору, что здесь присутствует нечто утомительное и даже сложное, но не предполагающее ярких озарений. Тогда читатель волен решать, насколько сильно он хочет сам разобраться во всех подробностях или ему достаточно заверений автора — и тогда можно сказать: «Ладно, верю тебе на слово».
Теперь независимо от вашего мнения об уместности употребления подобной фразы в конкретной ситуации и от корректности использования её автором вы должны понимать, что она должна значить на самом деле. Фраза «Из этого легко следует, что…» не значит
Если ты сразу этого не видишь, ты дурак
И она не значит
Это не должно занять больше двух минут
Но человек, незнакомый с математическим словарём, может её неправильно понять и столкнётся с разочарованием. Это помимо вопроса о том, что «утомительная задача» для одного человека может оказаться сложнейшей проблемой для другого. Поэтому автор должен правильно оценивать свою аудиторию.
Знай себя
Тексты пишутся с расчётом на читателей определённого уровня. Убедитесь, что вы являетесь таким читателем или желаете сделать всё, чтобы присоединиться к их числу.
Из Томаса Элиота, «Песнь Симеона»:
Господи, зимнее солнце ползёт меж снежных вершин,
Римские гиацинты заполыхали в чашах;
Время застыло — упрямый немой властелин,
Жду дуновения смерти душой облегчённой,
Словно пушинка на старческой длани. Один.
Пыль под солнцем и память по закоулкам
Чаю прохлады, что веет для смертных долин.
Lord, the Roman hyacinths are blooming in bowls and
The winter sun creeps by the snow hills;
The stubborn season has made stand.
My life is light, waiting for the death wind,
Like a feather on the back of my hand.
Dust in sunlight and memory in corners
Wait for the wind that chills towards the dead land.
Например, стихотворение Элиота в значительной степени предполагает, что читатели или знают, кто такой Симеон, или желают выяснить это. Оно также предполагает, что читателем будет или опытный читатель поэзии, или тот, кто хочет приобрести такой опыт. Автор предполагает, что читатели либо знают, либо разберутся в аллюзиях здесь. Это выходит за рамки простых вещей вроде того, кем был Симеон. Например, почему гиацинты «римские»? Почему это важно?
Элиот предполагает, что читатель будет читать медленно и обратит внимание на картинки: автор сопоставляет пыль и память, сравнивает старость с зимой, сравнивает ожидание смерти с пушинкой на обратной стороне ладони и т.д. Он предполагает, что читатель воспримет это как поэзию; в некотором смысле, он предполагает, что читатель знаком со всей поэтической традицией. Он должен заметить, что нечётные строчки рифмуются, а остальные нет, и т.д.
Самое главное, он предполагает, что читатель будет подключать к чтению не только свой ум, но также свои эмоции и воображение, которое нарисует образ старика, уставшего от жизни но вынужденного цепляться за неё, ожидающего некоего важного события.
Большинство математических книг тоже написано с некоторыми предположениями об аудитории: что они знают определённые вещи, что они достигли определённого уровня «математической зрелости» и проч. Прежде чем начать читать, убедитесь в соответствии тому, что автор ожидает от вас.
Пример математической записи
Чтобы поэкспериментировать с представленными здесь принципами, я включил в него небольшой математический фрагмент, часто называемый парадоксом дней рождения. Первая часть — это точная математическая статья, описывающая проблему и её решение. Вторая часть — вымышленная попытка Читателя понять статью, используя соответствующий протокол чтения. Тема статьи — вероятность. Она доступна смышлёному и мотивированному читателю даже без математического образования.
Парадокс дней рождения
Профессор в классе из 30-ти случайных студентов часто предлагает поспорить, что как минимум у двоих человек в классе одинаковый день рождения (месяц и день, необязательно год). Вы примете спор? А если в классе меньше студентов? Примете тогда предложение поспорить?
Предположим, что дни рождения человек равномерно распределены по 365 дням года (для простоты не учитываем високосные годы). Докажем, что вероятность одинакового дня рождения (месяц и день) по крайней мере у двоих из них равна:
Какова вероятность, что среди 30-ти случайных людей в комнате попадутся хотя бы двое с одинаковым днём рождения? Для эта вероятность будет 71%, то есть профессор будет выигрывать спор в 71 случаях из 100 на длинной дистанции. Как выясняется, при 23-х учениках в классе вероятность составляет примерно 50%.
Вот доказательство: Пусть будет искомой вероятностью. Пусть будет вероятностью, что у всех разные дни рождения. Теперь найдём , вычислив количество наборов из дней рождения без дубликатов и разделив его на общее количество возможных наборов из дней рождения. Затем найдём .
Общее количество наборов из дней рождения без дубликатов:
Это потому что для первого ДР возможно 365 вариантов, для второго — 364и так далее для человек. Общее количество дней рождения без всяких ограничений равняется просто , потому что для каждого из дней рождения есть 365 вариантов. Таким образом, равняется
Решение для даёт и, следовательно, наш результат.
Попытки нашего читателя понять парадокс дней рождения
В этом разделе наивный Читатель пытается понять смысл последних нескольких абзацев. Реплики Читателя — метафорическое выражение его мыслей вслух, а комментарии Профессионала представляют собой исследовательскую работу, которую должен проделать Читатель. Соответствующие протоколы выделены жирным шрифтом и вставлены в соответствующие места повествования.
Выглядит, что Читатель как будто схватывает вещи очень быстро. Но будьте уверены, что в реальности между комментариями Читателя проходит немало времени и что я оставил за скобками многие его замечания, которые ведут в тупик. Понять, что он испытывает, можно только если читать между строк и представить образ его мыслей. Думать за него — часть ваших собственных усилий.
Знай себя
Читатель (Ч): Я ничего не знаю о вероятностях, я смогу в этом разобраться?
Профессионал (П): Давай попробуем. Возможно, придётся делать большие отступления на каждом шаге.
Ч: Что означает фраза «30 случайных (хаотичных) студентов»?
«Когда я беру слово, оно означает то, что я хочу, ни больше и ни
меньше»
П: Хороший вопрос. Фраза не означает, что у нас 30 ошалевших или больных на голову людей. Она означает, что мы должны предположить, что дни рождения этих 30-ти человек не зависят друг от друга и что каждый день рождения одинаково вероятен для каждого человека. Чуть далее автор более формально описывает это: «Предположим, что дни рождения человек равномерно распределены по 365 дням года».
Ч: Разве это не очевидно? Зачем специально это оговаривать?
П: Да, предположение кажется очевидным. Автор просто устанавливает основное условие. Это предложение гарантирует, что всё нормально, а решение не предполагает какой-либо воображаемой причудливой научной фантастики.
Ч: Что ты имеешь в виду?
П: Например, автор не ищет решения вроде такого: все живут в Стране Независимости и родились 4-го июля, так что шансы на совпадение дней рождения двух и более людей составляют 100%. Математикам не нравятся решения такого рода. Кстати, предположение также подразумевает, что мы не учитываем високосные годы. То есть никто в этой задаче не родился 29-го февраля. Читай дальше.
Ч: Не понимаю эту длинную формулу, Что такое ?
П: Автор решает проблему для произвольного количества человек, не просто для 30-ти. С этого момента автор называет количество человек .
Ч: Я по-прежнему не понимаю. Какой ответ?
Не будь пассивным читателем – попробуй примеры
П: Ну если нужен ответ только для 30-ти, просто установи .
Ч: Окей, но это сложно посчитать. Где мой калькулятор? Посмотрим: 365×364×363×. ×336. Это утомительно, и результат даже не помещается на экране. Здесь написано:
Если даже зная формулу я не могу вычислить результат, как я могу понять, откуда взялась формула?
П: Ты прав, что здесь получается не точный результат, но если продолжить дальше и поделить, то ответ будет не слишком далёк от точного.
Ч: Всё это как-то некомфортно. Я бы хотел вычислить точное значение. Есть другой способ произвести вычисления?
П: Сколько множителей у тебя в числителе? Сколько в знаменателе?
Ч: Ты имеешь в виду 365 как первый множитель, 364 как второй? Тогда получается 30 множителей вверху. Также 30 множителей внизу (30 копий 365).
П: Теперь можешь вычислить результат?
Ч: А, понятно. Я могу спарить каждый множитель из числителя с каждым множителем знаменателя, так что получится 365/365 для первого множителя, затем умножить на 364/365 и так далее для всех 30-ти множителей. Так что результат всегда поместится в моём калькуляторе. (Через несколько минут)… Так, я получил 0,29368, если округлить до пяти знаков.
П: Что значит это число?
Не теряй большой картины
Ч: Я забыл, что делал. Так, посмотрим. Я искал ответ для . Число 0,29368 — это все вычисления, кроме вычитания из единицы. Если продолжить, получится 0,70632. А теперь что это значит?
П: Тут полезно больше узнать о вероятностях, но по-простому это означает, что в группе из 30-ти человек у двух или более совпадут дни рождения в 70 632 из 100 000 случаев, то есть примерно в 71% случаев.
Ч: Интересно. Я бы сам не догадался. Хочешь сказать, что в моём классе из 30-ти студентов довольно высока вероятность, что по крайней мере у двух человек будет одинаковый день рождения?
П: Да, правильно. Можешь принимать ставки до того, как узнал их даты рождения. Многие думают, что такое совпадение маловероятно. Вот почему некоторые авторы называют это парадоксом дней рождения.
Ч: Так вот почему я должен читать математику, чтобы заработать пару долларов?
П: Понимаю, что для тебя это может быть неким стимулом, но надеюсь, что математика также вдохновляет тебя и без всяких денежных перспектив.
Ч: Интересно, какой результат будет для других значений . Попробую сделать ещё несколько вычислений.
П: Хорошая мысль. Мы даже можем составить графическое изображение из всех твоих вычислений. Можно составить график количества людей и вероятностей совпадения дней рождения, хотя это можно оставить на другой раз.
Ч: О, смотри, автор сделал некоторые вычисления за меня. Он говорит, что для ответ около 71%; я тоже получил такую цифру. А для получается около 50%. Это имеет смысл? Думаю, что имеет. Чем больше людей, тем выше вероятность совпадения дней рождения. Эй, я опережаю автора. Неплохо. Ладно, продолжим.
П: Хорошо, теперь сам скажешь, когда продолжить.
Не читай слишком быстро
Ч: Кажется, что мы добрались до доказательства. Оно должно объяснить, почему формула работает. Что это за ? Думаю, что означает “probability ” (вероятность), но что означает ?
П: Автор вводит новую величину. Он использует просто потому что это следующая буква в алфавите после , но — это тоже вероятность, причём имеющая близкое отношение к . Пришло время взять минутку на раздумье. Что такое и почему оно равняется ?
Ч: — это вероятность, что ни у кого в комнате не совпадают дни рождения. Почему автора волнует этот вопрос? Разве нам не нужна другая вероятность, что дни рождения совпадают?
П: Хорошее замечание. Автор не говорит этого явно, но между строк ты можешь понять, что он понятия не имеет, как напрямую вычислить . Вместо этого он вводит вероятность , которая предположительно равна . Вероятно, после этого автор должен показать, как вычисляется . Кстати, когда ты закончишь статью, ты можешь задаться вопросом, как вычислить напрямую. Это прекрасное продолжение для идей, представленных здесь.
Ч: Всему своё время.
П: Ладно. Итак, теперь мы знаем , что дальше?
Ч: Затем мы можем получить . Если , то . Хорошо, но почему ? Автор полагает, что это очевидно?
П: Да, он так полагает, и что ещё хуже, он даже не говорит нам, что это очевидно. Вот эмпирическое правило: когда автор явно говорит, что это истина или это очевидно, то следует потратить 15 минут и убедить себя, что так оно и есть. Если автор даже не беспокоиться о том, чтобы это сказать, но подразумевает это, то процесс займёт немного больше времени.
Ч: Как я пойму, что нужно остановиться и подумать?
П: Просто будь честен с собой. Если появились сомнения, остановись и подумай. Если слишком устал, иди посмотри телевизор.
Ч: Так почему ?
П: Давай вообразим особый случай. Если вероятность совпадения двух и более дней рождения 1/3, то какова вероятность не получить совпадение?
Ч: Это 2/3, потому что вероятность отсутствия события обратна вероятности наступления события.
Сделай идею свой собственной
П: Ну, следует быть осторожным при использовании слов вроде обратна, но ты прав. На самом деле ты открыл одно из первых правил, которое изучают в теории вероятностей. А именно, что вероятность отсутствия события равна единице минус вероятность наступления события. Теперь перейдём к следующему абзацу.
Ч: Там вроде объясняется, чему равняется — в длинной и сложной на вид формуле. Я никогда такую не пойму.
П: Формула для тяжела для понимания, и автор рассчитывает на твоё усердие, упорство и/или имеющиеся знания, чтобы разобраться в ней.
Ч: Он как будто вычисляет все вероятности чего-то и делит их на общее количество вероятностей, что бы это ни значило. Понятия не имею, почему он так делает.
П: Может быть, могу помочь тебе с некоторой информацией по этому предмету. Вероятность наступления определённого исхода в математике определяется так: общее количество возможных вариантов этого исхода делится на общее количество всех вариантов исхода. Например, вероятность выбросить четвёртку на кубике равна 1/6. Поскольку там одна четвёрка и шесть возможных исходов. Какова будет вероятность, что ты выбросишь четвёрку или тройку?
Ч: Ну, я думаю, 2/6 (или 1/3), потому что общее количество возможных исходов по-прежнему осталось шесть, но у меня есть два варианта удачного исхода.
П: Хорошо. Теперь более сложный пример. Что насчёт вероятности выбросить четыре в сумме при бросании двух кубиков? Есть три варианта получить такую сумму (1-3, 2-2, 3-1), в то время как общее количество комбинаций равно 36. Это 3/36 или 1/12. Посмотри на следующую таблицу 6×6 и сам убедись в этом.
Что насчёт вероятности выбросить семь в сумме?
Ч: Погоди, что значит 1-1? Разве это не равняется 0?
П: Извини, я виноват. Я использовал знак минуса как тире, просто имея в виду пару чисел, так что 1-1 означает выбросить единички на обоих кубиках.
Ч: Ты не мог бы придумать лучшую запись?
П: Ну может я могу или должен сделать это, но запятые выглядят хуже, а слэш будет похож на деление, и всё остальное тоже может вводить в заблуждение. В любом случае, мы не собираемся публиковать эту расшифровку.
Ч: Слава богу. Ну, теперь-то я знаю, что ты имеешь в виду. Я могу получить семь в сумме шестью способами: 1-6, 2-5, 3-4, 4-3, 5-2 или 6-1. Общее количество исходов по-прежнему 36, так что получается 6/36 или 1/6. Это странно, почему вероятность выпадения четырёх отличается от вероятности выпадения семи?
П: Потому что не каждая сумма одинаково вероятна. Здесь ситуация отличается от простого вращения колеса с цифрами от 2 до 12 в одинаковых интервалах. В этом случае у каждой из 11 цифр одинаковая вероятность выпадения 1/11.
Ч: Хорошо, теперь я эксперт. Вероятность вычисляется просто подсчётом?
П: Иногда да. Хотя рассчитать бывает непросто.
Ч: Ясно, давай продолжим. Кстати, автор реально ожидал, что я всё это знаю? Мой друг проходит курс вероятности и статистики, но я не уверен, что он знает все эти вещи.
П: Маленький раздел математики содержит в себе много информации. Да, автор ожидает от читателя знания всего этого или что тот найдёт эту информацию и усвоит её, как это сделали мы. Если бы меня здесь не было, тебе пришлось бы задавать эти вопросы самому себе и находить ответы путём размышлений, в учебниках и справочниках или консультируясь с другом.
Ч: Так что вероятность совпадения дней рождения у двух человек — это количество возможных наборов из дней рождения без дубликатов, поделенное на общее количество возможных наборов из дней рождения.
П: Отличное резюме.
Ч: Мне не нравится использование , так что давай использовать 30. Возможно, тогда будет проще усвоить обобщение .
П: Отличная мысль. Часто бывает полезным проанализировать особый случай, чтобы понять общий случай.
Ч: Так сколько наборов из 30-ти дней рождения есть вообще? Я не могу посчитать. Думаю, что мне придётся ещё больше ограничить условия. Давай притворимся, что у нас всего два человека.
П: Хорошо. Теперь ты размышляешь как математик. Рассмотрим . Сколько здесь возможных комбинаций дней рождения?
Ч: Я считаю дни рождения с 1 по 365, не учитывая високосные годы. Тогда вот все возможные комбинации:
П: Когда ты пишешь 1-1, ты имеешь в виду 1-1=0, как вычитание?
Ч: Хватит меня дразнить. Ты точно знаешь, что я имею в виду.
П: Да, я знаю, и могу отметить хороший выбор способа записи. Теперь сколько здесь пар дней рождения?
Ч: Для двух человек получается 365×365 вариантов.
П: А сколько вариантов, если не учитывать совпадающие дни рождения?
Ч: Нельзя использовать 1-1, 2-2, 3-3… 365-365, так что выходит
Общее количество вариантов выходит 365×364, потому что в каждой строке теперь 364 пары вместо 365.
П: Хорошо. Ты здесь немного спешишь, но всё равно на 100% прав. Теперь можешь обобщить для 30-ти человек? Каково общее количество возможных наборов из 30-ти дней рождения? Попробуй догадаться. У тебя это хорошо получается.
Ч: Ну если пробовать догадаться (хотя это в реальности не совсем догадка, в конце концов, я уже знаю формулу), то я бы сказал, что для 30-ти человек нужно 30 раз умножить 365×365×. ×365, для общего количества возможных наборов ДР.
П: Точно. Математики пишут 365 30 . А каково общее количество наборов из 30-ти дней рождения без повторений?
Ч: Я знаю, что ответ должен быть 365×364×363×362×. ×336 (то есть начать с 365 и каждый раз умножать на число с вычитанием единицы 30 раз), но я не уверен, что действительно понимаю, почему именно так. Возможно, сначала нужно рассмотреть случай с тремя людьми и найти способ увеличения до 30-ти?
П: Блестящая мысль. Давай закончим на сегодня. Общая картина для тебя понятна. Когда отдохнёшь и у тебя будет больше времени, можешь вернуться и заполнить последний пробел в понимании.
Ч: Большое спасибо; это был хороший опыт. Увидимся позже.
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
- цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
- буквы латинского и греческого алфавитов ((a, b, c, d, α, β, γ, δ) и т.д.)
- знаки математических действий ( (+, -, times , div), и т.д.);
- скобки (), [], <>.
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
- 258 – конкретное числодвести пятьдесят восемь;
- (a + b) – сумма любых двух чисел;
- (x + 24 = 78) – уравнение с неизвестным первым слагаемым икс.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
- числа, обозначенные цифрами или буквами,
- знаки математических действий, которые связывают эти числа математическими действиями;
- вспомогательные знаки – скобки.
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
- запись только знака;
- запись, не обозначающая математического действия над числами (когда знаки не связывают собой числа и не указывают на последовательность действий);
- запись, в которой присутствуют знаки сравнения (в этом случае запись является уравнением или неравенством, сравнивающем два и более выражений).
Например, это НЕ математические выражения:
- (
- +
- ((div 8-59)
- (35cdot 12(+74)
- (a+5=12)
- (38+87

Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
- между числовым и буквенным множителем: (5cdot x = 5x)
- между буквенными множителями: (acdot b = ab)
- между числовым множителем и скобкой: (3cdot (d+c)=3(d+c))
- между буквенным множителем и скобкой: (acdot (b+c)=a(b+c))
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
- (2+3) – суммачисел 2 и 3
- (5cdot 4) – произведение чисел 5 и 4
- (24div 6) – частноечисел 24 и 6
- (35-5) – разность чисел 35 и 5
Более сложные выражения, называют по последнему выполняемому действию:
- ((a+b)-c) – разность суммы чисел a и b и числа c
- ((a+b)cdot (a-b)) – произведение суммы чисел a и b и разности чисел a и b
- (adiv (ccdot d)) – частное числа a и произведения чисел c и d
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
- Сумма первых пяти натуральных чисел – (1+2+3+4+5)
- Произведение всех однозначных чисел – (1cdot 2cdot 3cdot 4cdot 5cdot 6cdot 7cdot 8cdot 9)
- Сумма всех двузначных чётных чисел – (10+12+14+…+94+96+98)
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
- Определить порядок действий в выражении
- Прочитать, начиная с последнего действия
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
- (35cdot (28-12)) – Произведение числа 35 и разности чисел 28 и 12
- (35cdot (28-12)+64) – Сумма произведения числа 35 с разностью чисел 28 и 12, и числа 64.
- (35cdot (28-12)+64–32div 16) – Разность суммы произведения числа 35 и разности чисел 28 и 12 с числом 64, и частного чисел 32 и 16
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью (v_<1>) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: (v_=3cdot v_<1>);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: (v_
= v_<1>-15).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
- формула расстояния (s = vcdot t) (или (s = vt) ) – это запись зависимости значения пройденного расстояния от значений скорости движения и времени движения (Расстояние – это скорость, умноженная на время).
- формула периметра прямоугольника (P=2(a+b)) – это запись зависимости величины периметра
прямоугольника от его длины и ширины (Периметр прямоугольника равен удвоенной сумме
двух его разных сторон).
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2
Если вычислить правую часть, то можно узнать чему равна переменная x
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
Вычисляем правую часть и находим значение x
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства позволяет узнать чему равно x
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда .
Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда .
Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное.
Чтобы выразить число 15 мы поступили следующим образом:
То есть умножили частное 3 на делитель 5.
Теперь представим, что в равенстве вместо числа 15 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5.
А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Теперь представим, что в равенстве вместо числа 5 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства . Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вычислим правую часть, получим значение x равное 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение . Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение и подставим вместо x
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.
Отсюда .
Вернемся к исходному уравнению и подставим вместо x найденное значение 2
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы вычли из обеих частей уравнения число 10 . В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2
Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 4x , а в правой части число 4
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x , а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения .
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение . Корень этого уравнения, как и уравнения равен 4. Значит эти уравнения равносильны.
Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись:
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом:
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 5
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения равен 5 . Значит эти уравнения равносильны.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение . Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 9
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно . Теперь найдем значение переменной B . То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно
Видим, что значение переменной B , как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение . Чему равен корень этого уравнения?
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения . Это есть произведение минус единицы и переменной x
То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение на самом деле выглядит следующим образом:
Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .
или разделить обе части уравнения на −1 , что еще проще
Итак, корень уравнения равен 5 . Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения на минус единицу:
После раскрытия скобок в левой части образуется выражение , а правая часть будет равна 10
Корень этого уравнения, как и уравнения равен 5
Значит уравнения и равносильны.
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1 .
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения на −1 можно записать подробно следующим образом:
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения на −1 , мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение . Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77 , и разделим обе части на 7
Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2
Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5
Уравнения вида мы решали выражая неизвестное слагаемое:
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак:
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда .
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения:
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение и убеждаемся, что при этих значениях левая часть равняется нулю:
Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x , левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .
Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s .
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения определить время. Для этого нужно выразить переменную t .
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
А расстояние равно 100 км
Тогда буквенное уравнение примет следующий вид
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение . Выразите из данного уравнения x
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение . Выразите из данного уравнения x
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение . Выразите из данного уравнения x
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение примет вид .
Отсюда .
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
[spoiler title=”источники:”]
[/spoiler]
Одним из важных ключей, открывающих двери к пониманию и успехам в математике (да и не только), является чтение.
Умение читать, а главное, понимать прочитанное важно не только при чтении художественной литературы, но и при решении математических задач.
Поэтому достойный уровень ребёнка в чтении просто необходим для успешного решения математических задач. Он даёт ученику понимание того, о чём именно идёт речь в задаче, чего не хватает для ответа на главный вопрос, а что, наоборот, является лишней информацией.
Чем так важно чтение?
Понимание
условия задачи предоставляет возможность точно определить ход решения, если
формулировка условия отличается от привычной, к которой выработан алгоритм
решения во время проработки основных типов задач. Без понимания смысла условия
задачи даже небольшое отклонение её формулировки от привычного условия может
привести ребёнка в состояние ступора.
Школьник просто обязан читать много, не только для повышения своего культурного, духовного, образовательного уровня, но и для развития своего мозга, способности думать, размышлять, мыслить.
Необходимо
с самого раннего возраста проводить с ребёнком беседы о прочитанном, определять
его понимание текста, наводящими вопросами учить раскрывать суть, выявлять
важное и полезное.
Информация, которая поступает в наш мозг в словесной и письменной форме, требует от него гораздо больших аналитических и творческих усилий, чем поданная в видеоряде или картинках. В картинках (например, в популярных ныне комиксах) и видеоряде подаются уже сформированные образы. Да, они вызывают чувственные, эмоциональные реакции, но не дают возможности мозгу самостоятельно проанализировать, нарисовать, создать в своем воображении образ того, о чем идет речь.
А развивается именно то, что напрягается. Чтение и общение, то есть, письменная и словесная формы принятия информации, полноценны. Они объединяют эмоции и логику, чувственное восприятие и аналитику. Поэтому, читая и общаясь, наш мозг развивается во всех направлениях.
Научившись читать, нельзя долго задерживаться на чтении простых текстов, составленных из односложных предложений. Необходимо постепенно и настойчиво увеличивать сложность читаемого.
Как связано чтение и математика?
Читая сложные тексты, в которых присутствуют различные литературные приёмы, например, причастные и деепричастные обороты, фразеологизмы, аллегории, и т.д., ребёнок учится тому, что одни и те же слова, написанные в разных комбинациях и ситуациях, могут передавать разные смыслы.
Отталкиваясь
от примеров, увиденных им в литературе, ребёнок учится самостоятельно
складывать слова в стройные, осмысленные предложения и тексты.
Именно сложные тексты обеспечивают необходимую базу для логики. Научившись логически преобразовывать наиболее знакомый ему с детства материал – слово, ребёнок переносит это умение на абстрактные понятия – числа. А оперирование абстрактными понятиями даёт огромное развитие логическому аппарату человека, что в свою очередь положительно сказывается не только на математических способностях, но и на других сферах жизни.
Подписывайтесь на новые интересные и полезные материалы блога:
Вам также пригодится:
Описание презентации по отдельным слайдам:
-

1 слайд
Подготовила: Рябова Я.Н.,
Студентка 49 группы ТПК
Проверила: Киреева И.А.
Алгоритмы чтения произведения и деления -

2 слайд
Алгоритм чтения выражения
на умножение:
15 умножить на 4, получится 60.
Первый множитель 15, второй множитель 4, произведение 60.
Произведение чисел 15 и 4 равно 60.
Если 15 увеличить в 4 раза получится 60.
По 15 взять 4 раза, получится 60.
Четырежды пятнадцать – шестьдесят.
= 60
Примеры на умножение читаются по разному.
15
4
I Множ.
II Множ.
Произв.
15
60
15
15
15
15
60 -

3 слайд
Алгоритм чтения выражения на деление:
Если 84 разделить на 42 получится 2.
Если 84 уменьшить в 42 раза получится 2.
Делимое 84, делитель 42, частное 2.
Частное 84-ти и 42-х равно двум.Примеры на деление читаются по разному.
84
:
42
= 2
Дел-ое
Дел-ль
Частное
Изначально, формулы были придуманы математиками для того, чтобы описать простые физические явления. Например формула скорости: скорость = путь/время. Эта формула говорит о том, что если двигаться с одинаковой скоростью, то за определенное время мы пройдем определенное расстояние. То есть она показывает связь между двумя изменяющимися величинами: путь и время. Если же одно и то же расстояние два человека пройдут с разной скоростью, то они потратят на это разное время, и первым финиширует тот, кто шел с большей скоростью.
Таким образом, формулы нужны для более короткой записи (математическими символами или буквами) взаимосвязей между некоторыми величинами (смотрите пример в статье).
Решение заданий с формулами обычно подразумевает нахождение какой-либо величины, зная остальные величины входящие в формулу.
Все, что требуется в данном задании – подставить вместо букв их значения и посчитать. U = 2 • 10 = 20 В.
Встречаются задания и посложнее. Например:
Для начала нужно выразить величину, которую нужно найти (то есть, чтобы эту величину и остальные величины разделял знак равно). Для этого нужно избавиться от лишних величин, стоящих возле Sinα.
Разделим обе части на 1/2 d
1d2. В результате получим: = Sinα.
Теперь осталось подставить числа и посчитать: Sinα = = 0,4.
Из закона всемирного тяготения F = G выразите массу m и найдите её величину (в килограммах), если F = 13,4 Н, r = 5 м, M = 5·109 кг и гравитационная постоянная G = 6,7 ·10-11.
Первым действием разделим обе части на G, чтобы масса была отделена от других величин знаком равно.
Получим:
F : G = m
F : = m
F • = m
= m
Теперь подставляем численные значения и находим наконец-то массу:
= m
m = 1000.
Таким образом происходит решение задач на расчет по формулам.
boeffblog.ru
Ответы@Mail.Ru: Как научиться понимать математику?
Да уж, даже незнаю что и ответить. А так хочется чтоб не только
понимали, но еще и любили. Как интересно в математике, словно
в гиганских шахматах, где великое множество различных фигур,
где само поле странным образом изгибается, рвется, сварачивается
в немыслемые узлы. Где столько интересных вопросов и проблем,
что даже простые числа вдруг оказываются такими непослушными,
и вот уже столько веков недают спать спокойно лучшим математикам
мира. А научится можно, если небрать готовые формулы, а самому (ой)
попробовать вывести их из более простых. Вот простой пример:
65^2 как сосчитать. Оказывается просто: нужно 6 умножить на (6+1),
получим 42, и приписать 25, вот и ответ 4225. Так можно любое
двухзначное число оканчивающееся на пять возводить в квадрат.
И таких примеров можно найти великое множество. Если есть
хотя бы маленький интерес к этой великой науке. Да еще бы
хорошего наставника, который бы мало по малу открывал
маленькие таинственные дверки в жутких лабиринтах страшных
математических формул. Ведь за каждой такой формулой, иной раз
скрывается кропотливый многолетний труд. Вот ведь сосчитал же
голландец Лудольф 35 верных знаков числа pi(3,1415…)! Причем
без всяких калькуляторов!!
Считать научись!!!
В математике и понимать нечего. Это как бы аксиоматическая наука. Соображать надо, когда решаешь примеры и задачи. Но тут есть только один способ: для того, чтобы научиться решать задачи, надо решать задачи. У меня в школе был уникальный учитель математики. Он задавал примеры так: от номера такого-то …и до конца параграфа, кого на сколько хватит.
А понимать надо естественные науки: физику, химию, биологию.
Я думаю, чтобы понимать математику нужно знать ее историю. Ведь каждый термин, каждое понятие не явились с потолка, они не выдуманы, а появились как ответ на поставленный жизнью (или каким-либо человеком) вопрос. Каждое математическое понятие прежде чем оформилось прошло длинный исторический путь. Я думаю, что просмотрев этот путь, ученик проникнется уважением к этому понятию (читай к мыслителям) , и знания его будут увереннее.
А вообще, чтобы что-либо понимать, надо ЗАГОРЕТЬСЯ. И здесь многое зависит от учителя, и от окружения.
Еще в математике надо уметь отделять второстепенное, научиться мыслить рассчетными схемами (к гению это конечно не относится) .
Сам я дилетант.
Математика гавно!!!
математика самый легкий предмет я его тяну спокойно даже без обьяснений учителей даже контрохи на 5 пишу без подготовки
математика гавно считать надо
как понять физику и математику?
Наибольшие трудности с математикой возникают у школьников и студентов с гуманитарным складом ума. Их проблема именно в том и заключается, что они не могут проникнуть в сущность законов точных наук. Но даже люди, далекие от точных расчетов, смогут значительно продвинуться в познании математической теории при систематических занятиях.
2.
Начните заново. Математика, как и любая другая точная наука требует знания и понимания всех формул с самого 1 урока. Вдумчиво читайте формулировки теорем и способы их доказательства. Разбирайте до тех пор, пока у вас не останется ни тени сомнения. Спрашивайте у учителя все, что вам не ясно.
3.Прочитав несколько тем из учебника алгебры или геометрии, вы заметите, что в них применяется несколько методов доказательств – где-то проще объяснить методом от противного, а где-то найти решение при помощи индукции. Старайтесь их запоминать. Это в целом очень полезно для развития логического мышления. Не оставляйте никакого недопонимания в теории. Дальше это непонимание будет накручиваться как снежный ком, и вы придете к тому, от чего начали. Старайтесь при доказательстве каждой теоремы представить, как это знание вам пригодится в практике.
4.Несколько тысяч лет назад основатель геометрии Евклид сказал, что в математике нет царских путей. Если вам сложно понимать ее законы, то универсальных легких способов вы не найдете. Занимайтесь регулярно, старайтесь находить решение не по готовым формулам, а выводить его из более простых. Например, любое оканчивающееся на 5 двузначное число можно легко возвести в степень. Для этого достаточно умножить первую цифру умножить на нее же с прибавленной единицей и рядом приписать 25.Попробуйте возвести число 85 в квадрат: 8*(8+1)=72. Припишите 25 и получите число 7225. Это и есть 85². Старайтесь при этом не пользоваться калькулятором.
Надо полюбить математике. А потом если ты в школе делать все домашние задания. Если не понимаешь тему подойти в преподавателю и попроси, чтобы тебе объяснили.
touch.otvet.mail.ru
Как запоминать формулы по математике
Голова идёт кругом от множества математических формул, которые необходимо знать. Зубрёжка и шпаргалки — удел слабых. А вот тем, кто хочет стать в математике сильнее, мы подскажем несколько советов, как запоминать формулы по математике так, чтобы они не выветрились из головы до контрольной, экзамена или ЦТ.
Понимай формулу
В школе учат читать формулы, потому что так ты запоминаешь их суть, а не просто сочетание символов. Возьмём простой пример:
Если ты будешь заучивать только последовательность переменных, рискуешь «потерять» всю формулу, когда забудешь символ или знак.
Задействуй все виды памяти
Читай формулы вслух, прописывай на листке по нескольку раз, пока не запомнишь. Задействуй все виды памяти, делая упор на ведущую. Визуальная и двигательная память вместе дают больший эффект. Конечно, потенциал для запоминания у каждого разный. Есть специальные методики, которые помогают тренировать память.
Вот ещё несколько советов, как запомнить формулы
Обязательно делай формулы наглядными: обводи формулу в рамку, пиши её другим цветом. Так будет легче найти в конспекте и запомнить. А лучше выписывай формулы в отдельный блокнот, структурируя их по темам. Помечай, в какого рода задачах та или иная формула пригодится, в чём её особенность. Заведи привычку пополнять список формул. Подобный «дневник наблюдений за формулами» поможет освежить в памяти важную информацию перед контрольной, экзаменом или ЦТ по математике.
Многие школьники ещё вот что делают: когда раздают проштампованные черновики, ты берёшь и сразу же записываешь на них важные формулы, которые тебе тяжело даются. За полчаса до ЦТ ты эти формулы зрительно запомнил, а потом быстренько написал. Это экономит время. Особенно такой лайфхак хорош в тригонометрии. Чем больше знаешь формул, тем лучше.
Дмитрий Судник, преподаватель математики в образовательном центре Адукар
 Заучивание формул похоже на заучивание стихов: вызубрив только слова, прочесть стих выразительно не получится. А вот когда прочувствуешь содержание, научишься правильно расставлять паузы, произведение зазвучит и отложится в памяти надолго
Заучивание формул похоже на заучивание стихов: вызубрив только слова, прочесть стих выразительно не получится. А вот когда прочувствуешь содержание, научишься правильно расставлять паузы, произведение зазвучит и отложится в памяти надолго
Проверяй себя
Нужно постоянно возвращаться к выученному материалу, чтобы не забыть его. Попробуй метод «Две карточки», он подойдёт для запоминания формул приведения, сокращённого умножения, тригонометрических формул. Возьми две стопки карточек разного цвета, на одной напиши левую часть формулы, а на другой — правую. Раздели таким образом все формулы, что тебе нужно запомнить, затем перемешай обе стопки. Тяни по порядку карточку с левой частью формулы и подбирай её продолжение среди «правых» и наоборот.
Карточки хороши и в геометрии
Чтобы запомнить формулы по геометрии, заведи себе карточки по темам («Формулы площади», «Фомулы для треугольника», «Фомулы для квадрата» и т. д.) и записывай в них информацию следующим образом.
Можно фиксировать формулы в отдельном блокноте и всегда был под рукой — как тебе удобно
Будь на позитиве
Если ты учишь что-либо из-под палки, мозг сам желает избавиться от груза знаний. Воспринимай заучивание формул как хорошее упражнение для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужную формулу для решения. И конечно же, решай как можно больше тестов и задач для подготовки к контрольной, экзамену или ЦТ!
ЦТ по математике — это типовые задачи: чем больше тестов решаешь, тем выше шанс встретить что-то похожее на ЦТ. Невозможно подготовиться к ЦТ по одной задаче. Но когда ты прорешал 100 задач, то 101 задача не вызовет затруднений.
Дмитрий Судник, преподаватель математики в образовательном центре Адукар
***
Если материал был для тебя полезен, не забудь поставить «мне нравится» в наших соцсетях ВКонтакте, Instagram, Facebook, ASKfm и поделись постом с друзьями. А мы сделаем ещё больше материалов, которые пригодятся тебе для учёбы.
Перепечатка материалов с сайта adukar.by возможна только с письменного разрешения редакции. [email protected]
adukar.by
Zero To Hero
У меня непростые отношения с матанализом: с одной стороны он демонстрирует всю красоту и мощь математики, а с другой — агонию математического образования.
Математический анализ связывает различные темы в элегантной, но довольно сложной для ума манере. Ближайшая аналогия, которая приходит мне на ум, — Дарвиновская теория эволюции: стоит ее понять, и весь мир видится с позиции выживания. Вы понимаете, почему лекарства привели к резистентным микробам (выживает наиболее приспособленный). Вы понимаете, почему сахар и жир сладкие на вкус (вкус стимулирует потребление высококалорийных продуктов в условиях дефицита резервов организма). И все эти моменты складываются в единую, логическую картину.
Матанализ таким же образом проливает свет на всю систему математики. Не кажется ли вам, что все эти формулы как-то связаны?
Так и есть. Но большинство из нас изучают эти формулы независимо друг от друга. Математический анализ позволяет начать с «длина окружности = 2 * π * r» и вывести остальные формулы для вычисления площади круга, сферы и даже объема шара — древним грекам очень бы пригодился подобный подход.
К сожалению, матанализ олицетворяет собой все трудности в изучении математики. Большинство уроков объясняются на натянутых, неправдоподобных примерах, заумных доказательствах и банальном заучивании, которое напрочь убивает интуицию.
Так действительно не должно происходить.
Математика, искусство и идеи
Кое-что я понял еще со школы: математика — не самая сложная часть математики; самое тяжелое — мотивация к ее освоению. Особенно, умение не терять энтузиазм, несмотря на:
- Преподавателей, больше сконцентрированных на штамповке публикаций и своей карьере, чем на преподавании
- Небеспочвенные опасения, что математика — это сложно, скучно, непопулярно или «не ваш предмет»
- Учебники и учебные планы, больше нацеленные на получение прибыли и хорошую статистику по тестированиям знаний, чем на пояснение сущности предмета.
‘Плач математика’ [pdf] — отличное эссе на эту тему, которое вызвало бурный резонанс среди многих прочитавших его:
«…если бы мне пришлось создавать механизм с единственной целью разрушить природное любопытство ребенка и его любовь к моделированию, вряд ли бы у меня получилось лучше, чем это уже реализовано — у меня бы просто не хватило фантазии, чтобы тягаться с такими бесчувственными, унылыми идеями, которые воплощены в современных методах изучения математики».
Представьте изучение изобразительного искусства так: Детки, никакого рисования в детском садике. Вместо этого, давайте-ка изучим химию лакокрасочных изделий, физику света и анатомию глаза. После 12 лет изучения этих аспектов, если дети (точнее уже подростки) всё еще не возненавидят искусство, они смогут начать рисовать самостоятельно. В конечном итоге, они теперь владеют полноценным фундаментом для того, чтобы начать уважать искусство. Верно?
Также и с поэзией. Представьте изучение этой цитаты (формулы):
«Но главное: будь верен сам себе; Тогда, как вслед за днем бывает ночь, Ты не изменишь и другим.» —Вильям Шекспир, Гамлет
Это элегантный способ сказать «будь собой» (и если это означает непочтительно писать о математике, пусть будет так). Но если бы мы рассматривали поэзию на уроке математики, вместо поиска смысла мы бы занялись подсчётом количества слогов, анализировали пятистопный ямб, разметкой существительных, глаголов и прилагательных.
Математика и поэзия — это как разные способы пояснить, охарактеризовать одно и то же. Формулы — это средства к достижению цели, способ выражения математической истины.
Мы забыли, что математика оперирует идеями, это не машинальное маниппулирование формулами, которые выражают эти идеи.
Ну это всё понятно, так в чем же твоя великая мысль?
Вот, что я не буду делать: я не буду пересказывать уже написанные учебники. Если вам нужны ответы здесь и сейчас, есть масса вебсайтов, видеоуроков и 20-минуток в помощь.
Вместо этого давайте освоим основные положения матанализа. Уравнений недостаточно — я хочу моментов озарения, чтобы вы действительно видели их смысл и понимали язык математики.
Формальный математический язык — это просто способ коммуникации. Графики, информативные анимированные модели и разговор простым языком могут дать больше знаний, чем целая страница заумных доказательств.
Но матанализ — это сложно!
Я думаю, что любой человек сможет понять основные положения матанализа. Нам не обязательно быть поэтами, чтобы наслаждаться произведениями Шекспира.
Вам будет гораздо проще, если вы знаете алгебру и интересуетесь математикой. Не так давно, чтение и письмо были работой специально обученных писцов. А сегодня это может сделать любой 10-летний ребенок. Почему?
Потому что мы этого ожидаем. Ожидания играют огромную роль в развитии возможностей. Так что ожидайте, что матанализ — это просто еще один предмет. Некоторые люди доходят до мельчайших подробностей (писатели/математики). Но остальные из нас могут просто восторгаться происходящим и попытаться его понять. Я бы хотел, чтобы каждый освоил основные понятия матанализа и сказал «Вот это да!».
Так о чем же матанализ?
Некоторые определяют матанализ как «область математики, которая изучает пределы, дифференцирование, интегрирование функций с одной или более переменных». Это определение верно, но оно совсем не полезно для новичков.
Вот мой ход: Матанализ делает с алгеброй то, что алгебра сделала с арифметикой.
- Арифметика — это манипуляция числами (сложение, умножение и т.д.).
- Алгебра находит связи между числами: a2 + b2 = c2 — очень известная связь, описывающая соотношение сторон в прямоугольном треугольнике. Алгебра находит целые наборы чисел — если вы знаете a и b, вы можете вычислить и c.
- Матанализ находит связи между уравнениями: вы можете видеть, как одно уравнение (длина окружности = 2 * π * r) связано с другим (площадь круга = π * r2).
Используя матанализ, мы можем спросить самые разные вопросы:
- Как уравнение растет и сокращается? Наращивается со временем?
- Когда оно достигнет самой высокой/низкой точки?
- Как мы используем переменные, которые постоянно меняются? (Тепло, движение, популяции, …).
- И многое, многое другое!
Алгебра и матанализ решают задачи вместе: матанализ находит новые уравнения, а алгебра их решает. Как эволюция, матанализ расширяет ваше понимание того, как работает матушка-природа.
Пример, пожалуйста
Представим, что мы знаем уравнение длины окружности (2 * π * r), и нам нужно найти площадь. С чего начнем?
Представьте, что заполненный диск круга — это как набор матрешек.
Тут есть два способа нарисовать этот диск:
- Нарисовать окружность и закрасить ее
- Нарисовать набор колец толстым маркером
Количество «пространства» (площадь) должно быть одинаковым в обоих случаях, верно? И сколько пространства занимает кольцо?
Самое большое кольцо имеет радиус «r», и длина окружности кольца вычисляется как 2 * π * r. По мере того, как кольца уменьшаются, окружность также становится меньше, но всё равно сохраняется соотношение 2 * π * текущий радиус. Последнее кольцо больше похоже на булавочную головку, и длину окружности уже не вычислишь.
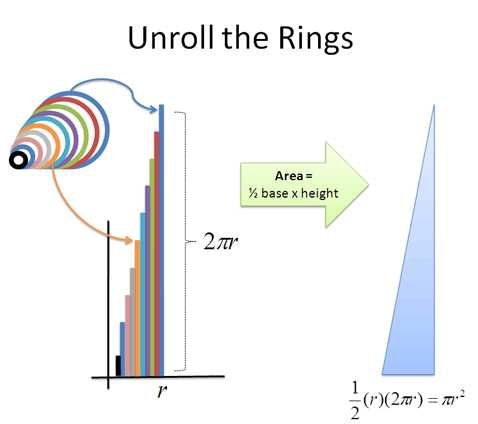
А теперь начинается самое интересное. Давайте раскрутим эти кольца и выровняем их. Что произойдет?
- У нас получится набор линий, который составит зубчатый треугольник. Но если взять более тонкие кольца, то треугольник становится уже менее зубчатым (об этом мы еще поговорим в других статьях).
- С одной стороны будет самое маленькое кольцо (0), а с другой — самое большое (2* π * r)
- Кольца имеют радиусы от 0 до «r». Для каждого возможного радиуса из этого диапазона (от 0 до r), мы просто помещаем раскрученное кольцо на свое место.
- Общая площадь «кольцевого треугольника» = 1/2 основания * высоту = 1/2 * r *(2 * π * r) = π * r2, а это и есть формула поиска площади круга!
Ух ты! Общая площадь колец = площадь треугольника = площадь круга!
(Изображение из Википедии)
Это был простой пример, но вы уловили основную идею? Мы взяли диск, разделили его, и сложили части вместе немного другим путем. Матанализ показал, что диск и кольцо тесно связаны друг с другом: диск — это действительно набор колец. Это очень популярная тема в матанализе: Большие предметы состоят из более мелких предметов. И иногда именно с этими мелкими предметами работается проще и понятнее.
Немного о примерах
Множество примеров в матанализе основано на физике. Это, конечно, замечательно, но бывает сложно их воспринимать: честно, далеко не всегда удается держать в голове разные физические формулы вроде формулы скорости объекта.
Я предпочитаю начать с простых визуальных примеров, потому что именно так и работает наш мозг. Кольцо/круг, которое мы исследовали — вы бы могли смоделировать то же самое из нескольких отрезков трубок разного диаметра: разделить их, выровнять и уложить в грубый треугольник, чтобы убедиться, что математика действительно работает. С простой физической формулой такое вряд ли удастся провернуть.
Немного о математической строгости (для фанатиков этой науки)
Я чувствую, как математики-педанты жгут свои клавиатуры. Поэтому я вставлю всего несколько слов о «строгости». Знаете ли вы, что мы не учим матанализ способами, которыми его открыл Ньютон или Лейбниц? Они использовали интуитивные идеи «флюксии» и «бесконечно малых величин», которые были заменены пределами, потому что «Конечно, это работает на практике. Но работает ли это в теории?».
Мы создали сложные механические модели, чтобы «точно» доказать матанализ, но мы утратили интуитивное восприятие предмета в процессе таких доказательств.
Мы смотрим на сладость сахара с точки зрения химии мозга, вместо того, чтобы пояснять это языком науки «В сахаре много энергии. Ешьте его».
Я не хочу (и не могу) преподавать матанализ студентам или обучать ученых. Но будет ли плохо, если каждый сможет понимать матанализ на том «неточном» уровне, на котором его понимал Ньютон? Чтобы это также изменило мир для вас, как когда-то изменило для него?
Преждевременная концентрация на точности рассредоточивает учеников и делает математику сложной для изучения. Вот хороший пример: число е технически определено пределом, но открыто оно было именно с помощью интуитивной догадки о росте. Натуральный логарифм может выглядеть как интеграл, или время, которому нужно расти. Какие объяснения лучше помогут новичкам?
Давайте немного порисуем от руки, а в химию погрузимся уже по ходу дела. Приятных вычислений.
(P.S: Один любезный читатель создал анимированное слайд-шоу powerpoint, которое помогает презентовать эту идею более наглядно (лучше посмотреть ее в PowerPoint, там будут видны анимации). Спасибо!)
Перевод статьи «A Gentle Introduction To Learning Calculus»
zero2hero.org
Как научиться понимать математику? | Учебный блог
Алгебра, геометрия, высшая математика… Некоторых эти слова заставляют нервно грызть ногти и хвататься за голову. Да, математика действительно требует серьезного подхода и старания, но и не только способность.
Проблема в том, что для многих математика ассоциируется с такими терминами как «дипломная», «курсовая», «контрольная», «семестровая» и другие виды отчетных работ. К счастью, сегодня это совсем не проблема, так как существуют такие сайты, как 5orka.ru, которые помогают справиться с выполнением таких работ. Важно полюбить математику.
Именно постоянная работа и интересные упражнения превратят математику в сплошное удовольствие с интересными задачами и примерами. И не обязательно без понимания сути заучивать формулы и зазубривать теоремы из аксиом, они сами «отложатся» в вашей голове с помощью специальных упражнений на основе математической логики.
Почему не все понимают математику?
Для школьников и студентов с гуманитарным направлением изучения математики может превратиться в сплошной кошмар. Это возникает ввиду отсутствия понимания всей сущности математических законов. Что же тогда делать? Как постичь все тайны математического мира когда все желания изучать эту науку отпали?
Первые шаги для понимания математики
Чтобы научиться понимать математику, нужно начать изучать эту науку заново. Да, нужно изучить все формулы и начальные законы снова, с пониманием и умением объяснить собственными словами. Таким образом, вы будете иметь хорошее математическое основание, которое поможет при дальнейшем изучении и углублении в мир математики. Обязательно спрашивайте у преподавателей или учителей, что вам не ясно, ведь промедление с непонятным материалом как снежный шарик катится по снегу, набирая все больше снега на себя, может привести к плохим последствиям.
Учимся понимать способы решения математических задач
Не менее важным в овладении математики есть и способы решения математических задач. Они бывают разными: от противного, от противоположного, с помощью индукции… Но вы не сможете ими пользоваться, если не поймете сути метода. Именно поэтому вам необходимо сначала ознакомиться с основными методами, понять их, освоить и научиться использовать. Для этого нужно просматривать уже готовые задачи, представленные в учебниках, и логично в них разобраться.
Чтобы научиться понимать математику, старайтесь находить решение задачи собственным путем, а не по шаблону. Ведь каждая задача требует своего подхода и решения. Даже Евклид, основатель геометрии, говорил, что математика не имеет царских путей. Это означает, что для того, чтобы решать задачи и постичь мир математики, нужно иметь только ум, и ни чего более. А решать задачи можно и с помощью начальных формул и логических рассуждений.
Например, не обязательно подносить к квадрату двузначное число с 5 на конце, нужно только воспользоваться специально выведенной формуле. Например число 65. Сначала добавляем первую цифру с единицей, а затем ту первую цифру умножаем на полученное число: 6 * (6 + 1) = 42. Итак, мы получили 42, к которому нужно подставить 25 и вуаля — 4225, а это 65 в квадрате!
Конечно, именно изучение математики требует не только ваших усилий, но и консультации специалистов. В таком случае, вы можете воспользоваться помощью репетитора или онлайн-помощи, предоставляемой талантливыми математиками через программы-мессенджеры.
Поэтому, все в ваших руках! Не забывайте об этом и идите к своей цели!
xn--80ablbaanka7beun6ae4de9e.xn--p1ai
Математические формулы и методы их применения
|
Отношения между объектами…………………………………… |
— 16 — |
|
|
Прямые второго порядка…………………………………………….. |
— 17 — |
|
|
Окружность…………………………………………………………………… |
— 17 — |
|
|
Эллипс……………………………………………………………………………… |
— 17 — |
|
|
Гипербола……………………………………………………………………….. |
— 17 — |
|
|
Парабола………………………………………………………………………… |
— 18 — |
|
|
Системы координат…………………………………………………….. |
— 18 — |
|
|
Приложения……………………………………………………………………. |
— 18 — |
|
|
Аналитическая геометрия (R3)……………………………………….. |
— 19 — |
|
|
Плоскость………………………………………………………………………. |
— 19 — |
|
|
Прямая……………………………………………………………………………. |
— 19 — |
|
|
Расстояния…………………………………………………………………….. |
— 19 — |
|
|
Вектор…………………………………………………………………………….. |
— 20 — |
|
|
Отношения между объектами…………………………………… |
— 20 — |
|
|
Приложения……………………………………………………………………. |
— 21 — |
|
|
Матрицы……………………………………………………………………………… |
— 22 — |
|
|
Операции над матрицами…………………………………………… |
— 22 — |
|
|
Свойства определителей…………………………………………….. |
— 22 — |
|
|
Операции над определителями…………………………………… |
— 23 — |
|
|
Обратная матрица………………………………………………………. |
— 23 — |
|
|
Производные функций………………………………………………………… |
— 24 — |
|
|
Определение производной…………………………………………….. |
— 24 — |
|
|
Таблица производных……………………………………………………. |
— 24 — |
|
|
Правила дифференцирования……………………………………… |
— 25 — |
|
|
Логарифмическая производная…………………………………… |
— 25 — |
|
|
Параметрические функции…………………………………………. |
— 26 — |
|
|
Приложения……………………………………………………………………. |
— 26 — |
|
|
Пределы………………………………………………………………………………… |
— 27 — |
|
|
Свойства пределов………………………………………………………… |
— 27 — |
|
|
Замечательные (классические) пределы …………………… |
— 27 — |
|
|
Эквивалентность бесконечно-малых………………………… |
— 28 — |
|
|
Сравнение бесконечно-малых………………………………………. |
— 28 — |
|
|
Способы раскрытия неопределенностей………………….. |
— 28 — |
|
|
Исследование графика функции……………………………………….. |
— 29 — |
|
|
Дифференциальное исчисление…………………………………………. |
— 30 — |
|
|
Основные понятия………………………………………………………… |
— 30 — |
|
|
Интегралы…………………………………………………………………………… |
— 31 — |
|
|
Таблица интегралов…………………………………………………….. |
— 31 — |
|
|
Основные правила…………………………………………………………. |
— 32 — |
|
|
Подстановки Эйлера…………………………………………………….. |
— 33 — |
|
|
Универсальная тригонометрическая подстановка.. |
— 34 — |
|
|
Метод неопределённых коэффициентов…………………… |
— 34 — |
|
|
Андрей Ивашов |
— 58 — |
studfiles.net
Как понять математику?
Вопрос, как понять математику, чаще возникает у людей с гуманитарным складом ума. Проблема состоит в том, что математику необходимо именно понять, уловить суть, а заучивание формул и теорем, без первой составляющей становится бесполезным делом. При систематических занятиях даже люди, которым математика дается с трудом, могут научиться логически думать, сопоставлять и просчитывать на несколько шагов вперед, что просто необходимо при решении математических задач.
Если ребенок не понимает математику, помогите ему разбираться в сути явлений, где и откуда что-то берется, как это взаимосвязано, как получить то, чего не достает.
Вот инструкция для всех тех, кто ищет ответ на вопрос — не понимаю математику, что делать?
- Начните изучать материал с самого начала, так как в точных науках невозможно понять что-либо без знания предыдущего материала. С самого первого урока разберитесь в формулировках теорем и правил так, чтобы для вас эти строчки не были пустым звуком. Читая правило, пишите на бумаге из чего оно состоит, для чего необходимо. Так, возможно чертите схемки или пишите тезисы до тех пор, пока точно не будете уверенны в том, что вам все понятно. Не стесняйтесь переспрашивать учителя, если что-либо не уловили или не ясно. Потеряв нить рассуждения, придется начинать все заново.
- Если внимательно прочитать несколько тем из алгебры или геометрии, можно заметить, что постоянно применяется несколько методов доказательств – метод от противного или метод индукции. Запомните их раз и навсегда. Не допускайте пробелов в знаниях, так как недопонимание одной темы закрывает вам дверь в понимание следующей. Часто математику не понимают из-за слабых начальных знаний.
- Основоположник геометрии Евклид говорил, что в математике нет царских путей. Универсальных легких способов для понимания математических законов нет. Вашим спасением будет регулярные занятия, нахождение решений по готовым формулам, развитее логики, редкое использ
elhow.ru
