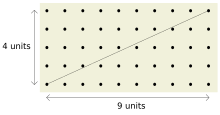
В «лесу», составленном на координатной плоскости из точек с целочисленными координатами, из начала координат «видны» только «деревья» со взаимно простыми координатами.
Взаимно простые числа — целые числа, не имеющие никаких общих делителей, кроме ±1. Равносильное определение[1]: целые числа взаимно просты, если их наибольший общий делитель (НОД) равен 1.
Например, взаимно просты числа 14 и 25, так как у них нет общих делителей; но числа 15 и 25 не взаимно просты, так как у них имеется общий делитель 5.
Для указания взаимной простоты чисел 


Это понятие было введено в книге VII «Начал» Евклида. Для определения того, являются ли два числа взаимно простыми, можно использовать алгоритм Евклида.
Понятие взаимной простоты естественным образом обобщается на любые евклидовы кольца[⇨].
Попарно взаимно простые числа[править | править код]
Если в наборе целых чисел любые два числа взаимно просты, то такие числа называются попарно взаимно простыми (или просто попарно простыми[3]). Для двух чисел понятия «взаимно простые» и «попарно простые» совпадают, для более чем двух чисел свойство попарной простоты более сильно, чем ранее определённое свойство взаимной простоты (в совокупности) — попарно простые числа будут и взаимно простыми, но обратное неверно[3]. Примеры:
- 8, 15 — не простые, но взаимно простые.
- 6, 8, 9 — взаимно простые (в совокупности) числа, но не попарно простые.
- 8, 15, 49 — попарно простые и взаимно простые (в совокупности).
Если числа 
- НОД
НОД
НОД
НОД
,
- где НОД – наибольший общий делитель.
Свойства[править | править код]
Все упомянутые в этом разделе числа подразумеваются целыми, если не оговорено иное.
- Дробь является несократимой тогда и только тогда, когда её числитель и знаменатель взаимно просты.
Таблица взаимной простоты чисел до 30[править | править код]
В каждой клетке стоит наибольший общий делитель её координат, и соответствующие взаимно-простым парам координат единицы выделены тёмным. Из описанного выше свойства следует, что средняя плотность тёмных клеток при расширении таблицы до бесконечности станет равна 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 |
| 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 |
| 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 |
| 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 |
| 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 |
| 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 |
| 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 |
| 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 12 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 4 | 1 | 6 |
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 2 | 1 | 2 | 1 | 2 | 7 | 2 | 1 | 2 | 1 | 2 | 1 | 14 | 1 | 2 | 1 | 2 | 1 | 2 | 7 | 2 | 1 | 2 | 1 | 2 | 1 | 14 | 1 | 2 |
| 15 | 1 | 1 | 3 | 1 | 5 | 3 | 1 | 1 | 3 | 5 | 1 | 3 | 1 | 1 | 15 | 1 | 1 | 3 | 1 | 5 | 3 | 1 | 1 | 3 | 5 | 1 | 3 | 1 | 1 | 15 |
| 16 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 16 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 |
| 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 18 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 9 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 18 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 9 | 2 | 1 | 6 |
| 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 20 | 1 | 2 | 1 | 4 | 5 | 2 | 1 | 4 | 1 | 10 | 1 | 4 | 1 | 2 | 5 | 4 | 1 | 2 | 1 | 20 | 1 | 2 | 1 | 4 | 5 | 2 | 1 | 4 | 1 | 10 |
| 21 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 1 | 3 | 1 | 1 | 3 | 1 | 7 | 3 | 1 | 1 | 3 | 1 | 1 | 21 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 1 | 3 |
| 22 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 11 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 22 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 24 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 8 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 8 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 24 | 1 | 2 | 3 | 4 | 1 | 6 |
| 25 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 25 | 1 | 1 | 1 | 1 | 5 |
| 26 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 13 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 26 | 1 | 2 | 1 | 2 |
| 27 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 27 | 1 | 1 | 3 |
| 28 | 1 | 2 | 1 | 4 | 1 | 2 | 7 | 4 | 1 | 2 | 1 | 4 | 1 | 14 | 1 | 4 | 1 | 2 | 1 | 4 | 7 | 2 | 1 | 4 | 1 | 2 | 1 | 28 | 1 | 2 |
| 29 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 29 | 1 |
| 30 | 1 | 2 | 3 | 2 | 5 | 6 | 1 | 2 | 3 | 10 | 1 | 6 | 1 | 2 | 15 | 2 | 1 | 6 | 1 | 10 | 3 | 2 | 1 | 6 | 5 | 2 | 3 | 2 | 1 | 30 |
Вариации и обобщения[править | править код]
Понятия простого числа, наибольшего общего делителя и взаимно простых чисел естественно обобщаются на произвольные евклидовы кольца, например, на кольцо многочленов или гауссовы целые числа. Обобщением понятия простого числа является «неприводимый элемент». Данное выше определение взаимно простых чисел не годится для произвольного евклидова кольца, поскольку в кольце могут быть делители единицы; в частности, НОД определяется с точностью до умножения на делитель единицы. Поэтому определение взаимно простых чисел следует модифицировать[6].
Элементы евклидова кольца называются взаимно простыми, если множество их наибольших общих делителей содержит только делители единицы.
Равносильные формулировки[6]:
Имеет также место лемма Евклида.
Практическое применение[править | править код]
Свойство взаимной простоты не только играет важную роль в теории чисел и коммутативной алгебре, но имеет ряд важных практических приложений, в частности, число зубьев на звёздочках и число звеньев цепи в цепной передаче стремятся делать взаимно простыми, что обеспечивает равномерность износа: каждый зуб звёздочки будет поочерёдно работать со всеми звеньями цепи.
Примечания[править | править код]
- ↑ 1 2 Взаимно простые числа. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 690.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — С. 139. — 703 с. — ISBN 5-03-001793-3.
- ↑ 1 2 Михелович, 1967, с. 28.
- ↑ Нестеренко Ю. В. Теория чисел. — М.: Издательский центр «Академия», 2008. — С. 40. — 272 с. — ISBN 9785769546464.
- ↑ Михелович, 1967, с. 64.
- ↑ 1 2 Ларин С. В. Алгебра и теория чисел. Группы, кольца и поля: учеб. пособие для академического бакалавриата. — 2-е изд. — М.: Юрайт, 2018. — С. 92—93. — 160 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-05567-2.
Литература[править | править код]
- Взаимно простые числа // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.
- Михелович Ш. Х. Теория чисел. — 2-е изд. — М.: Высшая школа, 1967. — 336 с.
В этом статье мы расскажем о том, что такое взаимно простые числа. В первом пункте сформулируем определения для двух, трех и более взаимно простых чисел, приведем несколько примеров и покажем, в каких случаях два числа можно считать простыми по отношению друг к другу. После этого перейдем к формулировке основных свойств и их доказательствам. В последнем пункте мы поговорим о связанном понятии – попарно простых числах.
Что такое взаимно простые числа
Взаимно простыми могут быть как два целых числа, так и их большее количество. Для начала введем определение для двух чисел, для чего нам понадобится понятие их наибольшего общего делителя. Если нужно, повторите материал, посвященный ему.
Взаимно простыми будут два таких числа a и b, наибольший общий делитель которых равен 1, т.е. НОД (a, b) =1.
Из данного определения можно сделать вывод, что единственный положительный общий делитель у двух взаимно простых чисел будет равен 1. Всего два таких числа имеют два общих делителя – единицу и минус единицу.
Какие можно привести примеры взаимно простых чисел? Например, такой парой будут 5 и 11. Они имеют только один общий положительный делитель, равный 1, что является подтверждением их взаимной простоты.
Если мы возьмем два простых числа, то по отношению друг к другу они будут взаимно простыми во всех случаях, однако такие взаимные отношения образуются также и между составными числами. Возможны случаи, когда одно число в паре взаимно простых является составным, а второе простым, или же составными являются они оба.
Это утверждение иллюстрирует следующий пример: составные числа -9 и 8 образуют взаимно простую пару. Докажем это, вычислив их наибольший общий делитель. Для этого запишем все их делители (рекомендуем перечитать статью о нахождении делителей числа). У 8 это будут числа ±1, ±2, ±4, ±8, а у 9 – ±1, ±3, ±9. Выбираем из всех делителей тот, что будет общим и наибольшим – это единица. Следовательно, если НОД (8, −9)=1, то 8 и -9 будут взаимно простыми по отношению друг к другу.
Взаимно простыми числами не являются 500 и 45, поскольку у них есть еще один общий делитель – 5 (см. статью о признаках делимости на 5). Пять больше единицы и является положительным числом. Другой подобной парой могут быть -201 и 3, поскольку их оба можно разделить на 3, на что указывает соответствующий признак делимости.
На практике довольно часто приходится определять взаимную простоту двух целых чисел. Выяснение этого можно свести к поиску наибольшего общего делителя и сравнению его с единицей. Также удобно пользоваться таблицей простых чисел, чтобы не производить лишних вычислений: если одно из заданных чисел есть в этой таблице, значит, оно делится только на единицу и само на себя. Разберем решение подобной задачи.
Условие: выясните, являются ли взаимно простыми числа 275 и 84.
Решение
Оба числа явно имеют больше одного делителя, поэтому сразу назвать их взаимно простыми мы не можем.
Вычисляем наибольший общий делитель, используя алгоритм Евклида: 275=84·3+23, 84=23·3+15, 23=15·1+8, 15=8·1+7, 8=7·1+1, 7=7·1.
Ответ: поскольку НОД (84, 275) =1, то данные числа будут взаимно простыми.
Как мы уже говорили раньше, определение таких чисел можно распространить и на случаи, когда у нас есть не два числа, а больше.
Взаимно простыми целые числа a1, a2, …, ak, k>2 будут тогда, когда они имеют наибольший общий делитель, равный 1.
Иными словами, если у нас есть набор некоторых чисел с наибольшим положительным делителем, большим 1, то все эти числа не являются по отношению друг к другу взаимно обратными.
Возьмем несколько примеров. Так, целые числа −99, 17 и −27 – взаимно простые. Любое количество простых чисел будет взаимно простым по отношению ко всем членам совокупности, как, например, в последовательности 2, 3, 11, 19, 151, 293 и 667. А вот числа 12, −9, 900 и −72 взаимно простыми не будут, потому что кроме единицы у них будет еще один положительный делитель, равный 3. То же самое относится к числам 17, 85 и 187: кроме единицы, их все можно разделить на 17.
Обычно взаимная простота чисел не является очевидной с первого взгляда, этот факт нуждается в доказательстве. Чтобы выяснить, будут ли некоторые числа взаимно простыми, нужно найти их наибольший общий делитель и сделать вывод на основании его сравнения с единицей.
Условие: определите, являются ли числа 331, 463 и 733 взаимно простыми.
Решение
Сверимся с таблицей простых чисел и определим, что все три этих числа в ней есть. Тогда их общим делителем может быть только единица.
Ответ: все эти числа будут взаимно простыми по отношению друг к другу.
Условие: приведите доказательство того, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.
Решение
Начнем с выявления их наибольшего общего делителя, после чего убедимся, что он не равен 1. Поскольку у отрицательных чисел те же делители, что и у соответствующих положительных, то НОД (−14, 105, 2 107, −91) =НОД (14, 105, 2 107, 91). Согласно правилам, которые мы привели в статье о нахождении наибольшего общего делителя, в данном случае НОД будет равен семи.
Ответ: семь больше единицы, значит, взаимно простыми эти числа не являются.
Основные свойства взаимно простых чисел
Такие числа имеют некоторые практически важные свойства. Перечислим их по порядку и докажем.
Если разделить целые числа a и b на число, соответствующее их наибольшему общему делителю, мы получим взаимно простые числа. Иначе говоря, a: НОД (a, b) и b: НОД (a, b) будут взаимно простыми.
Это свойство мы уже доказывали. Доказательство можно посмотреть в статье о свойствах наибольшего общего делителя. Благодаря ему мы можем определять пары взаимно простых чисел: достаточно лишь взять два любых целых числа и выполнить деление на НОД. В итоге мы должны получить взаимно простые числа.
Необходимым и достаточным условием взаимной простоты чисел a и b является существование таких целых чисел u0 и v0, при которых равенство a·u0+b·v0=1 будет верным.
Начнем с доказательства необходимости этого условия. Допустим, у нас есть два взаимно простых числа, обозначенных a и b. Тогда по определению этого понятия их наибольший общий делитель будет равен единице. Из свойств НОД нам известно, что для целых a и b существует соотношение Безу a·u0+b·v0=НОД (a, b). Из него получим, что a·u0+b·v0=1. После этого нам надо доказать достаточность условия. Пусть равенство a·u0+b·v0=1 будет верным, в таком случае, если НОД (a, b) делит и a, и b, то он будет делить и сумму a·u0+b·v0, и единицу соответственно (это можно утверждать, исходя из свойств делимости). А такое возможно только в том случае, если НОД (a, b)=1, что доказывает взаимную простоту a и b.
В самом деле, если a и b являются взаимно простыми, то согласно предыдущему свойству, будет верным равенство a·u0+b·v0=1. Умножаем обе его части на c и получаем, что a·c·u0+b·c·v0=c. Мы можем разделить первое слагаемое a·c·u0+b·c·v0 на b, потому что это возможно для a·c, и второе слагаемое также делится на b, ведь один из множителей у нас равен b. Из этого заключаем, что всю сумму можно разделить на b, а поскольку эта сумма равна c, то c можно разделить на b.
Если два целых числа a и b являются взаимно простыми, то НОД (a·c, b)=НОД (c, b).
Докажем, что НОД (a·c, b) будет делить НОД (c, b), а после этого – что НОД (c, b) делит НОД (a·c, b), что и будет доказательством верности равенства НОД (a·c, b)=НОД (c, b).
Поскольку НОД (a·c, b) делит и a·c и b, а НОД(a·c, b) делит b, то он также будет делить и b·c. Значит, НОД (a·c, b) делит и a·c и b·c, следовательно, в силу свойств НОД он делит и НОД (a·c, b·c), который будет равен c·НОД (a, b)=c. Следовательно, НОД (a·c, b) делит и b и c, следовательно, делит и НОД (c, b).
Также можно сказать, что поскольку НОД (c, b) делит и c, и b, то он будет делить и c, и a·c. Значит, НОД (c, b) делит и a·c и b, следовательно, делит и НОД (a·c, b).
Таким образом, НОД (a·c, b) и НОД (c, b) взаимно делят друг друга, значит, они являются равными.
Если числа из последовательности a1, a2, …, ak будут взаимно простыми по отношению к числам последовательности b1, b2, …, bm (при натуральных значениях k и m), то их произведения a1·a2·…·ak и b1·b2·…·bm также являются взаимно простыми, в частности, a1=a2=…=ak=a и b1=b2=…=bm=b, то ak и bm – взаимно простые.
Согласно предыдущему свойству, мы можем записать равенства следующего вида: НОД (a1·a2·…·ak, bm) =НОД (a2·…·ak, bm) =…=НОД (ak, bm) =1. Возможность последнего перехода обеспечивается тем, что ak и bm взаимно просты по условию. Значит, НОД (a1·a2·…·ak, bm) =1.
Обозначим a1·a2·…· ak=A и получим, что НОД (b1·b2·…· bm, a1·a2·…·ak) =НОД (b1·b2·…· bm, A)= НОД (b2·…·b·bm, A)=… =НОД (bm, A) =1. Это будет справедливым в силу последнего равенства из цепочки, построенной выше. Таким образом, у нас получилось равенство НОД (b1·b2·…·bm, a1·a2·…·ak) =1, с помощью которого можно доказать взаимную простоту произведений a1·a2·…·ak и b1·b2·…·bm
Это все свойства взаимно простых чисел, о которых бы мы хотели вам рассказать.
Понятие попарно простых чисел
Зная, что из себя представляют взаимно простые числа, мы можем сформулировать определение попарно простых чисел.
Попарно простые числа – это последовательность целых чисел a1, a2, …, ak, где каждое число будет взаимно простым по отношению к остальным.
Примером последовательности попарно простых чисел может быть 14, 9, 17, и −25. Здесь все пары (14 и 9, 14 и 17, 14 и −25, 9 и 17, 9 и −25, 17 и−25) взаимно просты. Отметим, что условие взаимной простоты является обязательным для попарно простых чисел, но взаимно простые числа будут попарно простыми далеко не во всех случаях. Например, в последовательности 8, 16, 5 и 15 числа не являются таковыми, поскольку 8 и 16 не будут взаимно простыми.
Также следует остановиться на понятии совокупности некоторого количества простых чисел. Они всегда будут и взаимно, и попарно простыми. Примером может быть последовательность 71, 443, 857, 991. В случае с простыми числами понятия взаимной и попарной простоты будут совпадать.
Взаимно простые числа


4.5
Средняя оценка: 4.5
Всего получено оценок: 184.
4.5
Средняя оценка: 4.5
Всего получено оценок: 184.
Взаимно простые числа тема достаточно сложная тема 6 класса математики. Как и простые числа, тема взаимно простых чисел используется для сложения и вычитания дробей. Чтобы не допускать ошибок в этой теме разберемся в вопросе подробнее.
Простые числа
Что такое простое число? Простое число делится только на единицу и на само себя. Например, число 13 является простым, так как нацело делится только на 1 и на 13. Секрет в том, что практически каждое число можно разделить на другое число. Но в простых числах важно именно деление нацело, дробные частные и деление с остатком не рассматривается.
Простые числа в знаменателях дробей означают, что для нахождения общего знаменателя нужно перемножить эти числа между собой. Разложить простые числа на множители невозможно. Поэтому НОД двух простых чисел это их произведение.
Числа, которые содержат в себе больше двух множителей, то есть делятся на несколько чисел, называются сложными. Сложные числа состоят из перемноженных простых.
Взаимно простые числа
Взаимно простыми числами называются числа, наибольший общий делитель которых равен единицы. Доказать факт того, что числа являются взаимно простыми можно только с помощью разложения чисел на простые множители. Если у чисел нет общих множителей, кроме 1, то они будут взаимно простыми.
При этом сами по себе взаимно простые числа могут быть сложными. Важен именно НОД двух чисел.
Нужно учитывать, что взаимно простыми могут быть не только два числа, но и 3, 4, 10 – любое множество чисел может быть взаимно простым.
Как определить взаимно простые числа?
Для того чтобы определить взаимно простые числа, можно воспользоваться двумя алгоритмами:
- Разложить каждое из чисел на множители и искать общие простые множители. Если такие есть, то числа не являются взаимно простыми. Если общих множителей нет, числа можно считать взаимно простыми.
- Делить каждое из чисел поочередно на простые множители. Этот способ проще в исполнении, так как не требует большой внимательности и сосредоточенности. Но такая проверка не подойдет для больших чисел, слишком долгой может получится проверка. Поэтому более надежным будет использовать первый вариант.
Относительно друг друга два простых числа всегда будут взаимно простыми. А если одно из чисел, делится на другое нацело, то эти числа точно не являются взаимно простыми.
Пример
Определим, являются ли взаимно простыми числа 1729 и 282
Определение начинается с разложения на множители:
1729=7*13*19
282=2*3*47
Обратите внимание, что для разложения таких чисел придется использовать метод перебора. Согласно таблице простых чисел каждый множитель проверяется, после чего деление продолжается. Подбирать множители нужно от маленьких чисел к большим, то есть от 2 и выше.
Как видно, общих множителей у двух чисел нет. Это значит, что числа можно считать взаимно простыми. Не нужно пугаться, если среди множителей попадаются достаточно большие числа. Среди учеников существует миф, что простые числа редко бывают больше 20, это не так. Просто такие числа проще использовать в задачах, чтобы набить руку. На экзамене или в контрольной сложность числа для разложения может быть абсолютно любой

Что мы узнали?
Мы поговорили о простых числах. Выяснили, что такое взаимно простые числа и обговорили некоторые их свойства. Привели примеры взаимно простых чисел. Обговорили неправильные мнения по поводу простых и взаимно простых чисел.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Ольга Оль
8/10
-

Валентина Дашинова
8/10
-

Саша Романов
7/10
-

Захар Забанов
10/10
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 184.
А какая ваша оценка?
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Простые и составные числа
Определение 1
Натуральное число $p$ называется простым числом, если у него только $2$ делителя: $1$ и оно само.
Делителем натурального числа $a$ называют натуральное число, на которое исходное число $a$ делится без остатка.
Пример 1
Найти делители числа $6$.
Решение: Нам надо найти все числа, на которые заданное число $6$ делится без остатка. Это будут числа: $1,2,3, 6$. Значит делителем числа $6$ будут числа $1,2,3,6.$
Ответ: $1,2,3,6$.
Значит, для того, чтобы найти делители числа надо найти все натуральные числа, на которые данное делится без остатка. Нетрудно заметить, что число $1$ будет являться делителем любого натурального числа.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Определение 2
Составным называют число, у которого кроме единицы и самого себя есть другие делители.
Примером простого числа может являться число $13$, примером составного число $14.$
Замечание 1
Число $1$ имеет только один делитель-само это число, поэтому его не относят ни к простым, ни к составным.
Взаимно простые числа
Определение 3
Взаимно простыми числами называются те, у которых НОД равен $1$.Значит для выяснения будут ли являться числа взаимно простыми необходимо найти их НОД и сравнить его с $1$.
Попарно взаимно простые
Определение 4
Если в наборе чисел любые два взаимно просты, то такие числа называются попарно взаимно простыми. Для двух чисел понятия «взаимно простые» и «попарно взаимно простые» совпадают.
«Взаимно простые числа, их свойства» 👇
Пример 2
$8, 15$ – не простые, но взаимно простые.
$6, 8, 9$ – взаимно простые числа, но не попарно взаимно простые.
$8, 15, 49$ – попарно взаимно простые.
Как мы видим, для того, чтобы определить являются ли числа взаимно простыми, необходимо сначала разложить их на простые множители. Обратим внимание на то, как правильно это сделать.
Разложение на простые множители
Например, разложим на простые множители число $180$:
$180=2cdot 2cdot 3cdot 3cdot 5$
Воспользуемся свойством степеней, тогда получим,
$180=2^2cdot 3^2cdot 5$
Такая запись разложения на простые множители называется канонической, т.е. для того чтобы разложить в канонической форме число на множители необходимо воспользоваться свойством степеней и представить число в виде произведения степеней с разными основаниями
Каноническое разложение натурального числа в общем виде
Каноническое разложение натурального числа в общем виде имеет вид:
$m=p^{n1}_1cdot p^{n2}_2cdot dots dots ..cdot p^{nk}_k$
где $p_1,p_2dots dots .p_k$- простые числа, а показатели степеней- натуральные числа.
Представление числа в виде канонического разложения на простые множества облегчает нахождение наибольшего общего делителя чисел, и выступает как следствие доказательства или определения взаимно простых чисел.
Пример 3
Найти наибольший общий делитель чисел $180$ и $240$.
Решение: Разложим числа на простые множества с помощью канонического разложения
$180=2cdot 2cdot 3cdot 3cdot 5$, тогда $180=2^2cdot 3^2cdot 5$
$240=2cdot 2cdot 2cdot 2cdot 3cdot 5$, тогда $240=2^4cdot 3cdot 5$
Теперь найдем НОД этих чисел, для этого выберем степени с одинаковым основанием и с наименьшим показателем степени, тогда
$НОД (180;240)= 2^2cdot 3cdot 5=60$
Составим алгоритм нахождения НОД с учетом канонического разложения на простые множители.
Чтобы найти наибольший общий делитель двух чисел с помощью канонического разложения, необходимо:
- разложить числа на простые множители в каноническом виде
- выбрать степени с одинаковым основанием и с наименьшим показателем степени входящих в состав разложения этих чисел
- Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
Пример 4
Определить, будут ли простыми, взаимно простыми числами числа $195$ и $336$.
Решение: Воспользуемся для разложения на множители каноническим разложением:
-
$195=3cdot 5cdot 13$
$336=2cdot 2cdot 2cdot 2cdot 3cdot 7=2^4cdot 3cdot 5$
-
$НОД (195;336) =3cdot 5=15$
Мы видим, что НОД этих чисел отличен от $1$, значит числа не взаимно простые. Также мы видим, что в состав каждого из чисел входят множители, помимо $1$ и самого числа, значит простыми числа так же являться не будут, а будут являться составными.
Пример 5
Определить, будут ли простыми, взаимно простыми числами числа $39$ и $112$.
Решение: Воспользуемся для разложения на множители каноническим разложением:
-
$39=3cdot 13$
$112=2cdot 2cdot 2cdot 2cdot 7=2^4cdot 7$
-
$НОД (39;112)=1$
Мы видим, что НОД этих чисел равен $1$, значит числа взаимно простые. Также мы видим, что в состав каждого из чисел входят множители, помимо $1$ и самого числа, значит простыми числа так же являться не будут, а будут являться составными.
Пример 6
Определить будут ли простыми, взаимно простыми числами числа $883$ и $997$.
Решение: Воспользуемся для разложения на множители каноническим разложением:
-
$883=1cdot 883$
$997=1cdot 997$
-
$НОД (883;997)=1$
Мы видим, что НОД этих чисел равен $1$, значит числа взаимно простые. Также мы видим, что в состав каждого из чисел входят только множители, равные $1$ и самому числу, значит числа будут являться простыми.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Главные понятия
Чтобы доказать, что числа взаимно простые (ВПЧ), учитываются их свойства. Запись считается правдивой, если выполняется одно из следующих условий: значение НОД равно 1, в задачах используются попарно ВПЧ. Чтобы понять слово «делитель», рассматривается конкретный пример: у 24 и 54 этот показатель равен 6. НОД может являться то число, на которое делятся без остатка m и n.
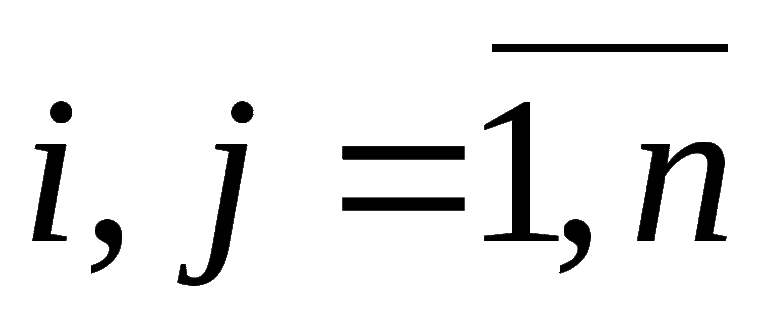
Показатель существует, и он определён, если значение m или n отлично от нуля. Понятие записывается различным набором символов. Рекомендуется следовать следующими записями:
- (m, n);
- gcd (m, n).
НОД (m, n) делится на все общие делители m и n. Если соблюдается условие для а: НОД (a, b)(a, b) и для b: НОД (a, b)(a, b), значит a и b — ВПЧ. С помощью такого свойства легко определяются подходящие пары.
Составные цифры
Два числа относительно друг друга будут взаимно простыми всегда. Аналогичные отношения формируются между составными цифрами. Возможно, что из пары m или n одно — составное, а другое — простое, либо две цифры составные (натуральные числа, у которых есть больше двух делителей). Чтобы подтвердить каноническое утверждение, рассматривается пара из 9 и 88. Её простота доказывается путём вычисления НОД.

Разложение 88: ±1, ±2, ±4, ±8±1, ±2, ±4, ±8. НОД (9): ±1, ±3, ±9±1, ±3, ±9. Из двух вариантов выбираются общие цифры, а из списка определяется самая большая. Из полного перечня подходит единица.
На практике часто определяется ВПЧ двух целых цифр. Алгоритм решения задач заключается в поиске НОД, его сравнении с единицей. Чтобы быстро и правильно найти пару, используется таблица, в которой есть числа, кратные одному и сами себе.
Описание нескольких групп признаков делимости (ПД) неизвестной а:
- ПД для 2, 4 вычисляется по последней цифре (самый маленький делитель равен двум).
- ПД на 3, 37 зависит от суммы цифр, из которых состоит число.
- Признак для 7 определяется после нахождения множителя, попарной суммы либо выполнения иных действий над цифрами а.
- ПД для 6, 12, 14. Основывается на иных признаках.
Задачи и доказательства
Числа a1, a2, …, akу, у которых есть положительный НОД, больший 11, не являются между собой взаимно обратными. Пример с последующей проверкой: 99, 17−99, 17 и −27−27 — простые. Любое количество цифр будет ВПЧ по отношению к другим членам совокупности. Но 12, −9, 90012, −9, 900 и −72−72 к этой категории не относятся.
Первое задание
Нужно найти число из 4 цифр, кратное 15. Это не дробь, знаменателя нет, но произведение составляющих равняется 60. Решение: чтобы результат делился на 15 без остатка, он должен делиться на 3 и 5. Из предполагаемого списка вычёркивается нуль, так как произведение бы равнялось 0, что невозможно. Можно прийти к выводу, что последняя цифра результата — 5.

Известно, что в ответе должно быть четыре цифры, из которых одна уже известна. Нужно найти оставшиеся три, которые находятся в ряду перед пятёркой, а при их умножении получается 12. Проверка предположения: 60:5=12. Полученный результат легко представить в виде нескольких вариантов со следующими тремя множителями:
- 1, 3 и 4;
- 1, 2 и 6;
- 2, 2 и 3.
По условию задачи, результат должен делиться на 15. Поэтому ответ будет состоять из трёх вариантов: 3225, 2325 и 2235.
Второй пример
Из 181615121 нужно зачеркнуть 3 цифры так, чтобы результат был кратным 12. Множители делителя: 3 и 4. Если их вычеркнуть, заданное число разделится на три и четыре, что объясняется их ПД:
- M кратно 4, если последние две цифры равны нулю либо их сумма делится на четыре без остатка.
- Если сумма составляющих цифр делится на три, тогда и само число кратно трём.
Учитывая ПД на 4, можно прийти к выводу, что последние две цифры из заданного числа не делятся на четыре. Поэтому из 181615121 вычёркивается единица.
Чтобы разделить 181615121 на три, необходимо просуммировать все составляющие, разделив на 3. Результат суммы равен 25 (3х8). Так как условие выполняется, вычеркивается последняя единица.
Воспользовавшись признаками делимости на 3 и 4, можно составить следующие уравнения:
- 25 = 3×8 + 1. Если вычеркнуть один, условия задачи не будут соблюдены, так как нужно удалить ещё две цифры.
- 25 = 3×7 + 4. Не подходит, так как при сложении не получается 4.
- 25 = 3×6 + 7. Если вычеркнуть шестую цифру либо единицу, кроме последней, сумма двух удалённых из списка будет равна семи.
Ответ: 181512, 811512 либо 181152.
Третье и четвёртое задания
Пример 3: необходимо определить шестизначное число, для записи которого используются 0 и 6, а также оно делится на 90. Решение: составляется уравнение 90 = 10х9. Результат делится на 9 и 10. В конце находится нуль, а сумма составных цифр делится на девять. Для записи используются три шестёрки, так как 3 х 6=18, а 18 кратно 9. Ответы: 666000, 660600, 606060, 600660.

Пример 4: нужно определить четырёхзначное число, которое делится на 45 без остатка. Все составные цифры разные и нечётные. Решение: следует составить уравнение с учётом условия задачи. Так как 45 = 9х5, то результат делится на пять и на девять. Одновременно он должен оканчиваться на 5, так как нуль считается чётным. Первые три цифры: 1, 3, 7, 9. Из списка выбираются те три числа, которые в сумме с пятёркой делятся на 9. К ним относятся: 1, 3, 9 и 5. Ответы: 9135, 3915,1935, 1395, 3195.
В условиях некоторых задач говорится о попарно простых числах (ППЧ). Понятие распространяется на последовательность целых цифр a1, a2, …, aka1, a2, …, ak, где каждая взаимно простая относительно других. Пример последовательности: 14, 9, 1714, 9, 17, и −25−25. Любая пара из списка будет взаимно простой. Последнее условие считается обязательным для ППЧ, но взаимно простые попарны не в каждом случае.
Другое понятие, которое встречается в задачах на рассматриваемую тему — совокупность ПЧ. Такие цифры всегда попарно и взаимно простые. Пример последовательности: 1, 443, 857, 99171, 443, 857, 991. У любой такой последовательности понятия попарности и взаимности совпадают.

