Как найти что либо в единицах

Как найти что либо в единицах

Опубликовано:

22 марта 2021, 15:23

Сантиметровая лента вокруг яблока
Единицы измерения: Freepick

Какие существуют единицы измерения и для чего они нужны? Люди часто используют в оценках числа, а потом сравнивают их. Меры величин помогают сделать этот процесс одинаковым для всех. Вот почему школьники по всему миру изучают одни и те же единицы измерения.

Меры длины

Величинами называют все, что поддается измерению. Так говорят о длине, площади, объеме, массе, времени, скорости. Величины — результат измерений, число, выраженное в определенных единицах. Последние известны как единица измерения.

Чтобы обозначить величину, пишут число, а рядом с ним указывают единицу, в которой проводилось измерение. К примеру, 3 см, 15 кг, 20 км, 2 мин. Для каждой величины общее число возможных значений не ограничено. Так, длина может быть 1 см, 10 см, 100 см и т. д. Одну и ту же величину в разных единицах выражают с помощью разных чисел.

Кроме того, одну и ту же величину могут выражать по-разному. Например, используются различные единицы измерения длины в зависимости от того, насколько она маленькая или большая. В школе используются такие из них:

  1. Наименьшая единица — миллиметр (мм). Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними.
  2. Следующей единицей стал сантиметр (см). На линейках сантиметры обозначаются числами. Один сантиметр состоит из десяти миллиметров. Между этими величинами ставится знак равенства, так как с их помощью обозначается одна и та же длина: 1 см = 10 мм.
  3. За сантиметром следует дециметр (дм). Один дециметр состоит из десяти сантиметров. Эти величины также равны, что обозначается следующим уравнением: 1 дм = 10 см.
  4. За дециметром следует метр (м), который содержит десять дециметров, то есть 1 м = 10 дм. В домашних условиях метр проще всего увидеть, если взять рулетку, длина которой часто составляет 1 метр. Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см).
  5. Самая большая единица в этой категории в рамках стандартной школьной программы — километр. Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее.

Существуют и более крупные меры, например мегаметры, гигаметры, тераметры, но они выходят за рамки знаний, необходимых школьнику.

Линейка

Сантиметры и миллиметры: Freepick

Таким образом, меры величин, с помощью которых можно измерить длину, таковы:

Меры длины

Меры длины: NUR.KZ

Меры веса

Массой называют величину, которая обозначает, сколько вещества содержит тело. В обиходе масса получила название вес. Часто при взвешивании говорят: «Вес этого вещества (материала, предмета) такой-то». Но на самом деле это не вес, а масса данного тела.

Таким образом, масса и вес — не одно и то же. Весом называют силу, которую тело прилагает к горизонтальной опоре. Вес измеряют в ньютонах. Масса же как величина отражает количество.

Как же выразить значение массы и что для этого надо знать? Основные единицы измерения массы таковы:

  1. Самая маленькая единица — миллиграмм (мг). Миллиграммы редко применяются на практике. Их используют химики и другие ученые, работа которых связана с маленькими количествами веществам. В обычной жизни редко отмеряем что-либо миллиграммами.
  2. Следующей единицей стал грамм (г). В граммах часто измеряют количество продуктов, когда составляют рецепты. Один грамм состоит из тысячи миллиграммов. Между этими величинами ставят знак равенства, так как они тождественны: 1 г = 1000 мг.
  3. Следующая единица — килограмм (кг). Это общепринятая единица измерения в мире, включенная в международную систему. Один килограмм содержит тысячу граммов, то есть: 1 кг = 1000 г.
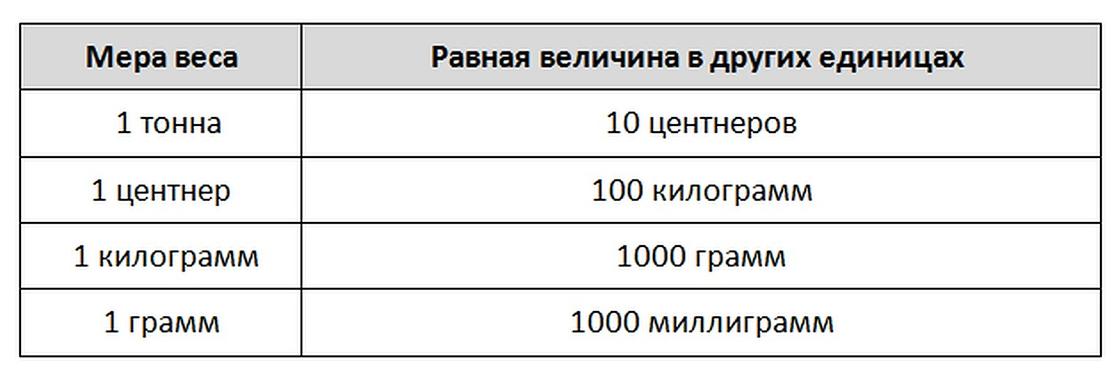
  4. За килограммом следует центнер (ц). В центнерах измеряется масса урожая, который собирают с небольших участков или масса различных грузов. Один центнер — это сто килограммов (1 ц = 100 кг).
  5. Тонна (т) — самое большое значение, с которым сталкиваются школьники, когда изучают массу предметов. Тонны используют, чтобы измерить большой груз и массу больших тел, таких как космические корабли или автомобили. Одна тонна состоит из тысячи килограмм (1 т = 1000 кг).

Гири

Измерение веса: Freepick

Если обобщить представленную выше информацию, то для измерения массы существует:

Меры веса

Меры веса: NUR.KZ

Меры объема

В каждом государстве устанавливают определенные единицы для измерений различных величин. Единица измерения, которую рассчитали точно, принимается как образец. Ее называют эталоном или образцом.

Существует стандарт килограмма, метра и т. п., на которые равняются во всех странах. Единицы, которые вошли в употребление и утверждены на государственном уровне, называют меры.

Меры могут быть однородными, если с их помощью измеряют величины одного рода. К примеру, ряд однородных мер для измерения объема таков:

  • 1 куб. метр = 1000 куб. дециметров;
  • 1 куб. дециметр = 1000 куб. сантиметров;
  • 1 куб. сантиметр = 1000 куб. миллиметров.

Кроме того, широко используется такая величина, как литр. С его помощью удобно обозначать вместимость сосудов. Литр — это объем, который соответствует одному кубическому дециметру (1 литр = 1 куб. дециметру). Эта единица получила свое название в память о виноделе Литре из Франции.

В древности объемы измерялись самыми разными единицами: сиеками, горстками, тинами, пурами, цибами, штофами, ложками (1 тина = 3 пуры = 9 сиеков = 720 горсток = 162 штофа = 208 литров). Но сейчас о них уже забыли, так как распространение получила единая унифицированная система.

Меры площади

Для удобства страны мира пользуются международной системой единиц СИ. Это французское сокращение, которое расшифровывается так: Le Système International d’Unités, SI.

Это система, в которой для наиболее распространенных величин определены общепринятые единицы измерения. Так, ученые пришли к соглашению измерять длину в метрах. Поэтому когда в задачах длины даются в других единицах измерения (например, в миллиметрах), то их переводят в метры.

Как измеряют площадь? С этой целью применяют разнообразные меры:

  1. Квадратным сантиметром обозначается квадрат, сторона которого равна одному сантиметру.
  2. Для квадратного дециметра следует представить квадрат со стороной длиной в один дециметр.
  3. Соответственно, квадратный метр — квадрат, сторона которого 1 м в длину.
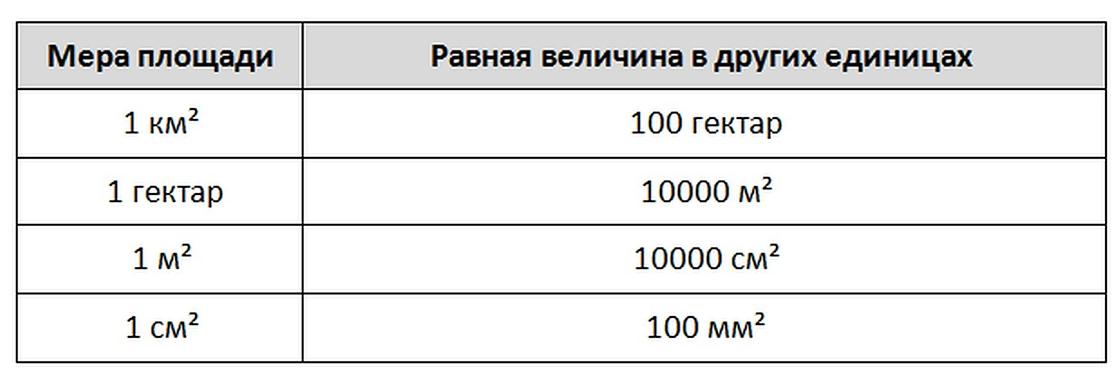
  4. Очень большие площади измеряют квадратными километрами. У такого квадрата сторона равняется одному километру.

Словосочетание «квадратный километр» сокращенно на письме отражается так: 2 км², 5 км², 15 км². В этих единицах обычно измеряют площади городов.

Для измерения площади используются:

Меры площади

Меры площади: NUR.KZ

Таковы основные единицы измерения, но в науке их арсенал гораздо шире. Людям нравится все измерять, а мир очень многогранен. Отсюда и разнообразие мер величин. К счастью, освоить и использовать их под силу каждому из нас.

Оригинал статьи: https://www.nur.kz/family/school/1904238-edinitsy-izmereniya-velichin-dlya-shkolnikov/

Источник

Единицы физических величин (единицы измерения), метрические системы, соотношения и переводы единиц измерения

Единицы физических величин. Общая информация

Единица физической величины (единица величины, единица, единица измерения) (англ. Measurement unit, unit of measurement, unit) — физическая величина фиксированного размера, которой условно по соглашению присвоено числовое значение, равное 1.

С единицей физической величины можно сравнить любую другую величину того же рода и выразить их отношение в виде числа. Применяется для количественного выражения однородных с ней физических величин.
Единицы измерения имеют присвоенные им по соглашению наименования и обозначения.

Различают основные и производные единицы.

Основные единицы в данной системе единиц устанавливаются для тех физических величин, которые выбраны в качестве основных в соответствующей системе физических величин. Так, Международная система единиц (СИ) основана на Международной системе величин (англ. International System of Quantities, ISQ), в которой основными являются семь величин: длина, масса, время, электрический ток, термодинамическая температура, количество вещества и сила света.
Соответственно, в СИ основными единицами являются единицы указанных величин.
Размеры основных единиц устанавливаются по соглашению в рамках соответствующей системы единиц и фиксируются либо с помощью эталонов (прототипов), либо путём фиксации численных значений фундаментальных физических постоянных.

Производные единицы определяются через основные путём использования тех связей между физическими величинами, которые установлены в системе физических величин.
Существует большое количество различных систем единиц, которые различаются как системами величин, на которых они основаны, так и выбором основных единиц.
Государство, как правило, законодательно устанавливает какую-либо систему единиц в качестве предпочтительной или обязательной для использования в стране.

Соотношение единиц измерения

Меры длины
1 км = 1 000 м
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см
1 см = 10 мм
1 мм = 1 000 мк

Меры площади  
1 км2 = 100 га = 10 000 а = 1 000 000 м2
1 га = 100 а = 10 000 м2
1 а = 100 м2 = 10 000 дм2
1 м2 = 100 дм2= 10 000 см2
1 дм2 = 100 см2= 10 000 мм2
1 см2 = 100 мм2
1 мм2 = 0,01 см2

Меры объема
1 м3 = 1 000 дм3
1 дм3= 1 000 см3
1 л = 1 дм3
1 см3 = 1 000 мм3
1 мм3 = 0,001 см3

Меры веса
1 т = 10 ц = 1 000 кг
1 ц = 100 кг
1 кг = 1 000 г
1 г = 1 000 мг
1 мг = 0,001 г

Меры времени   
1 век = 100 лет
1 год = 12 мес = 365 или 366 сут
1 мес = 30 сут или 31 сут (в феврале 28 или 29 сут)
1 неделя = 7 сут
1 сут = 24 ч= 86 400 сек
1 ч = 60 мин = 3 600 сек
1 мин = 60 с
1 сек = 1 000 мсек

Меры давления  
1 ат = 1 кГ/см2 = 735,66 мм рт. ст.
1 мм рт. ст. = 1,36 Г/см2

Меры тока  
1 ка = 1 000 а
1 а = 1 000 ма
1 ма = 1 000 мка

Меры напряжения и э.д.с. 
1 кв. = 1 000 в
1 в = 1 000 мв
1 мв = 1 000 мкв

Меры мощности
1 квт = 1 000 вт
1 вт = 1 000 мвт
1 мвт = 1 000 мквт

Меры сопротивления
1 Мом = 1 000 ком
1 ком = 1 000 ом.
1 ом = 0,001 ком

Меры частоты
1 Мгц = 1 000 кгц
1кгц = 1 000 гц

Меры количества информации

1 байт = 8 бит
1 Кб (1 Килобайт) = 210 байт == 1024 байт (~103 байт)
1 Мб (1 Мегабайт) = 220 байт = 1024 килобайт (~ 106 байт)
1 Гб (1 Гигабайт) = 230 байт = 1024 мегабайт (~ 109 байт)
1 Тб (1 Терабайт) = 240 байт = 1024 гигабайт (~ 1012 байт)
1 Пб (1 Петабайт) = 250 байт = 1024 терабайт (~1015 байт)
1 Эксабайт = 260 байт = 1024 петабайт (~1018 байт)
1 Зеттабайт = 270 байт = 1024 эксабайт (~1021 байт)
1 Йоттабайт = 280 байт = 1024 зеттабайт (~ 1024 байт)

Для  единиц измерения информации степени двойки (210, 220 и т.д.) являются точными значениями килобайт, мегабайт, гигабайт. А степени числа 10 (103, 106 и т.п.) – приблизительные значения, округленные в сторону уменьшения.
Такое приближение (или округление) вполне допустимо и является общепринятым 

Системы единиц измерения

Метрические системы

Метрическая система — общее название международной десятичной системы единиц, основанной на использовании метра и килограмма.
На протяжении двух последних веков существовали различные варианты метрической системы, различающиеся выбором основных единиц.

В настоящее время повсеместно признанной является Международная система единиц (СИ).
Метрическая система официально принята во всех государствах мира, кроме США, Либерии и Мьянмы (Бирма).

anr10

НУЖЕН АНГЛИЙСКИЙ?

6 лучших онлайн-школ и сервисов

Инглекс
englex.ru
обучение английскому языку по скайпу- живое общение с преподавателем

Skyeng
skyeng.ru
одна из крупнейших онлайн школ английского для аудитории СНГ

Фоксфорд
foxford.ru
эффективные курсы с погружением в англоязычную среду

Skillbox
eng.skillbox.ru
все программы английского языка

Puzzle English
puzzle-english.com
популярный онлайн-сервис для изучения английского языка

Lingualeo
lingualeo.com/ru
эффективный сервис для увлекательной практики языков

Основное отличие метрической системы от применявшихся ранее традиционных систем заключается в использовании упорядоченного набора единиц измерения. Для любой физической величины существует лишь одна главная единица и набор дольных и кратных единиц, образуемых стандартным образом с помощью десятичных приставок.
Тем самым устраняется неудобство от использования большого количества разных единиц (таких, например, как дюймы, футы, фадены, мили и т. д.) со сложными правилами преобразования между ними. В метрической системе преобразование сводится к умножению или делению на степень числа 10, то есть к простой перестановке запятой в десятичной дроби.

Основная используемая система
СИ
Неиспользуемые или малоиспользуемые системы
СГС
МКС
МКГСС
МТС
МСК
МКСЛ

Системы естественных единиц измерения

Атомная система единиц
Планковские единицы
Геометризованная система единиц
Единицы Лоренца — Хевисайда

Традиционные системы мер

Русская система мер
Английская система мер
Французская система мер
Китайская система мер
Японская система мер
Давно устаревшие (древнегреческая, древнеримская, древнеегипетская, древневавилонская, древнееврейская)

Международная система единиц СИ

Международная система единиц СИ (фр. Système international d’unités, SI) — система единиц физических величин, современный вариант метрической системы.
СИ принята в качестве основной системы единиц большинством стран мира и почти всегда используется в области техники, даже в тех странах, в которых в повседневной жизни используются традиционные единицы.
В этих немногих странах (например, в США) определения традиционных единиц были изменены таким образом, чтобы связать их фиксированными коэффициентами с соответствующими единицами СИ.

Полное официальное описание СИ вместе с её толкованием содержится в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure) и в дополнении к ней, опубликованных Международным бюро мер и весов (МБМВ) и представленных на сайте МБМВ –  bipm.org

Брошюра СИ издаётся с 1970 года, с 1985 года выходит на французском и английском языках, переведена также на ряд других языков, однако официальным считается текст только на французском языке.

Основные единицы СИ

Величина

Единица

Наименование

Символ
размерности

Наименование

Обозначение

русское

французское/
английское

русское

между
народное

Длина

L

метр

mètre/metre

м

m

Масса

M

килограмм

kilogramme/kilogram

кг

kg

Время

T

секунда

seconde/second

с

s

Сила электрического тока

I

ампер

ampère/ampere

А

A

Термодинамическая температура

Θ

кельвин

kelvin

К

K

Количество вещества

N

моль

mole

моль

mol

Сила света

J

кандела

candela

кд

cd

Наименования единиц СИ пишутся со строчной буквы, после обозначений единиц СИ точка не ставится, в отличие от обычных сокращений.
У этого правила есть исключение: обозначения единиц, названных фамилиями учёных, пишутся с заглавной буквы (например, ампер обозначается символом А).

Производные единицы

Остальные единицы СИ являются производными и образуются из основных с помощью уравнений, связывающих друг с другом физические величины используемой в СИ Международной системы величин.
Основная единица может использоваться и для производной величины той же размерности. Например, количество осадков определяется как частное от деления объёма на площадь и в СИ выражается в метрах. В этом случае метр используется в качестве когерентной производной единицы.
Определение СИ через фиксацию констант, в принципе не требует различать основные и производные единицы. Тем не менее, это разделение сохраняется по историческим причинам и для удобства.

Примеры производных единиц СИ, наименования и обозначения которых образованы с использованием наименований и обозначений основных единиц СИ

Величина

Единица

Наименование

Наименование

Обозначение
   

между
народное

русское

Площадь

квадратный метр

m

м

Объем, вместимость

кубический метр

m

м

Скорость

метр в секунду

m/s

м/с

Ускорение

метр на секунду в квадрате

m/s

м/с

Волновое число

метр в минус первой степени

m

м

Плотность

килограмм на кубический метр

kg/m

кг/м

Удельный объем

кубический метр на килограмм

m/kg

м/кг

Плотность электрического тока

ампер на квадратный метр

А/m

А/м

Напряженность магнитного поля

ампер на метр

А/m

А/м

Молярная концентрация компонента

моль на кубический метр

mol/m

моль/м

Яркость

кандела на квадратный метр

cd/m

кд/м

Производные единицы, имеющие специальные наименования и обозначения

Производные единицы могут быть выражены через основные с помощью математических операций — умножения и деления. Некоторым из производных единиц для удобства присвоены собственные наименования, такие единицы тоже можно использовать в математических выражениях для образования других производных единиц.

Величина

Единица измерения

Обозначение

Выражение через
основные единицы

русское
наименование

международное
название

русское

между
народное

Плоский угол

радиан

radian

рад

rad

м·м−1 = 1

Телесный угол

стерадиан

steradian

ср

sr

м2·м−2 = 1

Температура по шкале Цельсия

градус Цельсия

degree Celsius

°C

°C

K

Частота

герц

hertz

Гц

Hz

с−1

Сила

ньютон

newton

Н

N

кг·м·c−2

Энергия

джоуль

joule

Дж

J

Н·м = кг·м2·c−2

Мощность

ватт

watt

Вт

W

Дж/с = кг·м2·c−3

Давление

паскаль

pascal

Па

Pa

Н/м2 = кг·м−1·с−2

Световой поток

люмен

lumen

лм

lm

кд·ср

Освещённость

люкс

lux

лк

lx

лм/м² = кд·ср/м²

Электрический заряд

кулон

coulomb

Кл

C

А·с

Разность потенциалов

вольт

volt

В

V

Дж/Кл = кг·м2·с−3·А−1

Сопротивление

ом

ohm

Ом

Ω

В/А = кг·м2·с−3·А−2

Электроёмкость

фарад

farad

Ф

F

Кл/В = с4·А2·кг−1·м−2

Магнитный поток

вебер

weber

Вб

Wb

кг·м2·с−2·А−1

Магнитная индукция

тесла

tesla

Тл

T

Вб/м2 = кг·с−2·А−1

Индуктивность

генри

henry

Гн

H

кг·м2·с−2·А−2

Электрическая проводимость

сименс

siemens

См

S

Ом−1 = с3·А2·кг−1·м−2

Активность (радиоактивного источника)

беккерель

becquerel

Бк

Bq

с−1

Поглощённая доза 
ионизирующего излучения

грей

gray

Гр

Gy

Дж/кг = м²/c²

Эффективная доза 
ионизирующего излучения

зиверт

sievert

Зв

Sv

Дж/кг = м²/c²

Активность катализатора

катал

katal

кат

kat

моль/с

Существуют другие внесистемные единицы, такие как литр, которые не являются единицами СИ, но принимаются для использования вместе с СИ.

Единицы измерения по измеряемым величинам. Википедия

ru.wikipedia.org/wiki

Единицы измерения по отраслям науки. Википедия 

  • Единицы измерения в астрономии‎
  • Единицы измерения в информатике‎
  • Единицы измерения в медицине‎
  • Единицы измерения в физике‎
  • Единицы измерения в химии‎

Приставки СИ 

Приставки СИ (десятичные приставки) — приставки перед названиями или обозначениями единиц измерения физических величин, применяемые для формирования кратных и дольных единиц, отличающихся от базовой в определённое целое, являющееся степенью числа 10, число раз.
Десятичные приставки служат для сокращения количества нулей в численных значениях физических величин.
Рекомендуемые для использования приставки и их обозначения установлены Международной системой единиц (СИ), однако их использование не ограничено СИ, а многие из них восходят к моменту появления метрической системы (1790-е годы). 

Приставки для кратных единиц

Кратные единицы — единицы, которые в целое число раз (10 в какой-либо степени) превышают основную единицу измерения некоторой физической величины. Международная система единиц (СИ) рекомендует следующие десятичные приставки для обозначений кратных единиц:

Десятичный множитель

Приставка

Обозначение

Пример

русская

между
народная

русское

между
народное

101

дека

deca

да

da

дал — декалитр

102

гекто

hecto

г

h

гПа — гектопаскаль

103

кило

kilo

к

k

кН — килоньютон

106

мега

mega

М

M

МПа — мегапаскаль

109

гига

giga

Г

G

ГГц — гигагерц

1012

тера

tera

Т

T

ТВ — теравольт

1015

пета

peta

П

P

Пфлопс — петафлопс

1018

экса

exa

Э

E

Эм — эксаметр

1021

зетта

zetta

З

Z

ЗэВ — зеттаэлектронвольт

1024

иотта

yotta

И

Y

Иг — иоттаграмм

Приставки для дольных единиц

Дольные единицы составляют определённую долю (часть) от установленной единицы измерения некоторой величины.

Международная система единиц (СИ) рекомендует следующие приставки для обозначений дольных единиц:

Десятичный множитель

Приставка

Обозначение

Пример

русская

между
народная

русское

между
народное

10−1

деци

deci

д

d

дм — дециметр

10−2

санти

centi

с

c

см — сантиметр

10−3

милли

milli

м

m

мH — миллиньютон

10−6

микро

micro

мк

µ

мкм — микрометр

10−9

нано

nano

н

n

нм — нанометр

10−12

пико

pico

п

p

пФ — пикофарад

10−15

фемто

femto

ф

f

фл — фемтолитр

10−18

атто

atto

а

a

ас — аттосекунда

10−21

зепто

zepto

з

z

зКл — зептокулон

10−24

иокто

yocto

и

y

иг — иоктограмм

Семь основных единиц измерения (СИ)+площадь и объем

Базовые единицы СИ.  Международное бюро мер и весов  –   bipm.org/en/measurement-units

1

Единицы измерения массы (масса)

В настоящее время в Международной системе единиц (СИ) в качестве единицы измерения массы принят килограмм, являющийся одной из семи основных единиц СИ.

XXVI Генеральная конференция по мерам и весам c 20 мая 2019г. одобрила новое определение килограмма, основанное на фиксации численного значения постоянной Планка
Теперь килограмм измеряется не весом эталонного цилиндра, а энергией, необходимой для того, чтобы сдвинуть этот килограмм.

Тонна — 106 (1 000 000) граммов, или 1000 килограммов.
Центнер — 105 (100 000) граммов, или 100 килограммов.
Карат — 0,2 грамма.

Единицы массы в науке
Атомная единица массы (а. е. м., дальтон) = 1,660 538 921(73)⋅10−27 кг = 1,660 538 921(73)⋅10−24 г (в химии высокомолекулярных соединений и биохимии применяются также кратные единицы килодальтон, мегадальтон).
Солнечная масса M☉ = 1.98847(7)⋅1030 кг.
Электронвольт, 1 эВ = 1,782 661 845(39)⋅10−36 кг; применяются также кратные (килоэлектронвольт, кэВ; мегаэлектронвольт, МэВ, гигаэлектронвольт, ГэВ; тераэлектронвольт, ТэВ) и дольные (миллиэлектронвольт, мэВ) единицы.
Масса электрона me = 9,109 382 91(40)⋅10−31 кг.
Масса протона mp = 1,672 621 777(74)⋅10−27 кг.
Планковская единица массы MPl = 2,176 51(13)⋅10−8 кг.

2

Единицы измерения расстояния (расстояние)

Единицей измерения расстояния и одной из основных единиц в Международной системе единиц (СИ) является метр.

На практике применяются также кратные и дольные единицы метра, образуемые с помощью стандартных приставок СИ:

Кратные

Дольные

величина

название

обозначение

величина

название

обозначение

101 м

декаметр

дам

dam

10−1 м

дециметр

дм

dm

102 м

гектометр

гм

hm

10−2 м

сантиметр

см

cm

103 м

километр

км

km

10−3 м

миллиметр

мм

mm

106 м

мегаметр

Мм

Mm

10−6 м

микрометр

мкм

µm

109 м

гигаметр

Гм

Gm

10−9 м

нанометр

нм

nm

1012 м

тераметр

Тм

Tm

10−12 м

пикометр

пм

pm

1015 м

петаметр

Пм

Pm

10−15 м

фемтометр

фм

fm

1018 м

эксаметр

Эм

Em

10−18 м

аттометр

ам

am

1021 м

зеттаметр

Зм

Zm

10−21 м

зептометр

зм

zm

1024 м

иоттаметр

Им

Ym

10−24 м

иоктометр

им

ym

Единицы, применяемые в астрономии

  • радиус Луны (R☾) = 1737,10 км;
  • радиус Земли (R⊕) = 6371,0 км;
  • радиус Юпитера(R♃или RJ) = 69 911 км;
  • световая секунда = 299 792 458 м ;
  • радиус Солнца (R⊙) = 6,9551⋅105км;
  • световой месяц = 783934206048416.66… м
  • астрономическая единица = 149 597 870,700 км;
  • спат (единица длины)(англ.)= 1⋅1012 м;
  • световой год = 9 460 730 472 581 000 м ;
  • парсек= (648 000/π) а.е. (точно) ≈ 206264,806247 а.е. = 3,08567758491⋅1016м;
  • сириометр = 106а.е. = 149 597 870 700 000 000 м;

Единицы, применяемые в физике

  • планковская длина ≈ 1,616199(97)⋅10−35м;
  • ферми = 1 фм = 1⋅10−15м;
  • классический радиус электрона = 2,8179402894(58)⋅10−15м;
  • икс-единица = 1,00207⋅10−13м;
  • комптоновская длина волны электрона= 2,4263102175(33)⋅10−12м;
  • боровский радиус = 5,2917720859(36)⋅10−11м;
  • ангстрем = 1⋅10−10м;

Единицы измерения площади (площадь)

Квадратный метр (русское обозначение: м², международное: m²) — единица измерения площади в Международной системе единиц (СИ), а также в системах МТС и МКГСС.
1 м² равен площади квадрата со стороной в 1 метр.
1 м² = 1 са (сантиар);

Квадратный километр, 1 км² = 1 000 000 м²;
Гектар, 1 га = 10 000 м²;
Ар (сотка), 1 а = 100 м²:
Квадратный дециметр, 100 дм² = 1 м²;
Квадратный сантиметр, 10 000 см² = 1 м²;
Квадратный миллиметр, 1 000 000 мм² = 1 м²;
Барн, 1 б = 10−28 м².

Единицы измерения объёма (объём)

Объём — количественная характеристика пространства, занимаемого телом или веществом.

Кубический метр (кубометр) — единица объёма, производная в Международной системе единиц (СИ), а также в системах единиц МКГСС и МТС.
Одному кубическому метру равен объём куба с длиной ребра 1 метр.

От неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».

Единицы объёма жидкости

1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона

Русские
Ведро = 12,3 литра
Бочка = 40 вёдер = 492 литра

Английские
1 пинта = 0,568 литра
1 кварта (жидкостная) = 2 пинтам = 1,136 литра
1 галлон = 8 пинтам = 4,55 литра
1 галлон (амер.) = 3,785 литра

3

Единицы измерения температуры (температура)

Существует несколько различных единиц измерения температуры. Они делятся на относительные (градус Цельсия, градус Фаренгейта…) и абсолютные (Кельвин, градус Ранкина…).

Наиболее известными являются следующие:
Градус Цельсия (°C)
Градус Фаренгейта (°F)
Кельвин (K)
Градус Реомюра (°Ré, °Re, °R)
Градус Рёмера (°Rø)
Градус Ранкина (°Ra)
Градус Делиля (°Д или °D)
Градус Гука (°H)
Градус Дальтона (°Dа)
Градус Ньютона (°N)
Лейденский градус (°L или ÐL)
Планковская температура (TP)

Кельвин (русское обозначение: К; международное: K) — единица термодинамической температуры в Международной системе единиц (СИ), одна из семи основных единиц СИ. Определяется через значение постоянной Больцмана: 1,380649 × 10-23 Дж / К. Начало шкалы (0 К) совпадает с абсолютным нулём.

Градус Цельсия (обозначение: °C) —единица температуры, применяемая в Международной системе единиц (СИ) наряду с кельвином.
Используется всеми странами, кроме США, Багамских Островов, Белиза, Каймановых Островов и Либерии.

Согласно современному определению, один градус Цельсия равен одному кельвину (K), а ноль шкалы Цельсия установлен таким образом, что температура тройной точки воды равна 0,01 °C. В итоге шкалы Цельсия и Кельвина сдвинуты на 273,15 единиц:

Пересчёт в градусы Цельсия:
t_{C}=t_{K}-273,15}t_{C}=t_{K}-273,15 (температура тройной точки воды +0,01 °C).

Основные международные и российские документы, содержащие описание единиц СИ и регламентирующие их использование, называют градус Цельсия не единицей температуры, а единицей температуры Цельсия (фр. température Celsius, англ. Celsius temperature). Этот термин используется в Брошюре СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ)
В свою очередь температуру Цельсия (обозначение t) Брошюра СИ и ГОСТ 8.417-2002 определяют выражением t = T — T0, где T — термодинамическая температура, выражаемая в кельвинах, а T0 = 273,15 К.
В соответствии со сказанным градус Цельсия относится к производным единицам СИ, имеющим специальные наименования и обозначения.

Пересчёт температуры между основными шкалами

Шкала

Условное
обозначение

из Цельсия (°C)

в Цельсий

Фаренгейт

(°F)

[°F] = [°C] × 9⁄5 + 32

[°C] = ([°F] − 32) × 5⁄9

Кельвин

(K)

[K] = [°C] + 273,15

[°C] = [K] − 273,15

Ранкин (Rankin)

(°R)

[°R] = ([°C] + 273,15) × 9⁄5

[°C] = ([°R] − 491,67) × 5⁄9

Делиль (Delisle)

(°Д или °De)

[°De] = (100 − [°C]) × 3⁄2

[°C] = 100 − [°De] × 2⁄3

Ньютон (Newton)

(°N)

[°N] = [°C] × 33⁄100

[°C] = [°N] × 100⁄33

Реомюр (Réaumur)

(°Re, °Ré, °R)

[°Ré] = [°C] × 4⁄5

[°C] = [°Ré] × 5⁄4

Рёмер (Rømer)

(°Rø)

[°Rø] = [°C] × 21⁄40 + 7,5

[°C] = ([°Rø] − 7,5) × 40⁄21

Сравнение температурных шкал

Описание

Кельвин

Цельсий

Фаренгейт

Абсолютный нуль

0

−273,15

−459,67

Температура таяния смеси Фаренгейта (соль,лёд и хлорид аммония)

255,37

−17,78

0

Температура замерзания воды (Нормальные условия)

273,15

0

32

Средняя температура человеческого тела

309,75

36,6

98,2

Температура кипения воды (Нормальные условия)

373,15

100

212

Плавление титана

1941

1668

3034

Солнце

5800

5526

9980

4

Единицы измерения времени (время)

Современные единицы измерения времени основаны на периодах вращения Земли вокруг своей оси и обращения вокруг Солнца, а также обращения Луны вокруг Земли. Такой выбор единиц обусловлен как историческими, так и практическими соображениями: необходимостью согласовывать деятельность людей со сменой дня и ночи или сезонов.
Исторически основной единицей для измерения средних интервалов времени были сутки (часто говорят «день»), отсчитываемые по минимальным полным циклам смены солнечной освещённости (день и ночь).

В результате деления суток на меньшие временны́е интервалы одинаковой длины возникли часы, минуты и секунды.
Сутки делили на два равных последовательных интервала (условно день и ночь). Каждый из них делили на 12 часов. Дальнейшее деление часа восходит к шестидесятеричной системе счисления. Каждый час делили на 60 минут. Каждую минуту — на 60 секунд.
Таким образом, в часе 3600 секунд; в сутках — 24 часа, или 1440 минут, или 86 400 секунд.

Секунда (русское обозначение: с; международное: s) — единица измерения времени, является одной из семи основных единиц в Международной системе единиц (СИ) и одной из трёх основных единиц в системе СГС.
Представляет собой интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133, находящегося в покое при 0 К.

В астрономии используют обозначения ч, м, с (или h, m, s) в верхнем индексе: например, 13ч20м10с (или 13h20m10s).

Кратные и дольные единицы

С единицей измерения «секунда», как правило, используются только дольные приставки СИ (кроме деци- и санти-). Для измерения больших интервалов времени используются единицы минута, час, сутки, и т. д.

Кратные

Дольные

величина

название

обозначение

величина

название

обозначение

101 с

декасекунда

дас

das

10−1 с

децисекунда

дс

ds

102 с

гектосекунда

гс

hs

10−2 с

сантисекунда

сс

cs

103 с

килосекунда

кс

ks

10−3 с

миллисекунда

мс

ms

106 с

мегасекунда

Мс

Ms

10−6 с

микросекунда

мкс

µs

109 с

гигасекунда

Гс

Gs

10−9 с

наносекунда

нс

ns

1012 с

терасекунда

Тс

Ts

10−12 с

пикосекунда

пс

ps

1015 с

петасекунда

Пс

Ps

10−15 с

фемтосекунда

фс

fs

1018 с

эксасекунда

Эс

Es

10−18 с

аттосекунда

ас

as

1021 с

зеттасекунда

Зс

Zs

10−21 с

зептосекунда

зс

zs

1024 с

иоттасекунда

Ис

Ys

10−24 с

иоктосекунда

ис

ys

Эквивалентность другим единицам измерения времени

1 секунда равна:

• 1/60 минуты 

• 1/3 600 часа

• 1/86 400 суток (система единиц МАС)

• 1/31 557 600 юлианского года (система единиц МАС)

5

Сила электрического тока 

Средняя сила тока I – физическая величина , равная отношению заряда, прошедшего через поперечное сечение проводника за промежуток времени, к величине этого промежутка времени: I=△q/△t

Если сила тока со временем не меняется, то ток называется постоянным.
Сила тока в данный момент времени определяется так же по этой формуле, но промежуток времени должен быть очень малым.
Обычно обозначается символом I, от фр. intensité du courant.

Сила тока в Международной системе единиц (СИ) измеряется в амперах ((русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ.
1 А = 1 Кл/с.

В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов (устаревшее наименование — ампер-виток). Кроме того, ампер является единицей силы тока и относится к числу основных единиц в системе единиц МКСА.

На XXVI Генеральной конференции мер и весов было принято новое определение ампера, основанное на использовании численного значения элементарного электрического заряда. Формулировка вступила в силу 20 мая 2019 года.
В соответствии с данной формулировкой, Ампер, символ А, есть единица электрического тока в СИ. Она определена путём фиксации численного значения элементарного заряда равным 1,602 176 634⋅10−19, когда он выражен единицей Кл, которая равна А·с, где секунда определена через .△νCs
△νCs — частота излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.

6

Количество вещества

Количество вещества́ — физическая величина, характеризующая количество однотипных структурных единиц, содержащихся в веществе. Под структурными единицами понимаются любые частицы, из которых состоит вещество (атомы, молекулы, ионы, электроны или любые другие частицы).

Моль (русское обозначение: моль; международное: mol; устаревшее название грамм-молекула (по отношению к количеству молекул); от лат. moles — количество, масса, счётное множество) — единица измерения количества вещества в Международной системе единиц (СИ), одна из семи основных единиц СИ.

Значение одного моля определяется через число Авогадро, один моль — количество вещества, содержащее 6,022 140 76⋅1023 частиц (атомов, молекул, ионов, электронов или любых других объектов).
6,022 140 76 x 10 23 элементарных сущностей. Это число представляет собой фиксированное числовое значение постоянной Авогадро, N A , выраженное в единицах моль –1, и называется числом Авогадро.
Количество вещества (символ n ) в системе является мерой количества определенных элементарных сущностей. Элементарным объектом может быть атом, молекула, ион, электрон, любая другая частица или определенная группа частиц.

Кратные и дольные единицы

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ. Причём, единица измерения «иоктомоль» может использоваться лишь формально, так как столь малые количества вещества должны измеряться отдельными частицами (1 имоль формально равен 0,602 частицы).

Кратные

Дольные

величина

название

обозначение

величина

название

обозначение

101 моль

декамоль

дамоль

damol

10−1 моль

децимоль

дмоль

dmol

102 моль

гектомоль

гмоль

hmol

10−2 моль

сантимоль

смоль

cmol

103 моль

киломоль

кмоль

kmol

10−3 моль

миллимоль

ммоль

mmol

106 моль

мегамоль

Ммоль

Mmol

10−6 моль

микромоль

мкмоль

µmol

109 моль

гигамоль

Гмоль

Gmol

10−9 моль

наномоль

нмоль

nmol

1012 моль

терамоль

Тмоль

Tmol

10−12 моль

пикомоль

пмоль

pmol

1015 моль

петамоль

Пмоль

Pmol

10−15 моль

фемтомоль

фмоль

fmol

1018 моль

эксамоль

Эмоль

Emol

10−18 моль

аттомоль

амоль

amol

1021 моль

зеттамоль

Змоль

Zmol

10−21 моль

зептомоль

змоль

zmol

1024 моль

иоттамоль

Имоль

Ymol

10−24 моль

иоктомоль

имоль

ymol

Молярная масса — характеристика вещества, отношение массы вещества к количеству молей этого вещества, то есть масса одного моля вещества.

7

Сила света

Сила света Iν — физическая величина, одна из основных световых фотометрических величин. Характеризует величину световой энергии, переносимой в некотором направлении в единицу времени.

Количественно равна отношению светового потока, распространяющегося внутри элементарного телесного угла, к этому углу.
Понятие «сила света» возможно применять лишь для расстояний от источника света, существенно превышающих его линейные размеры.
Единица измерения в Международной системе единиц (СИ): кандела.

Канде́ла (от лат. candela — свеча; русское обозначение: кд; международное: cd) — единица силы света, одна из семи основных единиц Международной системы единиц (СИ).
Определена как «сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540⋅1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср».
Принята в качестве единицы СИ в 1979 году XVI Генеральной конференцией по мерам и весам.

Из определения следует, что значение спектральной световой эффективности монохроматического излучения для частоты 540⋅1012 Гц равно 683 лм/Вт = 683 кд·ср/Вт точно.
Выбранная частота соответствует длине волны 555,016 нм в воздухе при стандартных условиях и находится вблизи максимума чувствительности человеческого глаза, располагающегося на длине волны 555 нм. Если излучение имеет другую длину волны, то для достижения той же силы света требуется бо́льшая энергетическая сила света.

Световые фотометрические величины СИ   

ru.wikipedia.org

Преобразование единиц измерения.
Таблицы пересчета физических величин

Преобразование единиц — перевод физической величины, выраженной в одной системе единиц, в другую систему, обычно через коэффициент пересчёта.
ru.wikipedia.org

Длина

1 дюйм

= 2,54 см

1 миллиметр

= 0,03937 дюйма

1 фут

= 0,3048 м

1 сантиметр

= 0,3937 дюйма

1 ярд

= 0,9144 м

1 дециметр

= 0,3281 фута

1 род

= 5,0292 м

1 метр

= 3,281 фута

1 чейн

= 20,117 м

1 метр

= 1,094 ярда

1 фурлонг

= 201,17 м

1 декаметр

= 10,94 ярда

1 миля

= 1,6093 м

1 километр

= 0,6214 мили

1 морская миля

= 1,8532 м

1 километр

= 0,539 морской мили

Площадь

1 кв. дюйм

= 6,4516 кв. см

1 кв. сантиметр

= 0,1550 кв. дюйма

1 кв. фут

= 929,03 кв. см

1 кв. метр

= 1,550 кв. дюйма

1 кв. ярд

= 0,8361 кв. м

1 ар

= 119,60 кв. ярда

1 акр

= 4046,9 кв. м

1 гектар

= 2,4711 акра

1 кв. миля

= 259,0 га

1 кв. километр

= 0,3861 кв. мили

Объем

1 куб. дюйм

= 16,387 куб. см

1 куб. сантиметр

= 0,061 куб. дюйма

1 куб. фут

= 0,0283 куб. м

1 куб. дециметр

= 0,035 куб. фута

1 куб. ярд

= 0,7646 куб. м

1 куб. метр

= 1,308 куб. ярда

Меры сыпучих тел и жидкостей

Британия

США

1 пинта

= 0,5506 л

1 пинта

= 0,473 л

1 кварта

= 1,136 л

1 кварта

= 0,9463 л

1 галлон

= 4,546 л

1 галлон

= 3,785 л

1 пек

= 9,092 л

1 пек

= 8,809 л

1 бушель

= 36,369 л

1 бушель

= 35,24 л

Вес

1 унция

= 28,35 г

1 грамм

1 фунт

= 453,59 г

1 гектограмм

1 центнер

= 45,36 г

1 килограмм

1 короткая тонна

= 907,18 г

1 тонна

Энергия, тепло, работа

Единица
измерения энергии

Эквивалентные единицы

кДж

ккал

кВт ч

кГс м

кДж

1

0,239

0,00278

102,0

ккал

4,19

1

0,00116

427

кВт ч

3600

860

1

367200

кГс м

0,00981

0,00234

2,72 х 106

1

Давление

Пересчет

В

Па
(Паскаль)

Бар
(Бар)

мм рт. ст.
(миллиметр
ртутного столба)

мм вод. ст.
(миллиметр
водяного столба)

кгс/см2
(техническая атмосфера)

атм
(физическая атмосфера)

Из

1 Па

1

10-5

7,5 10-3

0,102

1,02 10-5

0,99 10-5

1 бар

105

1

750,1

10 200

1,02

0,987

1 мм рт. ст.

133

13,33 10-4

1

13,6

0,00136

0,001316

1 мм вод. ст.

9,81

0,9806 10-4

0,07355

1

0,0001

9,68 10-5

1 кгс/см2

98 100

0,9807

735,6

10 000

1

0,968

1 атм

101 300

1,013

760

10 330

1,033

1

 ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ

Общероссийский классификатор единиц измерения (ОКЕИ) ОК 015-94 (МК 002-97)

normativ.kontur.ru

Калькулятор перевода единиц измерения физических величин

calc.ru

❑ ПОМОЩЬ В УЧЕБЕ. ПОПУЛЯРНЫЕ СЕРВИСЫ И УСЛУГИ

TutorOnline
tutoronline.ru
репетиторы м онлайн-курсы для школьников и студентов

Фоксфорд
foxford.ru
онлайн-школа, поможет улучшить оценки, сдать ЕГЭ, ОГЭ

Автор24
a24help.ru
преподаватели и эксперты помогают учиться лучше

Напишем
napishem.ru
помощь в учебе для студентов

Всё сдал
vsesdal.com
онлайн-сервис помощи студентам

Kampus
kampus.ai
получение ответа на любой учебный вопрос в течение 30 минут

Инглекс
englex.ru
занятия по английскому с сильными преподавателями

Ваш Репетитор
repetitors.info
профессиональные репетиторы по всем предметам

Источник



С начала 5 класса мы с вами изучали только натуральные числа. Они исторически появились первыми как результат удовлетворения потребности человека в более удобном и качественном счете предметов. Но уже в те далекие времена люди поняли, что не все можно посчитать только такими числами, которые мы сегодня называем натуральные.

Поэтому, таким же естественным путем, каким были введены в жизнь человека натуральные числа, произошло появление дробных и смешанных чисел, речь о которых пойдет в следующих уроках. Этот же урок рассматривает одно из важнейших человеческих действий, которое напрямую привело к необходимости введения нового огромного класса чисел.

Измерение величин

Давайте представим, что нам нужно определить точное расстояние, к примеру, от одного конца комнаты до другого, то есть, узнать длину комнаты. Мы, конечно, можем при достаточных усилиях сделать это так, как в мультфильме «38 попугаев» – посчитать ее в мартышках, попугаях или слонятах. Но если мы так поступим, то мы не сможем сделать так, чтобы нас поняли другие, потому что размеры этих животных могут быть разные, и у каждого могут быть свои представления о них. Не водить же зверей все время с собой?

Поэтому, чтобы определить длину чего-либо, нам нужно взять известный всем размер. В нашем случае это метр. Мы берем его и откладываем последовательно по полу нашей комнаты от одной стены до другой столько раз, сколько сможем, создавая таким образом отрезки, каждый из которых равен метру.

Метр, которым мы измеряли длину комнаты – это длина, взятая нами в качестве единицы измерения другой длины. Поэтому, поскольку мы знаем величину этой единицы, и число раз, которое эта единица помещается в измеряемой нами длине, мы можем определить необходимый нам размер. Предположим, что у нас получилось 7 таких отрезков. Это значит, что длина комнаты 7 метров.

Определение

Единица измерения какой-либо величины – это известная всем величина, которая принята в качестве основной меры для измерения других величин этого же рода.

Например, метр – это единица измерения длины, а грамм – единица измерения массы.

Измерить величину – это означает определить, какое количество единиц измерения содержится в этой величине.

Можно выразить это определение более обобщенно.

Определение

Измерить величину – это означает определить, какое количество известных величин этого же рода, принятых в качестве единицы измерения, содержится в этой величине.

Меры измерений величин

Единицы измерения основных величин, как правило, определяются государствами в качестве обязательных или рекомендованных для использования. Для соблюдения стандартов создаются образцы этих единиц, которым должны соответствовать единицы измерений, используемые в повседневной жизни. Такие единицы, которые мы применяем в обиходе, называются мерами.

Однородные меры – это такие меры, которые применяются для измерения однородных величин.

Например, метр и сантиметр – это однородные меры, поскольку используются для измерения длины. Грамм и градус Цельсия – это не однородные меры, потому что грамм – это единица измерения массы, а градус Цельсия – температуры.

Отношение однородных мер – это показатель, который равен количеству меньших мер, содержащихся в большей мере. Иными словами, сколько раз можно в большей мере поместить меньшую.

Например, отношение сантиметра к миллиметру – это число 10.

Метрическая система мер

В России, как и в большинстве стран мира, принята метрическая система мер. То есть, в качестве единицы длина принят метр. Современное определение метра и историю становления и развития метрической системы измерений вы можете узнать из этой статьи.

Отношение соседних однородных мер (кроме площадей и объемов) в метрической системе равно 10, что совпадает с разрядом нашей системы счисления. Эта зависимость очень удобная, поскольку обеспечивает простое и быстрое совершение действий над числами, которыми выражены однородные меры.

Меры длины

Метр делится на десять одинаковых частей, которые называются дециметры (от латинского слова decimus – десять), каждый из них делится еще на десять равных частей, центиметры (от лат. cuntum – сто), или более привычное нам французское название сантиметры. Приставка, означающая 100, указывает на то, что один метр делится на 100 сантиметров (центиметров). Один сантиметр, в свою очередь, делится на 10 миллиметров (от латинского mille – тысяча), и т.д.

Соотношения величин вы можете всегда посмотреть в справочнике.

Кроме этого, метр также собирается в более крупные меры, по 10 более мелких частей в каждой. 10 метров – это декаметр (произошло от древнегреческого δέκα – десять), 100 метров – гектометр (древнегреческого ἑκατόν – сто), 1000 метров – километр (от древнегреческого χῑλιάς – тысяча).

Меры площади

Площади в метрической системе измеряются в квадратных мерах.

Так, один квадратный метр – это площадь квадрата, у которого сторона равна 1 метру, один квадратный километр – это площадь квадрата с длиной стороны 1 километр.

Одна квадратная мера площади состоит из 100 мер более низкого соседнего с ней разряда.

Так, 1 квадратный метр состоит из 100 квадратных дециметров, а он, в свою очередь, из 100 квадратных сантиметров.

Для обозначения площадей полей и лесов применяют два особых названия.

  • Ар (обозначается как а) соответствует квадратному декаметру, то есть, 100 квадратных метров.
  • Гектар (обозначается как га), то есть, квадратный гектометр, равен 100 ар, что соответствует 10000 квадратных метров.

Меры объема

Объемы измеряются кубическими мерами. Так, например, кубический метр (говорят также: «кубометр») – это объем такого куба, у которого длина одного ребра составляет 1 метр, кубический сантиметр – это объем куба с ребром 1 сантиметр.

Одна кубическая мера объема состоит из 1000 мер более низкого соседнего с ней разряда.

К примеру, один кубический дециметр состоит из 1000 кубических сантиметров, а один кубический сантиметр – из 1000 кубических миллиметров.

Меры веса

Конечно, с точки зрения физики правильно говорить масса, а не вес. Но мы используем эти слова в повседневном обиходе как синонимы, поэтому и я допускаю подобную трактовку в своих уроках математики.

Единицей измерения массы (веса) является грамм.

Грамм делится на десять равных частей, называемых дециграммы, каждый из которых делится еще на десять равных частей – сантиграммы (в одном грамме 100 сантиграмм), а они в свою очередь делятся на 10 миллиграмм каждый.

10 грамм образуют 1 декаграмм, 100 грамм (то есть, 10 декаграмм) составляют 1 гектограмм, 1000 грамм – килограмм.

Кроме этих мер свои названия имеют и более крупные группировки: в 1 центнере находится 100 килограмм, а в 1 тонне – 1000 килограмм.

Меры объема жидкостей

Объем жидких и сыпучих тел, а также объем вместимости сосудов измеряется в литрах.

Литр – это объем, который заполняет один килограмм воды при определенных условиях: нормальное атмосферное давление и максимальная плотность воды.

Если сравнивать эту меру с обычными мерами объема, то литр – это приближенно 1 кубический дециметр.

Литр делится на десять равных частей, называемых децилитры, каждый из которых делится еще на десять равных частей – центилитры (в одном литре 100 центилитров), а они в свою очередь делятся на 10 миллилитров каждый.

10 литров составляют 1 декалитр, 100 литров образуют гектолитр, 1000 литров – 1 килолитр.

Единицы измерения времени

Существуют две основные меры времени.

Сутки – это величина времени, приближенно равная одному обороту нашей планеты Земля вокруг своей оси.

Год – это такая величина времени, которая приближенно равна одному полному обороту Земли вокруг Солнца.

Сутки состоят из 24 частей, каждая из которых называются час. Сутки начинаются и заканчиваются в полночь, то есть, как только заканчиваются одни сутки, сразу же начинаются другие.

Часы в сутках считают сразу от 1 до 24, или разбивают на две части по 12 часов и считают от 1 до 12 (до полудня), а затем опять от 1 до 12 (уже до полуночи). При этом для уточнения периода суток добавляют: «до полудня», «после полудня» или указывают: «ночи», «утра», «дня» или «вечера».

Так, 15 часов – это 3 часа после полудня, или просто 3 часа дня, а 22 часа – это 10 часов после полудня, или 10 часов вечера.

Час делится на 60 минут, каждая минута состоит из 60 секунд.

Про год и летоисчисление вы узнаете больше из этой статьи.

Именованные числа

Определение.

Именованное число – это числовое выражение величины измерения совместно с указанием единиц измерения этой величины.

Отвлеченное число – это просто число без указания единицы измерения какой-либо величины.

Например, 12 деревьев, 3 килограмма, 135 литров – это именованные числа, а 12, 3 и 135 – отвлеченные.

Именованное число может состоять только из одной меры: 18 л, 312 км, 48 г, или из нескольких, но обязательно однородных: 5 кг 640 г, 12 м 72 см.

Нельзя в одном именованном числе смешивать меры разных величин, например, так: 12 кг 58 см или 15 л 12 г.

Простое именованное число – имеет в своем составе только одно наименование какой-либо величины.

Составное именованное число выражается несколькими единицами измерения одной и той же величины.

Именованные числа можно преобразовывать в более крупные или мелкие наименования однородных мер, то есть, увеличивать или уменьшать их разряд.

Превращением или укрупнением именованного числа называется его преобразование в более крупное наименование однородной меры.

Раздроблением именованного числа называется его преобразование в более мелкие единицы однородной меры.

Так, записав именованное число 5203 метра как 5 км 203 м, мы совершили превращение, а преобразовав 5 км 203 м в 5203 м, – раздробление.

Именованные числа называются равными, если они обозначают одну и ту же величину. При этом их записи могут отличаться. К примеру, 5 километров 203 метра и 5203 метра – это равные именованные числа.

Источник

Цена. Количество. Стоимость

В этом разделе научимся решать задачи и составлять таблицы по теме “Цена. Количество. Стоимость” и научимся находись зависимость между этими величинами.

Цена. Количество. Стоимость.

Стоимость – это то, что мы заплатили за всю покупку.

Задача 1: Наташа купила 5 открыток по 3 р. за каждую. Сколько стоила вся покупка?

Количество Цена Стоимость
5 шт. 3 р. ?

Чтобы узнать стоимость, нужно цену умножить на количество.

Цена. Количество. Стоимость.

Цена показывает сколько стоит один предмет.

Задача 2: Наташа купила 5 открыток и заплатила за них 15 р. Сколько стоила одна открытка?

Количество Цена Стоимость
5 шт. ? 15 р.

Чтобы найти цену, нужно стоимость разделить на количество.

Цена. Количество. Стоимость.

Количество показывает сколько предметов мы купили.

Задача 3: Наташа купила несколько открыток по 3 р. за каждую и отдала за покупку 15 р. Сколько открыток купила Наташа?

Количество Цена Стоимость
? 3 р. 15 р.

Чтобы найти количество, нужно стоимость разделить на цену.

Количественный и порядковый счёт

Математический счёт — это действие, позволяющее определить количество чего-либо. Счёт может быть количественным или порядковым.

Количественный

Количественный счёт — это определение количества предметов. Количественный счёт позволяет ответить на вопрос сколько? .

Например, чтобы узнать количество парт в классе или сколько деревьев растёт в саду, необходимо их сосчитать. Количественный счёт заключается в том, что, отделяя каждый раз один предмет за другим (на самом деле или только мысленно), мы называем количество отделённых предметов. Например, считая парты в классе, мы мысленно отделяем одну парту за другой и говорим: один, два, три, четыре, пять и т. д. Если при отделении последней парты мы сказали, например, восемь, значит, в классе всего восемь парт. Число восемь в этом случае является результатом счёта.

количественный и порядковый счет предметов

Результат счёта — это количество предметов, полученное в результате их счёта.

Результат счёта не зависит от того порядка, в каком считаются предметы.

Так, считая парты в классе, мы получим одно и то же число независимо от того, считаем ли мы от передних парт к задним или наоборот — от задних к передним. Важно только, чтобы при подсчёте парт, ни одна парта не была пропущена и ни одна не сосчитана два раза.

Число, при котором есть наименование тех единиц, от счёта которых оно получилось, называется именованным. В нашем случае, так как мы считали парты, число восемь является именованным (восемь парт). Число, у которого отсутствует наименование единиц, называется отвлечённым.

Порядковый

Порядковый счёт — это определение количества предметов и место каждого предмета относительно других. Порядковый счёт позволяет ответить на вопрос какой? (например, какой по счёту? или какой по порядку? ).

Например, для определения количества карандашей можно воспользоваться количественным счётом и посчитать карандаши в любом порядке:

количественный счет

Но если нужно узнать какой по счёту зелёный карандаш, то следует воспользоваться порядковым счётом. В этом случае каждый карандаш получает номер, указывающий каким по счёту он идёт:

порядковый счет

Так как карандаши расположены друг за другом, то зелёный карандаш будет третьим, если считать слева направо, и четвёртым, если считать справа налево.

При порядковом счёте, если считаются все предметы, то результатом счёта будет номер, указывающий порядок последнего посчитанного предмета. В нашем случае, так как последний посчитанный карандаш является шестым, то и общее количество предметов равно шести.

Номер — это порядковое число предмета в ряду других предметов.

Как найти количество правила в математике

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

Свойства сложения
Формула пути

= 50км, = 2ч, = 25км/ч

, 25км/ч = 50км : 2ч

, 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений
  • Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
  • Чтобы найти неизвестное уменьшаемое, надо к разности при­бавить вычитаемое.
  • Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
  • Чтобы найти неизвестный множитель, надо произведение раз­делить на известный множитель.
  • Чтобы найти неизвестное делимое, надо делитель умножить на частное.
  • Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Отрезок, прямая, луч
Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

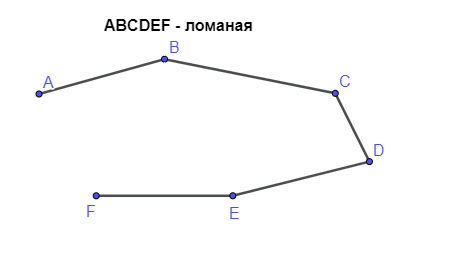
Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.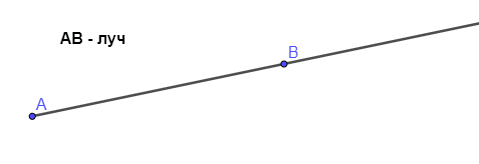

Угол, биссектриса угла

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

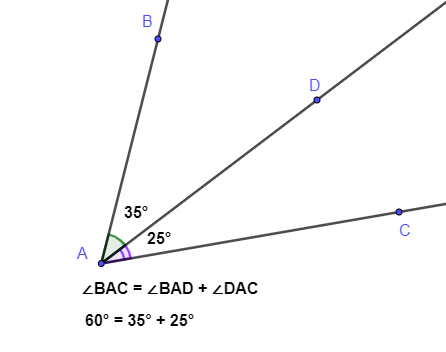
Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой
Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры
Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр
Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения
Умножение
  • Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.
  • Если один из двух множителей равен 1, то произведение равно второму множителю.
  • Если один из множителей равен нулю, то произведение равно нулю.
  • Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
  • Переместительный закон умножения:
  • Сочетательный закон умножения:
  • Распределительное свойство умножения относительно сложения:
  • Распределительное свойство умножения относительно вычитания:
Деление. Деление с остатком
Деление

Для натуральных чисел равенство является правильным, если является правильным равенство

В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

Деление с остатком

, где — делимое, — делитель, — неполное частное, — остаток, .

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

где — площадь основания параллелепипеда, — его высота.

Объем куба

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей
Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей
  • Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
  • Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
  • Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
  • Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
  • Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
  • Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
  • Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
  • Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

  • числитель разделить на знаменатель;
  • полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

  • целую часть числа умножить на знаменатель дробной части;
  • к полученному произведению прибавить числитель дробной части;
  • эту сумму записать как числитель неправильной дроби;
  • в его знаменателе записать знаменатель дробной части смешанного числа.
Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

  • с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
  • после чего сравнить полученные дроби поразрядно.
Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

  • все следующие за этим разрядом цифры отбросить.
  • если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4 , то последнюю из цифр, которые оставляют, не меняют ;
  • если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9 , то последнюю из цифр, которые оставляют, увеличивают на единицу.
Десятичные дроби: сложение, вычитание
Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

  • уравнять количество цифр после запятых;
  • записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
  • сложить полученные числа так, как складывают натуральные числа;
  • поставить в полученной сумме запятую под запятыми.
Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

  • уравнять количество цифр после запятых;
  • записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
  • выполнить вычитание так, как вычитают натуральные числа;
  • поставить в полученной разности запятую под запятыми.
Десятичные дроби: умножение, деление
Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

  • перемножить их как натуральные числа, не обращая внимания на запятые;
  • в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

  • перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
  • выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Процент

Процентом называют сотую часть величины или числа 1%=

Основные правила математики с примерами. 5 класс: 22 комментария

Спасибо большое! Я решил вспомнить материал по математике и вы мне с этим помогли

Уважаемая Наталья Владимировна! По структуре и подаче материала — это лучшее, что мне удалось найти на просторах интернета. Спасибо вам за труд!

Источник

математика единицы измерения классЧтобы сделать перевод единиц из одной единицы измерения в другую, нужно знать — из чего состоит та или иная единица измерения. Например, для перевода единиц длины нужно знать, что один сантиметр состоит из десяти миллиметров или один километр состоит из тысячи метров и т.д.

Итак, прежде чем приступить к правилам перевода единиц измерения одной единицы измерения в другую, давайте вспомним основные единицы измерения в математике«:

При этом единиц измерения существует гораздо больше. В том числе есть составные единицы измерения (например, скорость), для перевода которых необходимо перевести каждую составляющую. Например, для перевода скорости нужно перевести расстояние и время.

Перевод единиц измерения длины

Для того, чтобы перевести одну единицу измерения в другую, нужно число умножить или разделить на число, кратное 10 (10,100,1000 и т.д.) в зависимости от соотношения.

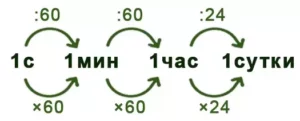
Чтобы переводить время из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения времени. То есть нужно знать, что к примеру один час состоит из шестидесяти минут или одна минута состоит из шестидесяти секунд и т.д.

Пример 7. Перевести единицы измерения времени: 2 минуты (мин) в секунды (с).
Число 2 умножаем на 60, так как 1мин = 60с.
Получаем: 2 мин =2 * 60 с = 120 с.

Пример 8. Перевести единицы измерения времени: 180 минут (мин) в часы (ч).
Число 180 делим на 60, так как 1 ч = 60мин.
Получаем: 180мин = 180: 60 = 3 ч.

Пример 9. Перевести единицы измерения времени: 10080 минут (мин) в сутки.
Если напрямую сделать перевод сложно, то его можно сделать в 2 этапа: мин → ч → сутки.
Число 10080 м сначала делим на 60 (1ч=60мин ), а затем делим на 24(1сутки=24ч)
Получаем: 1) 10080мин = 10080:60= 168ч.; 2)168ч=168:24=7 суток.

При переводе единиц измерения времени также применима схема, подсказывающая что применять — умножение или деление:

Свои вычисления вы можете проверить с помощью конвертера единиц измерения времени.

Перевод единиц измерения площади

Чтобы переводить площадь из одной единицы измерения в другую, нужно знать из чего состоят единицы измерения длины. Так как площадь — это величина составная, то для перевода нужно число умножить или разделить на число, кратное 10 (10,100,1000 и т.д.) в квадрате в зависимости от соотношения.

Пример 10. Перевести единицы измерения длины: 2 квадратных километра (км2) в квадратные метры (м2).
Число 2 умножаем на 10002, так как 1км2 = 1 0002 м2=1 000 000 м2.
Получаем: 2 км2 =2* 1 000 000 м2 = 2 000 000 м2

Свои вычисления вы можете проверить с помощью конвертера единиц измерения площади.

Перевод единиц измерения скорости

Чтобы переводить скорость из одной единицы измерения в другую, нужно знать из чего состоят единицы измерения длины и времени. Для перевода нужно отдельно перевести расстояние и время.

Для того, чтобы быстро и правильно определить действие умножения или деления при переводе единиц скорости, рассмотрим величину скорости как обыкновенную дробь:
— числитель — это расстояние
— знаменатель — это время.
Например, скорость 900 км/ч можно представить в виде дроби 900км/1ч.

Пример 11. Перевести 900 км/ч в км/мин.
1) Километры остаются, значит никаких действий не будет.
2) Переведем часы в минуты. Так как в одном часе 60минут, то нам нужно умножить на 60 минут. Но умножать мы будем знаменатель дроби: 900км/1час = 900 км/(1*60)мин.
Получаем: 900* 1 км : 60 мин = 15 км/мин.

Пример 12. Перевести 360 км/ч в м/с.
1) Переведем километры в метры, для этого умножаем на 1000, так как 1 км = 1000 м.
2) Переведем часы в секунды, для этого умножаем на 3600, так как 1 ч= 60 м = 3600 с. (умножать мы будем знаменатель, поэтому по факту это действие деления)
Получаем: 360 км/ч = (360*1000)м / (1*3600)с = 100 м/с.

Пример 13: перевести 1 м/с в км/ч.
1) Переведем метры в километры, для этого делим на 1000, так как 1 км = 1000 м.
1 км = 1000 м ⇒ 1 м = 0,001 км.
2) Переведем секунды в часы, для этого делим на 3600, так как 1 ч= 60 м = 3600 с.
1 ч= 60 м = 3600 с ⇒ 1 с = 1/3600 ч
Получаем: 1 м/с =  (1/1000)км / (1/3600)ч = 3600/1000 (км/ч) = 3,6 км/ч.

Свои вычисления вы можете проверить с помощью конвертера единиц измерения скорости.

Скачать программу  «Действия с именованными числами«. 
Группы заданий: 1) Единицы длины; 2) Единицы массы; 3) Единицы времени. Четыре типа карточек с разными видами заданий:  Преобразование; Сравнение; Сложение и вычитание; Умножение и деление.

В заключении

Умение преобразовывать именованные числа и совершать действия с ними пригодится не только для того, чтобы решать задачи по математике. Эти знания помогут купить нужное количество ткани, чтобы сшить одежду по определённым меркам, или посчитать время, которое ты затрачиваешь на какое-то дело. Навыки работы с именованными числами нужны, чтобы сделать ремонт или поменять валюту, и очень важны во многих профессиях, таких как продавец, повар, архитектор. Ещё именованные числа постоянно используются в науке, и знания о них пригодятся на уроках физики, химии, геометрии и черчения.

Источник

Добавить комментарий