Определить принадлежность точки отрезку, казалось бы, вполне себе тривиальная задача из школьного курса геометрии. Однако, есть определенные нюансы, которые заставляют усомниться в верности классической формулы:
Причины и постановка задачи
Запросы «как найти принадлежность точки отрезку» уводят на страницу «Пересечение прямых, угол и координаты пересечения», где есть пункт «Принадлежность точки отрезку». В нем рассматривается факт принадлежности точки отрезку, уже после того, как мы определили точку пересечения прямых. То есть точка уже принадлежит прямым, и это абсолютно точно. Осталось только определиться, точка в отрезке между двумя точками отрезка, либо где-то на прямой мимо них.
Людям свойственно искать готовые решения, и код, представленный в статье вряд ли удовлетворит запросу «как найти принадлежность точки отрезку, заданный двумя точками«. Поэтому здесь задачу так и сформулируем:
Есть отрезок, заданный точками P1(x1,y1) и P2 (x2,y2) . Необходимо определить, принадлежит ли точка P(x,y) этому отрезку.
Классическое уравнение
Предположим, вы делаете векторный редактор. Необходимо по курсору мыши определить попадает ли точка в ранее нарисованный отрезок. В этом многотрудном деле такая задача возникает всегда.
Для совместимости с Delphi 7 введем тип вещественной точки:
|
type {$IF CompilerVersion < 26} TxPoint = record X: Single; Y: Single; end; {$ELSE} // >= XE5 TxPoint = TPointF; {$IFEND} |
Почему бы не сделать сразу TPointF вместо типа TxPoint? Просто у меня гора старых исходников, где используется этот тип, а никакого TPointF не было ни в помине, ни в планах. Delphi 7 казалась вершиной инженерной мысли на тот момент.
В предложение uses дописываем следующее (ради TPointF, и чтобы компилятор XE не доставал хинтами):
|
interface uses Windows, SysUtils, Classes, Graphics, Controls, Forms, ... {$IF CompilerVersion > 25} // >= XE5 , System.Types {$IFEND} ; |
Почему именно XE5? Если честно, нет возможности проверить, не ставить же ради этого всю линейку дельфей. Но в XE5 вещественная точка точно есть, а в Delphi 7 ее точно нет. Вот этим и объясняется выбор версии компилятора в директиве. Одни говорят, что TPointF появился в XE2, другие — аж в Delphi 2010. Короче, с таким директивным условием будет работать везде и точка.
Пишем небольшую функцию, которая использует классическое уравнение прямой, проходящей через две различные точки на плоскости, представленное выше.
|
function PtInSegment(const P1, P2, P: TxPoint; const Epsilon: extended; var res: TxPoint): Integer; begin Result := 0; res := p; if // проверка Y-координаты SameValue(Abs(p1.Y–p.Y) + Abs(p2.Y–p.Y), Abs(p2.Y–p1.Y), Epsilon) and // проверка X-координаты SameValue(Abs(p1.X–p.X) + Abs(p2.X–p.X), Abs(p2.X–p1.X), Epsilon) and // используется классическая формула SameValue((p.x–p1.x)*(p2.y–p1.y) – (p.y–p1.y)*(p2.x–p1.x), 0, Epsilon) then Result := 3; end; |
SameValue — сравнивает два вещественных числа с учетом погрешности Epsilon. Находится в модуле Math, который надо подключить в предложении uses секции implementation.
Что происходит. Вначале проверяется допустимость координаты точки внутри координат отрезка. Условие необходимое, но недостаточное. Если координата может принадлежать отрезку, третьим условием проверяем нахождение точки на прямой, проходящей через точки отрезка.
Если мы попытаемся по координатам курсора мыши определить, попала ли точка в отрезок, нас ждет фиаско. Складывается ощущение, что формула не работает, алгебра — отстой, все в жизни не так.
Расширенная классика
Для начала навесим на функцию еще пару условий, чтобы определить попадание в точки, задающие отрезок.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
// сравнить две точки с учетом погрешности function PtEqual(const P1,P2: TxPoint; const Epsilon: extended = 0.0): Boolean; begin Result := SameValue(P1.X, P2.X, Epsilon) and SameValue(P1.Y, P2.Y, Epsilon); end; // классика с учетом попадания на точки P1 и P2 // режим нахождения на отрезке: 0 – мимо, 1 – p1, 2 – p2, 3 – между p1 и p2 function PtInSegmentEx(const P1, P2, P: TxPoint; const Epsilon: extended; var res: TxPoint): Integer; begin Result := 0; res := p; if PtEqual(P1, P, Epsilon) then Result := 1 else if PtEqual(P2, P, Epsilon) then Result := 2 else if SameValue(Abs(p1.Y–p.Y) + Abs(p2.Y–p.Y), Abs(p2.Y–p1.Y), Epsilon) and SameValue(Abs(p1.X–p.X) + Abs(p2.X–p.X), Abs(p2.X–p1.X), Epsilon) and SameValue((p.x–p1.x)*(p2.y–p1.y) – (p.y–p1.y)*(p2.x–p1.x), 0, Epsilon) then Result := 3; end; |
Ну, во-первых, вот и разгадка, куда делись значения 1 и 2 из результатов предыдущей функции. Во-вторых, теперь в конечные точки отрезка попадает отлично, но между ними по-прежнему не хочет работать.
На самом деле — математика по-прежнему царица наук, а мы пытаемся повенчать розу белую с черной жабой.
Выведем в интерфейс значения dx = (p2.x-p1.x), dy = (p2.y-p1.y) и т.д. Плюс результат работы функции (p.x-p1.x)*(p2.y-p1.y) — (p.y-p1.y)*(p2.x-p1.x). И убедимся, что при самых казалось бы максимально возможных приближениях к отрезку, результат ошеломляет своей двух- или трехзначной непохожестью на ноль.
Конечно, используя операцию умножения вместо деления, мы избегаем деления на ноль, укорачиваем код. Но при этом надо помнить, что умножение даже 1 на 12, это уже далеко от нуля, а если появляется еще и минус в разницах, то от нуля мы улетаем очень быстро и очень ощутимо.
На рисунке 2 прицел точно на линии, но разность координат, которую получаем из классического уравнения, и которая должна быть равна нулю, между тем равна:
f(x,y)=(x-x1) * (y2-y1) — (y-y1) * (x2-x1) = -16
Функция применима в точных расчетах, но не в векторном редакторе.
Модификация уравнения
Очевидно, надо вычислять как-то иначе. Например вычислять Y по имеющейся координате X и сравнивать с имеющейся координатой Y. Если разница меньше заданного Epsilon — точка принадлежит отрезку. Выразим Y из используемого уравнения прямой. Итак, дано:
Выразим Y:
И напишем еще одну функцию, в которой учтем ситуацию, когда (X2-X1) может быть равно нулю. Это ситуация вертикальной (или почти вертикальной) прямой.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
function PtInSeg(const P1, P2, P: TxPoint; const Epsilon: extended; var res: TxPoint): Integer; begin Result := 0; res := p; // сравнить с точкой P1 if PtEqual(P1, P, Epsilon) then begin res := p1; Result := 1; end else // сравнить с точкой P2 if PtEqual(P2, P, Epsilon) then begin res := p2; Result := 2 end else // проверить на вхождение в координатный допуск отрезка if SameValue(Abs(p1.Y–p.Y) + Abs(p2.Y–p.Y), Abs(p2.Y–p1.Y), Epsilon) and SameValue(Abs(p1.X–p.X) + Abs(p2.X–p.X), Abs(p2.X–p1.X), Epsilon) then begin Result := 3; // это почти вертикальная линия, Y уже проверен условием выше if SameValue(p1.X,p2.X,Epsilon) then begin res.x := p1.X + (p2.X – p1.X) / 2; Exit; end; // посчитать Y и сравнить с точкой P res.Y := (p.X–p1.x)*(p2.Y–p1.y)/(p2.X–p1.x) + p1.Y; if SameValue(p.Y, res.y, Epsilon) then Exit; Result := 0; end; end; |
Epsilon уже выступает, и как точность вычислений, и как допуск, при котором мы считаем, что точка на отрезке. Невозможно скрупулезно попасть мышкой в нужную точку отрезка, которая сама по себе уже есть огромное приближение к действительности. Все мы помним и любим Брезенхэма.
Но, даже если мы упростили себе процесс «попадания» в отрезок, мы должны знать точные координаты на отрезке. Для этого у нас и появился тип вещественной точки TxPoint и возвращаемый параметр res. В этой версии функции мы производим расчет реальной точки на отрезке.
На рисунке 3 расчетная точка и ее координаты выделена коричневым цветом.
Однако, все равно есть нюанс. Если линия сильно вертикальна, то есть расстояние (X2-X1) невелико, попадать в линию все равно трудно.
Связано с тем, что при уменьшении делителя, коим разность по X выступает в нашем случае, сильно вырастает результат, и чем расстояние (X2-X1) меньше, тем труднее попасть в Epsilon.
Итоговая функция
В стремлении к совершенству, всегда что-то незамысловатое, в пару строк кода, разрастается в какую-то все учитывающую портянку листинга.
Давайте проверять, что больше (X2-X1) или (Y2-Y1), и в зависимости от результата, будем высчитывать либо Y, либо X. Формулу для X не привожу, он очевидна.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
function PtInSegEx(const P1, P2, P: TxPoint; const Epsilon: extended; var res: TxPoint): Integer; var dx, dy, px, py: Single; begin Result := 0; res := p; if PtEqual(P1, P, Epsilon) then begin res := p1; Result := 1 end else if PtEqual(P2, P, Epsilon) then begin res := p2; Result := 2 end else begin // просто для понятности кода dx := (p2.X–p1.X); dy := (p2.Y–p1.Y); px := (p.X–p1.X); py := (p.Y–p1.Y); // линия почти вертикальна if SameValue(dx,0,Epsilon) then begin // во избежание деления на ноль. // ситуация мифическая, т.к. проверена уже выше в точках, но… if SameValue(dy,0) then res.X := p1.X + dx/2 else res.X := py*dx/dy + p1.x; // сравнить X точки с расчетным значением if SameValue(p.x, res.x, Epsilon) and // и проверить координату Y, которая должна быть в диапазон Y1..Y2 SameValue(Abs(p1.Y–p.Y) + Abs(p2.Y–p.Y), Abs(p2.Y–p1.Y), Epsilon) then Result := 3; exit; end; // линия почти горизонтальна if SameValue(dy,0,Epsilon) then begin // dx=0 уже отработан условием выше, деления на 0 не боимся res.Y := px*dy/dx + p1.Y; if SameValue(p.y, res.y, Epsilon) and SameValue(Abs(p1.x–p.x) + Abs(p2.x–p.x), Abs(p2.x–p1.x), Epsilon) then Result := 3; exit; end; // проверка координат точки на валидность координатам отрезка if SameValue(Abs(p1.Y–p.Y) + Abs(p2.Y–p.Y), Abs(p2.Y–p1.Y), Epsilon) and SameValue(Abs(p1.X–p.X) + Abs(p2.X–p.X), Abs(p2.X–p1.X), Epsilon) then begin // x2-x1 больше подходит в качестве делителя, // считаем и сравниваем Y if (abs(dx) > abs(dy)) then begin res.Y := px*dy/dx + p1.Y; if SameValue(p.Y, res.Y, Epsilon) then Result := 3; end else // иначе считаем и сравниваем X begin res.X := py*dx/dy + p1.x; if SameValue(p.x, res.X, Epsilon) then Result := 3; end; end; end; end; |
Почему такая большая функция получилась?
В функции помимо факта принадлежности точки отрезку, также осуществляется проверка на конечные точки — чтобы можно было менять их расположение мышкой. Также, функция возвращает «истинную» точку на отрезке, полученную из приближенной, содержащую погрешность Epsilon.
Можно сократить, не считать конечные точки, не анализировать «вертикальность» и «горизонтальность». Можно взять за настоящую ту точку, которую анализируем и не считать «истинную». Код в этом случае сильно сократиться. Поэтому лучше иметь полный комплект, из которого можно удалить «лишнее» на ваш взгляд.
Зачем нужны такие ощутимо большие проверки на вертикальность и горизонтальность. Ну, во-первых мы освобождаем от условий последний блок вычислений, во-вторых, если убрать, скажем, проверку на dy, погрешность станет в два раза меньше. Потому что отработает это условие: Abs(p1.Y-p.Y) + Abs(p2.Y-p.Y). Имея идеальную горизонтальную линию, подведя курсор на Epsilon допустимый интервал, мы получим в итоге Epsilon + Epsilon = 2 * Epsilon и условие конечно не сработает. Сработает, если подведем на расстояние в два раза меньшее Epsilon.
Если всех этих тонкостей не требуется, можно смело использовать либо эту, либо вообще эту функцию.
Классика всегда в моде или Математика — царица наук
Теперь давайте полученную в результате предыдущей функции вещественную точку res подставим в первую функцию. И убедимся, что теоретическая принадлежность точки отрезку работает прекрасно, просто в пространстве грубых целочисленных точек мы не в состоянии гарантированно получить такую точку, которая удовлетворила бы уравнению. Но если мы ее рассчитаем и получим значения с плавающей запятой — все заработает как надо.
На рисунке 5 добавлен результат функции f(x,y)=(x-x1) * (y2-y1) — (y-y1) * (x2-x1) для рассчитанной точки на отрезке. Он равен, как и следовало ожидать, нулю. А также результат вызова первой функции, которая использует это уравнение и возвращает 3, если точка принадлежит отрезку. Что мы воочию и видим.
1)Поэтому в графике надо избегать типов TPoint, даже если это вызывает необходимость постоянно их округлять для функций GDI.
2)Поэтому функция правильная, классическая формула работает, просто в пространстве компьютерных упрощений надо использовать ту же самую формулу, но в другом качестве.
Скачать
Друзья, спасибо за внимание!
Надеюсь, материал был полезен.
Не пропустите новых интересных штуковин, подписывайтесь на телегу. )))
Если есть вопросы, с удовольствием отвечу.
Исходники и исполняемый файл для GDI и Delphi 7. Проверен в XE 7, XE 10.
Исходники (Delphi 7, XE7, XE10) 11 Кб
Исполняемый файл (zip) 213 Кб
Исполняемый файл c GDI+ (zip) 216 Кб
Как подключить GDI+ в Delphi 7 и без проблем скомпилировать в XE 7, XE 10 читаем в этой статье. Там же забираем исходники.
Чтобы нарисовать отрезок, нажмите мышь и, не отпуская, ведите курсор. При отпускании отрезок зафиксируется. При повторном нажатии начнет рисоваться новый отрезок.
За концы отрезка можно таскать. Если попали на отрезок, т.е. видна коричневая точка, можно таскать весь отрезок.
Исходники намеренно выложены в D7 варианте.
При компиляции в XE10 следует снять галочку с Enable High-DPI
Просмотров 21.6к. Обновлено 23 ноября 2020
Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку, заданному координатами своего начала и конца.
Для реализации операций сравнения над вещественными данными напишем еще две функции: функцию EqPoint(), которая ,будет проверять, совпадают ли две точки на плоскости и функцию RealMoreEq() , которую будем использовать для проверки отношения «>=» (больше или равно). Причина ввода специальных функций нам уже известна.
Задача. Проверить, принадлежит ли точка отрезку.
Решение.
Пусть точки — начальная и конечные точки отрезка.
— произвольная точка на плоскости.
Вектор с началом в точке и концом в точке
будет иметь координаты (x2-x1, y2-y1).
Если P(x, y) – произвольная точка, то координаты вектора равны: (x-x1, y – y1).
Точка Р будет принадлежать отрезку если:
- Векторы в
и
коллинеарны (равно нулю их векторное произведение):
, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0
- Абсцисса точки P удовлетворяет условию:
или
. Иначе точка будет находиться на прямой левее или правее отрезка.
Program geom3;
Const _Eps: Real = 1e-3; {точность вычислений}
var x1,y1,x2,y2,x,y:real;
Function RealEq(Const a, b:Real):Boolean; {строго равно}
begin
RealEq := Abs(a-b)<= _Eps
End; {RealEq}
Function RealMoreEq(Const a, b:Real):Boolean; {больше или равно}
begin
RealMoreEq := a - b >= _Eps
End; {RealMoreEq}
Function EqPoint(x1,y1,x2,y2:real):Boolean;
{Совпадают ли две точки на плоскости}
begin
EqPoint:=RealEq(x1,x2)and RealEq(y1,y2)
end; {EqPoint}
Function AtOtres(x1,y1,x2,y2,x,y:real):Boolean;
{Проверка принадлежности точки P отрезку P1P2}
Begin
If EqPoint( x1,y1,x2,y2)
Then AtOtres:= EqPoint( x1,y1,x,y)
{точки P1 и P2 совпадают, результат определяется совпадением точек P1 и P}
Else
AtOtres := RealEq((x-x1)*(y2-y1)- (y-y1)*(x2-x1),0)and (RealMoreEq(x,x1)and
RealMoreEq( x2,x)Or RealMoreEq(x,x2)and RealMoreEq( x1,x))
end; {AtOtres}
begin {main}
writeln(Введите координаты точек: x1,y1,x2,y2,x,y');
readln( x1,y1,x2,y2,x,y);
if AtOtres(x1,y1,x2,y2,x,y)
then writeln('Да.')
else writeln('Нет.);
end. {main}
Результаты выполнения программы.
Введите координаты точек: x1, y1, x2, y2, x,y
0.5 1 2.5 2.8 1.203 1.633
Да.
Результаты тестирования в программе GeoGebra:
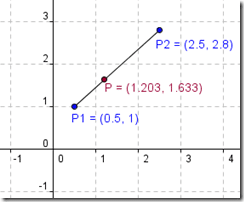
Сегодня мы написали функцию AtOtres() , которая проверяет принадлежность произвольной точки отрезку, заданному своими координатами.
Ввели еще две функции: EqPoint() и RealMoreEq() для реализации операций сравнения над вещественными данными. Первая проверяет, совпадают ли две точки на плоскости, вторая — используется для проверки отношения «>=».
На следующем уроке, на основе ранее написанных процедур, напишем процедуру определения координат точки пересечения двух отрезков.
На этом я с вами прощаюсь. До встречи на следующем уроке.
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
#1 15 июня 2004г. 11:15:36
- Олег
- Восстановленный участник
- На форуме с 21 мая 2004г.
- Сообщений: 9
- Спасибо: 0
Тема: Как определить принадлежит ли точка отрезку или нет?
Как определить принадлежит ли точка отрезку или нет?
#2 Ответ от VH 15 июня 2004г. 11:19:04
- VH
- Активный участник
- На форуме с 14 июня 2001г.
- Сообщений: 1,381
- Спасибо: 7
Re: Как определить принадлежит ли точка отрезку или нет?
Точка принадлежит отрезку, если сумма расстояний от этой точки до конечных точек отрезка равна длине отрезка.
#3 Ответ от AY 15 июня 2004г. 16:13:10
- AY
- Восстановленный участник
- На форуме с 22 августа 2003г.
- Сообщений: 465
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Очень интерестно проходит ли такая проверка.
Я в свое время для похожей задачи по двум точкам отрезка задавал уравнение прямой и подставлял в него координаты точки. Теоретически если точка на прямой уравнение обнуляется (aX+bY+c=0) на практике условие проходило если отрезок горизонтален или вертикален (точку получал указанием с привязкой к ближнему), ели нет погрешность приходилось учитывать (при конечной точности вычислений в данном случае это неизбежно) .
#4 Ответ от Alexander 15 июня 2004г. 19:48:21
- Alexander
- Восстановленный участник
- На форуме с 1 июня 2004г.
- Сообщений: 42
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Если устроит попробуйте использовать
функцию (vlax-curve-getParamatPoint <кривая> <точка>).
Если вернёт nil значит точка не лежит на кривой.
У Полещука написано <кривая> – VLA-объект,
но как показывает практика можно и имя примитива.
#5 Ответ от kserg 15 июня 2004г. 21:25:20
- kserg
- Активный участник
- На форуме с 2 апреля 2004г.
- Сообщений: 260
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Когда-то (в AutoCAD10) выходил из положения так :
(setq Nabor (ssget “_C” t1 t1))
,- где t1 – координаты точки [например, ‘(150 175 0)],
а затем, перебирал объекты, попавшие в набор “Nabor”, на предмет наличия среди них того самого отрезка…
#6 Ответ от Leonid 15 июня 2004г. 22:08:57
- Leonid
- Восстановленный участник
- На форуме с 16 июня 2003г.
- Сообщений: 389
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Я в свое время точно также как и AY пытался решить эту задачу на основе линейных уравнений. Оказалось, что камнем преткновения является погрешность вычислений. В итоге, метод работает ненадежно и неустойчиво. По-видимому, сама постановка вопроса -Точка принадлежит линии – при переводе в практическую плоскость нуждается в переосмыслении. А что есть прямая (линия), ведь это не более чем выдумка античных математиков…ведь она не имеет толщины, и следовательно – не существует. Я понимаю, все это звучит несколько академически, однако вопрос надо решать!
Давайте считать линией полосу конечной ширины, и при постановке задачи указывать эту ширину. Интересно было бы услышать мнение профессиональных математиков, например, специалистов по теории множеств.
#7 Ответ от Fantomas 16 июня 2004г. 01:28:17
- Fantomas
- Восстановленный участник
- На форуме с 7 декабря 2003г.
- Сообщений: 392
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Тоже недавно делал проверку принадлежности точки сфере. Естественно сравнение через EQUAL, смотря какая точность нужна…
Есть еще идея. Существует функция vlax-curve-getDistAtPoint <кривая> <точка> которая вычисляет расстояние между начальной точкой кривой (а в нашем случае отрезка) до точки на кривой. В случае если точка не лежит на кривой она возвратит Nil.
#8 Ответ от Миша 16 июня 2004г. 09:02:42
- Миша
- Восстановленный участник
- На форуме с 31 декабря 2001г.
- Сообщений: 322
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Public Function ТочкаНаПрямой(dblСписокКоордПрямой As Variant, XCoordТочки As Double, YCoordТочки As Double) As Boolean
Dim РасстояниеДоТочки As Double, РасстояниеПослеТочки As Double, ДлинаПрямой As Double
РасстояниеДоТочки = VBA.Sqr((XCoordТочки – dblСписокКоордПрямой(1)) ^ 2 + (YCoordТочки – dblСписокКоордПрямой(2)) ^ 2)
РасстояниеПослеТочки = VBA.Sqr((dblСписокКоордПрямой(3) – XCoordТочки) ^ 2 + (dblСписокКоордПрямой(4) – YCoordТочки) ^ 2)
ДлинаПрямой = VBA.Sqr((dblСписокКоордПрямой(3) – dblСписокКоордПрямой(1)) ^ 2 + (dblСписокКоордПрямой(4) – dblСписокКоордПрямой(2)) ^ 2)
If VBA.Round(РасстояниеДоТочки + РасстояниеПослеТочки, 7) = VBA.Round(ДлинаПрямой, 7) Then
‘Точка находится на прямой
ТочкаНаПрямой = True
Else
‘Точка находится вне прямой (ответ = расстояние от конца прямой до точки)
‘ ТочкаНаПрямой = (РасстояниеДоТочки + РасстояниеПослеТочки – ДлинаПрямой) / 2
ТочкаНаПрямой = False
End If
End Function
Эта функция работает без видимых и заметных сбоев уже долгое время. Весь секрет в том, что надо задавать как все нормальные люди точность своих вычислений, а не пытаться выполнить свою задачу с точностью до микрона там где требуется точность максимум до милиметра, и 7 знаков после запятой при единицах измерения мм вполне достаточно. Можете повысить точность до 12 чисел и выше, однако математические способности VBA уже начинают выдавать вместо 1 число 0,9999999999999999999999999999 и выражение 1=1 (при определёном задании и способах получения переменых) уже может не являться истиной. Прежде всего надо знать пределы математических возможностей программы с которой вы работаете и не тратить время на излишнюю точность а выдавать продукцию.
#9 Ответ от AY 16 июня 2004г. 10:22:31
- AY
- Восстановленный участник
- На форуме с 22 августа 2003г.
- Сообщений: 465
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Как уже писал, при теоретическом подходе учет пргрешности неизбежен, однако предположу, что функции (vlax-* могут контролировать и учитывать ее и выдавать достоверный результат. Может ли кто-нибудь подтвердить такое предположение?
#10 Ответ от Олег 16 июня 2004г. 15:33:27
- Олег
- Восстановленный участник
- На форуме с 21 мая 2004г.
- Сообщений: 9
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
*1.2 Аналитическая геометрия на плоскости.*
_1.2.1 Основные формулы в Декартовой системе координат._
P1(x1, y1), P2(x2, y2), P3(x3, y3), P4(x4, y4)
– Расстояние:
d(P1, P2) = sqrt((x1-x2)^2 + (y1-y2)^2)
– Угол между двумя веторами P1P2 P3P4:
(x2-x1)(x4-x3) + (y2-y1)(y4-y3) (P1P2, P3P4)
cos(al) = ——————————— = ——————-
d(P1, P2)*d(P3, P4) d(P1, P2)*d(P3, P4)
(x2-x1)(y4-y3) – (x4-x3)(y2-y1) [P1P2, P3P4]
sin(al) = ——————————— = ——————
d(P1, P2)*d(P3, P4) d(P1, P2)*d(P3, P4)
(x2-x1)(y4-y3) – (x4-x3)(y2-y1) [P1P2, P3P4]
tg (al) = ——————————— = ——————
(x2-x1)(x4-x3) + (y2-y1)(y4-y3) (P1P2, P3P4)
– Координаты x, y точки P, делящей P1P2 в отношении m/n = p/1
mx2 + nx1 x1 + qx2
x = ——— = ———;
n + m 1 + p
my2 + ny1 x1 + qx2
y = ——— = ———;
m + n 1 + p
– Соответственно, если P – середина (n=m), то
x2 + x1 y2 + y1
x = ——-; y = ——-;
2 2
#11 Ответ от Олег 16 июня 2004г. 15:36:27
- Олег
- Восстановленный участник
- На форуме с 21 мая 2004г.
- Сообщений: 9
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
– Координаты x, y точки P, делящей P1P2 в отношении m/n = p/1
mx2 + nx1 x1 + qx2
x = ——— = ———;
n + m 1 + p
my2 + ny1 x1 + qx2
y = ——— = ———;
m + n 1 + p
– Соответственно, если P – середина (n=m), то
x2 + x1 y2 + y1
x = ——-; y = ——-;
2 2
#12 Ответ от Олег 16 июня 2004г. 16:08:38
- Олег
- Восстановленный участник
- На форуме с 21 мая 2004г.
- Сообщений: 9
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
– Координаты x, y точки P, делящей P1P2 в отношении m/n = p/1
x = (mx2 + nx1)/(n + m)=(x1 + qx2)/(1 + p)
y = (my2 + ny1)/(n + m)=(y1 + qy2)/(1 + p)
съезжают дроби…
– Соответственно, если P – середина (n=m), то
x = (x2 + x1)/2 ; y = (y2 + y1)/2
#13 Ответ от Leonid 16 июня 2004г. 22:31:01
- Leonid
- Восстановленный участник
- На форуме с 16 июня 2003г.
- Сообщений: 389
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
В моей задаче рассматривалось взаимодействие множества линий на плоскости (чертежа), в частности, исследовался вопрос о наложении линий. Пришлось пойти на то, что “точка”
определялась как некая область, размеры которой зависят от погрешности вычислений. При зтом – увеличение точности
приводило к неустойчивости, слишком маленькую точку общую для двух линий программа не ловила, а снижение точности приводило к размытости критериев, программа на выполняла своих функций, т.е. возникали ложные наложения. В итоге, оптимальный вариант так и не был найден.
#14 Ответ от Олег 17 июня 2004г. 10:10:05
- Олег
- Восстановленный участник
- На форуме с 21 мая 2004г.
- Сообщений: 9
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
;| ф-ция проверяет принадлежит ли точка отрезку или нет;
возвращает t – если принадлежит и nil – если нет
аргументы: p – точка, lps – список из 2-х точек отрезка eps – допуск погрешности
1 – считаем расстояние (d) от точки до отрезка и сравниваем с eps
расстояние меньше eps
2 – Точка находиться между двумя перпендикулярами, проведенными
через концы отрезка (используется скалярное произведение)
создал – Уланов О. В. 6/16/04 10:21 PM дома;-) .
с помощью http://faqs.org.ru/science/geometry_faq.htm
|;
(defun pts (p lps)
(setq x (car p) y (cadr p)
x1 (caar lps) y1 (cadar lps)
x2 (caadr lps) y2 (cadadr lps)
eps 10e-10
d (/(sqrt(abs(-(*(- x x1)(- y2 y1))(*(- y y1)(- x2 x1)))))(sqrt(abs(+(- x2 x1)(sqrt(abs(- y2 y1)))))))
2p (*(+(*(- x x1)(- x2 x1))(*(- y y1)(- y2 y1)))(+(*(- x x2)(- x2 x1))(*(- y y2)(- y2 y1))))
); setq
(cond
((> d (sqrt eps)) nil)
((< 2p eps) t)
(t nil)
); cond
); defun
(defun c:pbs (/)
(while
(setq p (getpoint “nВыдели точку!!!”)
en (entget(car(entsel “nУкажи линию!!!”)))
lps (list(cdr(assoc 10 en))(cdr(assoc 11 en)))
); setq
(cond
((eq(pts p lps)t)(print “nТочка лежит на отрезке!!!”))
((eq(pts p lps)nil)(print “nТочка не лежит на отрезке!!!”))
(t nil)
); cond
); while
); defun
#15 Ответ от VH 17 июня 2004г. 16:40:52
- VH
- Активный участник
- На форуме с 14 июня 2001г.
- Сообщений: 1,381
- Спасибо: 7
Re: Как определить принадлежит ли точка отрезку или нет?
(defun isOnLine (_начальная _конечная _точка _допуск)
(apply
'(lambda (_до_начальной _длина_отрезка _до_конечной)
(equal (+ _до_начальной _до_конечной) _длина_отрезка _допуск))
(mapcar 'distance (list _точка _начальная _точка) (list _начальная _конечная _конечная)))
)
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
Содержание
- Геометрия 7 класс. Точка, прямая и отрезок
- Как обозначить прямую
- Задача № 1 из учебника Атанасян 7-9 класс
- Решение задачи
- Как обозначается пересечение прямых
- Взаимное расположение прямой и точек
- Сколько общих точек имеют две прямые
- Первый случай расположения прямых
- Второй случай расположения прямых
- Третий случай расположения прямых
- Задача № 3 из учебника Атанасян 7-9 класс
- Решение задачи
- Что такое отрезок
- Как определить принадлежит ли точка отрезку или нет?
- Сообщения 15
- #1 Тема от Олег 15 июня 2004г. 11:15:36
- Тема: Как определить принадлежит ли точка отрезку или нет?
- #2 Ответ от VH 15 июня 2004г. 11:19:04
- Re: Как определить принадлежит ли точка отрезку или нет?
- #3 Ответ от AY 15 июня 2004г. 16:13:10
- Re: Как определить принадлежит ли точка отрезку или нет?
- #4 Ответ от Alexander 15 июня 2004г. 19:48:21
- Re: Как определить принадлежит ли точка отрезку или нет?
- #5 Ответ от kserg 15 июня 2004г. 21:25:20
- Re: Как определить принадлежит ли точка отрезку или нет?
- #6 Ответ от Leonid 15 июня 2004г. 22:08:57
- Re: Как определить принадлежит ли точка отрезку или нет?
- #7 Ответ от Fantomas 16 июня 2004г. 01:28:17
- Re: Как определить принадлежит ли точка отрезку или нет?
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
На рисунке изображена прямая a и точки D, F, G и H . Точки F и G лежат на прямой a . Точки D и H не лежат на прямой a .
В тексте точку обозначают символом « (·)» . Принадлежность и непринадлежность точки прямой обозначают символами « ∈ » и « ∉ ». Знак принадлежности можно запомнить как зеркальное отображение буквы « Э » или как знак евро « € » .
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
- (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
- (·)G ∈ a — точка G принадлежит прямой a ;
- (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
- (·)H ∉ a — точка H не принадлежит прямой a .
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
- На рисунке изображены:
- Прямая a
- Прямая f
- Прямая CH
- Прямая DK
Точки D, E и F — лежат на одной прямой, поэтому: прямая DE , прямая EF и прямая DF — это три разных имени одной и той же прямой.
Задача № 1 из учебника Атанасян 7-9 класс
Проведите прямую, обозначьте её буквой a и отметьте точки A и B , лежащие на этой прямой, и точки P, Q и R , не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a , используя символы ∈ и ∉ .
Решение задачи
Обозначим её буквой a .
Отметим точки (·)A и (·)B , лежащие на прямой a .
Отметим точки (·)P, (·)Q и (·)R , не лежащие на прямой a .
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
На рисунке прямые a и b не пересекаются . Прямые b и c пересекаются .
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
В тексте пересечение прямых обозначают символом ∩ . Информацию на рисунке выше можно записать следующим образом:
- b ∩ c — прямые b и с пересекаются;
- a ∩ c — прямые a и с пересекаются.
Прямые e и g имеют общую точку M . Другими словами, прямые пересекаются в точке M . Геометрическими обозначениями пересечение прямых в точке записывается так:
e ∩ g = (·)M
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через любые две точки можно провести прямую, и притом только одну .
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Возможен вариант, что прямые f и e пересекаются и, значит, имеют одну общую точку (·)M .
Третий случай расположения прямых
Предположим, что прямые f и e имеют две или больше общих точек. Например, точки (·)A и (·)B .
Но мы знаем, что через две точки можно провести только одну прямую. Значит, прямые f и e совпадают и наше предположение, что у двух прямых может быть две или более общих точек неверно .
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Теперь прямая a пересекается с прямой b , прямая b пересекается с прямой c и прямая c пересекается с прямой a .
В этом случае у нас только одна точка пересечения всех прямых — точка (·)D .
Но возможен и другой вариант. Мы можем провести третью прямую c так, чтобы она не проходила через точку (·)D . Тогда получится три точки пересечения — (·)D, (·)E и (·)F .
Прямая a пересекается с прямой b в точке (·)D , прямая b пересекается с прямой c в точке (·)F и прямая c пересекается с прямой a в точке (·)E . Условие задачи выполнено.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
Две точки, ограничивающие отрезок, называются концами отрезка. У отрезка на рисунке выше концы называются S и T .
Сам отрезок можно назвать ST или TS . Когда изображают отрезок, оставшиеся от прямой хвосты можно не рисовать.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Источник
Как определить принадлежит ли точка отрезку или нет?
Форумы CADUser → Программирование → LISP → Как определить принадлежит ли точка отрезку или нет?
Чтобы отправить ответ, вы должны войти или зарегистрироваться
Сообщения 15
#1 Тема от Олег 15 июня 2004г. 11:15:36
- Олег
- Восстановленный участник
- На форуме с 21 мая 2004г.
- Сообщений: 9
- Спасибо: 0
Тема: Как определить принадлежит ли точка отрезку или нет?
Как определить принадлежит ли точка отрезку или нет?
#2 Ответ от VH 15 июня 2004г. 11:19:04
- VH
- Активный участник
- На форуме с 14 июня 2001г.
- Сообщений: 1,381
- Спасибо: 7
Re: Как определить принадлежит ли точка отрезку или нет?
Точка принадлежит отрезку, если сумма расстояний от этой точки до конечных точек отрезка равна длине отрезка.
#3 Ответ от AY 15 июня 2004г. 16:13:10
- AY
- Восстановленный участник
- На форуме с 22 августа 2003г.
- Сообщений: 465
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Очень интерестно проходит ли такая проверка.
Я в свое время для похожей задачи по двум точкам отрезка задавал уравнение прямой и подставлял в него координаты точки. Теоретически если точка на прямой уравнение обнуляется (aX+bY+c=0) на практике условие проходило если отрезок горизонтален или вертикален (точку получал указанием с привязкой к ближнему), ели нет погрешность приходилось учитывать (при конечной точности вычислений в данном случае это неизбежно) .
#4 Ответ от Alexander 15 июня 2004г. 19:48:21
- Alexander
- Восстановленный участник
- На форуме с 1 июня 2004г.
- Сообщений: 42
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Если устроит попробуйте использовать
функцию (vlax-curve-getParamatPoint ).
Если вернёт nil значит точка не лежит на кривой.
У Полещука написано — VLA-объект,
но как показывает практика можно и имя примитива.
#5 Ответ от kserg 15 июня 2004г. 21:25:20
- kserg
- Активный участник
- На форуме с 2 апреля 2004г.
- Сообщений: 260
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Когда-то (в AutoCAD10) выходил из положения так :
(setq Nabor (ssget «_C» t1 t1))
,- где t1 — координаты точки [например, ‘(150 175 0)],
а затем, перебирал объекты, попавшие в набор «Nabor», на предмет наличия среди них того самого отрезка.
#6 Ответ от Leonid 15 июня 2004г. 22:08:57
- Leonid
- Восстановленный участник
- На форуме с 16 июня 2003г.
- Сообщений: 389
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Я в свое время точно также как и AY пытался решить эту задачу на основе линейных уравнений. Оказалось, что камнем преткновения является погрешность вычислений. В итоге, метод работает ненадежно и неустойчиво. По-видимому, сама постановка вопроса -Точка принадлежит линии — при переводе в практическую плоскость нуждается в переосмыслении. А что есть прямая (линия), ведь это не более чем выдумка античных математиков. ведь она не имеет толщины, и следовательно — не существует. Я понимаю, все это звучит несколько академически, однако вопрос надо решать!
Давайте считать линией полосу конечной ширины, и при постановке задачи указывать эту ширину. Интересно было бы услышать мнение профессиональных математиков, например, специалистов по теории множеств.
#7 Ответ от Fantomas 16 июня 2004г. 01:28:17
- Fantomas
- Восстановленный участник
- На форуме с 7 декабря 2003г.
- Сообщений: 392
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Тоже недавно делал проверку принадлежности точки сфере. Естественно сравнение через EQUAL, смотря какая точность нужна.
Есть еще идея. Существует функция vlax-curve-getDistAtPoint которая вычисляет расстояние между начальной точкой кривой (а в нашем случае отрезка) до точки на кривой. В случае если точка не лежит на кривой она возвратит Nil.
Источник
Как проверить принадлежит ли точка отрезку
Как определить, принадлежит ли точка A(x,y) отрезку с концевыми точками B(x 1 ,y 1 ) и C(x 2 ,y 2 )?
Точки отрезка z можно описать уравнением
pOB+(1-p)OC=z, 0<=p<=1, OB и OC — векторы.
Если существует такое p, 0<=p<=1, что
pOB+(1-p)OC=A,
то A лежит на отрезке, иначе — нет.
Равенство расписывается по координатно так:
px 1 +(1-p)x 2 =x
py 1 +(1-p)y 2 =y
Из первого уравнения находим p, подставляем во второе: если получаем равенство и
0<=p<=1, то A на отрезке, иначе — нет.
Рабочая реализация более общей функции есть в разделе структуры геометрических данных.
Помогите с алгоритмом. Как проверить принадлежит ли точка А отрезку ВС? Координаты 2-х мерные (х,у).
procedure TForm1.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
if Start>0 then
begin
Back.Canvas.Rectangle(0,0,600,600);
if (LLine(19,580,X,Y)+LLine(X,Y,450,15)<=LLine(19,580,450,15)+0.01) then
begin
Back.Canvas.Pen.Color:=clGreen;
Back.Canvas.Rectangle(0,0,600,600);
end
else
Back.Canvas.Pen.Color:=clBlack;
Back.Canvas.MoveTo(19,580);
Back.Canvas.LineTo(450,15);
Back.Canvas.Pen.Color:=clRed;
Back.Canvas.MoveTo(19,580);
Back.Canvas.LineTo(X,Y);
Back.Canvas.LineTo(450,15);
Canvas.Draw(1,1,Back);
form1.Caption:=Floattostr(AB)+’=’+FloatToStr(LLine(19,580,X,Y)+LLine(X,Y,450,15));
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Start:=1;
end;
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
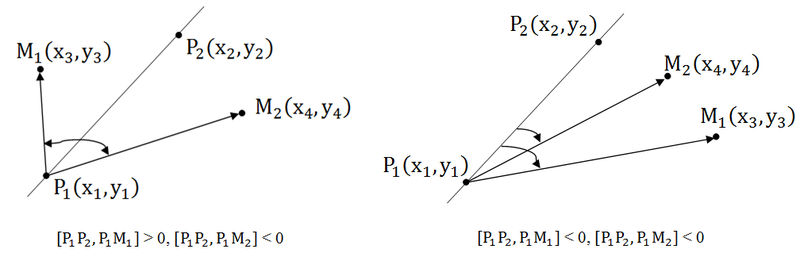
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] < 0 – точки лежат по разные стороны.
2. [P1P2, P1M1] * [P1P2, P1M2] > 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
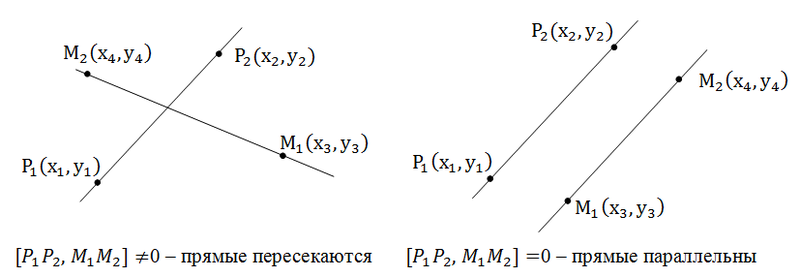
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
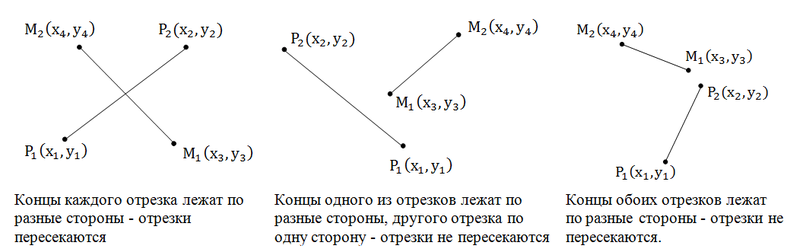
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] < 0 => [P1P2, P1M2] * [P1P2, P1M1] < 0. Аналогично
[M1M2, M1P1] * [M1M2, M1P2] < 0. Вы наверно думаете, почему не меньше либо равно. А потому, что возможен следующий случай, при котором векторное произведение как раз и равно нулю, но отрезки не пересекаются:
Поэтому нам необходимо сделать еще одну проверку, а именно: принадлежит ли хотя бы один конец каждого отрезка другому (принадлежность точки отрезку). Эту задачу мы уже решали.
Итак, для того чтобы отрезки имели общие точки необходимо и достаточно:
1. Концы отрезков лежат по разные стороны относительно другого отрезка.
2. Хотя бы один из концов одного отрезка принадлежит другому отрезку.
Задача №7
Расстояние от точки до прямой.
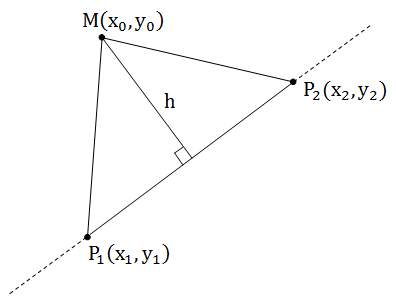
В предыдущей статье мы говорили о том, что геометрически косое произведение — это ориентированная площадь параллелограмма, поэтому SP1P2M = 0,5*[P1P2, P1M]. С другой стороны каждому школьнику известна формула для нахождения площади треугольника: половина основание на высоту.
SP1P2M = 0,5*h*P1P2.
Приравнивая эти площади, находим
По модулю взяли потому, что первая площадь ориентированная.
Если же прямая задана уравнением ax + by + c = 0, то уравнение прямой проходящей через точку M перпендикулярной заданной прямой есть: a(y — y0) – b(x — x0) = 0. Теперь спокойно можно решить систему из полученных уравнений, найти их точку пересечения и вычислить расстояние от исходной точки до найденной: оно будет ровно ρ = (ax0 + by0 + c)/√(a 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
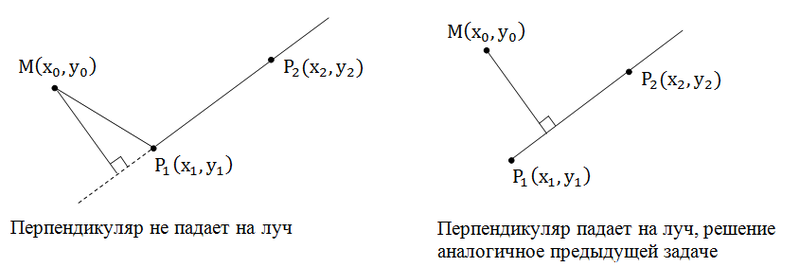
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) < 0 перпендикуляр не попадает на луч
2. (P1M, P1P2) ≥ 0 перпендикуляр попадает на луч
Задача №9
Расстояние от точки до отрезка.
Решение
Рассуждаем аналогично предыдущей задаче. Если перпендикуляр не падает на отрезок, то ответом будет минимальное из расстояний от данной точки до концов отрезка.
Чтобы определить попадает ли перпендикуляр на отрезок нужно по аналогии с предыдущей задачей использовать скалярное произведение векторов. Если перпендикуляр не падает на отрезок, то либо угол MP1P2 либо угол MP2P1 будут тупыми. Поэтому по знаку скалярных произведений мы можем определить попадает ли перпендикуляр на отрезок или нет:
Если (P1M, P1P2) < 0 или (P2M, P2P1) < 0 то перпендикуляр не падает на отрезок.
Задача №10
Определить количество точек прямой и окружности.
Решение
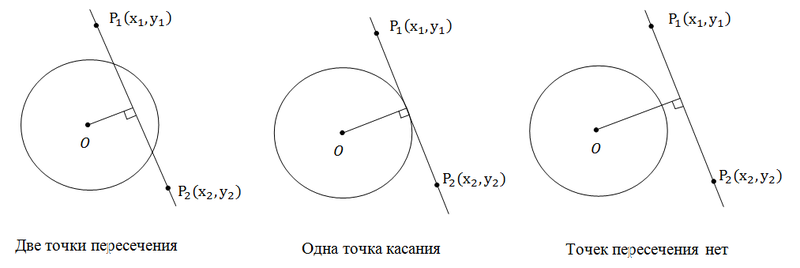
Прямая и окружность может иметь нуль, одну или две точки пересечения. Давайте посмотрим на рисунки:
Здесь из рисунков и так все понятно. Мы имеем две точки пересечения, если расстояние от центра окружности до прямой меньше радиуса окружности. Одну точку касания, если расстояние от центра до прямой равно радиусу. И наконец, ни одной точки пересечения, если расстояние от центра окружности до прямой больше радиуса окружности. Поскольку задача нахождения расстояние от точки до прямой была уже нами решена, то и эта задача тоже решена.
Задача №11
Взаимное расположение двух окружностей.
Решение
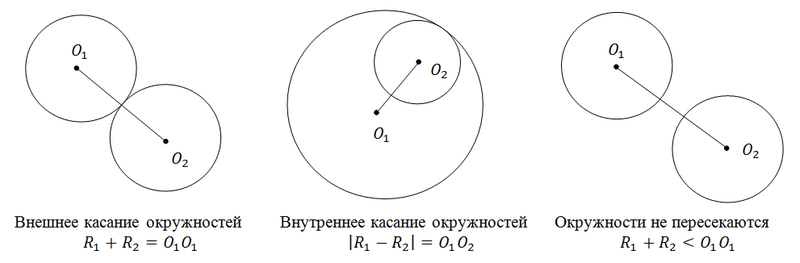
Возможные случаи расположения окружностей: пересекаются, касаются, не пересекаются.
Рассмотрим случай, когда окружности пересекаются, и найдем площадь их пересечения. Эту задачу я очень люблю, так как потратил на ее решение изрядное количество времени (было это давно — на первом курсе).
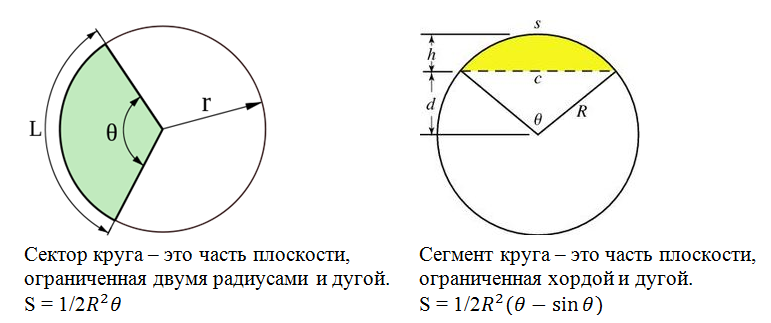
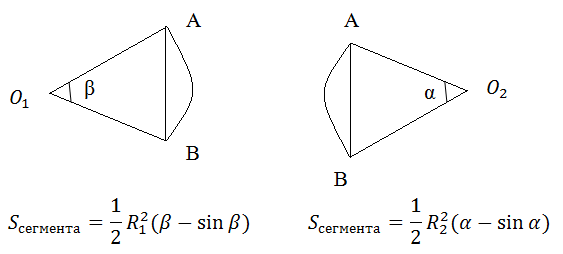
Вспомним теперь, что такое сектор и сегмент.
Пересечение кругов состоит из двух сегментов O1AB и O2AB.
Казалось бы необходимо сложить площади этих сегментов и все. Однако, все не так просто. Необходимо еще определить всегда ли эти формулы верны. Оказывается, нет!
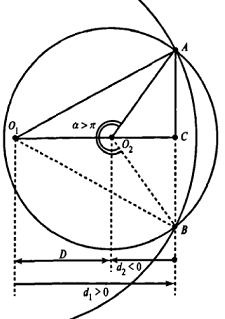
Рассмотрим случай, когда центр второго круга O2 совпадает с точкой C. В этом случае d2 = 0 и за значение α примем α = π. В этом случае имеем полукруг с площадью 1/2 πR2 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.