Как найти что значит формула - Сайт, где вы сможете решить свои вопросы

Эта статья об обозначениях элементарной математики; Для более общего контекста см. Математические обозначения.

Математи́ческая фо́рмула (от лат. formula — уменьшительное от forma — образ, вид) в математике, а также физике и других естественных науках — символическая запись высказывания (которое выражает логическое суждение^[1]), либо формы высказывания^[2]. Формула, наряду с термами, является разновидностью выражения формализованного языка.
В более широком смысле формула — всякая чисто символьная запись (см. ниже), противопоставляемая в математике различным выразительным способам, имеющим геометрическую коннотацию: чертежам, графикам, диаграммам, графам и т. п.

Основные виды (численных) формул[править | править код]

Как правило, в формулу входят переменные (одна или более), причём сама формула представляет собой не просто выражение, а некое суждение. Такое суждение может утверждать что-то о переменных, а может — о применяемых операциях. Точный смысл формулы зачастую подразумевается из контекста и его невозможно понять непосредственно из её вида. Можно выделить три распространённых случая:

Формула должна сообщить, как искать значения переменной (уравнения и т. п.);
Формула (записываемая как «искомое = выражение») определяет величину через свои параметры (аналогично присваиванию в программировании и иногда записывается через диграф «:=» как в языке Pascal, но в принципе может считаться вырожденным частным случаем уравнения);
Формула является собственно логическим утверждением: тождеством (например, аксиомой), утверждением теоремы и т. п.

Уравнения[править | править код]

Уравнение — формула, внешняя (верхняя) связка которого представляет собой бинарное отношение равенства. Однако важная особенность уравнения заключается также в том, что входящие в него символы делятся на переменные и параметры (присутствие последних, впрочем, необязательно). Например, $x^{2}=1$ является уравнением, где x — переменная. Значения переменной, при которых равенство истинно, называются корнями уравнения: в данном случае таковыми являются два числа 1 и −1. Как правило, если уравнение на одну переменную не является тождеством (см. ниже), то корни уравнения представляют собой дискретное, чаще всего конечное (возможно и пустое) множество.

Если в уравнение входят параметры, то его смысл — для заданных параметров найти корни (то есть значения переменной, при котором равенство верно). Иногда это можно сформулировать как нахождение неявной зависимости переменной от параметра (параметров). Например $x^{2}=a$ понимается как уравнение на x (это обычная буква для обозначения переменной, наряду с y, z и t). Корнями уравнения является квадратный корень из a (считается, что их имеется два, разных знаков).
Подобная формула, сама по себе, задаёт лишь бинарное отношение между x и a и её можно понимать в обратную сторону, как уравнение на a относительно x. В данном элементарном случае, речь может идти скорее об определении a через x: $a=x^{2}$ .

Тождества[править | править код]

Тождество — суждение, верное при любых значениях переменных. Обычно, под тождеством подразумевают тождественно верное равенство, хотя снаружи тождества может стоять и неравенство или какое-либо другое отношение. Во многих случаях тождество можно понимать как некое свойство используемых в нём операций, например тождество a+b=b+a утверждает коммутативность сложения.

С помощью математической формулы довольно сложные предложения могут быть записаны в компактной и удобной форме. Формулы, становящиеся истинными при любом замещении переменных конкретными объектами из некоторой области, называются тождественно-истинными в данной области. Например: «для любых a и b имеет место равенство ${displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ ». Данное тождество можно вывести из аксиом сложения и умножения в коммутативном кольце, которые сами по себе также имеют вид тождеств.

Тождество может и не включать в себя переменные и являться арифметическим (или каким-то ещё) равенством, как например ${displaystyle 6^{3}=3^{3}+4^{3}+5^{3}}$ .

Приближённые равенства[править | править код]

Например:
— приближённое равенство при малых ;

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Неравенства[править | править код]

Формула-неравенство может пониматься в обоих описанных в начале раздела смыслах: как тождество (например, неравенство Коши — Буняковского) или же, подобно уравнению, как задача на отыскание множества (а точнее, подмножества области определения), которому может принадлежать переменная, или переменные.

Используемые операции[править | править код]

В данном разделе будут перечислены операции, используемые в алгебре, а также некоторые общеупотребительные функции из математического анализа.

Сложение и вычитание[править | править код]

Используются знаки «+» и «−» (последний на письме довольно слабо отличим от дефиса).
Унарный минус чаще используется лишь при первом (левом) слагаемом, поскольку другие случаи, типа «a + (−b)» и «a − (−b)», ничем не отличаются по смыслу от более простых «a − b» и «a + b» соответственно.

По причине ассоциативности сложения, расстановка скобок для задания порядка выполнения сложения не имеет математического смысла.
В алгебре слагаемыми называют аргументы как сложения, так и вычитания. Порядок выполнения вычитания, при отсутствии скобок, таков, что вычитаемым оказывается лишь член, выписанный непосредственно справа от знака вычитания, а не результат выполнения операций каких-либо сложения и вычитания, записанных правее. Таким образом со знаком минус входят в сумму лишь те «слагаемые», непосредственно слева от которых знак «−» имеется.

Умножение[править | править код]

Знак умножения чаще всего опускается. Это не вызывает двусмысленности, поскольку переменные обозначаются обычно одиночными буквами, а выписывать умножение записанных цифрами констант друг на друга бессмысленно. В редких случаях, когда двусмысленности не избежать, умножение обозначается центрированным по вертикали символом точки «·». Символ «×» применяется лишь в школьной арифметике, в технических текстах (в особом контексте), а также некоторые системы вставляют его на месте знака умножения при переносе формулы на другую строку (обычно, перенос по знаку умножения избегается).

Деление[править | править код]

Деление в формулах записывается при помощи дробной черты. В школьной арифметике применяется также «÷» (обелюс).

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Возведение в степень[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Элементарные функции[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Абсолютная величина, знак и т. п.[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Приоритет операций и скобки[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Приоритет, ранг или старшинство операции или оператора — формальное свойство оператора/операции, влияющее на очерёдность его выполнения в выражении с несколькими различными операторами при отсутствии явного (с помощью скобок) указания на порядок их вычисления. Например, операцию умножения обычно наделяют бо́льшим приоритетом, чем операцию сложения, поэтому в выражении будет получено сначала произведение y и z, а потом уже сумма.

Примеры[править | править код]

Например:

— пример формулы, имеющей значение «ложь»;

— функция одного действительного аргумента;

$z={frac {y^{3}}{y^{2}+x^{2}}}$ — функция нескольких аргументов (график одной из самых замечательных кривых — верзьера Аньези);

— не дифференцируемая функция в точке (непрерывная ломаная линия не имеет касательной);

${displaystyle x^{3}+y^{3}=3axy}$ — уравнение, то есть неявная функция (график кривой «декартов лист»);

${displaystyle t_{n}=n!}$ — целочисленная функция;

${displaystyle y=y^{3}sin(nx)}$ — чётная функция;

— нечётная функция;

$f(P)={sqrt {x^{2}+y^{2}+z^{2}}}$ — функция точки, расстояние от точки до начала (декартовых) координат;

${displaystyle y={frac {1}{x-3}}}$ — разрывная функция в точке x=3 ;

— параметрически заданная функция (график циклоиды);

${displaystyle y=ln(x), x=e^{y}}$ — прямая и обратная функции;

${displaystyle f(x)=int limits _{-infty }^{x}|f(t)|,dt}$ — интегральное уравнение.

В филателии[править | править код]

Математические формулы нередко изображаются на почтовых марках разных стран, например, на посвящённых известным учёным, представляя открытые ими закономерности. Примечательна серия почтовых марок, посвящённая самим математическим формулам. Это почтовый выпуск Никарагуа 1971 года — серия из 10 почтовых марок под названием «10 математических формул, которые изменили лик Земли» (исп. Las 10 formulas matematicas que cambiaron la faz de la Tierra). На них представлены теорема Пифагора, закон Архимеда, закон Ньютона, формула Циолковского, формула де Бройля, формула Эйнштейна и др. На обратной стороне каждой марки помещено описание соответствующей формулы (Sc #877-881,C761-C765).

См. также[править | править код]

Алгебраическое выражение — математическое обозначение, не выражающее законченную мысль.
Выражение (математика)
Интерполяционные формулы
Рекуррентная формула
Трансцендентная функция
Формула Симпсона
Формула Эйлера
ISO 31

Примечания[править | править код]

↑ Чупахин, Бродский, 1977, с. 200.
↑ Колмогоров, Драгилин, 2006, с. 13—15.

Литература[править | править код]

Чупахин И.Я., Бродский И.Н. Формальная логика. — Ленинград: Издательство Ленинградского университета, 1977. — 357 с.
Колмогоров А.Н., Драгилин А.Г. Математическа логика. — М.: КомКнига, 2006. — 240 с. — ISBN 5-484-00520-5.

Ссылки[править | править код]

Большая советская энциклопедия (недоступная ссылка с 28-08-13 [3549 дней])
Самые красивые физические и математические формулы
Красивые формулы элементарной математики (недоступная ссылка с 28-08-13 [3549 дней])
М. Я. Выгодский. Справочник по высшей математике (недоступная ссылка)
Н. К. Верещагин, А. Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. (недоступная ссылка)

Источник

Содержание

КАК ВЫЧИСЛИТЬ ФОРМУЛУ ВЕЩЕСТВА
1.Понятие простейшей и истинной формулы вещества
2.Массовая доля химического элемента: что означает и как высчитывается
3.Как определить формулу вещества по массовым долям элементов
4.Как определить формулу органического соединения
4.1. Как определить формулу органического соединения
по общей молекулярной формуле вещества
4.2. Как определить формулу органического соединения
по продуктам его сгорания
5. Как определить формулу вещества: комбинированные задачи
Значение слова «формула»
фо́рмула

КАК ВЫЧИСЛИТЬ ФОРМУЛУ ВЕЩЕСТВА

Способов, как определить формулу вещества, достаточно много. Все зависит от исходных данных. Наиболее разнообразны подобные вычисления в органической химии. И это не удивительно, так как органических соединений значительно больше, чем неорганических.

1.Понятие простейшей и истинной формулы вещества

В одних задачах на определение формулы вещества необходимо найти его простейшую формулу, а в других – истинную. В чем разница?

Простейшая , или иными словами, эмпирическая формула , указывает на соотношение атомов в молекуле (или в формульной единице, если речь идет о не ковалентном соединении).

Так, например: СН₂ – простейшая формула алкена – показывает, что на каждый 1 атом углерода приходится 2 водородных атома. То есть существует соотношение 1:2. Поэтому для нахождения простейшей (эмпирической) формулы вещества важно рассчитать количество вещества атомов, которые входят в его состав, то есть n(C) и n(H).

Истинная формула , или иначе молекулярная , отражает действительное количество атомов всех элементов в молекуле.

Например, для пропилена, относящегося к классу алкенов, истинная (молекулярная) формула будет C₃H₆. Она говорит о том, что молекула данного вещества включает 3 атома С и 6 атомов Н. Это вполне соответствует простейшей формуле, отвечающей соотношению атомов 1:2. Для нахождения истинной (молекулярной) формулы соединения требуется посчитать его относительную молекулярную (Mr) или молярную массу (M).

2.Массовая доля химического элемента: что означает и как высчитывается

Массовая доля – это отношение массы компонента системы к массе системы, выраженное в процентах или долях от единицы.

Ну, а теперь проще.

Молекула имеет массу. Все атомы в молекуле также имеют свои массы. Атомов одного химического элемента в молекуле может быть 1 или несколько. Важна масса всех атомов одного элемента. Если ее разделить на массу молекулы, то получится массовая доля этого элемента. Ее выражают либо в процентах, которые всегда меньше 100%, либо в долях от единицы, которые всегда меньше 1.

Массовая доля элемента обозначается греческой буквой «омега» — ω . И записывается, например, так: ω(Н), ω(Сl), ω(С) и т.д. и рассчитывается:

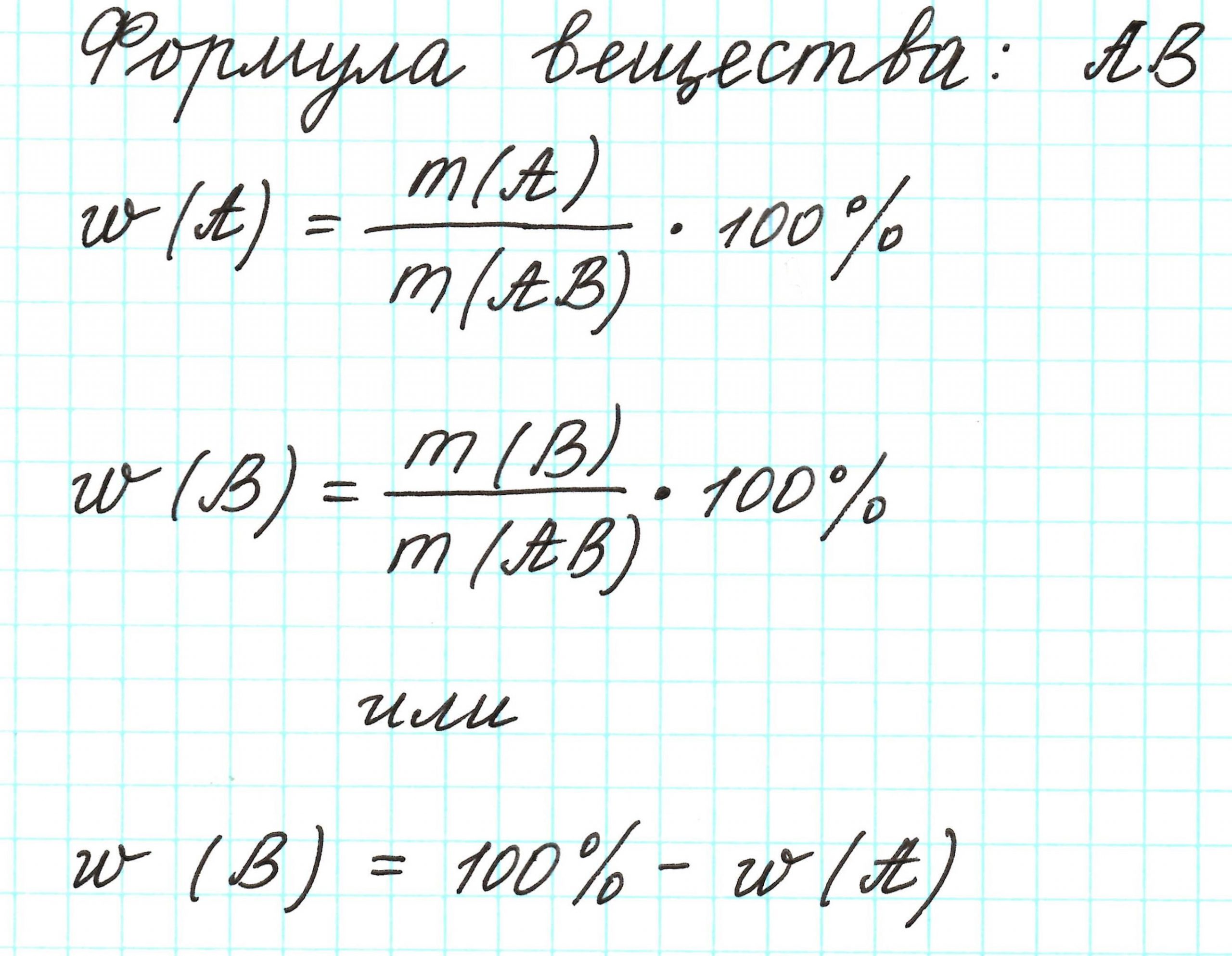
Пример 1. Каковы массовые доли элементов в оксиде железа (III) Fe₂O₃.

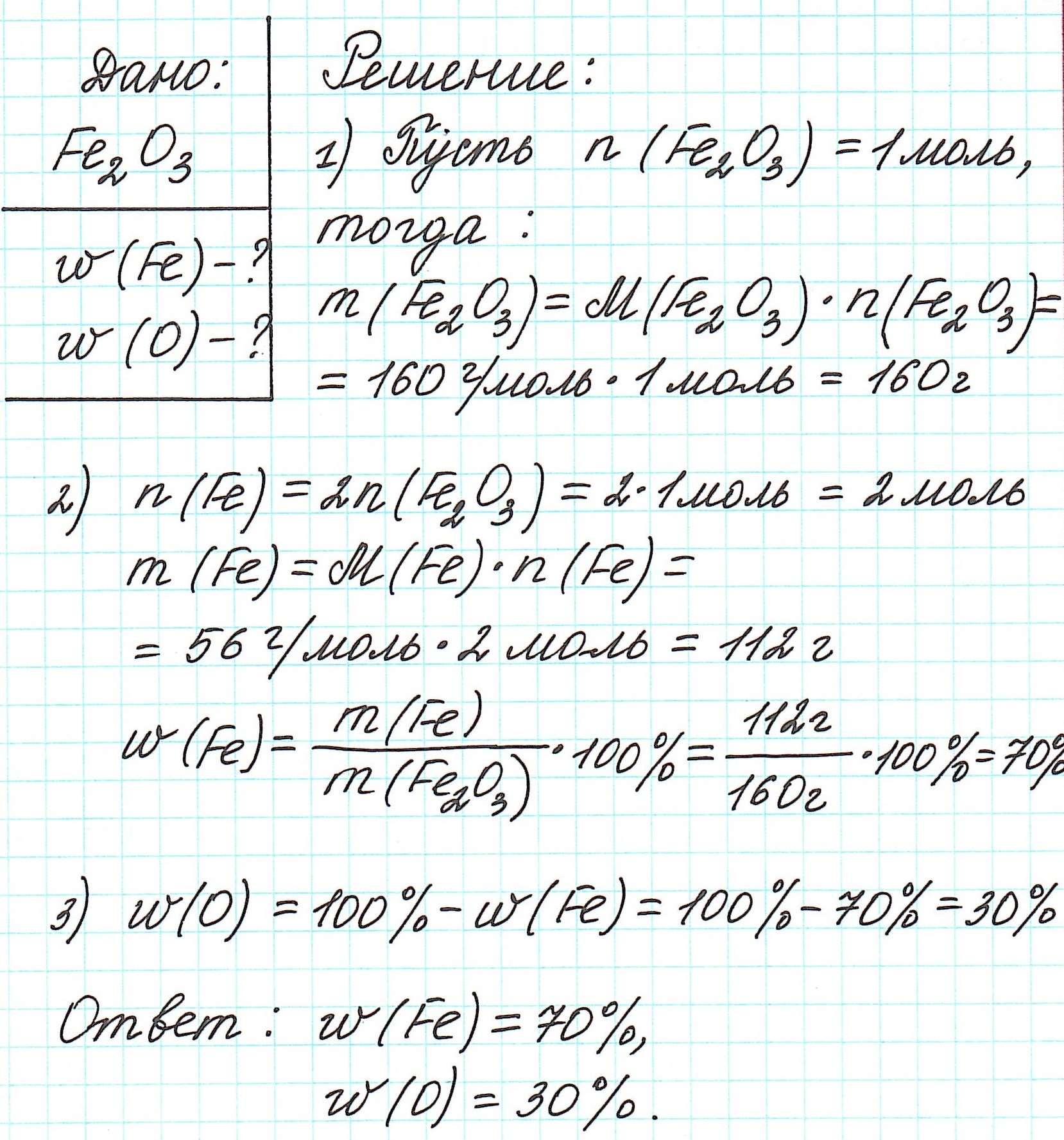
3.Как определить формулу вещества по массовым долям элементов

Нахождение формулы вещества по массовым долям элементов применимо как к органическим, так и к неорганическим соединениям.

Пример 2. Сероуглерод содержит 15,8% углерода по массе. Какова простейшая формула этого вещества?

Поскольку речь идет о массовых долях элементов, то необходимо знать массу вещества. В нашем случае – массу сероуглерода. В условии задачи о ней ничего не говорится. Поэтому допускаем, что масса вещества равна 100 г.

Почему 100 г? Это «круглое» число, и его использование облегчает все расчеты. Так как в итоге будем находить соотношения количеств веществ элементов, то какое-то особенное значение массы вещества не играет никакой роли.

Попробуйте ради эксперимента принять массу сероуглерода равной 23 г, 467 г и т.п. Результат будет один и тот же.

Допустим, что атомов углерода в молекуле х, а атомов серы – у. В таком случае формула вещества примет вид: С_хS_у.

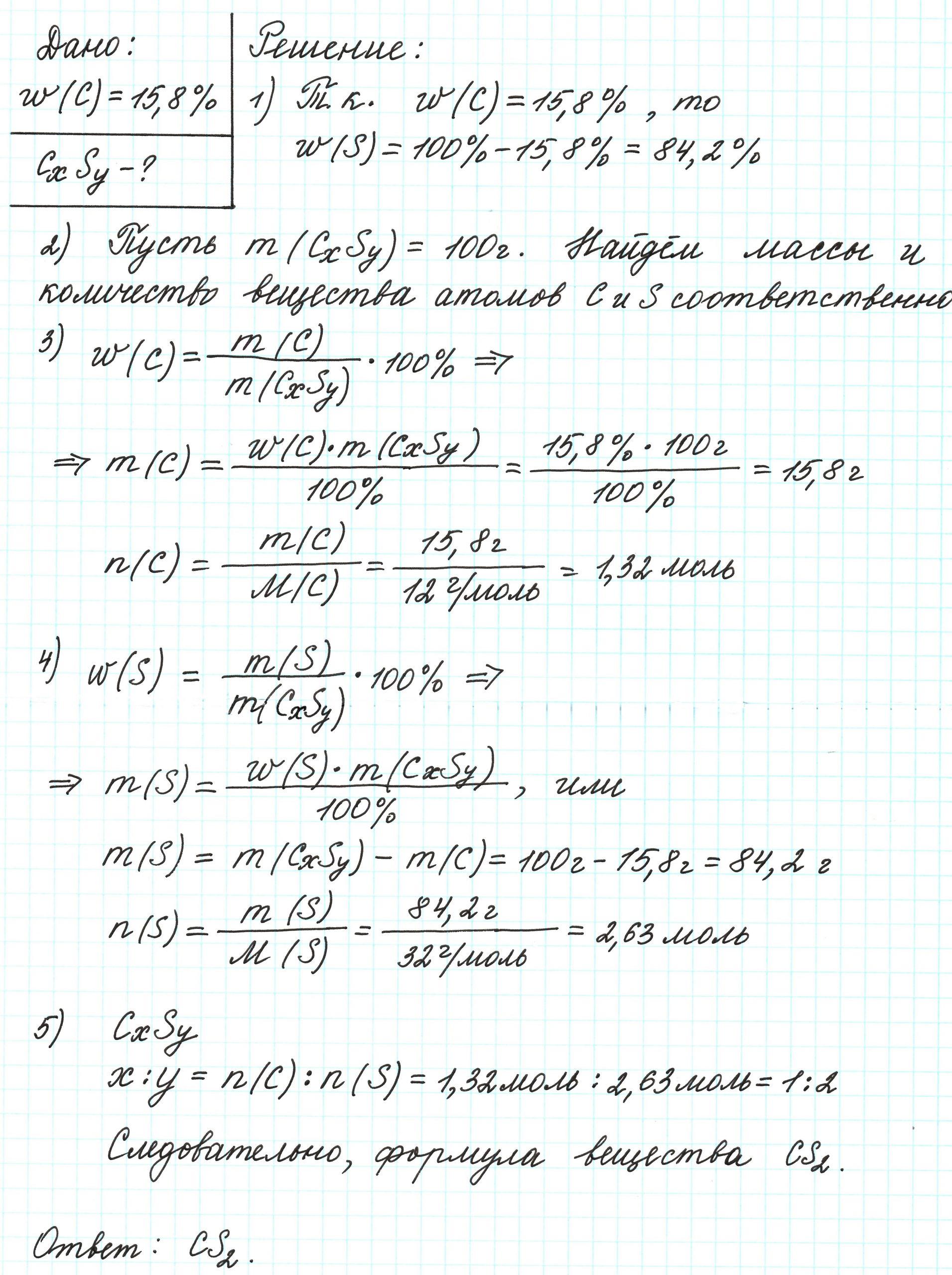
Пример 3. Содержание углерода в углеводороде составляет 83,33%. Плотность паров соединения по водороду – 36. Какова молекулярная формула углеводорода?

Из данных задачи следует, что углеводород может находиться в газообразном состоянии, так как известна плотность его паров . Эта величина в сегда требуется для нахождения молярной (относительной молекулярной) массы вещества . Как она находится и что это такое читайте подробнее здесь.

Чтобы не загромождать записи, массовую долю элементов будем считать не в процентах, а в долях от единицы.

Пусть вас не удивляет получившаяся простейшая формула. Ведь, исходя из определения простейшей формулы, на каждый 1 атом углерода приходится 2,4 атома водорода. Это всего лишь соотношение. Соединения с формулой СН_2,4 в принципе не существует. Не всегда простейшая и истинная формулы совпадают друг с другом.

А если полученная формула СН_2,4 вас все же смущает, вы можете решать задачу и вторым способом. Но это несколько более сложный способ, когда требуется составить и решить уравнение с двумя неизвестными.

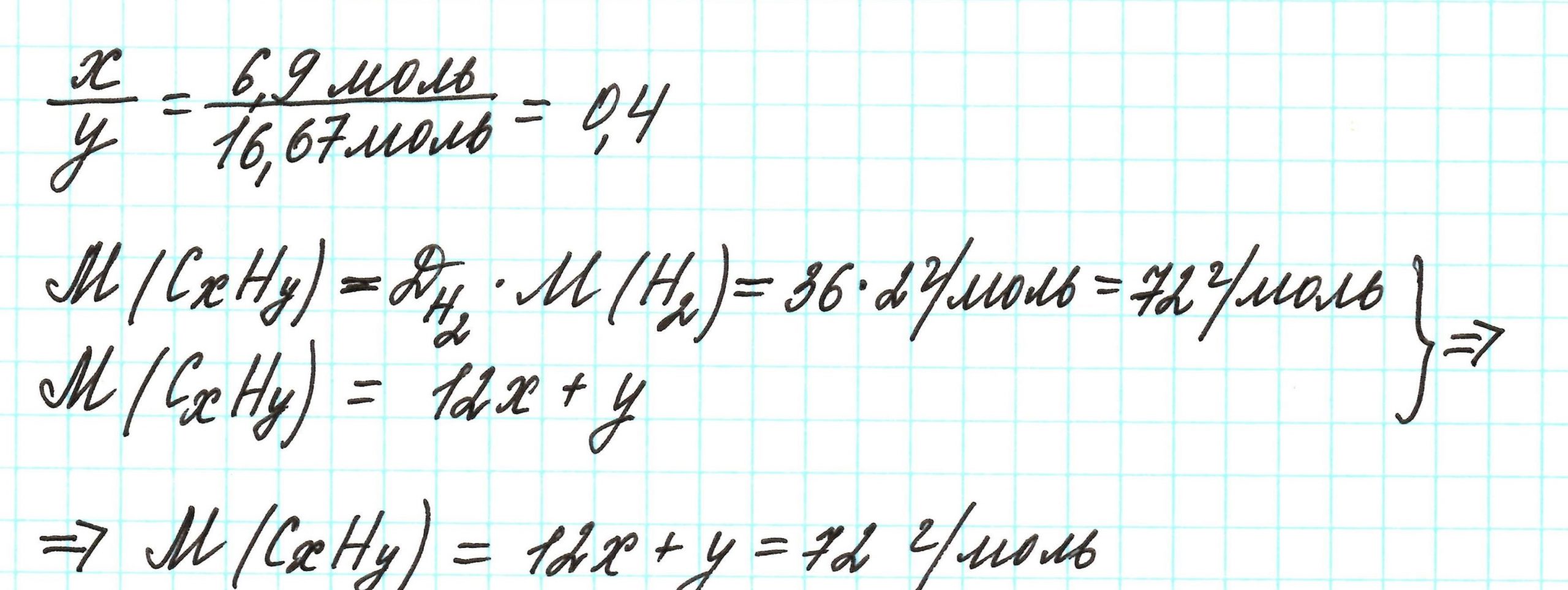
Не все химические вещества являются бинарными, то есть состоят из атомов двух химических элементов. Но в любом случае, алгоритм решения задачи тот же.

Пример 4. Некоторая кислота содержит водород (2,2%), иод (55,7%) и кислород (42,1%). Определите простейшую формулу этой кислоты.

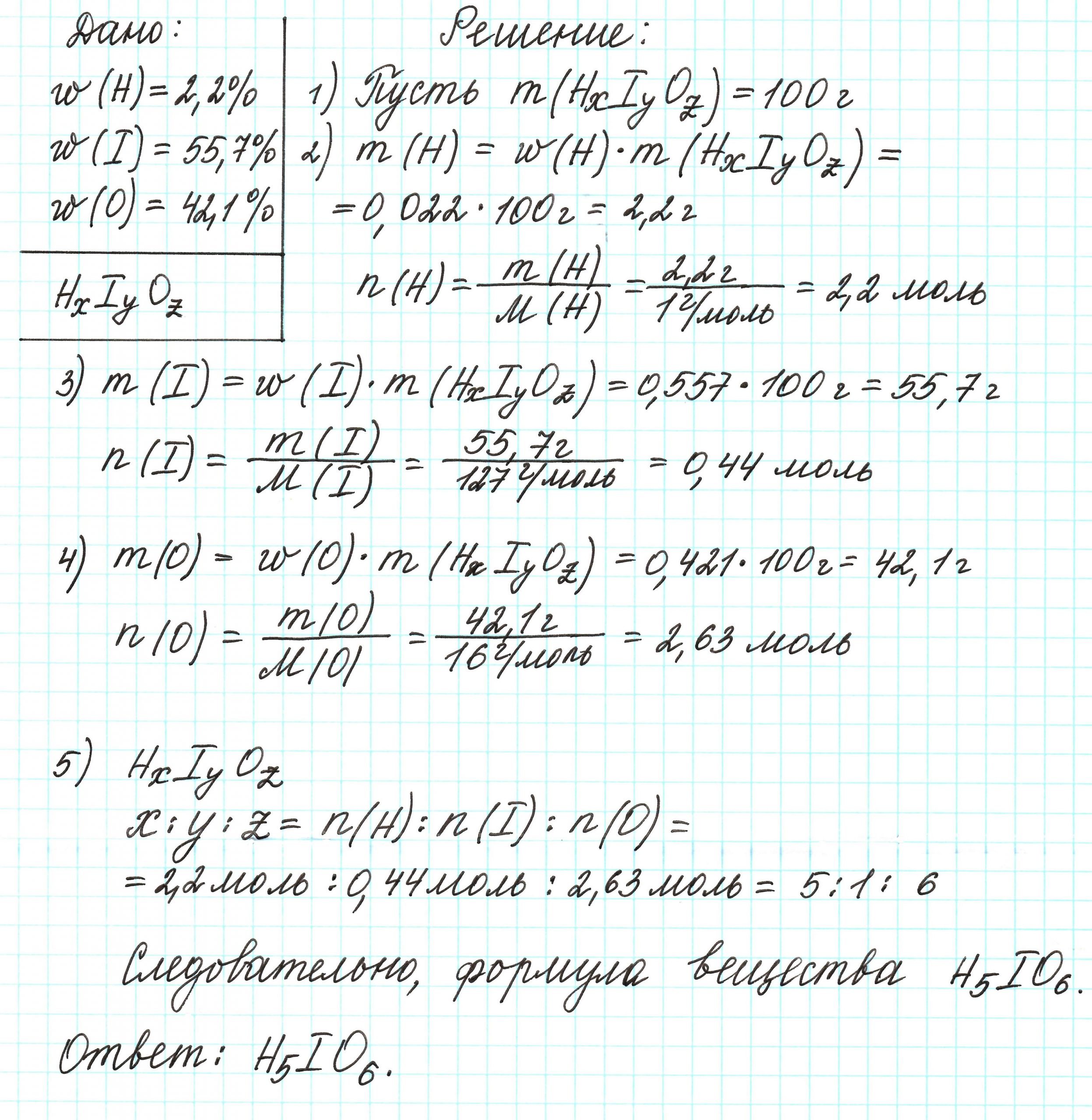
4.Как определить формулу органического соединения

Определить формулу органического вещества можно не только зная массовые доли элементов в его составе.

4.1. Как определить формулу органического соединения

по общей молекулярной формуле вещества

Органические вещества сгруппированы по самостоятельным классам на основе общности строения и свойств. Каждый класс соединений характеризуется своей общей молекулярной формулой. Особенно это наглядно видно на примере углеводородов.

Если другие органические вещества рассматривать как их производные, в молекулы которых введена какая-либо функциональная группа, то и для них также можно составить общую молекулярную формулу.

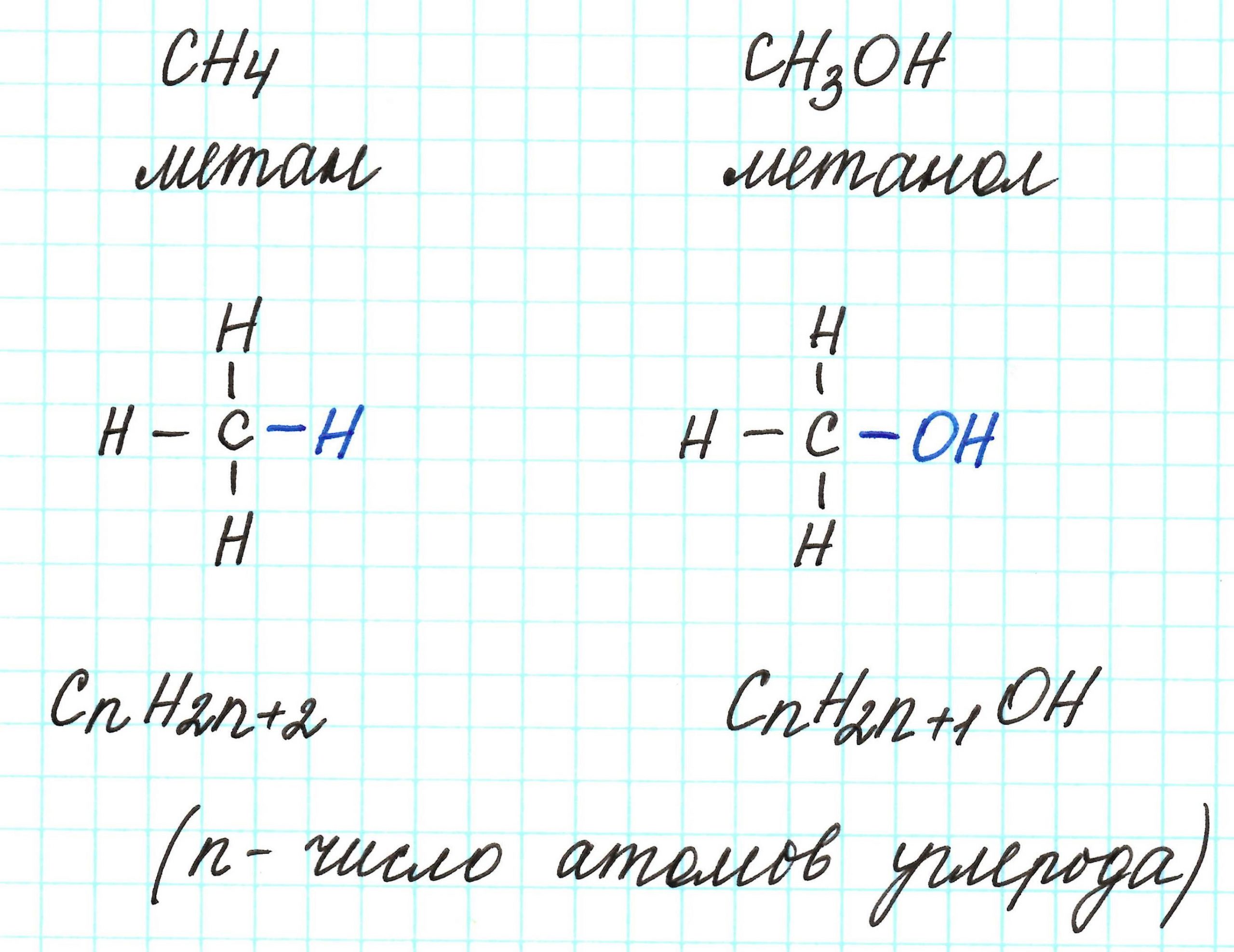
К слову, метан СН₄ является представителем алканов, в молекулах которых на n атомов углерода и приходится 2n+2 атомов водорода. Алканы имеют общую молекулярную формулу, отражающую их состав: С_nH₂_n₊₂.

Предельные одноатомные спирты можно рассматривать как производные алканов, в молекулах которых 1 атом водорода замещен на гидроксильную группа –ОН. Таким образом, их общая молекулярная формула такая: С_nH₂_n₊₁ОН.

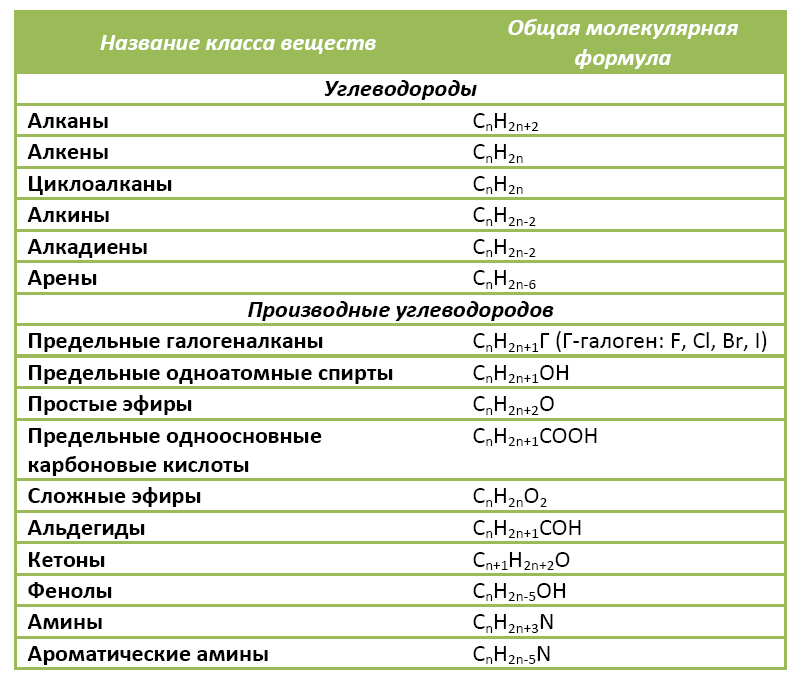
Ниже в таблице приведены общие молекулярные формулы основных классов органических соединений.

Разберем примеры решения задач с использованием общей молекулярной формулы вещества.

Пример 5. Плотность паров по воздуху некоторого алкана 4,414. Какова формула алкана?

4.2. Как определить формулу органического соединения

по продуктам его сгорания

Это еще один распространенный тип задач на определение формулы органического соединения.

Необходимо запомнить и понять основные моменты:

— так как все органические вещества содержат атомы С, Н, а также атомы О (кислородсодержащие соединения), то всегда при их сгорании выделяется углекислый газ СО₂ и образуется вода Н₂О;

— все углеродные атомы, входящие в состав органического соединения, окажутся в составе углекислого газа СО₂; следовательно, n(С) как в соединении, так и в СО₂ – это одна и та же величина;

— все атомы водорода Н, которые имеются в составе вещества, перейдут в состав воды Н₂О; следовательно, n(Н) и в данном веществе, и в Н₂О – это одна и та же величина;

— при сгорании веществ, включающих в себя азот (например, амины), кроме СО₂ и Н₂О, образуется еще и N₂.

Разберем несколько примеров.

Пример 6. Сожгли 7,2 г углеводорода. Плотность его паров по водороду составляет 36. В результате реакции образовалось 22 г оксида углерода (IV) и 10,8 г воды. Какова молекулярная формула соединения?

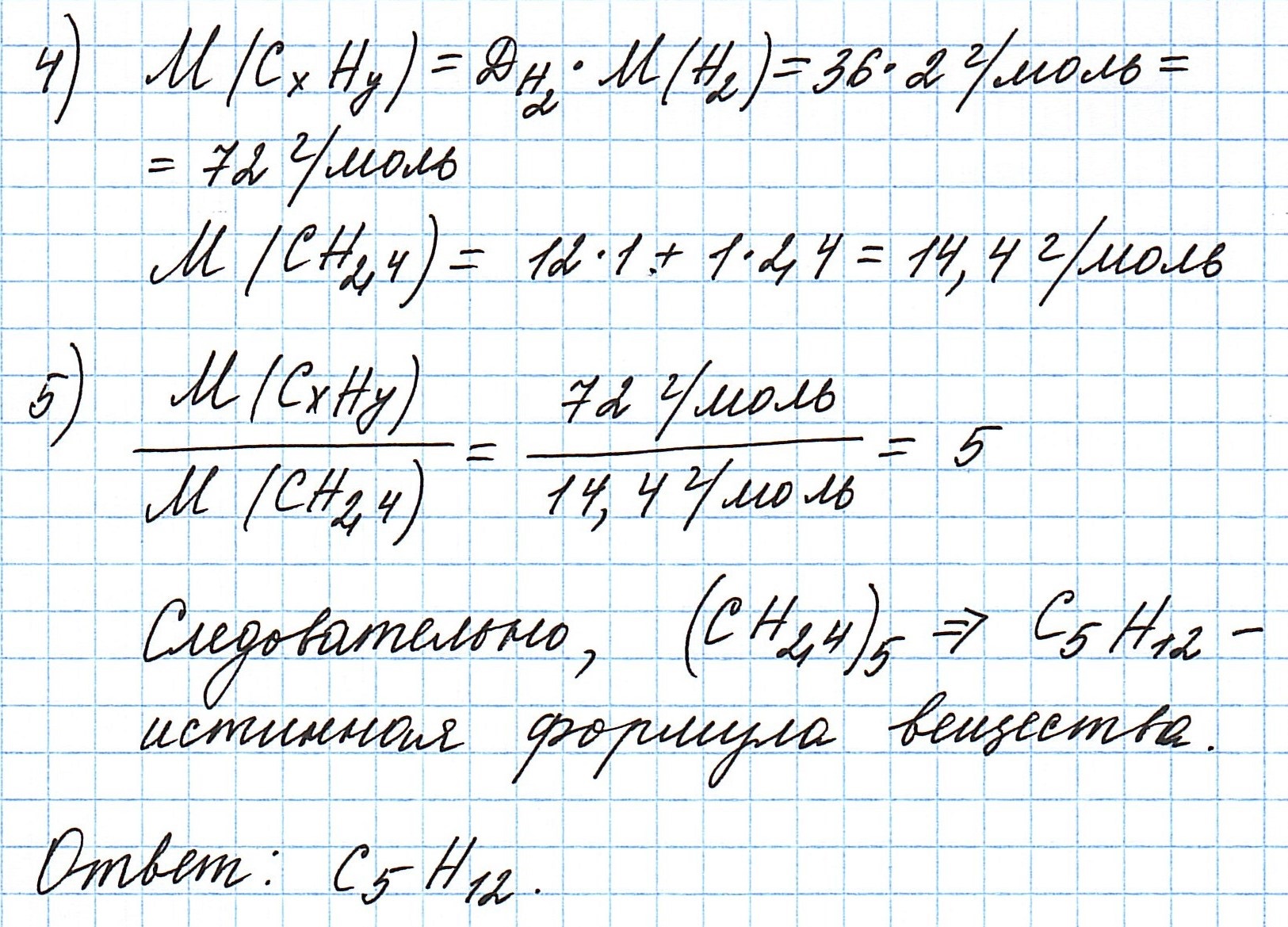
Пример 7. В результате сгорания 4,8 г органического соединения выделилось 3,36 л (н.у.) оксида углерода (IV) и образовалось 5,4 г воды. Плотность паров искомого соединения по кислороду равна 1. Вычислите молекулярную формулу вещества.

Пример 8. Результатом сжигания 0,31 г газообразного органического соединения, имеющего плотность 1,384 г/л, стало выделение 0,224 л (с.у.) оксида углерода (IV), 0,112 л азота и образование 0,45 г воды. Вычислите молекулярную формулу этого вещества.

5. Как определить формулу вещества: комбинированные задачи

Наибольший интерес и некоторую трудность представляют комбинированные задачи, сочетающие в себе необходимость найти формулу соединения:

— используя приемы, применяемые в рассмотренных выше задачах;

— используя сведения не только о химических, но и физических свойствах вещества.

Вот несколько примеров.

Пример 9. Какова молекулярная формула предельного углеводорода, при полном сгорании 8,6 г которого выделилось 13, 44 л (н.у.) оксида углерода (IV).

1) известен класс вещества, поэтому возможно применить его общую молекулярную формулу;

2) речь идет о сгорании вещества, поэтому количество атомов в составе молекулы будем искать, используя данные о продукте сгорания – СО₂.

Пример 10. Алкен нормального строения содержит двойную связь при первом углеродном атоме. Образец этого алкена массой 0,7 г присоединил бром массой 1,6 г. Вычислите формулу алкена и назовите его.

В предлагаемых условиях:

1) известен класс вещества, следовательно, применим его общую молекулярную формулу;

2) речь идет об одном из химических свойств: способности алкенов присоединять галогены по месту разрыва двойной связи.

Пример 11. После полного сжигания в кислороде арена, имевшего массу 0,92 г, выделился оксид углерода (IV). Пропуская газ через избыток раствора щелочи Ca(OH)₂, получили 7 грамм осадка. Какова молекулярная формула арена?

В предлагаемой задаче:

1) известен класс вещества;

2) речь идет о сжигании соединения и образовании в качестве продукта горения углекислого газа, который при взаимодействии со щелочью Са(ОН)₂ привел к выпадению осадка известной массы.

Следующий пример очень характерен для задач, встречающихся в заданиях второй части ЕГЭ по химии.

Пример 12. Некоторое соединение, образующее альдегид в реакции окисления, взаимодействует с избытком бромоводородной кислоты, образуя 9,84 г продукта (выход составляет 80% от теоретического), имеющего плотность паров по Н₂ 61,5. Определите строение этого соединения, а также его массу, вступившую в реакцию?

1) говорится о химических свойствах искомого соединения; анализируя их, приходим к выводу, что заданным веществом является предельный одноатомный спирт;

2) известна общая молекулярная формула предельных одноатомных спиртов;

3) более подробно говорится о взаимодействии заданного вещества с бромоводородной кислотой; спирт, реагируя с HBr, дает галогеналкан, для которого известны его масса, практический выход и относительная плотность по Н₂; именно от этих данных и нужно отталкиваться при решении данной задачи.

Итак, способов, как определить формулу вещества, действительно, множество. Мы рассмотрели лишь основные из них. Важно правильно уяснить понятия «простейшая формула вещества» и «истинная формула вещества», чтобы не путать их.

Чтобы самыми первыми узнавать о новых публикациях на сайте, присоединяйтесь в нашу группу ВКонтакте.

Пожалуйста, оцените публикацию и оставьте свой комментарий. Ваше мнение для нас важно!

Источник

Значение слова «формула»

1. Общее краткое определение какого-л. положения, закона, отношения и т. п., приложимое к частным случаям. Усвойте себе общий взгляд, общую формулу, и вы почти никогда не ошибетесь в частном приложении… если не измените ей сознательно или бессознательно. Герцен, Порядок торжествует! || Краткое и точное словесное выражение, определение чего-л. «Разделяй и властвуй» — старая политическая формула. А. Н. Толстой, Клянемся не осквернить святости нашей родины. || Стереотипная, шаблонная фраза, выражение. Это был один из тех неумелых и неразвитых захолустных врачей, которые из всех затруднений выходили с честью при помощи формулы: в известных случаях наша наука бессильна. Салтыков-Щедрин, Пошехонская старина. Ерофеич подмахивал обычную формулу: «А за него, неграмотного, по личной его просьбе» и т. д. Эртель, Гарденины.

2. Условное выражение (числами, буквами, специальными знаками) совокупности каких-л. величин, отношений, составов, элементов и т. п. Математическая формула (совокупность величин, выраженных числами и буквами и соединенных посредством математических знаков). Химическая формула (изображение химическими знаками состава и строения молекулы). □ — Илья Матвеевич, — сказал Игорь, — простите, пожалуйста, что мешаю. Я принес вам формулы расчетов. Кочетов, Журбины.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Формула (от лат. formula — форма, правило, предписание):

Формула в Microsoft Excel

Формула в судопроизводстве в Древнем Риме

Формула технических видов спорта — свод технических правил, предъявляемых к участвующим конструкциям.

Соревнование автомобилей в классе Формула-1

Соревнование автомобилей в классе Формула-1600

Соревнование автомобилей в классе Формула-4

Соревнование электромобилей в классе Формула Е

Соревнование скутеров в классе Формула-1

Формула — гоночный автомобиль с открытыми колёсами

«Формула» — журнал о Формуле-1 в России

«Формула любви» (фильм)

ФО’РМУЛА, ы, ж. [от латин. formula, букв. уменьш. от forma]. 1. Общее краткое и точное выражение (мысли, закона), определение (книжн.). — . У нас уже осуществлена в основном первая фаза коммунизма, социализм. Основным принципом этой фазы коммунизма является, как известно, формула: «от каждого — по его способностям, каждому — по его труду». Сталин. Ф. закона тяготения. 2. Выраженный условными знаками ряд математических величин в их функциональных зависимостях (мат.). 3. Условное буквенное выражение состава сложных веществ и химических процессов (хим.). Химическая ф. Ф. серной кислоты. Ф. горения.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

фо́рмула

1. краткое, точное определение какого-либо правила или закона ◆ ― Катет равен гипотенузе, умноженной на синус противолежащего угла или на косинус прилежащего. Запишите себе эту формулу ― я буду спрашивать на экзамене, и она имеет значение для дальнейшего чтения моего курса. И. Е. Репин, «Далёкое близкое», 1912–1917 г. (цитата из НКРЯ) ◆ Эти учёные были в плену авторитета великого Ньютона и в плену созданных им математических формул, хотя Ньютон, по существу, не может считаться первым апологетом «действия на расстоянии». В. П. Карцев, «Приключения великих уравнений», 1970 г. (цитата из НКРЯ) ◆ То, что бродило в его мыслях словесно, в частной формуле Гейзенберга нашло меру. Д. С. Данин, «Нильс Бор», 1969–1975 г. (цитата из НКРЯ)

2. краткое и точное словесное выражение, определение чего-либо ◆ Около этой упразднённой формулы ютились все его помыслы, и никакой иной комбинации он не только придумать, но и случайно представить себе не был в состоянии. М. Е. Салтыков-Щедрин, «Пошехонское «дело»», 1883 г. (цитата из НКРЯ) ◆ Тут всё дело в том, что мы, взрослые, если можно так выразиться, мыслим словами, словесными формулами, а маленькие дети ― вещами, предметами предметного мира. К. И. Чуковский, «От двух до пяти», 1933 г. (цитата из НКРЯ)

3. символическая запись чего-либо ◆ Углеводы ― группа природных органических соединений, химическая формула которых соответствует Сm (H₂O)_n, т.е. углерод + вода, отсюда название. Владимир Горбачёв, «Концепции современного естествознания», 2003 г. (цитата из НКРЯ)

Источник

Формула – что означает? Определение, значение, примеры употребления

Ищешь, что значит слово формула? Пытаешься разобраться, что такое формула? Вот ответ на твой вопрос:

Значение слова «формула» в словарях русского языка

Формула это:

формула (от — форма, правило, предписание):

Википедия

Формула

ж.

1.Выраженный условными знаками ряд математических величин в их функциональных зависимостях ( в математике ) .

2.Условное буквенное выражение состава сложных веществ и химических процессов ( в химии ) .

3. перен.Точное и краткое словесное определение чего-либо.

Большой современный толковый словарь русского языка

Формула

( лат. formula форма, правило)
1) точное общее определение какого-л, правила, отношения, закона и т. п., приложимое в определенных условиях ко всем частным случаям; вообще — всякое определение, выраженное в краткой форме;
2) мат. совокупность величин, выраженных числами и буквами и соединенных посредством математических знаков;
3) хим. сокращенное обозначение состава какого-л. соединения с помощью букв латинского алфавита, заменяющих названия элементов, и чисел, указывающих на количественное соотношение этих элементов в данном соединении ( напр. , nacl, H 2 O).

Новый словарь иностранных слов

Формула

ж.
1) Выраженный условными знаками ряд математических величин в их функциональных зависимостях (в математике).
2) Условное буквенное выражение состава сложных веществ и химических процессов (в химии).
3) перен. Точное и краткое словесное определение чего-л.

Новый толково-словообразовательный словарь русского языка Ефремовой

Формула

[

1. точное общее определение какого-л, правила, отношения, закона и т. п., приложимое в определенных условиях ко всем частным случаям; вообще — всякое определение, выраженное в краткой форме;

2. мат. совокупность величин, выраженных числами и буквами и соединенных посредством математических знаков;

3. хим. сокращенное обозначение состава какого-л. соединения с помощью букв латинского алфавита, заменяющих названия элементов, и чисел, указывающих на количественное соотношение этих элементов в данном соединении (напр., nacl, h2o).

Словарь иностранных выражений

Формула

символическая запись (с помощью химических знаков) химического состава и строения веществ Ф. молекулы. формула комбинация математических знаков, выражающая какое-нибудь утверждение Алгебраическая ф. формула краткое и точное словесное выражение, определение Изложить в сжатых формулах.

Словарь русского языка Ожегова

Формула

(лат. formula — образ, вид), комбинация математических знаков, выражающая какое-либо предложение; напр., формула a2 + b2 = c2 выражает связь длины с гипотенузы прямоугольного треугольника с длинами a и b его катетов.

Современный толковый словарь, БСЭ

Формула

формула ж.
1) Выраженный условными знаками ряд математических величин в их функциональных зависимостях (в математике).
2) Условное буквенное выражение состава сложных веществ и химических процессов (в химии).
3) перен. Точное и краткое словесное определение чего-л.

Толковый словарь Ефремовой

Формула

формулы, ж. (от латин. formula, букв. уменьш. от forma).

1. Общее краткое и точное выражение (мысли, закона), определение (книжн.). -…У нас уже осуществлена в основном первая фаза коммунизма, социализм. Основным принципом этой фазы коммунизма является, как известно, формула: “от каждого – по его способностям, каждому – по его труду”. Сталин. Формула закона тяготения.

2. Выраженный условными знаками ряд математических величин в их функциональных зависимостях (мат.).

3. Условное буквенное выражение состава сложных веществ и химических процессов (хим.). Химическая формула. Формула серной кислоты. Формула горения.

Толковый словарь русского языка Ушакова

Формула

ИЗОБРЕТЕНИЯ- в патентном праве — составленная по установленным нормативными документами правилам краткая словесная характеристика технической сущности изобретения, определяющая его объем. Ф.и. может быть однозвенной и многозвен-_ной и включать соответственно один или несколько пунктов.

Словарь экономических терминов

Формула

(от лат. formula v форма, правило, предписание) (математическая), комбинация математических знаков, выражающая какое-либо предложение; например, суть формулы: x 3 + y 3 < z (
1) 2 ` 2 4(
2) D ABC ~ D EFG (
3) 2 ` 2 5(
4) ( a + b )2 a 2 + 2 ab + b 2(
5) ,(
6) y- y (
7) (
8) что с помощью Ф. довольно сложные предложения могут быть записаны в компактной и удобной форме (см. Знаки математические ) . Некоторые Ф. [из написанных выше (
2), (
4), (
6)] выражают вполне определённые конкретные суждения и поэтому являются истинными [как (
2) и (
6)] или ложными [как (
4)]. Смысл других Ф. [из написанных выше (
1), (
3), (
5), (
7), (
8)] зависит от значения входящих в них переменных [например, (
1) превращается в истинную Ф. 13 + 23 < 19 при х 1, у 2, z 19 и в ложную Ф. 33 + 43 < 5 при х 3, у 4, z 5]. Ф. этого типа при таком понимании не являются истинными или ложными непосредственно, но становятся таковыми при замещении переменных конкретными объектами из какой-либо заранее выбранной области. Ф., становящиеся истинными при любом замещении переменных объектами из некоторой области, называются тождественно-истинными в данной области. Например, Ф. (
5) тождественно-истинна в области комплексных чисел, ф. (
8) тождественно-истинна в области дважды непрерывно-дифференцируемых функций от аргументов x и y . Ф., являющиеся истинными [как (
2) и (
6)] или тождественно-истинными в какой-либо области [как (
5) и (
8)], служат для записи математических законов. При этом тождественно-истинные Ф. часто понимаются как утверждения о всеобщности. Например, наиболее распространённое понимание Ф. (
5) состоит в том, что она считается сокращённой записью следующего утверждения: ‘для любых чисел а и b имеет место равенство ( a + b )2 a 2 + 2 ab + b

Большая советская энциклопедия, БСЭ

Формула

формула, -ы

Полный орфографический словарь русского языка

Формула

краткое, точное определение какого-либо правила или закона краткое и точное словесное выражение, определение чего-либо символическая запись чего-либо

Викисловарь

Где и как употребляется слово «формула»?

Кроме значения слова «формула» в словарях, рекомендуем также ознакомиться с примерами предложений и цитат из классической литературы, в которых употребляется слово «формула».

Так вы сможете гораздо легче понять и запомнить, как правильно употребляется слово «формула» в тексте и устной речи.

Примеры употребления слова «формула»

– Вы, наверное, требуете от меня какой-то математической формулы идеальной победы? – предположил он.

Поэтому здесь вы не найдёте магических формул, способных причинить вред, – сильных приворотов, присушек, способов нанести порчу.

Во-первых, он наверняка все свои отпуска проводит где-нибудь в горах на свежем воздухе и никогда не будет сидеть в помещении за выведением новых химических формул.

Формула является ответом на вопросы из кроссвордов

Символическая запись в математ.. 7 букв
Тождество, неравенство (матем.)
Закон в знаках
Ряд величин, выраженных условными знаками
Фильм Джона Эвилдсена
«Химическая реакция» в тетради ученика
«Общая крыша» для всех частных случаев
Символы химического состава
Фильм Питера Биллингсли «… любви для узников брака»
Фильм Марка Захарова «… любви»

Источник

Математическая формула (от лат. formula — уменьшительное от forma — образ, вид) — в математике, а также физике и прикладных науках, символическая запись высказывания (которое выражает логическое суждение^[1]), либо формы высказывания^[2]. Формула, наряду с термами, является разновидностью выражения формализованного языка.
В более широком смысле формула — всякая чисто символьная запись (см. ниже), противопоставляемая в математике различным выразительным способам, имеющим геометрическую коннотацию: чертежам, графикам, диаграммам, графам и т. п.

Содержание

1 Основные виды (численных) формул
- 1.1 Уравнения
- 1.2 Тождества
- 1.3 Приближённые равенства
- 1.4 Неравенства
2 Используемые операции
- 2.1 Сложение и вычитание
- 2.2 Умножение
- 2.3 Деление
- 2.4 Возведение в степень
- 2.5 Элементарные функции
- 2.6 Абсолютная величина, знак и т. п.
- 2.7 Приоритет операций и скобки
3 Примеры
4 Примечания
5 Литература
6 Ссылки
7 См. также

Основные виды (численных) формул

Формула должна сообщить, как искать значения переменной (уравнения и т. п.);
Формула (записываемая как «искомое = выражение») определяет величину через свои параметры (аналогично присваиванию в программировании и иногда записывается через диграф «:=» как в языке Pascal, но в принципе может считаться вырожденным частным случаем уравнения);
Формула является собственно логическим утверждением: тождеством (например, аксиомой), утверждением теоремы и т. п.

Уравнения

Если в уравнение входят параметры, то его смысл — для заданных параметров найти корни (то есть значения переменной, при котором равенство верно). Иногда это можно сформулировать как нахождение неявной зависимости переменной от параметра (параметров). Например $x^{2}=a$ понимается как уравнение на x (это обычная буква для обозначения переменной, наряду с y, z и t). Корнями уравнения является квадратный корень из a (считается, что их имеется два, разных знаков).
Следует отметить, что подобная формула, сама по себе, задаёт лишь бинарное отношение между x и a и её можно понимать в обратную сторону, как уравнение на a относительно x. В данном элементарном случае, речь может идти скорее об определении a через x: $a=x^{2}$ .

Тождества

Приближённые равенства

Например:
— приближённое равенство при малых ;

Неравенства

Используемые операции

Сложение и вычитание

Умножение

Деление

Возведение в степень

Элементарные функции

Абсолютная величина, знак и т. п.

Приоритет операций и скобки

Примеры

Например:

2+2=7 — пример формулы, имеющей значение «ложь»;

— функция одного действительного аргумента;

— не дифференцируемая функция в точке (непрерывная ломаная линия не имеет касательной);

${displaystyle x^{3}+y^{3}=3axy}$ — уравнение, то есть неявная функция (график кривой «декартов лист»);

${displaystyle t_{n}=n!}$ — целочисленная функция;

${displaystyle y=y^{3}sin(nx)}$ — чётная функция;

— нечётная функция;

$f(P)={sqrt {x^{2}+y^{2}+z^{2}}}$ — функция точки, расстояние от точки до начала (декартовых) координат;

${displaystyle y={frac {1}{x-3}}}$ — разрывная функция в точке x=3 ;

— параметрически заданная функция (график циклоиды);

${displaystyle y=ln(x), x=e^{y}}$ — прямая и обратная функции;

${displaystyle f(x)=int limits _{-infty }^{x}|f(t)|,dt}$ — интегральное уравнение.

Примечания

↑ Чупахин, Бродский, 1977, с. 200.
↑ Колмогоров, Драгилин, 2006, с. 13—15.

Литература

Чупахин И.Я., Бродский И.Н. Формальная логика. — Ленинград: Издательство Ленинградского университета, 1977. — 357 с.
Колмогоров А.Н., Драгилин А.Г. Математическа логика. — М.: КомКнига, 2006. — 240 с. — ISBN 5-484-00520-5.

Ссылки

Большая советская энциклопедия (недоступная ссылка с 28-08-13 [1893 дня])
Самые красивые физические и математические формулы
Красивые формулы элементарной математики (недоступная ссылка с 28-08-13 [1893 дня])
М. Я. Выгодский. Справочник по высшей математике (недоступная ссылка)
Н. К. Верещагин, А. Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. (недоступная ссылка)

См. также

Алгебраическое выражение — математическое обозначение, не выражающее законченную мысль.
Интерполяционные формулы
Формула конечных приращений
Формула Симпсона
Рекуррентная формула
Формула Эйлера
ISO 31
Трансцендентная функция

Источник

фо́рмула

Источник

Основные виды (численных) формул[править | править код]

Уравнения[править | править код]

Тождества[править | править код]

Приближённые равенства[править | править код]

Неравенства[править | править код]

Используемые операции[править | править код]

Сложение и вычитание[править | править код]

Умножение[править | править код]

Деление[править | править код]

Возведение в степень[править | править код]

Элементарные функции[править | править код]

Абсолютная величина, знак и т. п.[править | править код]

Приоритет операций и скобки[править | править код]

Примеры[править | править код]

В филателии[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

КАК ВЫЧИСЛИТЬ ФОРМУЛУ ВЕЩЕСТВА

1.Понятие простейшей и истинной формулы вещества

2.Массовая доля химического элемента: что означает и как высчитывается

3.Как определить формулу вещества по массовым долям элементов

4.Как определить формулу органического соединения

4.1. Как определить формулу органического соединения

по общей молекулярной формуле вещества

по продуктам его сгорания

Значение слова «формула»

фо́рмула

Формула – что означает? Определение, значение, примеры употребления

Значение слова «формула» в словарях русского языка

Формула это:

Формула

Формула

Формула

Формула

Формула

Формула

Формула

Формула

Формула

Формула

Формула

Формула

Где и как употребляется слово «формула»?

Примеры употребления слова «формула»

Формула является ответом на вопросы из кроссвордов

Содержание

Основные виды (численных) формул

Уравнения

Тождества

Приближённые равенства

Неравенства

Используемые операции

Сложение и вычитание

Умножение

Деление

Возведение в степень

Элементарные функции

Абсолютная величина, знак и т. п.

Приоритет операций и скобки

Примеры

Примечания

Литература

Ссылки

См. также

фо́рмула

Вам также может понравиться

Японские шоу как найти дочь

Уравнение зависимости пути от времени как найти

Как найти свою девушку книга

Добавить комментарий Отменить ответ