Как найти cos 630

The value of cos 630 degrees is 0. Cos 630 degrees in radians is written as cos (630° × π/180°), i.e., cos (7π/2) or cos (10.995574. . .). In this article, we will discuss the methods to find the value of cos 630 degrees with examples.

• Cos 630°: 0
• Cos (-630 degrees): 0
• Cos 630° in radians: cos (7π/2) or cos (10.9955742 . . .)

What is the Value of Cos 630 Degrees?

The value of cos 630 degrees is 0. Cos 630 degrees can also be expressed using the equivalent of the given angle (630 degrees) in radians (10.99557 . . .)

We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 630 degrees = 630° × (π/180°) rad = 7π/2 or 10.9955 . . .
∴ cos 630° = cos(10.9955) = 0

Explanation:

For cos 630°, the angle 630° > 360°. Given the periodic property of the cosine function, we can represent it as cos(630° mod 360°) = cos(270°). The angle 630°, coterminal to angle 270°, lies on the negative y-axis.
Thus, cos 630 degrees value = 0
Similarly, cos 630° can also be written as, cos 630 degrees = (630° + n × 360°), n ∈ Z.
⇒ cos 630° = cos 990° = cos 1350°, and so on.
Note: Since, cosine is an even function, the value of cos(-630°) = cos(630°) = 0.

Methods to Find Value of Cos 630 Degrees

The value of cos 630° is given as 0. We can find the value of cos 630 degrees by:

• Using Unit Circle
• Using Trigonometric Functions

Cos 630 Degrees Using Unit Circle

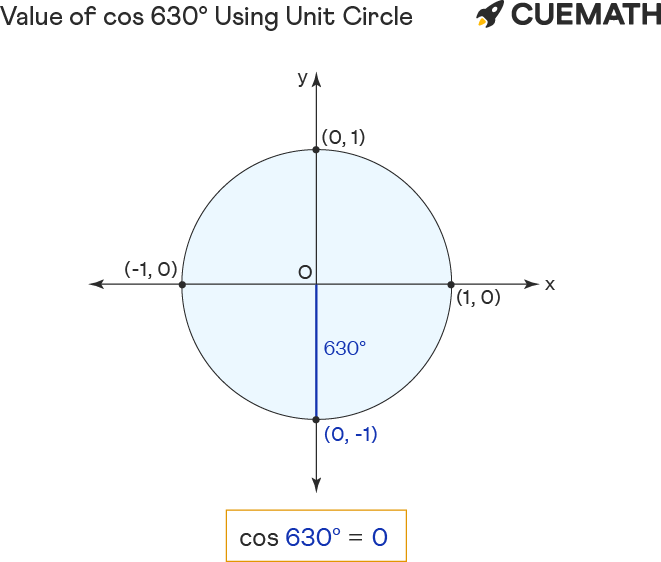
To find the value of cos 630 degrees using the unit circle, represent 630° in the form (1 × 360°) + 270° [∵ 630°>360°] ∵ cosine is a periodic function, cos 630° = cos 270°.

• Rotate ‘r’ anticlockwise to form 270° or 630° angle with the positive x-axis.
• The cos of 630 degrees equals the x-coordinate(0) of the point of intersection (0, -1) of unit circle and r.

Hence the value of cos 630° = x = 0

Cos 630° in Terms of Trigonometric Functions

Using trigonometry formulas, we can represent the cos 630 degrees as:

• ± √(1-sin²(630°))
• ± 1/√(1 + tan²(630°))
• ± cot 630°/√(1 + cot²(630°))
• ±√(cosec²(630°) – 1)/cosec 630°
• 1/sec 630°

Note: Since 630° lies on the negative y-axis, the final value of cos 630° is 0.

We can use trigonometric identities to represent cos 630° as,

• -cos(180° – 630°) = -cos(-450°)
• -cos(180° + 630°) = -cos 810°
• sin(90° + 630°) = sin 720°
• sin(90° – 630°) = sin(-540°)

☛ Also Check:

• cos 135 degrees
• cos 1 degrees
• cos 120 degrees
• cos 43 degrees
• cos 585 degrees
• cos 244 degrees

FAQs on Cos 630 Degrees

What is Cos 630 Degrees?

Cos 630 degrees is the value of cosine trigonometric function for an angle equal to 630 degrees. The value of cos 630° is 0.

How to Find the Value of Cos 630 Degrees?

The value of cos 630 degrees can be calculated by constructing an angle of 630° with the x-axis, and then finding the coordinates of the corresponding point (0, -1) on the unit circle. The value of cos 630° is equal to the x-coordinate (0). ∴ cos 630° = 0.

How to Find Cos 630° in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of cos 630° can be given in terms of other trigonometric functions as:

• ± √(1-sin²(630°))
• ± 1/√(1 + tan²(630°))
• ± cot 630°/√(1 + cot²(630°))
• ± √(cosec²(630°) – 1)/cosec 630°
• 1/sec 630°

☛ Also check: trigonometry table

What is the Value of Cos 630° in Terms of Cosec 630°?

Since the cosine function can be represented using the cosecant function, we can write cos 630° as -[√(cosec²(630°) – 1)/cosec 630°]. The value of cosec 630° is equal to -1.

What is the Value of Cos 630 Degrees in Terms of Cot 630°?

We can represent the cosine function in terms of the cotangent function using trig identities, cos 630° can be written as cot 630°/√(1 + cot²(630°)). Here, the value of cot 630° is equal to 0.

Вы зашли на страницу вопроса Вычислить с помощью формул приведения cos630 – sin1470 – ctg 1125?, который относится к
категории Математика. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.