Вместо слова альфа будем просто писать букву а. И здесь знак вопроса, вероятно, обозначает греческую букву Пи = 3,1416. Я понял так, что sina = 0,8. Надо найти угол «а» (то есть альфа), который больше Пи/2, но меньше, чем Пи, то есть угол а должен находится в промежутке Пи/2 < a < Пи (если заменить знак вопроса на букву Пи). А это вторая четверть, полный круг равен 2Пи = 360°. Итак, sina = 0,8. Здесь надо использовать из тригонометрии таблицу синусов. Пройдемся по таблице и найдем, что sin(53°8`) примерно равен 0,800. То есть, угол а = 53 градуса и 8 минут. Или а = 53,13°. А угол Пи/2 = 90°. Возьмем формулу из тригонометрии sin(Пи – а) = sina. Итак, находим, что наш угол а = Пи – а = 180° – 53,13° = 126,87°. Этот угол больше, чем Пи/2 (90°) и меньше, чем Пи = 180°.
Остальные функции находим по формулам. Для нахождения косинуса имеем
cosa = sqrt(1 – sin^2(а)). (1)
Где sin^2(а) – это sina в квадрате. Мы знаем, что sina = 0,800. Тогда синус в квадрате sin^2(а) = 0,8^2 = 0,64. Далее 1 – sin^2(а) = 1 – 0,64 = 0,36. По формуле (1) находим cosa = sqrt(1 – 0,64) = sqrt(0,36) = 0,6.
Для нахождения tga используем формулу tga = sina/cosa = 0,8/0,6 = 4/3 = 1,333… Для нахождения котангенса используем формулу ctga = 1/tga = 1/(4/3) =3/4 = 0,75. Только бы у меня не было ошибок при численных расчетах.
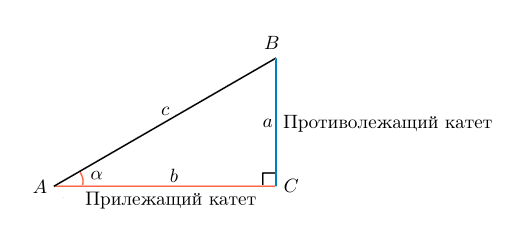
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
-
Определение
- График косинуса
- Свойства косинуса
- Обратная к косинусу функция
- Таблица косинусов
Определение
Косинус острого угла α (cos α) – это отношение прилежащего катета (b) к гипотенузе (c) в прямоугольном треугольнике.
cos α = b / c
Например:
b = 4
c = 5
cos α = b / c = 4 / 5 = 0.8
График косинуса
Функция косинуса пишется как y = cos (x). График называется косинусоидой и в общем виде выглядит следующим образом:
Косинусоида – периодическая функция с основным периодом T = 2π.
Свойства косинуса
Ниже в табличном виде представлены основные свойства косинуса с формулами:
Обратная к косинусу функция
Арккосинус x – это обратная к косинусу функция x, при -1≤x≤1.
Если косинус у равняется х (cos y = x), значит арккосинус x равен у:
arccos x = cos-1 x = y
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
Таблица косинусов
| x (°) | x (рад) | cos x |
| 180° | π | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | π/2 | 0 |
| 60° | π/3 | 1/2 |
| 45° | π/4 | √2/2 |
| 30° | π/6 | √3/2 |
| 0° | 0 | 1 |
microexcel.ru
|
Косинус угла cos(A) — есть отношение прилежащего катета b к гипотенузе c [ cos(A) = frac{b}{c} ] |
Косинус угла — cos(A), таблица
|
0° Косинус угла 0 градусов |
$ cos(0°) = cos(0) = 1 $ |
1.000 |
|
30° Косинус угла 30 градусов |
$ cos(30°) = cosBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{sqrt{3}}{2}normalsize $ |
0.866 |
|
45° Косинус угла 45 градусов |
$ cos(45°) = cosBig(Largefrac{pi}{4}normalsizeBig) = Largefrac{sqrt{2}}{2}normalsize $ |
0.707 |
|
60° Косинус угла 60 градусов |
$ cos(60°) = cosBig(Largefrac{pi}{3}normalsizeBig) = Largefrac{1}{2}normalsize $ |
0.500 |
|
90° Косинус угла 90 градусов |
$ cos(90°) = cosBig(Largefrac{pi}{2}normalsizeBig) = 0 $ |
0.000 |
Вычислить, найти косинус угла cos(A) и угол, в прямоугольном треугольнике
Вычислить, найти косинус угла cos(A) по углу A в градусах
Вычислить, найти косинус угла cos(A) по углу A в радианах
Косинус угла — cos(A) |
стр. 218 |
|---|
Что такое синус, косинус, тангенс, котангенс
18 мая 2022
Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
Содержание:
- Ключевые определения: синус, косинус, тангенс, котангенс.
- Почему эти значения зависят только от углов?
- Стандартные углы: 30°, 45°, 60°.
- Простейшие свойства синуса, косинуса, тангенса, котангенса.
- Тригонометрия на координатной сетке.
Никаких сложных формул и длинных решений. Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!
1. Ключевые определения
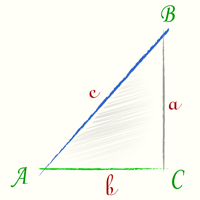
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Мы видим, что острый угол $alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $alpha $, назовём противолежащим:
Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.
1.1. Синус, косинус, тангенс, котангенс
Итак, пусть дан прямоугольный треугольник с острым углом $alpha $.
Тогда:
Определение 1. Синус угла $alpha $ — это отношение противолежащего катета к гипотенузе:
[sin alpha =frac{text{противолежащий катет}}{text{гипотенуза}}=frac{a}{c}]
Определение 2. Косинус угла $alpha $ — это отношение прилежащего катета к гипотенузе:
[cos alpha =frac{text{прилежащий катет}}{text{гипотенуза}}=frac{b}{c}]
Определение 3. Тангенс угла $alpha $ — это отношение противолежащего катета к прилежащему:
[operatorname{tg}alpha =frac{text{противолежащий катет}}{text{прилежащий катет}}=frac{a}{b}]
Определение 3. Котангенс угла $alpha $ — это отношение прилежащего катета к противолежащему:
[operatorname{ctg}alpha =frac{text{прилежащий катет}}{text{противолежащий катет}}=frac{b}{a}]
Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).
Рассмотрим пару примеров.
Задача 1. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Решение. Это классический прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5. Угол $alpha $ (он же — угол $A$ или угол $BAC$) образован прилежащим катетом $AB=3$гипотенузой $AC=5$. Следовательно катет $BC=4$ — противолежащий.
Имеем:
[begin{align}sin alpha& =frac{BC}{AC}=frac{5}{4} \ cos alpha& =frac{AB}{AC}=frac{3}{5} \ operatorname{tg}alpha& =frac{BC}{AB}=frac{4}{3} end{align}]
Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора. Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы.
Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:
[operatorname{ctg}alpha =frac{1}{operatorname{tg}alpha }]
Но об этом чуть позже.
Задача 2. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Это равнобедренный прямоугольный треугольник с катетами $AB=BC=1$. Найдём гипотенузу по теореме Пифагора:
[begin{align}{{ AC}^{2}} & ={{AB}^{2}}+{{BC}^{2}}=1+1=2 \ AC & =sqrt{2} \ end{align}]
Теперь найдём синус, косинус и тангенс:
[begin{align}sin alpha &=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos alpha &=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}alpha&=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)
1.2. Задачи для тренировки
Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.
Задача 3. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{5}{13} \ cos alpha &=frac{12}{13} \ operatorname{tg}alpha &=frac{5}{12} \ end{align}]
Задача 4. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{8}{17} \ cos alpha &=frac{15}{17} \ operatorname{tg}alpha &=frac{8}{15} \ end{align}]
Задача 5. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}}&={{3}^{2}}-{{1}^{2}}=9-1=8 \ l&=sqrt{8}=2sqrt{2} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{3} \ cos alpha&=frac{2sqrt{2}}{3} \ operatorname{tg}alpha&=frac{1}{2sqrt{2}}=frac{sqrt{2}}{4} \ end{align}]
Задача 6. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}} &={{2}^{2}}-{{1}^{2}}=4-1=3 \ l &=sqrt{3} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{2} \ cos alpha&=frac{sqrt{3}}{2} \ operatorname{tg}alpha&=frac{1}{sqrt{3}}=frac{sqrt{3}}{3} \ end{align}]
Как видим, считать синусы, косинусы и тангенсы совсем несложно. Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?
2. Теорема о единственности
Ключевая идея: синус, косинус, тангенс и котангенс зависят только от величины угла $alpha $ и никак не зависят от прямоугольного треугольника, в котором идут вычисления.
Такого не произойдёт. Потому что есть теорема о единственности.
2.1. Формулировка теоремы
Теорема. Значение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике определяются только величиной этого угла и никак не зависят от самого треугольника.
2.2. Доказательство
Рассмотрим произвольный острый угол $alpha $. Для удобства обозначим его вершину буквой $A$:
А затем впишем в него два произвольных прямоугольных треугольника — $ABC$ и $AMN$. Любым удобным способом. Например, можно вписать эти треугольники вот так:
А можно и вот так — это не имеет никакого значения:
Рассмотрим треугольники $ABC$ и $AMN$. Угол $A$ у них общий; углы [angle ABC=angle AMN=90{}^circ ] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:
[Delta ABCsim Delta AMN]
Из подобия треугольников следует двойное равенство
[frac{AB}{AM}=frac{BC}{MN}=frac{AC}{AN}]
Выпишем второе равенство — получим пропорцию
[frac{BC}{MN}=frac{AC}{AN}]
Попробуем выразить $sin alpha $. Вспомним основное свойство пропорции: произведение крайних членов равно произведению средних. Поэтому
[BCcdot AN=MNcdot AC]
Разделим обе части равенства на длину каждой гипотенузы — $AN$ и $AC$:
[begin{align}frac{BCcdot AN}{ANcdot AC} &=frac{MNcdot AC}{ANcdot AC} \ frac{BC}{AC} &=frac{MN}{AN} end{align}]
Однако по определению синуса имеем:
[begin{align}sin BAC &=frac{BC}{AC} \ sin MAN &=frac{MN}{AN} \ end{align}]
Получается, что $sin BAC=sin MAN$. Другими словами, вне зависимости от выбора треугольника для данного угла $alpha $ мы всегда будем получать одно и то же значение $sin alpha $.
То же самое касается и $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ — они зависят лишь от градусной меры угла $alpha $ и никак не зависят от конкретного прямоугольного треугольника, в котором они находятся. Теорема доказана.
3. Стандартные углы
Итак, значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ однозначно определяются величиной угла $alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $alpha $ нельзя найти точные значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
- Верно и обратное: для большинства «красивых» $sin alpha $, $cos alpha $ и т.д. нельзя подобрать подходящий угол $alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
[begin{array}{c|ccc} alpha& 30{}^circ& 45{}^circ & 60{}^circ \ hlinesin alpha & frac{1}{2} & frac{sqrt{2}}{2} & frac{sqrt{3}}{2} \ cos alpha & frac{sqrt{3}}{2} & frac{sqrt{2}}{2} & frac{1}{2} \ operatorname{tg}alpha& frac{sqrt{3}}{3} & 1 & sqrt{3} \ end{array}]
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $alpha =45{}^circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $angle A=angle B=45{}^circ $, получим:
[begin{align}sin 45{}^circ &=sin A=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos 45{}^circ &=sin A=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}45{}^circ&=sin A=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $alpha =30{}^circ $ и $alpha =60{}^circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $angle ABH=angle CBH=30{}^circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
[begin{align} sin{60}^circ &=sin A=frac{BH}{AB}=frac{sqrt{3}}{2} \ cos{60}^circ&=cos A=frac{AH}{AB}=frac{1}{2} \ operatorname{tg}{60}^circ&=operatorname{tg}A=frac{BH}{AH}=sqrt{3} \ end{align}]
И с углом 30°:
[begin{align} sin{30}^circ &=sin ABH=frac{AH}{AB} =frac{1}{2} \ cos{30}^circ &=cos ABH=frac{BH}{AB} =frac{sqrt{3}}{2} \ operatorname{tg}{30}^circ &=operatorname{tg} ABH=frac{AH}{BH} =frac{1}{sqrt{3}} =frac{sqrt{3}}{3} \ end{align}]
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $sin {50}^circ $? Или, быть может, $cos {10}^circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $alpha $:
[sin alpha =sin A=frac{BC}{AB}=frac{3}{5}=0,6]
Итак, мы знаем синус. Внимание, вопрос: каким должен быть угол $alpha $, чтобы $sin alpha =0,6$? Сколько градусов должно быть в угле $alpha $? Ответ: неизвестно.:)
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $alpha $, чтобы $sin alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
Мы можем посчитать лишь синус, косинус и тангенс для трёх табличных углов.
Например, $sin 30{}^circ $, $cos 45{}^circ $, $operatorname{tg}60{}^circ $ и т.д. А всякие $sin 15{}^circ $, $cos 25{}^circ $ или $operatorname{tg}89,5{}^circ $ — не сможем. По крайней мере пока.:)
И наоборот:
Зная $sin alpha $, $cos alpha $ или $operatorname{tg}alpha $, мы сможем назвать точный угол $alpha $ только в том случае, если все эти синусы, косинусы и тангенсы — среди табличных значений.
Например, мы точно знаем, что если $sin alpha =frac{sqrt{2}}{2}$, то $alpha =45{}^circ $. Но когда $sin alpha =0,6$, мы уже не можем назвать угол $alpha $ (хотя всегда можем построить такой угол).
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
4. Свойства синуса, косинуса, тангенса
Мы разберём три ключевых свойства:
- Связь между синусом, косинусом и тангенсом.
- Связь между острыми углами прямоугольного треугольника.
- Основное тригонометрическое тождество.
Свойствам 2 и 3 далее в курсе будут посвящены отдельные уроки. Но основные идеи полезно взять на вооружение уже сейчас.
4.1. Связь между синусом, косинусом и тангенсом
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Выразим синус, косинус:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
А теперь выразим тангенс и заметим, что
[operatorname{tg}alpha =frac{a}{b}=frac{a}{c}cdot frac{c}{b}=frac{sin alpha }{cos alpha }]
Точно так же можно выразить и котангенс:
[operatorname{ctg}alpha =frac{b}{a}=frac{b}{c}cdot frac{c}{a}=frac{cos alpha }{sin alpha }]
Более того, сам тангенс и котангенс тоже связаны:
[operatorname{tg}alpha cdot operatorname{ctg}alpha =frac{a}{b}cdot frac{b}{a}=1]
Мы получили три важнейших тригонометрических формулы:
Основные формулы тригонометрии:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha };quad operatorname{ctg}alpha =frac{cos alpha }{sin alpha };quad operatorname{tg}alpha cdot operatorname{ctg}alpha =1]
Эти формулы нужно знать наизусть. И понимать, откуда они берутся.
4.2. Связь между острыми углами
Рассмотрим прямоугольный треугольник $ABC$, где $angle C=90{}^circ $. Пусть градусная мера $angle A=alpha $ градусов:
Мы помним, что сумма острых углов прямоугольного треугольника равна 90°. Поэтому если $angle A=alpha $, то угол $angle B=90{}^circ -alpha $. Но тогда:
[sin alpha =sin A=frac{BC}{AB}=cos B=cos left( 90{}^circ -alpha right)]
То же самое и с косинусами:
[cos alpha =cos A=frac{AC}{AB}=sin B=sin left( 90{}^circ -alpha right)]
И даже с тангенсами и котангенсами:
[begin{align} operatorname{tg}alpha&=operatorname{tg}A=frac{BC}{AC} =operatorname{ctg}B=operatorname{ctg}left( {90}^circ -alpharight) \ operatorname{ctg}alpha&=operatorname{ctg}A=frac{AC}{BC} = operatorname{tg}B=tgleft( {90}^circ -alpha right) \ end{align}]
Другими словами, если вместо $alpha $ поставить ${90}^circ -alpha $, то исходная тригонометрическая функция поменяется на ко-функцию:
[begin{align}sin left( {90}^circ-alpharight) &=cos alpha \ cos left( {90}^circ-alpharight) &=sin alpha \ operatorname{tg}left( {90}^circ-alpharight) &=operatorname{ctg}alpha\ operatorname{ctg}left( {90}^circ-alpharight) &=operatorname{tg}alphaend{align}]
Но это ещё не всё. Есть гораздо более интересная формула.
4.3. Основное тригонометрическое тождество
Вновь рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Запишем выражения для $sin alpha $ и $cos alpha $:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
Далее заметим, что
[begin{align} {{sin }^{2}}alpha +{{cos }^{2}}alpha&={{left( frac{a}{c} right)}^{2}}+{{left( frac{b}{c} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{c}^{2}}} +frac{{{b}^{2}}}{{{c}^{2}}}= \ & =frac{{{a}^{2}}+{{b}^{2}}}{{{c}^{2}}} end{align}]
В числителе можем применить теорему Пифагора: ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$, поэтому
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =frac{{{c}^{2}}}{{{c}^{2}}}=1]
Правая часть этой формулы вообще не зависит от угла $alpha $.
Основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Это равенство связывает синус и косинус одного и того же угла и верно для всех $alpha $.
С помощью основного тригонометрического тождества можно вычислять косинус, зная синус, и наоборот.
Задача 7. Найдите $18cos alpha $ для острого угла $alpha $, если $sin alpha =frac{sqrt{65}}{9}$.
Решение. Запишем основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Подставим указанное значение $sin alpha $ и выразим $cos alpha $:
[begin{align}{{left( frac{sqrt{65}}{9} right)}^{2}}+{{cos }^{2}}alpha &=1 \ frac{65}{81}+{{cos }^{2}}alpha &=1 \ {{cos }^{2}}alpha &=frac{16}{81} \ cos alpha&=pm frac{4}{9} end{align}]
Поскольку косинус угла в прямоугольном треугольнике не может быть отрицательным, выбираем вариант $cos alpha ={4}/{9};$. Остаётся сделать финальный шаг:
[18cos alpha =18cdot frac{4}{9}=2cdot 4=8]
Вот и всё! Ответ: 8.
В следующем примере мы уже не будем подробно расписывать каждый шаг. Оформим всё так, как надо оформлять на контрольных и экзаменах.
Задача 8. Найдите $48operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{8}{sqrt{113}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-{{left( frac{8}{sqrt{113}} right)}^{2}}= \ & =1-frac{64}{113}=frac{49}{113} \ sin alpha&=pm frac{7}{sqrt{113}} end{align}]
Но ${0}^circ lt alpha lt {90}^circ $, поэтому $sin alpha gt 0$. Следовательно
[sin alpha =frac{7}{sqrt{113}}]
Найдём $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{7}{sqrt{113}}cdot frac{sqrt{113}}{8}=frac{7}{8}]
Окончательный ответ:
[48operatorname{tg}alpha =48cdot frac{7}{8}=6cdot 7=42]
Ответ: 42.
Заметка на будущее: замечание о том, что угол $alpha $ острый, весьма существенно. То, как мы сейчас определяем синусы, косинусы и тангенсы (через прямоугольный треугольник), называется геометрической тригонометрией. Её проходят в 8—9 классе.
Но в 10—11 классах появится алгебраическая тригонометрия, где синусы, косинусы и т.д. вполне могут быть отрицательными. И уже не получится просто так избавиться от минуса.
Но всё это будет чуть позже. А сейчас потренируемся.
Задача 9. ►
Найдите $52cos alpha $ для острого угла $alpha $, если $sin alpha =frac{5}{13}$.
Решение. Найдём $cos alpha $:
[begin{align}{{cos }^{2}}alpha &=1-{{sin }^{2}}alpha = \ &=1-frac{25}{169}=frac{144}{169} \ cos alpha&=pm frac{12}{13} end{align}]
Поскольку $cos alpha gt 0$ для острых $alpha $, выбираем $cos alpha ={12}/{13};$. Итого
[52cos alpha =52cdot frac{12}{13}=48]
Ответ: 48.
Задача 10. ►
Найдите $1+2operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{1}{sqrt{26}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-frac{1}{26}=frac{25}{26} \ sin alpha&=pm frac{5}{sqrt{26}} end{align}]
Поскольку $sin alpha gt 0$ для острых $alpha $, выбираем
[sin alpha =frac{5}{sqrt{26}}]
Считаем $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{5}{sqrt{26}}cdot frac{sqrt{26}}{1}=5]
Откуда
[1+2operatorname{tg}alpha =1+2cdot 5=11]
Ответ: 11.
5. Тригонометрия на координатной сетке
Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.
Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.
Звучит страшно, но на практике всё легко.:)
Задача 11. Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение. Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ на луч $BC$.
Треугольник $BAH$ — прямоугольный, причём угол $ABC$ — один из его острых углов. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{3}{4}=0,75]
Это и есть искомый тангенс.
Ответ: 0,75.
Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется. Попробуйте сами:
Задача 12. ►
Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение.
Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ к лучу $BC$.
Треугольник $BAH$ — прямоугольный с острым углом $ABC$. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{2}{4}=frac{1}{2}]
Ответ: 0,5.
Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.
Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.
Задача 13. Найдите тангенс угла $MNK$, изображённого на координатной сетке:
Решение. Луч $KN$ содержит лишь две точки в узлах координатной сетки — собственно, $K$ и $N$. Понятно, что если продолжить луч за точку $K$, мы найдём ещё много таких точек, но будем решать задачу с тем, что есть.
Заметим, что прямая $MN$ наклонена к линиям сетки под углом 45° и образует диагонали квадратов. Это значит, что перпендикуляр к ней тоже будет наклонён под углом 45°.
Дополнительное построение: отрезок $KH$ — диагональ одного из квадратов сетки.
Очевидно, что угол $NHK$ прямой, поэтому треугольник $KHN$ прямоугольный и содержит искомый острый угол $MNK$. Находим тангенс:
[operatorname{tg}MNK=frac{HK}{HN}=frac{sqrt{2}}{2sqrt{2}}=frac{1}{2}=0,5]
Здесь мы предположили, что сторона квадрата сетки равна 1. Но с тем же успехом можно считать, что сторона квадрата $a$:
[operatorname{tg}MNK=frac{HK}{HN}=frac{asqrt{2}}{2asqrt{2}}=frac{1}{2}=0,5]
Ответ: 0,5.
Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:
Задача 14. ►
Найдите тангенс угла $DEF$, изображённого на координатной сетке:
Решение.
Дополнительное построение: отрезок $DH$.
Очевидно, $EH=DH$, угол $EHD$ прямой. Следовательно, треугольник $EDH$ — прямоугольный и равнобедренный. Поэтому $operatorname{tg}DEF=1$.
Либо можно посчитать «напролом», полагая, что сторона квадрата сетки равна $a$:
[operatorname{tg}DEF=frac{asqrt{10}}{asqrt{10}}=1]
Ответ: 1.
Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.
К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:
И даже так (хотя вряд ли этот способ можно назвать рациональным):
Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)
Смотрите также:
- Радианная и градусная мера угла
- Как быстро запомнить таблицу синусов и косинусов
- Сложные логарифмические неравенства
- Сложные выражения с дробями. Порядок действий
- Задача B5: площадь фигур с вершиной в начале координат
- Обход точек в стереометрии — 2