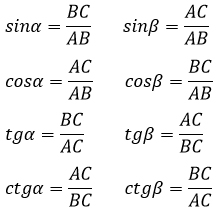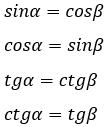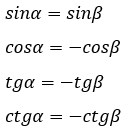Работа с внешними углами многоугольника с помощью тригонометрии
Определение
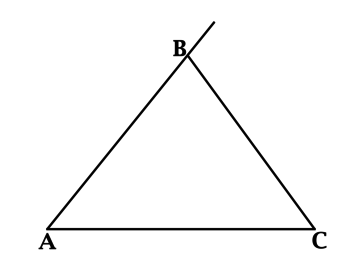
Смежные углы – это два угла, у которых общая вершина и сторона, а другие стороны образуют прямую.
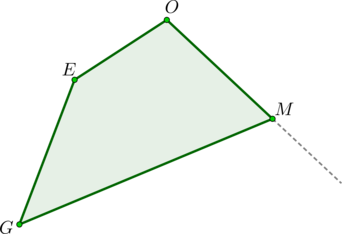
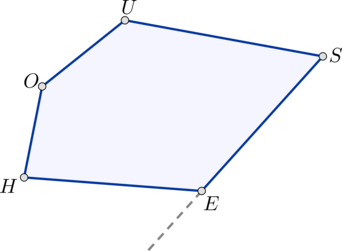
Внешний угол многоугольника – это угол, смежный с каким-нибудь внутренним углом многоугольника.
Утверждение
Для любого действительного (alpha) верно, что
(sinleft(pi – alpharight) = sinalpha),
(cosleft(pi – alpharight) = -cosalpha).
Следствия
Синусы смежных углов равны.
Косинусы смежных углов противоположны.
Следствия
Тангенсы смежных углов либо противоположны, либо оба не существуют (когда смежные углы равны (90^circ)).
Котангенсы смежных углов либо противоположны, либо оба не существуют (когда один из смежных углов развёрнутый).
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 октября 2021 года; проверки требуют 5 правок.
Смежные углы — это два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой. Таким образом, вместе смежные углы составляют развёрнутый угол, а сумма их угловых величин смежных всегда равна 
Таким образом, величина угла, являющимся смежным для угла величиной 

Так, например, для угла карп 

Тригонометрические соотношения[править | править код]
Синусы смежных углов равны. Их косинусы и тангенсы равны по величине, но имеют противоположные знаки (за исключением неопределённых значений).
См. также[править | править код]
- Угол
- Прилежащие углы
- Дополнительные углы
- Треугольник
Ссылки[править | править код]
- Никитин Н. Н. Геометрия. Смежные углы.
- Animated demonstration
- Angle definition pages
Что такое смежные углы: определение, теорема, свойства
В данной публикации мы рассмотрим, что из себя представляют смежные углы, приведем формулировку теоремы касательно них (в т.ч. следствия из нее), а также перечислим тригонометрические свойства смежных углов.
Определение смежных углов
Два прилежащих угла, внешними сторонами образующие прямую, называется смежными. На рисунке ниже это углы α и β.
Если два угла имеют одну общую вершину и сторону, они являются прилежащими. При этом внутренние области этих углов не должны пересекаться.
Принцип построения смежного угла
Одну из сторон угла протягиваем через вершину дальше, в результате чего образуется новый угол, смежный с исходным.
Теорема о смежных углах
Сумма градусов смежных углов равняется 180°.
Смежн. угол 1 + Смежн. угол 2 = 180°
Пример 1
Один из смежных углов равняется 92°, чему равен второй?
Решение, согласно рассмотренной выше теореме, очевидно:
Смежн. угол 2 = 180° – Смежн. угол 1 = 180° – 92° = 88°.
Следствия из теоремы:
Пример 2
Допустим, у нас есть угол, смежный с 75°. Он должен быть больше 90°. Давайте проверим это.
Воспользовавшись теоремой, находим значение второго угла:
180° – 75° = 105°.
105° > 90°, следовательно угол является тупым.
Тригонометрические свойства смежных углов
Источник
Углы. Смежные углы.
Какие углы называются смежными?
Смежными углами называется пара углов с общей вершиной и одной
общей стороной. 2 оставшиеся стороны делают продолжение друг
другу, образовывая прямую линию. Для угла 135 градусов смежным
будет угол равный 45 градусам. Для угла x градусов смежным
является угол (180 – x) градусов.

Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.
При пересечении 2-х прямых получается 4-ре пары смежных углов:
Но, так как ∠1 =∠4, ∠2 = ∠3 (как вертикальные), то достаточно рассматривать
только одну из этих пар.

Свойство смежных углов.
Чему равна сумма смежных углов?
Смежные углы равны: сумма смежных углов 180º.
Следствия из теоремы о смежных углах.
Тригонометрические соотношения.
противоположные знаки (исключение неопределенные значения).
Задание. Чему будет равна градусная мера угла α, когда градусная мера смежного ему угла = 70°?
Как найти смежный угол?
Решение. Из теоремы о смежных углах находим:
Источник
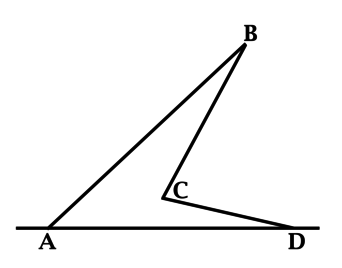
Работа с внешними углами многоугольника с помощью тригонометрии
Внешний угол многоугольника – угол, смежный с каким-нибудь внутренним углом многоугольника.
Задания, в которых школьникам необходимо найти внешние углы многоугольника, в ЕГЭ по математике традиционно встречаются из года в год. Правильно решать подобные задачи должны уметь выпускники, сдающие как базовый, так и профильный уровень аттестационного испытания. Школьники, которые освоили задания из раздела «Работа с внешними углами многоугольника», смогут справиться с ЕГЭ и рассчитывать на получение достойных баллов по итогам его прохождения.
Как подготовиться к экзамену?
Перед решением задач на нахождение внешних углов многоугольника в ЕГЭ стоит освежить в памяти определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике. Кроме того, для некоторых заданий могут потребоваться формулы основных тригонометрических тождеств.
Восполнить пробелы в знаниях, например, по теме «Вычисление синуса угла треугольника» и лучше усвоить информацию вам поможет образовательный проект «Школково». Для того чтобы выпускники могли успешно справляться с задачами на нахождение внешних углов треугольника в ЕГЭ, мы предоставляем возможность повторить определения и основные правила. Весь необходимый базовый материал вы найдете в разделе «Теоретическая справка». Наши специалисты подобрали соответствующую информацию.
Для закрепления теоретического материала мы предлагаем выполнить упражнения по теме «Работа с внешними углами многоугольника». Подборка простых и сложных заданий представлена в блоке «Каталог». Наши специалисты регулярно обновляют и дополняют упражнения.
Попрактиковаться в решении задач на нахождение внешних углов многоугольника, подобных тем, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.
Источник
Синус, косинус, тангенс и котангенс
Острые углы в прямоугольном треугольнике.
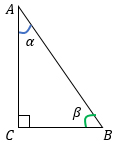
В геометрии определения синуса, косинуса, тангенса и котангенса мы изучаем на примере острых углов в прямоугольном треугольнике.
Возьмем прямоугольный треугольник АВС и распишем для него формулы для нахождения синуса, косинуса, тангенса и котангенса острых углов α и β.
Острые углы прямоугольного треугольника обладают очень интересными сверхспособностями, которые могут пригодится при решении геометрических задач.
Во-первых, их сумма равна 90°.
Смежные углы.
Теперь немного отстранимся от прямоугольных треугольников. Есть еще очень клевые формулы, но они подходят для смежных углов.
Пусть даны смежные углы α и β (напомню, что сумма смежных углов равна 180°).
Формулы приведения.
| Функции | Углы | ||||||||
| -α | 90°-α | 90°+α | 180°-α | 180°+α | 270°-α | 270°+α | 360°-α | 360°+α | |
| sin | -sinα | +cosα | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα |
| cos | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα | +cosα | +cosα |
| tg | -tgα | +ctgα | -ctgα | -tgα | +tgα | +ctgα | -ctgα | -tgα | +tgα |
| ctg | -ctgα | +tgα | -tgα | -ctgα | +ctgα | +tgα | -tgα | -ctgα | +ctgα |
Таблица значений тригонометрических функций для «прекрасных» углов.
| α | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | ||
| sinα | 1/2 | √2/2 | √3/2 | 1 | -1 | |||
| cosα | 1 | √3/2 | √2/2 | 1/2 | -1 | 1 | ||
| tgα | √3/3 | 1 | √3 | — | — | |||
| ctgα | — | √3 | 1 | √3/3 | — | — |
Осталось это всё запомнить и научиться применять на практике)
Вообще, достаточно запомнить информацию только про синусы и косинусы, а уже через них выводить значения тангенса и котангенса.
Еще рекомендую к прочтению статью про тригонометрические тождества.
Источник
Смежные углы и их свойства
Смежные углы и их свойства.
Смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными и лежат на одной прямой.
Смежные углы (понятие и определение):
Рис. 1. Смежные углы
В свою очередь, развернутый угол – это угол, градусная мера которого равна 180°.
Поэтому сумма величин смежных углов составляет 180 градусов.
Из этого следует, что величина угла β, являющимся смежным для угла величиной α градусов, будет (180° – α) градусов.
Свойства смежных углов:
1. Сумма величин смежных углов равна 180 градусам.
2. При пересечении двух прямых образуются две пары смежных углов.
Рис. 2. Смежные углы
Рис. 3. Смежные углы
4. В паре смежных углов один угол всегда тупой, а другой – острый либо оба угла являются прямыми.
5. Синусы смежных углов равны.
6. Косинусы и тангенсы смежных углов равны по величине, но имеют противоположные знаки.
Примечание: © Фото https://www.pexels.com, https://pixabay.com

Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Источник
Синус, косинус, тангенс и котангенс
Острые углы в прямоугольном треугольнике.
В геометрии определения синуса, косинуса, тангенса и котангенса мы изучаем на примере острых углов в прямоугольном треугольнике.
Вот и они:
Возьмем прямоугольный треугольник АВС и распишем для него формулы для нахождения синуса, косинуса, тангенса и котангенса острых углов α и β.
Острые углы прямоугольного треугольника обладают очень интересными сверхспособностями, которые могут пригодится при решении геометрических задач.
Во-первых, их сумма равна 90°.
Во-вторых, верны будут следующие равенства (доказать их верность очень легко – смотри предыдущие 8 формул):
Смежные углы.
Теперь немного отстранимся от прямоугольных треугольников. Есть еще очень клевые формулы, но они подходят для смежных углов.
Пусть даны смежные углы α и β (напомню, что сумма смежных углов равна 180°).
Для них будут верны следующие равенства (доказываются через формулы приведения, т.к. α = 180° – β):
Формулы приведения.
| Функции | Углы | ||||||||
| -α | 90°-α | 90°+α | 180°-α | 180°+α | 270°-α | 270°+α | 360°-α | 360°+α | |
| sin | -sinα | +cosα | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα |
| cos | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα | +cosα | +cosα |
| tg | -tgα | +ctgα | -ctgα | -tgα | +tgα | +ctgα | -ctgα | -tgα | +tgα |
| ctg | -ctgα | +tgα | -tgα | -ctgα | +ctgα | +tgα | -tgα | -ctgα | +ctgα |
Таблица значений тригонометрических функций для “прекрасных” углов.
| α | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| sinα | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| cosα | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tgα | 0 | √3/3 | 1 | √3 | – | 0 | – | 0 |
| ctgα | – | √3 | 1 | √3/3 | 0 | – | 0 | – |
Осталось это всё запомнить и научиться применять на практике)
Вообще, достаточно запомнить информацию только про синусы и косинусы, а уже через них выводить значения тангенса и котангенса.
Еще рекомендую к прочтению статью про тригонометрические тождества.
Успехов в подготовке!
С уважением, Васильева Анна.
math-public:opredelenie_i_svojstva_kosinusa
Содержание
Общее определение
-
Косинус острого угла равен отношению проекции к наклонной.
-
Косинус тупого угла равен косинусу смежного с ним угла, взятого с другим знаком.
-
Косинус прямого угла равен нулю.
-
Косинус развернутого угла равен минус единице.
Корректность определения косинуса
Значение косинуса угла не зависит от того, какую длину наклонной выбрать.
Доказательство
Первый способ.
Следует из корректности определения синуса и теоремы Пифагора.
Второй способ.
Следует из подобия треугольников.
Свойства косинуса
-
Косинус любого угла не больше $1$ и не меньше $-1$.
-
$cos{(180^circ-alpha)}=-cos{alpha}$.
-
При возрастании угла от $0^circ$ до $180^circ$ косинус убывает от 1 до -1.
-
Косинус однозначно определяет угол.
Доказательство
Докажем первый пункт теоремы.
Первое свойство следует из того, что проекция меньше наклонной.
Докажем второй пункт теоремы.
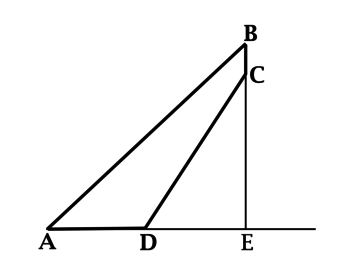
Второе свойство следует из того, что углы $180^circ-alpha$ и
$alpha$ являются смежными.
Докажем третий пункт теоремы.
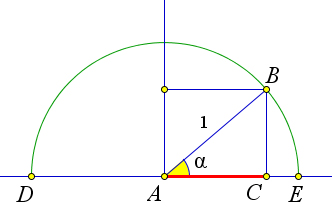
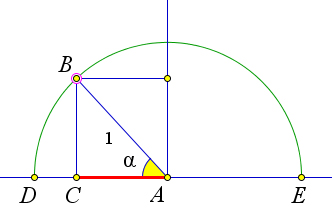
Рассмотрим окружность единичного радиуса с центром в точке $A$ и диаметром $DE$.
Пусть на прямой $DE$ задана числовая ось с началом в точке $A$ и единичным отрезком $AE$.
Проведем радиус $AB$ и получим угол $a BAE$ некоторой величины $alpha$.
Пусть точка $C$ является проекцией точки $B$ на прямую $DE$.
Тогда $cos{alpha}=AC$ при $alphaleqslant 90^circ$ и $cos{alpha}=-AC$ при $alpha>90^circ$.
Это означает, что $cos{alpha}$ равен координате точки $C$ на оси
$AE$.
Когда $alpha$ возрастает $0^circ$ до $180^circ$ (то есть,
когда точка $B$ пробегает полуокружность от точки $E$ до точки $D$),
точка $C$ пробегает диаметр $ED$ от точки $E$ до точки $D$.
При этом координата точки $C$, то есть $cos{alpha}$, убывает от $1$ до
$-1$.
Докажем четвертый пункт теоремы.
Пусть $cos{alpha}=cos{beta}$.
Докажем, что тогда $alpha=beta$.
Действительно, возможно три случая:
-
$alpha>beta$. Тогда по пункту 3 $cos{alpha}<cos{beta}$. Значит, этот случай не имеет места.
-
$alpha<beta$. Тогда по пункту 3 $cos{alpha}>cos{beta}$. Значит, этот случай не имеет места.
-
Следовательно, остаётся только третья возможность: $alpha=beta$.
· Последнее изменение: 2016/04/08 23:20 —
labreslav