Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2α, используя тригонометрические функции угла α. Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид nα записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin nαимеет то же значение, что и sin (nα). При обозначении sinn α имеем аналогичную запись(sin α)n. Использование записи применимо для всех тригонометрических функций со степенями n.
Ниже приведены формулы двойного угла:
sin 2α=2·sin α·cos αcos 2α=cos2 α-sin2 α, cos 2α=1-2·sin2 α, cos 2α=2·cos2 α-1tg 2α=2·tg α1-tg2 αctg 2α-ctg2 α-12·ctg α
Отметим, что данные формулы sin и cos применимы с любым значением угла α. Формула тангенса двойного угла справедлива при любом значении α, где tg 2α имеет смысл, то есть α≠π4+π2·z, z является любым целым числом. Котангенс двойного угла существует при любом α, где ctg 2α определен на α≠π2·z.
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin (α+β)=sin α ·cos β+cos α·sin βи косинуса суммы cos (α+β)=cos α ·cos β-sin α·sin β. Предположим, что β=α, тогда получим, что
sin (α+α)=sin α ·cos α+cos α·sin α=2·sin α·cos α и cos (α+α)=cos α ·cos α-sin α·sin α=cos2α-sin2α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2α= 2·sin α·cos α и cos 2α=cos2α-sin2α.
Остальные формулы cos 2α=1-2·sin2 α и cos 2α=2·cos2 α-1 приводят к виду cos 2α=cos 2α=cos2 α-sin2 α, при замене 1 на сумму квадратов по основному тождествуsin2 α+cos2 α=1. Получаем, что sin2 α+cos2 α=1. Так 1-2·sin2 α=sin2 α+cos2 α-2·sin2 α=cos2 α-sin2 α и 2·cos2 α-1=2·cos2 α-(sin2 α+ cos2 α)=cos2 α-sin2 α.
Для доказательства формул двойного угла тангенса и котангенса применим равенства tg 2α=sin 2αcos 2α и ctg 2α=cos 2αsin 2α. После преобразования получим, что tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α и ctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos α. Разделим выражение на cos2 α, где cos2 α≠0 с любым значением α, когда tg α определен. Другое выражение поделим на sin2 α, где sin2 α≠0 с любыми значениями α, когда ctg 2α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α=2·sin α·cos αcos2 αcos2 α-sin2 αcos2 α=2·sin2 αcos2 α1-sin2 αcos2 α=2·tg α1-tg2 αctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos=cos2 α-sin2 αsin2 α2·sin α·cos αsin2 α=cos2 αsin2 α-12·cos αsin α=ctg2 α-12·ctg α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2α для α=30°, применим значения тригонометрических функций для этих углов. Если α=30°, тогда 2α=60°. Проверим значения sin 60°=2·sin 30°·cos 30°, cos 60°=cos2 30°-sin2 30°.
Подставив значения, получим tg 60°= 2·tg 30°1-tg2 30° и ctg 60°=ctg230°-12·ctg 30°..
Известно, что sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3 и
sin 60°=32, cos 60°=12, tg 60°=3, ctg 60°=33, тогда отсюда видим, что
2·sin 30°·cos 30°=2·12·32=32, cos230°-sin230°=(32)2-(12)2=12,2·tg 30°1-tg230°=2·321-(33)=3
и ctg230°-12·ctg 30°=(3)2-12·3=33
Проведя вычисления, можно сделать вывод, что справедливость для α=30° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2α. В примере допускается применение формулы двойного угла 3π5. Тогда его необходимо преобразовать, в результате чего получим α=3π5:2=3π10. Отсюда следует, что формула двойного угла для косинуса будет иметь видcos3π5=cos23π10-sin23π10.
Представить sin 2α3 через тригонометрические функции, при α6.
Решение
Заметим, что из условия имеем 2α3=4·α6. Тогда использовав 2 раза формулу двойного угла, выразим sin2α3 через тригонометрические функции угла α6. Применяя формулу двойного угла, получим sin 2α3=2·sin α3·cos α3. После чего к функциям sin α3 и cos α3применим формулы двойного угла: sin 2α2=2·sin α3·cosα3=2·(2·sinα5·cosα6)·(cos2α6-sinα6)==4·sinα6·cos3α6-4·sin3α6·cosα6
Ответ: sin2α3=4·sinα6·cos3α6-4·sin3α6·cosα6.
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3α=sin(2α+α)=sin 2α·cos α+cos 2α·sin α=2·sin α·cosα·cos α+ (cos2 α-sin2α)·sin α==3·sin α·cos2α-sin3 α
При замене cos2α на 1-sin2α из формулы sin 3α=3·sin α·cos2α-sin3α, она будет иметь вид sin 3α=3·sin α-4·sin3 α.
Так же приводится формула косинуса тройного угла:
cos 3α=cos (2α+α)=cos 2α·cos α-sin 2α·sin α==(cos2 α-sin2 α)·cos α-2·sin α·cos α·sin α=cos3α-3·sin2α·cos α
При замене sin2 α на 1-cos2 α получим формулу вида cos 3α=-3·cos α+4·cos3 α.
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
tg 3α=sin 3αcos 3α=3·sin α·cos2 α-sin3 αcos3α-3·sin2α·cos α=3·sin α·cos2α-sin3αcos3αcos3α-3·sin2α·cos αcos3α==3·sin αcos α-sin3αcos3α1-3·sin2 αcos2 α=3·tg α-tg3α1-3·tg2α;ctg 3α=cos 3αsin 3α=cos3 α-3·sin2α·cosα3·sin α·cos2α-sin3α=cos3α-3·sin2α·cosαsin3α3·sin α·cos2α-sin3αsin3α==cos3αsin3α-3·cos αsin α3·cos2αsin2α-1=ctg3α-3·ctgα3·ctg2α-1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4α как 2·2α, тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5α в виде 3α+2α, что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Все формулы по тригонометрии
Основные тригонометрические тождества
$$sin^2x+cos^2x=1$$
$$tgx= frac{sinx}{cosx}$$
$$ctgx= frac{cosx}{sinx}$$
$$tgxctgx=1$$
$$tg^2x+1= frac{1}{cos^2x}$$
$$ctg^2x+1= frac{1}{sin^2x}$$
Формулы двойного аргумента (угла)
$$sin2x=2cosxsinx$$
begin{align}
sin2x &=frac{2tgx}{1+tg^2x}\
&= frac{2ctgx}{1+ctg^2x}\
&= frac{2}{tgx+ctgx}
end{align}
begin{align}
cos2x & = cos^2x-sin^2x\
&= 2cos^2x-1\
&= 1-2sin^2x
end{align}
begin{align}
cos2x & = frac{1-tg^2x}{1+tg^2x}\
&= frac{ctg^2x-1}{ctg^2x+1}\
&= frac{ctgx-tgx}{ctgx+tgx}
end{align}
begin{align}
tg2x & = frac{2tgx}{1-tg^2x}\
&= frac{2ctgx}{ctg^2x-1}\
&= frac{2}{ctgx-tgx}
end{align}
begin{align}
ctg2x & = frac{ctg^2x-1}{2ctgx}\
&= frac{2ctgx}{ctg^2x-1}\
&= frac{ctgx-tgx}{2}
end{align}
Формулы тройного аргумента (угла)
$$sin3x=3sinx-4sin^3x$$
$$cos3x=4cos^3x-3cosx$$
$$tg3x= frac{3tgx-tg^3x}{1-3tg^2x}$$
$$ctg3x= frac{ctg^3x-3ctgx}{3ctg^2x-1}$$
Формулы половинного аргумента (угла)
$$sin^2 frac{x}{2}= frac{1-cosx}{2}$$
$$cos^2 frac{x}{2}= frac{1+cosx}{2}$$
$$tg^2 frac{x}{2}= frac{1-cosx}{1+cosx}$$
$$ctg^2 frac{x}{2}= frac{1+cosx}{1-cosx}$$
begin{align}
tg frac{x}{2} & = frac{1-cosx}{sinx}\
&= frac{sinx}{1+cosx}
end{align}
begin{align}
ctg frac{x}{2} & = frac{1+cosx}{sinx}\
&= frac{sinx}{1-cosx}
end{align}
Формулы квадратов тригонометрических функций
$$sin^2x= frac{1-cos2x}{2}$$
$$cos^2x= frac{1+cos2x}{2}$$
$$tg^2x= frac{1-cos2x}{1+cos2x}$$
$$ctg^2x= frac{1+cos2x}{1-cos2x}$$
$$sin^2 frac{x}{2}= frac{1-cosx}{2}$$
$$cos^2 frac{x}{2}= frac{1+cosx}{2}$$
$$tg^2 frac{x}{2}= frac{1-cosx}{1+cosx}$$
$$ctg^2 frac{x}{2}= frac{1+cosx}{1-cosx}$$
Формулы кубов тригонометрических функций
$$sin^3x= frac{3sinx-sin3x}{4}$$
$$cos^3x= frac{3cosx+cos3x}{4}$$
$$tg^3x= frac{3sinx-sin3x}{3cosx+cos3x}$$
$$ctg^3x= frac{3cosx+cos3x}{3sinx-sin3x}$$
Формулы тригонометрических функций в четвертой степени
$$sin^4x= frac{3-4cos2x+cos4x}{8}$$
$$cos^4x= frac{3+4cos2x+cos4x}{8}$$
Формулы сложения аргументов
$$sin(alpha + beta) = sin alpha cos beta + cos alpha sin beta$$
$$cos(alpha + beta) = cos alpha cos beta – sin alpha sin beta$$
$$tg(alpha + beta)= frac{tg alpha + tg beta}{1 – tg alpha tg beta}$$
$$ctg(alpha + beta)= frac{ctg alpha ctg beta -1}{ctg alpha + ctg beta}$$
$$sin(alpha – beta) = sin alpha cos beta – cos alpha sin beta$$
$$cos(alpha – beta) = cos alpha cos beta + sin alpha sin beta$$
$$tg(alpha – beta)= frac{tg alpha – tg beta}{1 + tg alpha tg beta}$$
$$ctg(alpha – beta)= frac{ctg alpha ctg beta +1}{ctg alpha – ctg beta}$$
Формулы суммы тригонометрических функций
$$sinalpha + sinbeta = 2sin frac{alpha + beta }{2} cdot cos frac{alpha – beta }{2}$$
$$cosalpha + cosbeta = 2cos frac{alpha + beta }{2} cdot cos frac{alpha – beta }{2}$$
$$tgalpha + tgbeta = frac{sin(alpha + beta) }{cos alpha cos beta}$$
$$ctgalpha + ctgbeta = frac{sin(alpha + beta) }{cos alpha cos beta}$$
$$(sinalpha + cosalpha)^2= 1+sin2alpha$$
Формулы разности тригонометрических функций
$$sinalpha – sinbeta = 2sin frac{alpha – beta }{2} cdot cos frac{alpha + beta }{2}$$
$$cosalpha – cosbeta = -2sin frac{alpha + beta }{2} cdot sin frac{alpha – beta }{2}$$
$$tgalpha – tgbeta = frac{sin(alpha – beta) }{cos alpha cos beta}$$
$$ctgalpha – ctgbeta = – frac{sin(alpha – beta) }{sin alpha sin beta}$$
$$(sinalpha + cosalpha)^2= 1-sin2alpha$$
Формулы произведения тригонометрических функций
$$sinalpha cdot sinbeta = frac{cos(alpha – beta)-cos(alpha + beta)}{2}$$
$$sinalpha cdot cosbeta = frac{sin(alpha – beta)+sin(alpha + beta)}{2}$$
$$cosalpha cdot cosbeta = frac{cos(alpha – beta)+cos(alpha + beta)}{2}$$
begin{align}
tgalpha cdot tgbeta & = frac{cos(alpha – beta)-cos(alpha + beta)}{cos(alpha – beta)+cos(alpha + beta)}\
&= frac{tgalpha + tgbeta}{ctgalpha + ctgbeta}
end{align}
begin{align}
ctgalpha cdot ctgbeta & = frac{cos(alpha – beta)+cos(alpha + beta)}{cos(alpha – beta)-cos(alpha + beta)}\
&= frac{ctgalpha + ctgbeta}{tgalpha + tgbeta}
end{align}
$$tgalpha cdot ctgbeta = frac{sin(alpha – beta)+sin(alpha + beta)}{sin(alpha + beta)-sin(alpha – beta)}$$
На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.
Содержание:
- Основные тригонометрические тождества
- Формулы двойного угла
- Формулы тройного угла
- Формулы понижения степени
- Вторая степень
- Третья степень
- Четвертая степень
- Пятая степень
- Формулы половинного угла
- Формулы понижения степени половинного угла
- Формулы сложения аргументов
- Формулы вычитания аргументов
- Формулы суммы
- Формулы разности
- Формулы произведения
- Формулы произведения в степени
- Все формулы на одном листе
Все формулы тригонометрии
Основные тригонометрические тождества
tg alpha = dfrac {sin alpha}{ cos alpha} = dfrac{1}{ctg alpha}
ctg alpha = dfrac {cos alpha}{ sin alpha} = dfrac{1}{tg alpha}
sin ^2 alpha + cos ^2 alpha = 1
1+tg^2alpha=dfrac{1}{cos^2alpha}
1+ctg^2alpha=dfrac{1}{sin^2alpha}
tgalpha cdot ctgalpha=1
Формулы двойного угла (аргумента)
sin(2alpha)=2 cdot cos alpha cdot sin alpha
sin(2alpha)=dfrac{2 cdot tg alpha}{1+tg ^2 alpha}=dfrac{2 cdot ctg alpha}{1+ctg ^2 alpha}=dfrac{2}{tg alpha + ctg alpha}
cos(2alpha)=cos ^2 alpha- sin ^2 alpha = 2 cdot cos ^2 alpha- 1 = 1- 2 cdot sin ^2 alpha
cos(2alpha)=dfrac{1 -tg ^2 alpha}{1+tg ^2 alpha}=dfrac{ctg ^2 alpha- 1}{ctg ^2 alpha +1}=dfrac{ctg alpha-tg alpha}{ctg alpha + tg alpha}
tg(2alpha) = dfrac{2 cdot tg alpha}{1-tg ^2 alpha}=dfrac{2 cdot ctg alpha}{ctg ^2 alpha- 1}=dfrac{2}{ctg alpha- tg alpha}
ctg(2alpha) = dfrac{ctg ^2 alpha-1}{2 cdot ctg alpha}=dfrac{ctg alpha- tg alpha}{2}
Формулы тройного угла (аргумента)
sin(3alpha)=3 cdot sin alpha- 4 cdot sin ^3 alpha
cos(3alpha)= 4 cdot cos ^3 alpha- 3 cdot cos alpha
tg(3alpha)= dfrac{3 cdot tg alpha- tg ^3 alpha}{1-3 cdot tg ^2 alpha}
ctg(3alpha)= dfrac{ctg ^3 alpha- 3 cdot ctg alpha}{3 cdot ctg ^2 alpha -1}
Формулы понижения степени тригонометрических функций
Вторая степень
sin ^2 alpha = dfrac{1-cos(2alpha)}{2}
cos ^2 alpha = dfrac{1+cos(2alpha)}{2}
tg ^2 alpha = dfrac{1-cos(2alpha)}{1+cos(2alpha)}
ctg ^2 alpha = dfrac{1+cos(2alpha)}{1-cos(2alpha)}
(sin alpha- cos alpha)^2=1-sin(2 alpha)
(sin alpha+ cos alpha)^2=1+sin(2 alpha)
Третья степень
sin ^3 alpha = dfrac{3 cdot sin(alpha)-sin(3 alpha)}{4}
cos ^3 alpha = dfrac{3 cdot cos(alpha)+cos(3 alpha)}{4}
tg ^3 alpha = dfrac{3 cdot sin (alpha)-sin(3 alpha)}{3 cdot cos (alpha)+cos(3 alpha)}
ctg ^3 alpha = dfrac{3 cdot cos (alpha)+cos(3 alpha)}{3 cdot sin (alpha)-sin(3 alpha)}
Четвёртая степень
sin ^4 alpha = dfrac{3-4 cdot cos(2 alpha)+cos(4 alpha)}{8}
cos ^4 alpha = dfrac{3+4 cdot cos(2 alpha)+cos(4 alpha)}{8}
Пятая степень
sin ^5 alpha = dfrac{10 cdot sin(alpha)-5 cdot sin(3 alpha)+sin(5 alpha)}{16}
cos ^5 alpha = dfrac{10 cdot cos(alpha)+5 cdot cos(3 alpha)+cos(5 alpha)}{16}
Формулы половинного угла (аргумента)
sin Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1-cos alpha}{2}}
cos Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1+cos alpha}{2}}
tg Big( dfrac{alpha}{2} Big)= dfrac{1-cos alpha}{sin alpha}= dfrac{sin alpha}{1+cos alpha}
ctg Big( dfrac{alpha}{2} Big)= dfrac{1+cos alpha}{sin alpha}= dfrac{sin alpha}{1-cos alpha}
Формулы понижения степени половинного угла (аргумента)
sin ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{2}
cos ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{2}
tg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{1+cos alpha}
ctg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{1-cos alpha}
Формулы сложения аргументов
sin(alpha + beta)=sin alpha cdot cos beta + cos alpha cdot sin beta
cos(alpha + beta)=cos alpha cdot cos beta- sin alpha cdot sin beta
tg(alpha + beta)= dfrac{tg alpha + tg beta}{1-tg alpha cdot tg beta}
ctg(alpha + beta)= dfrac{ctg alpha cdot ctg beta-1}{ctg alpha + ctg beta}
Формулы вычитания аргументов
sin(alpha- beta)=sin alpha cdot cos beta- cos alpha cdot sin beta
cos(alpha- beta)=cos alpha cdot cos beta+ sin alpha cdot sin beta
tg(alpha- beta)= dfrac{tg alpha- tg beta}{1+tg alpha cdot tg beta}
ctg(alpha- beta)= dfrac{ctg alpha cdot ctg beta+1}{ctg beta – ctg alpha}
Формулы суммы тригонометрических функций
sin alpha+ sin beta=2 cdot sin big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)
cos alpha+ cos beta=2 cdot cos big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)
tg alpha + tg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}
ctg alpha + ctg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}
sin (alpha)+cos(alpha)=sqrt{2} cdot sin Big( alpha+ dfrac{pi}{4} Big)
Формулы разности тригонометрических функций
sin alpha- sin beta=2 cdot sin big( dfrac{alpha- beta}{2} big) cdot cos big( dfrac{alpha+ beta}{2} big)
cos alpha- cos beta=-2 cdot sin big( dfrac{alpha + beta}{2} big) cdot sin big( dfrac{alpha- beta}{2} big)
tg alpha- tg beta = dfrac{sin(alpha- beta)}{cos alpha cdot cos beta}
ctg alpha- ctg beta = dfrac{sin(alpha + beta)}{sin alpha cdot sin beta}
sin (alpha)-cos(alpha)=sqrt{2} cdot sin Big( alpha- dfrac{pi}{4} Big)
Формулы произведения тригонометрических функций
sin alpha cdot sin beta = dfrac{cos (alpha- beta)-cos(alpha + beta)}{2}
sin alpha cdot cos beta = dfrac{sin (alpha- beta)+sin(alpha + beta)}{2}
cos alpha cdot cos beta = dfrac{cos (alpha- beta)+cos(alpha + beta)}{2}
tg alpha cdot tg beta = dfrac{cos(alpha- beta)- cos(alpha+beta)}{cos(alpha- beta)+ cos(alpha+beta)}=dfrac{tg alpha + tg beta}{ctg alpha + ctg beta}
ctg alpha cdot ctg beta = dfrac{cos(alpha- beta)+ cos(alpha+beta)}{cos(alpha- beta)- cos(alpha+beta)}=dfrac{ctg alpha + ctg beta}{tg alpha + tg beta}
tg alpha cdot ctg beta = dfrac{sin(alpha- beta)+ sin(alpha+beta)}{sin(alpha+ beta)- sin(alpha-beta)}
Формулы произведения тригонометрических функций в степени
sin ^2 (alpha) cdot cos ^2 (alpha) = dfrac{1-cos(4 alpha)}{8}
sin ^3 (alpha) cdot cos ^3 (alpha) = dfrac{3 cdot sin(2 alpha)- sin(6 alpha)}{32}
sin ^4 (alpha) cdot cos ^4 (alpha) = dfrac{3-4 cdot cos(4 alpha)+ cos(8 alpha)}{128}
sin ^5 (alpha) cdot cos ^5 (alpha) = dfrac{10 cdot sin (2 alpha)-5 cdot sin(6 alpha)+sin (10 alpha)}{512}
Все формулы тригонометрии на одном листе
На этой картинке собраны все формулы тригонометрии для печати. Лист можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.

Основные тригонометрические формулы
Содержание
 Связи между тригонометрическими функциями одного угла Связи между тригонометрическими функциями одного угла |
 Тригонометрические функции суммы и разности двух углов Тригонометрические функции суммы и разности двух углов |
 Тригонометрические функции двойного угла Тригонометрические функции двойного угла |
 Формулы понижения степени для квадратов тригонометрических функций Формулы понижения степени для квадратов тригонометрических функций |
 Формулы понижения степени для кубов синуса и косинуса Формулы понижения степени для кубов синуса и косинуса |
 Выражение тангенса угла через синус и косинус двойного угла Выражение тангенса угла через синус и косинус двойного угла |
 Преобразование суммы тригонометрических функций в произведение Преобразование суммы тригонометрических функций в произведение |
 Преобразование произведения тригонометрических функций в сумму Преобразование произведения тригонометрических функций в сумму |
 Выражение тригонометрических функций через тангенс половинного угла Выражение тригонометрических функций через тангенс половинного угла |
 Тригонометрические функции тройного угла Тригонометрические функции тройного угла |
![]()
Связи между тригонометрическими функциями одного угла
Тригонометрические функции суммы и разности двух углов
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
Косинус двойного угла |
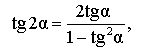 |
Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
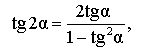 |
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
|
Выражение квадрата синуса через косинус двойного угла |
|
|
Выражение квадрата косинуса через косинус двойного угла |
|
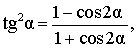 |
Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
Выражение тангенса через синус и косинус двойного угла
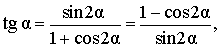

Преобразование суммы тригонометрических функций в произведение
| Сумма синусов |
|
|
| Разность синусов |
|
|
| Сумма косинусов |
|
|
| Разность косинусов |
|
|
| Сумма тангенсов |
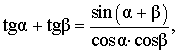 |
| Разность тангенсов |
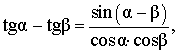 |
Преобразование произведения тригонометрических функций в сумму
| Произведение синусов |
|
|
| Произведение косинусов |
|
|
| Произведение синуса и косинуса |
|
|
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
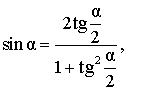 |
Выражение синуса угла через тангенс половинного угла |
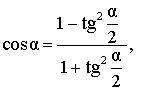 |
Выражение косинуса угла через тангенс половинного угла |
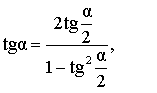 |
Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
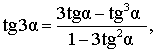 |
Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
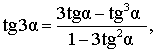 |
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••







