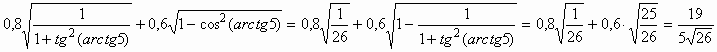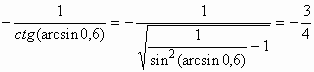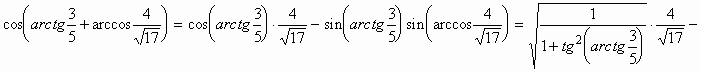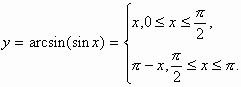Как найти ctg arccos - Сайт, где вы сможете решить свои вопросы

Найти котангенс арккосинуса ctg (arccos x) на основании определений косинуса, котангенса, арккосинуса и теоремы Пифагора очень легко. На чертеже прямоугольного треугольника этот способ решения демонстрируется наглядно.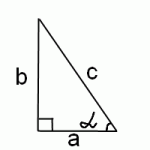Арккосинус икс — это такое число альфа, косинус которого равен x:

Поскольку косинус в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе, то в нашем случае

$[cos alpha = frac{a}{c}.]$

А нам нужен котангенс этого же угла альфа. Поскольку котангенс — это отношение прилежащего катета к противолежащему:

$[ctgalpha = frac{a}{b},]$

нам остается найти противолежаший катет b. По теореме Пифагора:

$[b = sqrt {{c^2} - {a^2}} , Rightarrow ctg(arccos x) = frac{a}{{sqrt {{c^2} - {a^2}} }},]$

где

$[x = frac{a}{c}.]$

Примеры.

1) Найти ctg (arccos (1/3)).

Арккосинус 1/3 равен числу α, значит cosα=1/3. А так как косинус — это отношение прилежащего катета к гипотенузе, то прилежащий катет a=1, гипотенуза c=3. Котангенс α равен отношению прилежащего катета к противолежащему. Противолежащий катет b находим по теореме Пифагора:

$[b = sqrt {{3^2} - {1^2}} = sqrt 8 = 2sqrt 2 , Rightarrow ctg(arccos frac{1}{3}) = frac{1}{{2sqrt 2 }} = frac{{sqrt 2 }}{4}.]$

2) Найти ctg (arccos (4/5)).

arccos (4/5)=α, значит cosα=4/5. Косинус равен отношению прилежащего катета к гипотенузе, отсюда a=4, c=5. По теореме Пифагора, b=3. Котангенс — это отношение прилежащего катета к противолежащему, значит ctg (arccos (4/5))=4/3.

Источник

Сферы применения правил обратных тригонометрических функций

Определение

Тригонометрия — раздел математики, объясняющий зависимость между сторонами и углами треугольника, правила используют для расчета углов.

Изучая постулаты тригонометрических функций, ученики и студенты часто задаются вопросом, где эти знания могут пригодиться. Сфер применения достаточно много. Астрономы используют понятия для расчёта положения небесных объектов, тригонометрия помогает выполнять чертежи и создавать архитектурные шедевры, выстраивать модель биологических ритмов. В морской и воздушной навигации, акустике и оптике, в анализе финансового рынка, статистике, медицине, химии, во многих областях используются тригонометрические вычисления. Поэтому так важно научиться применять и выводить формулы самостоятельно.

Обратные функции тригонометрии

Обратными называются функции, которые ещё называют арксинус, арккосинус, арктангенс, арккотангенс.

Название данный вид тригонометрической зависимости, получил от соответствующей прямой функции с приставкой арк — дуга. Взаимосвязь просматривается между длиной дуги единичной окружности и соответствующим определённым отрезком.

Правила обратной функции справедливы в пределах интервалов, например,

формула арксинуса возможна при:

[arcsin (sin mathrm{x})=mathrm{x} text { при }-frac{pi}{2} leq mathrm{x} leq frac{pi}{2}]

[arccos (cos mathrm{x})=mathrm{x} text { при } 0 leq mathrm{x} leq pi]

и так далее.

Формулы с обратными функциями тригонометрии

Уже были рассмотрены обратные тригонометрические функции. Они, как и другие функции имеют между собой связи и зависимости, которые можно выразить в виде формул и использовать для решения задач.

В данной работе мы рассмотрим основные формулы, в которых применяются функции тригонометрии. Разберём их виды, деление на группы, доказательства и способы решения задач с их помощью.

Группировка основных понятий

Сначала проведём группировку формул, для того чтобы сделать более понятной логику объяснений. И объединим все правила и доказательства в одну статью.

Синус от арксинуса для [alpha in(-1 ; 1) sin (arcsin alpha)=alpha, cos (arccos alpha)=alpha]

Тангенса от арктангенса для [alpha in(-infty, infty) operatorname{tg}(operatorname{arctg} alpha)=alpha, operatorname{ctg}(operatorname{arctg} alpha)=alpha].

Указанное в данных выражениях легко выводится из самих определений обратных функций тригонометрии. При необходимости найти arcsin tg, можно использовать приведённые формулы.

Тангенс, арктангенс, котангенс, арккотангенс, синус, арксинус, косинус, арккосинус и формулы

[text{Для }-frac{pi}{2} leq alpha leq frac{pi}{2} arcsin (sin alpha)=alpha],

[text{Для } leq alpha leq pi arccos (cos alpha)=alpha],

[text{Для }-frac{pi}{2}<alpha<frac{pi}{2} operatorname{arctg}(operatorname{tg} alpha)=alpha],

[text{Для } 0<alpha<pi operatorname{arcctg}(operatorname{ctg} alpha)=alpha].

В данном примере собраны тригонометрические выражения, достаточно очевидные, которые можно вывести из определений функций тригонометрии. Необходимо обратить внимание, на то, что высказывания будут верны, если «а» (угол, или числовое значение) будет входить в определённый предел. Если условие не выполняется, расчёт будет не верен и формулу использовать нельзя.

Соотношение между собой обратных тригонометрических функций противоположных чисел

Рассмотрим важное определение:

Обратные функции тригонометрии можно выразить через аркфункции противоположного положительного числа.

[text{Для }alpha in operatorname{open}-1,1] text { arccis }(-alpha)= -operatorname{arc} sin alpha, quad operatorname{arc} cos (-alpha)=pi -a r c cos alpha]

[text { Для } alpha in(-infty, infty) operatorname{arctg}(-alpha)= -operatorname{arctg} alpha, operatorname{arcctg}(-alpha)=pi-operatorname{arcctg} alpha]

Это значит, если расчёты имеют функции отрицательного числа, от них можно избавиться. Для этого необходимо преобразовать их в аркфункции положительных чисел. Такие вычисления проводить проще.

Формулы суммы: arcsin + arccos, arctg +arcctg

Правила суммы выглядят так:

Для [alpha in[-1,1] arcsin alpha+arccos alpha=frac{pi}{2}],

Для [alpha in[-infty, infty] operatorname{arctg} alpha+operatorname{arctg} alpha=frac{pi}{2}].

Отсюда видно, что arcsin определённого числа можно выразить через его arccos , и наоборот. Тоже правило касается и arctg и arcctg, которые выражаются аналогично.

Формулы связи между обратными и прямыми тригонометрическими функциями

Чтобы иметь возможность решить множество задач, требуется знание связей между прямыми тригонометрическими функциями, и их аркфункциями. Рассмотрим, как необходимо поступить, если нужно вычислить тангенс арксинуса. Ниже представлен список основных формул, которые помогут в решении таких задач.

[-1 leq alpha leq 1], [sin (arcsin alpha)=alpha]	[-1 leq alpha leq 1], [sin (arccos alpha) =sqrt{1-alpha^{2}}]	[-infty leq alpha leq+infty], [sin (operatorname{arctg} alpha)=frac{alpha}{sqrt{1+alpha^{2}}}]	[-infty leq alpha leq+infty], [sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
[-1 leq alpha leq 1], [cos (arcsin alpha)=sqrt{1-alpha^{2}}]	[-1 leq alpha leq 1], [cos (arccos alpha)=alpha]	[-infty leq alpha leq+infty], [cos (operatorname{arctg} alpha)=frac{1}{sqrt{1+a^{2}}}]	[-infty leq alpha leq+infty], [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
[-1<alpha<1], [operatorname{tg}(arcsin alpha)=frac{alpha}{sqrt{1-alpha^{2}}}]	[alpha in(-1,0) cup(0,1)], [operatorname{tg}(arccos alpha)=frac{sqrt{1-a^{2}}}{alpha}]	[-infty leq alpha leq+infty], [operatorname{tg}(operatorname{arctg} alpha)=alpha]	[alpha neq 0], [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{alpha}]
[alpha in(-1,0) cup(0,1)], [operatorname{ctg}(arcsin alpha)=frac{sqrt{1-alpha^{2}}}{alpha}]	[-1<alpha<1], [operatorname{ctg}(arccos alpha)=frac{alpha}{sqrt{1-a^{2}}}]	[alpha neq 0], [operatorname{ctg}(operatorname{arctg} alpha)=frac{1}{alpha}]	[-infty leq alpha leq+infty], [operatorname{ctg}(operatorname{arcctg} alpha)=alpha]

Таблица 1.

Примеры 1 — 2

Нужно найти косинус арктангенса из 5.

Решение. Для этого необходимо воспользоваться формулой следующего вида: [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]

Подставим необходимое значение: [cos (operatorname{arctg} sqrt{5})=frac{1}{sqrt{1+sqrt{5^{2}}}}=frac{2}{sqrt{6}}]

Определить синус арккосинуса [frac{1}{2}]
Решение. Реализовать решение нам поможет формула: [sin (arccos alpha)=sqrt{1-alpha^{2}}]

Ставим значение и получаем: [sin left(arccos frac{1}{2}right)=sqrt{1-left(frac{1}{2}right)^{2}}=frac{sqrt{3}}{2}]

Заметим, что непосредственное вычисление приведёт к тому же ответу: [sin left(arccos frac{1}{2}right)=sin frac{pi}{3}=frac{sqrt{3}}{2}]

Для правильного вычисления значений прямых и обратных тригонометрических функций, стоит вспомнить начальные материалы.

Доказательство формул синуса от арккосинуса, арккотангенса и арктангенса

Чтобы вывести формулы и разобрать их более наглядно, необходимо применить основные тригонометрические тождества и правила обратных тригонометрических функций, которые были выведены ранее.

Доказательство формул 1

Используя тождества получим:

[sin ^{2} alpha+cos ^{2} alpha=1]

[1+operatorname{ctg}^{2} alpha=frac{1}{sin ^{2} alpha}]

Вспомним тот факт, что tg α *ctg α= 1, следовательно

[sin alpha=sqrt{1-cos ^{2} alpha}, 0 leq alpha leq pi]

[sin alpha=frac{operatorname{tg} alpha}{sqrt{1+operatorname{tg}^{2} alpha}},-frac{pi}{2}<alpha<frac{pi}{2}]

[sin alpha=frac{1}{sqrt{1+c t g^{2} alpha}}, 0<alpha<pi]

Результатом станет вывод синуса через подходящие аркфункции в заданном условии.

В математическое выражение вместо α, ставим arccos α, получаем в итоге формулу синуса арккосинуса.

Во втором случае вместо α подставляем arctg α, соответственно получаем формулу синуса арктангенса.

В третьем варианте проводим аналогичную операцию и подставляем arcctg α для выражения формулы синуса арккотангенса.

Нет времени решать самому?

Наши эксперты помогут!

Доказательство формул для тангенса, обратных функций(arcsin, arccos, arcctg)

В данном разделе рассмотрим доказательство закона тангенса обратных функций тригонометрии.

Доказательство формул 2

Исходя из: [frac{sin alpha}{sqrt{1-sin alpha^{2}}},-frac{pi}{2}<alpha<frac{pi}{2}]Получим [operatorname{tg}(arcsin alpha)=frac{sin (arcsin alpha)}{sqrt{1-sin ^{2}(arcsin alpha)}}=frac{alpha}{sqrt{1-alpha^{2}}}]При условии [-1<alpha<1]
Из выражения [operatorname{tg} alpha=frac{sqrt{1-cos ^{2} alpha}}{cos alpha}, alpha inleft[0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright]]
Получаем [operatorname{tg}(arccos alpha)=frac{sqrt{1-cos ^{2}(arccos alpha)}}{cos (arccos alpha)}=frac{sqrt{1-alpha^{2}}}{alpha}] при условии [alpha in(-1,0) cup(0,1)].
Исходя из [operatorname{tg} alpha=frac{1}{operatorname{ctg} alpha}, alpha inleft(0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright)] получаем [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{operatorname{ctg}(operatorname{arcctg} alpha)}=frac{1}{alpha}] при условии, что [alpha neq 0].

Далее нам понадобятся понятия котангенсов арксинуса, арккосинуса, арктангенса. Напомним такое тригонометрическое равенство:

[operatorname{ctg} alpha=frac{1}{operatorname{tg} alpha}]

Применяя данное выражение можно вывести необходимые формулы, вставляя выражения тангенса обратных функций тригонометрии. Практически необходимо поменять местами числитель и знаменатель.

Выражение арксинуса с помощью арккосинуса, арктангенса и арккотангенса

Прямые и обратные функции в тригонометрии связаны между собой. Полученные в результате выведения формулы помогут найти связь и между обратными функциями тригонометрии, выразив одни аркфункции через другие. Рассмотрим примеры.

В первом случае меняем арксинус на арккосинус, а арктангенс на арккотангенс, получим следующие формулы арксинуса и арккосинуса:

[begin{aligned} &arcsin a=left{begin{array}{l} arccos sqrt{1-a^{2}}, 0 leq a leq 1 \ -arccos sqrt{1-a^{2}},-1 leq a<0 end{array}right. \ &arcsin a=operatorname{arctg} frac{a}{sqrt{1-a^{2}}},-1<a<1 \ &arcsin a=left{begin{array}{l} operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \ operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}-pi,-1 leq a<0 end{array}right. end{aligned}]

Для арккосинуса также есть свои формулы:

[begin{aligned} &arccos a=left{begin{array}{l} arcsin sqrt{1-a^{2}}, 0 leq a leq 1 \ pi-arcsin sqrt{1-a^{2}},-1 leq a<0 end{array}right. \ &arccos a=left{begin{array}{l} operatorname{arctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \ pi+operatorname{arctg} frac{sqrt{1-a^{2}}}{a},-1 leq a<0 end{array}right. \ &arccos a=operatorname{arcctg} frac{a}{sqrt{1-a^{2}}},-1<a<1 end{aligned}]

Выражения для арктангенса:

[begin{aligned} &operatorname{arctg} a=arcsin frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\ &operatorname{arctg} a=left{begin{array}{l} arccos frac{1}{sqrt{1+a^{2}}}, a geq 0 \ -arccos frac{1}{sqrt{1+a^{2}}}, a<0 end{array}right.\ &operatorname{arctg} a=operatorname{arcctg} frac{1}{a}, a neq 0 end{aligned}]

Последний блок формул покажет преобразование арккотангенса через другие обратные функции тригонометрии:

[begin{aligned} &operatorname{arcctg} a=left{begin{array}{l} arcsin frac{1}{sqrt{1+a^{2}}}, a geq 0 \ pi-arcsin frac{1}{sqrt{1+a^{2}}}, a<0 end{array}right.\ &operatorname{arctg} a=arccos frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\ &operatorname{arcctg} a=operatorname{arctg} frac{1}{a}, a neq 0 end{aligned}]

Рассмотренные формулы арксинуса, арккосинуса, арктангенса помогут в решении различных задач. Разберём доказательство с использованием основных определений обратных функций и ранее рассмотренных правил.

Возьмём arcsin [alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1] для выведения доказательства.

Мы имеем выражение [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] — число, которое имеет значение от минус половины [pi] до плюс половины [pi]. Используя выражение синуса арктангенса, получаем следующее:

[sin left(operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}right)=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+left(frac{alpha}{sqrt{1-alpha^{2}}}right)^{2}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+frac{alpha^{2}}{1-alpha^{2}}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{frac{1}{sqrt{1-alpha^{2}}}}=alpha]

Получается, что [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] с условием [-1<alpha<1] — арксинус числа [alpha].

Вывод: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1].

Другие подобные формулы доказываются по аналогичной схеме.

Рассмотрим пример применения полученных истин.

Пример 3

Необходимо вычислить синус арккотангенса — [sqrt{3}]
Решение. Для того чтобы провести решение задачи, необходимо использовать формулу связи арккотангенса и арксинуса: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}]

Подставим в неё [alpha=-sqrt{3}] и получим [-frac{1}{2}].

Используя непосредственное вычисление ответ был бы такой же: [sin (operatorname{arcctg}(-sqrt{3}))=sin frac{5 pi}{6}=frac{1}{2}]

Можно использовать и следующую формулу:

[sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]

[sin (operatorname{arcctg}(-sqrt{3}))=frac{1}{sqrt{1+(-sqrt{3})^{2}}}=frac{1}{2}]

Другие формулы, в которых используются обратные функции тригонометрии

Разобраны основные функции, которые чаще всего используются для решения задач. Но представлены не все формулы с обратными тригонометрическими функциями, есть некоторые специфичные, употребляемые редко, но они тоже полезны. Учить их нет смысла, лучше вывести при необходимости.

Пример 4

Разберём для примера одну такую формулу. Выглядит она так:

[sin ^{2} frac{alpha}{2}=sqrt{frac{1-cos alpha}{2}}]

Если представленный угол имеет значение больше нуля, но меньше Пи, то получаем:

[sin frac{arccos alpha}{2}=sqrt{frac{1-cos (arccos alpha)}{2}}]

[Leftrightarrow sin frac{arccos alpha}{2}=frac{sqrt{1-alpha}}{2}]

Здесь мы выводим следующую готовую формулировку, арксинус которой выведен через арккосинус:

[frac{arccos alpha}{2}=arcsin sqrt{frac{1-alpha}{2}}]

В тексте рассмотрены лишь некоторые, самые популярные виды связей между прямыми и обратными функциями тригонометрии. Главное не выучить наизусть данные постулаты, а научиться их применять и выводить, исходя из уже известных определений.

Удобно использовать инженерный вид калькулятора, на котором есть, необходимые для вычислений тригонометрические формулы и функции.

Источник

Задания, связанные с обратными
тригонометрическими функциями, часто
предлагаются на школьных выпускных экзаменах и
на вступительных экзаменах в некоторых ВУЗах.
Подробное изучение этой темы может быть
достигнуто только на факультативных занятиях
или на элективных курсах. Предлагаемый курс
призван как можно полнее развить способности
каждого ученика, повысить его математическую
подготовку.

Курс рассчитан на 10 часов:

1.Функции arcsin x, arccos x, arctg x, arcctg x (4 ч.).

2.Операции над обратными тригонометрическими
функциями (4 ч.).

3.Обратные тригонометрические операции над
тригонометрическими функциями (2 ч.).

Урок 1 (2 ч.) Тема: Функции y = arcsin x, y = arccos x,
y = arctg x, y = arcctg x.

Цель: полное освещение данного вопроса.

1.Функция y = arcsin х.

а) Для функции y = sin x на отрезке
существует обратная (однозначная) функция,
которую условились называть арксинусом и
обозначать так: y = arcsin x. График обратной функции
симметричен с графиком основной функции
относительно биссектрисы I – III координатных
углов.

<Рисунок1>

Свойства функции y = arcsin x .

1)Область определения: отрезок [-1; 1];

2)Область изменения: отрезок ;

3)Функция y = arcsin x нечетная: arcsin (-x) = – arcsin x;

4)Функция y = arcsin x монотонно возрастающая;

5)График пересекает оси Ох, Оу в начале
координат.

Пример 1. Найти a = arcsin . Данный пример подробно
можно сформулировать так: найти такой аргумент a ,
лежащий в пределах от до , синус которого равен .

Решение. Существует бесчисленное
множество аргументов, синус которых равен ,
например: и т.д. Но нас интересует только тот
аргумент, который находится на отрезке . Таким
аргументом будет . Итак, .

Пример 2. Найти 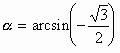.Решение. Рассуждая так же, как
и в примере 1, получим .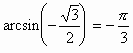

б) устные упражнения. Найти: arcsin 1, arcsin (-1), arcsin , arcsin (), arcsin , arcsin (), arcsin , arcsin (), arcsin 0.
Образец ответа: 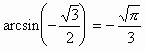, т.к. . Имеют ли смысл выражения: ; arcsin 1,5; ?

в) Расположите в порядке возрастания: arcsin, arcsin (-0,3),
arcsin 0,9.

II. Функции y = arccos x, y = arctg x, y = arcctg x (аналогично).

Урок 2 ( 2 ч) Тема: Обратные
тригонометрические функции, их графики.

Цель: на данном уроке необходимо
отработать навыки в определении значений
тригонометрических функций, в построении
графиков обратных тригонометрических функций с
использованием Д (у), Е (у) и необходимых
преобразований.

На данном уроке выполнить упражнения,
включающие нахождение области определения,
области значения функций типа: y = arcsin , y = arccos
(x-2), y = arctg (tg x), y = arccos .

Следует построить графики функций: а) y
= arcsin 2x; б) y = 2 arcsin 2x; в) y = arcsin ;

г) y = arcsin ; д) y = arcsin ; е) y = arcsin ; ж) y = |
arcsin | .

Пример. Построим график y = arccos

Д (у):
<= 1 или х² >= 1, т.е.
Е (у): ,
т.к. .
Функция четная, т.к. у (-х) = у (х).
Точки пересечения: с ОУ (х = 0) график не может
пересекаться, т.к. функция определена только при |
х | >= 1; с ОХ (у = 0) график пересекается в (-1; 0) и (1; 0),
т.к. = 1
лишь при х = ± 1.
В силу четности достаточно ее исследовать для х
>= 1.

Если х = 1, то у(1) = arccos 1 = 0. Если х –> + , то –> 0 ( > 0).

Значит, arccos –> , причем arccos < наименьшее у = 0 при х = ± 1,
наибольшего нет.

Функция в области определения неотрицательна,
т.е. arccos >= 0.
Дополнительные точки ;

<Рисунок2>

В домашнее задание можно включить
следующие упражнения: построить графики функций:
y = arccos ,
y = 2 arcctg x, y = arccos | x | .

Графики обратных функций

<Рисунок3>

Урок № 3 (2 ч.) Тема: Операции над
обратными тригонометрическими функциями.

Цель: расширить математические
познания (это важно для поступающих на
специальности с повышенными требованиями к
математической подготовке) путем введения
основных соотношений для обратных
тригонометрических функций.

Материал для урока.

Некоторые простейшие
тригонометрические операции над обратными
тригонометрическими функциями: sin (arcsin x) = x , i xi ?
1; cos (arсcos x) = x , i xi ? 1; tg (arctg x)= x , x I R; ctg (arcctg x) = x , x
I R.

Упражнения.

а) tg (1,5
+ arctg 5) = – ctg (arctg 5 ) = .

ctg (arctg x ) = ; tg (arcctg x ) = .

б) cos ( +
arcsin 0,6) = – cos (arcsin 0,6). Пусть arcsin 0,6 = a , sin a = 0,6;

– cos a =

cos (arcsin x ) = ; sin (arccos x) = .

Замечание: берем перед корнем знак “+”
потому, что a = arcsin x удовлетворяет .

в) sin (1,5
+ arcsin ).Ответ:
;

г) ctg ( +
arctg 3).Ответ: ;

д) tg ( –
arcctg 4).Ответ: .

е) cos (0,5
+ arccos ) .
Ответ: .

Вычислить:

a) sin (2 arctg 5) .

Пусть arctg 5 = a , тогда sin 2 a = или sin (2 arctg 5) = ;

б) cos ( + 2
arcsin 0,8).Ответ: 0,28.

в) arctg
+ arctg .

Пусть a = arctg , b = arctg ,

тогда tg (a + b ) = .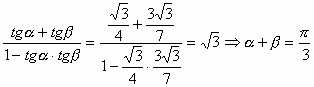

г) sin (arcsin + arcsin ).

д) Доказать, что для всех x I [-1; 1] верно arcsin x + arccos x
= .

Доказательство:

arcsin x = – arccos x

sin (arcsin x ) = sin ( – arccos x)

x = cos (arccos x )

x = x

Для самостоятельного решения: sin
(arccos ),
cos (arcsin )
, cos (arcsin ()), sin (arctg (- 3)), tg (arccos ) , ctg (arccos ).

Для домашнего решения: 1) sin (arcsin 0,6 + arctg 0 ); 2) arcsin
+ arcsin ; 3) ctg ( – arccos 0,6 ); 4)
cos (2 arcctg 5 ) ; 5) sin (1,5 – arcsin 0,8 ); 6) arctg 0,5 – arctg 3.

Урок № 4 (2ч.) Тема: Операции над
обратными тригонометрическими функциями.

Цель: на данном уроке показать использование
соотношений в преобразовании более сложных
выражений.

Материал для урока.

УСТНО:

а) sin (arccos 0,6), cos (arcsin 0,8);

б) tg (arcсtg 5), ctg (arctg 5);

в) sin (arctg -3), cos (arcсtg());

г) tg (arccos ), ctg (arccos()).

ПИСЬМЕННО:

1) cos ( arcsin + arcsin + arcsin ).

2) cos (arctg 5–arccos 0,8) = cos (arctg 5) cos (arccos 0,8) + sin (arctg 5) sin
(arccos 0,8) =

3) tg ( –
arcsin 0,6 ) = – tg (arcsin 0,6 ) =

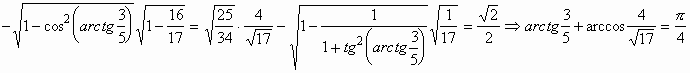
Самостоятельная работа поможет выявить
уровень усвоения материала

Для домашнего задания можно
предложить:

1) ctg (arctg + arctg + arctg ); 2) sin² (arctg 2 – arcctg ()); 3) sin (2
arctg + tg
( arcsin )); 4) sin (2
arctg ); 5)
tg ( (arcsin
))

Урок № 5 (2ч) Тема: Обратные
тригонометрические операции над
тригонометрическими функциями.

Цель: сформировать представление учащихся об
обратных тригонометрических операциях над
тригонометрическими функциями, основное
внимание уделить повышению осмысленности
изучаемой теории.

При изучении данной темы предполагается
ограничение объема теоретического материала,
подлежащего запоминанию.

Материал для урока:

Изучение нового материала можно начать с
исследования функции y = arcsin (sin x) и построения ее
графика.

1. ОДЗ: R

2. Е(y): .

3. Каждому x I R ставится в соответствие y I , т.е. <= y <= такое,
что sin y = sin x.

4. Функция нечетна: sin(-x) = – sin x ; arcsin(sin(-x)) = – arcsin(sin
x).

5. T = 2

6. График y = arcsin (sin x) на [0; ]:

a) 0 <= x <= имеем y = arcsin(sin x) = x, ибо sin y = sin x и <= y <= .

б)
<= x <=
получим y = arcsin (sin x) = arcsin ( – x) = – x, ибо

sin y = sin (
– x) = sinx , 0 <= – x <= .

Итак,

<Рисунок4>

Построив y = arcsin (sin x) на [0; ],
продолжим симметрично относительно начала
координат на [- ; 0], учитывая нечетность этой функции.
Используя периодичность, продолжим на всю
числовую ось.

Затем записать некоторые соотношения: arcsin
(sin a ) = a , если <= a <= ; arccos (cos a ) = a , если 0 <= a <= ; arctg (tg a ) =
a , если
< a < ;
arcctg (ctg a ) = a , если 0 < a < .

И выполнить следующие упражнения:a) arccos(sin
2).Ответ: 2 – ; б) arcsin (cos 0,6).Ответ: – 0,1 ; в) arctg (tg 2).Ответ: 2 – ;

г) arcctg(tg 0,6).Ответ: 0,9 ; д) arccos (cos ( – 2)).Ответ:2 – ; е) аrcsin
(sin ( –
0,6)). Ответ: – 0,6; ж) аrctg (tg 2) = arctg (tg (2 – )). Ответ:2 – ; з) аrcctg (tg
0,6). Ответ: – 0,6;

и) аrcsin (cos (2 arctg ( + 1))). Ответ:.

Для самостоятельного решения можно предложить
аналогичные задания:

arccos (sin 0,5); arctg (ctg ); arcsin (sin 1); arcsin (sin3); arcsin (sin4); arcsin (sin5);

arcsin (sin6); построить график y = arctg (tg x).

<Рисунок5>

Домашнее задание. Предложить любые задания
из приложения.

ПРИЛОЖЕНИЕ.

I.(1) Найти область определения: а) y=arcsin ; б)y= arctg 2x;
в)y= arctg
; г)y= arccos ; д)y=arctg ; е)y= arcctg ; ж) y= .

I.(2) Построить графики функций: a) y = arccos 2x; б) y = 2
arccos x; в) y = arccos (cosx); г) y = arctg (ctgx).

I.(3) В каких границах заключены дуги: а) 2 arcsin x; б) 2
arccos х; в) arctg x; г) – arctg x; д) arccos ; е) arctg x² – .

I.(4) Построить: а) arctg (- 0,3); б) arccos ; в) arcsin ; г) arcctg
(-1,5).

II.(1) Вычислить: а) arccos (sin 2);б) sin ; в) arcsin + arcsin ; г) sin ( + 2 arcsin ); д) arctg + arctg ; е) arctg – arctg3; ж)
tg ( – arcsin ); з) arctg + arccos .

II.(2) Вычислить: а) cos (2 arcsin ); б) tg (arccos ); в) sin
(arcctg );
г) ctg (arctg(-1)); д) cos (2 arcsin ()); е) sin (arcsin + arccos ); ж) cos (arccos () + arcsin );