Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика XVIII века Карла Шерфера и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: 
но они не прижились[1].
Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin−1, cos−1 для арксинуса, арккосинуса и т. п.[2], — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.
Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, 
означает множество углов 
, синус которых равен 
. Из множества значений каждой аркфункции выделяют её главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.
В общем случае при условии 
все решения уравнения 
можно представить в виде 
[3]
Основное соотношение[править | править код]
Функция arcsin[править | править код]
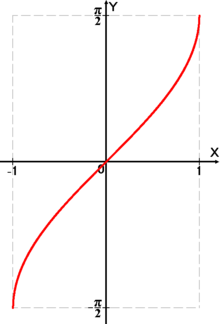
График функции 
Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.
Свойства функции arcsin[править | править код]
Получение функции arcsin[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок ![{displaystyle [-pi /2;pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e194f6091eb1b362d19112a5bffdab91ef2a07df)
, на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции относительно прямой 
.
Функция arccos[править | править код]
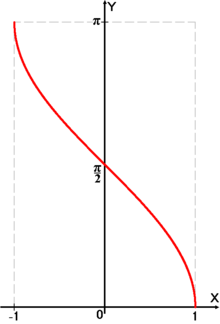
График функции 
Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.
Свойства функции arccos[править | править код]
Получение функции arccos[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок ![[0;pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/45ba33419dc889bf6c0c684b11285afda3437c95)
, на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции относительно прямой .
Функция arctg[править | править код]
График функции 
Аркта́нгенсом числа x называется такое значение угла 
выраженное в радианах, для которого 
Функция 
определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.
Свойства функции arctg[править | править код]
Получение функции arctg[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал 
, на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой .
Функция arcctg[править | править код]
График функции 
Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция 
определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго убывающей и всюду положительной.
Свойства функции arcctg[править | править код]
Получение функции arcctg[править | править код]
Дана функция 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал 
, на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой .
График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, 
) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы 
Функция arcsec[править | править код]
График функции 
Арксе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.
Свойства функции arcsec[править | править код]
Функция arccosec[править | править код]
График функции 
Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого 
Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей.
Свойства функции arccosec[править | править код]
Разложение в ряды[править | править код]
Производные от обратных тригонометрических функций[править | править код]
Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:
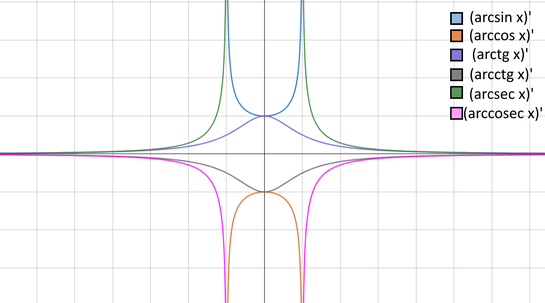
производные обратных тригонометрических функций
Функция  |
Производная  |
Примечание |
|---|---|---|
 |
 |
Доказательство Найти производную арксинуса можно при помощи взаимно обратных функций. |
 |
 |
Доказательство Найти производную арккосинуса можно при помощи данного тождества: |
 |
 |
Доказательство Найти производную арктангенса можно при помощи взаимнообратной функции: |
 |
 |
Доказательство Найти производную арккотангенса можно при помощи данного тождества: |
 |
 |
Доказательство Найти производную арксеканса можно при помощи тождества:
Теперь находим производную обеих частей этого тождества.
Получается.
|
 |
 |
Доказательство Найти производную арккосеканса можно при помощи данного тождества: |
![{displaystyle [sin(arcsin((x))]'=x'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be684108880964393fc7a90ba55f07de0e6d659a)
![{displaystyle D(cos(x))=[{frac {pi }{2}};-{frac {pi }{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1cb9db2cfdfe382a787aa5288735756e8dcb12e)
![{displaystyle [arcsin(x)+arccos(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3606594a168f2f06eb6faddfaac18f1c85324466)
![{displaystyle [tg(arctg(x))]'=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ce9406b214a5266d0bf8282fd6aae4b59602c66)
![{displaystyle [arctg(x)+arcctg(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f84cee67adf89ef76bfaa5c415907cce038d455)
![{displaystyle [arccosec(x)+arcsec(x)]'=({frac {pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4847d93af2226f3ab5e1ba20940ec8530526b49e)
Интегралы от обратных тригонометрических функций[править | править код]
Неопределённые интегралы[править | править код]
Для действительных и комплексных x:
Для действительных x ≥ 1:
- См. также Список интегралов от обратных тригонометрических функций
Использование в геометрии[править | править код]
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.
В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол.
Так, если катет длины 
является противолежащим для угла 
, то
Связь с натуральным логарифмом[править | править код]
Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:
См. также[править | править код]
- Обратные гиперболические функции
- Теорема Данжуа — Лузина
Примечания[править | править код]
Ссылки[править | править код]
- Weisstein, Eric W. Обратные тригонометрические функции (англ.) на сайте Wolfram MathWorld.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: «Советская Энциклопедия», 1982. — [dic.academic.ru/dic.nsf/enc_mathematics/3612/%D0%9E%D0%91%D0%A0%D0%90%D0%A2%D0%9D%D0%AB%D0%95 Т. 3. — с. 1135].
- Обратные тригонометрические функции — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1974. — Т. 18. — с. 225.
- Обратные тригонометрические функции // Энциклопедический словарь юного математика / Савин А.П. — М.: Педагогика, 1985. — С. 220—221. — 352 с.
- Построение графиков обратных тригонометрических функций онлайн
- Онлайн калькулятор: обратные тригонометрические функции
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных доменов
|
- Понятие арктангенса
- График и свойства функции y=arctgx
- Уравнение tgx=a
- Понятие арккотангенса
- График и свойства функции y=arcctgx
- Уравнение ctgx=a
- Формулы преобразований аркфункци
- Примеры
Определение тангенса и котангенса через отношение сторон прямоугольника и с помощью касательной к числовой окружности – см. §3 данного справочника.
Свойства функции y=tgx на всей области определения (xinmathbb{R}) – см. §6 данного справочника.
Свойства функции y=ctgx на всей области определения (xinmathbb{R}) – см. §7 данного справочника.
Определение и свойства взаимно обратных функций – см. §2 справочника для 9 класса.
п.1. Понятие арктангенса
В записи (y=tgx) аргумент x – это значение угла (в градусах или радианах), функция y – тангенс угла, действительное число в пределах от (-infty;) до (+infty). Т.е., по заданному углу мы находим тангенс.
Можно поставить обратную задачу: по заданному тангенсу найти угол. Но одному значению тангенса соответствует бесконечное количество углов. Например, если (tgx=1), то (x=fracpi4+pi k, kinmathbb{Z}); если (tgx=0), то (x=pi k, kinmathbb{Z}) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x главной ветвью тангенса: (-fracpi2leq xleq fracpi2) (правая половина числовой окружности, вся ось тангенсов).
Арктангенсом числа (a (ainmathbb{R})) называется такое число (xin[-fracpi2; fracpi2]), тангенс которого равен (a). $$ arctg a=x Leftrightarrow begin{cases} tgx=a\ -fracpi2leq xleq fracpi2 end{cases} $$
Например:
(arctgfrac{1}{sqrt{3}}=fracpi6, arctg(-sqrt{3})=-frac{pi}{3}, arctg1=fracpi4).
п.2. График и свойства функции y=arctgx
1. Область определения (xinmathbb{R}).
2. Функция ограничена сверху и снизу асимптотами (-fracpi2leq arctgxleq fracpi2).
Область значений (yinleft(-fracpi2; fracpi2right))
3. Функция стремится к максимальному значению (y_{max}=fracpi2 text{при} xrightarrow +infty)
Функция стремится к минимальному значению (y_{min}=-fracpi2 text{при} xrightarrow -infty)
Функция имеет две горизонтальные асимптоты (y=pmfracpi2).
4. Функция возрастает на всей области определения.
5. Функция непрерывна на всей области определения.
6. Функция нечётная: (arctg(-x)=-arctg(x)).
п.3. Уравнение tgx=a
 |
На оси тангенсов каждому углу на числовой окружности в интервале (-fracpi2leq xleq fracpi2) соответствует одно действительное число.
Например: |
 |
2) Решим уравнение (tgx=2) Числу (frac{1}{sqrt{3}}) на оси тангенсов соответствует угол (arctg2) на числовой окружности. Учитывая период тангенса (pi), получаем ответ: (x=arctg2+pi k) |
В общем случае:
Уравнение (tgx=a) имеет решения $$ x=arctga+pi k, kinmathbb{Z}, ainmathbb{R} $$
п.4. Понятие арккотангенса
По аналогии с арктангенсом, арккотангенс определяется на главной ветви котангенса: (0lt xlt pi) (верхняя половина числовой окружности, вся ось котангенсов).
Арккотангенсом числа (a (ainmathbb{R})) называется такое число (xin(0;pi)), котангенс которого равен (a). $$ arcctg a=x Leftrightarrow begin{cases} ctgx=a\ 0lt xlt pi end{cases} $$
Например:
(arcctgfrac{1}{sqrt{3}}=fracpi3, arcctg(-sqrt{3})=-frac{pi}{6}, arcctg1=fracpi4).
п.5. График и свойства функции y=arcctgx
1. Область определения (xinmathbb{R}).
2. Функция ограничена сверху и снизу асимптотами (0lt arcctgxlt pi).
Область значений (yin(0;pi))
3. Функция стремится к максимальному значению (y_{max}=pi text{при} xrightarrow -infty)
Функция стремится к минимальному значению (y_{min}=0 text{при} xrightarrow +infty)
Функция имеет две горизонтальные асимптоты (y=0 text{и} y=pi).
4. Функция убывает на всей области определения.
5. Функция непрерывна на всей области определения.
6. Функция ни чётная, ни нечётная.
п.6. Уравнение ctgx=a
В общем случае:
Уравнение (ctgx=a) имеет решения $$ x=arcctga+pi k, kinmathbb{Z}, ainmathbb{R} $$
Часто уравнение (ctgx=a) преобразуют в уравнение (tgx=frac{1}{a}), и ищут его корни.
Например:
1) (ctgx=sqrt{3})
(x=fracpi6+pi k)
Можно также преобразовать уравнение в (tg x=frac{1}{sqrt{3}})
Получаем тот же ответ: (x=fracpi6+pi k)
2) (ctgx=2)
(x=arcctg2+pi k)
Можно также преобразовать уравнение в (tg x=frac{1}{2})
Получаем ответ: (x=arctgfrac12+pi k)
Очевидно, что (arcctg 2=arctgfrac{1}{2}) (см. ниже формулы для аркфункций).
п.7. Формулы преобразования аркфункций
begin{gather*} arcsin(sinalpha)=alpha, alphainleft[-fracpi2;fracpi2right], arccos(cosalpha)=alpha, alphain[0;pi]\ arctg(tgalpha)=alpha, alphainleft(-fracpi2;fracpi2right), arcctg(ctgalpha)=alpha, alphain(0;pi) end{gather*}
begin{gather*} arcsin(-alpha)=-arcsinalpha, arccos(-alpha)=pi-arccosalpha\ arctg(-alpha)=-arctgalpha, arcctg(-alpha)=pi-arcctgalpha end{gather*}
begin{gather*} arcsinalpha+arccosalpha=fracpi2, arctgalpha+arcctgalpha=fracpi2 end{gather*}
Сводная таблица тригонометрических функций от аркфункций
| arcsin | arccos | arctg | arcctg | |
| sin | begin{gather*} a\ ain[-1;1] end{gather*} | begin{gather*} sqrt{1-a^2}\ ain[-1;1] end{gather*} | begin{gather*} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} | begin{gather*} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} |
| cos | begin{gather*} sqrt{1-a^2}\ ain[-1;1] end{gather*} | begin{gather*} a\ ain[-1;1] end{gather*} | begin{gather*} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} | begin{gather*} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather*} |
| tg | begin{gather*} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather*} | begin{gather*} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather*} | begin{gather*} a\ ainmathbb{R} end{gather*} | begin{gather*} frac{1}{a}\ ane 0 end{gather*} |
| ctg | begin{gather*} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather*} | begin{gather*} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather*} | begin{gather*} frac{1}{a}\ ane 0 end{gather*} | begin{gather*} a\ ainmathbb{R} end{gather*} |
Аркфункции, выраженные через другие аркфункции
| arcsin | |
| arccos | $$ arcsina= begin{cases} arccossqrt{1-a^2}, 0leq aleq 1\ -arccossqrt{1-a^2}, -1leq alt 0 end{cases} $$ |
| arctg | $$ arcsina=arctgfrac{a}{sqrt{1-a^2}}, -1lt alt 1 $$ |
| arcctg | $$ arcsina= begin{cases} arcctgfrac{sqrt{1-a^2}}{a}, 0lt aleq 1\ -arcctgfrac{sqrt{1-a^2}}{a}-pi, -1leq alt 0 end{cases} $$ |
| arccos | |
| arcsin | $$ arccosa= begin{cases} arcsinsqrt{1-a^2}, 0leq aleq 1\ pi-arcsinsqrt{1-a^2}, -1leq alt 0 end{cases} $$ |
| arctg | $$ arccosa= begin{cases} arcctgfrac{sqrt{1-a^2}}{a}, 0lt aleq 1\ pi+arctgfrac{sqrt{1-a^2}}{a}, -1leq alt 0 end{cases} $$ |
| arcctg | $$ arccosa=arcctgfrac{a}{sqrt{1-a^2}}, -1lt alt 1 $$ |
| arctg | |
| arcsin | $$ arctga=arcsinfrac{a}{sqrt{1+a^2}}, ainmathbb{R} $$ |
| arccos | $$ arctga= begin{cases} arccosfrac{1}{sqrt{1+a^2}}, ageq 0\ -arccosfrac{1}{sqrt{1+a^2}}, alt 0 end{cases} $$ |
| arcctg | $$ arctga=arcctgfrac{1}{a}, ane 0 $$ |
| arcctg | |
| arcsin | $$ arcctga= begin{cases} arcsinfrac{1}{sqrt{1+a^2}}, ageq 0\ pi-arcsinfrac{1}{sqrt{1+a^2}}, alt 0 end{cases} $$ |
| arccos | $$ arcctga=arccosfrac{a}{sqrt{1+a^2}}, ainmathbb{R} $$ |
| arctg | $$ arcctga=arctgfrac{1}{a}, ane 0 $$ |
п.8. Примеры
Пример 1. Найдите функцию, обратную арктангенсу. Постройте графики арктангенса и найденной функции в одной системе координат.
Для (y=arctgx) область определения (xinmathbb{R}), область значений (-fracpi2leq yleq fracpi2).
Обратная функция (y=tgx) должна иметь ограниченную область определения (-fracpi2leq xleq fracpi2) (главная ветвь) и область значений (yinmathbb{R}).
Строим графики:
Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.
Пример 2. Решите уравнения:
| a) (tg x=-1) (x=fracpi4+pi k) |
б) (ctgx=-1) (x=frac{3pi}{4}+pi k) Если решать через (tgx=-1) |
| в) (tg x=-5) (x=arctg(-5)+pi k=-arctg5+pi k) |
г) (ctgx=3) (x=arcctg3+pi k) Если решать через (tgx=frac13) |
Пример 3. Вычислите:
a) (2arccosleft(-frac12right)+arctg(-1)+arcsinfrac{sqrt{2}}{2}=2cdotfrac{2pi}{3}-fracpi4+fracpi4=frac{4pi}{3})
б) (arcsin1-arccosfrac{sqrt{3}}{2}-arctg(sqrt{-3})=arcsin1-fracpi3+fracpi3=arcsin1)
в) (arctg4+arcsin0-arccos1=arctg4+0-0=arctg4)
г) (5-2arccos0+arcsinfrac{sqrt{2}}{2}+3arccosfrac{sqrt{2}}{2}=5-2cdotfracpi2+fracpi4+3cdotfracpi4=5)
Пример 4. Постройте графики функций:
(a) y=arccosleft(frac{1}{x}right)+arccosleft(-frac{1}{x}right))
Сумма арккосинусов (arccosa+arccos(-a)=pi), где (-1leq aleq 1).
Получаем систему для определения ОДЗ: begin{gather*} -1leq frac{1}{x}leq 1Rightarrow 0leq frac{1}{x}+1leq 2Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{x+1}{x}leq 2 end{cases} Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{-x+1}{x}leq 0 end{cases} Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{x-1}{x}geq 0 end{cases} Rightarrow\ Rightarrow left[ begin{array}{l l} begin{cases} xgt 0\ x+1geq 0\ x-1geq 0 end{cases} \ begin{cases} xlt 0\ x+1leq 0\ x-1leq 0 end{cases} end{array} right. Rightarrow left[ begin{array}{l l} begin{cases} xgt 0\ xgeq 1 end{cases} \ begin{cases} xlt 0\ xleq -1 end{cases} end{array} right. Rightarrow xleq -1cup xgeq 1 end{gather*} Заметим, что используя модуль, тот же результат можно получить значительно быстрей: $$ -1leqfrac{1}{x}leq 1Leftrightarrow |frac{1}{x}|leq 1Leftrightarrow |x|geq 1 $$ Таким образом, ОДЗ – вся числовая прямая, кроме (xnotin(-1;1).) $$ y=arccosleft(frac{1}{x}right)+arccosleft(-frac{1}{x}right)Leftrightarrow begin{cases} y=pi\ xnotin (-1;1) end{cases} $$ Строим график:
(б) y=arcctg(sqrt{x})+arcctg(-sqrt{x}))
Сумма арккотангенсов (arcctga+arcctg(-a)=pi), где (ainmathbb{R})
ОДЗ ограничено требованием к подкоренному выражению: (xgeq 0)
$$ y=arcctgleft(sqrt{x}right)+arcctgleft(-sqrt{x}right)Leftrightarrow begin{cases} y=pi\ xgeq 0 end{cases} $$ Строим график:
Пример 5*. Запищите в порядке возрастания:
$$ arctgleft(fracpi4right), arcsinleft(fracpi4right), arctg1 $$
 |
Способ 1. С помощью числовой окружности.
Отмечаем точку (fracpi4) на оси синусов (ось OY) и точки (fracpi4) и 1 на оси тангенсов (касательная к окружности). |
| Способ 2. Аналитический Арктангенс – функция возрастающая: (fracpi4approx 0,79lt 1Rightarrow arctgleft(fracpi4right)lt arctg 1) Сравним (arctg1=fracpi4=arcsinleft(frac{sqrt{2}}{2}right)) и (arcsinleft(fracpi4right)) (frac{sqrt{2}}{2} ? fracpi4) – возведем в квадрат обе части (frac12 ? frac{pi^2}{16}Leftrightarrow 8 ? pi^2) (8ltpi^2Rightarrowfrac{sqrt{2}}{2}ltfracpi4 Rightarrow arcsinleft(frac{sqrt{2}}{2}right)lt arcsinleft(fracpi4right)Rightarrow 1lt arcsinleft(fracpi4right)) Получаем: $$ arctgleft(fracpi4right)lt underbrace{arctg1}_{=fracpi4} lt arcsinleft(fracpi4right) $$ |
Пример 6*. Решите уравнения:
a) (arccosx=arctgx)
ОДЗ определяется ограничением для арккосинуса: (-1leq xleq 1)
Арккосинус ограничен (0leq arccosxleq pi), арктангенс (-fracpi2leq arctgxltfracpi2)
Т.к. по условию они равны, ограничение сужается до (0leq arctgxlt fracpi2) и (0leq arccos xlt fracpi2) $$ arccosx=arctgxLeftrightarrow begin{cases} x=cos(arctgx)\ -1leq xleq 1\ 0leq arctgxltfracpi2\ 0leq arccosxltfracpi2 end{cases} Leftrightarrow begin{cases} x=cos(arctgx)\ -1leq xleq 1\ 0leq x\ 0lt xleq 1 end{cases} Leftrightarrow begin{cases} x=cos(arctgx)\ 0lt xlt 1 end{cases} $$ Для решения можно воспользоваться готовой формулой для (cos(arctgx)).
Выведем её. Пуcть (arctgx=varphi). Тогда (x=tgvarphi) и $$ cos(arctgx)=cosvarphi=sqrt{frac{1}{1+tg^2varphi}}=sqrt{frac{1}{1+x^2}} $$ Получаем уравнение: $$ x=sqrt{frac{1}{1+x^2}}Rightarrow x^2=frac{1}{1+x^2}Rightarrow x^2(1+x^2)=1Rightarrow x^4+x^2-1=0 $$ $$ D=1+4=5, x^2=frac{-1pmsqrt{5}}{2} $$ Квадрат числа не может быть отрицательным. Остаётся корень (x^2=frac{sqrt{5}-1}{2})
Откуда (x=pmsqrt{frac{sqrt{5}-1}{2}})
По условию (0lt xlt 1). Получаем (x=sqrt{frac{sqrt{5}-1}{2}})
Ответ: (sqrt{frac{sqrt{5}-1}{2}})
б) (arccos^2x+arcsin^2x=frac{5pi^2}{36})
Используем формулу для суммы: (arccosx+arcsinx=fracpi2)
Получаем: begin{gather*} arccos^2x+left(fracpi2-arccosxright)^2=frac{5pi^2}{36}\ arccos^2x+frac{pi^2}{4}-pi arccosx+arccos^2x=frac{5pi^2}{36}\ 2arccos^2x-pi arccosx+frac{pi^2}{9}=0\ D=(-pi)^2-4cdot 2cdot frac{pi^2}{9}=pi^2-frac89pi^2=frac{pi^2}{9}\ arccosx=frac{pipmfracpi3}{4}Rightarrow left[ begin{array} {l l} arccosx_1=fracpi6\ arccosx_2=fracpi3 end{array} right. Rightarrow left[ begin{array} {l l} x_1=cosfracpi6=frac{sqrt{3}}{2}\ x_2=cosfracpi3=frac12 end{array} right. end{gather*} Ответ: (left{frac12; frac{sqrt{3}}{2}right})
в) (arcsinfrac{sqrt{3x+2}}{2}=arcctgsqrt{frac{2}{x+1}})
ОДЗ определяется ограничением для арксинуса: ( -1leq frac{sqrt{3x+2}}{2}leq 1)
Арксинус ограничен (-fracpi2leq arcsinfrac{sqrt{3x+2}}{2}leqfracpi2), арккотангенс (0leq arcctgsqrt{frac{2}{x+1}}ltpi)
Т.к. по условию они равны, ограничение сужается до (0leq arcctgsqrt{frac{2}{x+1}}ltfracpi2) и (0leq arcsinfrac{sqrt{3x+2}}{2}ltfracpi2). begin{gather*} arcsinfrac{sqrt{3x+2}}{2}=arcctgsqrt{frac{2}{x+1}}Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ -1leqfrac{sqrt{3x+2}}{2}leq 1\ 0leq arcsinfrac{sqrt{3x+2}}{2}ltfracpi2\ 0leq arcctgsqrt{frac{2}{x+1}}ltfracpi2 end{cases} Leftrightarrow\ Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ -1leqfrac{sqrt{3x+2}}{2}leq 1\ 0leq frac{sqrt{3x+2}}{2}lt 1\ 0leq sqrt{frac{2}{x+1}} end{cases} Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ 0leq frac{sqrt{3x+2}}{4}lt 1\ frac{4}{x+1}geq 0 end{cases} end{gather*} Для ОДЗ получаем: $$ begin{cases} 0leq 3x+2lt 4\ x+1gt 0 end{cases} Rightarrow begin{cases} -2leq 3x lt 2\ xgt -1 end{cases} Rightarrow begin{cases} -frac23leq x lt frac23\ xgt -1 end{cases} Rightarrow -frac23leq xltfrac23 $$ ОДЗ: (-frac23leq xlt frac23)
Выведем формулу для синуса арккотангенса.
Пусть (arcctgx=varphi Rightarrow x=ctgvarphi)
Тогда (sin(arcctgx)=sinvarphi=sqrt{frac{1}{1+ctg^2varphi}}=sqrt{frac{1}{1+x^2}})
Правая часть уравнения: $$ sinleft(arcctgsqrt{frac{2}{x+1}}right)= sqrt{frac{1}{1+left(sqrt{frac{2}{x+1}}right)}}= sqrt{frac{1}{1+frac{2}{x+1}}}=sqrt{frac{x+1}{x+3}} $$ Подставляем: begin{gather*} frac{sqrt{3x+2}}{2}=sqrt{frac{x+1}{x+3}}Rightarrow frac{3x+2}{4}=frac{x+1}{x+3}Rightarrow (3x+2)(x+3)=4(x+1)Rightarrow\ Rightarrow 3x^2+11x+6=4x+4Rightarrow 3x^2+7x+2=0\ D=49-4cdot 3cdot 2=25\ x=frac{-7pm5}{6}Rightarrow left[ begin{array} {l l} x_1=-2 – text{ не подходит по ОДЗ}\ x_2=-frac13 end{array} right. end{gather*} Ответ: (-frac13)
Рассмотрим, как можно найти котангенс арктангенса ctg (arctg x) с помощью определений тангенса, котангенса и арктангенса.
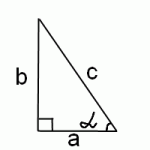Арктангенс икса — это такое число альфа, тангенс которого равен иксу:
arctg x=α, => tg α =x.
В прямоугольном треугольнике тангенс равен отношению противолежащего катета к прилежащему, в нашем случае tg α = b/a. А нам нужно найти котангенс этого же угла. Поскольку котангенс — это отношение прилежащего катета к противолежащему, то ctgα= a/b.
Значит, ctg (arctg x)=a/b, где x=b/a.
Пример.
Найти ctg (arctg 2/5).
Решение:
Рассуждаем аналогично. arctg 2/5=α, => tg α=2/5. А так как тангенс равен отношению противолежащего катета к прилежащему, то в нашем случае противолежащий катет a=2, прилежащий b=5.
А нам нужно найти котангенс этого же угла альфа. Поскольку котангенс равен отношению прилежащего катета к противолежащему, то ctg (arctg 2/5)=5/2.
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
для α∈-1, 1 sin(arccis α)=α, cos(arccos α)=α,для α∈(-∞, ∞) tg(arctg α)=α, ctg(arcctg α)=α
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
для -π2≤α≤π2 arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
для α∈-1, 1 arccis (-α)=-arcsin α, arccos (-α)=π-arccos α,для α∈(-∞, ∞) arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
для α∈-1, 1 arccis α+arccos α=π2,для α∈(-∞, ∞) arctg α+arcctg α=π2
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
| -1≤α≤1,sin (arcsin α)=α | -1≤α≤1,sin (arccos α)=1-α2 | -∞≤α≤+∞,sin (arctg α)=α1+α2 | -∞≤α≤+∞, sin (arcctg α)=11+α2 |
| -1≤α≤1,cos (arcsin α)=1-α2 | -1≤α≤1,cos (arccos α)=α | -∞≤α≤+∞,cos (arctg α)=11+α2 | -∞≤α≤+∞, cos (arcctg α)=11+α2 |
| -1<α<1,tg (arcsin α) =α1-α2 | α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α | -∞≤α≤+∞,tg (arctg α)=α | α≠0 ,tg (arcctg α)=1α |
| α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α | -1<α<1,ctg (arccos α)=α1-α2 | α≠0,ctg (arctg α)=1α | -∞≤α≤+∞, ctg (arcctg α)=α |
Теперь разберем примеры, как они применяются в задачах.
Вычислите косинус арктангенса из 5.
Решение
У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2
Подставляем нужное значение: cos(arctg5)=11+(5)2=26
Вычислить синус арккосинуса 12.
Решение
Для этого нам понадобится формула: sin (arccos α)=1-a2
Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций – косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin2α+cos2α=11+ctg2α=1sin2α
Вспомним, что tgα·ctgα=1. Из этого можно получить:
sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог – формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
- sinα=1-cos2α, 0≤α≤π
Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2
- sinα=tgα1+tgα, -π2<α<π2,
Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2
- sinα=11+ctg2α, 0<α<π
Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
- Из cosα=1-sin2α, -π2≤α≤π2 следует, что
cos(arcsin α)=1-sin2(arcsin α)=1-a2
- Из cosα=11+tg2α, -π2<α<π2 следует, что
- Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2
следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из tgα=sin α1-sin2α, -π2<α<π2. Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.
- Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем
tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).
- Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
ctgα=1tgα
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0
А так мы выразим арккосинус через остальные обратные функции:
arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1
Формула выражения арктангенса:
arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0
Последняя часть – выражение арккотангенса через другие обратные функции:
arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.
Мы знаем, что arctgα1-α2 – это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α
Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.
Вывод: arcsina=arctga1-a2, -1<a<1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Условие Вычислить синус арккотангенса минус корня из 3.
Решение
Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0
Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π
В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2 sin(arcctg(-3))=11+(-3)2=12
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
sin2α2=1-cosα2
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
sinα2=1-cosα2
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
arccosα2=arcsin1-α2
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
- Определение
- График арккотангенса
- Свойства арккотангенса
- Таблица арккотангенсов
Определение
Арккотангенс (arcctg или arccot) – это обратная тригонометрическая функция.
Арккотангенс x определяется как функция, обратная к котангенсу x.
Если котангенс угла у равен х (ctg y = x), значит арккотангенс x равняется y:
arcctg x = ctg-1 x = y
Примечание: ctg-1x означает обратный котангенс, а не котангенс в степени -1.
Например:
arctg 1 = ctg-1 1 = 45° = π/4 рад
График арккотангенса
Функция арккотангенса пишется как y = arcctg (x). График в общем виде выглядит следующим образом (0 < y < π, –∞ < x < +∞):
Свойства арккотангенса
Ниже в табличном виде представлены основные свойства арккотангенса с формулами.
Таблица арккотангенсов
| arcctg x (°) | arcctg x (рад) | x |
| 180° | π | -∞ |
| 150° | 5π/6 | -√3 |
| 135° | 3π/4 | -1 |
| 120° | 2π/3 | -1/√3 |
| 90 | π/2 | 0 |
| 60 | π/3 | 1/√3 |
| 45 | π/4 | 1 |
| 30 | π/6 | √3 |
| 0 | 0 | ∞ |
microexcel.ru
