Как найти целочисленные координаты графика функции - Сайт, где вы сможете решить свои вопросы

Приветствую Вас!

Как многим уже известно, профиль ЕГЭ по математике немного изменили. Убрали более простые задачи и внесли более сложные. Теперь нужно уметь решать задачи на сложную вероятность и вспомнить графики всех функций.

Рассмотрим задание №9 о графиках. На экзамене могут попасться примерно такие варианты:

Задание №9 из нового профиля ЕГЭ. Параболы, гиперболы, модули, синусоиды.

Как мне кажется, сами задания из этой серии не такие уж и простые. Хотя, если понимать в графиках, то решить все это вполне возможно. Меня удивили решения, которые даны у автора сайта. Может, просто еще все довольно сыровато, и позже будут предложены более развернутые объяснения? Вот одна из задач на параболу с решением:

Ну, если с (х-6)^2 и +8 боле менее понятно тем, кто разбирается в движении графиков по осям, то как быть с а=-4?

У меня, как всегда, свое видение на данную ситуацию, поэтому хочу предложить более простое решение, на мой взгляд, которое подойдет для любого задания такого типа.

Что мы здесь видим? – график расположен на клетчатой бумаге и указан единичный отрезок. Соответственно, видны координаты целочисленных точек. Так как нам нужно определить три коэффициента (а, в и с), то возьмем координаты трех точек и составим три уравнения.

Причем, возьмем общее уравнение параболы в стандартном виде: y=ax^2+bx+c. Все минуса и дробные коэффициенты, если таковые имеются, вылезут сами по себе.

Итак, выбираем “удобные” координаты, исходя из рисунка:

(0;-1), (2;4), (10;4). Подставим под х и у соответственно в общую формулу параболы и получим:

Все коэффициенты найдены. Теперь можно найти и f(3,5). Пусть это “рабоче-крестьянский” способ, зато, понятный, думаю, абсолютно всем.

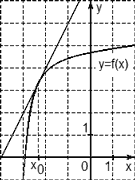
Теперь рассмотрим график с гиперболой:

С этим заданием всё боле менее ясно. разобрано по асимптотам и подставлено в коэффициенты. Но, здесь также можно использовать метод, приведенный выше, взяв за внимание только то, что график поднят по оси у на две единицы вверх, следовательно, свободный член с=2.

Далее, можно взять также с рисунка координаты двух точек и решить незамысловатую систему:

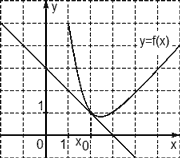
Теперь окунемся в модульный график. У многих боооольшие проблемы с модулями, даже элементарными, а тут такое..

Честно признаться, сама не очень понимаю откуда взяты такие равенства. Наверно, если разобраться, то в них есть смысл. Но, как то не очень хочется во всем этом копаться. Предпочитаю действовать простыми и понятными методами, и, по возможности не забивать голову лишней информацией.

Придержемся по прежнему вышеупомянутого способа и поставим все на свои места. Единственное что, существует один нюанс подмодульного выражения о котором нужно знать:

Линейные модульные графики все выглядят в виде “галочки”. Так вот, координата по иксу вершины этой “галочки”, это когда подмодульное выражение равно нулю. То есть, в данном случае bx+c=0. Из графика видно, что координата по иксу этой вершины равна 2, следовательно, 2b+c=0.

Далее: сам модуль раскрывается двумя способами, со знаком “+” и со знаком “-“. Правый луч “галочки”, это модуль, раскрытый с “+”, левый – с “-“.

Поясню, что все это значит:

Раскрыв модуль, мы получили два уравнения. Теперь, возьмем целочисленные координаты точек на графике и подставим в соответствующие уравнения:

Координаты синей точки в синее уравнение, красных – в красное. Помним еще об уравнении вершины “галочки”, 2b+c=0.

У нас, в данном уравнении 4 неизвестных – a,b,c,d. Следовательно, нам потребуется 4 уравнения. Поэтому, учитывая уравнение вершины, взяты координаты трех точек: (-1;4), (0;3), (3;4). Подставив под х и у, получим систему:

Ну, а теперь, когда известны все коэффициенты, можно решить то, что просят в задании: ах+d=0.

Теперь синусоиды:

Здесь довольно исчерпывающая информация. И, при изучении синусоидных графиков, формулы для нахождения коэффициентов а и d нужно знать. Далее выбирают точку на графике f(0)=1 и подставляют, определяя с, что собственно делали и мы до этого.

Обратите внимание, что коэф-т а берется по модулю, поэтому рассматривается два варианта уравнений по косинусу. Одно из которых не имеет целочисленного решения. Почему? А потому что, если cos с=-1, то с=Пи, что не является целым числом.

Разберем второй фрагмент решения, связанный с коэф-м b:

Полный период у косинуса 2П, поэтому именно он и прибавляется в скобку, но в связи с какими-либо обстоятельствами он может поменяться и, именно это зависит от коэф-та b. Здесь вновь обращаются к графику, из рисунка которого видно, что период составляет две единицы:

Теперь становится возможным вычислить саму b. Далее получаем формулу со всеми коэф-ми, что позволяет ответить на вопрос задачи.

Думаю, какие-то моменты я для кого-то прояснила.

Благодарю за внимание..

Источник

Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 26. Комбинаторные и вероятностные задачи к главе 3. ОТВЕТЫ на упражнения 26.1 — 26.7. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.

§ 26. Комбинаторные и вероятностные задачи к главе 3

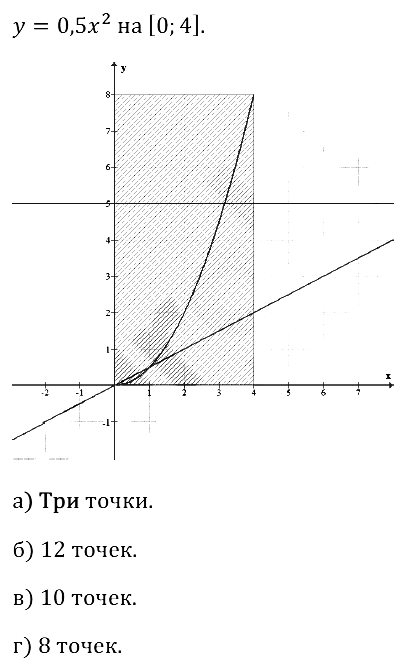
Задание № 26.1. Нарисуйте график функции у = 0,5х² на отрезке [0; 4]. Сколько точек с целыми координатами:
а) принадлежит этому графику;
б) лежит ниже графика и выше оси абсцисс;
в) лежит выше графика и ниже прямой у = 5;
г) лежит ниже графика и выше прямой у = 0,5х ?

Смотреть ответы на № 26.1

Задание № 26.2. Сколько точек, координаты которых – натуральные числа, лежит на графике функции:
а) у = 1/х; б) у = 5/х; в) у = 6/х; г) у = 12/х.

Смотреть ответы на № 26.2

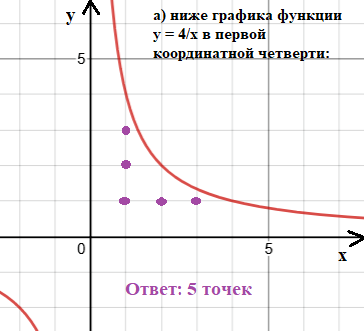
Задание № 26.3. Сколько точек с целочисленными координатами лежит:
а) ниже графика функции у = 4/х в первой координатной четверти*;
б) выше графика функции у = 5/х в третьей координатной четверти*;
в) ниже графика функции у = –3/x во второй координатной четверти*;
г) между графиками функций у = 2/x и у = –2/x (не включая точки на координатных осях)?

*- не на осях координат

Смотреть ответы на № 26.3

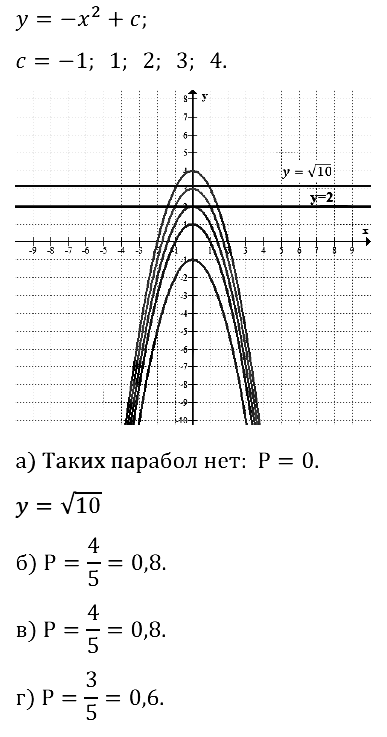
Задание № 26.4. В уравнении параболы у = –х² + с коэффициент с случайным образом выбирают из чисел –1, 1, 2, 3, 4. Какова вероятность того, что эта парабола:
а) не пересечёт четвёртую координатную четверть;
б) будет расположена ниже прямой у = √10;
в) пересечёт ось абсцисс в двух точках;
г) будет иметь хотя бы одну общую точку с прямой у = 2?

Смотреть ответы на № 26.4

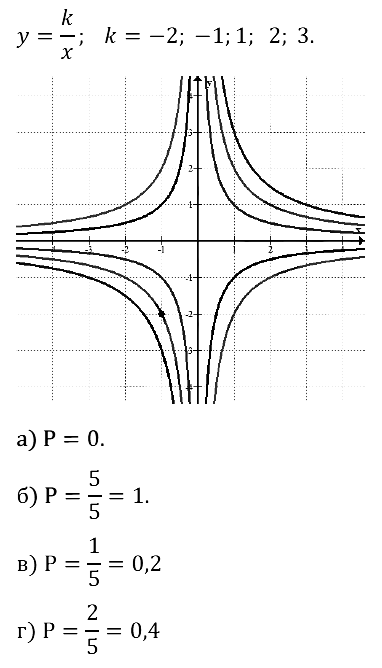
Задание № 26.5. Коэффициент k случайным образом выбирают из чисел –2, –1, 1, 2, 3. Какова вероятность того, что график функции у = k/x:
а) пересекает и первую, и вторую координатную четверть;
б) симметричен относительно начала координат;
в) проходит через точку (– 1, – 2);
г) содержит ровно две точки с целочисленными координатами?

Смотреть ответы на № 26.5

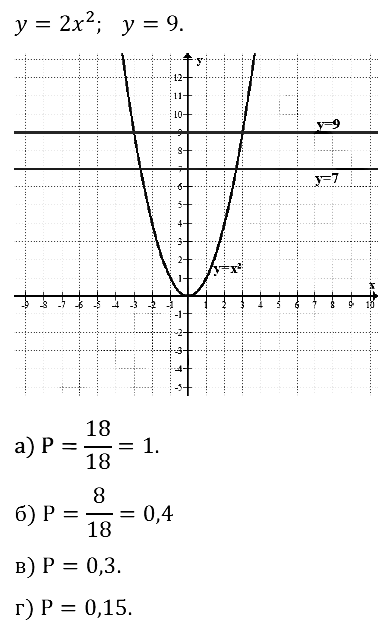
Задание № 26.6. Случайным образом выбирают точку с целочисленными координатами так, чтобы она лежала выше графика функции у = 2х² и ниже графика прямой у = 9. Какова вероятность того, что эта точка лежит:
а) выше оси абсцисс; в) левее оси ординат;
б) на оси ординат; г) выше прямой у = 7?

Смотреть ответы на № 26.6

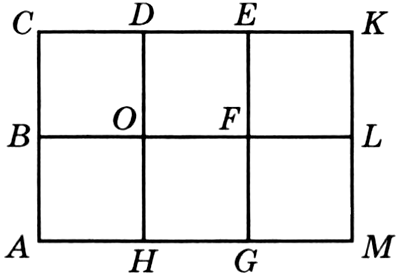
Задание № 26.7. В прямоугольнике АСКМ (рис. 69) надо пройти по отмеченным линиям из вершины А в вершину К, двигаясь только вверх или вправо. Сколько всего путей:
а) проходит через вершину М;
б) проходит через точку Н;
в) проходит через точку В;
г) можно проложить из вершины А в вершину К?

Смотреть ответы на № 26.7

Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 26. Комбинаторные и вероятностные задачи к главе 3. ОТВЕТЫ на упражнения 26.1 — 26.7. Вернуться в ОГЛАВЛЕНИЕ.

Источник

На графике дробно – линейной функции y = (10х + 52 / 5х + 2) найдите точки с целочисленными координатами.

Перед вами страница с вопросом На графике дробно – линейной функции y = (10х + 52 / 5х + 2) найдите точки с целочисленными координатами?, который относится к
категории Математика. Уровень сложности соответствует учебной программе для
учащихся 5 – 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.

Источник

15 марта 2011

В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:

Значение производной в некоторой точке x₀,
Точки максимума или минимума (точки экстремума),
Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x₀, и требуется найти значение производной в этой точке, применяется следующий алгоритм:

Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x₁; y₁) и B (x₂; y₂). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
Зная координаты, легко вычислить приращение аргумента Δx = x₂ − x₁ и приращение функции Δy = y₂ − y₁.
Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

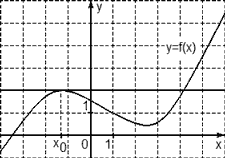
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x₂ − x₁ = −1 − (−3) = 2; Δy = y₂ − y₁ = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x₂ − x₁ = 3 − 0 = 3; Δy = y₂ − y₁ = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x₂ − x₁ = 5 − 0 = 5; Δy = y₂ − y₁ = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

Точка x₀ называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≥ f(x).
Точка x₀ называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x₀ известно, что f’(x₀) ≠ 0, то возможны лишь два варианта: f’(x₀) ≥ 0 или f’(x₀) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

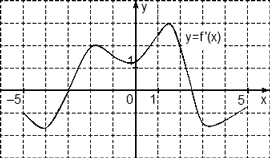
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

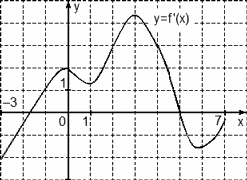
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

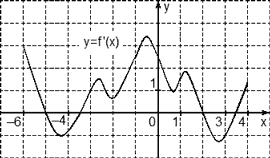
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂). Другими словами, чем больше значение аргумента, тем больше значение функции.
Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

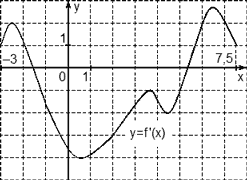
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

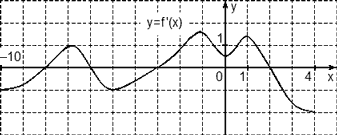
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l₁ = − 6 − (−8) = 2;
l₂ = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l₂ = 5.

Смотрите также: