Как найти целое число в арифметической прогрессии

Была ли эта статья полезной?

Арифметическая прогрессия — коротко о главном

Определение арифметической прогрессии:

Арифметическая прогрессия — это числовая последовательность, в которой разница между соседними числами одинакова и равна ( displaystyle d).

Например:

• ( {{a}_{1}}=3)
• ( displaystyle {{a}_{2}}=3+d=7~Rightarrow d=7-3=4)
• ( displaystyle {{a}_{3}}=7+4=11) и т.д.

Арифметическая прогрессия бывает возрастающей (( displaystyle d>0)) и убывающей (( displaystyle d<0)).

Формула нахождения n-ого члена арифметической прогрессии:

( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)) , где ( displaystyle n)– количество чисел в прогрессии.

Как найти член прогрессии, если известны его соседние члены:

( {{text{a}}_{text{n}}}=frac{{{text{a}}_{text{n}+1}}+{{text{a}}_{text{n}-1}}}{2}) — где ( displaystyle n) – количество чисел в прогрессии.

Сумма членов арифметической прогрессии:

1-й способ: ( {{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}), где ( displaystyle n) – количество значений.

2-й способ: ( displaystyle {{s}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n), где ( displaystyle n) – количество значений.

Числовая последовательность

Итак, сядем и начнем писать какие-нибудь числа. Например: ( displaystyle 4,text{ }7,text{ }-8,text{ }13,text{ }-5,text{ }-6,text{ }0,text{ }ldots )

Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ( displaystyle 7)). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать.

Это и есть пример числовой последовательности.

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.

Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и ( displaystyle n)-ное число) всегда одно.

Число с номером ( displaystyle n) называется ( displaystyle n)-ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, ( displaystyle a)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: ( displaystyle {{a}_{1}},text{ }{{a}_{2}},text{ }…,text{ }{{a}_{10}},text{ }…,text{ }{{a}_{n}}).

Арифметическая прогрессия — определения

Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна d.

Например:

( begin{array}{l}{{a}_{1}}=3\{{a}_{2}}=3+d=7~~~Rightarrow ~d=7-3=4\{{a}_{3}}=7+4=11end{array})

Такая числовая последовательность называется арифметической прогрессией.

Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность.

Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d.

Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:

• ( displaystyle 3;text{ }6;text{ }9;text{ }12;text{ }15;text{ }17ldots )
• ( displaystyle 1;text{ }12;text{ }23;text{ }34;text{ }45text{ }ldots )
• ( displaystyle -5;text{ }-1;text{ }3;text{ }7;text{ }11;text{ }15ldots )
• ( displaystyle -6;text{ }5;text{ }17;text{ }28;text{ }39ldots )

Разобрался? Сравним наши ответы:

Является арифметической прогрессией – 2, 3.

Не является арифметической прогрессией – 1, 4.

Вернемся к заданной прогрессии (( displaystyle 3;text{ }7;text{ }11;text{ }15;text{ }19ldots )) и попробуем найти значение ее 6-го члена.

Существует два способа его нахождения.

Нахождения n-ого члена арифметической прогрессии

Способ I

Мы можем прибавлять к предыдущему значению числа прогрессии ( d=4) , пока не дойдем до ( displaystyle 6)-го члена прогрессии. Хорошо, что суммировать нам осталось немного – всего три значения:

Способ II

А что если нам нужно было бы найти значение ( displaystyle 140)-го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.

А теперь очень важно! Чтобы облегчить себе работу, нужно найти закономерность, потом описать ее формулой и потом пользоваться этой формулой, чтобы вычислять в разы быстрее.

Это и есть математика!

Важно научиться находить закономерности, а потом уже запоминать формулы. Потому что, даже если ты забудешь формулу, ты сможешь ее вывести. И, самое главное, ты сможешь проверить подходит та или иная формула для решения задачи, а не просто подставлять их как обезьянка. 

Давай попробуем вывести формулу. Это легко и тебе понравится! Чтобы найти закономерности, надо пользоваться тем, что мы знаем.

Что мы знаем?

• У нас есть арифметическая прогрессия: 3, 7, 11, 15, 19 и т.д.
• У нас есть номера прогрессии: 1, 2, 3, 4, 5, и т.д.
• Мы все время прибавляем 4, значит разница прогрессии d = 4.

Чему равен 2-й член арифметической прогрессии? Попробуй сначала написать числами, а потом в более общем виде, заменив числа буквами.

7=3+4 или 7=3+d

Закономерности пока не видны. Ок. Идем дальше. Чему равен 3-й член арифметической прогрессии?

11=3+4+4 или 11=3+d+d

Похоже что вырисовывается закономерность! Чтобы узнать значение 2-го члена прогрессии, мы прибавляли одно d, а чтобы узнать 3-го — два d! Иными словами, нам надо прибавлять каждый раз на одно d меньше, чем номер члена прогрессии.

Давай проверим? Чему равен 4-й член арифметической прогрессии?

15=3+4+4+4 или 15=3+d+d+d

Бинго! Закономерность подтверждается. Теперь осталось описать закономерность формулой и пользоваться ею!

Если нам нужно найти значение числа прогрессии с порядковым номером n, мы прибавляем к первому члену арифметической прогрессии число d, которое на одно значение меньше порядкового номера искомого числа. 

А теперь запомни эту формулу и используй ее для быстрого счета. А если забудешь — то легко выведешь.

Например, посмотрим, из чего складывается значение ( displaystyle 4)-го члена данной арифметической прогрессии:

( begin{array}{l}{{a}_{4}}={{a}_{1}}+dleft( 4-1 right)\{{a}_{4}}=3+4left( 4-1 right)=15end{array})

Попробуй самостоятельно найти таким способом значение члена ( displaystyle n=6) данной арифметической прогрессии.

Рассчитал? Сравни свои записи с ответом:

( begin{array}{l}{{a}_{6}}={{a}_{1}}+dleft( 6-1 right)\{{a}_{6}}=3+4left( 6-1 right)=3+4cdot 5=3+20=23end{array})

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли ( displaystyle d) к предыдущему значению членов арифметической прогрессии.

Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)) – уравнение арифметической прогрессии.

Кстати, таким образом мы можем посчитать и ( displaystyle 140)-ой член данной арифметической прогрессии (да и ( displaystyle 169)-ый тоже можем, да и любой другой вычислить совсем несложно).

Попробуй посчитать значения ( displaystyle 140)-го и ( displaystyle 169)-го членов, применив полученную формулу.

( begin{array}{l}…\{{a}_{140}}={{a}_{1}}+dleft( 140-1 right)\{{a}_{140}}=3+4left( 140-1 right)=3+4cdot 139=3+556=559\{{a}_{169}}={{a}_{1}}+dleft( 169-1 right)\{{a}_{169}}=3+4left( 169-1 right)=3+4cdot 168=3+672=675end{array})

Возрастающие и убывающие арифметические прогрессии

Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего. 

Например:

( displaystyle begin{array}{l}4;text{ }6;text{ }8;text{ }10;text{ }12\-2;text{ }4;text{ }10;text{ }16;text{ }20end{array})

Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего. 

Например:

( displaystyle begin{array}{l}12;text{ }10;text{ }8;text{ }6;text{ }4\4;text{ }0;text{ }-4;text{ }-8;text{ }-12.end{array})

Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.

Проверим это на практике.

Нам дана арифметическая прогрессия, состоящая из следующих чисел: ( displaystyle 13;text{ }8;text{ }4;text{ }0;text{ }-4.)

Проверим, какое получится ( displaystyle 4)-ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:

( {{text{a}}_{text{n}}}={{text{a}}_{1}}+text{d}left( text{n}-1 right))

Заметим, что так как арифметическая прогрессия убывающая, то значение ( displaystyle d) будет отрицательным, ведь каждый последующий член меньше предыдущего.

( displaystyle d=8-13=-5)

( {{a}_{4}}={{a}_{1}}+dleft( 4-1 right))

Так как ( displaystyle d=-5), то:
( {{a}_{4}}=13-5left( 4-1 right)=13-15=-2)

Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.

Попробуй самостоятельно найти ( displaystyle 140)-ой и ( displaystyle 169)-ый члены этой арифметической прогрессии.

Сравним полученные результаты:

( begin{array}{l}{{a}_{140}}={{a}_{1}}+dleft( 140-1 right)\{{a}_{140}}=13-5left( 140-1 right)=13-5cdot 139=13-695=-682\{{a}_{169}}={{a}_{1}}+dleft( 169-1 right)\{{a}_{169}}=13-5left( 169-1 right)=13-5cdot 168=13-840=-827end{array})

Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)

Усложним задачу — выведем свойство арифметической прогрессии.

Допустим, нам дано такое условие:

( displaystyle 4;text{ }x;text{ }12ldots ) — арифметическая прогрессия, найти значение ( displaystyle x).

Легко, скажешь ты и начнешь считать по уже известной тебе формуле:

( {{a}_{n}}={{a}_{1}}+dleft( n-1 right))

Пусть ( displaystyle {{a}_{1}}=4), а ( displaystyle {{a}_{3}}=12), тогда:

( displaystyle begin{array}{l}{{a}_{3}}={{a}_{1}}+dleft( 3-1 right)\12=4+2d~~Rightarrow ~d=frac{12-4}{2}=4\{{a}_{2}}=x={{a}_{1}}+d\{{a}_{2}}=x=4+4=8end{array})

Абсолютно верно.

Получается, мы сначала находим ( displaystyle d), потом прибавляем его к первому числу и получаем искомое ( displaystyle x).

Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа ( displaystyle 4024;~x;6072)?

Согласись, есть вероятность ошибиться в вычислениях.

А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы?

Конечно да, и именно ее мы попробуем сейчас вывести.

Обозначим искомый член арифметической прогрессии как ( {{text{a}}_{text{n}}}), формула его нахождения нам известна – это та самая формула, выведенная нами в начале:

( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)), тогда:

• предыдущий член прогрессии это ( {{a}_{n}}-d): ( {{a}_{n-1}}={{a}_{1}}+dleft( n-1 right)-d)
• последующий член прогрессии это ( {{a}_{n}}+d): ( {{a}_{n+1}}={{a}_{1}}+dleft( n-1 right)+d)

Просуммируем предыдущий и последующий члены прогрессии:

( {{a}_{1}}+dleft( n-1 right)-d+{{{a}}_{1}}+text{d}left( text{n}-1 right)+text{d}=2left( {{a}_{1}}+dleft( n-1 right) right)text{ }!!~!!text{ })

Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними.

Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на ( 2).

( {{a}_{n}}=frac{{{a}_{n+1}}+{{a}_{n-1}}}{2}) – свойство членов арифметической прогрессии.

Попробуем посчитать значение ( x), используя выведенную формулу:

( x=frac{4+12}{2}=8)

Все верно, мы получили это же число. Закрепим материал.

Посчитай значение ( x) для прогрессии ( displaystyle 4024;~x;6072) самостоятельно, ведь это совсем несложно.

( x=frac{4024+6072}{2}=5048)

Молодец! Ты знаешь о прогрессии почти все!

Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» – Карл Гаусс…

Сумма первых n членов арифметической прогрессии

Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу:

«Сосчитать сумму всех натуральных чисел от ( displaystyle 1) до ( displaystyle 40) (по другим источникам до ( displaystyle 100)) включительно».

Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…

Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.

Допустим, у нас есть арифметическая прогрессия, состоящая из ( displaystyle 6)-ти членов: ( displaystyle 6;text{ }8;text{ }10;text{ }12;text{ }14;text{ }16…)

Нам необходимо найти сумму данных ( displaystyle 6) членов арифметической прогрессии.

Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму ( displaystyle 100) ее членов, как это искал Гаусс?

Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.

Попробовал? Что ты заметил? Правильно! Их суммы равны

А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии?

Конечно, ровно половина всех чисел, то есть ( frac{6}{2}=3).

Исходя из того, что сумма двух членов арифметической прогрессии равна ( 22), а подобных равных пар ( 3), мы получаем, что общая сумма равна:

( displaystyle Stext{ }=text{ }22cdot 3text{ }=text{ }66).

Таким образом, формула для суммы первых ( displaystyle n) членов любой арифметической прогрессии будет такой:

( displaystyle {{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}), где ( displaystyle n) – количество значений.

В некоторых задачах нам неизвестен ( displaystyle n)-й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу ( displaystyle n)-го члена. ( {{a}_{n}}={{a}_{1}}+dleft( n-1 right))

Что у тебя получилось?

( displaystyle {{S}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n), где ( displaystyle n) – количество значений.

Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма ( displaystyle 40) чисел, начиная от ( displaystyle 1)-го, и сумма ( displaystyle 100) чисел начиная от ( displaystyle 1)-го.

Сколько у тебя получилось?

У Гаусса получилось, что сумма ( displaystyle 100 ) членов равна ( displaystyle 5050), а сумма ( displaystyle 40 ) членов ( displaystyle 820).

Так ли ты решал?

• ( {{S}_{40}}=frac{left( 1+40 right)cdot 40}{2}=frac{41cdot 40}{2}=frac{1640}{2}=820)
• ( {{S}_{100}}=frac{left( 1+100 right)cdot 100}{2}=frac{101cdot 100}{2}=5050)

На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.

Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.

Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.

Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется ( displaystyle 6) блочных кирпичей.

Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?

В данном случае прогрессия выглядит следующим образом:

Разность арифметической прогрессии ( displaystyle ~=text{ }dtext{ }=text{ }-1).

Количество членов арифметической прогрессии ( displaystyle=6).

Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).

Способ 1.

Сошлось?

Молодец, ты освоил сумму ( displaystyle n)-ных членов арифметической прогрессии.

Конечно, из ( displaystyle 6) блоков в основании пирамиду не построишь, а вот из ( displaystyle 60)?

Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.

Справился?

Верный ответ – ( displaystyle 1830) блоков:

( begin{array}{l}{{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}\{{S}_{60}}=frac{left( 60+1 right)cdot 60}{2}=frac{61cdot 60}{2}=61cdot 30=1830.end{array})

У этого термина существуют и другие значения, см. Прогрессия.

Арифмети́ческая прогре́ссия — числовая последовательность вида

то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага, или разности прогрессии):

^[1]

Любой член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому, т. е. он выражается формулой^[2]:

Арифметическая прогрессия является монотонной последовательностью. При она является возрастающей, а при  — убывающей. Если , то последовательность будет стационарной. Эти утверждения следуют из соотношения для членов арифметической прогрессии.

Свойства[править | править код]

Общий член арифметической прогрессии[править | править код]

Член арифметической прогрессии с номером может быть найден по формулам

где  — первый член прогрессии,  — её разность,  — член арифметической прогрессии с номером .

Отметим, что в формулах общего члена -й член прогрессии есть линейная функция. Об этом говорит следующая теорема.

Характеристическое свойство арифметической прогрессии[править | править код]

Последовательность есть арифметическая прогрессия для любого её элемента выполняется условие

Тождество арифметической прогрессии[править | править код]

Следствие 1. Всякий член арифметической прогрессии вырази́м^[5] через любую пару других членов.

Следствие 2. Для того, чтобы число являлось членом данной арифметической прогрессии с членами и , необходимо и достаточно, чтобы было натуральным число

Формулировка ещё одного признака арифметической прогрессии.

Следствие 3 [критерий]. Числовая последовательность является арифметической прогрессией в том и только в том случае, если выполняется тождество арифметической прогрессии для всех членов данной последовательности. Другими словами, чтобы каждый член был вырази́м через любую пару остальных членов последовательности.

Сумма первых n членов арифметической прогрессии[править | править код]

Сумма первых членов арифметической прогрессии может быть найдена по формулам

, где  — первый член прогрессии,  — член с номером ,  — количество суммируемых членов.

 — где  — первый член прогрессии,  — второй член прогрессии  — член с номером .

, где  — первый член прогрессии,  — разность прогрессии,  — количество суммируемых членов.

, если  — нечётное натуральное число.

Доказательство

Запишем сумму двумя способами:  — та же сумма, только слагаемые идут в обратном порядке. Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали: Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде . Воспользуемся формулой общего члена арифметической прогрессии: Получили, что каждое слагаемое не зависит от и равно . В частности, . Поскольку таких слагаемых , то Третья формула для суммы получается подстановкой вместо . Что и так непосредственно следует из выражения для общего члена. Замечание: Вместо в первой формуле для суммы можно взять любое из других слагаемых , так как они все равны между собой.

Формулировка ещё одного факта: для всякой арифметической прогрессии при любом выполняется равенство:

Примечание: — сумма первых членов арифметической прогрессии.

Доказательство
1. Очевидно, что или Прибавим к обеим частям и получим, что 2. Покажем, что Это так, поскольку можно написать верное равенство: Из него следует, что 3. Теперь докажем, что Перепишем последнее как Но гораздо лучше представить это равенство в виде Видно, что это характеристическое свойство арифметической прогрессии. Значит, действительно 4. А следовательно, 5. Тем самым, что и требовалось доказать.

Предыдущее свойство имеет обобщение.

Для любых натуральных , , выполняется комплементарное свойство сумм:

Ещё один признак арифметической прогрессии.

Сумма членов арифметической прогрессии от n-го до m-го[править | править код]

Сумма членов арифметической прогрессии с номерами от до может быть найдена по формулам

, где  — член с номером ,  — член с номером ,  — количество суммируемых членов.

где  — член с номером ,  — разность прогрессии,  — количество суммируемых членов.

Произведение членов арифметической прогрессии[править | править код]

Произведением первых членов арифметической прогрессии называется произведение от до , то есть выражение вида Обозначение: .

Свойство произведения:

Число множителей-скобок равно , а в самом произведении их составляет «штук».^[10]

Сходимость арифметической прогрессии[править | править код]

Арифметическая прогрессия расходится при и сходится при . Причём

Доказательство
Записав выражение для общего члена и исследуя предел , получаем искомый результат.

Связь между арифметической и геометрической прогрессиями[править | править код]

Пусть  — арифметическая прогрессия с разностью и число . Тогда последовательность вида есть геометрическая прогрессия со знаменателем .

Доказательство
Проверим характеристическое свойство для образованной геометрической прогрессии: Воспользуемся выражением для общего члена арифметической прогрессии: Итак, поскольку характеристическое свойство выполняется, то  — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения .

Следствие: если последовательность положительных чисел образует геометрическую прогрессию, то последовательность их логарифмов образует арифметическую прогрессию.

Арифметические прогрессии высших порядков[править | править код]

Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:

1, 4, 9, 16, 25, 36, …

разности которых образуют простую арифметическую прогрессию с разностью 2:

3, 5, 7, 9, 11, …

Треугольные числа также образуют арифметическую прогрессию второго порядка, их разности образуют простую арифметическую прогрессию

Тетраэдральные числа образуют арифметическую прогрессию третьего порядка, их разности являются треугольными числами.

Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.

Если  — арифметическая прогрессия порядка , то существует многочлен , такой, что для всех выполняется равенство ^[11]

Примеры[править | править код]

Формула для разности[править | править код]

Если известны два члена арифметической прогрессии, а также их номера в ней, то можно найти разность как

.

Сумма чисел от 1 до 100[править | править код]

Согласно легенде, школьный учитель математики юного Гаусса, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050.
Действительно, легко видеть, что решение сводится к формуле

то есть к формуле суммы первых чисел натурального ряда.

См. также[править | править код]

• Геометрическая прогрессия
• Арифметико-геометрическая прогрессия

Примечания[править | править код]

Литература[править | править код]

• Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, 1986. — 544 с.

Ссылки[править | править код]

• Арифметическая прогрессия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890. — Т. II. — С. 98.

При изучении алгебры в общеобразовательной школе (9 класс) одной из важных тем является изучение числовых последовательностей, к которым относятся прогрессии -геометрическая и арифметическая. В данной статье рассмотрим арифметическую прогрессию и примеры с решениями.

Что собой представляет арифметическая прогрессия?

Чтобы это понять, необходимо дать определение рассматриваемой прогрессии, а также привести основные формулы, которые далее будут использованы при решении задач.

Арифметическая или алгебраическая прогрессия – это такой набор упорядоченных рациональных чисел, каждый член которого отличается от предыдущего на некоторую постоянную величину. Эта величина называется разностью. То есть, зная любой член упорядоченного ряда чисел и разность, можно восстановить всю арифметическую прогрессию.

Приведем пример. Следующая последовательность чисел будет прогрессией арифметической: 4, 8, 12, 16, …, поскольку разность в этом случае равна 4 (8 – 4 = 12 – 8 = 16 – 12). А вот набор чисел 3, 5, 8, 12, 17 уже нельзя отнести к рассматриваемому виду прогрессии, поскольку разность для него не является постоянной величиной (5 – 3 ≠ 8 – 5 ≠ 12 – 8 ≠ 17 – 12).

Важные формулы

Приведем теперь основные формулы, которые понадобятся для решения задач с использованием арифметической прогрессии. Обозначим символом a n n-й член последовательности, где n – целое число. Разность обозначим латинской буквой d. Тогда справедливы следующие выражения:

1. Для определения значения n-го члена подойдет формула: a n = (n-1)*d+a 1 .
2. Для определения суммы первых n слагаемых: S n = (a n +a 1)*n/2.

Чтобы понять любые примеры арифметической прогрессии с решением в 9 классе, достаточно запомнить эти две формулы, поскольку на их использовании строятся любые задачи рассматриваемого типа. Также следует не забывать, что разность прогрессии определяется по формуле: d = a n – a n-1 .

Пример №1: нахождение неизвестного члена

Приведем простой пример прогрессии арифметической и формул, которые необходимо использовать для решения.

Пусть дана последовательность 10, 8, 6, 4, …, необходимо в ней найти пять членов.

Из условия задачи уже следует, что первые 4 слагаемых известны. Пятое можно определить двумя способами:

1. Вычислим для начала разность. Имеем: d = 8 – 10 = -2. Аналогичным образом можно было взять любые два других члена, стоящих рядом друг с другом. Например, d = 4 – 6 = -2. Поскольку известно, что d = a n – a n-1 , тогда d = a 5 – a 4 , откуда получаем: a 5 = a 4 + d. Подставляем известные значения: a 5 = 4 + (-2) = 2.
2. Второй способ также требует знания разности рассматриваемой прогрессии, поэтому сначала нужно определить ее, как показано выше (d = -2). Зная, что первый член a 1 = 10, воспользуемся формулой для n числа последовательности. Имеем: a n = (n – 1) * d + a 1 = (n – 1) * (-2) + 10 = 12 – 2*n. Подставляя в последнее выражение n = 5, получаем: a 5 = 12-2 * 5 = 2.

Как видно, оба способа решения привели к одному и тому же результату. Отметим, что в этом примере разность d прогрессии является отрицательной величиной. Такие последовательности называются убывающими, так как каждый следующий член меньше предыдущего.

Пример №2: разность прогрессии

Теперь усложним немного задачу, приведем пример, как

Известно, что в некоторой 1-й член равен 6, а 7-й член равен 18. Необходимо найти разность и восстановить эту последовательность до 7 члена.

Воспользуемся формулой для определения неизвестного члена: a n = (n – 1) * d + a 1 . Подставим в нее известные данные из условия, то есть числа a 1 и a 7 , имеем: 18 = 6 + 6 * d. Из этого выражения можно легко вычислить разность: d = (18 – 6) /6 = 2. Таким образом, ответили на первую часть задачи.

Чтобы восстановить последовательность до 7 члена, следует воспользоваться определением алгебраической прогрессии, то есть a 2 = a 1 + d, a 3 = a 2 + d и так далее. В итоге восстанавливаем всю последовательность: a 1 = 6, a 2 = 6 + 2=8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14, a 6 = 14 + 2 = 16, a 7 = 18.

Пример №3: составление прогрессии

Усложним еще сильнее условие задачи. Теперь необходимо ответить на вопрос, как находить арифметическую прогрессию. Можно привести следующий пример: даны два числа, например, – 4 и 5. Необходимо составить прогрессию алгебраическую так, чтобы между этими помещалось еще три члена.

Прежде чем начинать решать эту задачу, необходимо понять, какое место будут занимать заданные числа в будущей прогрессии. Поскольку между ними будут находиться еще три члена, тогда a 1 = -4 и a 5 = 5. Установив это, переходим к задаче, которая аналогична предыдущей. Снова для n-го члена воспользуемся формулой, получим: a 5 = a 1 + 4 * d. Откуда: d = (a 5 – a 1)/4 = (5 – (-4)) / 4 = 2,25. Здесь получили не целое значение разности, однако оно является рациональным числом, поэтому формулы для алгебраической прогрессии остаются теми же самыми.

Теперь добавим найденную разность к a 1 и восстановим недостающие члены прогрессии. Получаем: a 1 = – 4, a 2 = – 4 + 2,25 = – 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, что совпало с условием задачи.

Пример №4: первый член прогрессии

Продолжим приводить примеры арифметической прогрессии с решением. Во всех предыдущих задачах было известно первое число алгебраической прогрессии. Теперь рассмотрим задачу иного типа: пусть даны два числа, где a 15 = 50 и a 43 = 37. Необходимо найти, с какого числа начинается эта последовательность.

Формулы, которыми пользовались до настоящего времени, предполагают знание a 1 и d. В условии задачи об этих числах ничего неизвестно. Тем не менее выпишем выражения для каждого члена, о котором имеется информация: a 15 = a 1 + 14 * d и a 43 = a 1 + 42 * d. Получили два уравнения, в которых 2 неизвестные величины (a 1 и d). Это означает, что задача сводится к решению системы линейных уравнений.

Указанную систему проще всего решить, если выразить в каждом уравнении a 1 , а затем сравнить полученные выражения. Первое уравнение: a 1 = a 15 – 14 * d = 50 – 14 * d; второе уравнение: a 1 = a 43 – 42 * d = 37 – 42 * d. Приравнивая эти выражения, получим: 50 – 14 * d = 37 – 42 * d, откуда разность d = (37 – 50) / (42 – 14) = – 0,464 (приведены лишь 3 знака точности после запятой).

Зная d, можно воспользоваться любым из 2 приведенных выше выражений для a 1 . Например, первым: a 1 = 50 – 14 * d = 50 – 14 * (- 0,464) = 56,496.

Если возникают сомнения в полученном результате, можно его проверить, например, определить 43 член прогрессии, который задан в условии. Получим: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Небольшая погрешность связана с тем, что при вычислениях использовалось округление до тысячных долей.

Пример №5: сумма

Теперь рассмотрим несколько примеров с решениями на сумму арифметической прогрессии.

Пусть дана числовая прогрессия следующего вида: 1, 2, 3, 4, …,. Как рассчитать сумму 100 этих чисел?

Благодаря развитию компьютерных технологий можно эту задачку решить, то есть последовательно сложить все числа, что вычислительная машина сделает сразу же, как только человек нажмет клавишу Enter. Однако задачу можно решить в уме, если обратить внимание, что представленный ряд чисел является прогрессией алгебраической, причем ее разность равна 1. Применяя формулу для суммы, получаем: S n = n * (a 1 + a n) / 2 = 100 * (1 + 100) / 2 = 5050.

Любопытно отметить, что эта задача носит название “гауссовой”, поскольку в начале XVIII века знаменитый немецкий еще будучи в возрасте всего 10 лет, смог решить ее в уме за несколько секунд. Мальчик не знал формулы для суммы алгебраической прогрессии, но он заметил, что если складывать попарно числа, находящиеся на краях последовательности, то получается всегда один результат, то есть 1 + 100 = 2 + 99 = 3 + 98 = …, а поскольку этих сумм будет ровно 50 (100 / 2), то для получения правильного ответа достаточно умножить 50 на 101.

Пример №6: сумма членов от n до m

Еще одним типичным примером суммы арифметической прогрессии является следующий: дан такой чисел ряд: 3, 7, 11, 15, …, нужно найти, чему будет равна сумма его членов с 8 по 14.

Задача решается двумя способами. Первый из них предполагает нахождение неизвестных членов с 8 по 14, а затем их последовательное суммирование. Поскольку слагаемых немного, то такой способ не является достаточно трудоемким. Тем не менее предлагается решить эту задачу вторым методом, который является более универсальным.

Идея заключается в получении формулы для суммы алгебраической прогрессии между членами m и n, где n > m – целые числа. Выпишем для обоих случаев два выражения для суммы:

1. S m = m * (a m + a 1) / 2.
2. S n = n * (a n + a 1) / 2.

Поскольку n > m, то очевидно, что 2 сумма включает в себя первую. Последнее умозаключение означает, что если взять разность между этими суммами, и добавить к ней член a m (в случае взятия разности он вычитается из суммы S n), то получим необходимый ответ на задачу. Имеем: S mn = S n – S m + a m =n * (a 1 + a n) / 2 – m *(a 1 + a m)/2 + a m = a 1 * (n – m) / 2 + a n * n / 2 + a m * (1- m/2). В это выражение необходимо подставить формулы для a n и a m . Тогда получим: S mn = a 1 * (n – m) / 2 + n * (a 1 + (n – 1) * d) / 2 + (a 1 + (m – 1) * d) * (1 – m / 2) = a 1 * (n – m + 1) + d * n * (n – 1) / 2 + d *(3 * m – m 2 – 2) / 2.

Полученная формула является несколько громоздкой, тем не менее сумма S mn зависит только от n, m, a 1 и d. В нашем случае a 1 = 3, d = 4, n = 14, m = 8. Подставляя эти числа, получим: S mn = 301.

Как видно из приведенных решений, все задачи основываются на знании выражения для n-го члена и формулы для суммы набора первых слагаемых. Перед тем как приступить к решению любой из этих задач, рекомендуется внимательно прочитать условие, ясно понять, что требуется найти, и лишь затем приступать к решению.

Еще один совет заключается в стремлении к простоте, то есть если можно ответить на вопрос, не применяя сложные математические выкладки, то необходимо поступать именно так, поскольку в этом случае вероятность допустить ошибку меньше. Например, в примере арифметической прогрессии с решением №6 можно было бы остановиться на формуле S mn = n * (a 1 + a n) / 2 – m * (a 1 + a m) / 2 + a m , и разбить общую задачу на отдельные подзадачи (в данном случае сначала найти члены a n и a m).

Если возникают сомнения в полученном результате, то рекомендуется его проверять, как это было сделано в некоторых приведенных примерах. Как находить арифметическую прогрессию, выяснили. Если разобраться, то это не так сложно.

Если каждому натуральному числу n

поставить в соответствие действительное число a n

, то говорят, что задано числовую последовательность

:

a
1
,
a
2
,
a
3
, . . . ,
a n

, . . .
.

Итак, числовая последовательность — функция натурального аргумента.

Число a
1

называют первым членом последовательности

, число a
2
— вторым членом последовательности

, число a
3
— третьим

и так далее. Число a n

называют n-м членом последовательности

, а натуральное число n
— его номером

.

Из двух соседних членов a n

и a n
+1

последовательности член a n
+1

называют последующим

(по отношению к a n

), а a n

— предыдущим

(по отношению к a n
+1

).

Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.

Часто последовательность задают с помощью формулы n-го члена

, то есть формулы, которая позволяет определить член последовательности по его номеру.

Например,

последовательность положительных нечётных чисел можно задать формулой

a n
=
2n –
1,

а последовательность чередующихся 1

и -1

— формулой

b
n =
(-1) n
+1 .
◄

Последовательность можно определить рекуррентной формулой
,
то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.

Например,

если a
1
= 1

, а a n
+1
= a n
+ 5

a
1
= 1,

a
2
= a
1
+ 5 = 1 + 5 = 6,

a
3
= a
2
+ 5 = 6 + 5 = 11,

a
4
= a
3
+ 5 = 11 + 5 = 16,

a
5
= a
4
+ 5 = 16 + 5 = 21.

Если а 1
= 1, а 2
= 1, a n
+2
= a n
+ a n
+1
,
то первые семь членов числовой последовательности устанавливаем следующим образом:

a 1
= 1,

a 2
= 1,

a 3
= a 1
+ a 2
= 1 + 1 = 2,

a 4
= a 2
+ a 3
= 1 + 2 = 3,

a 5
= a 3
+ a 4
= 2 + 3 = 5,

a
6
= a
4
+ a
5
= 3 + 5 = 8,

a
7
= a
5
+ a
6
= 5 + 8 = 13. ◄

Последовательности могут быть конечными

и бесконечными

.

Последовательность называется конечной

, если она имеет конечное число членов. Последовательность называется бесконечной

, если она имеет бесконечно много членов.

Например,

последовательность двузначных натуральных чисел:

10, 11, 12, 13, . . . , 98, 99

конечная.

Последовательность простых чисел:

2, 3, 5, 7, 11, 13, . . .

бесконечная. ◄

Последовательность называют возрастающей

, если каждый её член, начиная со второго, больше чем предыдущий.

Последовательность называют убывающей

, если каждый её член, начиная со второго, меньше чем предыдущий.

Например,

2, 4, 6, 8, . . . , 2n
, . . .
— возрастающая последовательность;

1, 1 / 2 , 1 / 3 , 1 / 4 , . . . , 1 / n
, . . .
— убывающая последовательность. ◄

Последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают, называется монотонной последовательностью

.

Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.

Арифметическая прогрессия

Арифметической прогрессией

называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.

a
1
,
a
2
,
a
3
, . . . ,
a n
, . . .

является арифметической прогрессией, если для любого натурального числа n

выполняется условие:

a n
+1
= a n
+ d
,

где d

— некоторое число.

Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:

а 2
– a
1
= а 3
– a
2
= . . . = a n
+1
– a n
= d
.

Число d

называют разностью арифметической прогрессии
.

Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.

Например,

если a
1
= 3, d
= 4
, то первые пять членов последовательности находим следующим образом:

a 1
=3,

a 2
= a 1
+ d
= 3 + 4 = 7,

a 3
= a 2
+ d
= 7 + 4 = 11,

a 4
= a 3
+ d
= 11 + 4 = 15,

a
5
= a
4
+ d
= 15 + 4 = 19. ◄

Для арифметической прогрессии с первым членом a
1

и разностью d

её n

a n
= a 1
+ (n
– 1)d.

Например,

найдём тридцатый член арифметической прогрессии

1, 4, 7, 10, . . .

a 1
=1, d
= 3,

a 30
= a 1
+ (30 – 1)d =
1 + 29·
3 = 88. ◄

a n-1
= a 1
+ (n
– 2)d,

a n
= a 1
+ (n
– 1)d,

a n
+1
= a
1
+ nd
,

то, очевидно,

каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.

числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.

Например,

a n
= 2n
– 7

, является арифметической прогрессией.

Воспользуемся приведённым выше утверждением. Имеем:

a n
= 2n
– 7,

a n-1
= 2(n –
1) – 7 = 2n
– 9,

a n+1
= 2(n +
1) – 7 = 2n
– 5.

Следовательно,

a n+1 + a n-1	=	2n – 5 + 2n – 9	= 2n – 7 = a n ,
2	2

◄

Отметим, что n

-й член арифметической прогрессии можно найти не толь через a
1

, но и любой предыдущий a k

a n
= a k
+ (n
– k
)d
.

Например,

для a
5

можно записать

a 5
= a 1
+ 4d
,

a 5
= a 2
+ 3d
,

a 5
= a 3
+ 2d
,

a 5
= a 4
+ d
. ◄

a n
= a n-k
+ kd
,

a n
= a n+k
– kd
,

то, очевидно,

любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.

Кроме того, для любой арифметической прогрессии справедливо равенство:

a m + a n = a k + a l
,

m + n = k + l.

Например,

в арифметической прогрессии

1) a
10
= 28 = (25 + 31)/2 = (a
9
+
a
11
)/2;

2) 28 = a 10
= a 3
+ 7d
= 7 + 7·3 = 7 + 21 = 28;

3) a 10
= 28 = (19 + 37)/2 = (a 7 + a 13
)/2;

4) a 2 + a 12 = a 5 + a 9
,
так как

a 2 + a 12
= 4 + 34 = 38,

a 5 + a 9
= 13 + 25 = 38. ◄

S n
= a 1 + a 2 + a 3 + . . .
+
a n
,

первых n

членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:

Отсюда, в частности, следует, что если нужно просуммировать члены

a k
, a k
+1
, . . . ,
a n
,

то предыдущая формула сохраняет свою структуру:

Например,

в арифметической прогрессии 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .

S
10
= 1 + 4 + . . . + 28 = (1 +
28) ·

10/2 = 145;

10 + 13 + 16 + 19 + 22 + 25 + 28 = S
10
–
S
3
= (10 + 28
) ·

(10
– 4 + 1)/2 = 133. ◄

Если дана арифметическая прогрессия, то величины a
1
, a n
, d
, n
и
S

n

связаны двумя формулами:

Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.

Арифметическая прогрессия является монотонной последовательностью. При этом:

• если d
  > 0

  , то она является возрастающей;

• если d
  < 0

  , то она является убывающей;

• если d
  = 0

  , то последовательность будет стационарной.

Геометрическая прогрессия

Геометрической прогрессией

называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.

b
1
,
b
2
,
b
3
, . . . ,
b n
, . . .

является геометрической прогрессией, если для любого натурального числа n

выполняется условие:

b n
+1
= b n
·

q
,

где q
≠ 0

— некоторое число.

Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:

b
2
/ b
1
= b
3
/ b
2
= . . . = b n
+1
/ b n
= q
.

Число q

называют знаменателем геометрической прогрессии
.

Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.

Например,

если b
1
= 1, q
= -3
, то первые пять членов последовательности находим следующим образом:

b 1
= 1,

b 2
= b 1
·

q
= 1 ·

(-3) = -3,

b 3
= b 2
·

q
= -3 ·

(-3) = 9,

b 4
= b 3
·

q
= 9 ·

(-3) = -27,

b
5
= b
4
·

q
= -27 ·

(-3) = 81. ◄

b
1

и знаменателем q

её n

-й член может быть найден по формуле:

b n
= b
1
·

q n
-1
.

Например,

найдём седьмой член геометрической прогрессии 1, 2, 4, . . .

b
1
= 1, q
= 2,

b
7
= b
1
· q
6
=
1 · 2 6 = 64
. ◄

b n-1
= b 1
·

q n
-2 ,

b n
= b 1
·

q n
-1 ,

b n
+1
= b
1
·

q n
,

то, очевидно,

b n
2
= b n
-1
·

b n
+1
,

каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.

Так как верно и обратное утверждение, то имеет место следующее утверждение:

числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.

Например,

докажем, что последовательность, которая задаётся формулой b n
= -3 · 2 n

, является геометрической прогрессией. Воспользуемся приведённым выше утверждением. Имеем:

b n
= -3 · 2 n
,

b n
-1
= -3 · 2 n
-1
,

b n
+1
= -3 · 2 n
+1

.

Следовательно,

b n
2
= (-3 · 2 n
) 2 = (-3 · 2 n
-1
) · (-3 · 2 n
+1
) = b n
-1
·
b n
+1

,

что и доказывает нужное утверждение. ◄

Отметим, что n

-й член геометрической прогрессии можно найти не только через b
1

, но и любой предыдущий член b k

, для чего достаточно воспользоваться формулой

b n
= b k
·

q n
– k
.

Например,

для b
5

можно записать

b 5
= b 1
·

q
4 ,

b 5
= b 2
·

q 3
,

b 5
= b 3
·

q 2
,

b 5
= b 4
·

q
. ◄

b n
= b k
·

q n
– k
,

b n
= b n
–
k
·

q k
,

то, очевидно,

b n
2
= b n
–
k
·
b n
+
k

квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.

Кроме того, для любой геометрической прогрессии справедливо равенство:

b m
·
b n
=
b k
·
b l
,

m
+
n
=
k
+
l
.

Например,

в геометрической прогрессии

1) b
6
2 = 32 2 = 1024 = 16 ·

64 = b
5
·

b
7
;

2) 1024 = b
11
= b
6
·

q
5
= 32 ·

2 5 = 1024;

3) b
6
2 = 32 2 = 1024 = 8 ·

128 = b
4
·

b
8
;

4) b
2
·

b
7
=
b
4
·

b
5
,
так как

b
2
·

b
7
=
2 ·

64 = 128,

b
4
·

b
5
= 8 ·

16 = 128. ◄

S n
= b
1
+
b
2
+
b
3
+ . . . +
b n

первых n

членов геометрической прогрессии со знаменателем q
≠

0
вычисляется по формуле:

А при q
= 1

— по формуле

S n
= nb
1

Заметим, что если нужно просуммировать члены

b k
, b k
+1
, . . . ,
b n
,

то используется формула:

S n – S k -1 = b k + b k +1 + . . . + b n = b k ·	1 – q n – k +1	.
1 – q

Например,

в геометрической прогрессии 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .

S
10
= 1 + 2 + . . . + 512 = 1 ·

(1 – 2 10) / (1 – 2) = 1023;

64 + 128 + 256 + 512 = S
10
–
S
6
= 64 ·

(1 – 2 10-7+1) / (1 – 2) = 960. ◄

Если дана геометрическая прогрессия, то величины b
1
, b n
, q
, n
и S n

связаны двумя формулами:

Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.

Для геометрической прогрессии с первым членом b
1

и знаменателем q

имеют место следующие свойства монотонности

:

• прогрессия является возрастающей, если выполнено одно из следующих условий:

b
1
> 0

и

q
> 1;

b
1
< 0

и

0 < q
<
1;

• прогрессия является убывающей, если выполнено одно из следующих условий:

b
1
> 0

и

0 < q <
1;

b
1
< 0

и

q
> 1.

Если q <
0

, то геометрическая прогрессия является знакопеременной: её члены с нечётными номерами имеют тот же знак, что и её первый член, а члены с чётными номерами — противоположный ему знак. Ясно, что знакопеременная геометрическая прогрессия не является монотонной.

Произведение первых n

членов геометрической прогрессии можно рассчитать по формуле:

P n
= b 1 ·

b 2 ·

b 3 ·

. . . ·

b n
= (b 1 ·

b n
) n
/ 2
.

Например,

1 ·

2 ·


4 ·


8 ·


16 ·


32 ·


64 ·


128 = (1 ·

128) 8/2 = 128 4 = 268 435 456;

3 ·

6 ·

12 ·

24 ·

48 = (3 ·

48) 5/2 = (144 1/2) 5 = 12 5 = 248 832.◄

Бесконечно убывающая геометрическая прогрессия

Бесконечно убывающей геометрической прогрессией

называют бесконечную геометрическую прогрессию, модуль знаменателя которой меньше 1

, то есть

|q
| <
1

.

Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю

1 < q <
0

.

При таком знаменателе последовательность знакопеременная. Например,

1, – 1 / 2 , 1 / 4 , – 1 / 8 , . . . .

Суммой бесконечно убывающей геометрической прогрессии

называют число, к которому неограниченно приближается сумма первых n

членов прогрессии при неограниченном возрастании числа n

. Это число всегда конечно и выражается формулой

S = b 1 + b 2 + b 3 + . . . =	b 1	.
1 – q

Например,

10 + 1 + 0,1 + 0,01 + . . . = 10 / (1 – 0,1) = 11 1 / 9
,

10 – 1 + 0,1 – 0,01 + . . . = 10 / (1 + 0,1) = 9 1 / 11
. ◄

Связь арифметической и геометрической прогрессий

Арифметическая и геометрическая прогрессии тесно связаны между собой. Рассмотрим лишь два примера.

a
1
,
a
2
,
a
3
, . . .

d

, то

b a
1
, b a
2
, b a
3
, . . .
b d

.

Например,

1, 3, 5, . . .

— арифметическая прогрессия с разностью 2

и

7 1 , 7 3 , 7 5 , . . .

— геометрическая прогрессия с знаменателем 7

2

. ◄

b
1
,
b
2
,
b
3
, . . .

— геометрическая прогрессия с знаменателем q

, то

log a b 1
, log a b 2
, log a b 3
, . . .
— арифметическая прогрессия с разностью log a
q

.

Например,

2, 12, 72, . . .

— геометрическая прогрессия с знаменателем 6

и

lg

2, lg

12, lg

72, . . .
— арифметическая прогрессия с разностью lg

6

. ◄

Задачи по арифметической прогрессии существовали уже в глубокой древности. Они появлялись и требовали решения, поскольку имели практическую необходимость.

Так, в одном из папирусов Древнего Египта, имеющем математическое содержание, – папирусе Райнда (XIX век до нашей эры) – содержится такая задача: раздели десять мер хлеба на десять человек, при условии если разность между каждым из них составляет одну восьмую меры».

И в математических трудах древних греков встречаются изящные теоремы, имеющие отношение к арифметической прогрессии. Так, Гипсикл Александрийский (II век составивший немало интересных задач и добавивший четырнадцатую книгу к «Началам» Евклида, сформулировал мысль: «В арифметической прогрессии, имеющей четное число членов, сумма членов 2-ой половины больше суммы членов 1-ой на квадрату 1/2 числа членов».

Обозначается последовательность an. Числа последовательности называются ее членами и обозначаются обычно буквами с индексами, которые указывают порядковый номер этого члена (a1, a2, a3 … читается: «a 1-ое», «a 2-ое», «a 3-тье» и так далее).

Последовательность может быть бесконечной или конечной.

А что же такое арифметическая прогрессия? Под ней понимают получаемую сложением предыдущего члена (n) с одним и тем же числом d, являющимся разностью прогрессии.

Если d<0, то мы имеем убывающую прогрессию. Если d>0, то такая прогрессия считается возрастающей.

Арифметическая прогрессия называется конечной, если учитываются только несколько ее первых членов. При очень большом количестве членов это уже бесконечная прогрессия.

Задается любая арифметическая прогрессия следующей формулой:

an =kn+b, при этом b и k – некоторые числа.

Абсолютно верно утверждение, являющееся обратным: если последовательность задается подобной формулой, то это точно арифметическая прогрессия, которая имеет свойства:

1. Каждый член прогрессии – среднее арифметическое предыдущего члена и последующего.
2. Обратное: если, начиная со 2-ого, каждый член – среднее арифметическое предыдущего члена и последующего, т.е. если выполняется условие, то данная последовательность – арифметическая прогрессия. Это равенство одновременно является и признаком прогрессии, поэтому его, как правило, называют характеристическим свойством прогрессии.
   Точно так же верна теорема, которая отражает это свойство: последовательность – арифметическая прогрессия только в том случае, если это равенство верно для любого из членов последовательности, начиная со 2-ого.

Характеристическое свойство для четырёх любых чисел арифметической прогрессии может быть выражено формулой an + am = ak + al, если n + m = k + l (m, n, k – числа прогрессии).

В арифметической прогрессии любой необходимый (N-й) член найти можно, применяя следующую формулу:

К примеру: первый член (a1) в арифметической прогрессии задан и равен трём, а разность (d) равняется четырём. Найти нужно сорок пятый член этой прогрессии. a45 = 1+4(45-1)=177

Формула an = ak + d(n – k) позволяет определить n-й член арифметической прогрессии через любой ее k-тый член при условии, если он известен.

Сумма членов арифметической прогрессии (подразумевается 1-ые n членов конечной прогрессии) вычисляется следующим образом:

Sn = (a1+an) n/2.

Если известны и 1-ый член, то для вычисления удобна другая формула:

Sn = ((2a1+d(n-1))/2)*n.

Сумма арифметической прогрессии, которая содержит n членов, подсчитывается таким образом:

Выбор формул для расчетов зависит от условий задач и исходных данных.

Натуральный ряд любых чисел, таких как 1,2,3,…,n,…- простейший пример арифметической прогрессии.

Помимо арифметической прогрессии существует еще и геометрическая, которая обладает своими свойствами и характеристиками.

Или арифметическая – это вид упорядоченной числовой последовательности, свойства которой изучают в школьном курсе алгебры. В данной статье подробно рассмотрен вопрос, как найти сумму арифметической прогрессии.

Что это за прогрессия?

Прежде чем переходить к рассмотрению вопроса (как найти сумму арифметической прогрессии), стоит понять, о чем пойдет речь.

Любая последовательность действительных чисел, которая получается путем добавления (вычитания) некоторого значения из каждого предыдущего числа, называется алгебраической (арифметической) прогрессией. Это определение в переводе на язык математики принимает форму:

Здесь i – порядковый номер элемента ряда a i . Таким образом, зная всего одно начальное число, можно с легкостью восстановить весь ряд. Параметр d в формуле называется разностью прогрессии.

Можно легко показать, что для рассматриваемого ряда чисел выполняется следующее равенство:

a n = a 1 + d * (n – 1).

То есть для нахождения значения n-го по порядку элемента следует n-1 раз добавить разность d к первому элементу a 1 .

Чему равна сумма арифметической прогрессии: формула

Прежде чем приводить формулу для указанной суммы, стоит рассмотреть простой частный случай. Дана прогрессия натуральных чисел от 1 до 10, необходимо найти их сумму. Поскольку членов в прогрессии немного (10), то можно решить задачу в лоб, то есть просуммировать все элементы по порядку.

S 10 = 1+2+3+4+5+6+7+8+9+10 = 55.

Стоит учесть одну интересную вещь: поскольку каждый член отличается от последующего на одно и то же значение d = 1, то попарное суммирование первого с десятым, второго с девятым и так далее даст одинаковый результат. Действительно:

11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.

Как видно, этих сумм всего 5, то есть ровно в два раза меньше, чем число элементов ряда. Тогда умножая число сумм (5) на результат каждой суммы (11), вы придете к полученному в первом примере результату.

Если обобщить эти рассуждения, то можно записать следующее выражение:

S n = n * (a 1 + a n) / 2.

Это выражение показывает, что совсем не обязательно суммировать подряд все элементы, достаточно знать значение первого a 1 и последнего a n , а также общего числа слагаемых n.

Считается, что впервые до этого равенства додумался Гаусс, когда искал решение на заданную его школьным учителем задачу: просуммировать 100 первых целых чисел.

Сумма элементов от m до n: формула

Формула, приведенная в предыдущем пункте, дает ответ на вопрос, как найти сумму арифметической прогрессии (первых элементов), но часто в задачах необходимо просуммировать ряд чисел, стоящих в середине прогрессии. Как это сделать?

Ответить на этот вопрос проще всего, рассматривая следующий пример: пусть необходимо найти сумму членов от m-го до n-го. Для решения задачи следует представить заданный отрезок от m до n прогрессии в виде нового числового ряда. В таком представлении m-й член a m будет первым, а a n станет под номер n-(m-1). В этом случае, применяя стандартную формулу для суммы, получится следующее выражение:

S m n = (n – m + 1) * (a m + a n) / 2.

Пример использования формул

Зная, как найти сумму арифметической прогрессии, стоит рассмотреть простой пример использования приведенных формул.

Ниже дана числовая последовательность, следует найти сумму ее членов, начиная с 5-го и заканчивая 12-м:

Приведенные числа свидетельствуют, что разность d равна 3. Используя выражение для n-го элемента, можно найти значения 5-го и 12-го членов прогрессии. Получается:

a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;

a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.

Зная значения чисел, стоящих на концах рассматриваемой алгебраической прогрессии, а также зная, какие номера в ряду они занимают, можно воспользоваться формулой для суммы, полученной в предыдущем пункте. Получится:

S 5 12 = (12 – 5 + 1) * (8 + 29) / 2 = 148.

Стоит отметить, что это значение можно было получить иначе: сначала найти сумму первых 12 элементов по стандартной формуле, затем вычислить сумму первых 4 элементов по той же формуле, после этого вычесть из первой суммы вторую.

        Суперполезная формула! Позволяет легко и просто (и главное — быстро!) искать любой член арифметической прогрессии! Да-да, любой! Какой хотите.) А заодно и массу других самых разных задач по прогрессии решать. Имеет смысл освоить и разобраться, правда?

        Вот поэтому осваиваем и разбираемся. В этом уроке.)

Вывод и смысл формулы n-го члена

        Итак, прошу любить и жаловать:

a_n = a₁ + (n-1)·d

        Это и есть формула n-го члена арифметической прогрессии, собственной персоной.) Какие-то индексы, буковки непонятные. Ничего страшного! Сейчас всё расшифрую.

        В формуле:

        a₁ — первый член арифметической прогрессии;

        d — разность арифметической прогрессии;

        n — номер члена;

        a_n — энный (n-й) член арифметической прогрессии.

        Как вы видите, большая часть входящих в формулу буковок (первый член, разность прогрессии, номер члена) уже должна быть вам хорошо знакома из прошлого урока. Если не читали, настоятельно рекомендую заглянуть. Там всё просто и доступно. Осталось лишь разобраться, что же такое n-й член.

        Мы с вами знаем (надеюсь), что любую арифметическую прогрессию в общем виде всегда можно записать в виде последовательности чисел:

        a₁, a₂, a₃, a₄, a₅, …

        Символ a₁ означает первый член прогрессии, a₂ — второй член, a₅ — пятый и так далее. Если нас интересует, скажем, десятый член прогрессии, то работаем с a₁₀. Если сто тридцатый, то, соответственно, с a₁₃₀. Элементарно, Ватсон!)

        А как можно обозначить в общем виде любой член арифметической прогрессии прогрессии с любым номером? Тоже элементарно! Вот так:

        a_n

        Это и есть n-й член арифметической прогрессии. Под буковкой n здесь скрываются сразу все номера членов: и 1, и 23 и 101 — все без исключения!

        И что нам даёт такая запись? Казалось бы, всего лишь вместо цифры буковка появилась — и что из этого? А вот что.

        Запись эта представляет собой очень мощный инструмент для работы с арифметической прогрессией. Сомневаетесь? Не надо.) Используя обозначение a_n, мы можем легко и просто искать любой член любой арифметической прогрессии! Как? Читаем дальше.)

        Возвращаемся снова к нашей формуле:

a_n = a₁ + (n-1)·d

        Со всеми обозначениями мы успешно разобрались, а теперь разбираемся, в чём же её суть.

        Эта формула позволяет нам найти любой член арифметической прогрессии по его номеру “n“.

        Заманчиво, правда? Знаем номер члена — сразу же можем найти и сам этот член! Естественно, для этого нам надо знать ещё первый член a₁ и разность прогрессии d. Ну так без этих двух ключевых параметров конкретную прогрессию и не задашь вовсе.

        Формула эта связывает четыре главных параметра любой арифметической прогрессии — а_n, a₁, d и n. Именно вокруг этих четырёх параметров и крутятся все-все задачки по прогрессии!

        Откуда же берётся эта формула и как её запомнить? А то уж больно часто сомнения грызут — то ли n там, то ли n-1, то ли n+1… Особенно на контрольных и экзаменах.

        Спокойствие! Сейчас мы с вами эту формулку выведем! Не очень строго, правда, но зато с полным пониманием всего происходящего. Что, как и откуда. И у вас сразу же отпадут все сомнения!

        Итак, рисуем числовую ось и последовательно отмечаем на ней члены нашей прогрессии:

        

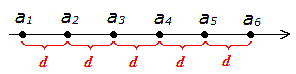
        А теперь смотрим на рисунок и соображаем. Чему равен второй член прогрессии?

        Второй член равен первому члену плюс одно d:

        a₂ = a₁ + 1·d

        А третий член чему равен?

        Не вопрос! Третий член равен первому члену плюс два d:

        a₃ = a₁ + 2·d

        Ну как, улавливаете закономерность? Я же не просто так некоторые слова и цифры выделяю жирным шрифтом! Нет? Что ж, ладно. Ещё один шаг.)

        Чему равен четвёртый член?

        Четвёртый член равен первому члену плюс три d:

        a₄ = a₁ + 3·d

        Пора бы уже догадаться, что количество интервалов (т.е. d) всегда на единичку меньше, чем номер нужного нам члена n. Поэтому до номера n количество интервалов всегда будет n-1.

        Стало быть, наша формула, уже безо всяких сомнений, будет вот такой:

a_n = a₁ + (n-1)·d

        Вот и весь секрет.)

        Совсем строгое доказательство данной формулы проводится так называемым методом математической индукции. Но метод этот — для особых гурманов.) Не каждый с ходу разберётся и поймёт, что к чему. А вот по картинке всё просто и наглядно! Да и вообще, картинка — очень мощный инструмент решения многих математических задач! И не только по прогрессиям. Так что не пренебрегаем ими. Скажем, в сложной боевой обстановке ЕГЭ вы переволновались и подзабыли случайно эту формулу. Ну, вот не помните, с кем не бывает! Ничего страшного. Есть пара-тройка минуток времени – рисуем картинку, отмечаем члены прогрессии и промежутки между членами — и всё сразу становится как на ладони!

        Разумеется, всё от конкретной задачи зависит. Бывают и такие задачи, рисовать картинку к которым весьма затруднительно, а то и вовсе невозможно. Тогда — только формула, да…) Ибо формула — это тяжёлая артиллерия, позволяющая подключить к решению задачи весь мощный арсенал математики — уравнения, неравенства, системы и т.д. Картинку ведь в уравнение не вставишь!

        Ну что, коли уж мы заговорили о задачках, то пора бы уже и порешать!

Решение задач с помощью формулы n-го члена арифметической прогрессии.

        Прямое применение формулы.

        Начнём с прямого применения формулы. В самом конце прошлого урока была вот такая задачка:

        В арифметической прогрессии известно, что a₁ = 4 и d = 0,4. Найдите a₁₄₁.

        Конечно, эту задачку можно и безо всяких формул решить. Исходя из смысла арифметической прогрессии. Прибавлять себе по 0,4 да считать. Часок-другой…)

        Зато по формуле решение осуществляется в одну строчку и занимает меньше минуты! Можете засекать время.)

        Итак, у нас имеются все данные для применения формулы.

        Известен первый член: a₁ = 4.

        Известна также разность прогрессии: d = 0,4.

        Остаётся только сообразить, чему равен номер члена n. Не вопрос! Нам надо найти a₁₄₁. Так прямо и пишем:

        a₁₄₁ =

        А вот здесь сосредотачиваемся! Вместо индекса n у нас появилось конкретное число 141. Что вполне естественно. Ибо нас интересует член прогрессии номер сто сорок один. Вот именно это и будет наше n! Именно это значение n = 141 мы и подставим в формулу n-го члена в скобки.

        Подставляем все наши данные в формулу и считаем:

        a₁₄₁ = 4 + (141-1)·0,4 = 4+56 = 60

        Вот и всё, никаких фокусов. Так же быстро можно найти и четыреста третий член, и тысяча первый — любой! Какой хотим, такой и отыщем. Просто подставляем нужный номер в формулу вместо индекса n и в скобки. И считаем.)

        Рассмотрим теперь задачку похитрее.

        В арифметической прогрессии с разностью 3 пятнадцатый член равен 50. Найдите первый член этой прогрессии.

        Ну и как вам? Знаете, с чего начинать? Если знаете — вперёд и с песнями. Не знаете? Что ж, тогда подскажу.

        Пишем формулу n-го члена арифметической прогрессии!

        Да-да! Прямо на черновике или в тетрадке.)

        a_n = a₁ + (n-1)·d

        А теперь глядим внимательно на нашу формулу и соображаем, какие данные у нас уже есть, а чего не хватает.

        Во-первых, нам известна разность прогрессии d:

        d = 3

        Во-вторых, нам известен пятнадцатый член прогрессии. Так и пишем:

        a₁₅ = 50

        Всё? Не-а! У нас есть ещё номер n! Дело в том, что в условии a₁₅ = 50 скрыты сразу два параметра прогрессии. Это, во-первых, значение самого пятнадцатого члена (50) и, во-вторых, его номер (15). То есть, n=15.

        Вот теперь уже можно подставить все известные нам данные в формулу:

        50 = a₁ + 3·(15-1)

        Решаем это простенькое линейное уравнение и получаем ответ:

        a₁ = 8

        Вот и все дела.)

        Ещё одна популярная задачка:

        Найдите разность арифметической прогрессии (a_n), если

        a₁ = 6; a₂₁ = -14.

        Первый шаг тот же самый: пишем формулу n-го члена арифметической прогрессии!

        a_n = a₁ + (n-1)·d

        А теперь снова соображаем, что нам дано по условию задачи:

        a₁ = 6

        a₂₁ = -14

        n = 21

        Вот и всё. Всю ценную информацию из условия скачали. Подставляем наши известные величины в формулу и считаем банальную арифметику:

        -14 = 6 + (21-1)·d

        -14 = 6 + 20d

        -20 = 20d

        d = -1

        Всё. Это правильный ответ.)

        Так, задачки на поиск a_n, a₁ и d порешали. Осталось научиться ещё номер члена находить.)

        Известно, что число 43 является членом арифметической прогрессии (a_n) c первым членом, равным 3 и разностью 0,4. Найдите номер этого члена.

        Вы удивитесь, но первый шаг снова точно такой же.

        Пишем формулу!

        a_n = a₁ + (n-1)·d

        На первый взгляд кажется, что здесь две неизвестные величины — a_n и n. Но a_n — это какой-то член арифметической прогрессии под номером n. И этот член нам известен! Это 43. Нам неизвестен номер n этого члена. Так этот самый номер, как раз, и требуется отыскать!

        Подставляем член прогрессии 43 в формулу n-го члена вместе с остальными известными нам параметрами:

        43 = 3 + (n-1)·0,4

        Считаем простецкую арифметику и выражаем номер n:

        (n-1)·0,4 = 40

        n-1 = 100

        n = 101

        Готово дело.)

        Как вы видите, запись формулы в общем виде и подстановка в неё известных величин — весьма популярный приём в решении очень многих задач на прогрессии! Если вы, конечно, умеете выражать переменную из формулы. Ну так без этого умения математику можно и вовсе не изучать. Как, впрочем, и остальные точные науки тоже, да…

        А теперь ещё одна задачка на эту тему, но более творческая.

        Определите, будет ли число 74 членом арифметической прогрессии

        (a_n): -5,6; -4; -2,4; …

        Снова (да-да!) пишем формулу:

        a_n = a₁ + (n-1)·d

        Начинаем подставлять известные нам данные. Гм… не подставляется что-то…

        Что, не видите никаких данных? Серьёзно? Ну, тогда срочно к окулисту. Без обид.) Что же всё-таки можно увидеть из предложенной нам последовательности? Первый член видим? Видим! Это -5,6. А разность d? Пока не видим, но… её можно посчитать, да.) Если, конечно, вы в курсе, что такое разность арифметической прогрессии:

        d = -4 — (-5,6) = 1,6

        Ну вот, уже кое-что. Осталось лишь разобраться с неизвестным нам номером n и загадочным числом 74. В предыдущей задачке нам прямым текстом было указано, что дан именно член прогрессии. А здесь про число 74 ничего непонятно — член оно, не член… Что делать?

        Что-что… Включим смекалку! Мы предположим, что число 74 — это всё-таки член нашей прогрессии! С неизвестным номером n. И снова попробуем отыскать, найти этот номер! Смело подставляем в формулу все наши числа:

        74 = -5,6 + (n-1)·1,6

        И выражаем n:

        (n-1)·1,6 = 79,6

        n — 1 = 49,75

        n = 50,75

        Во как! Номер получился дробный! А дробных номеров в прогрессиях не бывает. Уравнению ведь без разницы, с какими числами работать — целыми, дробными, отрицательными. Уравнение со всякими работает.) Вот оно нам честно и ответило: “В этой арифметической прогрессии число 74 имеет номер 50,75!”

        И какой же вывод можно сделать из полученного результата? Да! Число 74 не является членом нашей прогрессии! Оно находится где-то между пятидесятым и пятьдесят первым членами. Вот, если бы наш номер получился натуральным, то тогда — да, число 74 было бы членом нашей прогрессии. С найденным номером n.

        А так, ответ задачи: нет.

        Более сложные задачи.

        Рассмотрим теперь более хитрые задачки на применение формулы n-го члена. Например, такую:

        Известно, что в арифметической прогрессии a₃ = 2,1 и a₆ = 6,3. Найдите a₄.

        Эту задачку мы с вами уже решали в прошлом уроке. Для её успешного решения мы рисовали с вами вот такую незамысловатую картинку:

        

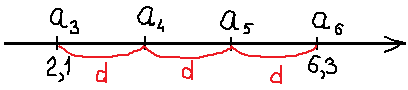
        Из этой картинки мы легко определили разность прогрессии d и затем так же легко, прямо по смыслу арифметической прогрессии, посчитали нужный нам четвёртый член.

        Получили ответ: a₄ = 3,5.

        Вспомнили? Отлично!

        То был графический способ. А сейчас мы с вами решим эту же задачку, но другим способом! Аналитическим.) С помощью формулы n-го члена, да. Нам ведь с формулой размяться нужно, правда?) Вот и разминаемся.

        Итак, что нам дано в условии задачи? Нам даны два члена некоторой арифметической прогрессии. А именно — третий и шестой её члены.

        Вот и расписываем их по формуле n-го члена!

        Именно так! Просто берём формулу n-го члена арифметической прогрессии и поочерёдно подставляем в неё известные нам данные для каждого члена.

        Для третьего члена a₃ = 2,1 получим:

        2,1 = a₁ + (3-1)·d

        2,1 = a₁ + 2d

        Так, отлично. Одно уравнение составилось.

        То же самое проделываем и для шестого члена a₆ = 6,3.

        Получим:

        6,3 = a₁ + (6-1)·d

        6,3 = a₁ + 5d

        Итак, мы получили два уравнения. Эти два уравнения относятся к одной и той же прогрессии. Стало быть, они должны выполняться одновременно. И, следовательно, они должны быть записаны в виде системы уравнений.

        Вот так:

        

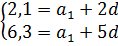
        Всё. Мы перевели задание по арифметической прогрессии в чистую алгебру. И дальше можно уже временно вообще забыть про прогрессию и просто решить эту систему уравнений.

        Системка не самая трудная. Решаем самым простым способом — подстановкой. Из первого уравнения выражаем a₁ и подставляем во второе:

        

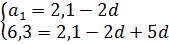
        Приводим подобные во втором уравнении и получаем:

        

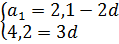
        Из второго уравнения легко находится d:

        d = 1,4

        Подставляем d = 1,4 в первое уравнение и получаем первый член:

        a₁ = 2,1-2·1,4

        a₁ = 2,1-2,8

        a₁ = -0,7

        Вот и отлично. Знаем первый член a₁, знаем разность d. И теперь мы без проблем можем найти любой интересующий нас член прогрессии. В том числе и четвёртый, да.)

        Пишем формулу n-го члена для n = 4:

        a₄ = a₁ + (4-1)·d = a₁ + 3d

        Подставляем найденные числа и считаем:

        a₄ = a₁ + 3d = -0,7+3·1,4 = -0,7+4,2 = 3,5

        Вот и всё. Как и следовало ожидать, ответ получился тем же самым.)

        Ну как, хлопотно? Да, я согласен. Но зато аналитическому способу (алгебре) любые задачи по плечу! Если её знать, конечно.) А вот картинка годится лишь для маленьких кусочков прогрессии.

        Например, такая задачка:

        Известно, что в арифметической прогрессии a₈₁ = 26 и a₂₇₁ = 83. Найдите a₁₁.

        Что, неохота картинку рисовать да безошибочно пальчиком считать промежутки? И правильно! Не надо.) Зато второму способу, алгебре, совершенно безразлично, какие числа стоят в задании! Большие числа или маленькие… Алгебра — это тяжёлая артиллерия. С любыми числами справляется.)

        Снова, как и в предыдущей задаче, расписываем каждый член прогрессии по формуле n-го члена:

        26 = a₁ + 80d

        83 = a₁ + 270d

        Объединяем эти уравнения в систему:

        

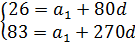
        А дальше решаем точно так же, как и в предыдущей задаче. Один в один. Дорешайте, чего уж там!

        Должно получиться:

        a₁₁ = 5

        Рассмотрим ещё более хитрую задачку. С подвохом. Если невнимательно читать задание…

        Сумма первого и седьмого членов возрастающей арифметической прогрессии равна 14, а произведение третьего и шестого членов равно 10. Найдите двадцатый член прогрессии.

        Что, внушает? Решение по картинке и “на пальцах” не катит, да… Попробуем перевести всё задание в чистую алгебру? А та — всё сможет.)

        Ничего не боимся и используем главное правило всей математики: “Не знаешь, что нужно, делай что можно.”

        Вот и прикидываем, что в этой эпичной задачке можно сделать. Можно хотя бы расписать все данные нам члены (1-й, 7-й, 3-й, 6-й) в виде формул n-го члена, подставляя те числа, которые даны в условии.

        Вот и расписываем каждый член! Прямо по формуле!

        Ну, с первым членом всё и так ясно. Его вообще расписывать не надо.) Идём дальше.

        Для седьмого члена мы можем записать:

        a₇ = a₁ + (7-1)·d = a₁ + 6d

        Третий член:

        a₃ = a₁ + (3-1)·d = a₁ + 2d

        Шестой член:

        a₆ = a₁ + (6-1)·d = a₁ + 5d

        А дальше снова читаем задачку и скачиваем всю остальную полезную информацию. А именно — связь между членами.

        Сумма первого и седьмого членов равна 14:

        a₁ + a₁ + 6d = 14

        2a₁ + 6d = 14

        Так, одно уравнение готово. Читаем дальше.)

        Произведение третьего и шестого членов равно 10:

        (a₁ + 2d)(a₁ + 5d) = 10

        Получили два уравнения. Раз они относятся к одной и той же прогрессии, то должны выполняться одновременно. Объединяем наши полученные уравнения в систему:

        

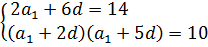
        Вот и всё. Всю ценную информацию по прогрессии мы скачали и записали в виде системы уравнений. А дальше дело за алгеброй. Решение систем —  уже её работа. И наша с вами, к сожалению, тоже, да…

        Начнём с первого уравнения. Оно попроще будет. Выражаем из него a₁. Для этого переносим 6d вправо и делим всё на двойку. Обычные тождественные преобразования, да.)

        2a₁ = 14 — 6d

        a₁ = 7 — 3d

        Теперь, ясное дело, подставляем это выражение во второе уравнение:

        (7 — 3d + 2d)(7 — 3d + 5d) = 10

        Приводим подобные в скобках:

        (7 — d)(7 + 2d) = 10

        Раскрываем скобки, приводим подобные и собираем всё слева:

        49 + 14d — 7d — 2d² — 10 = 0

        -2d² + 7d + 39 = 0

        Решаем это квадратное уравнение (помножив обе части на минус 1) и получаем корни:

        d₁ = -3

        d₂ = 6,5

        А вот и обещанный подводный камень! Что дальше? Получилось два значения разности d! Какое из них выбрать? Тупик?

        Вовсе нет! Просто ещё раз внимательно читаем условие задачи в поисках дополнительной информации! Там зачем-то употребляется слово “возрастающей”. А составители задач излишним словоблудием обычно не занимаются, да.) Вспоминаем из первого урока, что у возрастающей арифметической прогрессии разность всегда положительна.

        Стало быть, из двух вариантов выбираем d = 6,5.

        Так, отлично. Разность прогрессии найдена. По первому уравнению системы считаем первый член:

        a₁ = 7 — 3d = 7 – 3·6,5 = -3,5

        Вот, практически, и всё. Что там от нас в задаче требуют? Двадцатый член? Да, пожалуйста!

        a₂₀ = a₁ + (20 — 1)·d = -3,5 + 19·6,5 = 120

        Ответ: 120

        А теперь мы рассмотрим с вами ещё несколько коротких и простых задачек. Они, по своей сути, и вправду очень простые, но многих учеников ставят в тупик своей непривычностью и нестандартной подачей условия. Вот и пугается народ. И спотыкается на ровном месте, теряя драгоценные баллы на экзамене…

        Работаем с видоизменённой формулой!

        Первым делом, давайте с вами вспомним, как мы обычно задаём любую арифметическую прогрессию? Варианта два:

        1) Отдельными параметрами прогрессии (скажем, a₁ и d или a₁ и a_n и т.п.);

        2) В виде последовательности чисел.

        Например:

        (a_n): 1, 5, 9, 13, 17, …

        К этим двум вариантам задания прогрессии мы уже попривыкли.) Но оказывается, есть ещё и третий вариант задания арифметической прогрессии! А именно – в виде формулы n-го члена. Да-да! Любую арифметическую прогрессию в общем виде можно задать формулой её n-го члена. Для каждой прогрессии — своей.)

        Смотрите сами.

        Пусть, например, в арифметической прогрессии a₁ = 3 и d = 5. Запишем для неё формулу n-го члена:

        a_n = 3 + 5·(n-1)

        Раскрываем скобки и упрощаем:

        a_n = -2 + 5n

        Это выражение — тоже формула n-го члена! Только не общая, а уже для конкретной прогрессии. Задачки с такой видоизменённой формулой очень часто попадаются на экзамене. И частенько народ, не подумав, тут же радостно ответ пишет и… приехали.) Чем же эта формула так коварна? Здесь есть подводный камень: некоторые, глядя на формулу, сразу думают, что первый член — минус два. Хотя реально первый член — тройка…

        Например, такая задачка на основе реального варианта ОГЭ:

        Арифметическая прогрессия задана условием a_n = 5 — 1,5n. Найдите сумму первого и девятого её членов.

        Здесь прогрессия задана не совсем привычно. Формула какая-то… Ничего страшного. Бывает.) Эта формула — тоже формула n-го члена арифметической прогрессии. Она тоже позволяет найти любой член прогрессии по его номеру!

        Вот и ищем наши члены. Начинаем с первого члена. Тот, кто думает, что первый член — пятёрка, фатально ошибается! Потому что формула в задаче — видоизменённая. И первый член прогрессии в ней спрятан. Не беда, сейчас мы его отыщем.)

        Просто берём и подставляем n=1 в формулу:

        a₁ = 5 — 1,5·1 = 3,5

        Вот так! Первый член — три с половиной! А вовсе не пятёрка…

        Подставляем теперь n=9 и считаем девятый член:

        a₉ = 5 — 1,5·9 = -8,5

        Ну и считаем требуемую сумму:

        a₁ + a₉ = 3,5 + (-8,5) = -5

        Ответ: -5

        Вот и все дела. Теперь, надеюсь, видоизменённая формула n-го члена арифметической прогрессии не поставит вас навечно в тупик.)

        Работаем с рекуррентной формулой!

        Рассмотрим теперь ещё один сюрприз. Частенько в задачах на арифметическую прогрессию встречается ещё одно обозначение — a_n+1. Это, как вы уже, наверное, догадались, “эн плюс первый” член прогрессии. Всё очень просто. Это член прогрессии, номер которого больше номера n на единичку. И всё.) Например, если в какой-нибудь задаче мы берём за a_n третий член, то a_n+1 будет четвёртым членом. И тому подобное.

        Чаще всего обозначение a_n+1 встречается в так называемых рекуррентных формулах. Не пугаемся этого страшного слова!) Рекуррентная формула – это всего лишь способ задания любого члена арифметической прогрессии через предыдущий член. И всё.) Это ещё один, четвёртый способ задания арифметической прогрессии. Поработаем и с ним.

        Допустим, арифметическая прогрессия нам задана рекуррентной формулой:

        a_n+1 = a_n+4

        a₁ = 3

        Можно посчитать второй член этой прогрессии? Легко! Если за a_n принять первый член прогрессии a₁, то второй член будет, как раз, a₁₊₁ = a₂. Первый член нам уже дан отдельно. Это тройка. Вот и считаем по формуле:

        a₂ = a₁ + 4 = 3+4 = 7

        Третий член можно посчитать через второй:

        a₃ = a₂ + 4 = 7+4 = 11

        Четвёртый можно посчитать через третий, пятый – через четвёртый, и так далее. Продолжая эту цепочку, можно таким способом добраться до любого интересующего нас члена. А как можно посчитать сразу, скажем, 25-й член a₂₅? К сожалению, никак… Пока предыдущий, 24-й член, не узнаем, 25-й не посчитаем. В этом и состоит принципиальное отличие рекуррентной формулы от формулы n-го члена. Рекуррентная формула работает по принципу домино, только через предыдущий член, в то время как формула n-го члена — через первый и позволяет сразу находить любой член прогрессии по его номеру. Не просчитывая всю последовательность по порядочку.)

        Кстати, а как вы думаете, почему в рекуррентной формуле

        a_n+1 = a_n+4

        a₁ = 3

        первый член a₁ нам задан отдельно? Ответ прост: для последовательного подсчёта членов рекуррентным способом, нам всегда необходима некая точка отсчёта. А именно — некоторый стартовый член, с которого следует начинать. Это, кстати, не обязательно может быть именно первый член. Можно начать счёт со второго члена, с третьего — с любого! С того члена, который дополнительно указан в условии в качестве стартового.

        Подведём итог. Как вы видите, если число последовательно просчитываемых членов не очень большое (скажем, три или пять), то рекуррентные формулы вовсе не так уж и плохи на практике. А вот если считать предстоит много, то уже начинаются неудобства, да…

        К счастью, в арифметической прогрессии рекуррентную формулу очень легко превратить в обычную. Как? Просто посчитать пару последовательных членов, вычислить разность d, найти первый член (если надо), записать формулу n-го члена в привычном виде, да и работать с ней.

        В ОГЭ подобные задания частенько встречаются. Например, такая задачка:

        Арифметическая прогрессия задана условиями:

        a_n+1 = a_n+2,8

        a₂ = 3

        Найдите 112-й член этой прогрессии.

        Здесь прогрессия задана рекуррентным способом. Ну и ничего страшного. Любой член прогрессии можно посчитать через предыдущий. Второй член нам уже известен. Это тройка. Через него можно посчитать третий член, через третий — четвёртый и так далее вплоть до нужного нам 112-го члена. Мрачноватая перспектива, вообще-то.) А времени на экзамене немного, да…

        Но! У нас же есть такой мощный инструмент, как формула n-го члена! Которая сразу выдаст нам любой член с любым номером! Вот и запустим её в дело. Для начала просто запишем в тетрадке:

        a_n = a₁ + (n-1)·d

        А теперь смотрим на формулу и соображаем, какие данные у нас уже есть, а что нужно дополнительно посчитать.

        Пока у нас есть только номер члена n = 112. А вот первого члена a₁ и разности d — пока не хватает. Не беда, сейчас отыщем!

        Читаем ещё раз задачку и видим, что:

        a_n+1 = a_n+2,8    и    a₂ = 3

        Можно посчитать третий член по известному второму? Можно!

        Считаем:

        a₃ = a₂+2,8 = 3+2,8 = 5,8

        Ну вот. Теперь нам стали известны два последовательных члена прогрессии — второй и третий. Считаем разность прогрессии:

        d = a₃ — a₂ = 5,8 — 3 = 2,8

        Внимание! Ещё раз напоминаю, что разность прогрессии d — это не просто разница между двумя соседними членами! Это именно разность между членом и предыдущим членом! Стало быть, для определения разности, надо всегда от члена с большим номером отнять член с меньшим номером.

        Кстати сказать, а можно ли было сразу найти разность прогрессии, не вычисляя третий член? Можно! Давайте ещё разок посмотрим на нашу рекуррентную формулу:

        a_n+1 = a_n+2,8

        Переводим формулу на человеческий язык: каждый член (a_n+1) больше предыдущего члена (a_n) на 2,8. Прямо по смыслу и определению арифметической прогрессии, величина 2,8 и есть разность d! Вот и всё.)

        Так, разность прогрессии найдена. Осталось отыскать первый член. Не вопрос! Второй член нам уже дан по условию, а разность мы нашли только что. Вот и отнимаем разность прогрессии от второго члена:

        a₁ = a₂ — d = 3 — 2,8 = 0,2

        Вот и финишная прямая. Подставляем все чиселки в формулу n-го члена и считаем 112-й член:

        a₁₁₂ = a₁ + (112-1)·d = 0,2 + 111·2,8 = 311

        Ответ: 311

        Ну как, прониклись? Мощная штука формула n-го члена, правда? Тогда решаем самостоятельно.

        Для разминки:

        1. Записаны первые три члена арифметической прогрессии:

        20; 17; 14; …

        Какое число стоит в этой арифметической прогрессии на 91-м месте?

        2. В третьем ряду киноконцертного зала 34 места, а в пятнадцатом — 58 мест. Сколько мест в одиннадцатом ряду, если считать число мест в каждом ряду арифметической прогрессией?

        Эта чуть покруче будет:

        3. Дана арифметическая прогрессия:

        32; 31,6; 31,2; …

        Найдите номер первого отрицательного члена этой прогрессии.

        Картинку рисовать муторно, да. Слишком уж медленно наша прогрессия к отрицательным числам приближается… Но вы же формулу n-го члена знаете! Вперёд! Ну, и элемент творчества небольшой надо проявить, да.)

        А вот это уже не разминка:

        3. Известно, что в арифметической прогрессии a₆ = 6 и a₂₅₁ = -190. Найдите a₁₀₁.

        4. Третий член арифметической прогрессии в три раза меньше шестого, а сумма второго и пятого членов равна 16. Найдите пятнадцатый член этой прогрессии.

        5. Сумма восьмого и четырнадцатого членов убывающей арифметической прогрессии равна нулю, а произведение третьего и двенадцатого членов равно -32. Найдите девятнадцатый член прогрессии.

        Задачки попроще, для отдыха:

        6. Арифметическая прогрессия задана условием: a_n = -0,6+8,6n. Найдите произведение первого и шестнадцатого её членов.

        7. Арифметическая прогрессия задана условиями:

        a_n+1 = a_n — 0,3

        a₁ = 10

        Найдите 51-й член прогрессии.

        Ответы (в беспорядке): 54; -5; 82; -70; -250; 1096; -16; 50;

        Ну вот и второй этап знакомства с арифметической прогрессией успешно пройден! Осталось ещё научиться быстро складывать её члены. Такие задачки тоже часто встречаются! Об этом — в следующем уроке.