Как найти целое число в математике

Как найти целое, если известна его часть? Например, 3/8 торта весит 300 грамм. Как узнать, сколько весит весь торт? Нахождение целого по его части Если у нас известна какая-либо часть (доля) от целого, то можно всегда “восстановить” целое. При этом нужно помнить, что часть от целого числа может быть выражена либо в виде дроби (обычно обыкновенной), либо в виде процента. Рассмотрим оба случая. 1) Часть числа – это обыкновенная дробь. В этом случае для нахождения целого нужно число, соответствующее данной части, разделить на дробь. Для того, чтобы число разделить на обыкновенную дробь, нужно умножить его на знаменатель дроби и разделить на числитель. _ Пример 1: Специалист отдела кадров получил премию 2000 рублей, что составляет 1/15 часть от его месячной зарплаты. Требуется узнать, сколько составляет зарплата у данного сотрудника. Решение: Зарплата = 2000 / (1/15) = 2000 * 15 = 30000 рублей. Значит, сотрудник получает зарплату 30000 рублей в месяц. _ Пример 2: Было засеяно пшеницей 12 гектаров поля, что составляет 3/5 от его общей площади. Нужно посчитать, чему равна площадь поля. Решение: Площадь поля = 12 / (3/5) = 12 * (5/3) = 20 гектаров. 2) Часть числа представлена в процентах. Если доля от целого является процентом, а не обыкновенной дробью, то подобные задачи можно решать с помощью составления пропорции. _ Пример: Цена апельсинов со скидкой равна 120 рублей, величина скидки равна 20%. Нужно узнать, сколько стоили апельсины изначально. Решение: Так как скидка = 20%, то от исходной цены апельсинов осталось 100% – 20% = 80%. 80% – 120 рублей. 100% – x рублей. 0,8x = 120 рублей. x = 120 / 0,8 = 150 рублей. Таким образом, до скидки апельсины стоили 150 рублей. модератор выбрал этот ответ лучшим Алиса в Стран­е [363K] 3 года назад  Часть числа может быть выражена в виде десятичной или простой дроби, в виде процентов, что по сути то же самое, что десятичная дробь, всем понятно, что 0,1 это 10%, например. Если известна часть числа в абсолютном выражении и то, какую часть она составляет от целого, то нет ничего проще, чем определить это целое. Допустим, 20 яблок это 25 % от всех яблок, надо 20 поделить на 0,25, чтобы определить общее количество яблок, 20/0,25 = 80, вот так мы нашли целое по его части. Еще один пример разберем, 12 мест в автобусе это 1/3 от всех мест в автобусе, как найти общее число всех мест в автобусе, делим 12 на 1/3, то есть по правилам деления на дробь умножаем 12 на 3, получается 36. Ну и в итоге решим задачку автора из его вопроса: 300 граммов делим на 3/8 получаем 800 граммов. smile­6008 [28.5K] 3 года назад  В математике и жизни бывают случаи, когда необходимо найти число, зная только его часть. Для этого можно использовать различные способы расчётов, использовать дроби , но удобнее всего рассчитать в процентном соотношении. Итак мы знаем, что 300 грамм составляют 3/8 торта. Нужно узнать сколько же весит торт целиком. Переводим в процентное соотношение, поделим 8 на 3, получим 0,26666 в процентах – это 26,6%. Теперь найдём 100 %, для этого посчитаем пропорцию. 26,6% = 300 ;100 % = x. X = 26,6*300/100.Получае­м 799,8 округляем по закону округление в большую сторону, получаем 800 гр весит весь торт. [поль­зоват­ель забло­киров­ан] [3.3K] 5 лет назад  Для лучшего понимания процесса можно делать так (хотя математически это нерационально). Узнайте чему равна ОДНА часть. Для этого заданное число разделите на количество заданных частей в дроби, их 3. 300 делим на 3, получаем 300/3=100 Это одна восьмая часть. Целое – это восемь восьмых, потому предыдущий результат умножаем на 8, получаем 100*8=800 Если же дробь задана, как десятичная, т.е. 0.375, то представляем её, как натуральную (это 375/1000) и поступаем точно так же. Узнаём, чему равна одна тысячная часть 300/375=0.8 Ну, а далее узнаём чему равно само целое 0.8*1000=800 Эл Лепсо­ид [139K] 5 лет назад  В общем случае, конечно, следует прибегнуть к составлению пропорции, поставив в соответствие к имеющейся части ее вес, а к целому (т.е. единице) – неизвестную “х”. Но, поскольку, у нас во второй части пропорции стоит “1”, то решить задачу можно значительно проще: просто разделить на величину известной части. В нашем случае получается: 300/(3/8) = 300*8/3 = 800. Таким образом, весь торт будет весить 800 грамм. СТА 1106 [295K] 3 года назад  3/8- означает, что на три части из восьми приходится 300 грамм. Требуется узнать вес целого, в данном случае, торта. Для этого нужно узнать, что приходится на одну часть. Можно решить методом пропорции, мой любимый метод. Итак: 3 части – 300 грамм. 8 частей – Х грамм. Решаем пропорцию. 8 × 300 ÷ 3 = 800 грамм. Общий алгоритм решения следующий. Зная, сколько приходится на долю от целого, нужно определить, сколько приходится на единицу измерения ( грамм, килограмм, метр, час и т.д). Затем зная это, просто умножает на все количество долей, на которое поделён данный предмет. В данном случае- это восемь частей. Второй вариант решения задачи. 300 : 3 × 8 = 800 грамм. Ответ. 800 грамм , в обоих вариантах таз решения задачи. Проще не бывает. Надо число означающее часть разделить на количество этих частей и полученный результат умножить на целое. Получим число выражающее целую часть. Пример: Дано 4/15 равняется 40. Делим сорок на четыре и умножаем на 15. Получаем сумму в 150 – это и будет целое. Или 2/10 равняется 40. Делим сорок на два, получаем двадцать. Умножаем двадцать на десять, получаем двести. Целое число двести. Maste­r-Marga­rita [135K] 5 лет назад  Чтобы узнать, сколько весит торт в данном случае, надо провести следующие арифметический действия: (300*8)/3=800 грамм. То есть, чтобы найти целое нужно часть умножить на знаменатель дроби и разделить на числитель дроби. В данном случае числитель – 3, а знаменатель – 8. Рина1­9 [31.1K] 5 лет назад  Сначала найдём чем у равна 1 часть из всех имеющихся. А затем умножим её на общее число всех частей. На данном примере. Известно, что 3/8 торта весит 300 г, т.е. 3 части из 8 на которые был нарезан торт или, по другому, 3 куска торта из 8 нарезанных кусочков весят 300 г. Тогда 1 кусочек будет весить: 300/3=100 г. Теперь находим чему будет весить все 8 кусков, т.е. весь торт. 100*8=800 г Бекки Шарп [71.2K] 3 года назад  Если 3/8 торта весит 300 грамм, то сначала узнаем сколько весит одна часть. 300/3=100 грамм. Теперь умножаем на 8 и получаем, что весь торт весит 800 грамм. Приведем еще пример как найти целое число, если известна часть. В классе присутствует 27 человек и это 3/4 общего количества. Сколько человек в классе? Решить задачу можно так: 27 : 3/4 = 36 человек. Знаете ответ?

Целые числа

Представьте плитку шоколада или пиццу, они могут быть целыми или разрезанными на части, так же и с числами! Узнайте, что такое целые числа и как часто мы их используем в нашей жизни.

Что такое целые числа

Целые числа — это все положительные, все отрицательные числа и ноль. Никаких дробных частей в целых числах не бывает!

Например, к целым будут относиться числа: -12, -381, -5, 0, 32, 164, 978.

Как вы помните, в математике числа, которые мы используем для счета называются натуральными. Таким образом, можно сказать, что целые числа — это натуральные числа, ноль и отрицательные числа.

Выведем основные заключения:

• Целое число может быть не только положительным. 
• Число 0 – целое число.
• Целое число не может включать дробную часть. Значит, такие числа, как 1½, 3 ¼ и 7 ⅚, не являются целыми числами, а 1, 3 и 7 — целыми.
• Целое число не может включать десятичный элемент. Это означает, что такие числа как 3,5 или 9,12 не являются целыми, а 3 или 9 — целые числа.

Как обозначаются целые числа

Множество целых чисел обозначается буквой «Z».

Z = {∞ … -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, … ∞}

Множество целых чисел бесконечно, поэтому нельзя определить, сколько всего существует целых чисел. По этой же причине нельзя назвать наибольшее целое число либо наименьшее целое число.

Положительные и отрицательные целые числа

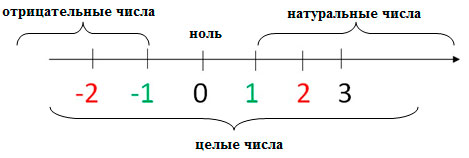
Множество целых чисел состоит из положительных и отрицательных чисел. Рассмотрите числовой луч: справа от нуля находятся положительные числа, а слева — отрицательные числа.

Отрицательные целые числа — это целые числа, которые меньше нуля. Записывают отрицательные числа всегда со знаком минус.
Например: – 12, – 135, – 74, – 3009.

Положительные целые числа — это целые числа, которые больше нуля. Записывают положительные числа без какого-то знака.
Например: 35, 14, 1004, 7286.

Свойства целых чисел при сложении и умножении

Закономерности при выполнении арифметических действий с целыми числами определяют основные свойства целых чисел. Все свойства сложения и умножения натуральных чисел будут подходить и для целых чисел.

Сумма и произведение двух целых чисел всегда будет целым числом. Например, два целых числа 2 и 6.

2 + 6 = 8 — целое число;

2 × 6 = 12 — целое число.

Переместительное свойство

Сумма или произведение целых чисел будут одинаковы, даже если порядок чисел поменять местами.

a + b = b + a

2 + 6 = 6 + 2

 8 = 8

a ⋅ b = b ⋅ a

2 ⋅ 6 = 6 ⋅ 2

12 = 12

Это свойство работает независимо от знака.

( – 2) + 6 = 6 + ( – 2)

4 = 4

2 ⋅ ( – 6) = ( – 6) ⋅ 2

 – 12 = – 12.

Сочетательное свойство

Сложение целого числа с суммой двух целых чисел равно сложению суммы двух первых чисел с третьим.

a + (b + c) = (a + b) + c

5 + (2 + 3) = (5 + 2) + 3

Умножение целого числа на произведение двух целых чисел равно произведению суммы двух первых чисел с третьим.

a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c

5 ⋅ (2 ⋅ 3) = (5 ⋅ 2) ⋅ 3

Умножение целого числа на сумму двух целых чисел равно сумме произведений первого со вторым и первого с третьим числом.

a ⋅ (b + c) = a ⋅ b + a ⋅ c

5 ⋅ (2 + 3) = 5 ⋅ 2 + 5 ⋅ 3

25 = 25

При умножении целого числа на ноль результат будет всегда равен нулю.

a ⋅ 0 = 0 или – a ⋅ 0 = 0

5 ⋅ 0 = 0 или – 5 ⋅ 0 = 0

Свойства целых чисел при вычитании

Разность равных целых чисел будет всегда равна нулю.

a – a = 0

Распределительное свойство

Вычитание суммы двух целых чисел из другого целого числа.

a – (b + c) = (a – b) – c

Вычитание целого числа из суммы двух целых чисел.

(a + b) – c = (a – с) + b = a + (b – c)

Сочетательное свойство

Умножение целого числа на разность двух целых чисел равно разности произведений первого и второго числа с первым и третьим числом.

a ⋅ (b – c) = a ⋅ b – a ⋅ c

5 ⋅ (6 – 4) = 5 ⋅ 6 – 5 ⋅ 4

10 = 10

Це́лые чи́сла — расширение множества натуральных чисел^[1], получаемое добавлением к нему нуля и отрицательных чисел^[2]. Необходимость рассмотрения целых чисел продиктована невозможностью в общем случае вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего. Введение нуля и отрицательных чисел делает вычитание такой же полноценной операцией, как сложение^[3].

Вещественное число является целым, если его десятичное представление не содержит дробной части (но может содержать знак). Примеры вещественных чисел:

Числа 142857; 0; −273 являются целыми.

Числа 5½; 9,75; −12,07 не являются целыми.

Множество целых чисел обозначается (от нем. Zahlen — «числа»^[4]). Изучением свойств целых чисел занимается раздел математики, называемый теорией чисел.

Положительные и отрицательные числа[править | править код]

Согласно своему построению, множество целых чисел состоит из трёх частей:

1. Натуральные числа (или, что то же самое, целые положительные). Они возникают естественным образом при счёте (1, 2, 3, 4, 5…)^[5].
2. Ноль — число, обозначаемое . Его определяющее свойство: для любого числа .
3. Целые отрицательные числа.

Отрицательные числа при записи помечаются спереди знаком минус: Для каждого целого числа существует и единственно противоположное ему число, обозначаемое и обладающее тем свойством, что Если положительно, то противоположное ему отрицательно, и наоборот. Ноль противоположен самому себе^[2].

Абсолютной величиной целого числа называется это число с отброшенным знаком^[6]. Обозначение:

Примеры:

Алгебраические свойства[править | править код]

Во множестве целых чисел определены три основные арифметические операции: сложение, обратное к сложению вычитание и умножение. Имеется также важная операция, специфическая для натуральных и целых чисел: деление с остатком. Наконец, для целых чисел определён порядок, позволяющий сравнивать числа друг с другом.

Сложение и вычитание[править | править код]

Следующая таблица иллюстрирует основные свойства сложения^[7] для любых целых :

Свойство	Алгебраическая запись
Коммутативность (переместительность)
Ассоциативность (сочетательность)
Свойство нуля
Свойство противоположного элемента

При сложении и вычитании целых чисел выполняются следующие правила знаков^[7][8], которые следует учитывать при раскрытии скобок:

Правила сложения целых чисел^[9].

1. При сложении целых чисел с одинаковыми знаками надо сложить их абсолютные величины и приписать ей знак слагаемых. Пример; .
2. При сложении целых чисел с разными знаками надо сравнить их абсолютные величины, из большей вычесть меньшую и приписать результату знак того слагаемого, у которого абсолютная величина больше. Примеры: .
3. Вычитание для целых чисел всегда выполнимо, и результат можно найти как Пример: .
4. Геометрически сложение можно наглядно представить как смещение числа вдоль числовой оси (см. рисунок в начале статьи), причём прибавление положительного числа вызывает смещение направо, а отрицательного — налево. Например, для числа прибавление к нему означает смещение его вправо на 4 единицы; наглядно видно, что получается . Аналогично , смещая влево на 4 единицы, получим в результате .
5. Вычитание можно наглядно представить аналогично, но в этом случае, наоборот, вычитание положительного числа вызывает смещение влево, а отрицательного — вправо. Например, смещает на 7 единиц к числу , а смещает его вправо к числу .

Умножение и возведение в степень[править | править код]

Умножение чисел далее обозначается или (только в случае буквенных обозначений) просто . Следующая таблица иллюстрирует основные свойства умножения^[7] для любых целых :

Свойство	Алгебраическая запись
Коммутативность (переместительность)
Ассоциативность (сочетательность)
Свойство единицы
Свойство нуля
Дистрибутивность (распределительность) умножения относительно сложения

При умножении целых чисел выполняются правила знаков^[7][8], которые следует учитывать при раскрытии скобок:

Следствие: произведение чисел с одинаковыми знаками положительно, с разными — отрицательно.

Возведение в натуральную степень целых чисел определяется так же, как и для натуральных чисел:

Свойства возведения в степень целых чисел такие же, как у натуральных:

Нулевая степень[править | править код]

В дополнение к этому определению, принято соглашение о нулевой степени: для любого целого кроме нуля. Основанием для такого соглашения служит желание сохранить приведенные выше свойства и для нулевого показателя степени: откуда ясно, что

Упорядоченность[править | править код]

 — линейно упорядоченное множество. Порядок в нём задаётся соотношениями:

Целое число положительно, если оно больше нуля, отрицательно, если меньше нуля. Положительными целыми числами являются натуральные числа и только они. Отрицательные числа — это числа, противоположные положительным. Ноль не является ни положительным, ни отрицательным. Любое отрицательное число меньше любого положительного^[2].

Для любых целых чисел справедливы следующие соотношения^[10].

1. Если , то для любого будет .
2. Если и , то .
3. Если и , то .
4. Если и , то .

Для сравнения двух отрицательных чисел существует правило: больше то число, у которого абсолютная величина меньше^[10]. Например, .

Делимость[править | править код]

Деление с остатком[править | править код]

Операция деления, вообще говоря, не определена на множестве целых чисел. Например, нельзя разделить на  — нет такого целого числа, которое, умноженное на , даст . Но можно определить так называемое деление с остатком^[11]:

Для любых целых (где ) существует единственный набор целых чисел такой, что , где

Здесь a — делимое, b — делитель, q — (неполное) частное, r — остаток от деления (всегда неотрицателен). Если остаток равен нулю, говорят, что деление выполняется нацело^[11].

Примеры

На операции деления с остатком основаны теория сравнений и алгоритм Евклида.

Деление нацело. Делители[править | править код]

Как определено выше, число делится (нацело) на число , если существует целое число такое, что . Символическая запись: . Существуют несколько равносильных словесных формулировок указанной делимости^[12]:

Каждое целое число , не равное нулю или , имеет 4 тривиальных делителя: . Если других делителей нет, число называется простым^[13].

Понятие наибольшего общего делителя двух целых чисел, разложение целого числа на простые множители и основная теорема арифметики для целых чисел практически совпадают (с возможным учётом знака) с аналогами этих понятий для натуральных чисел^[14].

Целые и вещественные числа[править | править код]

Существуют практические задачи, в которых необходимо округлить вещественное значение до целого, то есть заменить его на ближайшее (в ту или иную сторону) целое. Поскольку выполнять округление можно разными способами, для уточнения можно использовать «символы Айверсона»^[15]:

 — ближайшее к целое в меньшую сторону (функция «пол», англ. floor, или «целая часть»). Традиционно используются также обозначение Гаусса или обозначение Лежандра .

 — ближайшее к целое в бо́льшую сторону (функция «потолок», англ. ceiling).

В зависимости от особенностей постановки задачи, могут встретиться и другие методы: округлить до ближайшего целого или отсечь дробную часть (последний вариант для отрицательных отличается от функции «целая часть»).

Другой класс задач, связывающих целые и вещественные числа — приближение вещественного числа отношением целых, то есть рациональным числом. Доказано, что любое вещественное число можно с любой желаемой точностью приблизить рациональным, наилучшим инструментом для такого приближения служат непрерывные (цепные) дроби^[16].

История[править | править код]

Развитие математики началось с навыков практического счёта (один, два, три, четыре…), поэтому натуральные числа возникли ещё в доисторический период как идеализация конечного множества однородных, устойчивых и неделимых предметов (людей, овец, дней и т. п.). Сложение появилось как математическая модель таких важных событий, как объединение нескольких множеств (стад, мешков и т. д.) в одно, а вычитание отражало, наоборот, отделение части множества. Умножение для натуральных чисел появилось в качестве, так сказать, пакетного сложения: 3 × 4 означало сумму «3 раза по 4», то есть 4 + 4 + 4. Свойства и взаимосвязь операций открывались постепенно^[17][18].

Начальным шагом на пути расширения натуральных чисел стало появление нуля; первыми этот символ стали применять, по-видимому, индийские математики. Вначале ноль применялся не как число, а как цифра при позиционной записи чисел, затем постепенно стал признаваться и как полноценное число, обозначающее отсутствие чего-либо (например, полное разорение торговца)^[19].

Отрицательные числа впервые стали использовать в древнем Китае и в Индии, где их рассматривали как математический образ «долга». Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал «правило знаков» и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными^[20].

В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который также трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Свободно использовали отрицательные числа Никола Шюке (1484 год) и Михаэль Штифель (1544)^[20].

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Легализация отрицательных чисел привела к многочисленным удобствам — например, перенос слагаемых уравнения в другую его часть стал возможен независимо от знака этого слагаемого (ранее, скажем, уравнения и считались принципиально различными)^[21].

Тем не менее теория отрицательных чисел долго находилась в стадии становления. Паскаль, например, считал, что , так как «ничто не может быть меньше, чем ничто»^[22]. Оживлённо обсуждалась странная пропорция  — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Валлис считал, что отрицательные числа меньше нуля, но в то же время больше, чем бесконечность^[23]. Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия. Гаусс в 1831 году считал нужным разъяснить, что отрицательные числа принципиально имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам (например, неприменимы при счёте людей)^[24].

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Гюнтер Грассман)^[25].

Применение[править | править код]

В прикладных науках[править | править код]

Целые числа широко применяются при исследовании объектов, которые по своей природе или по особенностям постановки задачи неделимы (например, люди, суда, строения, иногда дни и т. п.). Отрицательные числа также могут найти применение в таких моделях — скажем, при планировании торговых сделок можно продажи обозначать положительными числами, а покупки — отрицательными. Пример из физики — квантовые числа, играющие фундаментальную роль в микромире; все они — целые (или полуцелые) числа со знаком^[26].

Для решения возникающих при этом задач разработаны специальные математические методы, учитывающие специфику проблем. В частности, решение в целых числах алгебраических уравнений (разных степеней) рассматривает теория «диофантовых уравнений»^[27]. Вопросы целочисленной оптимизации исследует целочисленное программирование^[28].

В информатике[править | править код]

Тип целое число — зачастую один из основных типов данных в языках программирования. Целые типы данных обычно реализуются как фиксированный набор битов, один из которых кодирует знак числа, а прочие — двоичные цифры. Современные компьютеры имеют богатый набор команд для арифметических операций с целыми числами^[29].

Место в общей алгебре[править | править код]

С точки зрения общей алгебры, относительно сложения и умножения является бесконечным коммутативным кольцом с единицей, без делителей нуля (область целостности). Кольцо целых чисел является евклидовым (и, следовательно, факториальным) и нётеровым кольцом, но не является артиновым. Если расширить это кольцо, добавив к нему всевозможные дроби (см. поле частных), получится поле рациональных чисел (); в нём уже выполнимо любое деление, кроме деления на ноль^[30][31].

Относительно операции сложения является абелевой группой, и, следовательно, также циклической группой, так как каждый ненулевой элемент может быть записан в виде конечной суммы 1 + 1 + … + 1 или (−1) + (−1) + … + (−1). Фактически, является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе . Относительно умножения не образует группу, поскольку во множестве целых чисел деление, вообще говоря, невозможно^[30].

Множество целых чисел с обычным порядком является упорядоченным кольцом, но не является вполне упорядоченным, так как, например, среди отрицательных чисел нет наименьшего. Однако его можно сделать вполне упорядоченным, если определить нестандартное отношение «меньше или равно»^[32], которое обозначим и определим следующим образом:

если либо либо либо и

Тогда порядок целых чисел будет таким: В частности, будет наименьшим отрицательным числом. с новым порядком будет вполне упорядоченным множеством, но уже не будет упорядоченным кольцом, так как этот порядок не согласован с операциями кольца: например, из , прибавив слева и справа 1, получаем неверное неравенство

Любое упорядоченное кольцо с единицей и без делителей нуля содержит одно и только одно подкольцо, изоморфное ^[33].

Логические основания[править | править код]

Расширение натуральных чисел до целых, как и любое другое расширение алгебраической структуры, ставит множество вопросов, основные из которых — как определить операции над новым типом чисел (например, как определить умножение отрицательных чисел), какие свойства они тогда будут иметь и (главный вопрос) допустимо ли такое расширение, не приведёт ли оно к неустранимым противоречиям. Для анализа подобных вопросов надо сформировать набор аксиом для целых чисел.

Аксиоматика целых чисел[править | править код]

Проще всего определить аксиоматику множества целых чисел , если опираться на уже построенное множество натуральных чисел (которое предполагается непротиворечивым, а свойства его — известными). Именно, определим как минимальное кольцо, содержащее множество натуральных чисел. Более строго, аксиомы целых чисел следующие^{[34] [35]}.

Z1: Для всяких целых чисел определена их сумма .

Z2: Сложение коммутативно: . Для краткости оговорку «для всяких » далее, как правило, опускаем.

Z3: Сложение ассоциативно:

Z4: Существует элемент 0 (ноль) такой, что .

Z5: Для всякого целого числа существует противоположный ему элемент такой, что

Z6: Для всяких целых чисел определено их произведение .

Z7: Умножение ассоциативно:

Z8: Умножение связано со сложением распределительными (дистрибутивными) законами:

Z9: Множество целых чисел содержит подмножество, изоморфное множеству натуральных чисел . Для простоты далее это подмножество обозначается той же буквой .

Z10 (аксиома минимальности): Пусть  — подмножество , включающее и такое, что операция вычитания не выводит за пределы . Тогда совпадает со всем .

Из этих аксиом вытекают как следствия все прочие свойства целых чисел, в том числе коммутативность умножения, упорядоченность, правила деления нацело и деления с остатком^[36]. Покажем, например, как вводится порядок целых чисел. Будем говорить, что , если есть натуральное число. Аксиомы порядка легко проверяются. Из определения сразу следует, что все натуральные числа больше нуля (положительны), а все противоположные им меньше нуля (отрицательны). Для натуральных чисел новый порядок совпадает со старым^[37].

Приведённая аксиоматика целых чисел категорична, то есть любые её модели изоморфны как кольца^[38].

Непротиворечивость[править | править код]

Стандартный способ доказать непротиворечивость новой структуры — смоделировать (интерпретировать) её аксиомы с помощью объектов другой структуры, чья непротиворечивость сомнений не вызывает. В нашем случае мы должны реализовать эти аксиомы на базе пар натуральных чисел^[39].

Рассмотрим всевозможные упорядоченные пары натуральных чисел . Чтобы смысл дальнейших определений стал понятен, сразу поясним, что мы намерены в дальнейшем каждую такую пару рассматривать как целое число например, пары или будут изображать единицу, а пары или будут изображать

Далее определим^[40]:

1. Пары и считаются равными, если . Это связано с тем, что, как показано в примерах, любое целое число можно представить бесконечным числом пар.
2. Сложение: сумма пар и определяется как пара .
3. Умножение: произведение пар и определяется как пара .

Нетрудно проверить, что результаты сложения и умножения не меняются, если любую пару мы заменим на равную ей, то есть новая пара-результат будет равна прежней (в указанном определением 1 смысле равенства). Несложно также убедиться, что описанная структура пар удовлетворяет всему приведенному перечню аксиом целых чисел. Положительные числа моделируются парами , в которых , ноль изображают пары вида , а пары с соответствуют отрицательным числам^[40].

Эта модель позволяет прояснить, как из аксиом целых чисел однозначно следуют их свойства; покажем это для «правила знаков». Например, умножив два «отрицательных числа» и , у которых , мы по определению получим пару . Разность равна , это число положительно, поэтому пара-произведение изображает положительное целое число, следовательно, произведение отрицательных чисел положительно. Любое другое правило (скажем, «произведение отрицательных чисел отрицательно») сделало бы теорию целых чисел противоречивой.

Описанная модель доказывает, что приведенная аксиоматика целых чисел непротиворечива. Потому что если бы в ней было противоречие, то это означало бы противоречие и в базовой для данной модели арифметике натуральных чисел, которую мы заранее предположили непротиворечивой^[39].

Мощность множества[править | править код]

Множество целых чисел бесконечно. Хотя натуральные числа составляют лишь часть множества целых чисел, целых чисел столько же, сколько натуральных, в том смысле, что мощность множества целых чисел такая же, как и множества натуральных — оба они счётные^[41].

Вариации и обобщения[править | править код]

Некоторые алгебраические структуры по своим свойствам похожи на кольцо целых чисел . Среди них:

Примечания[править | править код]

Литература[править | править код]

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 стр.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
• Нечаев В. И. Числовые системы. — М.: Просвещение, 1975. — 199 с.
• Энциклопедия элементарной математики (в 5 томах). — М.: Физматгиз, 1951. — Т. 1. — С. 160—168. — 448 с.

Начнем с нахождения неизвестной части от известного целого.

Как правило, целое принимается за единицу. Например, – необходимо разделить поровну торт, массой 2 кг на 8 человек. Найти массу одного кусочка.

Каждый присутствующий получит: 1 : 8 = 1/8 от всего торта. Тогда масса одного кусочка: 2 * 1/8 = 2 : 8 = 1/4 = 0,25 (кг) = 250 (г)

Таким образом, для нахождения части от целого необходимо целое разделить на количество частей (в данном случае 8), или умножить целое на дробь, выражающую эту часть (в данном случае 1/8).

——————————–  

В решении задач часто возникают ситуации, когда вопрос нахождения части от целого не ограничивается простым делением целого на количество частей. Например:

В свежих фруктах находится 60% воды. Найти массу сухих фруктов, получившихся из 12 кг свежих.

Так как воды в свежих фруктах 60% или 6/10 от всего количества, то сухих фруктов получится: 1 – 6/10 = 4/10 от всей массы свежих фруктов. Так как вся масса – 12 кг, то масса сухих фруктов:

                 12 * 4/10 = 48/10 = 4,8 (кг)

Следует обратить внимание на то, что при умножении числа на дробь безразлично, в каком порядке выполнять действия: можно умножить число на числитель, а потом разделить полученный результат на знаменатель, или можно число разделить на знаменатель, а потом полученный результат умножить на числитель:

12 * 4/10 = 12 * 4 : 10 = 12 : 10 * 4 = 1,2 * 4 = 4,8

=================================

Теперь рассмотрим, как находить целое, если известна его часть.

Возьмем, для примера, задачу с сухофруктами и изменим условие: Известно, что при сушке свежих фруктов получилось 7,2 кг сухих. Определить массу свежих фруктов, если известно, что масса воды составляет в них 60% от веса.

Так как 7,2 кг – это фрукты без воды, то от полной массы свежих фруктов 7,2 кг составляют: 100 – 60 = 40% или 0,4.

Тогда масса свежих фруктов: 7,2 : 0,4 = 7,2 : 4/10 = 7,2 * 10/4 = 72/4 = 18 (кг)  

Таким образом, чтобы найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.

Формулировки с числителями и знаменателями несколько запутаны и, часто, не поддаются логическому осмыслению. Гораздо проще запомнить через действия с дробями: в случае нахождения части от целого, – умножение на дробь, в случае нахождения целого от части, – деление на дробь. А то, что деление на дробь равнозначно умножению на дробь, обратную данной, на мой взгляд, значительно проще для понимания..))    

Что такое целые числа

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о ЦЕЛЫХ ЧИСЛАХ.

Это весьма обширное понятие из математики, с которым школьники сталкиваются уже в 5 классе. Быстрее разобраться помогут репетиторы по математике онлайн: объяснят тему понятным языком и дадут интерактивные задания для закрепления новых знаний.

Целые числа — это…

Целые числа – это все положительные, все отрицательные числа и ноль. Главное, чтобы они не содержали дробной части.

Согласно этому определению, к целым числам можно отнести:

-1256, -35, -9, 0, 14, 95, 2020

и так далее. Ведь у них нет дробной части. А вот числа:

0.5, 13.1319, ½, -¾, — 237.3

и так далее не могут считаться целыми, так как у них есть какие-то цифры после запятой или они являются дробью.

Все многообразие целых чисел называется множеством целых чисел. Это официальный математический термин. И обозначается он буквой Z.

В это множество входят и так называемые натуральные числа (это что?). Это все те, которые имеют положительное значение, но опять же без дробной части. Проще говоря, все числа, которые мы используем при счете. Например, 1, 2, 5, 10, 100 и так далее.

Множество натуральных чисел обознается буквой N. И зависимость его и множества целых чисел наглядно показана на следующем рисунке.

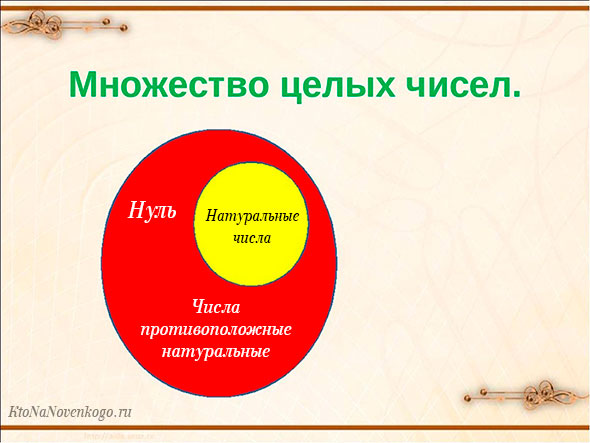
Отсюда можно сделать важный вывод:

Любое натуральное число автоматически является еще и целым. Но при этом далеко не каждое целое число является еще и натуральным.

А можно представить это и в таком варианте. Целые числа — это:

1. Натуральные числа;
2. Ноль;
3. Отрицательные числа.

Каким бы определением вы не пользовались, главное, чтобы было все понятно.

История изучения целых чисел

Опять же эту историю нужно разделить на три части. Ведь изучение натуральных чисел, а также открытие нуля и отрицательных чисел происходило независимо друг от друга. Да еще и в разных странах.

Изучение натуральных чисел

Тут все максимально просто. Эти числа возникли, как только человеку понадобилось считать – будь то куски мяса или количество бревен для дома.

Более точное изучение натуральных чисел начинается в Древнем Египте и Древней Месопотамии, а это более 6 тысяч лет назад.

А современные математики опираются на то, что после себя оставил древнегреческий ученый Пифагор. Он как раз активно собирал египетские и вавилонские данные, а после отразил их в своих трудах.

Открытие нуля

Конечно, египтяне, вавилоняне и даже греки знали о существовании нуля. Но не считали его числом, а потому не пользовались им. Это, кстати, приносило им немало сложностей. Они порой часами решали задачки, которые нынешний школьник посчитает за минуту.

Но официально число ноль появилось в 5-м веке. И «изобрели» его в Индии. Дело в том, что у местных жителей всегда существовало убеждение, что «ничто – это тоже что-то». Даже понятие Нирвана, которое обозначает состояние небытие, зародилось именно в Индии.

Потому-то там и придумали символ, который обозначал бы «ничто». Авторами его стали математики Брахмагупта и Ариабхата.

Как видите, индийский символ нуля очень похож на современный. Ну, разве что приплюснут и больше напоминает правильную окружность. Форма выбрана не случайно. По индийским поверьям, ноль символизирует круговорот жизни и мироздания. Его еще называют «змея вечности».

Когда арабы завоевали часть Индии, они переняли все математические знания. А во время крестовых походов многое, в том числе и цифры, перекочевали в Европу. Хотя потребовалось еще несколько сотен лет, чтобы «ноль» стал неотъемлемой частью европейской науки.

Открытие отрицательных чисел

Отрицательные числа первыми начали изучать китайцы во 2 веке до нашей эры. Их использовали в торговле и называли «долгами». А обычные числа – «имуществом». А для записи отрицательных чисел использовали перевернутый вид.

А вот в Европе к ним очень долго относились пренебрежительно, считая «несуществующими» и «абсурдными». Лишь в 12 веке математик Леонардо Фибоначчи (автор знаменитого числового ряда) описал их в своей книге «Книга Абака».

В середине 16 века математик Михаил Штифель посвятил им целый раздел в своей книге «Полная арифметика».

Но признание они получили лишь в 17 веке, после того как известный Рене Декарт создал свою систему координат.

В ней он также использовал нуль, привязав к нему положительные и отрицательные числа. Одни находились справа от него, а другие – слева.

Свойства целых чисел

Всем целым числам свойственны следующие характеристики:

1. Замкнутость. При математических действиях с целыми числами, за исключением деления, получаются только целые числа.

   Если А и В – целые, то А+В=целое, А-В=целое и А*В=целое

2. Ассоциативность. При сложении или умножении трех и более целых чисел их можно менять местами, и результат не изменится.

   (А + В) + С = А + (В + С)

3. Коммутативность. При перестановке мест слагаемых (множителей) – сумма (произведение) не меняется.

   А + В = В + А, А * В = В * А

4. Если ноль участвует в сложении или вычитании, то значение остается неизменным.

   А + 0 = 0, А – 0 = 0

5. Противоположность. При сложении одинаковых чисел с разными знаками, получается всегда ноль.

   А + (-А) = 0

6. Разность знаков. При умножении чисел с разными знаками, результат всегда отрицательный. Если знаки одинаковые, то результат всегда положительный.

   А * А = АА, А * (-А) = -АА, (-А) * (-А) = АА

Добавим: точно такое же правило действует и при делении. Минус на минус дают плюс. А минус на плюс или плюс на минус всегда дают минус.

Вместо заключения

Мы уже рассказали, с каким трудом в нашу жизнь попали отрицательные числа. Но сегодня они широко используются не только в математике.

1. География. Высоту гор измеряют положительными значениями, а вот глубину водоемов – отрицательными. А уровень моря является нулем.
2. История. Понятие «наша эра» разделила историю на положительное летоисчисление и отрицательное. Все, что происходило, более 2 тысяч лет назад можно описать как «в минус 125 году» или «в -3000 лет». Хотя больше принято говорить «125 год до н.э» и «3000 лет до н.э.».
3. Медицина. Для определения остроты зрения врачи используют понятия отрицательных и положительных диоптрий. Идеальное зрение – это ноль. Минус – близорукость (не видит вдалеке), а плюс – дальнозоркость (не видит вблизи).
4. Физика. Есть такие понятия, как положительно и отрицательно заряженные частицы. Одни называются протонами, а другие – электронами.

Ну и, наконец, слова положительный и отрицательный используются и в более разговорном смысле, как синонимы хорошего и плохого.

Например, в книгах и фильмах обязательно есть положительные и отрицательные герои. Также и наши черты характера, эмоции и поступки можно разделить на эти две категории.