Как найти целое количество решений

Метод подсчёта количества решений

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.

В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.

Общая форма интересующего нас уравнения:

где n и m — положительные целые числа.

Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.

Нам нужен метод

Давайте начнём с частного случая общего уравнения:

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

Число решений в этом случае равно 10.

Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.

Значит, нужен эффективный метод.

Разрабатываем метод

Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:

Одним из решений было (5, 0). Давайте преобразуем его в:

Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.

В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.

Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

Это то же самое число, что мы получили методом прямого счёта!

Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.

Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

Простейшее решение этого уравнения:

Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:

math4school.ru

Уравнения в целых числах

Немного теории

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

не имеет ненулевых рациональных решений для всех натуральных n > 2.

Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

способ перебора вариантов;

применение алгоритма Евклида;

представление чисел в виде непрерывных (цепных) дробей;

разложения на множители;

решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;

метод бесконечного спуска.

Задачи с решениями

1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

в) 201х – 1999у = 12.

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

Поскольку числа 5 и 7 взаимно простые, то

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x₀ = 1273·12 = 15276, y₀ = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

3. Решить в целых числах уравнение:

а) x 3 + y 3 = 3333333;

б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).

а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;

б) в целых числах уравнение x + y = x 2 – xy + y 2 .

а) Решим данное уравнение как квадратное относительно переменной у. Получим

у = х + 9 или у = 16 – х.

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х имеем

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

б) Рассмотрим данное уравнение как квадратное уравнение относительно x:

x 2 – (y + 1)x + y 2 – y = 0.

Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?

Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид

Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:

y = xn = n(2n 2 +1) = 2n 3 +n.

Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).

6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.

Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.

Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.

Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.

Поэтому все числа x, y, z, u чётны. Тогда можно записать, что

и исходное уравнение примет вид

Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x₁, y₁, z₁, u₁ нечётны, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится на 8. А если ровно два из этих чисел нечётно, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится даже на 4. Значит,

и мы получаем уравнение

Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

7. Докажите, что уравнение

(х – у) 3 + (y – z) 3 + (z – x) 3 = 30

не имеет решений в целых числах.

Воспользуемся следующим тождеством:

(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .

если х = 1, то у 2 = 1,

если х = 3, то у 2 = 9.

Этим случаям соответствуют следующие пары чисел:

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

9. Решите следующую систему уравнений в натуральных числах:

a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).

3abc > 0, то a 3 > b 3 + c 3 ;

таким образом имеем

b 2 2 + х = у 4 + у 3 + у 2 + у.

Разложив на множители обе части данного уравнения, получим:

х(х + 1) = у(у + 1)(у 2 + 1),

х(х + 1) = (у 2 + у)(у 2 + 1)

Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:

Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х₅ = 5, х₆ = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:

Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)

Задачи без решений

1. Решить в целых числах уравнение:

б) х 2 + у 2 = х + у + 2.

2. Решить в целых числах уравнение:

а) х 3 + 21у 2 + 5 = 0;

б) 15х 2 – 7у 2 = 9.

3. Решить в натуральных числах уравнение:

4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение

5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.

Линейные диофантовы уравнения с двумя переменными

Калькулятор решает линейные диофантовы уравнения с двумя переменными.

Сначала калькулятор, теория под ним.

Линейные диофантовы уравнения с двумя переменными

Диофантово уравнение с двумя неизвестными имеет вид:

где a, b, c — заданные целые числа, x и y — неизвестные целые числа.

Для нахождения решений уравнения используется Расширенный алгоритм Евклида (исключая вырожденный случай, когда a = b = 0 и уравнение имеет либо бесконечно много решений, либо же не имеет решений вовсе).
Если числа a и b неотрицательны, тогда с помощью расширенного алгоритма Евклида мы можем найти их наибольший общий делитель g, а также такие коэффициенты и , что:
.

Утверждается, что если число c делится на g, то диофантово уравнение имеет решение; в противном случае диофантово уравнение решений не имеет. Это следует из очевидного факта, что линейная комбинация двух чисел по-прежнему должна делиться на их общий делитель.

То есть если c делится на g, тогда выполняется соотношение:

т. е. одним из решений диофантова уравнения являются числа:

Если одно из чисел a и b или они оба отрицательны, то можно взять их по модулю и применить к ним алгоритм Евклида, как было описано выше, а затем изменить знак найденных коэффициентов и в соответствии с настоящим знаком чисел a и b соответственно.

Если мы знаем одно из решений, мы можем получить выражение для всех остальных решений, которых бесконечное множество.

Итак, пусть g = НОД (a,b), выполняется условие:
.

Тогда, прибавив к число и одновременно отняв от , мы не нарушим равенства:

Этот процесс можно повторять сколько угодно, т. е. все числа вида:

,
где k принадлежит множеству целых чисел, являются множеством всех решений диофантова уравнения.

[spoiler title=”источники:”]

http://math4school.ru/uravnenija_v_celih_chislah.html

http://planetcalc.ru/3303/

[/spoiler]

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения. 

В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений. 

Общая форма интересующего нас уравнения: 

где n и m — положительные целые числа.

Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения. 

Нам нужен метод

Давайте начнём с частного случая общего уравнения: 

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

Число решений в этом случае равно 10.

Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.

Значит, нужен эффективный метод.

Разрабатываем метод

Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения: 

Одним из решений было (5, 0). Давайте преобразуем его в:

Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций. 

В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём. 

Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

Это то же самое число, что мы получили методом прямого счёта!

Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.

Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

Простейшее решение этого уравнения:

Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:

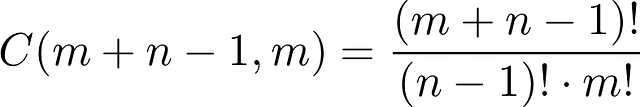
Это наш конечный результат.

---

Originally published at https://physicsgarage.com on April 26, 2020.

Читайте также:

• Связный список в деталях
• 7 способов раскрыть жульничество аналитика данных
• Лучшие фреймворки для ИИ и машинного обучения в веб-разработке

---

Перевод статьи Julia Fisher: A Method of Counting The Number of Solutions

Уравнения в целых числах – уравнения с двумя и более неизвестными переменными и целыми коэффициентами. Решениями таких уравнений являются целые числа. Также такие уравнения называются диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который изучал такие уравнения еще до нашей эры.

При решении уравнений в целых и натуральных числах можно выделить следующие способы.

1 способ. Метод перебора вариантов.

Решим уравнение  $ (x-2)(y+3)=4 $  в целых числах.

Так как x и у целые числа, совершим перебор вариантов:

$ {x-2=1;; y+3=4rightarrow;x=3;;y=1\ x-2=4;; y+3=1rightarrow;x=6;;y=-2\ x-2=-1;; y+3=-4rightarrow;x=1;;y=-7\ x-2=-4;; y+3=-1rightarrow;x=-2;;y=-4\ x-2=2;; y+3=2rightarrow;x=4;;y=-1\ x-2=-2;; y+3=-2rightarrow;x=0;;y=-5\} $

Ответ: (3; 1), (6; -2), (1; -7), (-2; -4), (4; -1), (0; -5).

Решим уравнение 10х + 10у = 2019 в целых числах.

Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

Пусть нужно решить уравнение в целых числах:  $ 5x+4y=22. $

Методом перебора находим решение  $ x_1=2;;y_1=3. $

Получаем систему уравнений:

$ {begin{cases}5x=4y=22\5cdot2=4cdot3=22end{cases}\ 5(x-2)=4(y-3)=0\ 5(x-2)=-4(y-3)} $

$ x-2=frac{-4(y-3)}{5} $

Из полученного равенства видно, что число (х – 2) будет целым тогда и только тогда, когда (у – 3) делится на 5, т.е. у – 3 = 5n, где n какое-нибудь целое число.

Имеем:

$ { y=3+5n\ x-2=-4cdotfrac{5n}{5}=-4n\ x=2-4n} $

Тем самым все целые решения исходного уравнения можно записать в таком виде:

$ (2-4n;;3=5n),; где; n in Z. $

Ответ:  $ (2-4n;;3=5n),; где; n in Z. $

2 способ. Алгоритм Евклида

Пусть нужно решить уравнение в целых числах:  $ 5x+7y=6. $

Сделаем это с помощью Алгоритма Евклида. Ищем НОД чисел 5 и 7 с помощью него:

НОД (5, 7) = НОД (5, 7-5) = НОД (5, 2) = НОД (5 – 2∙2, 2) = НОД (1, 2) = 1

Запишем этот процесс в обратном порядке:

$ 1=2-1=2-(5-2cdot2)=2cdot3-5cdot1=(7-5)cdot3-5cdot1=7cdot3-5cdot4. $

То есть:

$ 1=5cdot(-4)+7cdot3 $

Тогда:

$ { 1cdot6=5cdot(-4)cdot6+7cdot3cdot6\ 6=5cdot(-24)+7cdot18\ 6=5x+7y} $

Тогда  $ { x=-24 ;и ; y=18} $  является решением уравнения.

Общее решение записывается в виде:

$ { x=-24+7n; ; y=18+5n,} $  где n – любое целое число.

Выполним проверку:

$ { 5(-24+7n)+7(18+5n)=6\ -120+35n+126+35n=6\ 70n=0} $

$ { n} $  – любое целое.

Верно.

Это не всевозможные способы решения. Зачастую для решения диофантовых уравнений требуются более тонкие рассуждения, связанные с делимостью, перебором остатков, оценками частей уравнения, тождественными преобразованиями и т.п.

Пример.

Решим уравнение:

$ 3^{x}+4^{y}=5^{z} $

Разложить на множители и выразить переменную мы здесь не можем. Воспользуемся методом перебора остатков.

Если левая часть уравнения в целых числах кратна какому-то числу, то и другая обязательно должна быть кратна этому же числу. Отсюда следует, что и остатки от деления обеих частей уравнения на одно и то же число будут давать одинаковые остатки.

Будем делать выводы о делимости одной части уравнения на какое-либо число (или смотреть, какой остаток от деления при этом получается) и проверять, при каких значениях переменных вторая часть уравнения также делится на это число (либо даёт такой же остаток).

Левая часть кратна 5. И остатки от деления на 5 у обеих частей также будут равны.

Про пятёрку уже сказали, что правая часть делится на неё без остатка, значит и левая тоже должна делиться.

Рассмотрим остатки от деления на 4.

Z	$ 5^{z} $	Остаток при делении на 4
1	5	1
2	25	1
3	125	1
4	625	1

Видим простую закономерность, что 5 в любой степени при делении на 4 будет давать остаток 1.

Теперь левая часть: будет делиться на 4 без остатка.

Рассмотрим остатки от деления на 4 числа  $ 3^{x} $

Z	$ 3^{x} $	Остаток при делении на 4
1	3	3
2	9	1
3	27	3
4	81	1
5	243	3

И так далее. Закономерность: при чётных х остаток 1, при нечётных остаток 3.

Отсюда делаем вывод, что х – число чётное, значит, мы можем представить его как х = 2n.

Теперь рассмотрим остатки при делении обеих частей на 3.

Правая часть:

Z	$ 5^{z} $	Остаток при делении на 3
1	5	2
2	25	1
3	125	2
4	625	1

И так далее. Видим закономерность, что при чётных z остаток равен 1, при нечетных z остаток равен 2.

Рассмотрим левую часть. Число  $ 3^{x} $  даёт остаток 0 при делении на 3.

Рассмотрим остатки от деления на 3 числа  $ 4^{y} $

Z	$ 4^{y} $	Остаток при делении на 3
1	4	1
2	16	1
3	64	1
4	256	1
5	1024	1

Получается, что левая часть при делении на 3 может давать только остаток 1. Значит, и правая тоже. Это происходит при чётных z.

Вернёмся к нашему уравнению  $ 3^{x}+4^{y}=5^{z} $

Рассмотрев все остатки от деления, мы делаем выводы, что х и z – чётные числа. Тогда х = 2n, z = 2m, где m, n натуральные. Подставим в уравнение:

$ 3^{2n}+4^{y}=5^{2m} $ , заметим также, что  $ 4^{y}=2^{2y} $

Теперь мы можем разложить на множители, используя формулу разности квадратов:

$ 2^{2y}=5^{2m}-3^{2n} $

$ (5^{m}-3^{n})(5^{m}+3^{n})=2^{2y} $ . Получается, что обе скобки должны быть степенями двойки. Мы не можем сделать никаких обоснованных выводов. Наша группировка неудачная. Попробуем иначе:

$ { 5^{2m}-2^{2y}=3^{2n}\ (5^{m}-2^{y})(5^{m}+2^{y})=3^{2n}} $

Теперь у нас обе скобки являются произведением троек. Рассмотрим такую ситуацию,

$ acdot b=3^{2n} $ , это означает, что и а, и b кратны 3. Либо одно из чисел кратно 3, а другое равно 1.

Рассмотрим случай, когда и а, и b кратны трём. Вспомним основные свойства делимости.

Ключевым признаком здесь будет второй: в нашем случае разность a-b также будет делиться на 3.

Рассмотрим разность скобок:

$ 5^{m}+2^{y}-(5^{m}-2^{y})=2cdot 2^{y} $  – это число никогда не будет кратно 3. Значит, в нашем произведении один из множителей равен 1, а другой равен 3²ⁿ. Так как  $ 5^{m}+2^{y}> 1 $ ,

$ 5^{m}-2^{y}=1,5^{m}+2^{y})=3^{2n} $ Итак, мы с вами уже решаем немного другое уравнение, с переменными m и n, которые зависят от х и у. И пришли к выводу, что  $ 5^{m}+2^{y}=1 $

m	$ 5^{m} $	y	$ 2^{y} $
0	1	0	1
1	5	1	2
2	25	2	4
3	125	3	8

Эта таблица показывает, что  $ 5^{m}+2^{y}=1 $  только в одном случае при m = 1, y = 2. При их увеличении разница между и будет всё больше, поэтому это единственное решение.

Тогда z = 2m = 2, x = 2.

Ответ: (2, 2, 2)

Найти целые цешения системы неравенств

В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.

Найти целые решения системы неравенств — одно из заданий такого рода.

1) Найти целые решения системы неравенств:

7x — 5\ 5 — x

Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:

— 5 — 3\ — x + 6x

После упрощения разделим обе части каждого неравенства на b» href=»http://www.algebraclass.ru/axb/» target=»_blank»>число, стоящее перед иксом. При делении на положительное число знак неравенства не меняется:

— 8___left| <:2 >0> right.\ 5x 0> right. end right.]» title=»Rendered by QuickLaTeX.com»/>

— 4\ x

Отмечаем решения неравенств на числовых прямых. Решением системы является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).

Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:

Из промежутка (-4;2) выбираем целые решения.

Ответ: -3; -2; -1; 0; 1.

2) Какие целые решения имеет система неравенств?

17 — 4x end right.]» title=»Rendered by QuickLaTeX.com»/>

Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком

17 — 37 end right.]» title=»Rendered by QuickLaTeX.com»/>

Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:

0> right.\ — 4x > — 20___left| <:( – 4)

Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:

Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.

Ответ: -2; -1; 0; 1; 2; 3; 4.

В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.

3) Сколько целых решений имеет система неравенств?

Переносим неизвестные в одну сторону, известные — в другую:

0> right. end right.]» title=»Rendered by QuickLaTeX.com»/>

Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:

Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:

Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.

4) Сколько целых чисел являются решениями системы неравенств?

Неизвестные — в одну сторону, известные — в другую с противоположным знаком:

0> right. end right.]» title=»Rendered by QuickLaTeX.com»/>

При делении обеих частей неравенства на положительное число знак неравенства не изменяется, при делении на отрицательное число — меняется на противоположный:

Решение неравенств отмечаем на числовых прямых.

Множество решений системы состоит из единственного элемента — <2>. 2 — целое число, следовательно, решением данной системы является одно целое число.

Источник

Метод интервалов, решение неравенств

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

где x — переменная,

Квадратное неравенство можно решить двумя способами:

• графический метод;
• метод интервалов.

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

1. D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2. D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
3. D

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

если a 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.

Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.

Когда квадратный трехчлен корней не имеет (D

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.

Разложим квадратный трехчлен на множители.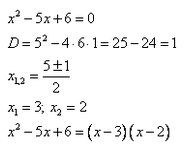

Неравенство примет вид:

Проанализируем два сомножителя:

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Построим чертеж.

Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.

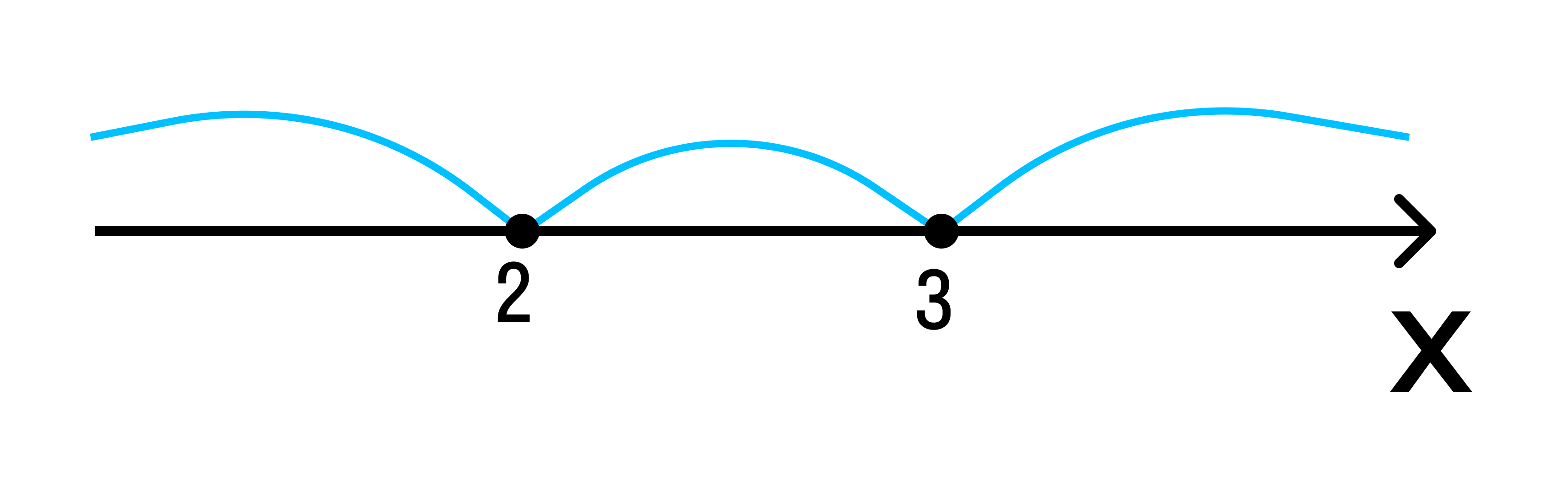
Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

• (25 — 3) (25 — 2) = 22*23 = 506 > 0

Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.

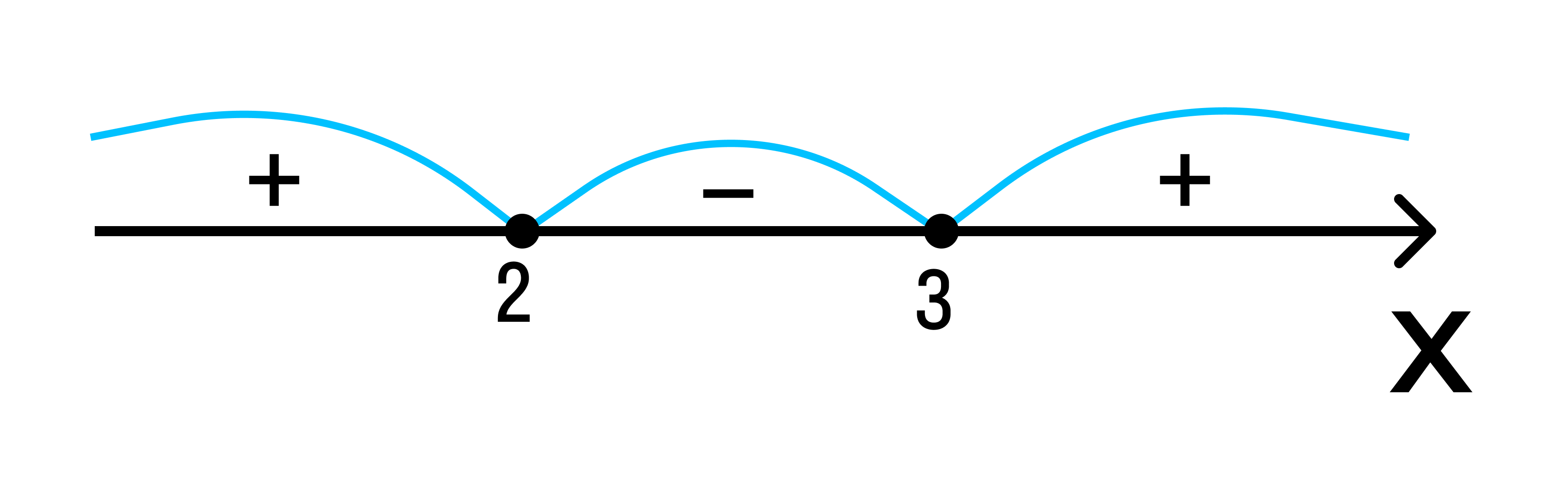
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.

Если (х — 3) * (х — 2) > 0:

Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Решение линейных неравенств

Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.

Символ	Название	Тип знака
>	больше	строгий знак (число на границе не включается )
строгий знак (число на границе не включается )
≥	больше или равно	нестрогий знак (число на границе включается )
≤	меньше или равно	нестрогий знак (число на границе включается )

Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.

В отличии от уравнения в неравенстве вместо знака равно « = » используют любой знак сравнения: « > », « », « ≤ » или « ≥ ».

Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени.

Рассмотрим пример линейного неравенства.

Как решить линейное неравенство

Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом « 1 ».

При решении линейных неравенств используют правило переноса и правило деления неравенства на число.

Правило переноса в неравенствах

Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.

При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на противоположный .

Вернемся к нашему неравенству и используем правило переноса.

Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.

Нарисуем числовую ось для неизвестного « x » и отметим на ней число « 14 ».

При нанесении числа на числовую ось соблюдаются следующие правила:

• если неравенство строгое, то число отмечается как «пустая» точка. Это означает, что число не входит в область решения;
• если неравенство нестрогое, то число отмечается как «заполненная» точка. Это означает, что число входит в область решения.

Заштрихуем на числовой оси по полученному ответу « x » все решения неравенства, то есть область слева от числа « 14 ».

Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство « x − 6 » даст верный результат.

Возьмем, например число « 12 » из заштрихованной области и подставим его вместо « x » в исходное неравенство « x − 6 ».

Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.

Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.

Решением неравенства называют множество чисел из заштрихованной области на числовой оси.

В нашем примере ответ « x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее « 14 ») будет являться решением неравенства « x − 6 ».

Правило умножения или деления неравенства на число

Рассмотрим другое неравенство.

Используем правило переноса и перенесём все числа без неизвестного, в правую часть.

Теперь нам нужно сделать так, чтобы при неизвестном « x » стоял коэффициент « 1 ». Для этого достаточно разделить и левую, и правую часть на число « 2 ».

При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.

• Если неравенство умножается (делится) на положительное число, то
  знак самого неравенства остаётся прежним .
• Если неравенство умножается (делится) на отрицательное число, то
  знак самого неравенства меняется на противоположный .

Разделим « 2x > 16 » на « 2 ». Так как « 2 » — положительное число, знак неравенства останется прежним.

Рассмотрим другое неравенство.

Разделим неравенство на « −3 ». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.

Источник