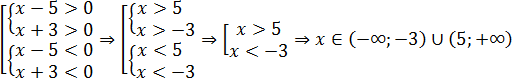Как найти целое решение неравенства на отрезке - Сайт, где вы сможете решить свои вопросы

При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
 Напомним свойства числовых неравенств.
 1. Если а > b , то b < а; наоборот, если а < b, то b > а.
 2. Если а > b и b > c, то а > c. Точно так же, если а b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.

Замечание.

Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
 5. Если а > b и c < d, то а – c > b – d; если а d, то а – c b и m – положительное число, то m а > m b и , т.е. обе части неравенства можно умножить или разделить на одно и то же положительное число ( знак неравенства остаётся тем же ).
 Если же а > b и n – отрицательное число, то n а < n b и , т.е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при этом знак неравенства нужно переменить на противоположный.
 7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а² > b², и если а < b, то а² < b², т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.

8. Если а > b, где а, b > 0, то и если а < b , то .

Виды неравенств и способы их решения

1. Линейные неравенства и системы неравенств

Пример 1. Решить неравенство .
 Решение:
 .
 Ответ: х < – 2.

Пример 2. Решить систему неравенств
    Решение:
         .
    Ответ: (– 2; 0].

Пример 3. Найти наименьшее целое решение системы неравенств

    Решение:

    Ответ:

2. Квадратные неравенства

Пример 4. Решить неравенство х² > 4.
    Решение:
        х² > 4   (х – 2)∙(х + 2) > 0.
        Решаем методом интервалов.

Ответ:

3. Неравенства высших степеней

Пример 5. Решить неравенство (х + 3)∙(х² – 2х + 1) > 0.
    Решение:

    Ответ: .

Пример 6. Найти середину отрезка, который является решением неравенства 4х² – 24х + 24 < 4у², где .
 Решение:
 Область определения неравенства: .
 С учётом области определения 4х² – 24х + 24 < 4у² будет равносильно неравенству

Решаем методом интервалов.

        Решение неравенства: .
        Середина отрезка: .
    Ответ: .

4. Рациональные неравенства

Пример 7. Найти все целые решения, удовлетворяющие неравенству .
    Решение:

Методом интервалов:

        Решение неравенства: .
        Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
    Ответ: – 6; – 5; – 4; 1.

5. Иррациональные неравенства

Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.

Пример 8. Решить неравенство .
    Решение:
        Область определения: .
        Так как арифметический корень не может быть отрицательным числом, то .
    Ответ: .

Пример 9. Найти все целые решения неравенства .

Решение:

Область определения .

– быть отрицательным не может, следовательно, чтобы произведение было неотрицательным достаточно потребовать выполнения неравенства , при этом учитывая область определения. Т.е. исходное неравенство равносильно системе .

Целыми числами из этого отрезка будут 2; 3; 4.

Ответ: 2; 3; 4.

Пример 10. Решить неравенство .

Решение:

Область определения:

Преобразуем неравенство: . С учётом области определения видим, что обе части неравенства – положительные числа. Возведём обе части в квадрат и получим неравенство, равносильное исходному.

т.е. , и этот числовой отрезок включён в область определения.

Ответ: .

Пример 11. Решить неравенство .

Решение:

Раскрываем знак модуля.

Объединим решения систем 1) и 2): .

Ответ: .

6. Показательные, логарифмические неравенства и системы неравенств

Пример 12. Решите неравенство .

Решение:

Ответ: .

Пример 13. Решите неравенство .

Решение:

Ответ: .

Пример 14. Решите неравенство .

Решение:

Ответ: .

Пример 15. Решите неравенство .

Решение:

Ответ: .

Задания для самостоятельного решения

Базовый уровень

Целые неравенства и системы неравенств

1) Решите неравенство 2х – 5 ≤ 3 + х.

2) Решите неравенство – 5х > 0,25.

3) Решите неравенство .

4) Решите неравенство 2 – 5х ≥ – 3х.

5) Решите неравенство х + 2 < 5x – 2(x – 3).

6) Решите неравенство
.

7) Решите неравенство (х – 3) (х + 2) > 0.

8) Решить систему неравенств

9) Найдите целочисленные решения системы неравенств .

10) Решить систему неравенств .

11) Решить систему неравенств

12) Найти наименьшее целое решение неравенства

13) Решите неравенство .

14) Решите неравенство .

15) Решите неравенство .

16) Решите неравенство .

17) Найдите решение неравенства , принадлежащие промежутку .

18) Решить систему неравенств

19) Найти все целые решения системы

Рациональные неравенства и системы неравенств

20) Решите неравенство .

21) Решите неравенство .

22) Определите число целых решений неравенства .

23) Определите число целых решений неравенства .

24) Решите неравенство .

25) Решите неравенство 2^x<16 .

26) Решите неравенство .

27) Решите неравенство .

28) Решите неравенство .

29) Найдите сумму целых решений неравенства на отрезке [– 7, 7].

30) Решите неравенство .

31) Решите неравенство .

Иррациональные неравенства

32) Решите неравенство .

33) Решите неравенство

34) Решите неравенство .

Показательные, логарифмические неравенства и системы неравенств

35) Решите неравенство .

36) Решите неравенство .

37) Решите неравенство .

38) Решите неравенство .

39) Решите неравенство .

40) Решите неравенство 49∙7^х < 7^{3х + 3}.

41) Найдите все целые решения неравенства .

42) Решите неравенство .

43) Решите неравенство .

44) Решите неравенство 7^x+1-7^x<42 .

45) Решите неравенство log₃(2x²+x-1)>log₃2 .

46) Решите неравенство log_0,5(2x+3)>0 .

47) Решите неравенство .

48) Решите неравенство .

49) Решите неравенство .

50) Решите неравенство log_x+112>log_x+12 .

51) Решите неравенство log_x9<2.

52) Решите неравенство .

Повышенный уровень

53) Решите неравенство |x-3|>2x.

54) Решите неравенство 2│х + 1| > х + 4.

55) Найдите наибольшее целое решение неравенства .

56) Решить систему неравенств

57) Решить систему неравенств .

58) Решите неравенство .

59) Решите неравенство 25•2^x-10^x+5^x>25 .

60) Решите неравенство .

Ответы

1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) ; 8) (-2;0]; 9) – 1; 10) х ≥ 7,5; 11); 12) 1; 13); 14) х ≤ – 0,9; 15) х < – 1; 16) х < 24; 17); 18) ; 19) 3, 4, 5;

20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26); 27) (– 3; 17); 28)

; 29) – 10; 30) (0; + ∞); 31); 32) [1;17); 33) x > 17; 34) х ≥ 2; 35); 36) х < 2; 37) х > 0; 38) х ≤ 3; 39) х > – 3,5; 40) х > – 0,5; 41) 0, 1, 2, 3, 4, 5; 42) х < 3; 43) ; 44) х < 1; 45) ; 46) (– 1,5; – 1); 47) х < 0; 48); 49) ; 50) х > 0; 51) ; 52) ; 53) х < 1; 54); 55) – 1; 56) ; 57) [3,5; 10]; 58) (0, 1); 59) (0; 2); 60)

Источник

Метод интервалов: решение простейших строгих неравенств

12 ноября 2017

Домашнее задание
Ответы

Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:

(x − 5)(x + 3) > 0

Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:

Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:

x² − 2x − 15 > 0

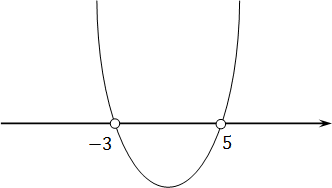
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:

Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.

Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.

Почему эти методы неэффективны?

Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.

Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:

(x − 7)(x − 1)(x + 4)(x + 9) < 0

Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.

Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.

Что такое метод интервалов

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:

Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.

Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.

На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:

Задача. Решите неравенство:

(x − 2)(x + 7) < 0

Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:

(x − 2)(x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.

Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:

Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:

f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;

Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.

Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.

Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:

Вернемся к исходному неравенству, которое имело вид:

(x − 2)(x + 7) < 0

Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.

Задача. Решите неравенство:

(x + 9)(x − 3)(1 − x) < 0

Шаг 1: приравниваем левую часть к нулю:

(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.

Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.

Шаг 2: отмечаем все корни на координатной прямой:

Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:

f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.

Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:

Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:

(x + 9)(x − 3)(1 − x) < 0

Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:

x ∈ (−9; 1) ∪ (3; +∞)

Это и есть ответ.

Замечание по поводу знаков функции

Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.

Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:

Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.

Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.

Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.

Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:

(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;

Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.

Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:

Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.

«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.

На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:

f (x) = (x − 1)(2 + x)(7 − x)

Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.

Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.

Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:

(+) · (+) · (−) = (−)

Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:

Исходное неравенство имело вид:

(x − 1)(2 + x)(7 − x) < 0

Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:

x ∈ (−2; 1) ∪ (7; +∞)

Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:

Задача. Решите неравенство:

x(2x + 8)(x − 3) > 0

Заменяем неравенство уравнением и решаем его:

x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.

Отмечаем все три корня на координатной прямой (сразу со знаками):

Справа на координатной оси стоит плюс, т.к. функция имеет вид:

f (x) = x(2x + 8)(x − 3)

А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:

x ∈ (−4; 0) ∪ (3; +∞)

Смотрите также:

Метод интервалов: случай нестрогих неравенств
Тест по методу интервалов для строгих неравенств
Сводный тест по задачам B12 (2 вариант)
Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
Формулы приведения: ускоряем вычисления в тригонометрии
Задачи B4: перевозка груза тремя фирмами

Источник

Сколько целых решений имеет неравенство -18

Для того, чтобы определить сколько целых решений имеет неравенство — 18 < х < 174 выполним следующие действия.

Алгоритм решения задачи

вспомним определение целого числа;
выясним входят ли концы отрезка в решение неравенства;
найдем число отрицательных решений неравенства;
найдем число положительных решений неравенства;
найдем количество целых решений неравенства.

Определение целого числа

Давайте вспомним определение целого числа в математике.

Натуральные числа, противоположные им числа и 0 называются целыми числами.

Теперь выясним входят ли концы отрезка в решение неравенства.

Знаки в заданном неравенстве — 18 < х < 174 строгие и при изображении этих точек на координатной прямой они будут выколотыми и не будут являться решением неравенства.

Найдем количество целых решений неравенства — 18 < х < 174

Чтобы посчитать число целых решений неравенства можно поступить двумя способами:

1) выписать все целые числа удовлетворяющие неравенству и сосчитать их;

2) методом логических рассуждений вычислить число отрицательных решений, число положительных решений и не забыть про ноль.

Давайте решим наше задание вторым способом.

Рассмотрим отрезок (- 18; 0). На нем целых чисел, удовлетворяющих нашему неравенству будет 17 (так как -18 не входит и число 0 мы посчитаем отдельно).

0 будем считать за 1 решение неравенства.

Рассмотрим отрезок (0; 174). На нем целых чисел, удовлетворяющих неравенству 173.

Сложим число всех найденных решений на каждом из рассмотренных отрезков и получим:

Что значит найти целые решения системы неравенств. Найти целые цешения системы неравенств. Соблюдение вашей конфиденциальности на уровне компании

В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.

Найти целые решения системы неравенств — одно из заданий такого рода.

1) Найти целые решения системы неравенств:

Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:

Title=»Rendered by QuickLaTeX.com»>

После упрощения разделим обе части каждого неравенства на . При делении на положительное число знак неравенства не меняется:

Title=»Rendered by QuickLaTeX.com»>

Отмечаем решения неравенств на числовых прямых. является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).

Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:

Из промежутка (-4;2) выбираем целые решения.

Ответ: -3; -2; -1; 0; 1.

2) Какие целые решения имеет система неравенств?

Title=»Rendered by QuickLaTeX.com»>

Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком

Title=»Rendered by QuickLaTeX.com»>

Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:

Title=»Rendered by QuickLaTeX.com»>

Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:

Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.

Ответ: -2; -1; 0; 1; 2; 3; 4.

В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.

3) Сколько целых решений имеет система неравенств?

Переносим неизвестные в одну сторону, известные — в другую:

Title=»Rendered by QuickLaTeX.com»>

Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:

Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:

Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.

4) Сколько целых чисел являются решениями системы неравенств?

Неравенство это выражение с, ≤, или ≥. Например, 3x — 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно. Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений . Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .

Линейные неравенства

Принципы решения неравенств
Для любых вещественных чисел a, b, и c :
Принцип прибавления неравенств : Если a Принцип умножения для неравенств : Если a 0 верно, тогда ac Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.

Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами .

Пример 1 Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x — 5 b) 13 — 7x ≥ 10x — 4
Решение
Любое число, меньше чем 11/5, является решением.
Множество решений есть Чтобы сделать проверку, мы можем нарисовать график y 1 = 3x — 5 и y 2 = 6 — 2x. Тогда отсюда видно, что для x
Множеством решений есть , или (-∞, 1]. График множества решений изображён ниже.

Двойные неравенства

Когда два неравенства соединены словом и , или , тогда формируется двойное неравенство . Двойное неравенство, как
-3 и 2x + 5 ≤ 7
называется соединённым , потому что в нём использовано и . Запись -3 Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.

Пример 2 Решите -3 Решение У нас есть

Множество решений или x > 3>. Мы можем также написать решение с использованием обозначения интервала и символ для объединения или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.

Для проверки, нарисуем y 1 = 2x — 5, y 2 = -7, и y 3 = 1. Заметьте, что для или x > 3>, y 1 ≤ y 2 или y 1 > y 3 .

Неравенства с абсолютным значением (модулем)

Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x| |x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.

Например,
|x| |y| ≥ 1 эквивалентно y ≤ -1 или y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.

Пример 4 Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2| b) |5 — 2x| ≥ 1

Решение
a) |3x + 2|

Множеством решением есть
b) |5 — 2x| ≥ 1
Множеством решением есть или x ≥ 3>, или (-∞, 2] .

Весь выше прописанный алгоритм записывается так:

3 · x + 12 ≤ 0 ; 3 · x ≤ − 12 ; x ≤ − 4 .

Ответ: x ≤ − 4 или (− ∞ , − 4 ] .

Указать все имеющиеся решения неравенства − 2 , 7 · z > 0 .

Решение

Из условия видим, что коэффициент a при z равняется — 2 , 7 , а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.

Производим деление обеих частей уравнения на число — 2 , 7 . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (− 2 , 7 · z) : (− 2 , 7) 0 ; z , ≥) :

Числовое неравенство вида b , ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.

Решить неравенство 0 · x + 7 > 0 .

Решение

Данное линейное неравенство 0 · x + 7 > 0 может принимать любое значение x . Тогда получим неравенство вида 7 > 0 . Последнее неравенство считается верным, значит любое число может быть его решением.

Ответ : промежуток (− ∞ , + ∞) .

Найти решение неравенства 0 · x − 12 , 7 ≥ 0 .

Решение

При подстановке переменной x любого числа получим, что неравенство получит вид − 12 , 7 ≥ 0 . Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.

Ответ: решений нет.

Рассмотрим решение линейных неравенств, где оба коэффициента равняется нулю.

Определить не имеющее решение неравенство из 0 · x + 0 > 0 и 0 · x + 0 ≥ 0 .

Решение

При подстановке любого числа вместо x получим два неравенства вида 0 > 0 и 0 ≥ 0 . Первое является неверным. Значит, 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет бесконечное количество решений, то есть любое число.

Ответ : неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.

Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.

Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0 . Иначе придется вычислять при помощи другого метода.

Метод интервалов – это:

введение функции y = a · x + b ;
поиск нулей для разбивания области определения на промежутки;
определение знаков для понятия их на промежутках.

Соберем алгоритм для решения линейных уравнений a · x + b , ≥) при a ≠ 0 с помощью метода интервалов:

нахождение нулей функции y = a · x + b , чтобы решить уравнение вида a · x + b = 0 . Если a ≠ 0 , тогда решением будет единственный корень, который примет обозначение х 0 ;
построение координатной прямой с изображением точки с координатой х 0 , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
определение знаков функции y = a · x + b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, 0 .

Решение

Из алгоритма следует, что для начала нужно найти корень уравнения − 3 · x + 12 = 0 . Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.

Нужно определить знаки на промежутках. Чтобы определить его на промежутке (− ∞ , 4) , необходимо произвести вычисление функции y = − 3 · x + 12 при х = 3 . Отсюда получим, что − 3 · 3 + 12 = 3 > 0 . Знак на промежутке является положительным.

Определяем знак из промежутка (4 , + ∞) , тогда подставляем значение х = 5 . Имеем, что − 3 · 5 + 12 = − 3 , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.

Из чертежа видно, что искомое решение имеет вид (− ∞ , 4) или x 0 и 0 , 5 · x − 1 ≥ 0 . Их решениями будут значения x 2 и x ≥ 2 . Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.

решением неравенства 0 , 5 · x − 1 0 считается промежуток, гре функция располагается выше О х;
решением 0 , 5 · x − 1 ≥ 0 считается промежуток, где график выше О х или совпадает.

Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y = a · x + b , а правая – y = 0 , причем совпадает с О х.

Построение графика функции y = a · x + b производится:

во время решения неравенства a · x + b 0 производится определение промежутка, где график изображается выше О х;
во время решения неравенства a · x + b ≥ 0 производится определение промежутка, где график находится выше О х или совпадает.

Решить неравенство — 5 · x — 3 > 0 при помощи графика.

Решение

Необходимо построить график линейной функции — 5 · x — 3 > 0 . Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с О х — 5 · x — 3 > 0 получим значение — 3 5 . Изобразим графически.

Решение неравенства со знаком > , тогда необходимо обратить внимание на промежуток выше О х. Выделим красным цветом необходимую часть плоскости и получим, что

Необходимый промежуток является частью О х красного цвета. Значит, открытый числовой луч — ∞ , — 3 5 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки — 3 5 также являлось бы решением неравенства. И совпадало бы с О х.

Ответ : — ∞ , — 3 5 или x 0 , 7 · (x − 1) + 3 ≤ 4 · x − 2 + x , x — 3 5 — 2 · x + 1 > 2 7 · x .

Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.

При сведении неравенства 5 − 2 · x > 0 к линейному, представляем его таким образом, чтобы оно имело вид − 2 · x + 5 > 0 , а для приведения второго получаем, что 7 · (x − 1) + 3 ≤ 4 · x − 2 + x . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:

7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0

Это приводит решение к линейному неравенству.

Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.

Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:

раскрыть скобки;
слева собрать переменные, а справа числа;
привести подобные слагаемые;
разделить обе части на коэффициент при x .

Решить неравенство 5 · (x + 3) + x ≤ 6 · (x − 3) + 1 .

Решение

Производим раскрытие скобок, тогда получим неравенство вида 5 · x + 15 + x ≤ 6 · x − 18 + 1 . После приведения подобных слагаемых имеем, что 6 · x + 15 ≤ 6 · x − 17 . После перенесения слагаемых с левой в правую, получим, что 6 · x + 15 − 6 · x + 17 ≤ 0 . Отсюда имеет неравенство вида 32 ≤ 0 из полученного при вычислении 0 · x + 32 ≤ 0 . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.

Ответ : нет решений.

Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 5 2 · x − 1 ≥ 1 является показательным уравнением, которое сводится к решению линейного вида 2 · x − 1 ≥ 0 . Эти случаи будут рассмотрены при решении неравенств данного вида.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Решение целых и дробно рациональных неравенств

Продолжаем разбирать способы решения неравенств, имеющих в составе одну переменную. Мы уже изучили линейные и квадратные неравенства, которые представляют из себя частные случаи рациональных неравенств. В этой статье мы уточним, неравенства какого типа относятся к рациональным, расскажем, на какие виды они делятся (целые и дробные). После этого покажем, как правильно их решать, приведем нужные алгоритмы и разберем конкретные задачи.

Понятие рациональных равенств

Когда в школе изучают тему решения неравенств, то сразу берут рациональные неравенства. На них приобретаются и оттачиваются навыки работы с этим видом выражений. Сформулируем определение данного понятия:

Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обоих частях рациональные выражения.

Отметим, что определение никак не затрагивает вопрос количества переменных, значит, их может быть сколь угодно много. Следовательно, возможны рациональные неравенства с 1 , 2 , 3 и более переменными. Чаще всего приходится иметь дело с выражениями, содержащими всего одну переменную, реже две, а неравенства с большим количеством переменных обычно в рамках школьного курса не рассматривают вовсе.

Таким образом, мы можем узнать рациональное неравенство, посмотрев на его запись. И с правой, и с левой стороны у него должны быть расположены рациональные выражения. Приведем примеры:

x > 4 x 3 + 2 · y ≤ 5 · ( y − 1 ) · ( x 2 + 1 ) 2 · x x — 1 ≥ 1 + 1 1 + 3 x + 3 · x 2

А вот неравенство вида 5 + x + 1 < x · y · z не относится к рациональным, поскольку слева у него есть переменная под знаком корня.

Все рациональные неравенства делятся на целые и дробные.

Целое рациональное равенство состоит из целых рациональных выражений (в обеих частях).

Дробно рациональное равенство – это такое равенство, которое содержит дробное выражение в одной или обеих своих частях.

Например, неравенства вида 1 + x — 1 1 3 2 2 + 2 3 + 2 11 — 2 · 1 3 · x — 1 > 4 — x 4 и 1 — 2 3 5 — y > 1 x 2 — y 2 являются дробно рациональными, а 0 , 5 · x ≤ 3 · ( 2 − 5 · y ) и 1 : x + 3 > 0 – целыми.

Мы разобрали, что из себя представляют рациональные неравенства, и выделили их основные типы. Можем переходить дальше, к обзору способов их решения.

Как решать целые неравенства

Допустим, что нам требуется найти решения целого рационального неравенства r ( x ) < s ( x ) , которое включает в себя только одну переменную x . При этом r ( x ) и s ( x ) представляют собой любые целые рациональные числа или выражения, а знак неравенства может отличаться. Чтобы решить это задание, нам нужно преобразовать его и получить равносильное равенство.

Начнем с перенесения выражения из правой части в левую. Получим следующее:

вида r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ )

Мы знаем, что r ( x ) − s ( x ) будет целым значением, а любое целое выражение допустимо преобразовать в многочлен. Преобразуем r ( x ) − s ( x ) в h ( x ) . Это выражение будет тождественно равным многочленом. Учитывая, что у r ( x ) − s ( x ) и h ( x ) область допустимых значений x одинакова, мы можем перейти к неравенствам h ( x ) < 0 ( ≤ , > , ≥ ) , которое будет равносильно исходному.

Зачастую такого простого преобразования будет достаточно для решения неравенства, поскольку в итоге может получиться линейное или квадратное неравенство, значение которого вычислить несложно. Разберем такие задачи.

Условие: решите целое рациональное неравенство x · ( x + 3 ) + 2 · x ≤ ( x + 1 ) 2 + 1 .

Решение

Начнем с переноса выражения из правой части в левую с противоположным знаком.

x · ( x + 3 ) + 2 · x − ( x + 1 ) 2 − 1 ≤ 0

Теперь, когда мы выполнили все действия с многочленами слева, можно переходить к линейному неравенству 3 · x − 2 ≤ 0 , равносильному тому, что было дано в условии. Решить его несложно:

Ответ: x ≤ 2 3 .

Условие: найдите решение неравенства ( x 2 + 1 ) 2 − 3 · x 2 > ( x 2 − x ) · ( x 2 + x ) .

Решение

Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.

( x 2 + 1 ) 2 − 3 · x 2 − ( x 2 − x ) · ( x 2 + x ) > 0 x 4 + 2 · x 2 + 1 − 3 · x 2 − x 4 + x 2 > 0 1 > 0

В итоге наших преобразований мы получили неравенство, которое будет верным при любых значениях x , следовательно, решением исходного неравенства может быть любое действительное число.

Ответ: любое действительно число.

Условие: решите неравенство x + 6 + 2 · x 3 − 2 · x · ( x 2 + x − 5 ) > 0 .

Решение

Из правой части мы ничего переносить не будем, поскольку там 0 . Начнем сразу с преобразования левой части в многочлен:

x + 6 + 2 · x 3 − 2 · x 3 − 2 · x 2 + 10 · x > 0 − 2 · x 2 + 11 · x + 6 > 0 .

Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.

Начнем с вычисления корней квадратного трехчлена − 2 · x 2 + 11 · x + 6 :

D = 11 2 — 4 · ( — 2 ) · 6 = 169 x 1 = — 11 + 169 2 · — 2 , x 2 = — 11 — 169 2 · — 2 x 1 = — 0 , 5 , x 2 = 6

Теперь на схеме отметим все необходимые нули. Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.

Нам будет нужна область параболы, расположенная над осью абсцисс, поскольку в неравенстве у нас стоит знак > . Нужный интервал равен ( − 0 , 5 , 6 ) , следовательно, эта область значений и будет нужным нам решением.

Ответ: ( − 0 , 5 , 6 ) .

Бывают и более сложные случаи, когда слева получается многочлен третьей или более высокой степени. Чтобы решить такое неравенство, рекомендуется использовать метод интервалов. Сначала мы вычисляем все корни многочлена h ( x ) , что чаще всего делается с помощью разложения многочлена на множители.

Условие: вычислите ( x 2 + 2 ) · ( x + 4 ) < 14 − 9 · x .

Решение

Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.

( x 2 + 2 ) · ( x + 4 ) − 14 + 9 · x < 0 x 3 + 4 · x 2 + 2 · x + 8 − 14 + 9 · x < 0 x 3 + 4 · x 2 + 11 · x − 6 < 0

В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени. Применим метод интервалов для его решения.

Сначала вычисляем корни многочлена, для чего нам надо решить кубическое уравнение x 3 + 4 · x 2 + 11 · x − 6 = 0 . Имеет ли оно рациональные корни? Они могут быть лишь в числе делителей свободного члена, т.е. среди чисел ± 1 , ± 2 , ± 3 , ± 6 . Подставим их по очереди в исходное уравнение и выясним, что числа 1 , 2 и 3 будут его корнями.

Значит, многочлен x 3 + 4 · x 2 + 11 · x − 6 может быть описан в виде произведения ( x − 1 ) · ( x − 2 ) · ( x − 3 ) , и неравенство x 3 + 4 · x 2 + 11 · x − 6 < 0 может быть представлено как ( x − 1 ) · ( x − 2 ) · ( x − 3 ) < 0 . С неравенством такого вида нам потом будет легче определить знаки на промежутках.

Далее выполняем оставшиеся шаги интервального метода: рисуем числовую прямую и точки на ней с координатами 1 , 2 , 3 . Они разбивают прямую на 4 промежутка, в которых нужно определить знаки. Заштрихуем промежутки с минусом, поскольку исходное неравенство имеет знак < .

Нам осталось только записать готовый ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .

Ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .

В некоторых случаях выполнять переход от неравенства r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) к h ( x ) < 0 ( ≤ , > , ≥ ) , где h ( x ) – многочлен в степени выше 2 , нецелесообразно. Это распространяется на те случаи, когда представить r ( x ) − s ( x ) как произведение линейных двучленов и квадратных трехчленов проще, чем разложить h ( x ) на отдельные множители. Разберем такую задачу.

Условие: найдите решение неравенства ( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) ≥ 2 · x · ( x 2 − 2 · x − 1 ) .

Решение

Данное неравенство относится к целым. Если мы перенесем выражение из правой части влево, раскроем скобки и выполним приведение слагаемых, то получим x 4 − 4 · x 3 − 16 · x 2 + 40 · x + 19 ≥ 0 .

Решить такое неравенство непросто, поскольку придется искать корни многочлена четвертой степени. Оно не имеет ни одного рационального корня (так, 1 , − 1 , 19 или − 19 не подходят), а искать другие корни сложно. Значит, воспользоваться этим способом мы не можем.

Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя x 2 − 2 · x − 1:

( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) − 2 · x · ( x 2 − 2 · x − 1 ) ≥ 0 ( x 2 − 2 · x − 1 ) · ( x 2 − 2 · x − 19 ) ≥ 0 .

Мы получили неравенство, равносильное исходному, и его решение даст нам искомый ответ. Найдем нули выражения в левой части, для чего решим квадратные уравнения x 2 − 2 · x − 1 = 0 и x 2 − 2 · x − 19 = 0 . Их корни – 1 ± 2 , 1 ± 2 5 . Переходим к равенству x — 1 + 2 · x — 1 — 2 · x — 1 + 2 5 · x — 1 — 2 5 ≥ 0 , которое можно решить методом интервалов:

Согласно рисунку, ответом будет — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .

Ответ: — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .

Добавим, что иногда нет возможности найти все корни многочлена h ( x ) , следовательно, мы не можем представить его в виде произведения линейных двучленов и квадратных трехчленов. Тогда решить неравенство вида h ( x ) < 0 ( ≤ , > , ≥ ) мы не можем, значит, решить исходное рациональное неравенство тоже нельзя.

Как решать дробно рациональные неравенства

Допустим, надо решить дробно рационально неравенств вида r ( x ) < s ( x ) ( ≤ , > , ≥ ) , где r ( x ) и s ( x ) являются рациональными выражениями, x – переменной. Хотя бы одно из указанных выражений будет дробным. Алгоритм решения в этом случае будет таким:

Определяем область допустимых значений переменной x .
Переносим выражение из правой части неравенства налево, а получившееся выражение r ( x ) − s ( x ) представляем в виде дроби. При этом где p ( x ) и q ( x ) будут целыми выражениями, которые являются произведениями линейных двучленов, неразложимых квадратных трехчленов, а также степеней с натуральным показателем.
Далее решаем полученное неравенство методом интервалов.
Последним шагом является исключение точек, полученных в ходе решения, из области допустимых значений переменной x , которую мы определили в начале.

Это и есть алгоритм решения дробно рационального неравенства. Большая часть его понятна, небольшие пояснения требуются только для п. 2 . Мы перенесли выражение из правой части налево и получили r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) , а как потом привести его к виду p ( x ) q ( x ) < 0 ( ≤ , > , ≥ ) ?

Сначала определим, всегда ли можно выполнить данное преобразование. Теоретически, такая возможность имеется всегда, поскольку в рациональную дробь можно преобразовать любое рациональное выражение. Здесь же у нас есть дробь с многочленами в числителе и знаменателе. Вспомним основную теорему алгебры и теорему Безу и определим, что любой многочлен n -ной степени, содержащий одну переменную, может быть преобразован в произведение линейных двучленов. Следовательно, в теории мы всегда можем преобразовать выражение таким образом.

На практике разложение многочленов на множители зачастую оказывается довольно трудной задачей, особенно если степень выше 4 . Если мы не сможем выполнить разложение, то не сможем и решить данное неравенство, однако в рамках школьного курса такие проблемы обычно не изучаются.

Далее нам надо решить, будет ли полученное неравенство p ( x ) q ( x ) < 0 ( ≤ , > , ≥ ) равносильным по отношению к r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) и к исходному. Есть вероятность, что оно может оказаться и неравносильным.

Равносильность неравенства будет обеспечена тогда, когда область допустимых значений p ( x ) q ( x ) совпадет с областью значений выражения r ( x ) − s ( x ) . Тогда последний пункт инструкции по решению дробно рациональных неравенств выполнять не нужно.

Но область значений для p ( x ) q ( x ) может оказаться шире, чем у r ( x ) − s ( x ) , например, за счет сокращения дробей. Примером может быть переход от x · x — 1 3 x — 1 2 · x + 3 к x · x — 1 x + 3 . Либо это может происходить при приведении подобных слагаемых, например, здесь:

x + 5 x — 2 2 · x — x + 5 x — 2 2 · x + 1 x + 3 к 1 x + 3

Для таких случаев и добавлен последний шаг алгоритма. Выполнив его, вы избавитесь от посторонних значений переменной, которые возникают из-за расширения области допустимых значений. Возьмем несколько примеров, чтобы было более понятно, о чем идет речь.

Условие: найдите решения рационального равенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x x — 3 2 · x + 1 .

Решение

Действуем по алгоритму, указанному выше. Сначала определяем область допустимых значений. В данном случае она определяется системой неравенств x + 1 · x — 3 ≠ 0 x — 3 2 ≠ 0 x — 3 2 · ( x + 1 ) ≠ 0 , решением которой будет множество ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .

Далее нам надо сделать так, чтобы в правой части неравенства получился 0 . Выполняем перенос выражения из правой части влево с противоположным знаком и получаем неравенство, равносильное исходному:

x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) ≥ 0

После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю ( x − 3 ) 2 · ( x + 1 ) :

x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) = = x · x — 3 + 4 · x + 1 + 3 · x x — 3 2 · x + 1 = x 2 + 4 · x + 4 ( x — 3 ) 2 · ( x + 1 )

Сворачиваем выражение в числителе, применяя формулу квадрата суммы:

x 2 + 4 · x + 4 x — 3 2 · x + 1 = x + 2 2 x — 3 2 · x + 1

Областью допустимых значений получившегося выражения является ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) . Мы видим, что она аналогична той, что была определена для исходного равенства. Заключаем, что неравенство x + 2 2 x — 3 2 · x + 1 ≥ 0 является равносильным исходному, значит, последний шаг алгоритма нам не нужен.

Используем метод интервалов:

Видим решение ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) , которое и будет решением исходного рационального неравенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x ( x — 3 ) 2 · ( x + 1 ) .

Ответ: ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .

Условие: вычислите решение x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 .

Решение

Определяем область допустимых значений. В случае с этим неравенством она будет равна всем действительным числам, кроме − 2 , − 1 , 0 и 1 .

Переносим выражения из правой части в левую:

x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 > 0

Далее выполняем преобразование левой части. Сначала преобразуем первую дробь:

x + 3 x — 1 — 3 x x + 2 = x + 3 — x — 3 x x + 2 = 0 x x + 2 = 0 x + 2 = 0

Учитывая получившийся результат, запишем:

x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 0 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 ( x + 1 ) · x — 1 = = — x — 1 ( x + 1 ) · x — 1 = — x + 1 ( x + 1 ) · x — 1 = — 1 x — 1

Для выражения — 1 x — 1 областью допустимых значений будет множество всех действительных чисел, за исключением единицы. Мы видим, что область значений расширилась: в нее были добавлены − 2 , − 1 и 0 . Значит, нам нужно выполнить последний шаг алгоритма.

Поскольку мы пришли к неравенству — 1 x — 1 > 0 , можем записать равносильное ему 1 x — 1 < 0 . С помощью метода интервалов вычислим решение и получим ( − ∞ , 1 ) .

Исключаем точки, которые не входят в область допустимых значений исходного равенства. Нам надо исключить из ( − ∞ , 1 ) числа − 2 , − 1 и 0 . Таким образом, решением рационального неравенства x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 будут значения ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .

Ответ: ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .

В заключение приведем еще один пример задачи, в котором окончательный ответ зависит от области допустимых значений.

Условие: найдите решение неравенства 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 .

Решение

Область допустимых значений неравенства, заданного в условии, определяет система x 2 ≠ 0 x 2 — x + 1 ≠ 0 x — 1 ≠ 0 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≠ 0 .

Решений у этой системы нет, поскольку

x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 = = ( x + 1 ) · x 2 — x + 1 x 2 — x + 1 — ( x — 1 ) · x + 1 x — 1 = = x + 1 — ( x + 1 ) = 0

Значит, исходное равенство 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 не имеет решения, поскольку нет таких значений переменной, при которой оно имело бы смысл.

Источник

taghaleviowh979

Вопрос по алгебре:

Найти целые решения неравенства на отрезке [-3;3]
Распишите как можно подробней пожалуйста
9^x-3^x-6>0

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Ответы и объяснения 1

tilrgra

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат – это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Источник

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Неравенства

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

> больше,

≥ больше или равно,

< меньше,

≤ меньше или равно,

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

a x b a x ≥ b

где a и b – любые числа, причем a ≠ 0, x – переменная.

Примеры линейных неравенств:

3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0

Решить линейное неравенство – получить выражение вида:

x < c x ≤ c x > c x ≥ c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.

Смысл выколотой точки в том, что сама точка в ответ не входит.

Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.

Смысл жирной точки в том, что сама точка входит в ответ.

Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.

Таблица числовых промежутков

Неравенство	Графическое решение	Форма записи ответа
x < c		x ∈ ( − ∞ ; c )
x ≤ c		x ∈ ( − ∞ ; c ]
x > c		x ∈ ( c ; + ∞ )
x ≥ c		x ∈ [ c ; + ∞ )

Алгоритм решения линейного неравенства

Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:

a x b a x ≥ b

Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.

Если a > 0 то неравенство приобретает вид x ≤ b a .

Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .

Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.

Примеры решения линейных неравенств:

№1. Решить неравенство 3 ( 2 − x ) > 18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 − 3 x > 18

− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )

Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x ∈ ( − ∞ ; − 4 )

№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x + 4 ≥ 3 x + 3 − 14

6 x − 3 x ≥ 3 − 14 − 4

3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.

x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x ∈ [ − 5 ; + ∞ )

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

Примеры:

№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x − 1 ≤ 6 x − 1

6 x − 6 x ≤ − 1 + 1

0 ≤ 0

Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.

Ответ:

x – любое число
x ∈ ( − ∞ ; + ∞ )
x ∈ ℝ

№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x + 6 − 9 x > − 8 x + 48

− 8 x + 8 x > 48 − 6

0 > 42

Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.

Ответ: x ∈ ∅

Квадратные неравенства

Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .

Отметить на числовой прямой корни трехчлена.

Если знак неравенства строгий > , < , точки будут выколотые.

Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).

Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Выбрать подходящие интервалы (или интервал).

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.

Записать ответ.

Примеры решения квадратных неравенств:

№1. Решить неравенство x 2 ≥ x + 12.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

x 2 ≥ x + 12

x 2 − x − 12 ≥ 0

x 2 − x − 12 = 0

a = 1, b = − 1, c = − 12

D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .

Точки -3 и 4 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

№2. Решить неравенство − 3 x − 2 ≥ x 2 .

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

− 3 x − 2 ≥ x 2

− x 2 − 3 x − 2 ≥ 0

− x 2 − 3 x − 2 = 0

a = − 1, b = − 3, c = − 2

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1

x 1 = − 2, x 2 = − 1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0

Это значит, что знак на интервале, в котором лежит точка 0 будет − .

Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.

Точки -2 и -1 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ [ − 2 ; − 1 ]

№3. Решить неравенство 4 < x 2 + 3 x .

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

4 < x 2 + 3 x

− x 2 − 3 x + 4 < 0

− x 2 − 3 x + 4 = 0

a = − 1, b = − 3, c = 4

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1

x 1 = − 4, x 2 = 1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:

− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0

Это значит, что знак на интервале, в котором лежит точка 2, будет -.

Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .

Точки -4 и 1 будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )

№4. Решить неравенство x 2 − 5 x < 6.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

x 2 − 5 x < 6

x 2 − 5 x − 6 < 0

x 2 − 5 x − 6 = 0

a = 1, b = − 5, c = − 6

D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1

x 1 = 6, x 2 = − 1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:

x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.

Точки -1 и 6 будут в круглых скобках, так как они выколотые

Ответ: x ∈ ( − 1 ; 6 )

№5. Решить неравенство x 2 < 4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

x 2 < 4

x 2 − 4 < 0

x 2 − 4 = 0

( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2

x 1 = 2, x 2 = − 2

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:

x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .

Точки -2 и 2 будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 2 ; 2 )

№6. Решить неравенство x 2 + x ≥ 0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.

x 2 + x ≥ 0

x 2 + x = 0

x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1

x 1 = 0, x 2 = − 1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:

x 2 + x = 1 2 + 1 = 2 > 0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):

f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.

Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Нанести нули числителя и нули знаменателя на ось x.

Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.

Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.

Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.

Расставить знаки на интервалах.

Выбрать подходящие интервалы и записать ответ.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

Приравниваем числитель к нулю f ( x ) = 0.

x − 1 = 0

x = 1 – это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.

Приравниваем знаменатель к нулю g ( x ) = 0.

x + 3 = 0

x = − 3 – это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Привести неравенство к виду f ( x ) g ( x ) ≤ 0.

3 ( x + 8 ) ≤ 5

3 ( x + 8 ) − 5 x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

− 5 x − 37 x + 8 ≤ 0

Приравнять числитель к нулю f ( x ) = 0.

− 5 x − 37 = 0

− 5 x = 37

x = − 37 5 = − 37 5 = − 7,4

x = − 7,4 – ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.

Приравнять знаменатель к нулю g ( x ) = 0.

x + 8 = 0

x = − 8 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0

Это значит, что знак на интервале, в котором лежит точка 0 будет -.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.

В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

Приравнять числитель к нулю f ( x ) = 0.

x 2 − 1 = 0

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

x 1 = 1, x 2 = − 1 – нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.

Приравнять знаменатель к нулю g ( x ) = 0.

x = 0 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Системы неравенств

Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств – это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

{ x + 4 > 0 2 x + 3 ≤ x 2

Алгоритм решения системы неравенств

Решить первое неравенство системы, изобразить его графически на оси x.

Решить второе неравенство системы, изобразить его графически на оси x.

Нанести решения первого и второго неравенств на ось x.

Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Примеры решений систем неравенств:

№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2 x − 3 ≤ 5

2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

x ≤ 4 ;

Графическая интерпретация:

Точка 4 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

7 − 3 x ≤ 1

− 3 x ≤ 1 − 7

− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.

x ≥ 2

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.

Ответ: x ∈ [ 2 ; 4 ]

№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2 x − 1 ≤ 5

2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

x ≤ 3

Графическая интерпретация:

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

1 < − 3 x − 2

3 x < − 1 − 2

3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.

x < − 1

Графическая интерпретация решения:

Точка -1 на графике выколотая, так как знак неравенства строгий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.

Ответ: x ∈ ( − ∞ ; − 1 )

№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

3 x + 1 ≤ 2 x

3 x − 2 x ≤ − 1

x ≤ − 1

Графическая интерпретация решения:

Решаем второе неравенство системы

x − 7 > 5 − x

x + x > 5 + 7

2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

x > 6

Графическая интерпретация решения:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

Ответ: x ∈ ∅

№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

x + 4 > 0

x > − 4

Графическая интерпретация решения первого неравенства:

Решаем второе неравенство системы

2 x + 3 ≤ x 2

− x 2 + 2 x + 3 ≤ 0

Решаем методом интервалов.

− x 2 + 2 x + 3 = 0

a = − 1, b = 2, c = 3

D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16

D > 0 – два различных действительных корня.

x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .

Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.

Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )

Скачать домашнее задание к уроку 8.

Источник

Виды неравенств и способы их решения

1. Линейные неравенства и системы неравенств

2. Квадратные неравенства

3. Неравенства высших степеней

4. Рациональные неравенства

5. Иррациональные неравенства

6. Показательные, логарифмические неравенства и системы неравенств

Задания для самостоятельного решения

Базовый уровень

Целые неравенства и системы неравенств

Рациональные неравенства и системы неравенств

Иррациональные неравенства

Показательные, логарифмические неравенства и системы неравенств

Повышенный уровень

Ответы

Метод интервалов: решение простейших строгих неравенств

Почему эти методы неэффективны?

Что такое метод интервалов

Замечание по поводу знаков функции

Сколько целых решений имеет неравенство -18

Алгоритм решения задачи

Определение целого числа

Найдем количество целых решений неравенства — 18 < х < 174

Что значит найти целые решения системы неравенств. Найти целые цешения системы неравенств. Соблюдение вашей конфиденциальности на уровне компании

Линейные неравенства

Двойные неравенства

Неравенства с абсолютным значением (модулем)

Решение целых и дробно рациональных неравенств

Понятие рациональных равенств

Как решать целые неравенства

Как решать дробно рациональные неравенства

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Есть сомнения?

Неравенства

Вам также может понравиться

Как найти скорость через сопротивление воздуха

Как найти ллойда фоллаут 2

На флешку не копируются файлы больше 4 гб как исправить

Добавить комментарий Отменить ответ