Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.
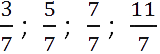
Обратите внимание, что в двух первых дробях (
и
)
числители меньше знаменателей. Такие дроби называют правильными.
Запомните!
![]()
У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь
всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробь
имеет числитель равный знаменателю (такие дроби
равны единицы), а дробь
имеет числитель больший знаменателя. Такие
дроби называют неправильными.
Запомните!
![]()
У неправильной дроби числитель равен или больше знаменателя.
Поэтому неправильная дробь или равна единице или больше единицы.
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.
Пример. Выделим целую часть из неправильной дроби
.
- Разделим в столбик числитель на знаменатель.
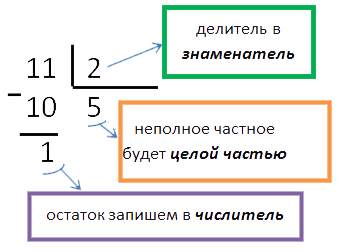
- Теперь запишем ответ.
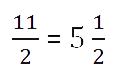
Запомните!
![]()
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно
выполнить и обратное действие, то есть представить смешанное число в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
- Умножаем целую часть на знаменатель.
3 · 5 = 15
- Прибавляем числитель.
15 + 2 = 17
- Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
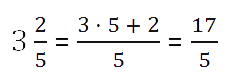
Любое смешанное число можно представить как сумму целой и дробной части.
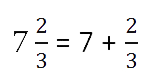
Запомните!
![]()
Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.
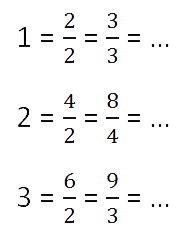
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
7 сентября 2020 в 18:33
Ксюша Островская

Профиль
Благодарили: 0
Сообщений: 1

Ксюша Островская
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
7 сентября 2020 в 20:33
Ответ для Ксюша Островская
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
= 55 : 66 = 5 : 6.
0
Спасибо
Ответить
14 декабря 2016 в 16:32
Руслан Потапов

Профиль
Благодарили: 0
Сообщений: 2

Руслан Потапов
Профиль
Благодарили: 0
Сообщений: 2
50
найдите числитель неправильной обыкновенной
дроби.равной смешанному числу.
помогите пожалуйста решением.
0
Спасибо
Ответить
15 декабря 2016 в 16:45
Ответ для Руслан Потапов
Амина Гилазиева

Профиль
Благодарили: 0
Сообщений: 2

Амина Гилазиева
Профиль
Благодарили: 0
Сообщений: 2
я думаю что это дродь
0
Спасибо
Ответить
15 декабря 2016 в 16:46
Ответ для Руслан Потапов
Амина Гилазиева

Профиль
Благодарили: 0
Сообщений: 2

Амина Гилазиева
Профиль
Благодарили: 0
Сообщений: 2
а числитель 71
0
Спасибо
Ответить
16 декабря 2016 в 19:33
Ответ для Руслан Потапов
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Чушь полная, конечно.
0
Спасибо
Ответить
18 октября 2016 в 10:44
Светлана Черемисова

Профиль
Благодарили: 0
Сообщений: 1

Светлана Черемисова
Профиль
Благодарили: 0
Сообщений: 1
Найдите целые значения а, при которых дробь принимает целые значения:
0
Спасибо
Ответить
18 октября 2016 в 18:00
Ответ для Светлана Черемисова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
±2.
0
Спасибо
Ответить
2 апреля 2016 в 19:01
Валерия Аралушкина

Профиль
Благодарили: 0
Сообщений: 1

Валерия Аралушкина
Профиль
Благодарили: 0
Сообщений: 1
Вычитание дроби из единицы и вычитание дроби из натурального числа.
5-7/10 10-3/5 9-5/9 7-5/11 8-2/5
Помогите я не очень понимаю как это делать!
0
Спасибо
Ответить
3 апреля 2016 в 12:22
Ответ для Валерия Аралушкина
Марина Доценко

Профиль
Благодарили: 0
Сообщений: 1

Марина Доценко
Профиль
Благодарили: 0
Сообщений: 1
5-7/10=5/1-7/10=50/10-7/10=43/10=4 целых и 3/10.
10-3/5=10/1-3/5=50/5-3/5=47/5=9 целых 2/5
9-5/9=9/1-5/9=81/9-5/9=76/9=8 целых 4/9
7-5/11=7/1-5/11=77/11-5/11=72/11=6 целых 6/11
8-2/5=8/1-2/5=40/5-2/5=38/5=7целых 3/5
0
Спасибо
Ответить
11 января 2016 в 23:48
Алинчик Плышевская

Профиль
Благодарили: 0
Сообщений: 1

Алинчик Плышевская
Профиль
Благодарили: 0
Сообщений: 1
Привет, помогите понять как сложить и вычетать смешаные числа?
0
Спасибо
Ответить
12 января 2016 в 19:05
Ответ для Алинчик Плышевская
Janina Kutovska

Профиль
Благодарили: 0
Сообщений: 2

Janina Kutovska
Профиль
Благодарили: 0
Сообщений: 2
смотри:
Сложение дробейСложение дробей с одинаковыми знаменателями.Определение. Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | б | = | + б |
| С | С | С |
Примеры сложения дробей с одинаковыми знаменателямиПример 1. Найти сумму двух дробей с одинаковыми знаменателями:
| 1 | + | 2 | = | 1 + 2 | = | 3 |
| 5 | 5 | 5 | 5 |
Пример 2. Найти сумму двух дробей с одинаковыми знаменателями:
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание дробей с равными знаменателями
Сложение обыкновенных дробей.Определение. Чтобы сложить две обыкновенные дроби, следует:привести дроби к наименьшему общему знаменателю;сложить числители дробей, а знаменатель оставить без изменений;сократить полученную дробь;Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.Примеры сложения обыкновенных дробейПример 3. Найти сумму двух дробей:
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | = | 3 | = | 3 | = | 1 |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
Пример 4. Найти сумму двух дробей:
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух обыкновенных дробей
Сложение смешанных чиселОпределение. Чтобы сложить смешанные дроби, надо:привести дробные части этих чисел к наименьшему общему знаменателю;отдельно сложить целые части и отдельно дробные части;если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;сократить полученную дробь.Примеры сложения смешанных чиселПример 5. Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
Пример 6. Найти сумму двух смешанных чисел:
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | = 4 | 5 |
| 24 | 24 | 24 | 24 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух смешанных чисел
Вычитание дробейВычитание дробей с одинаковыми знаменателями.Определение. Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | – | б | = | – б |
| С | С | С |
Примеры вычитания дробей с одинаковыми знаменателямиПример 7. Найти разность двух дробей с одинаковыми знаменателями:
| 3 | – | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
Пример 8. Найти разность двух дробей с одинаковыми знаменателями:
| 8 | – | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание дробей с равными знаменателями
Вычитание обыкновенных дробей.Определение. Чтобы вычесть из одной обыкновенной дроби другую, следует:привести дроби к наименьшему общему знаменателю;из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменений;сократить полученную дробь.
Примеры вычитания обыкновенных дробейПример 9. Найти разность двух дробей:
| 5 | – | 1 | = | 5 | – | 1·3 | = | 5 | – | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
Пример 10. Найти разность двух дробей:
| 3 | – | 1 | = | 3·3 | – | 1·5 | = | 9 | – | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух обыкновенных дробей
Вычитание смешанных чисел.Определение. Чтобы выполнить вычитание смешанных чисел, надо:привести дробные части этих чисел к наименьшему общему знаменателю;если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;отдельно выполнить вычитание целых частей и отдельно дробных частей;сократить полученную дробь.
Примеры вычитания смешанных чиселПример 11. Найти разность двух смешанных чисел:
| 2 | 1 | – | 1 | 1 | = | 2 | 1·3 | – | 1 | 1·2 | = | (2 — 1) | + | 3 | – | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
Пример 12. Найти разность двух смешанных чисел:
| 3 | 1 | – | 1 | 3 | = | 3 | 1·4 | – | 1 | 3·3 | = | 3 | 4 | – | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | – | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
Пример 13. Найти разность двух смешанных чисел:
| 1 | 1 | – | 3 | 2 | = | 1 | 1 | – | 3 | 2·2 | = | 1 | 1 | – | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | – | 3 | = | -2 | – | 3 | = | -2 | – | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух смешанных чиселДробиВиды дробей (обыкновенная правильная, неправильная, смешанная, десятичная)Основное свойство дробиСокращение дробиПриведение дробей к общему знаменателюПреобразование неправильной дроби в смешанное числоПреобразование смешанного числа в неправильную дробьСложение и вычитание дробейУмножение дробейДеление дробейСравнение дробейПреобразование десятичной дроби в обыкновенную дробьОнлайн калькуляторы дробейОнлайн упражнения с дробями
0
Спасибо
Ответить
12 января 2016 в 19:06
Ответ для Алинчик Плышевская
Janina Kutovska

Профиль
Благодарили: 0
Сообщений: 2

Janina Kutovska
Профиль
Благодарили: 0
Сообщений: 2
![]()
0
Спасибо
Ответить
8 сентября 2015 в 23:36
Лариса Краснова

Профиль
Благодарили: 0
Сообщений: 1

Лариса Краснова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
5 сентября 2016 в 14:12
Ответ для Лариса Краснова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
=25 ? + = 25 ? = 25 ? = 24=24,25
0
Спасибо
Ответить
8 сентября 2015 в 18:48
Никита Парфёнов

Профиль
Благодарили: 0
Сообщений: 1

Никита Парфёнов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
5 сентября 2016 в 9:14
Ответ для Никита Парфёнов
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В таком виде не ясна задача и решить её не возмонжо.
0
Спасибо
Ответить
8 сентября 2015 в 0:32
Sparkiss Princess

Профиль
Благодарили: 0
Сообщений: 1

Sparkiss Princess
Профиль
Благодарили: 0
Сообщений: 1
Всем привет! Помогите пожалуйста в решении примеров со смешанными дробями!
1.) 2
? 51
:11 · (21
? 9,8 : 2,8 · 4
) +
2.) 48
? ( 66,4 — 66,25) · (1
+
) + 28, 2: 5 ? 44, 2
3.) 12
? 0,5 ? 5
· 1
: (
+ 1
· 1,5) · 0,62
4.) 7, 025 ? (11
+ 22
? 33
) · 7,8 + (65
? 64) : 0,5
5.) 97
? 3
? 8,5 ? ( 2
+ 28,2 : 2) · 0,2 ·
22,5
Заранее спасибо! ![]()
0
Спасибо
Ответить
5 сентября 2016 в 14:21
Ответ для Sparkiss Princess
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Принцип решения таких примеров сводится к большой внимательности и применения нескольких простейших правил:
1) Последовательность действий в первую очередь действие в скобках, далее умножение/деление, далее сложение/вычитание
2) Правила перевода обыкновенных дробей в десятичные. Подробно можно почитать вот здесь: http://math-prosto.ru/index.php?page=pages/convert-decimal/convert-decimal2.php
3)Действия с десятичными дробями. О них можно подробнее почитать здесь: math-prosto.ru/index.php?page=pages/decimal/decimal1.php
В случаях, когда решение осложняется периодическими дробями, можно воспользоваться обратными действиями и перевести десятичные дроби в обыкновенные. Подробнее можно прочесть здесь http://math-prosto.ru/index.php?page=pages/decimal/decimal1.php
0
Спасибо
Ответить
5 апреля 2015 в 12:10
Кристина Тишина

Профиль
Благодарили: 0
Сообщений: 1

Кристина Тишина
Профиль
Благодарили: 0
Сообщений: 1
[1
*0,27-3
*0,15] ? 1500*[ ? 0,1]3
0
Спасибо
Ответить
14 апреля 2016 в 10:27
Ответ для Кристина Тишина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Преобразуем и решим.
(1 · -3 · ) ?1500 · (-0,001)=( ?) +1,5=( ? )+1,5= ? +1,5= ?0,14+1,5=1,36
Ответ:1,36
0
Спасибо
Ответить
14 апреля 2016 в 10:28
Ответ для Кристина Тишина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Решил пойти с конца форума и ответить на неотвеченные задачи =) Камни не кидайте, что так долго отвечал =)
0
Спасибо
Ответить
Задача. В шестом классе (20) девочек, что составляет
57
всех учащихся класса.
Сколько всего учеников в классе?
| Вопросы к задаче | Ответы |
| 1. Какая величина принята за целое? | 1. За целое принято количество всех учеников класса |
| 2. Известна ли целая величина? | 2. Целое не известно |
| 3. Какую величину нужно найти? | 3. Количество всех учеников класса, или целое по его части |
| 4. Как найти величину, которая приходится на 17? | 4. (20 : 5 = 4) ученика составляют одну часть |
| 5. Как найти величину, которая составляет целое? | 5. (4 · 7 = 28) количество всех учеников класса |
Ответ: всего в шестом классе (28) учеников.
Чтобы найти целое по его части, необходимо число, соответствующее части, разделить на числитель
и результат умножить на знаменатель дроби, которая выражает эту часть.
Пример:
1. найди число, если
23
его равны (26):
(26 : 2 · 3 = 13 · 3 = 39).
2. Найди число, если
34
его равны (45):
(45 : 3 · 4 = 15 · 4 = 60).
как выделить целую часть от дроби
Ученик
(108),
закрыт
10 лет назад
Бульбозавр ☺☺☺
Высший разум
(737454)
10 лет назад
Как найти целую часть от дроби Правила записи чисел, имеющих дробную часть, предусматривают несколько форматов, основными из которых являются «десятичный» и «обыкновенный» . Обыкновенные дроби, в свою очередь, могут быть записаны в форматах, называемых «неправильными» и «смешанными» . Для выделения целой части из дробного числа каждого из этих вариантов записи удобнее применять различающиеся способы.
Правила записи чисел, имеющих дробную часть, предусматривают несколько форматов, основными из которых являются «десятичный» и «обыкновенный» . Обыкновенные дроби, в свою очередь, могут быть записаны в форматах, называемых «неправильными» и «смешанными» . Для выделения целой части из дробного числа каждого из этих вариантов записи удобнее применять различающиеся способы.
1. Отбросьте дробную часть, если надо выделить целое число из положительной дроби, записанной в смешанном формате. В такой дроби целая часть пишется перед дробной – например, 12 ⅔. В этой дроби целой частью будет число 12. Если смешанная дробь имеет отрицательный знак, то полученное таким способом число уменьшайте на единицу. Необходимость этого действия вытекает из определения целой части числа, согласно которому она не может быть больше значения исходной дроби. Например, целой частью дроби -12 ⅔ является число -13.
2. Разделите без остатка числитель исходной дроби на ее знаменатель, если она записана в неправильном обыкновенном формате. Если исходное число имеет положительный знак, то полученный результат и будет целой частью. Например, целая часть дроби 716/51 равна 14. Если же исходное число отрицательно, то и здесь от результата следует отнять единицу – например, вычисление целой части дроби -716/51 должно дать число -15.
3. Считайте ноль целой частью положительной дроби, записанной в обыкновенном формате и при этом не являющейся ни смешанной, ни неправильной. Например, это относится к дроби 48/51. Если исходная дробь меньше нуля, то, как и в предыдущих случаях, результат нужно уменьшить на один. Например, целой частью дроби -48/51 следует считать число -1.
4. Отбросьте все знаки, стоящие после десятичной запятой, если выделить целую часть надо из положительного числа, записанного в формате десятичной дроби. В этом случае именно разделительная запятая и отделяет дробную часть от целой. Например, целой частью десятичной дроби 3,14 является число 3. И для этого формата действует определение, согласно которому целая часть не может быть больше исходного числа, поэтому и здесь полученное описанным способом значение для отрицательного числа надо уменьшать на единицу. Например, целая часть десятичной дроби -3,14 должна быть равна -4.
Содержание материала
- Обращение числа с целой и дробной частями в неправильную дробь
- Видео
- Неправильные дроби. Выделение целой части
- Дробь означает деление
- Как устроена обыкновенная дробь
- Основное свойство дроби
- Свойства дробей
- Как выделить целую часть из неправильной дроби
Обращение числа с целой и дробной частями в неправильную дробь
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Например,  .
.
 .
.
Вообще, чтобы записать число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к произведению прибавить числитель дробной части. Полученная сумма будет числителем дроби, а знаменателем будет знаменатель дробной части.

Видео
Неправильные дроби. Выделение целой части
Если числитель меньше знаменателя, такая дробь называется правильной. В противном случае (т.е. когда числитель больше или хотя бы равен знаменателю) дробь называется неправильной, и в ней можно выделить целую часть.
Целая часть записывается крупным числом спереди перед дробью и выглядит так (отмечена красным):

Чтобы выделить целую часть в неправильной дроби, надо выполнить три простых шага:
- Найдите, сколько раз знаменатель помещается в числителе. Другими словами, найдите максимальное целое число, которое при умножении на знаменатель все равно будет меньше числителя (в крайнем случае — равно). Это число и будет целой частью, поэтому записываем его спереди;
- Умножьте знаменатель на целую часть, найденную в предыдущем шаге, а результат вычтите из числителя. Полученный «огрызок» называется остатком от деления, он всегда будет положительным (в крайнем случае — ноль). Записываем его в числитель новой дроби;
- Знаменатель переписываем без изменений.
Ну как, сложно? На первый взгляд, может быть и сложно. Но стоит немного потренироваться — и вы будете делать это почти устно. А пока взгляните на примеры:
Задача. Выделите целую часть в указанных дробях:


Во всех примерах целая часть выделена красным цветом, а остаток от деления — зеленым.
Обратите внимание на последнюю дробь, где остаток от деления оказался равным нулю. Получается, что числитель полностью разделился на знаменатель. Это вполне логично, ведь 24 : 6 = 4 — суровый факт из таблицы умножения.
Если все делать правильно, числитель новой дроби обязательно будет меньше знаменателя, т.е. дробь станет правильной. Отмечу также, что лучше выделять целую часть в самом конце задачи, перед записью ответа. Иначе можно значительно усложнить вычисления.
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь  . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
. Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:

Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:

Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Основное свойство дроби
Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.
Например, рассмотрим дробь  . Умножим её числитель и знаменатель на одно и то же число, например на число 2
. Умножим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь  . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби  и
и  равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь  (один кусок из двух), а второй иллюстрирует дробь
(один кусок из двух), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями  и
и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь  . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
. Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь  . Если верить основному свойству дроби, то дроби
. Если верить основному свойству дроби, то дроби  и
и  равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь  (четыре куска из восьми), а второй иллюстрирует дробь
(четыре куска из восьми), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
(два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями  и
и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
 где a, b, k — натуральные числа.
где a, b, k — натуральные числа.
- Дробь не имеет значения, если знаменатель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как выделить целую часть из неправильной дроби
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления будет целой частью числа, остаток — числителем, а делитель — знаменателем. Например,  .
.

Теги
Начнем с довольно простой, но в то же время интересной темы, в которой школьники зачастую делают ошибки – нахождение дроби от числа.
Что такое часть от целого? Если у нас есть некоторое значение и нам необходимо вычислить некоторую долю или дробь от этого значения. Например, зная вес пиццы, найти вес нескольких ее кусочков.
При этом нужная доля может быть выражена как в виде обыкновенной дроби, так и в виде десятичной дроби или процентов. Для нахождения процента от числа стоит предварительно перевести проценты в десятичную дробь, просто разделив на 100. Например, 28 % = 0,28.
Для того, чтобы найти, сколько весят x кусочков пиццы, порезанной на равные y кусков, нужно общий вес пиццы разделить на y и умножить на x. Допустим, пицца весит Q грамм. То есть нам необходимо найти вес x/y части пиццы.
Немного парадоксальная ситуация: нужно найти часть, а мы умножаем, а не делим. Но на самом деле никакого парадокса в этом нет, если вспомнить, что дробь, вернее, горизонтальная черта дроби – это деление.
Да и при умножении на десятичную дробь меньше 1 мы тоже получим значение меньшее, чем исходное.
Немного запутать может ситуация, когда целая часть выражена в виде обыкновенной или десятичной дроби. Не стоит обращать на это внимание. Алгоритм действий точно такой же.
Рассмотрим еще несколько примеров.
Для закрепления материала предлагаем несколько примеров для самостоятельного решения. Ответы размещайте в комментариях.
Надеемся, эта тема была вам интересна. Если что-то осталось непонятным, задавайте вопросы в комментариях.
Завтра разберемся, как найти число, если нам известна только его часть.
Ставим лайки, подписываемся, в комментариях пишем темы, которые вам хотелось бы разобрать, задаем вопросы.
До скорой встречи!
